Characterizing Loop Dynamics and Ligand Recognition in Human- and Avian-Type Influenza Neuraminidases via Generalized Born Molecular Dynamics and End-Point Free Energy Calculations

Abstract

The comparative dynamics and inhibitor binding free energies of group-1 and group-2 pathogenic influenza A subtype neuraminidase (NA) enzymes are of fundamental biological interest and relevant to structure-based drug design studies for antiviral compounds. In this work, we present seven generalized Born molecular dynamics simulations of avian (N1)- and human (N9)-type NAs in order to probe the comparative flexibility of the two subtypes, both with and without the inhibitor oseltamivir bound. The enhanced sampling obtained through the implicit solvent treatment suggests several provocative insights into the dynamics of the two subtypes, including that the group-2 enzymes may exhibit similar motion in the 430-binding site regions but different 150-loop motion. End-point free energy calculations elucidate the contributions to inhibitor binding free energies and suggest that entropic considerations cannot be neglected when comparing across the subtypes. We anticipate the findings presented here will have broad implications for the development of novel antiviral compounds against both seasonal and pandemic influenza strains.

Introduction

Avian influenza virus type A, subtype H5N1, is becoming the world’s largest pandemic threat due to its high virulence and lethality in birds, quickly expanding host reservoir, and high rate of mutations.(1) Antigenic drift has given rise to new strains that are resistant to existing drugs, and antigenic shift is resulting in new virulent subtypes of the flu virus, underscoring the need to design novel therapeutics. Influenza’s two major membrane glycoproteins, hemagglutinin (HA) and neuramindase (NA), together play important roles in the interactions with host cell surface receptors. NA facilitates viral shedding by cleaving terminal sialic residues on host cell surface proteoglycans, which are bound by HA.(2)

The neuraminidase enzymes are phylogenetically categorized into two groups: group-1, which includes N1, N4, N5, and N8, and group-2, which includes N2, N3, N6, N7, and N9.(3) Although active-site residues are largely conserved across both groups, different NA subtypes exhibit varied drug susceptibility(4) and resistance profiles.^5,6 Since the first NA crystal structure was published in 1983,(7) a number of structure-based computational studies against the group-2 subtypes have added significant insight to our understanding of substrate recognition and inhibitor design. Currently available NA inhibitors, including oseltamivir(8) and zanamivir,(9) have been designed against crystal structures of group-2 enzymes (ref (2) and references therein). Oseltamivir, which has been stockpiled by many nations in efforts to avert a possible pandemic, is the only orally available drug effective against H5N1; yet, oseltamivir-resistant strains have already been isolated.^10,11 These factors combine to easily motivate additional drug discovery efforts against H5N1.

Recent studies of the avian-type N1 enzyme have enriched our understanding of the binding process. The first crystal structures of a group-1 NA in apo form and in complex with currently available drugs(12) revealed that, although the binding pose of oseltamivir was similar to that seen in previous crystallographic complexes,^7,13 the 150-loop adopted a distinct conformation, opening a new cavity adjacent to the active site. Under certain crystallization conditions, however, the 150-loop adopted the same closed conformation as previously seen in group-2 NA structures, suggesting a slow conformational change may occur upon inhibitor binding.(12) It was conjectured that the new structural observation of the N1 strain’s open 150-loop could be exploited in structure-based drug discovery efforts.

Despite this detailed structural information, the interpretation of the loop dynamics based on crystal structures alone is a difficult task. To complement the crystallographic structures, all-atom explicit solvent molecular dynamics (MD) simulations of the apo and oseltamivir-bound systems were carried out.(14) The extensive simulations suggested that the 150-loop and adjacent binding site loops may be even more flexible than observed in the crystal structures.(14) In the apo simulations, the 150-loop was seen to open more widely than observed in the crystal structures, and its motion was often coupled to an outward movement of the adjacent 430-loop. These coupled motions significantly expanded the active-site cavity, increasing its solvent-accessible surface area compared with both the open and closed crystal structures. Subsequent computational solvent mapping (CS-map) experiments assessed the ability of small, solvent-sized molecules to bind within close proximity to the sialic acid binding region and the newly discovered 150- and 430-cavities.(15) The consensus binding sites (i.e., hot spots) of these probes, as determined by the CS-Map algorithm, have been shown to relate directly to experimental druggability and are thus able to identify important binding site features.¹⁶⁻¹⁸ Mapping analyses of the nonredundant MD conformations revealed the presence of additional hot spot regions in the 150- and 430-loop regions, confirming the druggability of these newly revealed sites. Furthermore, small-molecule docking to the new 150- and 430-cavities indicated favorable binding of several compounds to these areas, in addition to the sialic acid binding site.(19)

A complete understanding of the comparative human- and avian-type neuraminidase structural dynamics is lacking, despite the relevance of this knowledge to antiviral development. Our current understanding of the active-site dynamics for these medically relevant enzymes is predominantly based on X-ray crystallography experiments(12) and the aforementioned explicitly solvated MD simulations of the open 150-loop N1 enzyme. In this work, in order to assess the dynamical differences in the 150-loop, 430-loop, and sialic acid binding regions between the avian and human subtypes, we present a series of generalized Born molecular dynamics (GB MD)(20) simulations of the N1 and N9 NA enzymes. GB MD, which employs a continuum representation of the solvent water molecules and salt ions, offers computational efficiency over the more rigorous Poisson−Boltzmann solvers or explicit solvent simulations.(21) The implicit solvent approach essentially reduces solvent friction and has been shown to enhance conformational sampling for a wide variety of peptide, protein, and nucleic acid systems.²²⁻²⁵ To date, however, the application of GB MD to larger biomolecular systems, such as the neuraminidase enzyme, has been much fewer in number than its application to smaller proteins and peptides. This work therefore presents an important methodological example that highlights the utility of employing generalized Born implicit solvent models for elucidating the dynamics and energetics of large protein systems.

Although crystallographic experiments provide critical time/ensemble-averaged structure and ligand binding information, atomic-level simulations yield additional insights and relevant biophysical information that is otherwise inaccessible with standard experimental techniques. As oseltamivir does not rely on water-mediated interactions with the protein active site, unlike other sialic acid analogue NA inhibitors,(26) the N1 and N9 oseltamivir-bound systems are particularly well suited for treatment with implicit solvent. The comparative dynamics that we present here allow us to gain insights into the flexibility of the 150- and 430-loops, which are important due to their proximity to the sialic acid binding site. A more complete understanding of the dynamical differences between the subtypes, especially in the 150- and 430-loop regions, may assist in the design of antiviral compounds that are able to take advantage of the newly revealed ligand binding areas. Here we show that the extensive conformational sampling gained through the GB MD simulations allows us to attain a significantly enhanced conformational sampling speedup, as compared to explicit solvent MD. The dynamics of residues that have been shown by computational solvent mapping to be potentially important in the binding of ligands to this expanded area are investigated and discussed, and a comparison of the resulting structures to the explicitly solvated MD simulations is provided. Finally, end-point free energy calculations provide quantitative insight into oseltamivir recognition.

Methods

Generalized Born Solvent Simulations

Molecular dynamics simulations were initiated from crystallographic coordinates. The seven systems used in our simulations are listed in Table 1. The closed-loop oseltamivir-bound N1 simulation started from one of the monomers from the 2HU4 (PDB code) structure. The open-loop oseltamivir-bound N1 simulation started from one of the monomers from the 2HTY structure. The closed-loop N9 oseltamivir-bound simulation was initiated from one of the monomers from the 2QWK structure. For each of the monomer systems, several residues on the N-terminus were removed (first six residues in N1, V83−N88; first nine residues in N9, R82−G90). Coordinates of the three corresponding apo systems were obtained by removing the inhibitor oseltamivir, respectively. To study the impact of the adjacent subunits on loop structure and dynamics, a tetramer system comprised of the closed-loop N1 neuraminidase in complex with oseltamivir (2HU4) was also simulated. To compare with experiment, protonation states for histidines and other titratable groups were determined at pH 6.5 by the PDB2PQR web server and manually verified.(27) Hydrogen atoms were added by using the LEAP module in AMBER. The FF99SB force field, which has modifications to backbone torsional terms, was used for the protein.(28) Parameters for oseltamivir were obtained from ANTECHAMBER module using the Generalized Amber force field (GAFF)(29) with RESP HF 6-31G* charges as described previously.(14) All MD simulations were carried out with Amber 8.(30) Temperature was maintained by using Langevin dynamics with a collision frequency of 5 ps⁻¹. The time step was 2 fs, and all bonds involving hydrogen were constrained with the SHAKE algorithm with a tolerance of 10⁻⁴ Å.

Table 1. Description of Simulations^a.

system name	crystal structure	description	simulation time, ns	no. of atoms
N1ac	2HU4	N1-apo, closed	16	5389
N1ao	2HTY	N1-apo, open	16	5389
N1hc	2HU4	N1-holo, closed	15.9	5433
N1ho	2HU0	N1-holo, open	16	5433
N9a	2QWK	N9-apo, closed	16	5526
N9h	2QWK	N9-holo, closed	16	5568
N1-tetramer	2HU4	N1 tetramer, holo, closed	5	21732

^aSeven simulations of the N1 (group-1, avian) and N9 (group-2, human) neuraminidases are summarized with their system name, initial PDB structure identifier, brief description, total simulation time, and number of atoms. The system names listed here are used throughout the figures and text.

Solvation effects were modeled implicitly by using the generalized Born model. The GB model has been demonstrated to provide improved conformational sampling as compared to simulations with explicit representation of solvent molecules. The improved sampling arises from an acceleration of transitions due to the lack of solvent viscosity, as well as through reduced cost of calculating forces of explicit solvent. A modified GB model (GB^OBC, igb = 5) was employed for more accurate solvation of large proteins.(23) The Born radii were adopted from Bondi with modification (mbondi2) and an offset of 0.09 Å. The scaling factors for Born radii were taken from the Tinker modeling package. The salt concentration was set to 0.2 M. A reaction field cutoff (rgbmax = 25 Å) was used to speed-up the calculation of effective Born radii. No cutoff was used for the long-range interactions for the monomer systems, while a cutoff of 50 Å was used for the tetramer system.

Each GB simulation consisted of two stages, equilibration and production. During equilibration, the starting structure was minimized for 2000 steps to remove close contacts and then gradually heated to 300 K at 50 K intervals during six simulations of 200 ps. Positional restraints on backbone atoms were gradually decreased from 3 to 0 kcal/(mol·Å²) in several stages. All production simulations were at 300 K and fully unrestrained. Each production run was ∼16 ns for the monomer systems and ∼5 ns for the tetramer system. System performance benchmarks are as follows: for the tetramer system, 0.8 ns per day using 1024 processors on the IBM BlueGene/L platform at San Diego Supercomputer Center; for the monomer system, 9 ns per day on the NCSA Abe platform using 256 processors (32 nodes), and 2 ns per day on the IBM BlueGene/L machine using 256 processors.

Clustering

In order to generate reduced, representative structural ensembles for the simulations and for the CS-Map calculations, root-mean-square deviation (RMSD) conformational clustering was performed, based on a previously reported clustering algorithm.(31) To be able to compare to previous clustering results, the gromos method within GROMACS (g_cluster) was employed.(33) Structures were extracted in 10 ps intervals over each of the simulations; 1.6 × 10³ trajectory structures for each simulation were superimposed using all C_α atoms to remove overall rotation and translation. The RMSD-clustering was performed on a subset of 62 residues that line the entire binding-site area, which we define here as the binding-site residues: 117−119, 133−138, 146−152, 156, 179, 180, 196−200, 223−228, 243−247, 277, 278, 293, 295, 344−347, 368, 401, 402, and 426−441. These residues were clustered into batches of similar configurations using the atom-positional RMSD of all atoms (including side chains and hydrogen atoms) as the similarity criterion. A cutoff of 1.3 Å was chosen on the basis of previous work using explicit solvent.(15)

End-Point Free Energy Calculations

Using equidistant snapshots extracted from the GB MD trajectories, the total binding free energy was computed using the MM-GBSA scheme.^34,35 For computational efficiency, a single trajectory approach was used and the calculations were performed on ∼800 snapshots with a sampling interval of 20 ps.

where E_MM represents the sum of electrostatic, van der Waals, and internal energies (we note that the internal energies cancel out in eq 2 due to the single trajectory approach). ΔG_solvation is the desolvation free energy penalty, estimated from GB and solvent-accessible surface area (SASA) calculations which yield G_polar and G_nonpolar. A surface tension coefficient (γ) of 0.0072 kcal/(mol·Å²) is used to calculate the nonpolar solvation free energy contribution. The modified GB model (GB^OBC, igb = 2),(23) the modified Born radii (mbondi2), and 0.2 M salt concentration were adopted, to be consistent with the GB MD simulations. We tried 10 different MM-PB(GB)SA postprocessing schemes, including IGB5. The best results (i.e., most closely reproduced experimental binding constants) were obtained with IGB2. TΔS is the product of temperature (at 300 K) and solute entropy, derived from normal-mode analyses of the solute coordinates after energy minimization of solute structures to within a root-mean-square of the energy gradient of 1.0⁻⁵ kcal/(mol·Å). The normal-mode analysis was carried out on eight snapshots at 2 ns sampling intervals due to its prohibitive computational cost on large protein−ligand systems. The minimum TΔS results were selected to compute the total binding free energy in eq 1.

Results and Discussion

The seven simulations with various starting conditions allow us to investigate the comparative dynamics of the avian- and human-type neuraminidase enzymes in several states, including the apo and oseltamivir-bound N1 enzyme starting with the open 150-loop crystal structure (N1ao, N1ho, respectively), the apo and oseltamivir-bound N1 enzyme starting with the closed 150-loop crystal structure (N1ac, N1hc), the apo and oseltamivir-bound N9 crystal structures (N9a, N9h), and the tetramer closed 150-loop oseltamivir-bound N1 (Table 1). As the human-type N9 enzyme has never been crystallized with the 150-loop in the open conformation, the starting conditions are with a closed 150-loop. Overall, the backbone RMSD establishes that all of the systems are stable during the trajectories (Supporting Information, Figure S1).

RMSD-Based Clustering

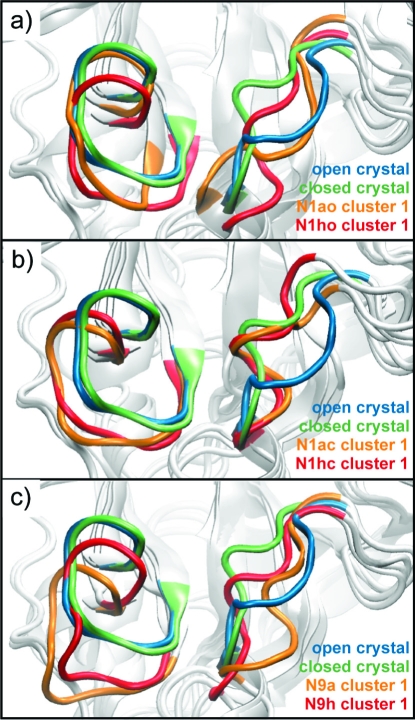
An RMSD-based clustering analysis of 62 residues lining the binding site allows us to compare the relative structural populations of N1 and N9 in the different trajectories. The clustering procedure was performed in a manner identical to that described by Landon et al.(15) (using a 1.3 Å cutoff) and thus provides a basis of comparison for the explicit solvent and GB MD simulation cluster structures (Table 2). The central member structures of the most dominant clusters for each of the simulations illustrate the range of structural fluctuation in this loop region (Figure 1). The clustering results indicate that the GB MD simulations enhance the conformational sampling of the N1 enzyme, as compared to the explicit solvent simulations, while maintaining the relative population trends established in the latter.

Table 2. Clustering Results: Total Number of Clusters at 1.3 Å RMSD Cutoff for Each System and Number of Clusters Representing 90% of the Ensemble.

system	total no. of clusters	90% ensemble
N1ac	55	11
N1ao	85	21
N1hc	36	6
N1ho	39	8
N9a	55	14
N9h	32	6
N1ao - explicit solv	51	10
N1ho - explicit solv	27	5

Figure 1.

Motions of the 150- and 430-loops. Loop conformations are shown in cartoon representation for the most dominant configurations of (a) the N1-apo-closed (orange) and the N1-oseltamivir-bound-closed (red), (b) the N1-apo-open (orange) and the N1-oseltamivir-bound-open (red), and (c) the N9-apo-closed (orange) and the N9-oseltamivir-bound-closed (red) trajectories. The N1 open (blue) and N1 closed (green) crystal structures are shown for comparison.

The clustering analysis indicates several relevant features of the N1 dynamics. First, regardless of the open vs closed 150-loop configuration, the apo systems are more flexible in the binding-site region compared to the oseltamivir-bound systems. These results are consistent with the explicitly solvated simulations.(14) Second, the relative cluster populations of the open 150-loop N1 systems indicate that the GB simulations are able to sample a larger conformational space than the explicitly solvent simulations, despite the fact that the GB simulations were 1 order of magnitude shorter in time scale. This is due to the reduced solvent friction in the GB MD simulations and highlights the utility of the GB method for exploring receptor conformational space. In terms of the comparative dynamics between the N1 and N9 systems, both the N1 and N9 apo systems are represented by 55 clusters, indicating that the dynamics are similar between the subtypes in the absence of substrate. In contrast, the N1hc system has more clusters than the N9h system, suggesting that the N9 subtype is more stable than the N1 subtype when oseltamivir is bound.

Active-Site and Hot-Spot Residue Dynamics

The dynamics of residues lining the sialic acid, 150-, and 430-cavities are of interest for drug design investigations as well as to better understand the fundamental basis of molecular recognition in the neuraminidase enzymes. In order to characterize the dynamics of residues within the N1 and N9 systems, a root-mean-square fluctuation (RMSF) analysis was performed (Supporting Information, Figure S2). The dynamics of hot-spot residues (Table 3; Supporting Information, Figure S3) are of particular interest, as they have been suggested to provide additional opportunities for drug discovery that could potentially mitigate the effects of drug resistance.(15)

Table 3. RMSF per Hot-Spot Residue for the Six Simulations^a.

		N1ao	N1ac	N1ho	N1hc	N9a	N9h
Sialic Acid Region
R	118	0.57	0.54	0.51	0.51	0.42	0.48
E	119	0.56	0.55	0.65	0.61	0.44	0.48
R	224	0.47	0.49	0.48	0.61	0.42	0.43
E	227	0.48	0.53	0.52	0.65	0.44	0.45
S	246	1.13	1.01	1.02	1.31
E	277	0.57	0.6	0.49	0.56	0.47	0.41
R	371	0.77	0.78	0.83	0.8	0.79	0.73
Y	406	0.47	0.55	0.48	0.54	1	0.55
150-Loop Region
V	116	0.68	0.64	0.49	0.69	0.51	0.55
Q	136	0.81	0.74	0.87	0.77	0.78	0.79
V	149	2.31	1.53	1.21	2.82
D	151	1.52	0.99	0.71	1.66	0.98	0.69
R	152	1.26	0.96	0.79	1.32	0.95	0.79
S	153	1.22	0.94	0.83	1.23	0.97	0.85
P	154	1.24	0.98	0.93	1.22
R	156	0.69	0.64	0.59	0.62	0.54	0.59
W	178	0.56	0.5	0.77	0.57	0.44	0.44
S	179	0.48	0.47	0.66	0.51	0.4	0.41
S	195	0.64	0.6	0.64	0.79	0.54	0.56
G	196	0.77	0.76	0.81	1.19	0.72	0.74

^aThe first column lists the residue type, the second column lists the residue number, and the third through eighth columns list the RMSF per residue for the N1-apo-open, N1-apo-closed, N1-holo-open, N1-holo-closed, N9-apo, and N9-holo systems, respectively.

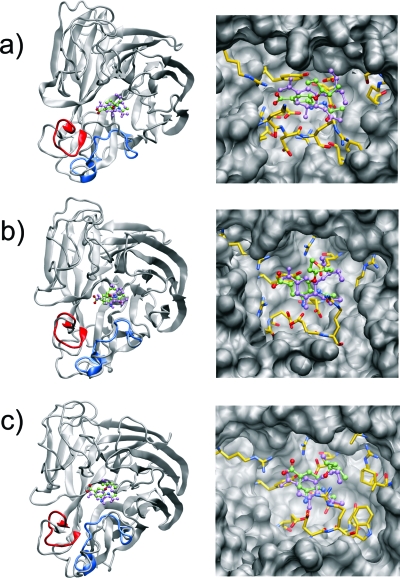
Our analysis again reveals several interesting features of N1 vs N9 dynamics. Most notably, with the exception of Y406, all the hot-spot residues lining the sialic acid cavity in N9 exhibit much lower RMSF values than the same residues in the N1 strain (Table 3). This is also illustrated in the equilibrium binding poses of oseltamivir, which, in the N9 subtype, undergoes the least amount of movement from the original crystal structure pose versus the N1 subtypes (Figure 2). The increased positional fluctuations of the sialic acid binding residues in the N1 subtype may contribute to the reduced efficacy of several known inhibitors against N1.^36,37 In addition, the N9h system shows significant stabilization of the 150-loop upon binding of oseltamivir (Table 3). The increased rigidity in this area substantiates available crystallographic data that, to date, have not provided evidence of 150-loop mobility in the N9 subtype.

Figure 2.

Equilibrium orientations of oseltamivir in the different binding sites. Overall orientations (left panel) and active-site interactions (right panel) of oseltamivir bound to (a) the N1-closed, (b) the N1-open, and (c) the N9-closed system. The original conformations of the 150- and 430-loops are shown in blue and red, respectively, to highlight the loop motion observed in the course of the dynamics. Active-site residues within 4 Å of oseltamivir are shown explicitly. The original conformation of oseltamivir is shown in violet for comparison.

The presence of oseltamivir in the closed 150-loop N1 system actually increases the RMSF of the sialic acid and 150-loop hot-spot residues (Table 3). This is in contrast to both the open 150-loop N1 and N9 systems, which exhibit reduced fluctuations in the 150-loop in the presence of oseltamivir. The stabilization of the 150-loop residues in the N1ho system is in agreement with the explicitly solvated MD simulations.(14) Taken together, these findings suggest relative structural instability of the N1 system in this region due to the presence of inhibitor as compared to N9, lending support to the potential importance of targeting the 150- and 430-cavities for developing inhibitors that bind more strongly to the N1 subtype.

At approximately 6 ns into the N1hc trajectory, a strained salt bridge forms between R152 and the carboxylate group of oseltamivir. This salt bridge interaction persists for the remainder of the simulation. As this interaction is not seen in any of the other GB or explicit solvent simulations, it is likely that this salt bridge is an artifact of the continuum solvent approach. The formation of overstabilized salt bridges, especially those involving arginine residues, is a known weakness of the GB model.(38) In all other trajectories, R152, which is within a stable region of the 150-loop, forms varying salt bridge interactions with neighboring aspartate residues in the protein. Hot-spot residue RMSF values for N1hc simulation time segments before (0−5.2 ns) and after (10.0−15.2 ns) formation of the strained salt bridge indicate that the positional fluctuations of residues in the vicinity of R152 are slightly dampened after the salt bridge is formed (data not shown). The trends in RMSF values for both time segments, however, are the same as the mean values reported in Table 3.

Dynamics of the 150- and 430-Loops

The crystal structures of the N1 enzyme published by Russell et al. first revealed the flexibility of the 150-loop.(12) Adjacent to the sialic acid binding site, the outward movement of the 150-loop expanded the N1 active site and was suggested to present a new opportunity for antiviral drug design. Explicitly solvated MD simulations presented by Amaro et al. sampled a single open−close loop transition in chain D of the oseltamivir bound system, as demonstrated by the instantaneous RMSD of the 150-loop from the closed (2HU4) and open (2HTY) 150-loop crystal structures during 40 ns of tetramer simulations (Figure 1 in ref (14)). In addition, the explicit MD sampled a so-called “wide-open” 150-loop structure that significantly altered the size and topology of the N1 binding pocket. In this work, a similar analysis of the six monomer systems provides dynamical and structural insights into this region.

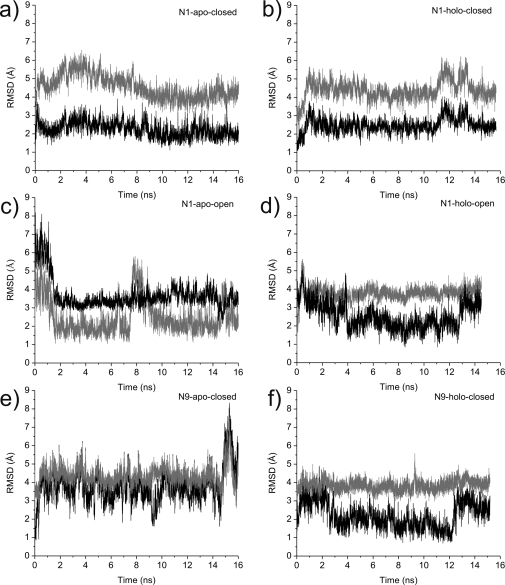
For the open 150-loop N1 system, the apo and holo systems each demonstrate two open−close loop transition events (Figure 3). In comparison to the explicit solvent MD, which sampled only one transition event in the N1ho system over 160 ns of simulation, the four loop transition events sampled here point to the advantage of the GB method for sampling conformational transitions on a much faster time scale compared to explicit solvent MD. Similar to the explicit solvent MD, the most dominant central member cluster structure of the N1 apo system is significantly more open than the open 150-loop crystal structure (Figure 1). The general agreement between the resulting structures determined by both computational methods substantiates the idea that the N1 subtype generally exists in a more open conformation in the absence of ligand. By contrast, the closed 150-loop N1 systems remain relatively stable across the trajectories, and no loop transition events are sampled (Figure 3).

Figure 3.

Open−closed loop transitions. Root-mean-square deviations of the 150-loop (comprising residues N146−R152) from the MD with respect to the open (gray) and closed (black) crystal structures are shown for the N1-apo-closed (a), the N1-oseltamivir-bound-closed (b), the N1-apo-open (c), the N1-oseltamivir-bound-open (d), the N9-apo-closed (e), and the N9-oseltamivir-bound-closed (f) structures.

In the (closed-loop) apo N9 system, the open−close loop transition analysis indicates that the enzyme adopts an intermediate conformation (Figure 3). This is also illustrated in the most dominant cluster representative structure, which indicates that the 150-loop in the apo N9 system takes on characteristics of both the closed and open loops but is definitively more open. Our analysis indicates that the most populated structure in the N9a system has an open 150-cavity. This structural finding suggests that, in the absence of inhibitor, both subtypes take on a more relaxed and open conformation in the 150-loop region. In contrast, the holo N9 system remains in a more closed conformation throughout (Figures 1 and 3).

It is also worth noting that, in each of the most dominant structures extracted from all six monomer simulations, the 430-loop adopts a more open conformation (Figure 1). These results reveal motion in the 430-loop region for the N9 enzyme and, more broadly, indicate that motion in the 430-loop region is independent of bound ligand. Importantly, this suggests that compounds designed to target the more open 430-cavity have the potential to be viable against both N1 and N9 subtypes.

End-Point Free Energy Calculations

In order to quantify the individual contributions to oseltamivir binding in the N9 and N1 systems, end-point energy calculations were performed. The theory of end-point energy, also known as MM-PB(GB)SA, calculations relies on a set of assumptions, elegantly reviewed in ref (39). A simple thermodynamic cycle and single-trajectory postprocessing allows the efficient computation of the various contributions. Here, the application of the MM-GBSA approach allows us to decompose the terms that contribute to ligand binding while providing relative free energies of binding that correlate well with experimental data for both N9 and N1 subtypes (Table 4).^36,37,40 The absolute values of the binding free energies, however, are off by approximately 5−7 kcal/mol in all three cases, which is not surprising given the assumptions present in the underlying theory and also considering that we neglected to include the internal energy change (i.e., strain energy) for oseltamivir binding. Regarding the latter, Masukawa et al. showed that the range of ligand strain energy may be in the range of −5 to 5 kcal/mol for known inhibitors of NA, although they recognized the inherent difficulty in determining accurate absolute quantities due to insufficient sampling.(26)

Table 4. End-Point Free Energy Calculations with MM-GBSA^a.

contribution	N9	N1-open	N1-closed
ΔEelec	−189.2 (0.6)	−210.2 (1.0)	−205.5 (0.6)
ΔEVDW	−24.2 (0.2)	−24.8 (0.2)	−26.8 (0.2)
ΔGsolv,polar	173.2 (0.6)	193.0 (0.8)	186.7 (0.5)
ΔGsolv,nonpolar	−5.1 (0.01)	−5.0 (0.01)	−5.1 (0.01)
−TΔS(vib)	−0.2	5.3	9.6
−TΔS(total)	23.6	29.2	33.5
ΔGbinding	−21.7 (0.8)	−17.8 (1.2)	−17.1 (0.8)
ΔGbinding,exp	−15.2 to −12.0	−13.3 to −12.8	−13.3 to −12.8

^aThe average contributions to the oseltamivir binding free energies to the N9, N1-open, and N1-closed systems over the 16 ns trajectories are given in kcal/mol; standard errors of the mean are given in parentheses. ΔE_elec and ΔE_VDW are the molecular mechanics electrostatic and van der Waals contributions, respectively. ΔG_{solv, polar} is the polar component of the solvation free energy, whereas ΔG_{solv, nonpolar} is the nonpolar component. TΔS is the contribution from the rotational (rot), translational (trans), and vibrational (vib) entropies. Experimental binding free energies (ΔG_{binding, exp}) are provided for comparison.^36,37,40.

In theory, if the configurational space sampling is sufficient, the N1 open- and closed-loop systems should converge to the same binding free energy, since they are the same enzyme (merely different starting configurations of the 150-loop). Although our results are not identical between the two systems, it is promising that they are within the standard error of the mean for each. A plot of the convergence of the binding free energies as a function of trajectory length indicates that the differences between running 1 and 16 ns in terms of the enthalpic contributions are minor (Supporting Information, Figure S4). It also indicates that the salt bridge artifact between R152 and oseltamivir in the N1hc system (which was not present before 6 ns) has a negligible effect on the binding free energy.

The absolute values of the electrostatics terms are similar to those recently published by Chachra and Rizzo for the N1 system, using explicit solvent simulations.(41) Although they and others⁴²⁻⁴⁴ have shown that within a single NA enzyme, the electrostatics term trends well with experimental binding free energies, our results suggest this is not the case when comparing across human and avian subtypes. Notably, it is only with the inclusion of the entropic component that the free energies of binding agree with what is known experimentally (Table 4). Our work indicates that the N1 systems (whether initiated from a closed- or open-150 loop) pay a larger entropic penalty upon binding oseltamivir. These results are in good correspondence with the loop transition sampling events (Figure 3) and the per-residue RMSF values (Table 3), which indicate increased flexibility in the N1 subtype. Thus, we would expect the N1 systems to pay a higher entropic penalty upon complexation with oseltamivir, as compared to N9, which appears to be intrinsically less flexible. Future antiviral development efforts against the N1 subtype may benefit from considering these entropic contributions.

Tetramer GB MD Simulations

As a control for our monomer simulations, we also present data from a 5 ns GB simulation of the closed 150-loop N1 tetramer system. The tetramer system, with 21 732 atoms (Table 1), exhibited excellent parallel performance scaling: we were able to generate 0.8 ns per day when scaled to 1024 processors on the IBM BlueGene machine at the San Diego Supercomputer Center.

The comparison of the tetramer N1hc system to the monomer N1hc system reveals largely similar behavior, especially in the sialic acid, 150-, and 430-loop regions. The open−close loop transition behavior was also similar for each of the monomers within the tetramer (Figure 3; Supporting Information, Figure S5). Neither of the closed-loop systems exhibits significant motion in the 150-loop. The exception is chain B of the tetramer, in which the 150- and 430-loops (data not shown) shift to a more open conformation after ∼ 3 ns. Notably, the interaction of R152 with the carboxylate group of oseltamivir occurs in two of the four chains of the tetramer, indicating the intermittent occurrence of this interaction. We anticipate that this extended arginine interaction may occur in all four chains if the tetramer simulations were run for longer than 5 ns. Again we note that this salt bridge is likely overstabilized and could be an artifact of the GB electrostatics.

A comparison of the RMSF difference per residue of the tetramer to the monomer systems does indicate slight structural variation between the simulations in a region far from the active site. In particular, in the monomer simulations, a helix on the opposite side of the 430-loop, comprised of residues D103−F115 (hereafter referred to as the “110-helix”), exhibited larger RMSF values (Supporting Information, Figure S6) and in several cases appeared to completely unravel. In the physiologically relevant tetrameric form of the enzyme, the 110-helix makes contact to a neighboring subunit. Correspondingly, in the tetramer simulation, the contacts formed among the subunits appear to stabilize this region. The percentage of secondary structure formed (α helix) within the core of this 110-helix (residues S105−G109) as a function of simulation time was investigated (Table 5 and Figure S6) and indicates that the tetrameric contacts play a role in stabilizing this region of the enzyme. Although the tetramer simulation was performed only for the N1 enzyme, we expect similar results for the N9 subtype. Recent explicit solvent simulations of the monomer form of the N9 subtype also indicate that restrained dynamics were necessary to maintain the proper backbone fold,(41) whereas explicit solvent simulations of the tetramer enzyme were stable.(14) Our work here supports these observations, although the increased structural fluctuations are localized to the 110-helix and the termini strand, not generalizable to the entire protein backbone.

Table 5. Comparison of the 110-Helix Helical Character for the Tetramer and Monomer Simulations.

	α helix (%)	3-10-helix (%)
tetramer chain A	63.6	25.6
tetramer chain B	54.9	33.9
tetramer chain C	67.3	25.6
tetramer chain D	47.8	19.7
monomer	17.7	16.1

Conclusions

This study points to the promise and utility of generalized Born implicit solvent models for elucidating the dynamics and energetics of large-scale atomistic protein systems. The reduced solvent friction in the simulations enhances the receptor conformational space sampling for the N1 and N9 neuraminidase enzymes, as compared to explicitly solvated MD simulations. The 16 ns GB MD trajectories sample twice as many open−close loop transition events as compared to 160 ns of explicit solvent simulations, suggesting a conformational sampling speed-up of at least 10 times that of equivalent explicit solvent simulations. Our work also shows that end-point free energy calculations performed with the MM-GBSA protocol are able to recapture experimentally known oseltamivir binding profiles, thus providing an important computational framework to understand the various contributions to substrate recognition in the neuraminidase enzymes. Moreover, our estimates of the entropic contributions to the binding free energies suggest that these contributions cannot be neglected when comparing binding affinities across the subtypes.

This work also provides several provocative insights into the structural dynamics of the avian- and human-type NA enzymes, including that the apo N9 enzyme may also present 150- and 430-cavities to antiviral compounds. Especially promising is the persistence of the open 430-cavity in both the oseltamivir-bound and apo systems. Consequently, we anticipate that novel antiviral compounds targeting the recently discovered 150- and 430-cavities in the N1 subtype may also be effective against N9, and we suggest the targeting of these new pockets as a general anti-influenza drug development strategy. This could have important implications for developing new therapeutics that maintain efficacy over currently known resistant strains, for both seasonal and potentially pandemic influenza subtypes.

Supporting Information Available

Figures S1−S6; complete ref (9). This material is available free of charge via the Internet at http://pubs.acs.org.

Funding Statement

National Institutes of Health, United States