Description of phosphate hydrolysis reactions with the Self-Consistent-Charge Density-Functional-Tight-Binding (SCC-DFTB) theory. 1. Parameterization

Abstract

Phosphate chemistry is involved in many key biological processes yet the underlying mechanism often remains unclear. For theoretical analysis to effectively complement experimental mechanistic analysis, it is essential to develop computational methods that can capture the complexity of the underlying potential energy surface and allow for sufficient sampling of the configurational space. To this end, we report the parameterization of an approximate density functional theory, Self-Consistent-Charge Density-Functional Tight-Binding (SCC-DFTB) method for systems containing phosphorus. Compared to high-level density functional theory and ab initio (MP2 and G3B3) results, the standard second-order parameterization is shown to give reliable structures for a diverse set of phosphate compounds but inaccurate energetics. With the on-site third-order terms included, referred to as SCC-DFTBPA, calculated proton affinities of phosphate compounds are substantially improved, although it remains difficult to obtain reliable proton affinity for both phosphates and compounds that do not contain phosphorus, indicating that further improvement in the formulation of SCC-DFTB is still a challenge to meet. To make SCC-DFTB applicable to phosphate reactions in the current (on-site-third-order-only) formulation, a “reaction-specific” parameterization, referred to as SCC-DFTBPR, is developed based on hydrolysis reactions of model phosphate species. Benchmark calculations in both the gas-phase and solution-phase indicate that SCC-DFTBPR gives reliable structural properties and semi-quantitative energetics for phosphate hydrolysis reactions. Since the number of reaction-specific parameters is small, it is likely that SCC-DFTBPR is applicable to a broad set of phosphate species. Indeed, for 56 reaction exothermicities and 47 energy barriers related to RNA catalysis model reactions collected from the QCRNA database, which involve molecules rather different from those used to parameterize SCC-DFTBPR, the corresponding root-mean-square difference between SCC-DFTBPR and high-level DFT results is only 5.3 kcal/mol. We hope that the parameterized SCC-DFTB models will complement NDDO based reaction-specific models (e.g., AM1-d/PhoT) and high-level ab initio QM/MM methods in better understanding the mechanism of phosphate chemistry in condensed phase, particularly biological systems.

I. INTRODUCTION

Phosphorus is the one of the most abundant elements on earth. It is part of many essential biological components such as lipids, bones, genetic materials, energy rich molecules (e.g., ATP) and signaling molecules (e.g., GTP).^1,2 Most of the phosphorus in living systems exists in the form of phosphate, and the hydrolysis of phosphate is a key reaction involved in many fundamental life processes such as energy production and signal transduction. In molecular motors, for example, regulation of ATP hydrolysis by the conformational dynamics of the system is the key to the mechanochemical coupling in these amazing “nanomachines”.^3–6 Revealing the mechanism of phosphate hydrolysis and factors that regulate the hydrolysis activity, therefore, is crucial to the understanding of many essential biological processes.

Unfortunately, phosphate reactions are, in general, fairly complex and there are many possible reaction pathways.^7–15 Which pathway dominates is expected to depend rather sensitively on the environment.¹⁶ Experimental investigations in this context are complicated by the fact that the interpretation of typical data, such as kinetic isotope effects and linear free energy relations, is often not straightforward.^11,12 This explains why the precise mechanism of phosphate hydrolysis, especially in biomolecules such as phosphatases¹⁷ and ribozymes,¹⁸ remains controversial after many decades of studies and debates. Theoretical studies, in principle, are powerful in complementing experimental work for detailed mechanistic analysis. However, phosphate chemistry poses a major challenge to theory due to the intrinsic complexity and sensitivity to the environment. Employing a hybrid quantum mechanical/molecular mechanical (QM/MM) framework^19–23 is promising, but only with a sufficiently reliable QM method, an adequate treatment of the QM/MM interactions and sufficient amount of conformational sampling.^24,25

The importance of conformational sampling makes approximate QM methods such as semi-empirical methods based on the Neglect-of-Diatomic-Differential-Overlap (NDDO) approximation uniquely valuable in this context. Unfortunately, the popular NDDO based methods such as MNDO,²⁶ AM1²⁷ and PM3,²⁸ in general give rather poor results for phosphate reactions and therefore can not be used without improvements.^29,30 Considering the importance of d orbitals in describing the structure and energetics of phosphate compounds, extensions have been made for MNDO^31–33 and AM1^30,34 to include d orbitals in the corresponding Hamiltonians; the extension to AM1 was done largely for specific reactions involving phosphoryl transfers rather than a general parameterization. Despite notable improvements^35,36 and successful applications^37–39, the general results indicate that these methods are still not sufficiently robust for general mechanistic studies.

One important issue relevant to the mechanistic study of phosphate chemistry concerns the prediction of proton affinities. In many elementary steps in the phosphate hydrolysis, for example, protons are transferred between the nucleophile, the phosphate and the leaving group; proton transfers involving molecules in the nearby environment (such as water molecules that may act as “proton relays”^40–42) have been proposed to play a catalytic role. Therefore, predicting accurate, or at least balanced, proton affinities for different reactive motifs is essential. In this regards, the popular NDDO approaches require major improvements. In a recent benchmark study by Range et al.,²⁹ 16 model molecules representing the nucleophiles, phosphate compounds and leaving groups involved in biologically important phosphoryl transfer reactions have been studied with high level ab initio, density functional theories (DFT) and several semi-empirical methods. It was found that all semi-empirical methods, which include AM1, PM3, MNDO, MNDO/d and SCC-DFTB⁴³ (see below), all have rather large errors in the calculated proton affinities; the root-mean-square errors (RMSE) are 19.1, 13.8, 27.4, 31.0 and 17.4 kcal/mol, respectively. If it is only the proton affinity that is of interest, simple correction schemes can be developed.²⁹ For the purpose of analyzing reaction mechanisms, however, more sophisticated modifications have to be introduced.

In the past few years, our groups have been actively pursuing the development and application of an approximate density functional theory, the self-consistent-charge density-functional-tight-binding (SCC-DFTB) method, originally proposed by one of us.⁴³ This was driven by its reasonable balance in computational efficiency (comparable to AM1 and PM3) and accuracy, which is essential to condensed phase studies. The SCC-DFTB method has been applied successfully to a range of problems involving biomolecules, such as conformational energies of peptides^44–47 and catalysis in several enzymes^25,48–52. Furthermore, the SCC-DFTB approach has been benchmarked for reaction energies, geometries and vibrational frequencies for small molecules in comparison to the G2 approach,⁵³ and a large set of experimental data for organic molecules^54,55. An empirical dispersion correction has also been developed,⁵⁶ which was found crucial for predicting reliable nucleic acid base-stacking interactions⁵⁶ and the relative stability of α and 3₁₀ helices in proteins.⁵⁷

Considering those attractive features and the fact that it is straightforward to include d orbitals in the method (as been done for sulfur⁵⁸), it seems natural to pursue the parameterization of SCC-DFTB for phosphorus. Another important motivation in this regard is that SCC-DFTB has been recently extended to include specific third-order terms,^25,59–61 which were found to dramatically improve the calculated proton affinities. Since reliable proton affinities are important in the mechanistic analysis of phosphate chemistry, as discussed above, the advantage of SCC-DFTB over other semi-empirical methods becomes apparent.

In this work, we report the parameterization of SCC-DFTB for phosphorus. Two sets of parameters have been developed, which work better for proton affinities of phosphate compounds and the hydrolysis reactions of phosphates, respectively, as compared to high-level ab initio calculations. With the current SCC-DFTB model, which includes on-site third-order contributions (vide infra), it seems difficult to describe both classes of properties with high accuracy using a single set of parameters and the precise reason is under investigation. In the next section, we briefly summarize the SCC-DFTB methodology and the procedures for parameterization. We then present data from the parameterization process and discuss trends in the results, which are followed by additional benchmark calculations of gas phase models, which have been studied by York et al.⁶² using high-level ab initio calculations, as well as solution calculations with a QM/MM framework. Finally, we draw a few conclusions. In a separate publication, we further test the robustness of the model in the context of phosphate hydrolysis in solution and enzymes using SCC-DFTB/MM simulations. A brief summary on the performance of the parameterization and the application to ATP hydrolysis in the molecular motor myosin have been reported recently.⁵

II. COMPUTATIONAL METHODS

In this section, we first briefly review the formulation of SCC-DFTB as used in the parameterization for phosphorus. We then present details regarding the parameterization procedure and additional benchmark systems for further validating the fitted parameters.

A. Theory: SCC-DFTB

As described in detail in several previous publications,^43,63 the standard SCC-DFTB approach is based on a second-order expansion of the density functional theory energy around a reference density, ρ₀,

$$\begin{array}{ccc}E& =& {\displaystyle \sum _i^{\mathit{\text{occ}}}\langle {\Psi }_i\left|{\widehat{H}}^0\right|{\Psi }_i\rangle }+\frac{1}{2}{\displaystyle \iint \prime }\left({\frac{1}{|\overrightarrow{r}-\overrightarrow{r}\prime |}+\frac{{\delta }^2{E}_{\mathit{\text{xc}}}}{\mathrm{\Delta }\rho \mathrm{\Delta }\rho \prime }|}_{{\rho }_0}\right)\delta \rho \delta \rho \prime \\ & -& \frac{1}{2}{\displaystyle \iint \prime }\frac{{\rho }_0^{\prime }{\rho }_0}{|\overrightarrow{r}-\overrightarrow{r}\prime |}+E_{\mathit{\text{xc}}}\left[{\rho }_0\right]-{\displaystyle \int V_{\mathit{\text{xc}}}}{\rho }_0+E_{\mathit{\text{cc}}}\end{array}$$ (1)

where Ĥ⁰ = Ĥ [ρ₀] is the effective Kohn-Sham Hamiltonian evaluated at the reference density ρ₀ and the Ψ_i are Kohn-Sham orbitals. E_xc and V_xc are the exchange-correlation energy and potential, respectively, and E_cc is the core-core repulsion energy. With a minimal basis set, a monopole approximation for the second-order term and the two-center approximation to the integrals, the SCC-DFTB total energy is given in the following form,

$$E={\displaystyle \sum _{i\mu \nu }{c}_{\mu }^i{c}_{\nu }^i{H}_{\mu \nu }^0+\frac{1}{2}{\displaystyle \sum _{\alpha \beta }{\gamma }_{\alpha \beta }\mathrm{\Delta }}}{q}_{\alpha }\mathrm{\Delta }{q}_{\beta }+\frac{1}{2}{\displaystyle \sum _{\alpha \beta }U\left[R_{\alpha \beta };{\rho }_0^{\alpha },{\rho }_0^{\beta }\right]}$$ (2)

where $c_{\mu /\nu }^i$ are orbital coefficients, Δq_α/β are the Mulliken charges on atom α/β and γ_αβ is the approximate second-order kernel derived based on two interacting spherical charges. The last pair-wise summation gives the so-called repulsive potential term, which is the core-core repulsion plus double counting terms and defined relative to infinitely separated atomic species.

As discussed in our recent work,^25,59–61 it was found that further including the third-order contribution can substantially improve calculated proton affinity for a set of biologically relevant small molecules, even with only the on-site terms included. Since proton affinity is of great relevance to phosphate chemistry, as emphasized above, we choose to adopt the same formulation. The corresponding expression for the SCC-DFTB total energy is^25,59,61

$$E={\displaystyle \sum _{i\mu \nu }{c}_{\mu }^i{c}_{\nu }^i{H}_{\mu \nu }^0+\frac{1}{2}{\displaystyle \sum _{\alpha \beta }{\gamma }_{\alpha \beta }\mathrm{\Delta }}}{q}_{\alpha }\mathrm{\Delta }{q}_{\beta }+\frac{1}{2}{\displaystyle \sum _{\alpha \beta }U\left[R_{\alpha \beta };{\rho }_0^{\alpha },{\rho }_0^{\beta }\right]}+\frac{1}{6}{\displaystyle \sum _{\alpha }{U}_{\alpha }^d\mathrm{\Delta }{q}_{\alpha }^3}$$ (3)

where $U_{\alpha }^d$ is the derivative of the Hubbard parameter of atom α with respect to atomic charge. In our recent study,⁶¹ $U_{\alpha }^d$ is regarded as a fixed parameter for each element type; in other words, the Hubbard parameter is taken to be linearly dependent on the atomic charge. For phosphorus containing compounds, a complicating factor is that the oxygen atoms on the phosphorus tend to be highly charged, thus the linear charge dependence of the Hubbard parameter may no longer be valid. To take this deviation from the linear behavior into account, we add an additional charge dependent term to the Hubbard charge derivative; i.e.,

$$U_{\alpha }^d\left(q\right)=U_{0\alpha }^d+D_0\mathit{\text{exp}}\left[-{\mathrm{\Gamma }}_0{\left(\mathrm{\Delta }{q}_{\alpha }-Q_0\right)}^2\right]$$ (4)

where the charge-independent parameter $\left(U_{0\alpha }^d\right)$ is dependent on the element type whereas the three parameters associated with the Gaussian (D₀, Γ₀,Q₀) are taken to be independent of element type to minimize the number of parameters. The choice of the Gaussian functional form is entirely empirical and designed to avoid undesired behavior of the Hubbard derivative for large charges.

B. Reference systems and parameter fitting

To parameterize an effective SCC-DFTB approach for phosphorus compounds and phosphate chemistry, the parameterization procedure is divided into several stages. First, the atomic properties (basis functions, zero-order Hamiltonian matrix elements, Hubbard parameter) for P are derived based on a set of rather well-defined protocols involving atomic calculations.^43,63 The pair-wise repulsive potentials between P and O, N, C, H for a second-order SCC-DFTB approach are then fitted based on small molecule compounds and B3LYP calculations. With these parameters held fixed, the Hubbard derivatives are then fitted based on more specific properties such as proton affinity or phosphate hydrolysis reaction energetics. With the current third-order formulation, it seems difficult to develop a single set of Hubbard derivatives to simultaneously produce reliable proton affinities and phosphate hydrolysis energetics (see below). Therefore, two sets of Hubbard derivative parameters have been developed based on proton affinity and phosphate hydrolysis reactions, respectively; for clarity, they are referred to as SCC-DFTBPA and SCC-DFTBPR, respectively (see Table I). The phosphate hydrolysis set of parameters is further tested with additional benchmark calculations using results from the QCRNA database established by the York group.⁶² These gas phase calculations are finally supplemented with potential of mean force calculations for monophosphate ester hydrolysis in solution with SCC-DFTBPR/MM simulations.

TABLE I.

Different sets of parameterizations of the SCC-DFTB approach for phosphate^a

Notationb	Reference datac	$U_{P,O,C,H}^d$	D0,Г0,Q0
	Second-order parameterization
2nd-order	13 small molecules (see main text)	—	—
	Third-order parameterizations
3rd-order	—	−0.07, −0.17, −0.16, −0.16	—
SCC-DFTBPA	Proton affinity, 18 P-compounds	−0.07, −0.20, −0.22, −0.23	−0.06, 17.9, 0.86
Mix-optimized	Proton affinities, 5 P- and 11 non-P compounds	−0.10, −0.15, −0.24, −0.15	−0.08 37.5, 0.83
SCC-DFTBPR	37 phosphate reaction energetics	−0.07, −0.22, −0.24, −0.08	−0.09, 16.1, 0.75

^a$U_{\alpha }^d$ is the Hubbard derivative defined in Eq.3; D₀,Г₀,Q₀ are Gaussian parameters defined in Eq.4.

^bThe notations are used in all tables.

^c“P-compounds” indicate phosphorus containing compounds; “non-P compounds” indicate compounds that do not contain phosphorus. For the list of compounds, see Table 3 and Table 4.

1. Atomic properties and repulsive potentials

Since the parameterization procedure for SCC-DFTB has been reported in details in previous articles for several elements,^43,63 we only include a very short description here. The atomic properties include the Slater basis functions, the reference density (ρ₀) and the chemical hardness (Hubbard) parameter; these are determined based on atomic DFT calculations with an in-house program TWOCENT. Once these are established, other quantities such as the second-order kernel γ_AB can be determined.^43,63 The matrix elements for the effective Kohn-Sham Hamiltonian with the reference density can also be calculated and tabulated; the exchange-correlation functional used is the one of Perdew, Burke and Ernzerhof (PBE).⁶⁴

For the repulsive potential, $U\left[R_{\alpha \beta };{\rho }_0^{\alpha },{\rho }_0^{\beta }\right],$, five different pairs need to be derived (P-P and P-O/N/C/H). Accordingly, several small molecules are chosen and full DFT (B3LYP^65–67/6-311G**) calculations are calculated as a function of specific bond distances. The repulsive potential is then calculated as the difference between the full DFT potential energy curve and the electronic contribution from SCC-DFTB at the same structures,

$$U\left[R_{\alpha \beta };{\rho }_0^{\alpha },{\rho }_0^{\beta }\right]=\left[E^{\mathit{\text{DFT}}}(R_{\alpha \beta })-E^{\mathit{\text{DFT}}}(\infty )\right]-{\displaystyle \sum _{i\mu \nu }{c}_{\mu }^i{c}_{\nu }^i{H}_{\mu \nu }^0(R_{\alpha \beta })-\frac{1}{2}{\displaystyle \sum _{\alpha \beta }{\gamma }_{\alpha \beta }\mathrm{\Delta }{q}_{\alpha }}}\mathrm{\Delta }{q}_{\beta }$$ (5)

The repulsive potential is fitted into a cubic spline and truncated to zero in the 2.2–3.2 Å range. The specific molecules used for parameterizing different repulsive potentials are: PH₃, PCH, HPCH₂, H₂PCH₃, PN, HPNH, H₂PNH₂, P₂, HPPH, H₂PPH₂, OPH, H₃PO₄ and ${\text{H}}_4{\text{PO}}_5^{-}$.

2. Hubbard derivative related parameters

Similar to our recent work on using third-order terms to improve SCC-DFTB proton affinities,^25,59, the Hubbard derivative related parameters are optimized using a Genetic Algorithm^68,69 by minimizing the penalty function defined as

$$X=\frac{{\Sigma }_i{w}_i{\left(Y_i^{\mathit{\text{ref}}}-Y_i^{\mathit{\text{SCC}}}\right)}^2}{{\Sigma }_i{w}_i}$$ (6)

where the summation is over all properties of interest in a particular optimization set (see below), w_i is the weight of a specific property and $Y_i^{\mathit{\text{ref}}}/Y_i^{\mathit{\text{SCC}}}$ are the values of the i-th property from reference calculation (see below) and SCC-DFTB calculation with a specific set of Hubbard derivative related parameters $\left(U_{0\alpha }^d,D_0,{\mathrm{\Gamma }}_0,Q_0\right),$ respectively. During the Genetic Algorithm (GA) optimization, the properties of interest include proton affinities/reaction energetics and the root-mean-square gradient (GRMS) of the molecule at the reference geometry, addressing both energetic and structural information; the corresponding weights in χ are 10 and 1, respectively. The micro-GA technique⁶⁸ is applied with a population of 10 chromosomes for 100 generations with uniform crossovers.

SCC-DFTBPA: Proton affinity of phosphate compounds

Eighteen phosphate species of biological relevance (see Table 3) are chosen as the reference system to optimize the Hubbard derivative related parameters. A subset of these molecules were used as benchmark systems in the previous work of Range et al.,²⁹ who found that all semi-empirical methods including the standard SCC-DFTB have significant systematic errors. As the high-level reference, geometries are optimized at the B3LYP/6-31G(d) level and the energetics are obtained at the G3B3⁷⁰ level. Benchmark calculations by Range et al.²⁹ showed that this combination gives systematically reliable energetics compared to experimental values. For the purpose of making comparison and establishing a less expensive reference level for the subsequent parameterization involving larger molecules, MP2 with the G3Large basis set is also carried out; the G3Large was modified based on the 6-311+G(3df,2p) basis set for G3⁷¹ calculations.

Table 3.

Comparison of proton affinities from different parameterizations of SCC-DFTB and ab initio methods for 18 Phosphorus Containing Molecular Systems^a

			SCC-DFTBd
Moleculesb	G3B3	MP2c
			2nd-order	3rd-order	SCC-DFTBPA
H3PO4	334.0	−1.5	27.3	13.7	5.0
H2PO4−	463.6	−1.1	36.7	15.2	1.9
DMPHe	336.2	−1.5	19.9	9.7	2.9
MMPe	336.7	−1.6	22.2	10.3	2.4
MMP−e	460.5	−1.2	31.7	14.2	3.5
PH3OH	201.6	−2.0	1.6	−2.0	−2.9
PH2OHOH	201.6	−1.9	7.4	1.6	0.1
PHOHOHOH	200.8	−1.7	14.7	6.9	4.6
PH2(OH)=O	336.6	−1.6	13.2	4.9	−1.9
PH(OH)(OH)=O	334.7	−1.5	20.9	9.9	2.0
P(O)(OH)(-O-CH2CH2-O-)	336.3	−1.7	18.0	7.5	1.0
P(OH)(OH)(-O-CH2CH2-O-)(OH*)	359.0	−2.0	6.9	7.6	0.8
P(OH*)(OH)(-O-CH2CH2-O-)(OH)	350.4	−1.7	16.8	5.7	−2.3
P(OH*)(OH)(-O-CH2CH2-O-)(OCH3)	351.2	−1.6	12.0	2.3	−5.4
P(OH)(OCH3)(-O-CH2CH2-O-)(OH*)	359.6	−1.9	6.3	−3.5	−0.4
P(OH*)(OCH3)(-O-CH2CH2-O-)(OH)	353.0	−1.7	13.7	3.9	−3.9
P(OH)(OH)(OH)(OH*)(OH)_ax	357.3	−1.8	14.2	10.8	4.2
P(OH)(OH)(OH)(OH*)(OH)_eq	347.0	−1.9	24.2	−18.5	−1.1
Error Analysisf
MAXE		−2.0	36.7	−18.5	−5.4
RMSE		1.7	19.3	9.5	3.0
MUE		1.7	17.1	8.2	2.6
MSE		−1.7	17.1	5.6	0.6

^a)The proton affinity (PA) of A⁻ is defined as the negative of the enthalpy change for the gas phase reaction A⁻ _(g)+H⁺ _(g)→AH_(g). In the current calculations, 0 K electronic energies instead of the room temperature enthalpy are used without zero point energy correction. All quantities are given in kcal/mol. For G3B3, such calculated PA values are given; for all other methods, the errors relative to G3B3 results are given (positive error indicates overestimation).

^b)All molecules correspond to the protonated species (AH). Asterisk “*”, “ax” (axial) and “eq” (equatorial) are used to identify the acidic proton.

^c)The basis set used is G3Large, which is a basis set used in the G3 method (see http://chemistry.anl.gov/compmat/g3theory.htm).

^d)See Table 1 for the notations used to label different parameterizations of the SCC-DFTB approach. As discussed in previous studies, a value of 141.8 kcal/mol is included to account for the self-interaction energy of the H atom.

^e)“DMPH” refers to dimethyl hydrogen phosphate; “MMP” refers to P(O)(OH)(OH)(OCH₃); “MMP-” refers to P(O)(O)(OH)(OCH₃)⁻.

^f)MAXE: largest error; RMSE: root-mean-square error, defined as <(err)²>^1/2; MUE: mean unsigned error; MSE: mean signed error.

Rigorously speaking, the proton affinity of molecule A⁻ is the negative of the enthalpy change for the gas-phase reaction A⁻(g)+H⁺(g)→AH(g) at the room temperature, which involves thermal vibrational contributions. To avoid a large number of vibrational calculations in the parameterization process, we consistently consider only the potential energy contribution in both the reference calculations and SCC-DFTB calculations during the GA optimization. Another subtle point is that the energy of proton in SCC-DFTB is not zero due to the definition of the repulsive potential in the total energy expression;⁶³ however, once a value (141.8 kcal/mol) is selected, the results are consistent among all SCC-DFTB calculations.

To test if the parameters optimized based on phosphate proton affinities are transferrable to non-phosphate compounds, a set of 11 small molecules including water, alcohols and carboxylic acids are also considered. A set of Hubbard derivative parameters are optimized based on the proton affinities of both phosphate and non-phosphate molecules, although the result is rather disappointing (see below), which suggests that further improvements in the SCC-DFTB formalism are needed to predict accurate proton affinities for a broad range of molecules that include both second and third row elements.

SCC-DFTBPR:Phosphate Hydrolysis

As discussed above, a balanced treatment for the proton affinities of phosphate, the nucleophile and the leaving group is required (but not sufficient) for a reliable description of phosphate hydrolysis reactions. Since this seems difficult to achieve even with the third-order extension of SCC-DFTB, we choose to pursue a more pragmatic avenue by fitting the Hubbard derivative parameters based on results for a set of representative phosphate hydrolysis reactions. The underlying assumption is that errors in the proton affinity of different species can cancel out to yield satisfactory reaction energies. An additional advantage of using reaction properties for parameterization is that both reaction energy and barrier can be taken into account. We emphasize that the number of parameters is rather small, which include five $U_{0\alpha }^d$ values for P, O, N, C, H and three element-independent Gaussian parameters, D₀, Γ₀,Q₀. Therefore, we hope that parameters optimized based on phosphate hydrolysis are reasonably transferrable to other phosphate reactions with similar characteristics, such as phosphoryl transfer reactions; this will be tested with the additional benchmark calculations discussed below.

The reference reactions include the hydrolysis of dimethyl monophosphate ester (DMP) and monomethyl monophosphate ester (MMP) with different protonation states (see Table 5). Several considerations account for this choice. First, the hydrolysis of MMP and DMP are basic models^8,72 for the hydrolysis of nucleotides (e.g., ATP, GTP) and the scission reactions in many ribozyme systems, respectively. Second, different protonation states for the reactant stress the effects due to pH changes or pK_a shifts induced by the macromolecular environment, which may have important biological implications.⁴² For instance, the phosphorane intermediate is a short-lived species with -2 charge; for the neutral and monoanionic species, the lifetime is long enough for pseudorotation.^73–75 Finally, the small size of DMP and MMP allows us to perform relatively high-level ab initio calculations as reference.

Table 5.

Comparison of exothermicity and barrier height from SCC-DFTB and high-level ab initio calculations for 37 elementary steps in the hydrolysis of MMP and DMP^a

Processb	ab initio	SCC-DFTB Single point	SCC-DFTBPR Optimizationi	MP2//SCC- DFTBPRj
com1→ts1 (MMP,B)	31.0c/−1.7d	−0.9e/−3.0f/0.4g/3.1h	1.1	−0.9
com1→int1 (MMP,E)	30.6/−1.4	−2.1/−2.2/0.7/2.1	1.4	−0.8
com1→ts1_2 (MMP,B)	41.5/−2.1	1.2/−0.3/2.4/5.3	−3.4	−1.6
com1→int1_2 (MMP,E)	31.0/−1.1	−4.4/−0.6/1.6/3.1	1.9	−0.1
int1_2→ts2_1 (MMP,B)	11.9/−2.0	−2.5/−2.1/−3.3/−2.3	---k
int1_2→ts2_2 (MMP,B)	3.6/0.1	−5.4/−5.0/−5.2/−5.0	0.3	6.1
int1_2→com2 (MMP,E)	−28.8/−0.9	2.5/0.6/0.2/0.4	−0.4	−0.8
com1→diss_tsa (MMP,B)	36.8/−4.2	4.7/4.0/2.4/4.8	2.6	0.2
com1→diss_int (MMP,E)	19.6/−6.4	−7.1/−6.0/−3.5/−2.8	−2.9	−1.0
com1_w2→ts1_2_w2 (MMP,B)	39.9/−2.1	−8.2/−9.4/−6.1/−3.7	−5.4	−2.5
com1_w2→int1_2a_w2 (MMP,E)	28.0/0.8	−5.4/−2.5/−1.2/0.8	0.2	−1.1
int1_2a_w2→int1_2_w2 (MMP,E)	0.4/−1.7	0.4/0.7/1.2/1.0	1.7	1.5
int1_2_w2→ts2_0_w2 (MMP,B)	11.4/−0.5	−3.7/−7.3/−5.2/−3.8	−7.3	−1.1
com1_da→ts1_da (MMP,B)	55.0/−8.4	−22.5/−12.3/−9.2/−10.1	−8.9	0.0
com1_da→int_da (MMP,E)	4.5/−2.0	−2.9/−0.7/−1.8/−0.4	−12.1	−1.5
com1→ts1 (DMP,B)	38.6/−1.4	−0.9/−4.1/−0.8/3.1	−1.6	0.8
com1→int1 (DMP,E)j	35.4/−0.2	−5.6/−3.1/−0.5/0.2	−0.5	0.6
int1→int1_2 (DMP,E)	1.3/−0.7	−3.0/−0.9/−0.9/0.1	−4.0	2.0
int1_2→ts2 (DMP,B)	0.6/−0.5	0.5/−0.1/−0.6/−0.6	−0.5	−1.6
int1_2→com2 (DMP,E)	−35.2/−0.7	7.1/4.6/4.9/4.2	7.0	−1.3
n_com1→n_ts3 (DMP,B)	33.6/−1.4	4.9/4.3/1.0/3.5	1.2	−0.4
n_com1→n_int1 (DMP,E)	13.2/0.4	−3.7/−0.8/0.4/1.1	0.1	0.1
n_int1→n_ts4 (DMP,B)	22.9/−1.6	6.4/4.9/2.0/4.2	0.9	1.0
n_int1→n_com2 (DMP,E)	−15.8/−1.9	2.6/0.5/0.9/0.6	0.0	0.0
DMP_P→diss_ts (DMP,B)	40.9/−2.9	11.8/9.4/5.5/7.2	6.1	−0.8
DMP_P→diss_prod (DMP,E)	28.2/−3.8	0.6/−2.1/−2.7/−2.9	−2.6	−1.2
diss_prod2→diss_ts2 (DMP,B)	13.5/0.7	13.4/13.0/7.5/11.7	8.4	−0.5
diss_prod2→MMP_P (DMP,E)	−29.8/3.6	0.8/2.8/2.6/3.6	2.8	0.2
diss_w_reac→diss_w_ts (DMP,B)	20.9/−2.3	5.9/3.4/−0.2/2.0	−0.1	−0.4
diss_w_reac→diss_w_prod (DMP,E)	18.4/−2.6	4.8/1.2/−2.5/−1.3	−2.0	−0.3
diss_w_prod2→diss_w_ts2 (DMP,B)	1.9/0.2	2.5/2.7/1.1/3.7	1.8	−0.8
diss_w_prod2→diss_w_reac2 (DMP,E)	−21.0/2.7	−2.9/−0.5/0.9/1.5	0.4	0.3
n_w_com1→n_w_ts3 (DMP,B)	28.2/−1.8	−3.0/−2.3/−4.8/−2.0	---	---
n_w_com1→n_w_int1 (DMP,E)	13.1/1.0	−4.2/−1.3/0.0/0.7	−3.1	−0.5
n_w_int1→n_w_int2 (DMP,E)	−0.5/0.5	0.3/0.5/0.7/1.1	0.4	0.3
n_w_int2→n_w_ts4 (DMP,B)	15.1/−2.3	1.8/−0.5/−4.0/−2.3	---	---
n_w_int2→n_w_com2 (DMP,E)	−13.0/−2.0	1.2/−1.0/−0.4/−2.0	−1.3	0.6
Error Analysisl
MAXE	−8.4	−22.5/13.0/−9.2/11.7	−12.1	6.1
RMSE	2.5	6.1/4.6/3.3/3.9	4.0	1.4
MUE	1.9	4.4/3.3/2.4/2.9	2.8	1.0
MSE	−1.4	−0.4/−0.4/−0.4/0.8	−0.5	−0.2

^a)No zero-point corrections are included in either exothermicity or barrier heights. All quantities are given in kcal/mol.

^b)The processes are labeled in the following manner: e.g., “com1→ts1 (MMP,B)” refers to the reaction from the reactant “com1” to the transition state “ts1”, “MMP” in the parenthesis refers to the mono-methyl mono-phosphate ester model system, “B” in the parenthesis stands for “Barrier”. Similarly, “com1→int1 (DMP,E)” refers to the reaction from the reactant “com1” to the intermediate “int1”, “DMP” refers to the dimethyl di-phosphate ester model system, “E” stands for “Exothermicity”. For the structures, see Fig. S1 in the Supporting Materials.

^c)The number before the slash refers to the MP2/G3Large single point calculation based on the B3LYP/6-31+G** optimized structures. For more details about G3Large basis set, see http://chemistry.anl.gov/compmat/g3theory.htm.

^d)The number after the slash refers to the energy difference between the B3LYP result and the MP2/G3Large single point calculation at the B3LYP structure.

^e)The difference between the standard (second-order) SCC-DFTB and MP2/G3Large single point energies at the B3LYP/6-31+G(d,p) structures.

^f)The difference between the default 3^rd-order SCC-DFTB and MP2/G3Large single point energies at the B3LYP/6-31+G(d,p) structures..

^g)The difference between SCC-DFTBPR and MP2/G3Large single point energies at the B3LYP/6-31+G(d,p) structures.

^h)The difference between the “Mix-optimized 3^rd-order” SCC-DFTB and MP2/G3Large single point energies at the B3LYP/6-31+G(d,p) structures.

ⁱ⁾The difference between fully geometry-optimized SCC-DFTBPR energies and MP2/G3Large single point energies at the B3LYP/6-31+G(d,p) structures.

^j)The difference between MP2/G3Large single point energies at the SCC-DFTBPR structures and those at the B3LYP/6-31+G(d,p) structures.

^k)As discussed in the main text and illustrated in Fig. 2, only one transition state is found at the SCC-DFTBPR level.

^l)The errors are defined in the same manner as in Table 3. For the entry for “ab initio”, the errors are for the B3LYP/6-31+G(d,p) energies relative to the MP2/G3Large results.

Regarding the reaction mechanism, both dissociative and associative mechanisms are considered. In addition, pathways that involve water-assisted proton transfers, which have been proposed to be important for at least the dissociative mechanism,⁴⁰ are also included. All together, 37 gas-phase reaction energies (18 of which are energy barriers) involving 47 structures are included as the reference set; 15 reaction energies are based on MMP model reactions (8 energy barriers) and the remaining 22 are from DMP reactions with 10 energy barriers. Despite the relatively small size of the DMP and MMP systems, it is impractical to carry out G3B3 calculations. Instead, B3LYP/6-31+G(d,p) geometries and MP2/G3Large single point energies are used as reference. For all energy calculations, no zero-point correction or vibrational contribution has been included.

C. Benchmark calculations

1. Geometrical parameters

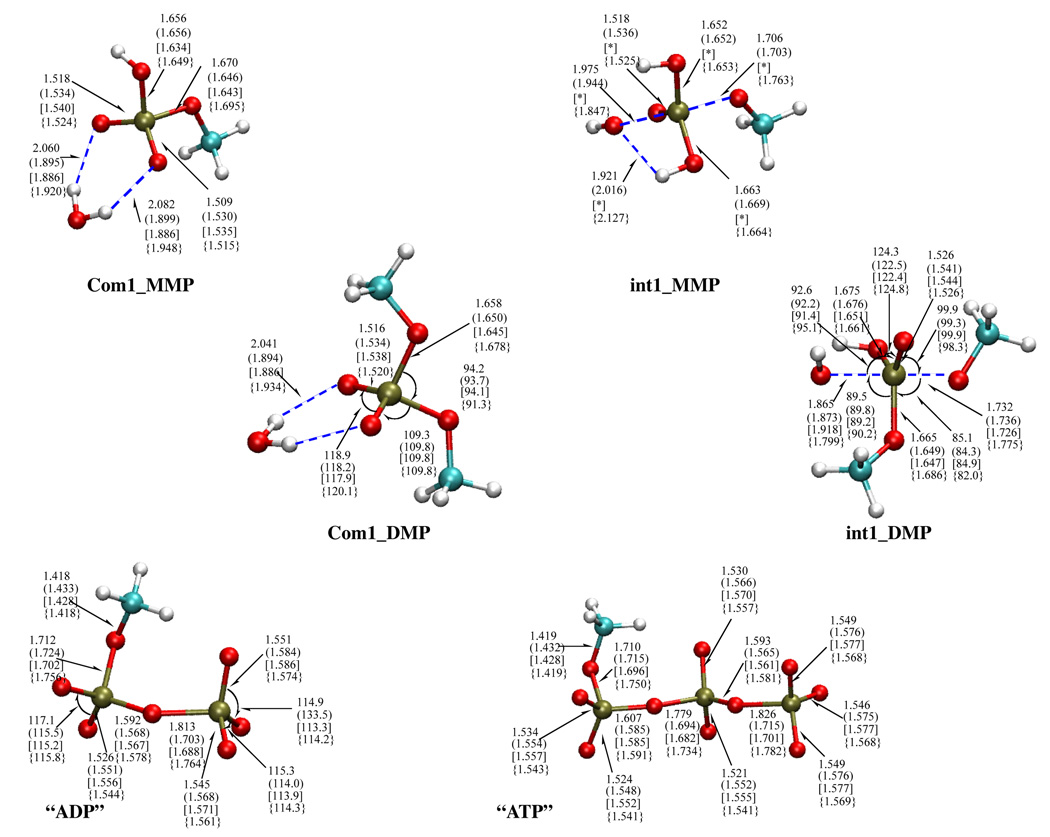
To test the performance of the different SCC-DFTB parameterization on structural properties, a series of common phosphate compounds are studied and the optimized gas-phase geometries are compared to those from B3LYP calculations with the 6-31+G(d,p) basis set. The list of compounds include inorganic phosphate with different protonation states $({\mathrm{H}}_3{\text{PO}}_4,{\mathrm{H}}_2{\text{PO}}_4^{-},{\mathrm{H}}_2{\text{PO}}_4^{2-}\text{and}{\text{PO}}_4^{3-})$ mono-phosphate esters (MMP, DMP), di-phosphate ester (model ADP, see Fig.1) and tri-phosphate ester (model ATP, see Fig.1).

FIG. 1.

Selected structures included in the SCC-DFTB parameterization protocol optimized at different levels; the first four are involved in the hydrolysis of small phosphate molecules, and the last two are models for ADP and ATP, respectively. Values without parentheses are from B3LYP/6-31+G** calculations; values with parentheses are from SCC-DFTBPR; values with brackets are from SCC-DFTBPA; values with curly brackets are from second-order SCC-DFTB parameterization. See Table 1 for the notation of different SCC-DFTB parameterizations. Distances are in Å, angles in degrees.

2. Additional phosphate hydrolysis reactions

As additional benchmark systems for the newly parameterized SCC-DFTBPR, all (19) RNA model reactions with the overall charge of -1 are selected from the QCRNA database established by the York group;⁶² these include 56 reaction energies and 47 barriers. These systems were consistently calculated at the B3LYP/6-311++G(3df,2p) level for energy and B3LYP/6-31++G(d,p) for structure by the York group. Both single point energy calculations and geometry optimizations are carried out at the SCC-DFTBPR level; for transition states, only single point energies are considered. Dipole moments are also compared. In a separate study,⁷⁶ selected pseudo-rotation barriers at the SCC-DFTBPR level are also compared to the QCRNA database, for which good agreement is found.

3. Explicit solvent simulations with SCC-DFTBPR/MM

Finally, to supplement the gas phase calculations, potential of mean force simulations are carried out with SCC-DFTBPR/MM to investigate if the parameterized model works in an explicit condensed phase environment. This is an important test since the ultimate goal is to use SCC-DFTBPR in enzyme simulations (for an initial application, see5).

The specific reaction studied is the first step for the hydrolysis of MMP in water. The stochastic boundary condition⁷⁷ is used as the simulation protocol. The MMP molecule is solvated with a water droplet of 22 Å radius. Only MMP and the lytic water are treated with SCC-DFTBPR while the rest of the water molecules are described with the modified version of TIP3P^78,79 in CHARMM.⁸⁰ The van der Waals parameters for the atoms in MMP are taken from the CHARMM force field for lipid⁸¹ without further optimization. The importance of QM van der Waals parameters in QM/MM simulations has been discussed in previous studies,⁸² and it was argued that in some cases allowing the van der Waals parameters to vary during the reaction can be important,⁸³ which we examine briefly here using the MMP system as an example (vide infra).

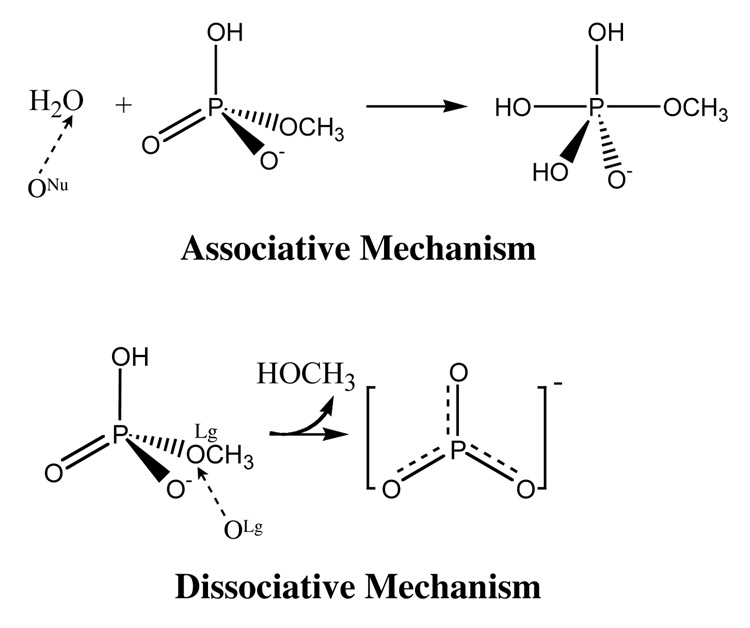
Both the associative and dissociative mechanisms (see Scheme 1) are considered and the according potentials of mean force surfaces are calculated with umbrella sampling.⁸⁴ For the associative mechanism, the P-O^Nu distance and the antisymmetric stretch describing the proton transfer from the lytic (nucleophilic) water to phosphate are defined as the reaction coordinates. For the dissociative mechanism, the reaction coordinates include the P-O^lg distance (where O^Lg is the oxygen atom of the leaving group, which is methanol in the current case) and the antisymmetric stretch that describes the intramolecular proton transfer between the protonated oxygen of MMP and O^Lg. In both cases, the antisymmetric stretch is defined as the distance of donor-proton minus the distance of acceptor-proton. Based on the defined reaction coordinates, two-dimensional potential of mean force (PMF) in solution are generated using umbrella sampling; for comparison, two-dimensional potential energy surface (PES) in the gas phase are also calculated using adiabatic mapping. A technical point is that the O-H bond in MMP needs to be constrained in calculations for the associative mechanism; otherwise, the proton of MMP is transferred back to the nucleophilic water as the latter transfers its proton to the unprotonated oxygen in MMP. In the umbrella sampling calculations, 122 and 108 windows are used for the associative and dissociative mechanisms, respectively, where each window includes 50 ps of MD simulations. The data from umbrella sampling are combined using the Weighted Histogram Analysis Method (WHAM) approach.⁸⁵

Scheme I.

Nonbonded interactions (electrostatic and van der Waals) are calculated without cutoffs. The bulk electrostatics are considered via GSBP^86,87 with an 24 Åinner region, which includes an additional 2 Å buffer region. The generalized reaction field matrix is evaluated using 400 spherical harmonics with an outer region dielectric constant of 80. Thermal collisions due to the bulk are included in the outer 2 Å of the 22 Å water sphere via Langevin dynamics⁸⁸ and the Langevin atom list is heuristically updated during the simulation. A 1 fs time step is used and the temperature is maintained at 298 K. Bonds involving hydrogen are constrained with the SHAKE algorithm⁸⁹ except for those involved in the proton transfer.

III. RESULTS AND DISCUSSIONS

In this section, we first briefly go over results for the structural properties of common phosphate compounds and then focus on the performance of the third-order parameterizations for proton affinities and hydrolysis reactions. Some of the gas-phase benchmark results are summarized in the first application of SCC-DFTBPR/MM although without detailed discussions.⁵

A. Structural properties

As shown in Table II, the structure of common phosphate compounds are well reproduced by all three parameterizations of the SCC-DFTB model. The bond distances and bond angles have RMS error in the range of 0.03 Å and 1.8 degrees, respectively. The results are equally impressive for species with rather complex electronic structures, such as “ADP/ATP” and pentavalent intermediate involved in the associative pathways of hydrolysis (see Fig.1). For the bridging P-O bonds in the model ADP and ATP species, the values from second-order SCC-DFTB agree better with B3LYP results, while both SCC-DFTBPR and SCC-DFTBPA tend to underestimate the distances. For most geometrical parameters, any one of the SCC-DFTB models can be used to give satisfying results. Hydrogen-bonding distances have larger errors, as illustrated in Com1_MMP and Com1 DMP in Fig.1, although this is not unique to phosphate species.^61,82

TABLE II.

Errors in structural properties of different parameterizations of the SCC-DFTB approach or common phosphate compounds^a

Geometrical Parameterb	Second-order	SCC-DFTBPAc	SCC-DFTBPR
P-O (Å)	0.03	0.04	0.03
O-P-O (°)	1.8	1.9	1.7

^aThe root-mean-square (RMS) errors are calculated relative to those from B3LYP/6-31+G(d,p) alculations.

^bIn total, 10 common phosphate compounds are included in the analysis (including MMP/DMP-water complexes, pentavalent intermediate structures for the hydrolysis of MMP/DMP, different protonation states for phosphoric acid, models for ADP and ATP). For selected structures, see Fig. 1.

^cWith SCC-DFTBPA, the pentavalent intermediate for MMP hydrolysis is not stable as an intermediate, and geometry optimization leads to the reactant state.

B. SCC-DFTBPA: proton affinities

For the 18 phosphorus containing species, large errors are seen in the gas-phase proton affinities with the standard second-order SCC-DFTB parameterization (see Table 3). The largest error is 36.7 kcal/mol for ${\text{H}}_2{\text{PO}}_4^{-}$, which is not unexpected for a highly charged species in the gas phase. The root-mean-square-error (RMSE) is 19.3 kcal/mol, similar to those reported for the second-order SCC-DFTB and other semi-empirical methods in the previous study.²⁹ With the on-site third-order terms, even without specific parameterization, the errors in the proton affinity reduce dramatically as also seen in our recent analysis for non-phosphate compounds (also see Table 4).⁶¹ The largest error becomes −18.5 kcal/mol and the RMSE is cut nearly half to 9.5 kcal/mol. With further optimizations, the results become very good with the largest error of −5.4 kcal/mol and RMSE of merely 3.0 kcal/mol. Similar to the observations in previous analysis, the Mulliken charges on the phosphate oxygen atoms are substantially modified with the third-order terms, which is related to the reduced error in proton affinity. Take MMP as an example. The Mulliken charges on the acidic oxygen atom are −0.566 and −0.816 before and after deprotonation, respectively, with the second-order SCC-DFTB; the corresponding values are −0.710 and −0.895, respectively, with the optimized third-order SCC-DFTB.

Table 4.

The different performances for SCC-DFTB including on-site third-order terms for non-phosphorus compounds and phosphate species.^a

		SCC-DFTBb
Molecules	G3B3
		2nd-order	3rd-order	Mix-optimized 3rd-order
	Non-phosphorus
water	398.4	26.5	−5.4 (1.3)	1.0 [−13.9]
methanol	392.6	4.5	−6.3 (−4.0)	−8.3 [−13.1]
ethanol	388.3	8.7	−2.8 (−0.5)	−4.3 [−9.3]
propanol	387.6	7.9	−3.5 (−1.1)	−4.8 [−9.8]
2-propanol	385.6	11.5	−0.5 (1.8)	−1.4 [−6.5]
formic acid	351.2	11.9	3.1 (4.2)	−0.9 [−6.8]
acetic acid	355.1	11.3	1.6 (2.9)	−2.8 [−8.4]
propanoic acid	354.5	11.2	1.9 (3.1)	−2.5 [−8.0]
phenol	356.7	5.5	0.2 (1.1)	−2.6 [−5.8]
p-methylphenol	357.9	4.6	−0.4 (0.4)	−3.1 [−6.2]
p-nitrophenol	334.6	0.9	−5.4 (−4.4)	−5.8 [−12.0]
CH2(OH)2	374.8	11.7	1.3 (3.4)	−4.7 [−10.1]
CH2(OH)(OCH3)	377.2	5.1	−1.1 (0.0)	−3.4 [−8.4]
CH(OH)3	361.9	18.0	3.7 (5.9)	−1.8 [−7.2]
CH(OCH3)2OH	365.7	9.5	2.5 (3.6)	−0.4 [−5.7]
	Error Analysis
MAXE		26.5	−6.3 (5.9)	−8.3 [−13.9]
RMSE		11.6	3.2 (3.0)	3.8 [9.1]
MUE		9.9	2.6 (2.5)	3.2 [8.7]
MSE		9.9	−0.7 (1.2)	−3.1 [−8.7]
	Phosphate
H3PO4	334.0	27.3	13.7	8.5 [1.6]
H2PO4 −	463.6	36.7	15.2	8.7 [3.7]
DMPH	336.2	19.9	9.7	5.0 [1.7]
MMP	336.7	22.2	10.3	5.2 [−0.1]
MMP−	460.5	31.7	14.2	10.1 [6.1]
PH3OH	201.6	1.6	−2.0	−2.0 [−3.0]
PH2OHOH	201.6	7.4	1.6	1.6 [−1.0]
PHOHOHOH	200.8	14.7	6.9	6.5 [3.0]
PH2(OH)=O	336.6	13.2	4.9	0.1 [−3.6]
PH(OH)(OH)=O	334.7	20.9	9.9	4.7 [−0.8]
	Error Analysis
MAXE		36.7	15.2	10.1 [6.1]
RMSE		22.1	10.0	6.1 [3.0]
MUE		19.6	8.8	5.2 [2.5]
MSE		19.6	8.4	4.8 [0.8]

^a)The PA values and errors (in kcal/mol) are defined in the same manner as in Table 3.

^b)See Table 1 for the notations used to label different SCC−DFTB approaches. The values in parentheses are obtained using a third-order approach optimized in Ref. 59 based on 32 non-phosphorus compounds. For the “Mix-optimized 3^rd-order” set, both non-phosphorus and phosphate molecules (shown in italics) are included to attempt to optimize a set of third-order parameters that work for both classes of molecules, although the results are not satisfying (see text). The numbers in bracket are based on the phosphate hydrolysis reaction parameter set (SCC−DFTBPR).

Despite these encouraging results, difficulties arise when we attempt to optimize the current third-order formulation for both phosphorus-containing compounds and species without phosphorus. The situation is illustrated in Table 4. Although the RMSE’s for both classes of compounds seem to be reasonable, 3.8 kcal/mol and 6.1 kcal/mol for the non-phosphorus-and phosphorus-containing compounds, respectively, the signs of error are opposite. For non-phosphorus compounds, the proton affinity is typically underestimated by a few kcal/mol, while the trend is the opposite for phosphorus-containing species. This is alarming because error will accumulate for reactions between, for example, a non-phosphorus nucleophile and a phosphate compound, which suggests that the calculated reaction energetics are likely poor (see discussions below). With the SCC-DFTBPR parameter set, the errors in the proton affinity follow the same trend: the non-phosphorus- and phosphorus-containing compounds tend to have errors of opposite signs.

The origin for the different trends is not clear and an interesting observation is that different optimal Hubbard derivatives for oxygen $\left(U_O^d\right)$ apply to two classes of compounds. The computed $U_{\mathrm{O}}^d$ based on atomic calculations is −0.17; the optimized value based on the proton affinity for 32 non-phosphorus compounds and 18 phosphorus-containing compounds is −0.14 and −0.20, respectively. The variation towards different directions indicates some intrinsic differences between the two classes of compounds although the precise origin is not clear; further improvements in the SCC-DFTB formalism, such as including the off-site third-order terms and the treatment of polarization, are likely required.

C. SCC-DFTBPR: phosphate hydrolysis reactions

The hydrolysis of MMP and DMP molecules have been studied by a number of groups using different ab initio and DFT methods,^{11,16,40,90–95} and the role of additional water as proton relay has been discussed for the dissociative⁴⁰ pathway. Our present calculations, which also include the hydrolysis of DMP in different protonation states and the effect of additional water in associative pathways, are largely consistent with previous studies. Overall (see Table 5 for energetics and Supporting Materials for structures), the barriers for DMP and MMP hydrolysis are rather similar and show a weak dependence on the protonation state; e.g., the barrier for the protonated form of DMP (charge neutral) in the gas phase is lower than that of the anionic species by ~ 5 kcal/mol along the associative pathway, and the additional water helps to further reduce the potential barrier (not free energy barrier) by another 5 kcal/mol. The role of the additional water on the dissociative potential barriers is much more significant, on the order of ~ 20 kcal/mol. Therefore, when the entropic factor is taken into consideration, the effect of an additional water as proton relay is likely small for associative pathway; a detailed analysis in the condensed phase using a QM/MM framework will be reported in the near future (Yang and Cui, work in progress).

The reference energetics are taken to be MP2/G3-Large, which has been shown to give reliable proton affinities compared to the more elaborate CBS and G3B3 methods.²⁹ Compared to the MP2/G3-Large data, the energetics at the B3LYP/6-31+G(d,p) are generally rather close with a difference typically smaller than 3 kcal/mol; the RMSE is 2.5 kcal/mol. In certain cases, especially when the phosphate is highly charged, the difference between B3LYP/6-31+G(d,p) and MP2/G3-Large can be rather substantial and as large as 8.4 kcal/mol (for com1_da→ts1_da, see Table 5).

When single point energies are calculated at the B3LYP/6-31+G(d,p) structures, the standard second-order SCC-DFTB gives rather large errors; the largest error is −22.5 kcal/mol and the RMSE is 6.1 kcal/mol. When the third-order terms are included, the errors decrease substantially even without specific parameterizations, especially for the dianionic cases; the largest error decreases to 13.0 kcal/mol and the RMSE becomes 4.6 kcal/mol. Using the “Mixed-optimized 3rd-order” parameter set based on PA comparisons, the reaction energies become slightly better, with the largest error of 11.7 kcal/mol and a RMSE of 3.9 kcal/mol. With further parameter optimizations (SCC-DFTBPR), the largest error becomes −9.2 kcal/mol and the RMSE is 3.3 kcal/mol, which are rather remarkable for a semi-empirical method without many reaction-specific parameters. The errors for the stable states are overall smaller than that for the transition states; e.g., the RMSE is 1.9 kcal/mol when only the stable states are considered.

The reliability of the parameterized SCC-DFTBPR is further tested by full structure optimizations for both stable and transition states using the ABNR⁸⁰ and CPR⁹⁶ algorithms implemented in CHARMM; care is taken to ensure that the same local minima/saddle-points are used when compared to the B3LYP structures. The errors in energies are largely consistent with those for SCC-DFTBPR single-point energies at B3LYP geometries and the RMSE increases only slightly to 4.0 kcal/mol. As shown in Table 6, the SCC-DFTBPR structures are rather similar to the B3LYP/6-31+G(d,p) results, with RMSE for P-O distances typically of 0.02 Å, and for O-P-O angles of ~ 2–3 degrees. The errors in the transition state structures are slightly larger, especially for the bond distance associated with the leaving group (RMSE of 0.08 Å). The encouraging aspect is that MP2/G3-Large single point energies at the SCC-DFTBPR structures are overall close to the reference (MP2/G3-Large//B3LYP/6-31+G(d,p)) values, with a RMSE of merely 1.4 kcal/mol. Large errors more than 2 kcal/mol occur very rarely, which suggest that the SCC-DFTBPR structures are usually satisfactory.

Table 6.

Errors in the SCC-DFTBPR optimized structures for species involved in the hydrolysis reactions included in the parameterization^a

		Error Analysisb
Structures	Propertya
		MAXE	RMSE	MUE	MSE
Stable states	P-Oc	0.41/−0.12	0.05/0.02	0.02/0.02	0.00/0.00
	O-P-Od	−11.8/7.8	2.3/1.9	1.4/1.3	−0.1/0.0
	P-ONu e	−0.40/−0.04	0.14/0.02	0.07/0.02	−0.03/0.01
Transition states	P-OLg f	−0.33/0.18	0.15/0.08	0.10/0.05	0.03/0.04
	P-O g	0.07	0.02	0.02	0.00
	O-P-Oh	11.5/6.5	2.9/2.5	2.0/1.9	0.0/−0.2

^a)The reference structures are optimized at the B3LYP/6-31+G(d,p) level. Bond distances are in Å and bond angles are in degrees.

^b)The errors are defined in the same manner as in Table 3.

^c)The number before the slash is the overall performance; the number after the slash excludes one extreme deviation from int1_2 of DMP.

^d)The number before the slash is the overall performance; the number after the slash excludes one extreme deviation from int1 of DMP.

^e)The distance between P and the nucleophilic oxygen (“O^Nu”); the number before the slash is the overall performance; the number after the slash excludes extreme deviations from ts1_2 and ts1_da of MMP.

^f)The distance between P and the key oxygen in the leaving group (“O^Lg”); the number before the slash is the overall performance; the number after the slash excludes one extreme deviation from ts2 and ts1_da of MMP.

^g)The distances between P and oxygen atoms not involved in the nucleophilic attack or the leaving group.

^h)The number before the slash is the overall performance; the number after the slash excludes one extreme deviation from ts1_2 of MMP.

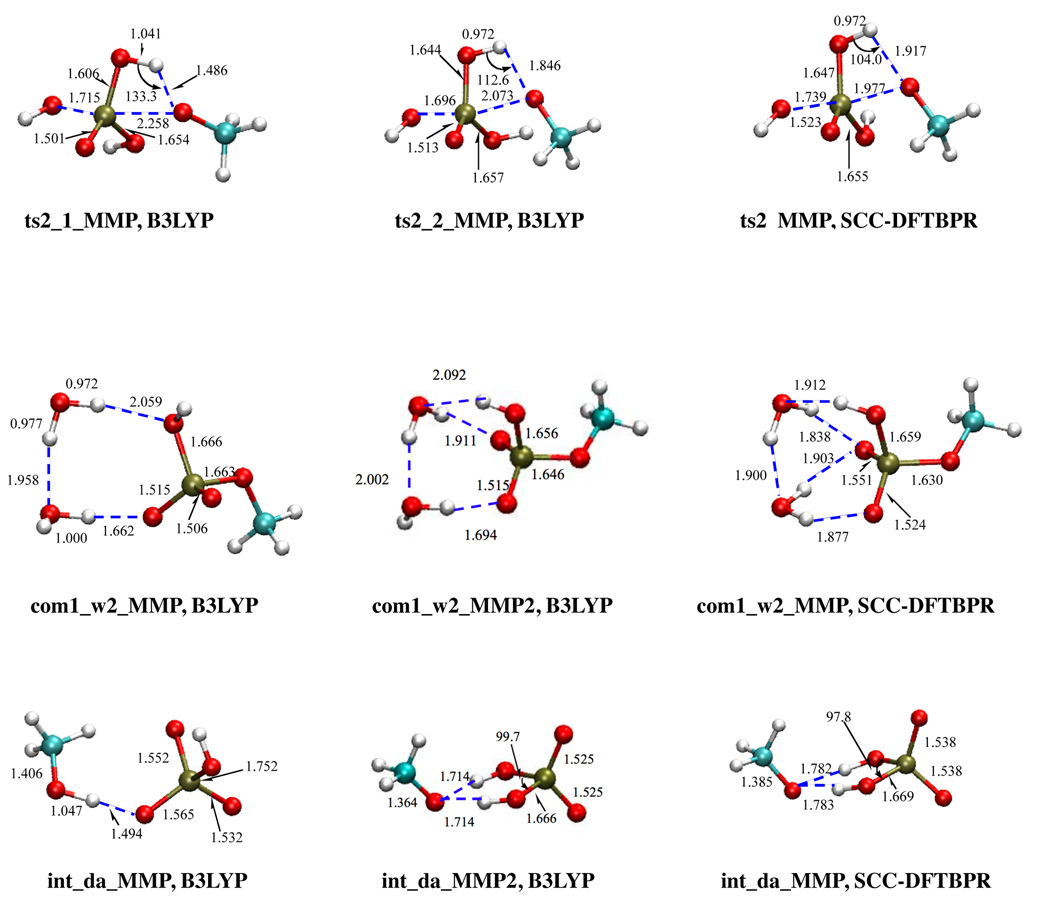
There are, however, cases where notable differences between SCC-DFTBPR and B3LYP results are observed. For the second step of MMP hydrolysis along the associative pathway (int1_2→com2), two pathways are obtained at the B3LYP/6-31+G(d,p) level with energy barriers of 9.9 and 3.7 kcal/mol, respectively, and differ in the orientation of the OH group in the equatorial plane of the phosphorane-like transition state (see Fig.2). When the OH forms a hydrogen-bond to the leaving group (-OCH₃), the corresponding transition state has a lower energy. At the SCC-DFTBPR level, however, only one transition state is obtained despite numerous attempts; the corresponding OH group is oriented in a position that is approximately the average of those in the two B3LYP transition states. For the dianionic species, the product-like complex (int_da_MMP in Fig.2) at the B3LYP level is featured with a very strong and short (1.494 Å) hydrogen bond between CH₃OH and ${\text{HPO}}_4^{2-}$. At the SCC-DFTBPR level, however, the proton on CH₃OH is transferred to ${\text{HPO}}_4^{2-}$ , which leads to a very different structure; interestingly, B3LYP optimization starting from the SCC-DFTBPR geometry led to a very similar structure, which is in fact lower than the original B3LYP structure by ~2.9 kcal/mol. The similar behavior is found for the molecular complex between two water and MMP, (com1_w2), where B3LYP optimization starting from SCC-DFTBPR geometry led to a structure with lower energy (~ 2 kcal/mol) than the original B3LYP structure. These findings not only confirm the robustness of SCC-DFTBPR for structural properties but also highlight the value of a fast method in exploring conformational space.

FIG. 2.

Structures for which significant discrepancy is found between independent B3LYP/6-31+G** and SCC-DFTBPR geometry optimizations. For com1_w2_MMP and int_da_MMP, B3LYP optimization starting from SCC-DFTBPR geometry located structure closer to the SCC-DFTBPR result and lower in energy than the original B3LYP structure. See main text (Sect. 3.3) for discussions. Distances are in Å angles in degrees.

D. Additional benchmark calculations with the QCRNA database

For the large number of energetics data points studied here (56 reaction energies and 47 barriers), single point values at the standard second-order SCC-DFTB level have larger errors (see Table 7 for a summary and Supporting Materials for details); the largest error is −24.6 kcal/mol and the RMSE is 10.3 kcal/mol. Similar errors are found when the structures are optimized (only for stable states). With SCC-DFTBPR, the errors are substantially smaller; for single point energetics, the largest error is 14.4 kcal/mol and the RMSE is only 5.6 kcal/mol. When the structures are optimized for the stable states, the corresponding values are 14.8 kcal/mol (see below) and 5.3 kcal/mol, respectively, which are rather encouraging. The RMSEs in the optimized P-O distances and O-P-O angles are 0.035 Å and 2.2 degree, respectively. The dipole moment for the structures are well described with both the second-order SCC-DFTB and SCC-DFTBPR, with RMSEs on the order of 0.5 Debye.

Table 7.

Benchmark results for SCC-DFTB for the 19 Phosphate Reactions from the QCRNA Database^a

		Error Analysisb
State	Propertyc
		MAXE	RMSE	MUE	MSE
Overall	Energy SP (2nd-order)e	−24.6	10.3	8.2	−6.0
	Energy SP (SCC-DFTBPR)	14.4	5.6	4.8	−0.2
Stable States	Energy SP (2nd-order)	−23.9	9.9	7.9	−4.6
	Energy SP (SCC-DFTBPR)	14.4	5.3	4.3	1.0
	Energy OPT (2nd-order)	−27.2	11.8	9.1	−6.1
	Energy OPT (SCC-DFTBPR)	14.8	5.3	4.5	−0.8
	P-O (Å) OPT (SCC-DFTBPR)d	0.45/0.19	0.07/0.035	0.03/0.02	0.00/0.00
	O-P-O (°) OPT (SCC-DFTBPR)e	−9.3	2.2	1.5	0.0
Transition states	Energy SP (2nd -order)	−24.6	10.6	8.7	−7.5
	Energy SP (SCC -DFTBPR)	12.8	6.0	5.4	−1.6
Dipole Moment f	2nd -order)	−1.2/−1.2	0.6/0.6	0.5/0.5	−0.4/−0.4
	SCC-DFTBPR	0.8/1.1	0.3/0.5	0.2/0.3	0.1/0.1

^a)The reference values are from the B3LYP calculations included in the QCRNA database (http://theory.chem.umn.edu/QCRNA/). The energies are in kcal/mol and dipole moments in Debye. For specific values, see Supporting Materials.

^b)The errors are defined in the same manner as in Table 3.

^c)“Energy” refers to reaction energy (energy relative to the reactant state); “SP” represents single point calculation at the QCRNA structures; “OPT” indicates full geometry optimization at the relevant SCC-DFTB level with the B3LYP reference structure as the initial guess.

^d)The number before the slash is the performance including all the P-O distances (in total, 327 P-O distances are studied); the number after the slash excludes one parameter from C6H5OH…P(O)(O)(-O-sugar-O-)_min2, (CH3)2CHOH…P(O)(O)(-O-sugar-O-)_min3, CH3OH…P(O)(O)(-O-CH2CH2-O-)_min3, CH3OH…P(O)(O)(-O-sugar-O-)_min3, HOH…P(O)(O)(-O-2'methyl-sugar-O-)_min3a, HOH…P(O)(O)(-O-CH2CH2-O-)_min3; the notation scheme follows the QCRNA convention (http://theory.chem.umn.edu/QCRNA/Nomenclature.html).

^e)In total, 568 O-P-O angles are analyzed.

^f)Numbers before slashes are from single point calculations at the DFT geometries from the QCRNA database; those after the slashes are after geometry optimization at the respective SCC-DFTB levels. The reference values are from QCRNA database at the level of B3LYP/6-311++G(3df,2p)//B3LYP/6-31++G(d,p).

Detailed analyses of results indicate that all larger errors (> 15 kcal/mol) in the standard SCC-DFTB approach occur in reactions that involve OH⁻ as a reactant, such as OH⁻ …P(O)(OCH₃)(-O-CH₂CH₂-O-) and OH⁻ … P(O)(OCH₃)(OCH₃)(OCH₃). With the third-order terms, the errors in those reactions typically reduce significantly to merely a few kcal/mol (for details, see Table S1 in Supporting Materials). The largest error at the SCC-DFTBPR level, 14.8 kcal/mol, is found for the exothermicity for the reaction between OH⁻ and P(O)(OH)(OH)(OCH₃), which has a very large value of −60.7 kcal/mol at the B3LYP/6-311++G(3df, 2p) level.

E. MMP hydrolysis with SCC-DFTBPR/MM simulations

1. Associative mechanism

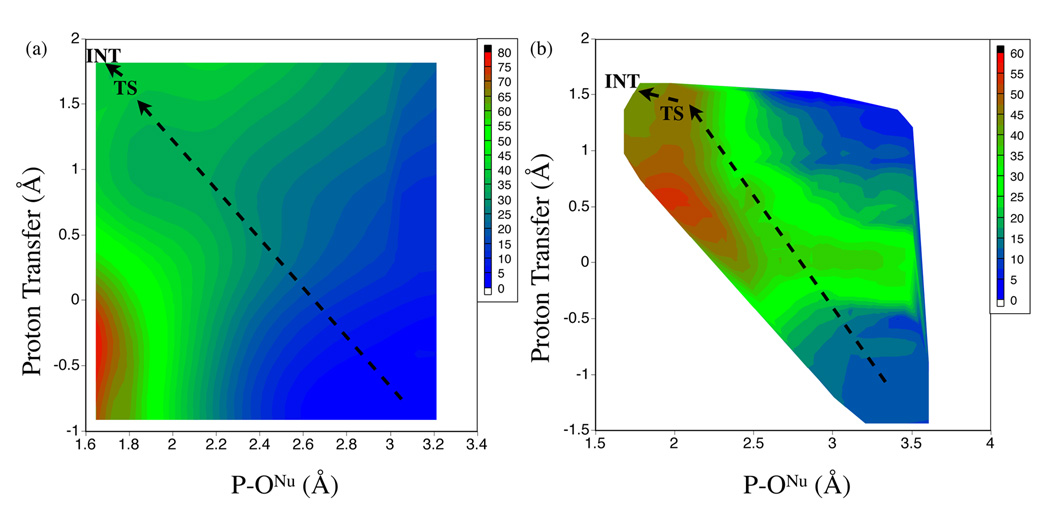
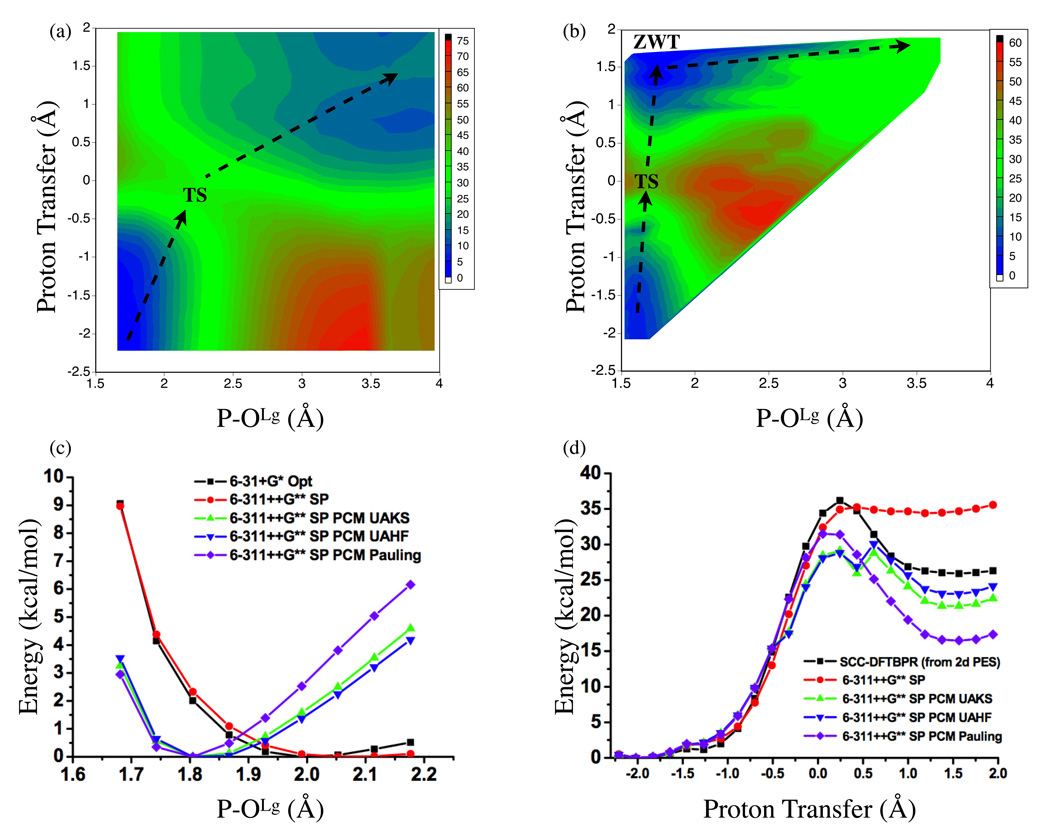
In the gas phase, the two-dimensional PES (Fig.3a) shows a high barrier of ~ 33 kcal/mol, which is consistent with the results of transition state optimization at the same SCC-DFTBPR level (32.1 kcal/mol, com1→ts1, Table 5). The transition state and intermediate regions are very flat on the two-dimensional PES, which is also seen in the optimization calculations; the intermediate is lower than the transition state by 0.1 kcal/mol at the SCC-DFTBPR level, and 0.4 kcal/mol at the B3LYP/6-31+G** level. The shape of the two-dimensional PES makes it clear that a strictly step-wise mechanism, in which the proton is first transferred to MMP to generate the nucleophilic hydroxide, is not energetically favorable. This is confirmed by comparing the adiabatic energy profile along the proton transfer coordinate with the P-O^Nu fixed at 3.0 Å at the SCC-DFTBPR and B3LYP/6-311++G**//SCC-DFTBPR levels. The results are purely uphill and numerically close at the two levels of calculations (data not shown); for example, at the proton transfer (anti-symmetric stretch) coordinate of −0.2, 0.2 and 0.4 Å, respectively, the B3LYP result is lower than SCC-DFTBPR by 0.8, 3.2 and 4.0 kcal/mol, respectively.

FIG. 3.

SCC-DFTBPR results (energies in kcal/mol) for the first step of the associative pathway for the hydrolysis of monomethyl phosphate (MMP). (a) Two-dimensional potential energy surface from adiabatic mapping calculations in the gas phase using SCC-DFTBPR. (b) Two-dimensional potential of mean force from umbrella sampling in solution using a SCC-DFTBPR/MM model. The O^Nu stands for the nucleophilic oxygen in water (see Scheme I), the proton transfer coordinate is the antisymmetric stretch that describes the proton transfer between the nucleophilic water and the basic oxygen in MMP.

In the solution phase, an equally late transition state is identified on the two-dimensional PMF (Fig.3b) with a barrier of ~ 34 kcal/mol. Clearly, solvation does not stabilize the transition state over the reactant in any major way in the associative pathway, which is reasonable since there is no major difference between the dipole moment of the transition state and the reactant complex; at the SCC-DFTBPR level, the values are 6.9 and 6.2 Debye for the reactant and transition state, respectively. Our value is close to the finding of Florian et al., who obtained a barrier of ~35 kcal/mol using a Langevin dipole model for solvation and structures from gas-phase reaction path optimizations.¹⁶

2. Dissociative mechanism

Without the “proton relay” mediated by water molecules, the first step of the dissociative pathway involves an intramolecular proton transfer to the leaving group, generating a complex between metaphosphate and methanol. In the gas-phase, the two-dimensional PES (Fig.4a) clearly shows a saddle point in which the proton is equally shared between the metaphosphate and the leaving group oxygen (proton transfer coordinate ~−0.1–0.0 Å) and the distance between the leaving group and phosphorus significantly lengthens by ~0.4 Å relative to MMP. The barrier is about 35 kcal/mol, which is close to the result of transition state search (com1→diss_tsa in Table 5) at both the SCC-DFTBPR (34.2 kcal/mol) and MP2 (36.8 kcal/mol) levels.

FIG. 4.

SCC-DFTBPR results (energies in kcal/mol) for the first step of the dissociative pathway for the hydrolysis of monomethyl phosphate (MMP). (a) Two-dimensional potential energy surface from adiabatic mapping calculations in the gas phase using SCC-DFTBPR. (b) Two-dimensional potential of mean force from umbrella sampling in solution using a SCC-DFTBPR/MM model. The O^Lg stands for the oxygen in the leaving group (see Scheme I), which is methanol in this case; the proton transfer coordinate is the antisymmetric stretch that describes the intramolecular proton transfer between the protonated oxygen in MMP and O^Lg. (c) Adiabatic mapping along the P-O^Lg distance with the proton transfer coordinate fixed at 0.0; structures are partially optimized at the B3LYP/6-31+G(d) level in the gas-phase, followed by single point continuum solvent calculations with the 6-311++G(d,p) basis and various sets of radii. (d) Adiabatic mapping along the proton transfer coordinate with the P-O^Lg distance fixed at ~1.824 Å; here structures are optimized with SCC-DFTBPR, followed by single point energy calculations at the B3LYP level in both gas-phase and continuum solvent model.

In solution, the two-dimensional PMF (Fig.4b) points to a transition state with a similar shared-proton feature but more compressed P-O^Lg distance of 1.7–1.8 Å. Physically speaking, the observed shift in the P-O^Lg distance in the transition state upon solvation is to be expected. Without breaking the P-O^Lg bond, the intra-molecular proton transfer leads to a species with significant charge separation, which is much better stabilized in solution than in the gas phase. Therefore, the transition state in the gas-phase has a substantially longer P-O^Lg distance than in solution. To quantitatively verify the solvation effect on the transition state structure observed in the SCC-DFTBPR based calculations, an adiabatic mapping scan in the gas phase along the P-O^Lg distance is first performed with the antisymmetric stretch proton transfer coordinate constrained at 0.0 Å; all other degrees of freedom are optimized at the B3LYP/6-31+G* level. Single point B3LYP/6-311++G** energies at these partially optimized structures are then compared between gas-phase and implicit solvent (PCM) calculations. As shown in Fig.4c, an energy minimum is found around the P-O^Lg distance of 2.0–2.1 Å in the gas phase, which is consistent with the 2d-PES shown in Fig.4a. With the implicit solvent model, however, the position of the energy minima along P-O^Lg is shifted to be around 1.8 Å, regardless of the atomic radii used in the B3LYP-PCM calculations. Therefore, the SCC-DFTBPR based results are consistent with B3LYP calculations in both the gas phase and solution, which is very encouraging.

The solution PMF barrier calculated at the SCC-DFTBPR/MM level is about 32 kcal/mol (Fig.4b), which is consistent with previous results obtained using various implicit solvent models. For example, Warshel and coworkers found a barrier of 34 kcal/mol by using MP2/6-31+G(d,p) energies and the Langevin dipole model for solvation;¹⁶ Bianciotto et al.⁹⁰ obtained a barrier of 33.5 kcal/mol using B3LYP and a modified double-ζ plus polarization valence basis set along with the PCM solvation model.

Despite these encouraging aspects of the SCC-DFTBPR/MM calculations, an unexpected feature is observed in the PMF. As shown in Fig.4b, a very low-energy region is found in the left-upper corner of the 2d-PMF, which corresponds to a zwitterionic intermediate. In fact, the current PMF calculations predict that this zwitterionic species is even more stable than the reactant state by ~ 3 kcal/mol. Such a zwitterionic intermediate has been discussed in the computational study of Bianciotto et al.,^90,91 who argued that the dissociative mechanism of the MMP hydrolysis in solution may follow a step-wise pathway that involves a stable zwitterionic intermediate produced by intramolecular proton transfer to the leaving group. Using B3LYP-PCM and a double-ζ plus polarization quality basis, Bianciotto et al. predicted that such an intermediate is ~ 21.2 kcal/mol higher than the reactant, which is at odds with the current SCC-DFTBPR/MM result.

Since the zwitterionic type of species has not been considered in the development of SCC-DFTBPR, it is possible that the stability of this structure is overestimated at the SCC-DFTBPR/MM level. To better understand the situation, several sets of calculations are carried out.

First, to explore the intrinsic performance of SCC-DFTBPR, adiabatic mapping calculations are carried out for MMP in the gas phase along the proton transfer coordinate while holding the P-O^Lg distance fixed at 1.824 Å. At these partially optimized structures at the SCC-DFTBPR level, B3LYP/6-311++G** single-point energy calculations are carried out in both the gas phase and with the PCM model for solution. In the gas phase, as shown in Fig.4d, SCC-DFTBPR and B3LYP agree well for the antisymmetric proton transfer coordinate below 0.4 Å; the agreement deteriorates quickly as the PT coordinate further increases. For example, with the proton transfer coordinate of 2.0 Å, the SCC-DFTBPR energy is lower than the B3LYP value by as much as 9 kcal/mol. At the B3LYP level, with the PCM model describing solvation, the partially optimized zwitterionic species varies in the range of 18–24 kcal/mol above the reactant, depending on the radii used; these values are largely consistent with the result of Bianciotto et al.^90,91, indicating that the SCC-DFTBPR structures are quite promising.

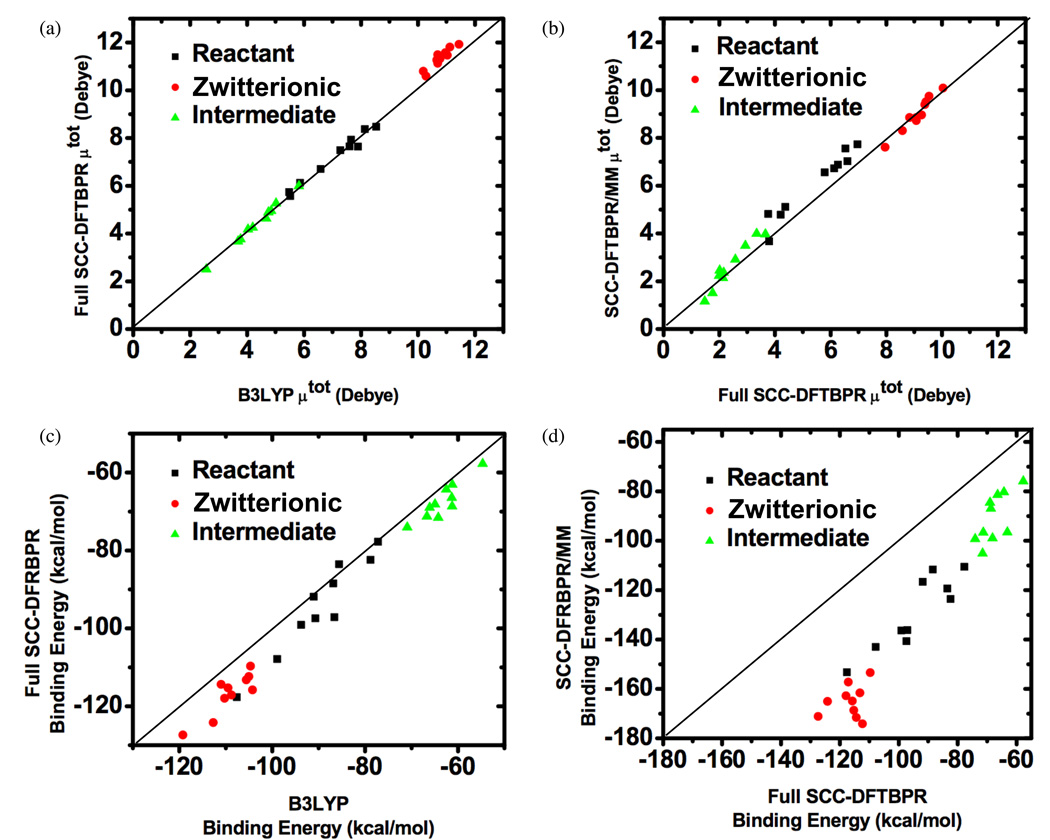
The ~ 9 kcal/mol error in the SCC-DFTBPR result for the zwitterionic species in the gas-phase doesn’t explain the significantly overestimated stability in solution by the SCC-DFTBPR/MM simulations. In fact, this discrepancy suggests that the current SCC-DFTBPR/MM simulations have significantly unbalanced treatment of solute-solvent interactions between the reactant and the zwitterionic species, with the latter significantly over-stabilized. This can be caused either by large errors in the predicted charge distribution (e.g., dipole moment) in the zwitterionic structure, or by non-optimal van der Waals parameters for the QM atoms used in the current simulations. To distinguish the two possibilities, we study the binding energies of the solute with nearby water molecules (~9–11) in the reactant (MMP), zwitterionic and “intermediate” (metaphosphate with a weakly bound methanol) states; for each case, 10 snapshots are taken from SCC-DFTBPR/MM trajectories. As shown in Fig.5a, the dipole moment of the solute at the SCC-DFTBPR level correlates very well with B3LYP/6-311++G** result, regardless of the chemical state of the solute. The dipole moment of the solute-water cluster is not sensitive to whether the water molecules are treated as MM or QM (Fig.5b). We do note, however, that the magnitude of charge separation in the zwitterionic state is substantially higher at the SCC-DFTBPR/MM level; e.g., the average net Mulliken charge on the metaphosphate is −1.54 with SCC-DFTBPR/MM, as compared to the value of ~−1.15 with full SCC-DFTBPR, and the value of ~−0.95 based on B3LYP NBO charges. Therefore, the electronic structure (or electron distribution) seems adequately described at the SCC-DFTBPR level even for the zwitterionic species and the MM treatment of the nearby solvent causes a higher degree of polarization in the solute.

FIG. 5.

Additional analysis for the reliability of the SCC-DFTBPR approach for the dissociative pathway in MMP hydrolysis. (a–b) Dipole moment of the solute in different chemical states (MMP, zwitterionic and intermediate state) calculated at different levels. (c–d) Binding energy between the solute and nearby water molecules (within the first solvation shell, see Fig. S10 in the Supporting Materials for the computed solvent distribution function) at different levels; SCC-DFTBPR/MM refers to calculations in which the solute is treated with SCC-DFTBPR and the water with MM, while SCC-DFTBPR and B3LYP indicates calculations where both the solute and water molecules are treated as QM.

The total binding energy between the solute and nearby water molecules, however, is significantly overestimated at the SCC-DFTBPR/MM level, especially when the solute is in the zwitterionic state (Fig.5c). In the MMP state, the average interaction between the solute and nearby water molecules is −129.1 kcal/mol with SCC-DFTBPR/MM, which is significantly larger than the value of −94.3 (−89.7) kcal/mol when all atoms are described with SCC-DFTBPR (B3LYP/6-311++G**); for the zwitterionic state, the corresponding values are −165.1, −116.7 and −109.1 kcal/mol. In other words, the MM treatment of the nearby water molecules preferentially stabilizes the zwitterionic species by almost 20 kcal/mol [e.g., (165.1-129.1)−(109.1-89.7)~ 17 kcal/mol!], which explains why the zwitterionic species is overstabilized in the SCC-DFTBPR/MM simulations. Therefore, these results vividly demonstrate that the quantitative accuracy of QM/MM simulations for reactions involving significant charge redistributions relies very sensitively on the treatment of QM/MM interactions. We emphasize that this is not a straightforward problem to “fix” by simply refitting the van der Waals parameters for the QM atoms based on simple solute-water dimers as commonly done in the literature;^21,82 in fact, such fitted QM van der Waals parameters are found to be very similar to the set used here in a recent QM/MM study of phosphoryl transfer reaction in water and tert-butanol solutions.⁷⁶ For highly charged solutes, the errors are due to the accumulative effects of a large number of solute-solvent interactions (e.g., more than 8 hydrogen bonds are involved in the MMP-water clusters studied here), thus a balanced treatment of QM/MM interactions over different chemical states of the solute likely calls for more sophisticated approaches that allow the QM non-bond parameters to vary during the reaction.⁸³ Another possibility is that the QM/MM interaction is better represented by a Klopman-Ohno form, which is substantially damped at the intermediate and short distances and more consistent with the way that charge-charge interactions are treated for the QM atoms in SCC-DFTB.⁶⁰ The simple Coulombic form is used in the integration of second-order SCC-DFTB with MM because this combination empirically compensates for the fact that SCC-DFTB Mulliken charges tend to be too low;^48,82 with modified Mulliken charges at the third-order level, however, it is possible that the Klopman-Ohno form becomes more appropriate. We leave the systematic analysis of these possibilities to future work (however, see Supporting Materials for some preliminary results). Along this line, it is encouraging to observe that the differential solute/solvent interaction between MMP and the zwitterionic species at the SCC-DFTBPR level (i.e., nearby water also treated as QM), −22.4(=94.3–116.7) kcal/mol, is very close to the value of −19.4(=89.7–109.1) kcal/mol at the B3LYP/6-311++G** level, which suggests that an attractive alternative is to treatment the first solvation shell at the QM level⁹⁷ and that SCC-DFTBPR seems adequate in this regard. A technical challenge for such calculations, however, is that the QM/MM interface needs to be updated in an adaptive fashion during the simulation^98–101, which in fact is not problematic if only thermodynamic quantities are of interest.

In summary, the combination of gas-phase adiabatic mapping, solution QM/MM PMF calculations and comparison to relevant B3LYP calculations in the gas-phase or with implicit solvent models indicate that the SCC-DFTBPR approach gives reliable structures, including transition states for both associative and dissociative pathways and the zwitterionic inter-mediate in the dissociative pathway. For structures with similar charge distributions (e.g., dipole moment), the SCC-DFTBPR/MM simulations give rather satisfying energetics as well; for describing the relative energetics of species with very different charge distributions, however, a simple treatment of the solute/solvent interaction at the traditional QM/MM level may not be sufficient.

IV. CONCLUSIONS

Despite extensive efforts from both experimental and theoretical studies, the precise mechanism of phosphate chemistry such as phosphate hydrolysis and phosphoryl transfer remains controversial. This is a major challenge to tackle because phosphate chemistry plays a key role in many essential biological processes such as energy/signal transduction and synthesis of protein and nucleic acids. From a theoretical stand point, the key is to develop effective computational methods that can balance accuracy and sampling efficiency, which, with the typical computational hardware, naturally points to the development of semi-empirical methods. There have been several such models established in recent years for specific types of phosphate reactions^30,33,34 based on the traditional NDDO framework although their general applicability still remains to be fully explored.

In this work, we make an attempt to parameterize an approximate density functional theory, SCC-DFTB, as an alternative approach for studying the chemistry of phosphorus containing systems in solution and biological systems. This is motivated by the recent success of SCC-DFTB for studying the structural and energetics of biological systems.^25,52,59 It is found that although a standard second-order formulation of SCC-DFTB gives good geometries compared to high-level density functional theories, further extensions are needed to obtain reliable proton affinity and reaction energies. Including the on-site third-order terms is found to improve the proton affinity significantly, although it remains difficult to obtain accurate proton affinity for both phosphorus containing compounds and those that do not contain phosphorus; it is possible that off-diagonal third-order terms are needed to resolve such difficulty. As a pragmatic approach, we have developed two sets of “reaction specific” parameterizations; SCC-DFTBPA for proton affinity of phosphates and SCC-DFTBPR for phosphate hydrolysis. The number of “reaction specific” parameters, however, is small (7 in total for O, N, C, H and P) and therefore SCC-DFTBPR is likely applicable to a broader set of phosphate reactions.

Benchmark calculations in the gas-phase and solution with a QM/MM framework indicate that the current parameterizations, particularly SCC-DFTBPR, generally give reliable structures and semi-quantitative energetics (e.g., with a RMSE of ~ 3–5 kcal/mol compared to high-level calculations). Therefore, these methods are attractive choices for exploring the gross features of the potential energy surfaces of condensed phase systems and for identifying amino acids and/or structural fluctuations that play an important role in controlling the chemical step.⁵ Higher level QM/MM calculations are still required for more quantitative understanding, although the number of variables in these much more expensive calculations can be substantially reduced by SCC-DFTB(PR) based studies. The solution phase bench-mark study for the zwitterionic species in the dissociative pathway of MMP hydrolysis also underlines the importance of carefully handling solute/solvent interactions for reactions involving highly charged species, which may require sophisticated treatment of van der Waals parameters for the QM atoms or describing the first solvation shell of the solute with a QM approach. Quantitative analysis along these lines and systematic comparison of the new SCC-DFTB models to NDDO based models for phosphate chemistry^30,33,34,102 remain important goals for the near future.

Supplementary Material

1_si_001. Supporting Materials.

The structures for all molecules (optimized at the SCC-DFTBPR level) involved in the parameterization process are included. The solvent radial distribution functions near MMP from SCC-DFTBPR/MM simulations are also included. Detailed comparison (energetics and dipole moment) of the second-order SCC-DFTB and optimized SCC-DFTBPR for selected molecules in the QCRNA databse is summarized.