Abstract
We introduce a novel algorithm for the design of fast slice-selective spatially-tailored magnetic resonance imaging (MRI) excitation pulses. This method, based on sparse approximation theory, uses a second-order cone optimization to place and modulate a small number of slice-selective sinc-like radio-frequency (RF) pulse segments (“spokes”) in excitation k-space, enforcing sparsity on the number of spokes allowed while simultaneously encouraging those that remain to be placed and modulated in a way that best forms a user-defined in-plane target magnetization. Pulses are designed to mitigate B1 inhomogeneity in a water phantom at 7 T and to produce highly-structured excitations in an oil phantom on an eight-channel parallel excitation system at 3 T. In each experiment, pulses generated by the sparsity-enforced method outperform those created via conventional Fourier-based techniques, e.g., when attempting to produce a uniform magnetization in the presence of severe B1 inhomogeneity, a 5.7-ms 15-spoke pulse generated by the sparsity-enforced method produces an excitation with 1.28 times lower root mean square error than conventionally-designed 15-spoke pulses. To achieve this same level of uniformity, the conventional methods need to use 29-spoke pulses that are 7.8 ms long.
Keywords: B1inhomogeneity mitigation, high field strength, magnetic resonance imaging (MRI) radio-frequency (RF) pulse sequence design, parallel transmission, sparse approximation, three-dimensional (3-D) RF excitation
I. Introduction
SLICE-SELECTIVE radio-frequency (RF) excitation pulses are ubiquitous throughout magnetic resonance imaging (MRI). They are widely used to excite only those magnetic spins within a thin slice of tissue while leaving spins outside the slice in alignment with B0, the system's magnetic main field. This type of excitation is extremely useful because it simplifies the encoding stage of the MRI experiment by permitting the system to record and reconstruct an image from only two dimensions of data. RF pulses that are not only able to excite a thin slice, but able to spatially-tailor the in-plane excitation (i.e., produce a varying in-plane flip angle) are also highly useful because they are able to reduce field of view (FOV) requirements in dynamic imaging applications [1], decrease susceptibility artifacts in functional MRI [2], and mitigate transmit profile inhomogeneity occurring at high field [3].
A. Spoke-Based Slice-Selective Pulses
In this work we focus on a class of slice-selective pulses comprised of segments that resemble sine cardinal (sinc) functions, which are applied in the presence of oscillating z gradients. We refer to these pulse segments as “spokes” [3]-[5] because as each is played, its trajectory in k-space is a straight line. These pulses rely on the small-tip angle approximation, where a Fourier relationship (approximately) holds between the energy deposited by the RF pulse and the resulting transverse magnetization, giving rise to excitation k-space [6]. In this regime, a rectangle-like slice profile along a logical z axis is achieved by placing a sinc-like RF pulse segment (a spoke) in the kz direction of excitation k-space [7]. In practice, a true sinc function along kz is replaced by a finite-length waveform [8], e.g., a Hanning-windowed sinc [5]. The time-bandwidth product of the pulse segment and its extent in kz influence the thickness and transition edges of the resulting thin-slice excitation.
Playing a single sinc-like spoke at (kx, ky) = (0, 0) (dc) in k-space is one way to excite a thin slice. This approach, where each of the system's excitation channels encodes a single amplitude and phase along the spoke, is known as RF shimming [4], the goal of which, typically, is to mitigate an inhomogeneous B1 field profile. A single frequency sample in (kx, ky), however, does not provide any ability to tailor the resulting in-plane excitation pattern when using a single-channel excitation system; even with a multichannel excitation system, significant tailoring is not possible with this approach. To strongly influence the in-plane excitation flip angle in each of these cases, one must place a number of spokes at various locations in (kx, ky), modulating the amplitude and phase of each to form a desired in-plane transverse magnetization [3]. Unlike RF shimming, this approach does not alter the B1 field profile—rather, it is the gradient modulation of the excitation process that produces the desired magnetization. In this multiple-spoke case, the complex weightings in (kx, ky) form the in-plane excitation, while the sinc-encoded kz traversals provide slice selectivity in z. Simultaneous slice selection and in-plane tailoring are possible due to the separability of the 3-D Fourier transform that relates the spatial excitation to the deposition of energy in k-space. Unfortunately, using multiple spokes has the negative consequence of increasing pulse duration. Thus, an ideal spoke-based pulse is one that not only achieves the user-specified in-plane excitation, but does so using as few spokes as possible.
B. Spoke-Based Pulse Applications
To date, spoke-based waveforms (also referred to as echo-volumnar trajectories) have been used to mitigate B1 inhomogeneity on a single-channel excitation system at 3 T [3] and perform spatially-tailored slice-selective excitations on multichannel excitation systems [5], [9]-[11]. In these cases, only small numbers of spokes were placed at low spatial frequencies because only smoothly-varying in-plane excitations were necessary.
There are many applications, however, where more than a few spokes are needed. For example, 25-spoke pulses were needed for signal recovery in -weighted functional MRI [12]. Another application of multispoke pulses is the mitigation of B1 inhomogeneity [13] that occurs in the human body at 4 T [14] and in the head at 7 T due to wavelength interference effects [15], [16] and tissue-conductive RF amplitude attenuation [17]. The presence of B1 inhomogeneity causes a system's transmit and receive profiles to exhibit high-frequency spatial variations. The nonuniformity of the transmit profile causes standard slice-selective pulses to produce a nonuniform flip angle across space, one that varies widely throughout the field of excitation (FOX), causing images to exhibit severe center-brightening, spatial contrast variation, and SNR nonuniformity despite the use of “homogeneous” excitation and reception coils [18]-[20]. In this situation, an ideal slice-selective mitigation pulse is one that produces a spatially-tailored excitation across the FOX that is the exact multiplicative inverse of the inhomogeneity, strongly flipping those regions where the B1-effect causes under-flipping of the magnetization and vice versa, such that when the pulse is applied, a uniform flip angle arises across the FOX. In practice, forming such a high-spatial-variation excitation requires spokes to be placed with care at both low and high frequencies throughout (kx, ky).
C. Conventional Spoke Placement
One way to achieve a desired high-variation in-plane excitation is to place a large number of spokes throughout (kx, ky), but this leads to lengthy, impractical pulses. A more intuitive approach is to compute the Fourier transform of the desired in-plane excitation and place spokes at (kx, ky) frequencies where the Fourier coefficients are largest in magnitude [12], [21]. We will show shortly, however, that this method yields suboptimal placements.
D. Sparsity-Enforced Spoke Placement
In this paper we introduce a spoke-based pulse design framework based on sparsity and simultaneous sparsity [22]-[27]. Our method is applicable to all of the problems mentioned above, yet general enough to apply to both conventional single-channel and multichannel parallel transmission systems [5], [9]-[11], [28], [29]. In our approach, we pose optimization problems that determine the minimal number of spokes needed to produce a user-defined in-plane excitation, the placement of these spokes in (kx, ky), and their proper amplitudes and phase modulations. For computational tractability, we use a convex relaxation [25], [26], [30]-[32], formulating a second-order cone (SOC) program [33] that promotes sparsity on a (kx, ky) grid of candidate spoke locations. This sparsity-enforcement algorithm discourages the use of many spokes while simultaneously encouraging those that remain to be placed and modulated in a way that best achieves the desired in-plane excitation. Preliminary results of this technique were presented in [34] and [35]. This design method automates spoke-based RF pulse design and frees the designer from the task of spoke placement. The method has several control parameters that allow designers to easily trade off pulse duration (number of spokes) with excitation fidelity (squared error relative to a target). This technique automatically generates echo-volumnar thin-slice excitation pulses, differing greatly from other automated design algorithms that optimize 2-D trajectories and produce pulses incapable of slice selection [36].
E. Overview of Experiments
The utility of the sparsity-enforced spoke placement method is demonstrated by conducting a B1 mitigation experiment in a head-shaped water phantom on a human scanner at 7 T, along with a spatially-selective excitation experiment on an eight-channel parallel transmission system at 3 T. In each experiment, the sparsity-enforced placement algorithm is compared to the conventional Fourier-based placement method and to an extension of the latter, which we call “inversion-based” placement. After demonstrating the superior performance of the sparsity-enforced placement algorithm, we proceed to characterize it in detail by exploring its sensitivity to its control parameters. Results for these various experiments are first obtained via Bloch-equation simulations and then validated with trials on the 7 T and 3 T systems; thus the sparsity-enforced method is investigated in both theory and practice.
F. Organization of the Paper
Section II covers background material on parallel excitation systems, RF excitation pulse design, transmit and receive profile estimation, and sparse approximation. Section III presents the conventional Fourier-based spoke placement method, the inversion-based technique, and the proposed sparsity-enforced algorithm. Section IV discusses how to design a set of RF pulses and gradients based on a chosen spoke placement pattern. Section V describes the 7 T and 3 T systems and their associated experiments, while Section VI presents and discusses the experimental results. Concluding remarks appear in Section VII.
II. Background
A. Parallel Excitation RF Pulse Design
1) System Overview
A parallel excitation system differs from a standard single-channel system in that its RF excitation coil is comprised of multiple elements, each capable of independent, simultaneous transmission. The presence of multiple elements allows one to undersample a given excitation trajectory and yet in many cases still form a high-fidelity version of the desired excitation; undersampling the trajectory is greatly beneficial because it reduces the distance one travels in k-space, which in turn reduces the duration of the corresponding pulse [5], [9]-[11], [28], [29]. This ability to “accelerate” in the Fourier domain and reduce pulse duration arises due to the extra degrees of freedom provided by the system's multiple transmit elements, in direct analogy with the concept of readout-side acceleration where the use of multiple reception coils permits one to undersample readout k-space and substantially reduce readout time [37], [38]. We now describe one way to design a set of P RF pulses to play through the elements of a P-channel parallel excitation system in order to generate a user-defined target excitation. This formulation, largely due to Grissom et al. [39], holds for P ≥ 1 and thus applies to both single- and multichannel systems.
2) Linearization
To establish a design methodology for RF pulses, assume for now that the set of gradient waveforms, G(t) = [Gx(t), Gy(t), Gz(t)]T, is fixed, i.e., the k-space trajectory, k(t) = [kx(t), ky(t), kz(t)]T, is predetermined, and that the spatial transmit profile (a map) of each array element is known. Finally, in order to make the design process tractable, we impose the small-tip angle approximation on the problem, enabling a Fourier-based design [6]. This results in the following system of linear equations:
| (1) |
where M0is the steady-state magnetization, r = [rx, ry, rz]T a spatial variable, t a temporal variable (sec), m(r) the approximate transverse magnetization due to the transmission of the RF pulses in the presence of the time-varying gradients (rad), γ the gyromagnetic ratio (rad/T/s), Sp(r) the complex-valued transmit profile of the pth coil (T/V), b1,p(t) the RF pulse played along the pth coil (volts), ΔB0(r) a field map of B0 inhomogeneity (rad/s), eiΔB0(r)(t–L) the phase accrual due to this inhomogeneity, L the duration of each waveform (sec), and [39].
3) Discretization
Discretizing (1) in space and time leads to
| (2) |
Here, is a diagonal matrix comprised of Ns samples of the pth spatial profile taken within a user-defined FOX, which in many cases is smaller than the FOV. The next matrix, , incorporates the effect of main field nonuniformity and brings energy placed in k-space into the spatial domain at the Ns locations where each coil profile is sampled. Formally, F(m, n) = iγM0ΔteiΔB0(rm)(tn–L)eirm·k(tn). Each of the are comprised of samples of the pth RF waveform, b1,p(t), spaced by Δt. Finally, Atot and btot are implicitly defined in (2) [39]. Users are free to choose how finely to sample the spatial and temporal variables in (1) and thus control whether m = Atotbtot is under- or over-determined [40], [41]. Furthermore, by sampling r only within the FOX, (2) becomes blind to the rest of the FOV and is freed from needless spatial constraints.
4) RF Waveform Generation
To excite a pattern d(r) using a P-channel system, P RF pulses are needed. To determine these pulses, one may form Ns samples of the desired pattern into the vector . Then, by estimating a ΔB0 map and each spatial coil profile, one may generate F, the Sps, and in turn Atot. Finally, a set of RF pulses that (approximately) achieves the desired excitation may be generated by solving
| (3) |
for btot. Solving (3) via direct inversion (or pseudoinversion) of Atot tends to result in poorly-conditioned btot vectors [42], so we instead solve the following Tikhonov-regularized problem [43] that penalizes the energy of the solution:
| (4) |
Setting δ to a small positive value and then solving (4) typically produces a btot with reasonable and voltages without seriously impacting the residual error [39], [40], [44]. In our work, we use the LSQR algorithm [45] to solve (4), which has been shown in practice to yield favorable multichannel pulse designs [42].
5) Spoke-Based RF Pulse Generation
For most spoke-based pulse designs, one fixes not only k(t) and d(r), but desired slice thickness and spoke type as well. In this work, slice thickness is fixed at 10 mm and each spoke is a Hanning-windowed sinc. For all T-spoke pulses, the spoke at dc in (kx, ky) has a time-bandwidth product of 4, while the T – 1 off-dc spokes have kz-lengths half that of the former. (Using shorter off-dc spokes lets one reduce the duration of a pulse without noticeably impacting slice selection performance [5].) Overall, these constraints fix the shape of the P RF pulses and all properties of the slice profile (e.g., sidelobes and sharpness) [3], [5], while still letting the user retain control over the amplitude and phase each channel encodes along each spoke.
For a T-spoke pulse on a P-channel system, these constraints cause major changes to (2) and (3). First, all but T columns of F are discarded, since only T locations in (kx, ky)-space (those where the spokes are located) are available for weighting. Further, each bp reduces from Nt to T elements. Finally, the FOX reduces to a 2-D in-plane region, leading to a far smaller Ns than in a 3-D case. The system now has only PT unknowns, giving the user control over PT weights to influence the in-plane excitation pattern.
B. Transmit and Receive Profile Estimation
In order to generate RF pulses for use on a P-channel system, one sees from (1) and (2) that estimates of the spatial transmit profiles, , are first required. In our work, we only need coil profile estimates in the 2-D plane where the thin-slice excitation occurs, so here r indexes samples only within a 2-D FOX.
1) Magnitude Estimation
Here we use a parametric fitting method to obtain |Sp(r)| in T/V. This technique also estimates |R(r)|, the system's receive profile magnitude. For fixed p, the following steps are performed: first, NV intensity images are collected. Each is obtained by playing a standard slice-selective pulse with duration τ through channel p (leaving all other P – 1 channels dormant) and reading out the result on the receive coil with a gradient-recalled echo (GRE). This pulse's peak transmit voltage, V, is varied from one image to another, and increased enough so that several high-flip images are obtained. Then, for all coordinates r in the FOX, the intensities of these NV images are fit to
| (5) |
where SIp,V is the intensity image due to playing the pulse with peak voltage V through channel p, |α(r)| = γτ|Sp(r)|, and E1(r) = e–TR/T1(r) [46]-[48]. In this work, experiments are conducted in uniform-T1 phantoms, so E1(r) is known.
2) Phase Estimation
To estimate the phase of each channel profile, we keep V constant and collect one low-flip image per channel; each phase profile is then simply the phase of each respective image. This yields the phase relative to the receive coil, which is sufficient [5], [42].
C. Sparse Approximation
1) Single-Vector Case
Consider a linear system of equations d = Fg, where , , , and d and F, are known. It is common to use the pseudoinverse of F, denoted F†, to determine ĝ = F†d as an (approximate) solution to the system of equations. When d is in the range of F, ĝ is the solution that minimizes ∥ĝ∥2, the Euclidean or norm of ĝ. When d is not in the range of F, no solution exists; ĝ minimizes ∥ĝ∥2 among the vectors that minimize ∥d–Fĝ∥2. In the design problems in this paper, it is necessary for the analogue to ĝ to have only a small fraction of its entries different from zero. We are faced with a sparse approximation problem of the form
| (6) |
where ∥·∥0 equals the number of nonzero elements of a vector. The subset of {1,2,...,N} where there are nonzero entries in g is called the sparsity profile. For general F, solving (6) essentially requires a search over the 2N – 1 nonempty sparsity profiles. The problem is thus computationally infeasible except for very small systems of equations (e.g., even for N = 30, one may need to search 1 073 741 823 subsets). Formally, the problem is NP-complete [22], [23].
For problems where (6) is intractable, a large body of research supports the relaxation of (6) [25]
| (7) |
This is a convex optimization and thus may be solved efficiently [49]. The solution of (7) does not always match the solution of (6)—if it did, the intractability of (6) would be contradicted—but certain conditions on F guarantee a match [26], [31] and (7) is generally a useful heuristic [50]. The optimization
| (8) |
has the same set of solutions as (7). The first term of (8) keeps residual error down, whereas the second promotes sparsity of g [25], [51]. As the control parameter, λ, is increased from zero to one, the algorithm yields sparser solutions and the residual error increases; sparsity is traded off with residual error.
2) Multiple-Vector Case (Simultaneous Sparsity)
Now suppose we have the system of equations
| (9) |
where and the are known. In the design problems posed in this paper, it is natural to constrain the number of positions in which any of the gps are nonzero. Thus we seek approximate solutions in which the gps are not only sparse, but the union of their sparsity patterns is small; this is called simultaneous sparsity [30], [32]. Unfortunately, optimal approximation with a simultaneous sparsity constraint is even harder than (6). Thus, we propose to use a relaxation similar to (8)
| (10) |
where and , i.e., the norm of the norms of the rows of G. This latter operator is a simultaneous sparsity norm: it penalizes the program (produces large values) when the columns of G have dissimilar sparsity profiles [30]. An equivalent way of writing (10), which will be useful later, is to replace ∥G∥s with , where , and , i.e., the nth element of this vector contains the norm of the nth row of G. Finally, by setting P = 1, one sees that (8) is a base case of (10).
To the best of our knowledge, (10) is a novel instance where simultaneous sparsity is required. To date, others have sought simultaneously sparse gps such that [d1...dP] = F[g1...gP] holds [30], [32], [52], whereas here we are seeking simultaneously sparse gps that solve (9). In other words, in prior work, there are many different ds and a single F, whereas here, we have a single d and many different Fs.
3) Solution via Second-Order Cone Programming
One may solve (10) using second-order cone (SOC) programming, a method that encapsulates conic, convex-quadratic [33], and linear constraints. Quadratic programming is not an option because the terms of (10) are complex. Second-order conic constraints are of the form s : ∥[sl,...,sn–1]T∥2 ≤ sn, and the generic format of an SOC program is
| (11) |
where , H is the complex conjugate, is the N-dimensional positive orthant cone, and the Lns are second-order cones [33]. SOC programs are useful because they can be solved via efficient interior point algorithms [53], [54]. To convert (10) into the SOC format, we first write
| (12) |
This makes the objective function linear, as required. Now we change variables, rewriting ∥G∥s ≤ q as , for n = 1,...,N, and 1Hy ≤ q, where 1 is an N × 1 vector of ones and y = [y1,...,yN]T. Letting z = dtot – Ftotgtot, we arrive at
| (13) |
With these steps, the problem is a fully-defined SOC program that may be implemented and solved numerically. In our work, we implement (13) in SeDuMi (self-dual-minimization) [53], and find that it is capable of solving problems in a reasonable amount of time (e.g., 3−25 min) when the number of unknowns, PN, is in the thousands. It is possible that a more efficient method for solving (10) can be found, but techniques for (10) lag behind those for (7) and (8).
III. Spoke Placement and Weighting Methods
We now describe three methods for determining the placement of spokes in (kx, ky) when designing a spoke-based RF waveform whose goal is to produce a user-defined in-plane target excitation, d(x, y), using a P-channel system whose coil profiles are known. The second and third methods will suggest spoke weights in addition to placement. Assume that the FOV is a rectangle, so when d(x, y) is sampled, its NFOV samples may be assembled into . Furthermore, assume the FOX is smaller than the FOV and not necessarily rectangular. It is discretized and comprised of NFOX < NFOV samples, which are a proper subset of the FOV samples. (The NFOV – NFOX pixels in the FOV but not in the FOX comprise a “don't care” region.) Finally, assume the system's P coil profiles are sampled within the FOX and assembled into the diagonal matrices . The goal now is to place spokes at T locations in (kx, ky) such that the resulting in-plane excitation is close (in the sense) to d(x, y) within the FOX (not the entire FOV).
A. Fourier-Based Spoke Placement
An intuitive way to determine where to place each spoke is to compute the discrete Fourier transform (DFT) of D and from the resulting discrete grid of (kx, ky) frequencies, choose the T whose Fourier coefficients are largest in magnitude [12], [21]. If the complex weights at these T locations are brought back into the spatial domain via an inverse transform, Plancherel's theorem implies that this image, D̂T, is the best approximation of D within the FOV [7], [55]. Unfortunately, there are problems with this method. 1) The FOX is typically smaller than the FOV, and the RF profile in the “don't care” region is not important. The Fourier method, however, has no concept of the FOX or the “don't care” region. This FOX–FOV mismatch means that the T chosen locations do not necessarily yield the best representation of d(x, y) within the FOX. 2) The influence of each spatial profile, Sp(r), is not accounted for, even though each has a major impact on the in-plane excitation. 3) There is no concept of transmit channels, so the method cannot suggest a weight for each channel to place at each spoke location.
B. Inversion-Based Spoke Placement
Single-Channel Derivation: This method retains the logic of the Fourier technique while accounting for its shortcomings. For now, assume the system has a single channel and imagine a grid of Nf arbitrarily-spaced points in (kx, ky) located at {k1,...,kNf}. Each is a Dirac delta that produces a complex exponential in the spatial domain. An arbitrary choice of complex weights at different points on this grid results in a nominal spatial domain excitation, which is related to the weighted grid by a Fourier transform. The nominal excitation is then multiplied (pointwise) by the coil profile to yield the actual excitation, m(x, y). One may sample this excitation within the FOX at {r1,...,rNFOX} and arrange the samples into . Likewise, the weights on the grid may be formed into . The relation between m and g is represented by , where F(m, n) = iγM0Δteirm·kn, where the nth column of F describes how the excitation at the rms is influenced by the weight at kn. When samples of the coil profile are arranged into , this leads to
| (14) |
This is analogous to the derivation in Section II-A, In short, (14) expresses the excitation that forms at a set of points in the FOX when an arbitrary set of complex weights is placed on an arbitrary k-space grid. For fixed kn, the column of F here is nearly identical to the column of its counterpart in Section II-A, except now there is no notion of time. For the most part, this is tolerable: kn is known rather than k(t) at time tn. The difference here is that time-dependent ΔB0 phase accrual cannot be incorporated because k's dependence on t is not yet known. Fortunately, if B0 is nearly homogeneous or pulse duration is short, then the column of F here (nearly) equals the column of its counterpart in Section II-A.
By sampling d(x, y) analogously to m(x, y), it is possible to form , and by solving d = SFg for g, the weighting of the (kx, ky) grid that best achieves the target excitation in the sense within the FOX may be obtained. This solution is generated via regularization rather than direct pseudoinversion
| (15) |
This yields a well-conditioned g that (approximately) solves the system and provides a set of grid weights that form the desired excitation. At this point, two pitfalls of the Fourier method have been mitigated: the coil profile has been explicitly incorporated and the unnecessary constraints on the excitation outside the FOX have been removed. Now, using the intuition that motivated the Fourier method, we decide to place spokes at the T points on the grid that correspond to the T largest-magnitude elements of g.
1) Multichannel Derivation
For multichannel systems, (14) generalizes to
| (16) |
analogously to (2). A regularization analogous to (15) is then applied to solve d = Atotgtot, yielding a well-conditioned solution, gtot, which is disassembled into , where gp contains the weights for channel p. When an element of gp is large in magnitude, channel p is using the corresponding grid point to strongly influence the resulting excitation, so placing a spoke here may be worthwhile. However, at this same location, imagine that the other P – 1 channels have weights of zero; should a spoke still be placed here, if only one channel suggests doing so, or should it be placed at an alternate location, one where each channel contributes toward the formation of d(x, y)?
The presence of multiple channels has led to a quandary about how to choose the T best spoke locations. A solution to this problem is to “compress” the energy of the resulting gp-weighted grids along the channel dimension using the norm. This produces a single grid that represents the overall energy placed at each (kx, ky) location by all P channels, denoted , where . Using this norm to combine the energy deposited by all P channels at the ith grid location has no sparsifying effects, so will not radically differ if one channel deposits a large amount of energy at the ith grid point, or if this same amount of total energy is contributed by many channels. Forming is sensible because when performing excitations using a multichannel system, it does not matter if it is one or many channels that place energy at a given point if such a deposition improves the excitation. Based on this reasoning, we reapply the intuition that inspired the Fourier-based method, and decide to place spokes at the T locations corresponding to the largest-magnitude elements of .
Unfortunately, using Tikhonov regularization to find gtot yields a dense solution, leading to a dense , one where all grid locations experience moderate amounts of energy deposition. Frequently, the energies at each of the T chosen locations are not much greater than the energies present at most other points. Up until this point, the magnitude of energy at a grid point has been used as proxy for whether that point is a good spoke location, but since the energies being deposited across all candidate locations are now similar, it is no longer clear if this intuition is useful. The ideal weights for each channel to place on the candidate grid have indeed been determined, but this process has not restricted the number of points at which a channel may deposit energy.
This is a serious drawback, because when T spokes are chosen, only T locations in (kx, ky) remain for the P channels to modulate and attempt to form d(x, y). Thus in practice, when all weights are zeroed out except those PT weights associated with the chosen locations, the resulting excitation does not closely resemble the desired one. The achieved excitation is of low quality because the PT chosen weights relied on the weights placed at all other grid locations to form an accurate excitation. To mitigate this problem, the PT weights need to be retuned (see Section IV). In short, this method does not encourage the channels to form the excitation by modulating only a small number of locations, despite the fact that only a small subset of candidate grid points are able to be retained for the final pulse design.
C. Sparsity-Enforced Spoke Placement
This method—our main contribution—resolves the problem of the former by finding a sparse that reveals a small set of spoke locations (and weights) that alone form a high-fidelity excitation. In Section VI, we demonstrate that this approach is superior to the inversion method at revealing a small number of locations at which to place spokes.
1) Single-Channel Derivation
Since P = 1, there is only one grid vector, g, and the system of equations we desire to solve is d = SFg. Rather than using Tikhonov regularization to reveal spoke locations, we instead promote the sparsity of g
| (17) |
Because of the relationship between sparsity and regularization [25], [51], this optimization yields a sparse g that approximately solves the system.
2) Multichannel Derivation
With P > 1 channels, the resulting excitation may be expressed as (16), so we again arrive at d = Atotgtot. To mitigate the inversion-based method's dense grid problem, we rely on sparse approximation and pose an optimization that promotes the sparsity of
| (18) |
This is equivalent to (10), the only difference being notational ( is used rather than ∥G∥s). With large enough λ, this method produces gps that approximately solve the system while also yielding a sparse . Typically, solving (18) yields a with many elements close to zero, with only several high-energy grid points. (The small grid weights are not exactly zero; this is because an regularization is used to promote sparsity rather than an ideal but computationally intractable penalty.)
In this way, the sparsity-enforced spoke placement reveals a small subset of the overall grid that alone is able to form the excitation. At this stage, T spoke locations are selected by choosing those points on the grid corresponding to the largest-magnitude elements of . In contrast with the inversion-based method, the PT weights associated with these T locations alone are typically able to generate a reasonable version of the desired excitation when other weights are zeroed out. This does not occur by chance. Rather, it is because the T columns of F in Atot are nearly identical to the T columns of the similarly-named matrix in Section II-A. (This claim holds if ΔB0 is small or the pulse will be of short duration, the latter of which is always the case for small T.) Thus this method determines a small set of spoke locations and weightings that form an acceptable-quality excitation. Like the inversion-based method, the weights undergo retuning (discussed next), but in many cases they do not radically change.
3) Necessity of Simultaneous Sparsity
What if rather than promoting the sparsity of , we simply promote that of gtot? This would produce a sparse gtot, and thus individually-sparse gp. But this does not encourage simultaneous sparsity among the gps, so their sparsity profiles differ, and thus when is formed, it is not necessarily sparse, contradicting our goal. Further, ∥gtot∥1 discourages solutions where many channels deposit energy at a single location, and thus penalizes solutions which are in fact useful.
4) Variants
One may modify (18) so that an rather than penalty is imposed on the system. Furthermore, if the conditioning of the gps is a concern, constraints may be placed on their and energies. These variants and their combinations are still SOC programs.
IV. Generation of Gradients, Retuned Weights, and RF Pulses
At this point, we have a P-channel system whose profiles are known and have used one of the methods to determine T locations at which to place spokes. Assume that ΔB0(r) and the gradient coil's amplitude and slew rate constraints are known, all spoke parameters are fixed, and the assumptions from Section III are in effect. To begin, a set of gradients must be designed to visit and traverse a spoke at each location in an efficient manner. To accomplish this, a genetic algorithm is used to find a near-optimal minimal-length Euclidean path through the T points. Knowing this short path allows us to design the gradients, G(t), to drive to each (kx, ky) coordinate in a way that minimizes pulse duration. The time-dependent k-space trajectory, k(t), is obtained in turn by integrating these gradients. Additionally, because the spoke parameters have been fixed, the shape of each channel's RF pulse is known.
The next task is to obtain the weight each channel should encode along each spoke location, i.e., to find PT weights that best generate d(x, y). If the Fourier method is used for placement, this step is necessary because it does not generate weights during the placement stage. If the inversion method is used, weight retuning is also a necessity (see Section III-B). If the sparsity-enforced method is used, the weights it generates often do form a reasonably-accurate excitation, but still benefit from retuning because they have a slight reliance on the various small weights that get discarded when only T locations are retained. Further, if ΔB0(r) ≠ 0, retuning helps the inversion and sparsity-enforced methods because the weights these techniques initially determine cannot take B0 inhomogeneity into account (see Section III-B).
We now apply the pulse design method of Section II-A. With k(t), the coil profiles, and ΔB0, we update the T columns of F to account for ΔB0 phase accrual and then generate Atot in (2). We then solve (4), generating the PT weights that the RF pulses should use to best produce the excitation. This concludes the design process. (Note that the PT weights may be obtained via an alternative approach, e.g., [9], [28], [56].)
V. System and Experiment Setup
A. B1 Mitigation in a Head-Shaped Water Phantom on a Single-Channel 7 T Scanner
1) Overview
Each placement method will design pulses that mitigate B1 inhomogeneity present in a head-shaped water phantom at 7 T using different numbers of spokes. Here, the ideal mitigation pulse is one that excites the multiplicative inverse of the inhomogeneity [3] and produces a uniform magnetization across the FOX. Each method will attempt to produce this ideal excitation.
2) Hardware
Work is conducted on a 7 T whole-body human scanner (Siemens Medical Solutions, Erlangen, Germany). The scanner is built around a 90-cm-diameter magnet (Magnex Scientific, Oxford, U.K.). The amplitude and slew rate of the system's head gradient coils are always constrained to 35 mT/m and 600 T/m/s, respectively. Potential gradient imperfections are minimized by operating at amplitude and slew rates below the hardware's maximum specifications and performing a one-time RF-gradient delay calibration. A single-channel, 28-cm-diameter, quadrature bandpass birdcage coil is used for transmission and reception [57], [58].
3) Spatial Profiles, Target Pattern, and Spoke Parameters
A GRE magnitude image of the head-shaped water phantom is obtained using a conventional low-flip slice-selective pulse with a repetition time (TR) of 20 ms, an echo time (TE) of 5 ms, a bandwidth (BW) of 390 Hz/pixel, and a FOV of 25.6 cm in each dimension. The dielectric properties of the water in the phantom cause its transmit and receive profiles to exhibit significant spatial variation, causing the resulting image intensity to be highly nonuniform. One sees from (5) that this image is linearly related to both the transmit profile and the receive profile when in the small-tip angle regime, because sin(α) ≃ α for small α.
We use this image—the combination of the transmit and receive profiles—as proxy for the transmit profile. Naturally, when one implements a mitigation pulse for in vivo use, one should mitigate only the transmit profile, as this achieves optimal contrast and SNR, but here we will mitigate the combination of profiles, for three reasons: 1) The combination exhibits more spatial variation than the transmit profile alone, making the spoke selection problem more challenging. 2) A pulse designed to mitigate this combination, rather than simply the transmit profile, produces a result that is easy to understand and evaluate, since it ideally will produce a uniformly image, whereas a pulse that mitigates only the transmit profile still produces a nonuniform image because the receive profile is not mitigated. 3) Evaluating the performance of a pulse that mitigates only the transmit profile is difficult because to do so we must quantify the postmitigation flip angle. In order to obtain a flip angle map via fitting, the pulse must be played at increasing voltages to obtain high-flip images (cf. Section II-B), but the spoke-based pulse does not maintain its intended excitation profile in this regime, because like all spoke-based designs, it relies on the small-tip angle approximation. This is in contrast with conventional RF pulses, which may be used to estimate the maps for each coil, but not to validate the flip angles of spoke-based pulses.
The hypothetical transmit profile to be mitigated appears in Fig. 1 in nT/V, with a 25.6 cm × 25.6 cm FOV and 4-mm resolution. The FOX is where the phantom is present. The in-plane target magnetization magnitude is a uniform 10° flip and target phase is zero. (We have no desire to shape the nearly-constant phase that occurs naturally across the target.) Spoke parameters for all designs are given in Section II-B. Based on these parameters and gradient constraints, the duration of a T-spoke pulse, L(T), is close to 0.26T+0.34 ms, i.e., each spoke adds roughly 1/4 ms to pulse duration. The in-plane (kx, ky) traversals take negligible time because most time is spent playing spokes in kz. Finally, ΔB0 is estimated from the phase of two GRE images (TE1 = 5 ms, TE2 = 6 ms).
Fig. 1.

Quantitative map of the head-shaped water phantom at 7 T (nT/V). This hypothetical transmit profile is generated by collecting a GRE magnitude image and scaling the resulting pixels.
4) Experiment Details: Simulations, Quality Metrics, and Validation Trial on Real System
First, simulations are conducted as a function of T to demonstrate the superior performance of the sparsity-enforced technique; here, we assume we know a good value for the sparsity-enforced method's λ parameter. The quality of the in-plane excitation produced by each method is evaluated by computing the within-FOX, in-plane root mean square error (RMSE) and maximum error between each resulting excitation and the desired magnetization. Because the desired pattern is in degrees, each of these error terms are in degrees as well. Further, because the resulting pulses are in volts, we calculate the rms (VRMS) and peak voltage (Vpeak) of each. After the simulations, a sparsity-enforced pulse is played on the scanner to show that the experimental result closely matches the one predicted via simulation. We then return to simulations and characterize how the sparsity-enforced placement algorithm behaves when provided grids of oversampled candidate spoke locations. Finally, we investigate how RMSE varies as a function of λ and T. Results appear in Section VI.
B. Phase-Encoded, Spatially-Selective Excitation in an Oil Phantom on an Eight-Channel 3 T Scanner
1) Overview
Here we evaluate how well the spoke placement methods design pulses that form a highly-structured excitation pattern in a 17-cm oil phantom, where the FOX is the phantom itself and transmission is conducted using an eight-channel parallel excitation system.
2) Hardware
The parallel system is built around a 3 T Magnetom Trio scanner (Siemens Medical Solutions, Erlangen, Germany). The coil array is composed of eight circular surface coils arranged on a 28-cm-diameter acrylic tube [59]. After a set of pulses is designed for use on the scanner, the eight resulting waveforms are transmitted simultaneously through their respective coils and modulated in magnitude and phase as dictated by the pulse design. The system's body coil is used for reception. The amplitude and slew rate constraints of the gradients are 35 mT/m and 150 T/m/s, respectively. Gradient imperfections are mitigated by operating in a region well within the hardware's maximum specifications; RF-gradient mismatch is prevented via a one-time delay calibration.
3) Spatial Profiles, Target Pattern, and Spoke Parameters
Spatial profiles are obtained by collecting ten images per channel and fitting the results to (5) using the Powell method [60]. The images are obtained by sending ten pulses through each of the eight transmit elements, one at a time, and receiving on the body coil using a GRE readout (TR = 20 ms, TE = 6 ms, BW = 390 Hz/pixel). This yields 25.6 cm × 25.6 cm FOV, 4-mm resolution magnitude and phase maps, half of which are in the high-flip regime. The profile magnitudes, in nT/V, are illustrated in Fig. 2. The smooth variations exhibited by each profile occur without smoothing the fitted results, leading us to believe that the fitting method is robust and accurate. Further, the method determines that the receive profile is smooth, varying less than 5% within the FOX. Spoke type and thickness are the same as in the single-channel case. The duration of a T-spoke pulse, L(T), fits well to 0.47T+0.65 ms; ΔB0 is again obtained from two phase maps.
Fig. 2.

Quantitative transmit profile magnitudes of the 3 T, eight-channel parallel excitation system (nT/V) obtained by collecting ten intensity images per channel and fitting to (5).
With the profiles of Fig. 2, it is possible to run the spoke placement algorithms and produce pulses. For all experiments, d(x, y) is the phase-encoded bifurcation depicted in Fig. 3. This target has a high degree of spatial selectivity, experiencing a 10° flip within only two thin “veins” and no flip across the rest of the FOX. The left vein is 90° out of phase with the right vein. Exciting this pattern is worthwhile because highly-structured excitations may have applications to clinical MRI. Furthermore, the strength of multichannel excitation will be demonstrated. Finally, the phase-encoded nature of this excitation may have applications to phase-contrast magnetic resonance angiography (MRA) [61], [62], perhaps allowing MRA concepts to be ported to general MRI.
Fig. 3.
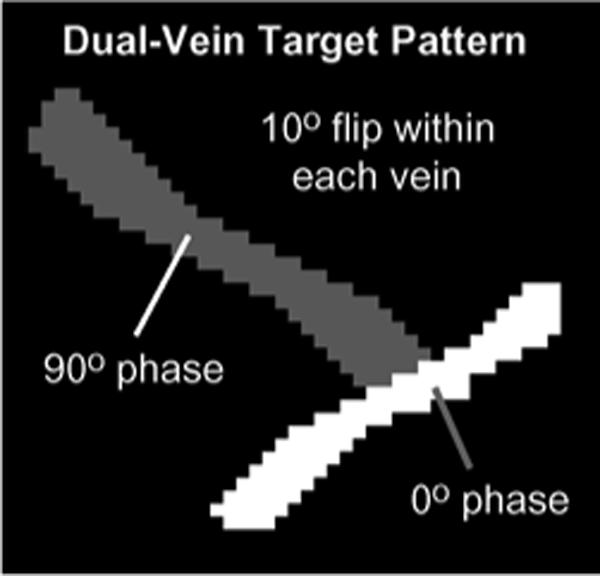
Dual-phase bifurcation target excitation used for all 3 T eight-channel system experiments. Within the two veins the target commands a 10° flip and zero flip elsewhere. Each branch is phase encoded: the left vein is 90° out of phase with the right. The ability to achieve this structured excitation pattern will show the strength of both multichannel excitation and sparsity-enforced spoke placement.
4) Experiment Details: Simulations, Quality Metrics and Validation Trial on Real System
Analogously to the single-channel system experiments, simulations are first conducted and RMSE and metrics are used to evaluate the performance of the different methods as a function of T. Voltages of the resulting pulses are also analyzed. Each design consists of eight RF pulses, so to succinctly present the data, the maximum peak and maximum RMS voltages observed across each set of eight waveforms are recorded. After the Bloch-simulated trials, a sparsity-enforced pulse is played on the scanner and the resulting excitation is compared to the one predicted via simulation. We then return to simulations, analyzing how the sparsity-enforced algorithm behaves when provided grids of candidate spoke locations with different extents in k-space, along with the method's sensitivity to its control parameter, λ.
VI. Results and Discussion
1) Single-Channel System: Bloch-Simulated Spoke Placement Analysis
Here, each method is used to place T = 1,...,40 spokes. Based on Section V, we are able to generate all matrices and vectors needed to run the placement and pulse design routines, e.g., 1138 within-FOX samples of the transmit profile, S(x, y), are used to form the spatial profile matrix, S, all elements of d are set to 10° based on the desired excitation d(x, y), etc. The pointwise inverse of the inhomogeneity, S−1(x, y), is provided as the desired excitation to the Fourier placement method (see Section III-A). The inversion-based method's Tikhonov parameter in (15) is set to 0.1, and the pulse design Tikhonov parameter in (4) is set to 0.001.
The frequency grid of candidate spoke locations provided to the inversion-based and sparsity-enforced methods is centered at dc, Nyquist-spaced at (1/25.6) cm−1, extends outward equally in both kx and ky, and is comprised of 172 points, leading to . Providing this same grid to the inversion and sparsity-enforced methods promotes fair comparisons between the algorithms. Ideally, this grid would extend further out in k-space to reach the maximum and minimum frequencies suggested by the transmit profile's 4-mm sample spacing, but using such a large grid increases the sparsity-enforced method's runtime to 25 min (versus 3 min for the 172-point grid). The smaller grid is acceptable, however, because the Fourier-based method—which selects spokes on the large, ideal grid—never chooses to place a spoke outside of this 172 region when T ≤ 40, i.e., the majority of k-space energy lies on the small grid. (Later we will show how grid extent affects the sparsity-enforced method's performance.)
The final step is to run the sparsity-enforced routine for R = 40 values of λ, solving (17) each time and storing each resulting weighted grid, g(r). When the sparsity-enforced method is used to place T spokes, R possible placements are evaluated—spoke locations being chosen based on the T maximum values of each g(r)—and the placement yielding the smallest residual error, , is retained. Thus when the sparsity-enforced method's results are presented, they implicitly assume that a good value for λ is known. (Later on, we will analyze sensitivity to λ.) We do not find it necessary to loop over the inversion-based method's Tikhonov term because we observe that once it is tuned past a certain threshold, all resulting solutions suggest essentially the same set of T spoke locations.
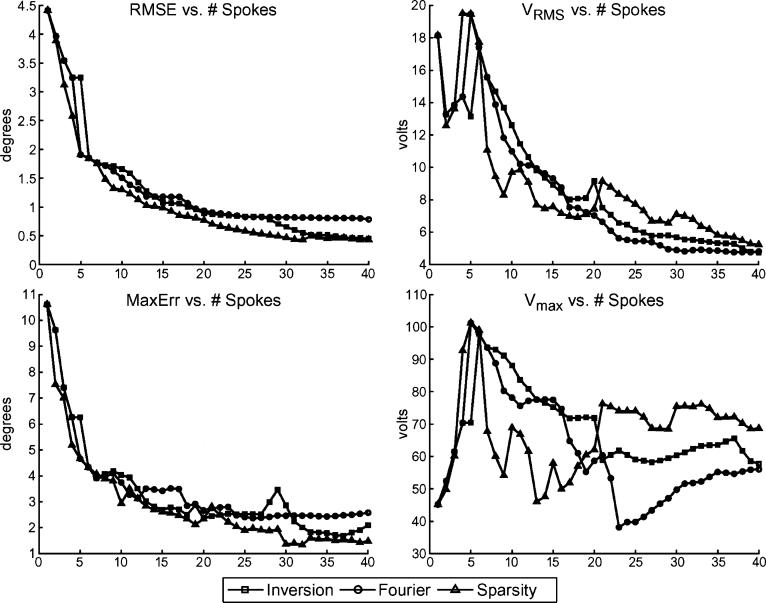
Each method designs pulses with T = 1,..., 40 spokes, which are then simulated. The RMSE and maximum error of each resulting excitation pattern with respect to the uniform target are computed, along with the voltage characteristics of each corresponding pulse. Fig. 4 depicts these results, illustrating how each metric varies with T. For each method, RMSE decreases with T, because using more spokes allows for more spatial tailoring and inhomogeneity mitigation. For fixed T, the Fourier method is outperformed by the inversion-based method, which in turn is outperformed by the sparsity-enforced technique. For all T, the sparsity-enforced placement method produces the lowest RMSE.
Fig. 4.
Bloch-simulated spoke placement algorithm comparisons for mitigating B1 inhomogeneity in the head-shaped water phantom at 7 T. Error and voltage statistics versus number of spokes used (T) are shown for the Fourier, inversion, and sparsity-enforced spoke placement methods. Upper-left: RMSE versus T. Lower-left: maximum error versus T. Upper-right: VRMS versus T. Lower-right: Vmax versus T. For all three algorithms, the duration of a T-spoke pulse is close to 0.26T + 0.34 ms.
When T < 15, the RMSE for each method is large, and the resulting magnetization still highly nonuniform. When T ∈ [15, 30], the sparsity-enforced method, on average, produces an excitation with 1.32 times lower RMSE relative to the inversion method. The inversion-based method's excitations, in turn, have on average 1.06 times lower RMSE than those due to the Fourier method. For T > 30, the RMSE of the sparsity-enforced and inversion methods converges, but the resulting pulses are over 8-ms long and thus impractical. Overall, it is clear that the sparsity-enforced method produces higher-quality excitations than the other methods for all practical pulse durations. To see the strength of the sparsity-enforced method, consider its 21-spoke 5.7-ms pulse with 0.68 RMSE. In order for the inversion method to produce the same quality excitation, a 29-spoke, 7.8-ms pulse is required. In other words, the sparsity-enforced pulse achieves the same quality excitation yet is 1.37 times shorter.
Unlike RMSE, maximum error does not vary smoothly with T, because the algorithms do not explicitly penalize error. In general, the maximum error curves of the inversion and sparsity-enforced methods are similar. The RMS voltages of pulses generated by each method exhibit a downward trend as T increases, because with more spokes, each individual spoke does not need to be modulated as intensely to form the excitation. Further, the peak voltages behave more erratically than the RMS voltages, analogously to how the error fluctuates more than RMSE. Finally, for T ∈ [10, 20], the sparsity-enforced method often has the lowest voltages among all methods, whereas for T > 20, its voltages are higher.
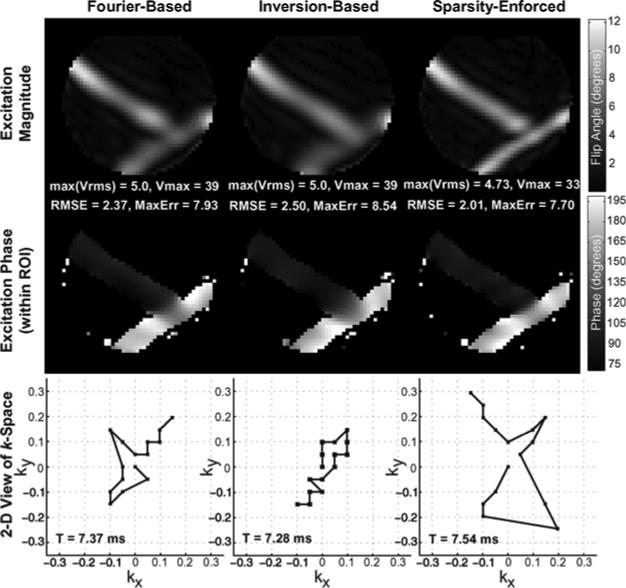
Fig. 5 depicts the results of each method when T = 21. The left, center, and right columns show the Fourier, inversion, and sparsity-enforced method's results, respectively. The top, middle, and bottom rows depict the simulated excitation before accounting for transmit profile nonuniformity, the resulting magnetization after accounting for inhomogeneity, and a 2-D view of k-space showing where each method places its spokes and how they are traversed in-plane. Metrics are also given in correspondence with those in Fig. 4. From the top row, one sees that each method produces an excitation that approximates the inverse of the nonuniform profile in Fig. 1. Looking at the middle row, one appreciates the ability of each method to produce a relatively flat magnetization. The bottom row shows that the Fourier and inversion methods cluster spokes around dc. The sparsity-enforced method, however, places its spokes further out on the grid, leading to an excitation with 1.28 times lower RMSE. This improvement is achieved with no increase in pulse duration and only a moderate voltage increase. The spoke placement determined by the sparsity-enforced algorithm is not obvious, but by placing spokes at slightly higher spatial frequencies, the sparsity-enforced method produces a nominal excitation that is less symmetric, better resembling the pointwise inverse of the transmit profile than the excitations produced by the other methods.
Fig. 5.
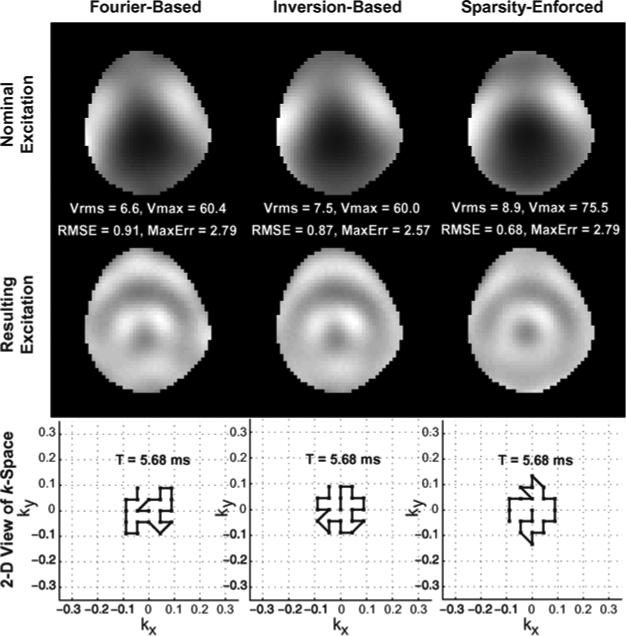
Bloch-simulated 21-spoke pulses designed by the Fourier, inversion, and sparsity-enforced spoke placement algorithms for mitigating B1 inhomogeneity in the head-shaped water phantom at 7 T. Columns, from left to right: results of the Fourier, inversion, and sparsity-enforced methods. Top row: excitations produced by each algorithm. Middle row: magnetizations after accounting for the inhomogeneity. Bottom row: 2-D view of k-space illustrating each spoke placement; each trajectory ends at the center of k-space. The sparsity-enforced pulse produces the lowest-RMSE excitation.
2) Single-Channel System Validation
To validate our simulations, we play the 21-spoke sparsity-enforced pulse from Fig. 5 on the scanner and perform a GRE readout. Since the pulse is designed to mitigate both the transmit and receive profiles, we validate our simulation by analyzing the magnitude of the readout image. Fig. 6 shows the RF magnitude and gradients of the 21-spoke pulse, along with the in-plane and through-plane result from the real system. The through-plane image demonstrates excellent slice selection. Further, there is a striking resemblance between the in-plane result and simulation (middle row, right column of Fig. 5). Note how Fig. 5 Fourier and inversion-based simulated patterns have two bright spots slightly north-west and north-east of center, whereas the simulated pattern and the scanner result in Fig. 6 have only a single bright spot northeast of center. This close match between the experimental and simulated result lends strong support to the simulation method and results.
Fig. 6.
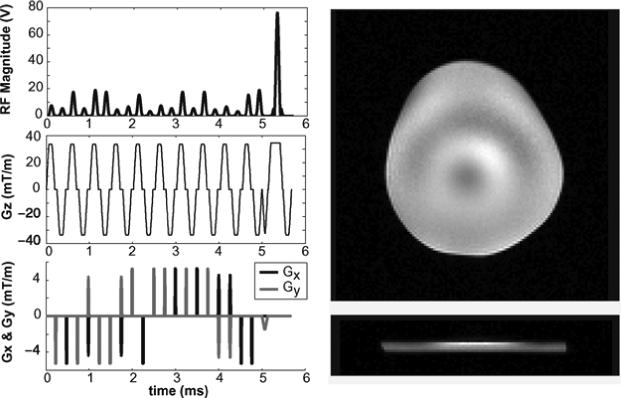
Experimental result in the head-shaped water phantom on the single-channel 7 T scanner. Here, the 21-spoke sparsity-enforced RF pulse whose simulations appear in Fig. 5 is played on the actual system. Left: RF waveform magnitude and gradients. Upper-right: in-plane scanner result. Lower-right: through-plane scanner result. This experimental result closely resembles the Bloch-simulated image in Fig. 5, validating the simulation methodology and proving that the pulse design process is feasible for use on real systems.
3) Multichannel System: Bloch-Simulated Spoke Placement Analysis
Here, each method places 1−40 spokes, and RMSE, error, VRMS, and Vpeak are calculated for each of the resulting 120 pulses and excitations. The goal here is to produce the dual-vein target in Fig. 3. Since there are 8 channels, the matrices are 8 times larger, e.g., Atot in (18) is now 1416 × (289 × 8). For all trials, the inversion method's Tikhonov value in (15) is 0.01 and the pulse design Tikhonov term in (4) is 0.01. The frequency grid is the same as in the single-channel experiment, so each gp vector (see Section III-B) is comprised of 289 elements. With these variables, it takes about 25 min to solve (18) for one value of λ.
Analogously to the single-channel experiment, the sparsity-enforced routine is run for R = 32 different values of λ, so when the method is requested to place T spokes, it evaluates R possible placements and chooses the one yielding the smallest error. Here, in contrast with the single-channel experiment, λ ∈ (10−9, 10−1). Small values of λ are necessary because the application of ∥·∥s to the gps results in grids with barely any energy when λ > 10−1.
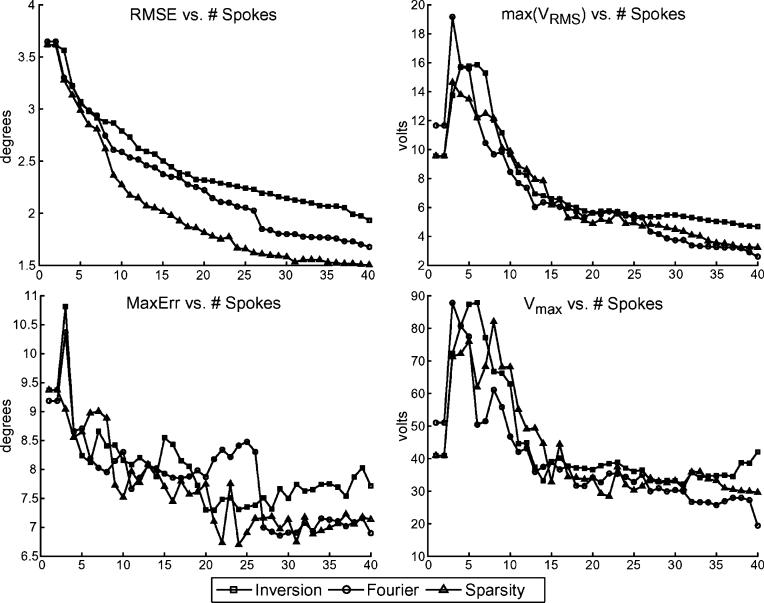
After these steps, the algorithms place 1−40 spokes and design pulses for each. Fig. 7 shows the error and voltage metrics of each method as a function of T. The RMSE plot shows that the sparsity-enforced routine outperforms the other methods. For T ∈ [10, 40], the sparsity-enforced technique, on average, has 1.18 times and 1.31 times lower RMSE than the Fourier and the inversion methods, respectively. Consider the sparsity-enforced method's 15-spoke, 7.5-ms pulse with 2.01 RMSE. For the Fourier method to attain this RMSE, a 26-spoke, 13-ms pulse is required, i.e., the sparsity-enforced pulse generates the same quality excitation yet is 1.73 times shorter in duration. In terms of voltages, all methods exhibit similar trends; this differs from the single-channel case where the sparsity-enforced method at times produced higher-voltage pulses. This means that the sparsity-enforced method produces pulses that yield higher-quality excitations without significantly increasing pulse duration, VRMS, or Vpeak.
Fig. 7.
Bloch-simulated spoke placement comparisons for forming the dual-vein target on the eight-channel parallel excitation system at 3 T. Error and voltage statistics versus number of spokes (T) are shown for the Fourier, inversion, and sparsity-enforced placement methods. Upper-left: RMSE versus T. Lower-left: maximum error versus T. Upper-right: max VRMS across all eight channels versus T. Lower-right: max Vpeak across all eight channels versus T. For all algorithms, the duration of a T-spoke pulse is close to 0.47T + 0.65 ms.
These error plots also reveal a surprising result: for all T, the inversion method performs worse than the Fourier one, even though the former was designed to account for pitfalls of the latter. This differs from the single-channel case of Fig. 4, where the inversion method outperformed the Fourier one. The inversion method fails here because of the “grid compression” step explained in Section III-B. This problem does not occur in the single-channel experiment because in the latter case there is only a single gp vector and the compacting of various grids to form a dense, problematic never occurs.
Fig. 8 shows each method's excitation and spoke placement for T = 15. Its left, middle, and right columns show the results of the Fourier, inversion, and sparsity-enforced techniques. The rows, from top to bottom, depict the simulated excitation magnitude, excitation phase, and spoke placement in (kx, ky). Each method succeeds, to some extent, in producing the desired excitation, but the sparsity-enforced method produces one that best resembles the target. Its excitation is better because it is not only less blurry than the others, its lower vein exhibits a degree of curvature not present in the veins of the other methods. This leads to the sparsity-enforced method's 2.01 RMSE, which is 1.18 and 1.24 times lower than those of the Fourier and inversion techniques. The sparsity-enforced method's spoke placement exhibits the same trend that it did in the single-channel case: it places spokes at slightly higher spatial frequencies than the Fourier method. The discussion about the poor performance of the inversion method (see Section III-B) is bolstered by its placement shown here: the dense grid causes the inversion-based technique to tightly cluster its spokes around dc, and because of this, its resulting excitation completely lacks distinct edges and is only a “lowpass” version of the target in Fig. 3.
Fig. 8.
Bloch-simulated 15-spoke pulses designed by the Fourier, inversion, and sparsity-enforced spoke placement algorithms for forming the dual-vein target on the eight-channel system at 3 T. Columns, from left to right: results of the Fourier, inversion, and sparsity-enforced spoke placement methods. Top row: excitation magnitudes. Middle row: excitation phases. Bottom row: 2-D view of k-space showing each method's spoke placement; each trajectory ends at the center of k-space. The sparsity-enforced excitation has the lowest RMSE, error, VRMS, and Vpeak.
4) Multichannel System Validation
Simulation results are validated by playing the 15-spoke sparsity-enforced pulse on the system. The magnitude and phase of the center slice are shown in Fig. 9, corresponding with the simulated images in the right column of Fig. 8. The experimental and simulated magnitude images are quite similar: there is a dark ridge in both images where the two veins intersect, the left vein in both images has barely any curvature, and the right vein of each image exhibits slight curvature. The lower-left of the experimental image contains ghosts of the left vein, an artifact not present in the simulation. We believe this occurs because gradient infidelities cause a spoke to be slightly misplaced in (kx, ky); this misplaced spoke ends up modulating spatial frequencies different from those intended, and because the system's coil profiles are being driven and superposed to cancel each other out in the majority of the FOX, this slight deviation perturbs the intended cancellation of the profiles and creates noticeable artifacts. In other words, commanding no flip in most of the FOX while asking for a 10° flip within two thin veins is an ill-conditioned problem.
Fig. 9.
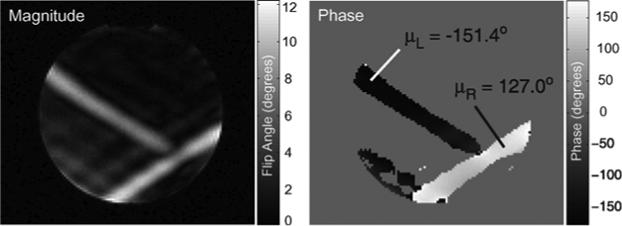
Experimental result in an oil phantom on the eight-channel 3 T system. Here, the 15-spoke sparsity-enforced RF pulse and gradients whose simulation results appear in Fig. 8 are played on the actual system followed by a GRE readout. This experimental result closely resembles the Bloch-simulated magnitude and phase of this same waveform in Fig. 8, validating the simulation methodology and showing that the proposed pulse design process is applicable to real multichannel systems.
The phase of the experimental image in Fig. 9 resembles the phase map predicted by the simulation in Fig. 8. On average, the phase in the left vein differs from that in the right vein by 81.6°, 8.4° off from the ideal 90° separation. The majority of this 8.4° error occurs where the two veins intersect. In the ideal target in Fig. 3, we see there is a sharp 90° phase cutoff between the left and right veins, whereas in the experimental map, there is a gradual change in phase in this region. This behavior is reasonable: it is unrealistic to think that the real system is capable of exciting a target with a discontinuity. Besides this difference, the observed magnitude and phase maps match closely with the simulated ones, lending credence to the simulation results and sparsity-enforced pulse design.
5) Sparsity-Enforced Placement: Grid Oversampling Analysis
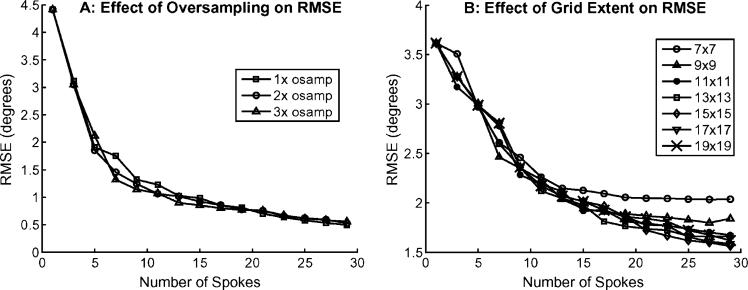
We have seen that the sparsity-enforced placement algorithm is superior to the other methods, yielding improvements in excitation quality with negligible changes to pulse duration and, at most, moderate increases in voltage. We now investigate how oversampling the grid of candidate spoke locations affects the sparsity-enforced algorithm's RMSE performance. This is done via simulations in the context of the single-channel system's inhomogeneity mitigation scenario. Here, for T = 1,3,...,29, we run the sparsity-enforced method using the 17 × 17 Nyquist grid discussed earlier, along with a 33 × 33 2×-oversampled grid and a 49 × 49 3×-oversampled grid. These oversampled grids extend out to nearly identical maximum and minimum spatial frequencies in k-space as does the Nyquist grid, so the only difference among the grids is their oversampling factor. With other parameters held constant, we run the sparsity-enforced method with various λs for each grid, design T-spoke pulses, and compute RMSE. The sparsity-enforced method's runtime increases when provided the oversampled grids, because they have roughly 4× and 8× as many candidate locations than does the Nyquist grid. Fig. 10(A) shows the results of this Bloch-simulated experiment. Here, RMSE as a function of oversampling factor is relatively constant, e.g., for T < 7, T > 17, oversampling the grid has no RMSE benefit. For fixed T ∈ [7, 15], RMSE decreases with increasing oversampling factor, but only slightly.
Fig. 10.
A: Single-channel B1 inhomogeneity mitigation experiment: RMSE versus number of spokes (T) when providing the sparsity-enforced method Nyquist-sampled, 2×-oversampled, and 3×-oversampled frequency grids of candidate locations. Grid oversampling seems to provide little RMSE benefit. B: Eight-channel system, dual-vein target: RMSE versus T for Nyquist-sampled frequency grids of candidate spoke locations that are 7 × 7,9 × 9,...,19 × 19 in size. Each grid is centered at DC and candidate points extent outward in kx and ky. The 11 × 11 grid yields reasonable RMSE results, suggesting that smaller grids may be used to decrease runtime. A: Effect of oversampling on RMSE. B: Effect of grid extent on RMSE.
6) Sparsity-Enforced Placement: Grid Extent Analysis
We now investigate whether increasing (reducing) the extent of the grid out to higher frequencies is of any benefit (detriment). Specifically, we alter the extent of the grid used in the multichannel experiment and measure RMSE. We run the sparsity-enforced algorithm using the original Nyquist-spaced 172 grid, along with Nyquist-spaced grids that are 72,92,...,152, and 192 in size. In terms of runtime relative to the 172 grid, the sparsity-enforced algorithm runs 5.9, 3.6, 2.4, 1.7, and 1.3 times faster when the 72 through 152 grids are used, and 1.2 times slower when the 192 grid is used. For each grid, we sweep over λ (like in the earlier experiments) and then compute the RMSE of various T-spoke pulses for T = 1,3,...,29. Fig. 10(B) shows RMSE as a function of grid extent and T. Grids of size 112 and up yield relatively the same RMSE, which means that runtime may be reduced without a loss of performance by using smaller grids.
Based on the grid-extent results in Fig. 10(B) and the over-sampling results in Fig. 10(A), it is sufficient for our applications to simply pick a Nyquist-sampled grid that extends out a moderate rather than far distance into k-space. There is no need to extend the grid to high spatial frequencies or oversample it by even a factor of two. The strength of the sparsity-enforced algorithm does not come from placing spokes at high or finely-sampled frequencies, but in simply tuning placements outward from low frequencies and making slight—but certainly not obvious—alterations to the placements suggested by the Fourier method.
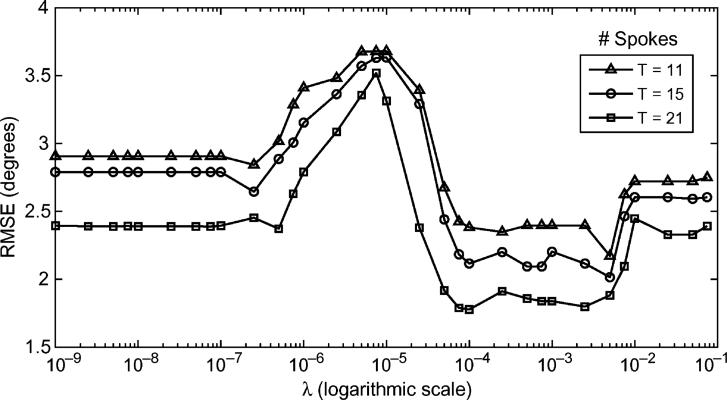
7) Sparsity-Enforced Placement: λ Sensitivity Analysis
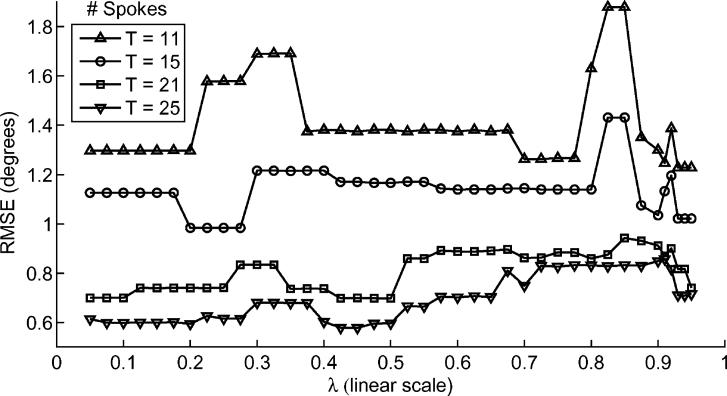
The single-channel simulation results presented in Fig. 4 assumed that a good choice of λ was known. We now do away with this assumption, presenting RMSE as a function of λ and T ∈ {11, 15, 21, 25} in Fig. 11. For small T, the choice of λ is crucial in order to best reduce RMSE, but as T increases, the algorithm's sensitivity to λ decreases significantly. Further, for fixed λ, RMSE does not exhibit a consistent trend across T.
Fig. 11.
Single-channel B1 inhomogeneity mitigation experiment: λ sensitivity analysis. The sparsity-enforced spoke placement algorithm's sensitivity to λ is analyzed when designing pulses comprised of 11, 15, 21, and 25 spokes. As T increases, sensitivity to λ decreases. Further, for fixed λ, RMSE does not exhibit a consistent trend across T.
Fig. 12 depicts the multichannel experiment's sensitivity results, showing RMSE as a function of λ and T ∈ {11, 15, 21}. As T increases, the RMSE versus λ curve moves smoothly downward. We are unsure why more erratic behavior occurs in the single-channel context (see Fig. 11).
Fig. 12.
Eight-channel system, dual-vein target: λ sensitivity analysis. The sparsity-enforced spoke placement algorithm's sensitivity to λ is analyzed when designing pulses comprised of 11, 15, and 21 spokes. For fixed λ, RMSE decreases smoothly with T, in contrast with the behavior in Fig. 11.
A fast technique for finding ideal values of λ is an open problem. We are investigating several approaches to automated selection: the “L-curve” method [63], universal parameter selection [64], and min–max parameter selection [65].
8) Runtime
In the single-channel experiments where a 172 grid is used, it takes approximately 3 min to solve (18) using our MATLAB SeDuMi implementation on a Linux-based computer with a 3.0-GHz Pentium IV processor. In the eight-channel case with the 172 grid, runtime increases nearly linearly to 25 min. In general, the random-access memory footprint of the SOC program ranges from 200−700 MB.
Runtime may be reduced via a multiresolution approach (as in [30]) by first running the algorithm with a coarse grid, noting which spoke locations are revealed, and then running the algorithm with a grid that is finely sampled around the locations suggested by the coarse result. This is faster than providing the algorithm a large, finely-sampled grid and attempting to solve the problem in one step. Further, because the desired solution to the spoke placement problem is sparse and the matrices involved are dense, solving this problem using iterative shrinkage techniques [66], [67], greedy-pursuit algorithms [25], [52], or special-purpose solvers (e.g., [68], [69]) may lead to major runtime improvements.
VII. Conclusion
We have introduced a novel algorithm for the design of fast, slice-selective MRI excitation pulses. The algorithm uses sparse approximation theory and a second-order cone optimization to place and modulate a small number of spokes in k-space to produce excitations that are capable of both exciting a thin slice and tailoring the in-plane magnetization.
The strength of sparsity-enforced spoke placement was demonstrated by designing fast, slice-selective RF pulses that mitigated B1 inhomogeneity present in a head-shaped water phantom on a 7 T single-channel system and that achieved a complex-valued target pattern using an eight-channel 3 T parallel excitation system. In both cases, the sparsity-enforced method outperformed conventional methods, producing excitations with lower RMSE when pulse duration across the methods was fixed, and producing pulses with significantly shorter durations when excitation quality across the methods was fixed. The simulation results presented throughout this paper were validated by experiments on both the single-channel 7 T system and the eight-channel 3 T parallel excitation system and showed that sparsity-enforced pulses are applicable in real scenarios. Throughout both experiments, the sparsity-enforced algorithm automated the task of spoke placement and the design of the corresponding gradients and RF waveforms, yielding placement patterns that were not obvious and would be difficult or impossible to design by hand, freeing the designer from the task of slice-selective pulse design. The algorithm was shown to be highly robust to the choice of many of its input parameters, such as the extent and sample spacing of the grid of candidate spoke locations, and relatively robust to the choice of its sparsity-enforcing control parameter, λ, when larger numbers of spokes were placed during the single-channel experiments and in general during the multichannel experiments.
With further investigation into automated λ selection and fast sparsity-enforcement algorithms, the sparsity-enforced pulse design method will have clinical impact in the areas of B1 inhomogeneity mitigation, multichannel parallel transmission, high-field imaging, and spatially-selective excitation, all of which comprise the vanguard of emerging MRI technology.
Acknowledgment
The authors would like to thank the reviewers for providing very useful advice.
This work was supported in part by the National Institutes of Health under Grant 1P41RR14075, Grant 1R01EB000790, Grant 1R01EB006847, and 1R01EB007942, in part by the National Science Foundation under Grant CCF-643836, in part by the United States Department of Defense National Defense Science and Engineering Graduate Fellowship F49620-02-C-0041, in part the MIND Institute, in part the A. A. Martinos Center for Biomedical Imaging, and in part by the R. J. Shillman Career Development Award.
Contributor Information
Adam C. Zelinski, Research Laboratory of Electronics, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology (MIT), Cambridge, MA 02139 USA..
Lawrence L. Wald, HST and the Department of Radiology, Harvard Medical School, Longwood, MA 02115 USA.
Elfar Adalsteinsson, Research Laboratory of Electronics, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology (MIT), Cambridge, MA 02139 USA and also with the Harvard-MIT Division of Health Sciences and Technology (HST), Cambridge, MA 02139 USA..
References
- 1.Hu X, Parrish T. Reduction of field of view for dynamic imaging. Magn. Reson. Med. 1994;31:691–694. doi: 10.1002/mrm.1910310618. [DOI] [PubMed] [Google Scholar]
- 2.Glover G, Lai S. Proc. Int. Soc. Magn. Reson. Med. (ISMRM) 1998. Reduction of susceptibility artifacts in BOLD fMRI using tailored RF pulses; p. 298. [Google Scholar]
- 3.Saekho S, Yip CY, Noll DC, Boada FE, Stenger VA. Fast-kz three-dimensional tailored radiofrequency pulse for reduced B1 inhomogeneity. Magn. Reson. Med. 2006;55(4):719–724. doi: 10.1002/mrm.20840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ulloa J, Hajnal JV. Proc. Int. Soc. Magn. Reson. Med. (ISMRM) Miami Beach, FL: 2005. Exploring 3D RF shimming for slice selective imaging; p. 21. [Google Scholar]
- 5.Setsompop K, Wald LL, Alagappan V, Gagoski BA, Hebrank F, Fontius U, Schmitt F, Adalsteinsson E. Parallel RF transmission with 8 channels at 3 Tesla. Magn. Reson. Med. 2006;56(5):1163–1171. doi: 10.1002/mrm.21042. [DOI] [PubMed] [Google Scholar]
- 6.Pauly JM, Nishimura D, Macovski A. A k-space analysis of small-tip angle excitation. J. Magn. Reson. 1989;81:43–56. doi: 10.1016/j.jmr.2011.09.023. [DOI] [PubMed] [Google Scholar]
- 7.Oppenheim AV, Schafer R. Discrete-Time Signal Processing. Prentice-Hall; Englewood Cliffs, NJ: 1989. [Google Scholar]
- 8.Bernstein MA, King KF, Zhou XJ. Handbook of MRI Pulse Sequences. Elsevier; New York: 2004. [Google Scholar]
- 9.Zhu Y. Parallel excitation with an array of transmit coils. Magn. Reson. Med. 2004;51(4):775–784. doi: 10.1002/mrm.20011. [DOI] [PubMed] [Google Scholar]
- 10.Ullmann P, Junge S, Wick M, Seifert F, Ruhm W, Hennig J. Experimental analysis of parallel excitation using dedicated coil setups and simultaneous RF transmission on multiple channels. Magn. Reson. Med. 2005;54(4):994–1001. doi: 10.1002/mrm.20646. [DOI] [PubMed] [Google Scholar]
- 11.Zhu Y, Watkins R, Gianquinto R, Hardy C, Kenwood G, Mathias S, Valent T, Denzin M, Hopkins J, Peterson W, Mock B. Proc. Int. Soc. Magn. Reson. Medicine (ISMRM) Miami Beach, FL: 2005. Parallel excitation on an eight transmit channel MRI system; p. 14. [Google Scholar]
- 12.Yip CY, Fessler JA, Noll DC. Advanced three-dimensional tailored RF pulse for signal recovery in T2*-weighted functional magnetic resonance imaging. Magn. Reson. Med. 2006;56(5):1050–1059. doi: 10.1002/mrm.21048. [DOI] [PubMed] [Google Scholar]
- 13.Bottomley PA, Andrew ER. RF magnetic field penetration, phase shift and power dissipation in biological tissue: Implications for NMR imaging. Phys. Med. Biol. 1978;23:630–643. doi: 10.1088/0031-9155/23/4/006. [DOI] [PubMed] [Google Scholar]
- 14.Bomsdorf H, Helzel T, Kunz D, Roschmann P, Tschendel O, Wieland J. Spectroscopy and imaging with a 4 Tesla whole-body MR system. NMR Biomed. 1988;1(3):151–158. doi: 10.1002/nbm.1940010308. [DOI] [PubMed] [Google Scholar]
- 15.Vaughan JT, Garwood M, Collins CM, Liu W, DelaBarre L, Adriany G, Anderson P, Merkle H, Goebel R, Smith MB, Ugurbil K. 7T vs. 4T: RF power, homogeneity, and signal-to-noise comparison in head images. Magn. Reson. Med. 2001;46(1):24–30. doi: 10.1002/mrm.1156. [DOI] [PubMed] [Google Scholar]
- 16.van de Moortele PF, Akgun C, Adriany G, Moeller S, Ritter J, Collins CM, Smith MB, Vaughan JT, Ugurbil K. B1 destructive interference and spatial phase patterns at 7T with a head transceiver array coil. Magn. Reson. Med. 2005;54:1503–1518. doi: 10.1002/mrm.20708. [DOI] [PubMed] [Google Scholar]
- 17.Collins CM, Wanzhan L, Schreiber W, Yang QX, Smith MB. Central brightening due to constructive interference with, without, and despite dielectric resonance. J. Magn. Reson. Imag. 2005;21(2):192–196. doi: 10.1002/jmri.20245. [DOI] [PubMed] [Google Scholar]
- 18.Jin J, Chen J. On the SAR and field inhomogeneity of birdcage coils loaded with the human head. Magn. Reson. Med. 1997;21:192–196. doi: 10.1002/mrm.1910380615. [DOI] [PubMed] [Google Scholar]
- 19.Collins CM, Li S, Smith MB. SAR and B1 field distributions in a heterogeneous human head model within a birdcage coil. Magn. Res. Med. 1998;40:847–856. doi: 10.1002/mrm.1910400610. [DOI] [PubMed] [Google Scholar]
- 20.Ibrahim TS, Lee R, Baertlein BA, Robitaille P-ML. B1 field homogeneity and SAR calculations in the high pass birdcage coil. Phys. Med. Biol. 2001;46:609–619. doi: 10.1088/0031-9155/46/2/324. [DOI] [PubMed] [Google Scholar]
- 21.Yip CY, Fessler JA, Noll DC. Proc. Int. Soc. Magn. Reson. Med. (ISMRM) Miami, FL: 2005. A novel, fast and adaptive trajectory in three-dimensional excitation k-space; p. 2350. [Google Scholar]
- 22.Davis G. Ph.D. dissertation. New York Univ.; Sep. 1994. Adaptive nonlinear approximations. [Google Scholar]
- 23.Natarajan BK. Sparse approximate solutions to linear systems. SIAM J. Comput. 1995;24(2):227–234. [Google Scholar]
- 24.Gorodnitsky IF, Rao BD. Sparse signal reconstruction from limited data using FOCUSS: A re-weighted minimum norm algorithm. IEEE Trans Signal Process. 1997 Mar.45(3):600–616. [Google Scholar]
- 25.Chen SS, Donoho DL, Saunders MA. Atomic decomposition by basis pursuit. SIAM J. Sci. Comput. 1999;20(1):33–61. [Google Scholar]
- 26.Donoho DL, Huo X. Uncertainty principles and ideal atomic decomposition. IEEE Trans. Inf. Theory. 2001 Nov.47(7):2845–2862. [Google Scholar]
- 27.Tropp JA. Ph.D. dissertation. Univ. Texas; Austin: 2004. Topics in sparse approximation. [Google Scholar]
- 28.Katscher U, Bornert P, Leussler C, van den Brink JS. Transmit SENSE. Magn. Reson. Med. 2003 Jan.49(1):144–150. doi: 10.1002/mrm.10353. [DOI] [PubMed] [Google Scholar]
- 29.Graesslin I, Vernickel P, Schmidt J, Findeklee C, Roschmann P, Leussler C, Haaker P, Laudan H, Luedeke KM, Scholz J, Buller S, Keupp J, Bornert P, Dingemans H, Mens G, Vissers G, Blom K, Swennen N, vd Heijden J, Mollevanger L, Harvey P, Katscher U. Proc. Int. Soc. Magn. Reson. Med. (ISMRM) Seattle, WA: 2006. Whole body 3T MRI system with eight parallel RF transmission channels; p. 129. [Google Scholar]
- 30.Malioutov DM, Cetin M, Willsky AS. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005 Aug.53(8):3010–3022. [Google Scholar]
- 31.Tropp JA. Just relax: Convex programming methods for identifying sparse signals. IEEE Trans. Inf. Theory. 2006 Mar.52(3):1030–1051. [Google Scholar]
- 32.Tropp JA. Algorithms for simultaneous sparse approximation: Part II: Convex relaxation. Signal Process. 2006;86(3):589–602. [Google Scholar]
- 33.Nemirovski A, Ben-Tal A. Lectures on Modern Convex Optimization. Analysis, Algorithms and Engineering Applications. SIAM; Philadelphia, PA: 2001. [Google Scholar]
- 34.Zelinski AC, Setsompop K, Goyal VK, Alagappan V, Fontius U, Schmitt F, Wald LL, Adalsteinsson E. Proc. Int. Soc. Magn. Reson. Med. (ISMRM) Berlin, Germany: 2007. Designing fast 3D RF excitations by optimizing the number, placement, and weighting of spokes in k-space via a sparsity-enforcement algorithm; p. 1691. [Google Scholar]
- 35.Setsompop K, Zelinski AC, Goyal VK, Wald LL, Adalsteinsson E. Proc. Int. Soc. Magn. Reson. Med. (ISMRM) Berlin, Germany: 2007. Sparse spokes slice-selective design for B1-inhomogeneity correction at 7T; p. 356. [Google Scholar]
- 36.Yip CY, Grissom WA, Fessler JA, Noll DC. Joint design of trajectory and RF pulses for parallel excitation. Magn. Reson. Med. 2007;58(3):598–604. doi: 10.1002/mrm.21262. [DOI] [PubMed] [Google Scholar]
- 37.Sodickson DK, Manning WJ. Simultaneous acquisition of spatial harmonics (SMASH): Fast imaging with radio frequency coil arrays. Magn. Reson. Med. 1997 Oct.38(4):591–603. doi: 10.1002/mrm.1910380414. [DOI] [PubMed] [Google Scholar]
- 38.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med. 1999 Nov.42:952–962. [PubMed] [Google Scholar]
- 39.Grissom WA, Yip CY, Zhang Z, Stenger VA, Fessler JA, Noll DC. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magn. Reson. Med. 2006;56(3):620–629. doi: 10.1002/mrm.20978. [DOI] [PubMed] [Google Scholar]
- 40.Yip CY, Fessler JA, Noll DC. Iterative RF pulse design for multidimensional, small-tip-angle selective excitation. Magn. Reson. Med. 2005;54(4):908–917. doi: 10.1002/mrm.20631. [DOI] [PubMed] [Google Scholar]
- 41.Katscher U, Graesslin I, Dingemans H, Mens G. Proc. Int. Soc. Magn. Reson. Med. (ISMRM) 2006. Experimental verification of over- and underdetermined transmit SENSE; p. 600. [Google Scholar]
- 42.Zelinski AC, Wald LL, Setsompop K, Alagappan V, Gagoski BA, Goyal VK, Hebrank F, Fontius U, Schmitt F, Adalsteinsson E. Comparison of three algorithms for solving linearized systems of parallel excitation RF waveform design equations: Experiments on an eight-channel system at 3 Tesla. Concepts Magn. Reson. Part B: Magn. Reson. Eng. 2007 Aug.31B(3):176–190. [Google Scholar]
- 43.Tikhonov AN. On the solution of incorrectly stated problems and a method of regularization. Dokl. Acad. Nauk SSSR. 1963;151:501–504. [Google Scholar]
- 44.Katscher U, Bornert P, van den Brink JS. Theoretical and numerical aspects of transmit SENSE. IEEE Trans. Med. Imag. 2004 Apr.23(4):520–525. doi: 10.1109/TMI.2004.824151. [DOI] [PubMed] [Google Scholar]
- 45.Paige CC, Saunders MA. LSQR: An algorithm for sparse linear equations and sparse least squares. ACM Trans. Math. Software. 1982 Mar.8(1):43–71. [Google Scholar]
- 46.Ernst RR, Anderson WA. Applications of Fourier transform spectroscopy to magnetic resonance. Rev. Sci. Instrum. 1966;37:93–102. [Google Scholar]
- 47.Wang J, Qiu M, Yang QX, Smith MB, Constable RT. Measurement and correction of transmitter and receivers induced nonuniformities in vivo. Magn. Reson. Med. 2005;53:408–417. doi: 10.1002/mrm.20354. [DOI] [PubMed] [Google Scholar]
- 48.Kerr AB, Cunningham CH, Pauly JM, Gianquinto RO, Watkins RD, Zhu Y. Proc. Int. Soc. Magn. Reson. Med. (ISMRM) Seattle, WA: 2006. Self-calibrated transmit SENSE; p. 14. [Google Scholar]
- 49.Boyd S, Vandenberghe L. Convex Optimization. Cambridge Univ. Press; Cambridge, U.K.: Mar. 2004. [Google Scholar]
- 50.Donoho DL. For most large underdetermined systems of linear equations, the minimal l1-norm near-solution approximates the sparsest near-solution. Commun. Pure Appl. Math. 2006 Jul.59(7):907–934. [Google Scholar]
- 51.Tibshirani R. Regression shrinkage and selection via the lasso. (ser. B).J. Roy. Statist. Soc. 1996 Nov.B 58(1):267–288. [Google Scholar]
- 52.Tropp JA, Gilbert AC, Strauss MJ. Algorithms for simultaneous sparse approximation: Part I: Greedy pursuit. Signal Process. 2006;86(3):572–588. [Google Scholar]
- 53.Sturm J. Using sedumi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optimizat. Methods Software. 1999;11−12:625–653. [Google Scholar]
- 54.Toh KC, Todd MJ, Tutuncu RH. SDPT3—A matlab software package for semidefinite programming,” Optimizat. Methods Software. 1999;11(12):545–581. [Google Scholar]
- 55.Luenberger DG. Optimization by Vector Space Methods. Wiley; New York: 1969. [Google Scholar]
- 56.Ullmann P, Junge S, Seifert F, Ruhm W, Hennig J. Proc. Int. Soc. Magn. Reson. Med. (ISMRM) Berlin, Germany: 2007. Parallel excitation experiments using a novel direct calibration technique for RF-pulse determination; p. 672. [Google Scholar]
- 57.Tropp J. Proc. Soc. Magn. Reson. Med. (SMRM) Berlin, Germany: 1992. The hybrid bird cage resonator; p. 4009. [Google Scholar]
- 58.Barberi EA, Gati JS, Rutt BK, Menon RS. A transmit-only/receive-only (TORO) RF system for high-field MRI/MRS applications. Magn Reson Med. 2000;43:284–289. doi: 10.1002/(sici)1522-2594(200002)43:2<284::aid-mrm16>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
- 59.Alagappan V, Wiggins GC, Potthast A, Setsompop K, Adalsteinsson E, Wald LL. Proc. Int. Soc. Magn. Reson. Med. (ISMRM) Seattle, WA: 2006. An 8 channel transmit coil for transmit sense at 3T; p. 121. [Google Scholar]
- 60.Powell MJD. A fast algorithm for nonlinearly constrained optimization calculations. Lecture Notes Math. 1978;630:144–157. [Google Scholar]
- 61.Dumoulin CL, Hart HR. Magnetic resonance angiography. Radiology. 1986;161:717–720. doi: 10.1148/radiology.161.3.3786721. [DOI] [PubMed] [Google Scholar]
- 62.Souza SP, Dumoulin CL. Phase-contrast magnetic resonance angiography. Proc. 11th Annu. Int. Conf. Eng. Med. Biol. Soc. 1989;2:514–515. [Google Scholar]
- 63.Hansen PC. Regularization tools: A matlab package for analysis and solution of discrete ill-posed problems. Numer. Algor. 1994;6:1–35. [Google Scholar]
- 64.Donoho DL, Johnstone IM. Ideal spatial adaptation by wavelet shrinkage. Biometrica. 1994 Aug.81(3):425–455. [Google Scholar]
- 65.Johnstone IM. On minimax estimation of a sparse normal mean vector. Ann. Stat. 1994 Mar.22(1):271–289. [Google Scholar]
- 66.Daubechies I, Defrise M, Mol CD. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Comm. Pure Appl. Math. 2004;57(11):1413–1457. [Google Scholar]
- 67.Elad M, Matalon B, Zibulevsky M. Image denoising with shrinkage and redundant representations. Proc. IEEE Comput. Vis. Pattern Recognit. 2006;2:1924–1931. [Google Scholar]
- 68.Saunders MA, Kim B. PDCO: Primal-dual interior method for convex objectives. [Online]. Available: http://www.stanford.edu/group/SOL/software/pdco.html.
- 69.Kim S-J, Koh K, Lustig M, Boyd S, Gorinevsky D. A method for large-scale-regularized least squares problems with applications in signal processing and statistics. Stanford Univ.; Stanford, CA: 2007. [Online]. Available: http://www.stanford.edu/~boyd/reports/l1_ls.pdf. [Google Scholar]