Parenchymal Texture Analysis in Digital Breast Tomosynthesis for Breast Cancer Risk Estimation: A Preliminary Study

Abstract

Rationale and Objectives

Studies have demonstrated a relationship between mammographic parenchymal texture and breast cancer risk. Although promising, texture analysis in mammograms is limited by tissue superimposition. Digital breast tomosynthesis (DBT) is a novel tomographic x-ray breast imaging modality that alleviates the effect of tissue superimposition, offering superior parenchymal texture visualization compared to mammography. Our study investigates the potential advantages of DBT parenchymal texture analysis for breast cancer risk estimation.

Materials and Methods

DBT and digital mammography (DM) images of 39 women were analyzed. Texture features, shown in studies with mammograms to correlate with cancer risk, were computed from the retroareolar breast region. We compared the relative performance of DBT and DM texture features in correlating with two measures of breast cancer risk: (i) the Gail and Claus risk estimates, and (ii) mammographic breast density. Linear regression was performed to model the association between texture features and increasing levels of risk.

Results

No significant correlation was detected between parenchymal texture and the Gail and Claus risk estimates. Significant correlations were observed between texture features and breast density. Overall, the DBT texture features demonstrated stronger correlations with breast percent density (PD) than DM (p ≤0.05). When dividing our study population in groups of increasing breast PD, the DBT texture features appeared to be more discriminative, having regression lines with overall lower p-values, steeper slopes, and higher R² estimates.

Conclusion

Although preliminary, our results suggest that DBT parenchymal texture analysis could provide more accurate characterization of breast density patterns, which could ultimately improve breast cancer risk estimation.

1. Introduction

The ability to estimate a woman’s risk of developing breast cancer risk is becoming increasingly important in clinical practice. Breast cancer risk assessment is used as a criterion to form guidelines for offering customized screening recommendations (1), to tailor individual breast cancer treatments (2), and to form preventive strategies (3), especially for women associated with a higher risk. Currently, breast cancer risk assessment is limited both by the existing epidemiological risk estimation models, and by the breast imaging methods that have been considered to date.

The current gold standards for breast cancer risk estimation, the Gail and Claus models (4, 5), are multivariate statistical models based primarily on non-modifiable demographic, clinical, and hereditary risk factors. With the exception of childbirth as a modifiable risk factor, the Gail model estimates the risk of breast cancer based on factors, such as age at menarche, first degree relatives with cancer, and prior biopsies (4). The Claus model relies on the assumption that susceptibility to breast cancer is primarily regulated by a rare autosomal dominant allele, and therefore estimates the risk of breast cancer based only on familial history of breast cancer, including ages at onset of relatives affected by breast cancer (5). Evaluation of the Gail model has shown that, despite its good calibration for population-based risk assessment, it has modest discriminatory accuracy at the individual level (6). Studies evaluating the accuracy of models that predict genetic susceptibility to breast cancer, including the Claus model, have shown that there is a potential to overestimate the expected number of women as high risk for a genetic mutation (7). Considering also that individual risk can be reduced due to interventions such as chemoprevention (8), the Gail and Claus models lack the desired flexibility to estimate adjustments to risk levels.

Breast parenchymal patterns, on the other hand, appear to be indicative of changes in modifiable risk factors for breast cancer, such as hormonal levels, diet, and body mass index (9–12). Starting from the pioneering work of Wolfe in 1976 (13), numerous studies have demonstrated a relationship between mammographic parenchymal patterns and the risk of developing breast cancer (14). Parenchymal patterns in x-ray breast images are formed by the distribution of fatty, glandular, and stromal breast tissues (15); the underlying assumption is that the composition of breast tissue appears to be related, through currently unknown biological mechanisms, with factors that are associated with the development of breast cancer (16, 17). Currently, growing evidence suggests that mammographic breast density is a strong independent risk factor for breast cancer, being indicative of a woman’s relative risk of developing breast cancer (18–21). Preliminary studies have shown the potential to increase the accuracy of the Gail model by including breast density descriptors (22–24); nevertheless, these improvements have been minimal, mostly due to the subjective nature of breast density assessment.

While the relationship between mammographic breast density and breast cancer risk has been clearly demonstrated, studies have also shown that a potential relationship exists between mammographic parenchymal texture and the risk of breast cancer (25, 26). Computerized analysis of digitized mammograms has shown the potential to distinguish the parenchymal patterns of BRCA1/2 gene mutation carriers using parenchymal texture features, particularly from the retroareolar breast region (27–31). These studies suggest that computer-extracted texture features could provide alternative, fully-automated, objective, and reproducible methods to identify parenchymal patterns that are associated with increased levels of risk.

Mammograms, however, are projection images in which the breast tissue layers are superimposed. For this reason, mammographic texture features reflect mixed properties of superficial skin and subcutaneous tissue overlapping deeper fibro-glandular (i.e., dense) and fatty (i.e., non-dense) tissues. Knowing that the risk of breast cancer is mainly associated with properties of the fibro-glandular tissue (i.e., breast density), superficial layers of skin or subcutaneous fat could be considered as anatomical noise to breast cancer risk estimation, and therefore reduce the predictive value of the computed texture features. To overcome this limitation of mammography, tomographic breast imaging could offer the ability to selectively analyze the fibro-glandular tissue texture, and ultimately provide more accurate measures to estimate risk (32).

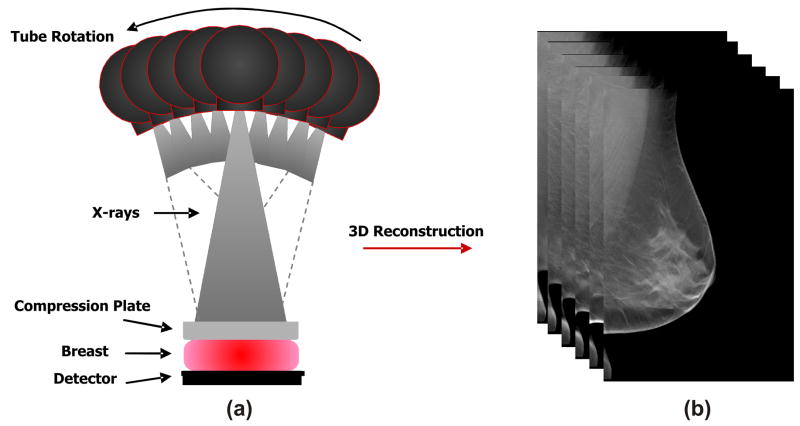
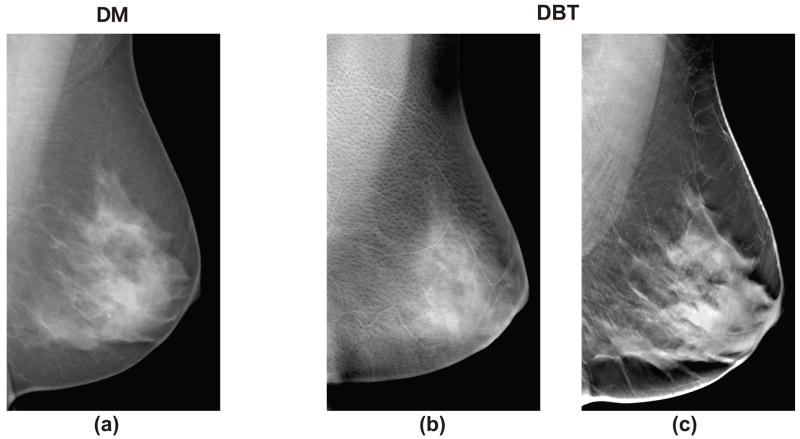
Digital breast tomosynthesis (DBT) is an emerging x-ray imaging modality in which tomographic images of the breast are reconstructed in 3D from multiple low-dose 2D x-ray source projection images that are acquired by varying the angle of the x-ray tube (33, 34) (Figure 1. a). By combining information from different projections, DBT filters out the adjacent anatomical structures, alleviating the effect of tissue superimposition (Figure 1. b). Clinical trials have shown that DBT provides superior tissue visualization and improved lesion conspicuity in comparison to projection mammography, resulting in higher sensitivity and specificity (35, 36). Compared to mammography (Figure 2. a), DBT also offers superior texture visualization, by separating the superficial skin and subcutaneous fat layers (Figure 2. b) from the deeper fibro-glandular parenchymal tissues (Figure 2. c). Therefore, DBT could offer the ability to selectively analyze the fibro-glandular tissue texture, having the potential to provide more accurate features to characterize parenchymal texture patterns, and ultimately provide more accurate means for breast cancer risk estimation.

Figure 1.

An illustrative example of (a) digital breast tomosynthesis acquisition geometry with (b) the reconstructed tomographic breast image.

Figure 2.

Differences in parenchymal texture in (a) a digital mammogram (DM) and (b–c) the digital breast tomosynthesis (DBT) tomographic slices for the same breast, where (b) the superficial skin layer, in which skin pore texture is visible, is separated from (c) the deeper fibro-glandular tissue layers.

In this paper we present an exploratory study that investigates the potential advantages of DBT parenchymal texture analysis for breast cancer risk estimation. Parenchymal patterns of 39 women were analyzed both in DBT images and their corresponding digital mammograms (DM). We compared the relative performance of the DBT and the DM texture features in correlating with two established measures of breast cancer risk: (i) the Gail and Claus model risk estimates, and (ii) mammographic breast density. Although preliminary, our results suggest that DBT parenchymal texture analysis could potentially provide more discriminative features for breast cancer risk estimation, in comparison to DM. To the best of our knowledge, our study is the first to investigate the potential advantages of DBT parenchymal analysis for breast cancer risk assessment, with the intention to offer instrumental evidence for the design of larger clinical studies in the future. The improved performance and low cost of breast DBT will likely fuel the rapid and broad dissemination of DBT as a breast cancer screening modality. Our long term goal is to develop DBT biomarkers that can be used to improve breast cancer risk estimation in clinical practice by providing Computer-Assisted Risk Estimation (CARe) for breast cancer.

2. Materials and Methods

Patient recruitment

The images included in our analysis have been retrospectively collected, under Institutional Review Board (IRB) protocol approval and HIPAA regulations, from a multimodality breast imaging clinical trial in the Radiology Department at the University of Pennsylvania^†. The goal of this clinical trial was to develop an understanding of the relative performance of new-generation breast imaging modalities. Eligible participants included women at high risk (>25% Gail and Claus lifetime risk), women with recently detected abnormalities, and follow-up of previous cancer patients. All women were volunteers who signed informed consent. From March 2002 to August 2007 a total of 886 women enrolled in the trial. Within the same day, the women were imaged with DM, whole breast ultrasound, MRI, PET, and optical imaging. The individual imaging results were reviewed in a consensus meeting of expert radiologists to determine relative performance of the breast imaging modalities; the associated clinical information for each woman, such as pathology, likelihood of malignancy, and Breast Imaging Reporting and Data System (BIRADS) (37) lesion characterization was also recorded as part of the study. During the period of August 2004 to August 2005, a prototype DBT system was operating under research investigation and DBT was offered as an option to the women participating in the clinical trial. During this period, a total of 52 women agreed to also receive DBT imaging.

Breast imaging

DBT and DM imaging was performed at the Breast Imaging Section of the Radiology Department at the University of Pennsylvania. The images were acquired with a commercial Full-Field Digital Mammography (FFDM) GE Senographe 2000D system (GE Healthcare, Chalfont St. Giles, U.K.), modified under IRB approval to perform DBT; the x-ray gantry was adapted to allow independent rotation of the x-ray tube, in order to acquire 9 source projection images by varying the x-ray tube angle from −25° to +25° in increments of 6.25° (38, 39). The breast was immobilized and compressed in a medio-lateral oblique (MLO) position with light compression force (50–70N) for DBT, and typical compression force (80–180N) for DM. Both DBT source projection images and DMs were acquired with spatial resolution of 0.1 mm/pixel and 12 bit gray level. A custom filtered-backprojection implementation was used to reconstruct the 3D DBT images at 0.22mm in-plane resolution and 15 bit gray level with 1mm tomographic slice spacing (40). The DM images were post-processed with the GE Premium View^™ algorithm (GE Healthcare, Chalfont St. Giles, U.K.). All images were stored in DICOM format in our laboratory’s Medical Imaging Resource Center (MIRC) database (41).

Study population and risk evaluation

Bilateral DBT and DM images from a total 39 women were retrospectively collected and analyzed for our study; women with bilateral breast cancer were not included in our study population. In addition, women with unilateral imaging, incomplete data and significant technical image artifacts were excluded. From the 39 women included in our study population, 30 were diagnosed with breast cancer. For the women diagnosed with cancer, only the contralateral breast was analyzed. Our earlier studies demonstrated a strong correlation of parenchymal texture between breasts, indicating that texture patterns appear to be inherent in a woman’s parenchyma (42); in our current study, parenchymal properties of the unaffected breast were considered as a surrogate of breast cancer risk. In order to obtain an assessment of each woman’s breast cancer risk profile, two different estimates were obtained: (i) the Gail and Claus model risk estimates and (ii) the mammographic breast density. Both of these measures are currently used in clinical practice to counsel women that seek risk assessment evaluation in order to receive customized breast screening (1–3, 19).

The Gail and Claus risk estimates were calculated for each woman using data acquired as part of their participation in the multimodality breast imaging trial (4, 5). The number of first degree relatives with breast cancer, the number of benign biopsies, the age at menarche and age at first live birth, and the woman’s race were used as inputs to the NCI’s breast cancer risk assessment tool (43), to calculate the Gail lifetime breast cancer risk estimate. In addition, a list of each woman’s first- and second-degree relatives with breast or ovarian cancer history, as well as the age of onset, was used to calculate the corresponding Claus lifetime breast cancer risk estimate (5).

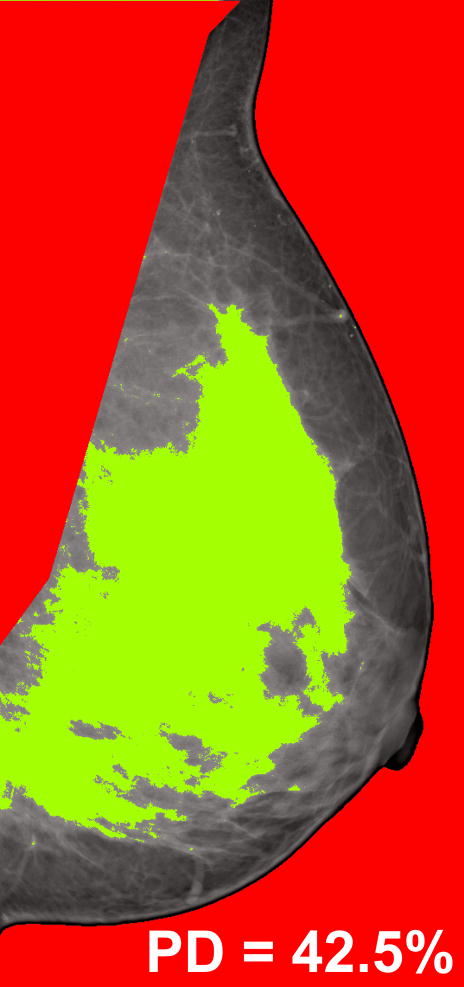
Mammographic breast density was estimated using Cumulus (Ver. 4.0 2006, University of Toronto), a widely validated software for breast percent density (PD) estimation (19, 44, 45). Cumulus provides the user with the ability to exclude image background and the pectoral muscle region; gray-level intensity thresholds are defined manually in order to segment the glandular tissue area within the breast. Breast PD is then computed on a continuous scale as the percentage of the total breast region occupied by glandular tissue (45) (Figure 3). In our study, breast PD estimation was performed by a breast imaging specialist with experience in using Cumulus (PRB) (39, 46, 47). To calculate intra-observer variability and reproducibility, the images were processed twice, with an interim time period of two months between the two readings (47); the average of the two breast PD estimates for each woman was used as a breast cancer risk surrogate in our experiments.

Figure 3.

Illustration of the Cumulus (Ver. 4, 2006) software thresholding technique used for mammographic breast percent density (PD) estimation: the image background and the pectoral muscle are excluded (in red), and the dense tissue is segmented by gray-level thresholding (in green). PD is then estimated as the percent of dense tissue within the delineated breast region.

Image analysis

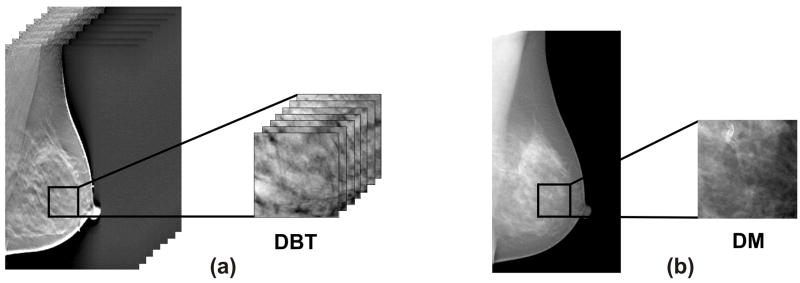
A region of interest (ROI) was manually segmented from the central breast region behind the nipple (i.e. retroareolar region) in each image. The physical dimensions of the ROIs were selected to be (2.5cm)³ for the DBT images, and (2.5cm)² for the DM images, based on previous suggestions in the literature (30). Corresponding to these physical dimensions, retroareolar 116×116×26 pixel ROIs at 0.22mm/pixel in-plane resolution and 1mm tomographic slice spacing were segmented from all the reconstructed DBT images; matching 256×256 pixel ROIs at 0.1mm/pixel resolution were segmented in the corresponding spatial location from the DM of the same breast. Examples of such ROIs are shown in Figure 4.

Figure 4.

An illustrative example of (a) a 3D ROI segmented from a reconstructed digital breast tomosynthesis (DBT) image and (b) the corresponding 2D ROI from the digital mammogram (DM) of the same breast.

To characterize the parenchymal pattern, texture features of skewness, coarseness, contrast, energy, homogeneity, and fractal dimension were estimated from all the DBT and DM ROIs. These texture features were originally defined for 2D image analysis, and have been previously used for breast cancer risk assessment in studies with digitized mammograms (27–31, 48).

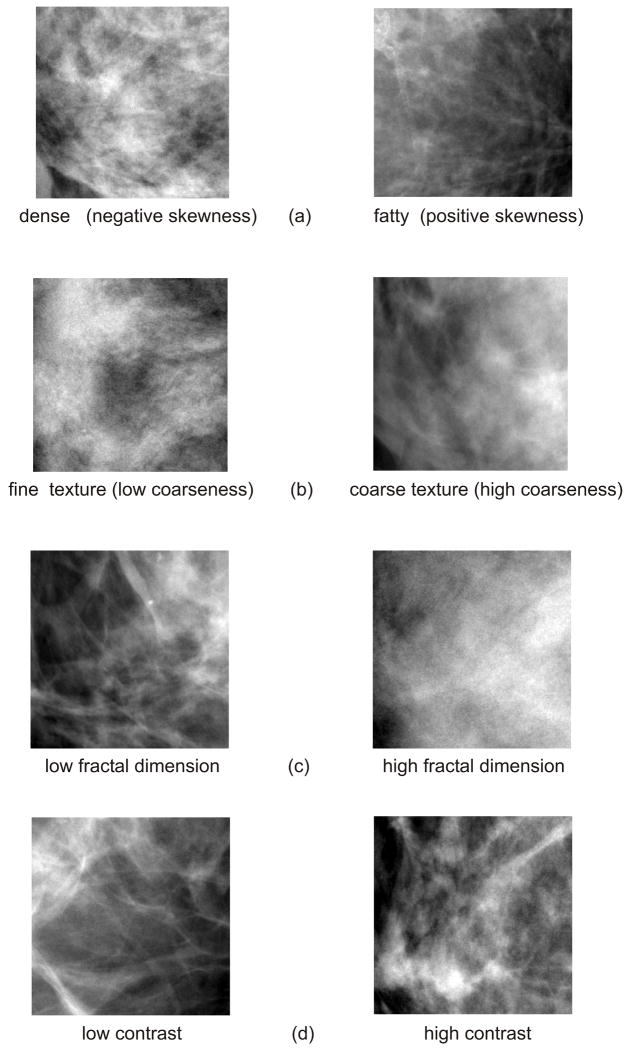
Skewness reflects the asymmetry of the gray-level pixel value distribution and has been used to assess parenchymal density (29, 45). When the image texture is predominantly composed of fat, the gray-level histogram is skewed to higher values and the skewness tends to be positive, whereas when the texture is primarily formed by dense tissue, the gray-level histogram is skewed to lower values, and the skewness values are negative. Coarseness reflects the local granularity (i.e. roughness) in image texture and is based on the computation of the neighborhood gray tone difference matrix (NGTDM) (29, 49). Small coarseness value for an ROI indicates fine texture with higher variation in gray level values in neighboring pixels, while high coarseness value indicates coarse texture, where neighboring pixels have similar gray level values. Contrast quantifies overall variation in image intensity, providing a measure of the intensity contrast between neighboring pixels over the entire image. Energy is a measure of texture uniformity of the gray-level spatial distribution. Homogeneity increases with less contrast in the image and is used to reflect the heterogeneity of the texture pattern. Fractal dimension indicates the measure of self-similarity in the texture pattern and the overall texture roughness at different scales. Figure 5 shows representative examples of mammographic texture patterns.

Figure 5.

Examples of various mammographic texture patterns: (a) skewness, (b) coarseness, (c) fractal dimension, and (d) contrast.

While texture analysis methods have been widely implemented for the analysis of 2D medical images (50), the available techniques for 3D texture analysis are currently limited. Few reports have been published in the literature that introduce 3D texture analysis methods for medical images (51–54). Recently Chen et al. demonstrated an extension of the conventional 2D co-occurrence texture analysis methods for 3D contrast-enhanced magnetic resonance images (54). In our study, two approaches were implemented for texture analysis in the 3D reconstructed DBT images: (i) tomographic and (ii) volumetric texture analysis.

Tomographic (2D) texture analysis

For each texture descriptor, a feature f_i, i=1,…, T was computed from each tomographic slice of the 3D DBT ROI (T=26 slices in each ROI, 1mm/slice), resulting to a feature vector F_T = [f₁,…, f_T] for each ROI. The mean of the feature vector, F̄_T, was used as the representative feature for the ROI.

Skewness is the third statistical moment and was computed as:

$$\mathit{skewness}=\frac{w_3}{w_2^{3/2}},w_k=\sum _{i=0}^{g_{max}}{n}_i{(i-\overline{i})}^k/N,N=\sum _{i=0}^{g_{max}}{n}_i,\overline{i}=\sum _{i=0}^{g_{max}}(i{n}_i/N)$$ (Eq. 1)

and n_i represents the number of times that gray level value i occurs in the image region, g_max is the maximum gray-level value, and N is the total number of image pixels.

Coarseness computation is based on the NGTDM (29, 49) of the gray-level values within the image region; this matrix is derived by estimating the difference between the gray-level value of each pixel and the average gray-level value of the pixels around a neighborhood window.

$$\mathit{coarseness}={\left(\sum _{i=0}^{g_{max}}{p}_{i}v(i)\right)}^{-1}\text{and}v(i)=\left\{\begin{array}{c}\sum \mid i={\overline{L}}_i\mid \mathit{for}i\in \left\{n_i\right\}if{n}_i\ne 0\\ 0\mathit{otherwise}\end{array}\right\},$$ (Eq. 2)

where v(i) is the NGTDM. In the above formulas, g_max is the maximum gray-level value, p_i is the probability that gray level i occurs, {n_i} is the set of pixels having gray level value equal to i, and L̄_i is given by:

$${\overline{L}}_i=\frac{1}{S-1}\sum _{k=-t}^t\sum _{l=-t}^{t}j(x+k,y+l),$$ (Eq. 3)

where j(x,y) is the pixel located at (x,y) with gray level value i, (k,l)≠(0,0) and S=(2t +1)² with t=1 specifying the neighborhood size around the pixel located at (x,y).

Contrast, Energy, and Homogeneity, as proposed originally by Haralick (55), require the computation of second-order statistics derived from the gray-level co-occurrence matrix; the spatial dependence of gray-levels is estimated by calculating the frequency of the spatial co-occurrence of gray-levels in the image (55).

$$\mathit{contrast}=\sum _{i=0}^{g_{max}}\sum _{j=0}^{g_{max}}\mid i-j{\mid }^{2}C(i,j),\mathit{energy}=\sum _{i=0}^{g_{max}}\sum _{j=0}^{g_{max}}C{(i,j)}^2,\mathit{homogeneity}=\sum _{i=0}^{g_{max}}\sum _{j=0}^{g_{max}}\frac{C(i,j)}{1+\mid i-j\mid }$$ (Eq. 4)

where g_max is the maximum gray-level value and C is the normalized co-occurrence matrix (55). To optimize the computation of the gray-level co-occurrence statistics, gray-level quantization was implemented (42). The co-occurrence frequencies were calculated symmetrically in the four directions around each pixel using a displacement vector d = (dx, dy) along x and y dimensions, where dx=dy=1 pixel offset. The texture features calculated in each of these four directions were averaged to create a single measure that was used in our experiments.

Fractal dimension (FD) was estimated based on the power spectrum of the Fourier transform of the image (48, 56). The 2D Discrete Fourier Transform (DFT) was performed using the Fast Fourier Transform (FFT) algorithm as:

$$F(u,v)=\sum _{m=0}^{M-1}\sum _{n=0}^{N-1}I(m,n)e^{-j(2\pi /\text{M})um}{e}^{-j(2\pi /N)vn},u=0,1,\dots ,M-1v=0,1,\dots N-1,$$ (Eq. 5)

where I is the 2D image region of size (M, N), and u and v are the spatial frequencies in the x and y directions. The power spectral density P was estimated from F(u,v) as:

$$P(u,v)=\mid F(u,v){\mid }^2.$$ (Eq. 6)

To compute the FD, P was averaged over radial slices spanning the FFT frequency domain. The frequency space was uniformly divided in 24 directions, with each direction uniformly sampled at 30 points along the radial component. To calculate the FD the least-squares-fit of the log(P_f) versus log(f) was estimated, where $f=\sqrt{u^2+v^2}$ denotes the radial frequency (56). The FD is related to the slope β of this log-log plot by:

$$FD=\frac{3D_T+2-\beta }{2}=\frac{8-\beta }{2},$$ (Eq. 7)

where D_T is the topological dimension, and is equal to D_T=2 for a 2D image.

Volumetric (3D) texture analysis

The conventional 2D texture descriptors were extended to 3D by considering a 3D neighborhood of voxels (i.e. volume elements), rather than a 2D neighborhood of pixels, when computing gray-level texture statistics.

Skewness was again computed as the third moment of the gray-level histogram as in Eq 1; however, the gray-level histogram of the ROI was estimated using the gray-level values from the entire 3D ROI volume, rather than separately for each tomographic plane. This is a valid 3D adaptation of the skewness definition, since skewness does not dependent on the spatial co-occurrence of gray-levels.

For coarseness, the local differences in gray-level values, required for the computation of the NGTDM, were estimated within a 3D neighborhood of voxels. More specifically the definition of L̄_i in Eq. 3 was modified as follows, to account for a 3D rather than a 2D neighborhood of voxels:

$${\overline{L}}_i=\frac{1}{S-1}\sum _{k=-t}^t\sum _{l=-t}^t\sum _{q=-t}^{t}j(x+k,y+l,z+q).$$ (Eq. 8)

Here j(x,y,z) is the voxel located at (x,y,z) with gray level value i, (k,l,z)≠(0,0,0), and S=(2t +1)³ with t =1 specifying the 3D voxel window around (x,y,z).

For contrast, energy, and homogeneity, the gray-level co-occurrence statistics, required for the computation of the co-occurrence matrix in Eq. 4, were estimated based on the spatial co-occurrence frequencies of voxel gray-level values within the entire 3D ROI volume similar to the approach of Chen et al. (54). A 3D displacement vector d = (dx, dy, dz) was defined around each voxel along the x, y, and z dimensions, where dx=dy=dz=1 is the voxel offset; resulting in 26 neighboring voxel-pairs in 13 independent symmetric directions. Texture features were calculated in each of these 13 directions and they were averaged to create a single measure that was used in our experiments.

Fractal dimension (FD) was estimated based on the power spectrum of the 3D Fourier transform of the image. The 3D DFT was performed for the entire 3D ROI using the FFT algorithm:

$$F(u,v,w)=\sum _{m=0}^{M-1}\sum _{n=0}^{N-1}\sum _{k=0}^{K-1}I(m,n,k)e^{-j(2\pi /\text{M})um}{e}^{-j(2\pi /N)vn}{e}^{-j(2\pi /K)wk},$$ (Eq. 9)

where I is the 3D image region of size (M, N, K), and u, v and w are the spatial frequencies in the x, y, and z directions respectively. The power spectral density (PSD) was estimated as:

$$P(u,v,w)=\mid F(u,v,w){\mid }^2.$$ (Eq. 10)

To compute the FD, P was averaged over radial sectors spanning the 3D FFT frequency domain. The frequency space was evenly divided in 24 azimuth and 12 zenith directions, and each direction was uniformly sampled at 30 points along the radial component. To calculate the FD, the least-squares-fit of the log(P_f) versus log(f) was estimated, where $f=\sqrt{u^2+v^2+w^2}$ denotes the radial frequency in spherical coordinates (56). The FD is related to the slope β of this log-log plot as defined in Eq. 7, and for D_T=3 in 3D:

$$FD=\frac{11-\beta }{2}.$$ (Eq. 10)

Texture association with Gail and Claus risk estimates

To assess the relationship between parenchymal texture descriptors and the Gail and Claus model breast cancer risk estimates, the Pearson correlation coefficient r (57) was computed between the continuous Gail and Claus lifetime risk estimates and the features of each individual parenchymal texture descriptor, along with associated p-values and 95% confidence intervals. The p-value was estimated to reflect the probability of having a correlation as large as the observed value by random chance when the true correlation is zero. The p-value was computed by transforming the r correlation coefficient into a t-statistic having n-2 degrees of freedom, where n was the number of women in our study population (n=39). The confidence bounds of the p-value were approximated using an asymptotic normal distribution of 0.5×log((1+r)/(1−r)), with an approximate variance equal to 1/(n−3) (58). These bounds are accurate by approximation when the sample has a multivariate normal distribution. The correlation coefficients and the corresponding p-values were used to compare the performance of DBT to that of DM.

Texture association with breast density estimates

To examine the association between parenchymal texture patterns and breast density, two approaches were followed:

1. For each texture descriptor, the Pearson correlation coefficient, and the associated p-value, was computed between the parenchymal texture features and the corresponding continuous breast PD estimates.

2. To further examine differences in texture patterns between groups of women at different risk levels, we compared the distributions of parenchymal texture features across categories of increasing breast PD; the risk of breast cancer is known to increase with increasing breast density (19). We divided our study population according to the recommendations published by Boyd et. al (19); the women were separated in groups of increasing breast PD as: Group 1: (0% ≤ PD < 10%), Group 2: (10% ≤ PD < 25%), Group 3: (25% ≤ PD < 50%), Group 4: (50% ≤ PD <75%), and Group 5: (75% ≤ PD < 100%). Linear regression models were estimated to predict parenchymal texture features using the increasing breast PD categories; estimates of R² values were used to assess goodness of fit. Statistical significance was determined using two-sided, 0.05-level tests. In addition to examining the association between individual texture features and increasing categories of breast density, the features were also combined into one representative parenchymal feature using principal component analysis (PCA) (59). Linear regression was also performed to model the association between increasing categories of breast PD and the PCA feature.

3. Results

Descriptive statistics

Age, breast PD and the Gail risk estimates for the women in our study population followed an approximate normal distribution (Lilliefors test, at α=0.05 significance level, p_age=0.49, p_Gail=0.16, p_PD=0.06). The women’s ages ranged from 31–80 years and their mean age (±std) was 51.4±12 years. Their Gail lifetime breast cancer risk ranged between 1.8%–30.3% with a mean (±std) of 10.5%±5.8%. The breast PD estimates ranged from 5.9%–82.8% with a mean of 38.9%±19.8%. The within-subject Pearson correlation coefficient for the two readings of breast PD estimation was 0.89 and the Jaccard coefficient (60) of the spatial correlation between the dense regions segmented at the different readings was 0.78±0.15. Due to the increased prevalence of women with no family history of breast cancer in our population (i.e., Claus lifetime risk equal to 0.0%), the corresponding Claus risk estimates did not follow a normal distribution (Lilliefors test, at α=0.01 significance level, p<0.001). Claus lifetime risk ranged from 0%–41.4%, with a mean of 5.8%.

Correlation between DBT and DM texture features

Table 1 shows the computed Pearson correlation coefficient r between the DBT features, computed both with the tomographic (i.e. 2D) and the volumetric (i.e. 3D) approach, and the DM texture features. Overall, significant correlations were observed between the 2D DBT and the DM texture features; fractal dimension demonstrated a particularly strong correlation (r=0.73, p<0.001). These correlations were, on average, lower between the 3D DBT features and the DM texture features. Overall, very strong correlations were observed between the 2D and the 3D DBT features; however, in this case, fractal dimension demonstrated a particularly low correlation (r=0.01, p=0.91).

Table 1.

Correlation between the digital breast tomosynthesis (DBT) and the digital mammography (DM) parenchymal texture features, with associated p-values in parentheses.

	Pearson Correlation Coefficients r (p-values)
	2D DBT†vs. DM	3D DBT‡vs. DM	2D DBT vs. 3D DBT
Skewness	−0.07 (0.65)	−0.08 (0.59)	0.99 (0.00)**
Coarseness	0.37 (0.02)*	0.25 (0.12)	0.97 (0.00)**
Contrast	0.46 (0.003)**	0.41 (0.008)**	0.98 (0.00)**
Energy	0.16 (0.31)	0.37 (0.02)*	0.79 (0.00)**
Homogeneity	0.50 (<0.001)**	0.51 (<0.001)**	0.98 (0.00)**
Fractal Dim	0.73 (<0.001)**	0.27 (0.09)	0.01 (0.91)

^†2D DBT: 2D tomographic texture features

^‡3D DBT: 3D volumetric texture features

^*for p ≤ 0.05,

^**for p ≤ 0.01

Texture Correlation with Gail and Claus risk estimates

Table 2 shows the computed Pearson correlation coefficient r, and associated p-values, between the parenchymal texture features and the corresponding Gail and Claus lifetime breast cancer risk estimates. Overall, low correlations were detected; with the exception of DBT skewness and Claus risk, no other correlation was statistically significant (p<0.05). For our study population, neither DBT nor DM appeared to be superior in correlating parenchymal texture patterns with the breast cancer risk estimates of the Gail and Claus models.

Table 2.

Correlation between digital mammography (DM) and digital breast tomosynthesis (DBT) parenchymal texture features and the Gail and Claus lifetime breast cancer risk estimates.

	Pearson Correlation Coefficients r (p-values)
	Gail Risk			Claus Risk
	DM	2D DBT	3D DBT	DM	2D DBT	3D DBT
Skewness	0.01 (0.97)	0.04 (0.81)	0.05 (0.74)	−0.07 (0.69)	0.32 (0.05)*	0.33 (0.04)*
Coarseness	0.06 (0.72)	0.03 (0.83)	0.03 (0.86)	−0.08 (0.61)	0.14 (0.39)	0.15 (0.35)
Contrast	0.00 (0.99)	−0.03 (0.86)	−0.04 (0.80)	−0.11 (0.50)	−0.09 (0.57)	−0.10 (0.55)
Energy	−0.24 (0.14)	−0.03 (0.85)	−0.11 (0.50)	−0.24 (0.13)	−0.20 (0.13)	−0.16 (0.34)
Homogeneity	0.01 (0.95)	0.02 (0.92)	0.02 (0.88)	0.20 (0.22)	0.09 (0.60)	0.10 (0.53)
Fractal Dim	0.02 (0.92)	0.19 (0.24)	−0.01 (0.95)	−0.02 (0.88)	−0.01 (0.94)	0.03 (0.85)

^*for p ≤ 0.05

Texture correlation with breast density

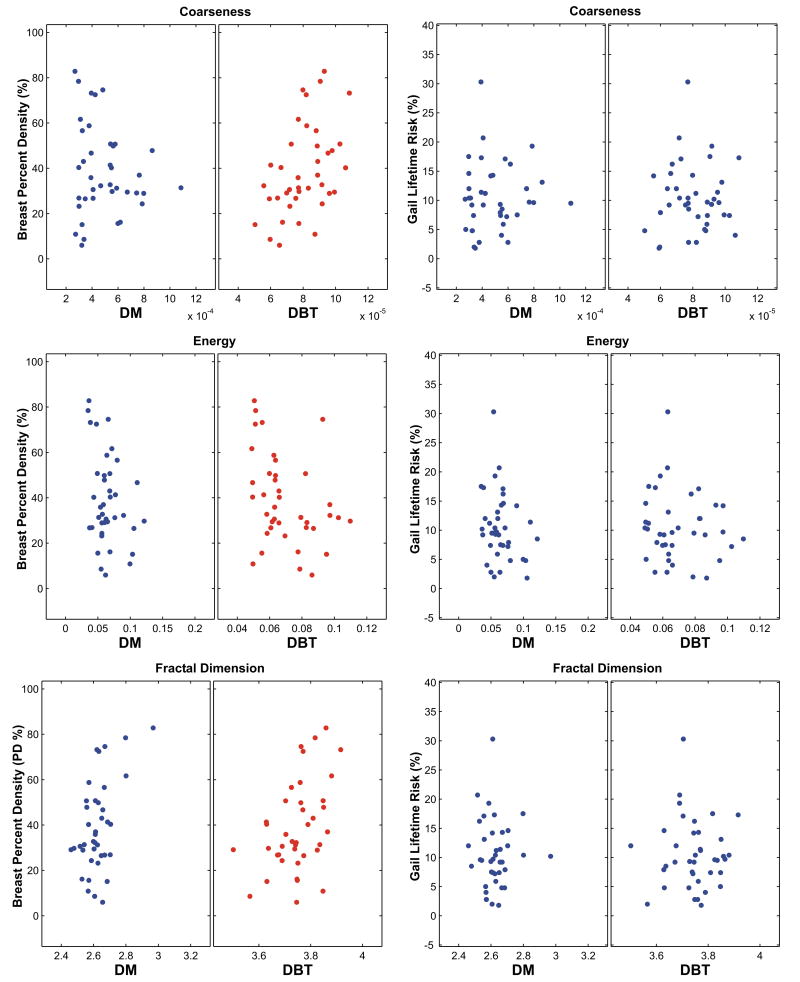
Table 3 shows the Pearson correlation coefficients r, with associated p-values, computed between the parenchymal texture features and the corresponding continuous breast PD estimates. With the exception of skewness, statistically significant correlations were detected for all the texture descriptors in either or both imaging modalities (p≤ 0.05); however, with the exception of coarseness, only the 3D texture features appeared to yield significant correlations for DBT. Overall, the 3D DBT parenchymal texture features appeared to have stronger correlation with breast percent density than the DM features. By comparing Table 3 to Table 2, it appears that parenchymal texture features correlate significantly higher with breast PD, than with the Gail and Claus risk estimates. Significant correlations were detected between the 3D DBT texture features and breast PD, for coarseness (p=0.003), contrast (p=0.05), energy (p=0.03), and fractal dimension (p=0.004). For DM significant correlations were detected for homogeneity (p=0.01), and fractal dimension (p=0.001). Figure 6 shows representative scatter-plots of DM and 3D DBT parenchymal features versus the breast PD estimates; the corresponding scatter-plots of the same texture features versus the Gail risk estimates are also shown for comparison on the right. While the Gail risk scatter-plots demonstrate no clear pattern of association between the texture features and the corresponding Gail risk estimates for either modality, a clearer pattern of association is visible between the parenchymal texture features and breast PD, and the directionality of the association can also be seen, particularly for DBT.

Table 3.

Pearson correlation coefficient r computed between parenchymal texture features and breast percent density (PD), for digital mammography (DM) and digital breast tomosynthesis (DBT). The corresponding p-values for the detected correlations are shown in parentheses.

	Pearson Correlation Coefficients r (p-values)
	Breast Percent Density (PD %)
	DM	2D DBT	3D DBT
Skewness	−0.18 (0.26)	0.18 (0.26)	0.18 (0.26)
Coarseness	0.15 (0.34)	0.40 (0.01)**	0.46 (0.003)**
Contrast	−0.25 (0.13)	−0.23 (0.15)	−0.31 (0.05)*
Energy	−0.29 (0.07)	−0.20 (−0.21)	−0.36 (0.03)*
Homogeneity	0.39 (0.01)**	0.16 (0.32)	0.26 (0.11)
Fractal Dim	0.50 (0.001)**	0.23 (0.16)	0.45 (0.004)**

^*for p ≤ 0.05,

^**for p ≤ 0.01

Figure 6.

Scatter-plots of the texture features versus breast percent density (PD) (left) and the Gail lifetime risk estimates (right), for digital mammography (DM) and digital breast tomosynthesis (DBT).

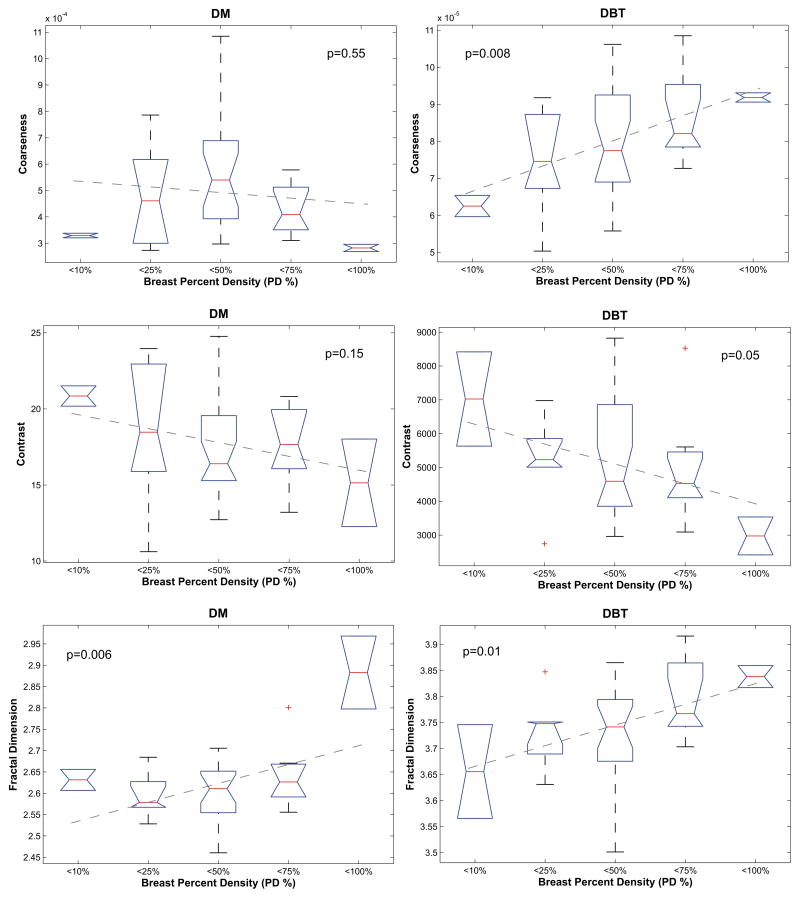
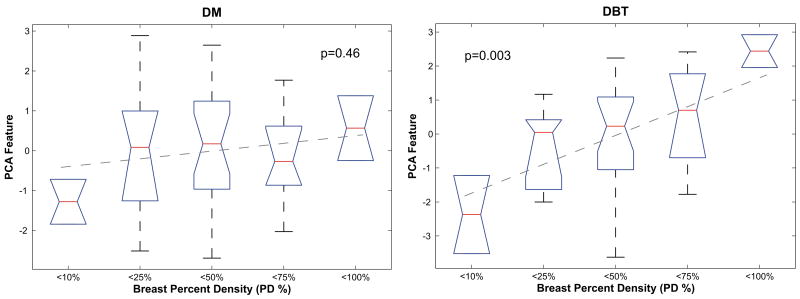
Figure 7 shows representative box-plots of the DM and the 3D DBT texture feature distributions within the groups of increasing breast PD. Fitted regression lines are shown which model the association between increasing breast PD and parenchymal texture features; to avoid over-fitting, considering our small sample size, only linear models were fitted. Figure 8 shows the corresponding box-plots for the PCA feature, computed from all the DM and the 3D DBT features respectively. Table 4 shows the corresponding regression beta b coefficients and R² estimates for the fitted models. In general, the association between breast PD and texture features was stronger for DBT than for DM, as evidenced by fitted regression lines with steeper slopes and more significant p-values. The strongest association with increasing breast PD was observed for the DBT PCA feature (R²=0.21, p=0.003).

Figure 7.

Box-plots with fitted regression lines and associated p-values for digital mammography (DM) and digital breast tomosynthesis (DBT) coarseness, contrast, and fractal dimension texture features versus the five groups of increasing breast percent density (PD): < 10%, 10%≤…< 25%, 25%≤…< 50%, 50%≤…<75%, and 75%≤…< 100%.

Figure 8.

Box-plots with fitted regression lines and associated p-values for digital mammography (DM) and digital breast tomosynthesis (DBT) PCA features versus the five groups of increasing breast percent density (PD): < 10%, 10%≤…< 25%, 25%≤…< 50%, 50%≤…<75%, and 75%≤…< 100%.

Table 4.

Beta b coefficients, R², and p-values for the fitted regression models of each texture descriptor, for digital mammography (DM) and digital breast tomosynthesis (DBT).

	DM			3D DBT
	b	R2	p-value	b	R2	p-value
Skewness	−0.08	0.01	0.50	0.06	0.03	0.33
Coarseness	−0.02×10−3	0.01	0.55	0.7×10−5	0.17	0.008**
Contrast	−0.91	0.05	0.15	−588	0.10	0.05*
Energy	−0.006	0.06	0.14	−0.005	0.07	0.09
Homogeneity	0.005	0.10	0.04*	0.009	0.08	0.09
Fractal Dim	0.04	0.18	0.006**	0.04	0.16	0.01**
PCA	0.19	0.01	0.46	0.84	0.21	0.003**

^*for p ≤ 0.05,

^**for p ≤ 0.01

4. Discussion

To date, breast density has been used as the main image-based surrogate of risk (19). However, certain limitations exist for using breast density as the prime imaging biomarker for breast cancer risk estimation. The current state-of-the art methods to estimate breast density are not fully-automated and therefore not accurately reproducible; breast density estimation is highly subjective to observer’s perception and subjectivity (21, 61). Some studies have investigated the development of fully-automated methods to quantify breast density (62); nevertheless these methods have not yet been validated with large clinical studies. In addition, breast density is currently evaluated as a global image measure that cannot be used to characterize spatially localized parenchymal patterns. Previous studies with mammograms have shown that certain regions within the breast, such as the retroareolar region, might be highly discriminative for breast cancer risk estimation (27–31, 48). Parenchymal texture analysis, on the other hand, could provide fully-automated, objective and reproducible features to characterize breast density patterns, and therefore complement and augment the current methods for breast cancer risk estimation.

In our study, parenchymal texture features were analyzed in DM and DBT clinical images using both 2D and 3D texture descriptors. Overall, moderate correlations were observed between the DM and the DBT texture features, indicating that parenchymal texture differs between the two imaging modalities. With the exception of fractal dimension, however, strong correlations were detected between the 2D DBT texture features and their 3D counterparts, suggesting that the observed differences in texture between DM and DBT are more likely to be attributed in the most part to the effect of tissue superimposition, rather than the selection of the particular feature extraction technique. In our particular study, however, the DBT images were anisotropic in resolution, which could potentially impact the computation of the 3D texture features. Currently, this issue is under investigation in the medical imaging literature, and no definitive work has been published. Mahmoud-Ghoneim et al. have applied 2D and 3D descriptors, similarly to our approach, to analyze the texture of gliomas in anisotropic 3D brain MRI images, without particularly accounting for the potential effect of texture anisotropy (52). Chen et al. have applied 3D texture descriptors to analyze the texture of breast lesions in contrast-enhanced 3D breast MRI images, but have accounted for anisotropy by performing a bi-linear interpolation to yield isotropic tomographic voxel resolution (54). Kovalev et al. have performed an extensive study on texture anisotropy in 3D images, using both simulated and real clinical data, concluding that no definitive solutions can be proposed, but rather suggestive approaches dependent on the particular modality of the available images and the type of pathology (63). Considering that our study is the first to perform parenchymal texture analysis in DBT images for breast cancer risk estimation, we intend to fully investigate this effect in our future studies when larger clinical datasets are available. Potential future studies could also include phantom data analysis to assess the effect of various DBT acquisition geometries on different feature extraction techniques (64).

The observed overall low correlation between parenchymal texture features and the Gail and Claus model lifetime breast cancer risk estimates could potentially be attributed to the small size of our dataset, and the particular patient selection criteria of the clinical multimodality imaging study; our study population could potentially be considered as a high risk population, as most of the women were diagnosed with unilateral breast cancer. However, it is important to note that the Gail lifetime risk estimates for the women in our population followed a normal distribution with an average of 10.5%, which is slightly lower than the 12.6% average lifetime risk of the general USA population (43). In a previous study with digitized mammograms, Huo et al. used multiple linear regression to examine the correlation between a set of parenchymal texture features, along with age, versus the Gail and Claus model risk estimates (27). Their study showed a moderate and statistically significant correlation between their linear regression risk estimate and the Gail and Claus risk model predictions. However, their linear regression model also considered age as a risk factor, which is known to also be a variable included in the Gail and Claus risk assessment models. Hence, the reported correlation could potentially be attributed mostly to the inclusion of age as a risk factor, rather than to the individual parenchymal texture features alone.

On the other hand, the observed low correlations between the individual parenchymal texture features and the Gail and Claus risk estimates persisted over all the texture descriptors in our study, regardless of the imaging modality; this could indicate that parenchymal texture is potentially an independent risk factor, unrelated to the conventional variables of the Gail and Claus risk estimation models (i.e., age, parity, age at menarche, number of relatives with cancer, number of prior biopsies, etc.). In support of this hypothesis, Palomares et al. have also reported that the Gail model variables do not fully account for the relationship between mammographic breast density, a correlate of parenchymal texture, and the calculated breast cancer risk estimates; in particular breast density also appears to have no significant correlation to age at menarche, nulliparity, and late age at first birth (65). If this hypothesis is further validated by larger clinical studies, parenchymal texture features could be considered as additional variables to the current epidemiological risk prediction models to further improve their discriminatory accuracy; such a discussion has already been raised in the scientific community (66–68). Some studies have already investigated the potential to improve the Gail model by also including image-based breast density descriptors (22–24, 69).

Our analyses demonstrated significant correlations between parenchymal texture features and breast density, which is an established independent risk factor for breast cancer (19). Although our results should be viewed as suggestive, due to the small size of our dataset, the association between parenchymal texture and breast density was overall more evident for the DBT than the DM texture features. In particular, significant correlations (i.e. p≤0.05) with continuous breast PD estimates were detected for 3D DBT coarseness, contrast, energy, and fractal dimension; for 2D DBT coarseness; and for 2D DM homogeneity and fractal dimension. When our study population was divided into sub-groups of increasing breast PD, 3D DBT texture analysis demonstrated a potential to provide more discriminative texture features than DM, as shown by the corresponding box-plots of the texture feature distributions and the fitted regression lines with overall lower p-values, steeper slopes and higher R² estimates. The superiority of DBT texture analysis in this case was particularly evident for the PCA, in which the 3D DBT feature demonstrated the highest statistical significance (p=0.003) and the best linear regression fit (R²=0.21), compared to DM (p=0.46, R²=0.01).

The improved performance of DBT features, compared to DM, could potentially be attributed to the effect of tissue superimposition. DBT parenchymal analysis can exclude tissue layers that are potentially irrelevant to risk assessment, such as the superficial skin layers and the surrounding subcutaneous fatty regions, which could be considered as anatomical structure noise for image-based breast cancer risk assessment. In DBT, texture analysis can be performed within spatially localized areas of the breast volume, such as the retroareolar fibro-glandular breast region which has been shown to be particularly characteristic for breast cancer risk assessment (27, 29–31). Although preliminary, our results also suggest that 3D texture analysis in DBT could potentially result in more discriminative features, than 2D texture analysis, for breast cancer risk estimation. The study of Chen et al. has also demonstrated the superiority of 3D texture descriptors, versus their 2D counterparts, in classifying breast tissue texture in 3D contrast-enhanced breast MRI images (54).

Our findings in DBT are in agreement with previous studies in mammograms, and further support the hypothesis that parenchymal texture features can be used as alternative, or even complementary, methods to quantify breast density patterns for breast cancer risk estimation. We observed that coarseness has a positive correlation with breast density, indicating that women at higher risk could potentially have coarser patterns of parenchymal texture; Huo et al., Li, et al. have also reported that BRCA1/2 gene mutation carriers, a population known to be at very high risk, appear to have coarser mammographic texture patterns with increasing breast density (28, 29). We also observed that contrast and energy appear to have a negative correlation with breast density, indicating that women at higher risk could potentially have parenchymal texture patterns with lower local variation of gray-levels, resulting in lower contrast values; these results also agree with the previous reports of Huo and Li (28, 29), who showed that high-risk women had mammographic texture patterns with lower contrast. Finally, fractal dimension demonstrated a strong association with breast percent density, having the lowest and most significant p-values; Li et al. have also shown in their studies that fractal dimension can provide highly discriminative measures for characterizing the mammographic patterns of high-risk women (31).

Our study, nevertheless, has certain limitations. The small sample size does not provide sufficient statistical power to connote general applicability of our results and to fully determine the superiority of the 3D versus the 2D texture analysis methods. This limitation is reflected by the moderately statistically significant p-values (i.e. p≤0.05) and the observed overall low R² values in the fitted regression models. However, since this is the first study to explore the potential advantages of DBT parenchymal analysis for breast cancer risk estimation, our intention was to evaluate proof-of-concept and demonstrate the instrumental evidence required to initiate the design of larger clinical studies in the future. Such larger studies will render the sufficient statistical power required to fully evaluate the potential advantages of DBT in breast cancer risk estimation and determine the optimal texture analysis techniques. Future approaches may also include investigating other areas of the breast than the retroareolar region, and evaluating the effect of inter-observer variability in ROI selection and breast density estimation (47). In addition, larger datasets will also offer the ability to further investigate the potential of combining multiple texture descriptors into a more comprehensive breast cancer risk estimation measure. Our results indeed demonstrate that combining multiple texture features using PCA could potentially yield more accurate risk estimation measures, as evidenced by the higher R² value in the corresponding linear regression fits.

Although preliminary, our results suggest that DBT parenchymal texture analysis could potentially provide more discriminative features for breast cancer risk estimation, in comparison to DM. This potential advantage, combined with the on-going advancements in improving the image quality and reconstruction algorithms for DBT (40, 70), could offer the opportunity to develop novel imaging biomarkers that can be used to improve breast cancer risk estimation. The improved performance and low cost of breast DBT will likely fuel the rapid and broad dissemination of DBT as a breast cancer screening modality (35, 71). Our ultimate goal is to improve breast cancer risk estimation by developing automated Computer-Assisted Risk Estimation (CARe) methods based on DBT parenchymal analysis. Establishing novel DBT imaging biomarkers for breast cancer risk estimation could be of great clinical advantage, for customizing detection, tailoring individual treatment and forming preventive strategies, especially for women associated with a higher risk.