Determining the helical tilt of membrane peptides using electron paramagnetic resonance spectroscopy

Abstract

Theoretical calculations of hyperfine splitting values derived from the EPR spectra of TOAC spin labeled rigid aligned α-helical membrane peptides reveal a unique periodic variation. In the absence of helical motion, a plot of the corresponding hyperfine splitting values as a function of residue number results in a sinusoidal curve that depends on the helical tilt angle that the peptide makes with respect to the magnetic field. Motion about the long helical axis reduces the amplitude of the curve and averages out the corresponding hyperfine splitting values. The corresponding spectra can be used to determine the director axis tilt angle from the TOAC spin label, which can be used to calculate the helical tilt angle due to the rigidity of the TOAC spin label. Additionally, this paper describes a method to experimentally determine this helical tilt angle from the hyperfine splitting values of three consecutive residues.

1. Introduction

The helical nature of nearly 80% of integral membrane proteins contributes to the importance of defining their topology and structure [1]. As almost no secondary structure is present in the loops, turns, and terminal regions (further disrupted by substantial internal motion), the identification and characterization of the α-helix in particular can be used to determine the three-dimensional structure of the protein embedded inside the membrane [1].

Previously, multiple studies have been performed to determine the structure and topology of α-helices through a variety of methods, which includes infrared spectroscopy [2], chemical modifications of a probe (i.e. using thiol-based cross-linking studies on multiple single-cysteine mutants)[3], x-ray diffraction experiments[4-8], electron microscopy[9], and magnetic resonance experiments[1,10-19]. Recently, solid-state NMR spectroscopic techniques have been developed that have shown the viability of using dipolar waves to determine helical tilt angles [1,10,20,21]. Dipolar waves, derived from PISA (polarity index slant angle) wheels based upon two-dimensional ¹H-¹⁵N heteronuclear dipolar/¹⁵N chemical shift PISEMA (polarization inversion with spin exchange at the magic angle) spectra, represent the mapping of a protein structure through the anisotropic nuclear spin interactions that occur in a sinusoidal nature due to the periodicity of α-helices. By fitting the sinusoidal oscillations of the ¹⁵N chemical shift and ¹H-¹⁵N dipolar coupling to known dipolar waves, the helical tilt angle of the protein with respect to the membrane can be calculated [1,10,20].

This article describes the existence of hyperfine waves, which also utilize the known periodicity of α-helices to map in a sinusoidal manner the hyperfine splitting values of consecutive residues derived from aligned electron paramagnetic resonance (EPR) spectra. Similar to dipolar waves, these waves are dependent on the structure and angle of the helix from which they are derived. Furthermore, this paper demonstrates the viability of using these hyperfine waves to experimentally determine the helical tilt angle of an α-helix with respect to the membrane normal and the magnetic field.

The α-helical M2δ domain of the nicotinic acetylcholine receptor (AChR) was used as a theoretical model for the development of this approach. The M2δ domain has been characterized previously through a variety of methods, including solution-state and solid-state NMR experiments by Opella and co-workers, EPR experiments utilizing the TOAC spin label in a bicelle, glass plates and nanotubes array studies, as well as molecular dynamic simulations, all of which resulted in a predicted helical tilt angle of 15° ± 4°[14,15,22,23]. This paper demonstrates the viability of using an EPR-based method that utilizes the 3.6 turn periodicity of most α-helices to identify the angle of its helical tilt.

2. Results

2.1 Determination of hyperfine splitting values from EPR spectra

The parallel (A_∥) and perpendicular (A_⊥) hyperfine splitting values can be obtained from EPR spectra when samples are aligned with the axis of motional averaging (the director axis, Z_D) parallel and perpendicular to the applied magnetic field, respectively. The values of A_∥ and A_⊥ can then be measured from the inner and outer extrema of the unaligned EPR spectrum. Similarly, A_exp can be obtained by measuring the difference between the low field and center field lines of the nitroxide EPR spectrum in an aligned media.

2.2 Hyperfine waves based upon A_exp values

Figure 1 shows simulated EPR spectra derived for residues 14-16 of M2δ, with a simulated helical tilt angle of 15° with respect to the membrane normal. When comparing the simulated A_exp values (A_sim) of consecutive residues in an α-helix such as the M2δ domain, the hyperfine splitting values were found to vary periodically. Therefore, A_sim values for all 23 residues were plotted as a function of residue number to more accurately characterize the hyperfine wave pattern.

Figure 1.

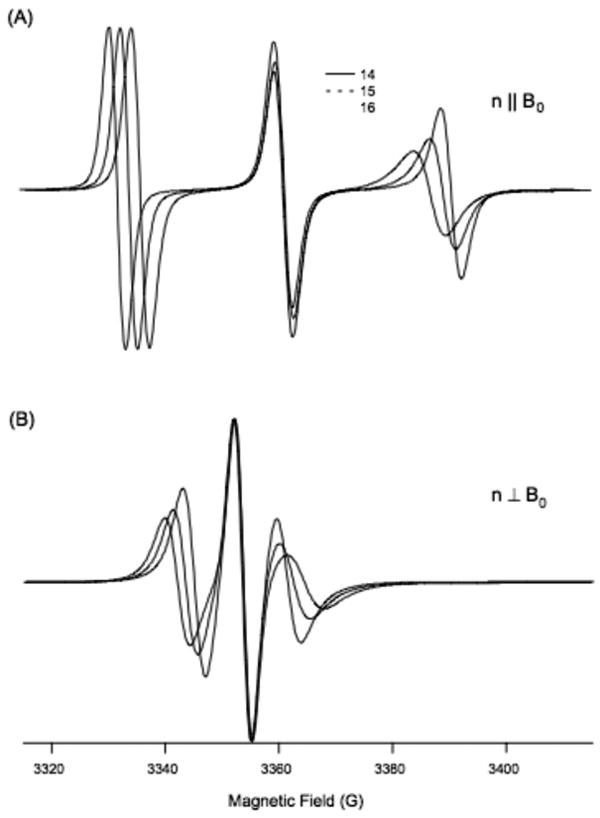
Simulation of EPR spectra for residues 14-16 demonstrating how the A_exp values change between these residues. (A) Parallel aligned (B) perpendicularly aligned with respect to the direction of magnetic field (B₀).

The sinusoidal nature of the wave suggests that the A_exp values are influenced by the periodic nature of the α-helix. Additionally, when the helical tilt angle was changed, the hyperfine waves were found to shift in both amplitude and position, as observed in Figure 2. For example, the A_sim values for an α-helix with a tilt angle of 0° results in a hyperfine wave with no amplitude and a constant A_sim value equal to 33 G. However, the A_sim values for an α-helix with a tilt angle of 30° results in a hyperfine wave with a significantly lower average hyperfine splitting value and larger wave amplitude.

Figure 2.

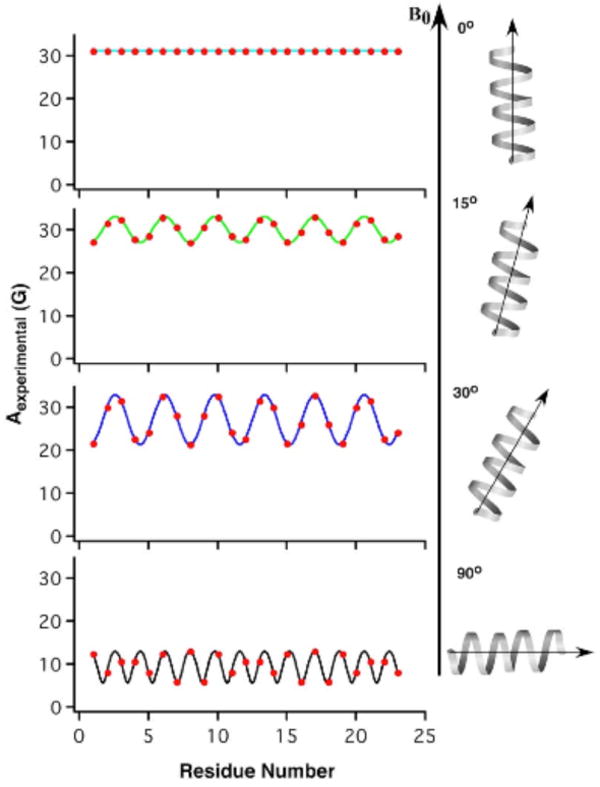
Hyperfine waves as a function of helical tilt angle, using predefined values for A_∥ (33.3 G), A_⊥ (5.6 G), β_D (21°), and α_D at residue 18 (-10°).

2.3 Derivation of hyperfine waves

To explain the sinusoidal nature of these waves, the geometry and dynamics of the individual residues from which the spectra were derived were analyzed. The EPR spectra simulated in this paper directly depend on the orientation of the TOAC spin label that is rigidly bound to the backbone of the protein at a specific residue, thus helping to characterize the secondary structure of the M2δ domain [24-27].

The values of A_∥ and A_⊥ obtained from the random powder sample EPR spectra correlate to the different orientations of the director axis of the TOAC-spin label with respect to the direction of the static magnetic field. However, as defined earlier, in an aligned media, A_∥ is the experimentally observed hyperfine splitting if the magnetic field is applied along the axis of motional averaging (director axis, Z_D) for the spin label. Similarly, if the magnetic field is applied perpendicular to the director axis, the observed hyperfine splitting value is A_⊥. In general, the following equation can be used when the magnetic field makes an angle (ψ) with the axis of motional averaging (Z_D):

$$A_{\text{exp}}=\sqrt{A_{\parallel }^2{\text{cos}}^2\psi +A_{\perp }^2{\text{sin}}^2\psi }$$ (1)

In this paper, the axis of motional averaging corresponds to the axis directed along the π-orbital, perpendicular to the N-O bond of the TOAC spin label attached at a specific residue (Fig. 3) [14]. In parallel-aligned samples, the director tilt angle with respect to the magnetic field (ψ) is equal to the director tilt angle with respect to the bilayer normal (ζ), while in perpendicular-aligned samples the two angles are different and must be resolved with an additional step [14].

Figure 3.

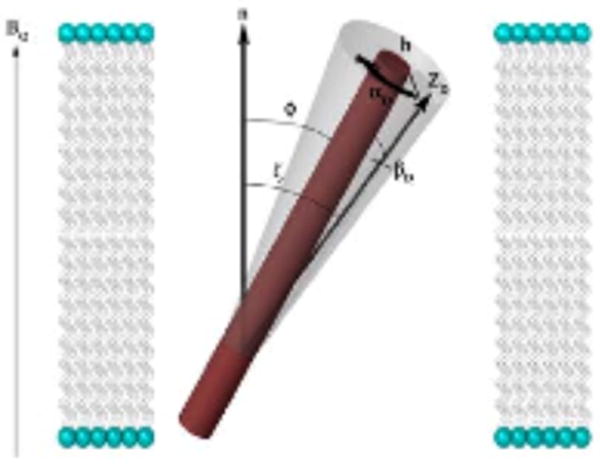
Illustration of an α-helix with attached TOAC spin label and applied magnetic field. φ represents the helical tilt angle, ζ, (equal to ψ in the parallel orientation) is the director tilt angle, which is directly measured in the EPR spectrum. Z_D is the director axis of the spin label and to the axis directed along the π-orbital, perpendicular to the N-O bond of the TOAC spin label (not shown). α_D is the rotation of the spin label around the helix and depends on the residue number, while β_D is the angle between the director axis and the helical axis.

From previous crystal structural studies of an α-helix containing the TOAC-spin label [26,28], it was found that the director axis makes an angle of approximately 21° with respect to the helical axis (β_D). The angle between the helix-director axis plane and the helix-bilayer normal plane varies at each residue depending on the periodicity of the α-helix, as the director axis rotates around the helix for consecutive residues. The specific rotation around the helix (α_D) at a specific residue was known in the case of the M2δ domain, and was found to be approximately 80° at Leu 18, (known because it is one of the pore-lining residues that faces the N-terminal or intracellular side of membrane)[14].

To relate the angle ζ obtained from the EPR spectra to the helical tilt angle (φ), a series of Euler angles were used (α, β, γ). α is defined as the rotation about the Z-axis of the initial coordinate system, β is the rotation performed about the Y' axis of the newly generated coordinate system, and γ is the rotation about the Z-axis, [14]. These rotations allowed for a mathematical relationship between the director tilt angle (ζ and the helical tilt angle (φ) to be established, as follows:

$$\text{cos}\zeta =\text{sin}\phi \text{sin}{\beta }_D\text{sin}{\alpha }_D+\text{cos}\phi \text{cos}{\beta }_D$$ (2)

When α_D is known beforehand for a particular residue of an α-helix, and the helical tilt axis is assumed to be rigid, the values for other residues can be extrapolated based upon the periodicity of the helix. Since there are approximately 3.6 residues per turn (for a full 360° rotation) in a model α-helix, the residues rotate approximately 100° between each residue. For most α-helices, the value of α_D is unknown, but as this paper will later demonstrate, the correct α_D frame is intrinsically linked to the helical tilt angle, and can be determined experimentally using the hyperfine waves.

As similarly observed in RDC NMR studies, it is possible to compose a single equation demonstrating the relationship between the periodic factor α_D and the hyperfine splitting value [30,31]. All the variables that contribute to the hyperfine splitting value can be resolved into an algorithm based upon equations (1) and (2):

$$\begin{array}{l}{A}_{\text{exp}}=[A_{\parallel }^2{\text{cos}}^2\{{\text{cos}}^{-1}(\text{sin}\phi \text{sin}{\beta }_D\text{sin}{\alpha }_D+\text{cos}\phi \text{cos}{\beta }_D)\}\\ +A_{\perp }^2{\text{sin}}^2\{{\text{cos}}^{-1}(\text{sin}\phi \text{sin}{\beta }_D\text{sin}{\alpha }_D+\text{cos}\phi \text{cos}{\beta }_D)\}]\end{array}$$ (3)

Equation 3 shows how keeping all the other variables constant, the A_exp value depends only on the value of α_D, clearly implicating this semi-variable as the source of the sinusoidal trend.

2.4 Variation in hyperfine waves

The influence of the helical tilt angle of a peptide on the hyperfine waves produced has been described previously. Several other factors can also alter the hyperfine waves, including the alignment of the sample, variation in the director tilt axis itself, motion about the helical axis, dynamic properties reflected in the A_∥ and A_⊥ values, and experimental conditions.

For example, while the TOAC spin-label is useful due to its rigid structure, there is some variation in the angle its director axis makes with respect to the helical axis (β_D) that affects the overall position of the hyperfine wave. Even so, this angle was found to only vary within a few degrees. Therefore, the overall effect on the hyperfine wave is minimal.

It should be noted that the hyperfine waves in Figure 2 were simulated using constant values for A_∥ (33.3 G) and A_⊥ (5.6 G), which were taken from experimentally derived values [14].

2.5 Determination of helical tilt angle using hyperfine waves

As described above, A_sim values were found to vary in a predictable manner primarily due to the periodicity of the α-helix and the helical tilt angle. Using these two parameters, a method was derived to experimentally determine the helical tilt angle using A_sim values from consecutive residues. While one residue would be sufficient theoretically to estimate the tilt angle for a given helix, the experimental variation in A_∥ and A_⊥, as well as changes in α_D, require that multiple residues be used to determine a more accurate value.

To account for the experimental variation of several parameters, a value for the acceptable error in the experimental hyperfine splitting was determined as the average experimental error for that protein. Based upon previous work with the M2δ domain, the acceptable error for this paper was determined to be ± 0.5 G for parallel-aligned samples. To demonstrate this method, only the parallel-aligned samples were used for simplification purposes, although perpendicular-aligned samples could be used instead or in conjunction if desired [22].

Due to the variation in the A_exp value (as a result of changes in A_∥, A_⊥, and α_D due to dynamic changes between different residues), a range of possible helical tilt angles are measured from one residue's spectrum. The width of this range depends upon a variety of factors, but the error associated with A_∥ and A_⊥ and the α_D value appear to be the most significant.

When the α_D value for a specific residue correlates to the plane of the bilayer normal and the helix being 180° to the plane of the helix and the director axis, the helical tilt angle range is the narrowest (because α_D is at its maximal value). At the same time, the A_exp values at these residues vary the most when comparing different tilt angles (or conversely, the helical tilt angles change the least for the same range of A_exp values). Thus, a small change in helical tilt angle is associated with a relatively large change in A_exp, and the A_exp value is more representative of a specific tilt angle. As observed in Table 1, residue 15, which has an α_D value corresponding to this optimal angle of rotation (290°), experiences a wide range of A_exp values at different tilt angles (31.2 G at 0°, 28.8 G at 10°, 25.6 G at 20°, etc.) than the other residues such as residue 14 (31.2 G at 0°, 31.7 G at 10°, 31.3 G at 20°, etc.) which have less than optimal rotation angles. Thus, the given A_exp value at residue 15 is much more indicative of a specific helical tilt angle and results in a narrower range of possible helical tilt angles. If the acceptable error is ± 0.5 G, the range of A_exp values associated with specific tilt angles within this error can be seen to much smaller for residue 15 than the other two residues. Furthermore, through the analysis of three consecutive residues, a helical tilt range that is relatively narrow will likely be determined as one of the residues will have the optimal or near-optimal α_D value, as observed in Figure 4.

Table 1.

Comparison of hyperfine splitting values from residues 14-16 of M2δ domain. Residues with certain α_D values experience wider ranges of A_exp values at different tilt angles depending on its α_D value, corresponding to antinodes in the waves.

Helical Tilt Angle	Hyperfine splitting value, Aexp (G)
	Residue Number
	14	15	16
0°	31.2 G	31.2 G	31.2 G
10	31.7	28.8	30.3
20	31.3	25.6	28.7
30	30.0	21.7	26.1
40	27.8	17.3	22.9
50	24.8	12.5	19.0
60	21.2	8.0	14.7
70	17.0	5.6	10.2
80	12.4	7.9	6.5
90	8.1	12.4	6.0
αD	30°	290°	190°

Figure 4.

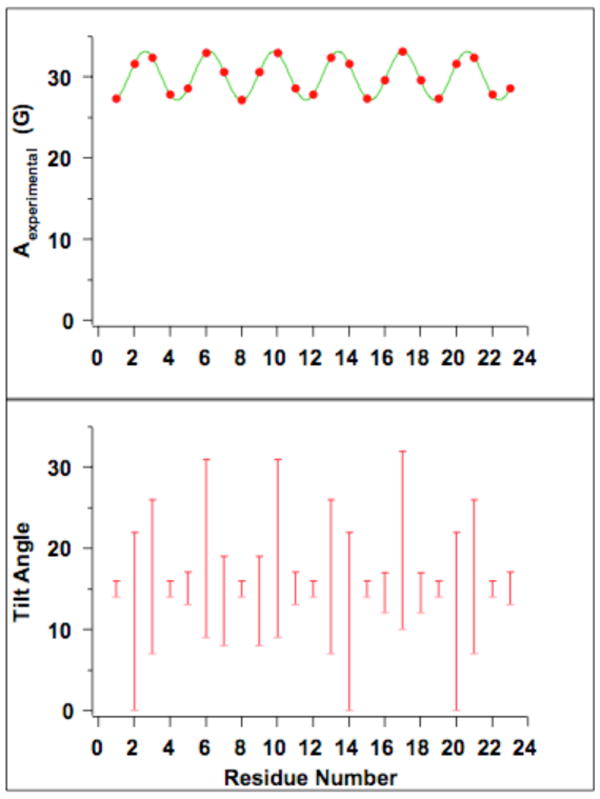
Helical tilt ranges as a function of residue number. Using simulated A_exp values corresponding to a tilt angle of 15°, helical tilt ranges were found. As can be seen in the figure, some residues result in helical tilt ranges that are much smaller than others, which is due to changes in the residues' orientation with respect to the magnetic field (changing values of α_D). Furthermore, a relatively narrow helical tilt range is found within three consecutive residues.

2.6 Simulated determination of helical tilt angle for a transmembrane peptide

This article uses simulated EPR spectra based upon available experimental data of TOAC-labeled M2δ domain residues. The procedures for synthesizing and purifying TOAC spin-labeled amino acids has previously been described in the literature [14]. The values of A_∥ and A_⊥ corresponding to TOAC-labeled M2δ, which are necessary to calculate the helical tilt angle, can be obtained from EPR spectra of aligned samples of this peptide, as described earlier [29]. The simulations assumed EPR spectra were collected on a Bruker EMX X-band CW-EPR spectrometer and acquired by taking a 42 s field-swept scan (3370 G center field, 100 G sweep width, 9.434 GHz microwave frequency, 100 kHz modulation frequency, 1.0 G modulation amplitude, and a microwave power of 10 mW) [14].

The simulated spectra presented here considered cases of both, a rigid helical axis where the peptide did not experience any rotational motion about the long axis of the helix. Simulated spectra of residues 14-16 from the M2δ domain, provided simulated A_exp values (A_sim), which were calculated using predefined values for A_∥ (33.3 G), A_⊥ (5.6 G), β_D (21°), various α_D rotations (ranging from -10° to 20° at residue 18, corresponding to correct and incorrect α_D frames), as well as the value for the simulated helical tilt angle of 15°.

To simplify matters, only parallel-aligned spectra were simulated. Furthermore, A_∥ and A_⊥ were not varied per residue as they would be experimentally.

Given these approximations, the ranges of helical tilt angles were found for each residue [14], from which the overall helical tilt range was found. When the correct α_D (-10°) was used, the helical tilt angle range was found to be between 14° and 16°, which agreed very closely to the simulated helical tilt angle of 15°. However, when the incorrect α_D values were used, as Figure 5 shows, inconsistent results were obtained, indicating the hyperfine waves were out of phase.

Figure 5.

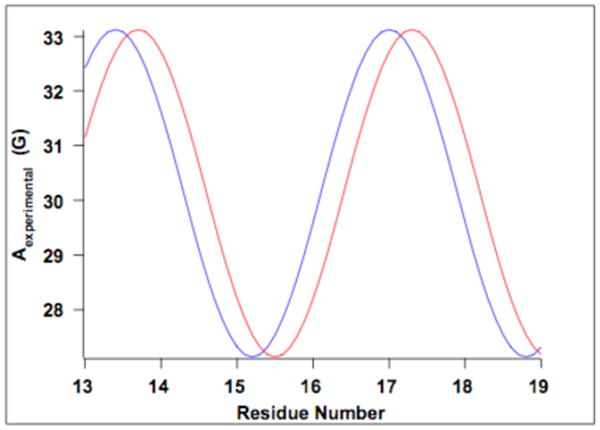
Hyperfine wave as a function of reside number and showing a shift in the hyperfine waves due to changing the α_D frame. The blue wave represents the correct α_D frame, while the red wave is out of phase by 30°. When the wave is out of phase, it shifts either to the right or to the left and causes the corresponding helical tilt angle ranges to become incompatible with each other as a result, which can be seen in Table 3.

To determine the range of helical tilt angles for a given hyperfine splitting value (from a specific residue), a custom script using MATLAB was created utilizing equations 1 and 2 discussed previously. The program simulated A_sim values by varying the possible helical tilt angle from 0°-90°, while keeping all the previously discussed parameters constant. The program then determined whether each value was within a specified error A_exp. Lastly, the program determined the maximum and minimum tilt angles corresponding to an acceptable A_sim. The hyperfine splitting values were calculated by using equations 1 and 2. While the simulated values could be calculated for either the perpendicular or parallel orientations in this case only the parallel orientation was analyzed.

The results for parallel oriented simulations can be viewed in Table 2, where A_sim values for residues 14-16 were used to determine the range of helical tilt angles within the acceptable error of the simulated values. For instance, only the A_sim values corresponding to helical tilt angles from 14-16° were within the ± 0.5 G acceptable error of the “experimental” 27.32 G simulated for residue 15. Well in concurrence, the A_sim values for residues 14 and 16 resulted in helical tilt ranges of 0°-22° and 12°-17° respectively. Ultimately, the final range of helical tilt angle values was determined by finding the range that was compatible with all the ranges found for each residue. In this case, the overall range was also 14°-16°.

Table 2.

Determination of helical tilt angle range for residues 14-16 of M2δ domain. Using “experimental” values simulated for a 15° tilt angle, the ranges were determined for each residue by determining which A_exp values were within the acceptable error of +/-0.5 G. By varying the simulated helical tilt angles from 0°-90°, the ranges were calculated by finding the lowest and highest tilt angles that had A_exp values within the acceptable error of the “experimental” value. The values in red, blue, and green represent the A_exp values that were within the acceptable error of the experimental A_exp for residues 14, 15, and 16, respectively. The bolded values represent the lower and upper limits of the ranges. Moreover, the overall range obtained from the three residues is the range that is compatible with all three ranges, 14°-16°.

Simulated Helical Tilt Angle	Hyperfine Splitting Value, Aexp (G)
	Residue Number
	14	15	16
0°	31.15	31.15	31.15
1	31.24	30.96	31.11
2	31.33	30.76	31.06
3	31.41	30.54	31.00
4	31.48	30.32	30.93
5	31.54	30.09	30.86
6	31.59	29.85	30.78
7	31.63	29.60	30.68
8	31.67	29.35	30.58
9	31.69	29.08	30.47
10	31.70	28.81	30.34
11	31.70	28.53	30.21
12	31.70	28.24	30.08
13	31.68	27.94	29.92
14	31.66	27.63	29.77
15	31.62	27.32	29.61
16	31.58	27.00	29.43
17	31.52	26.67	29.25
18	31.47	26.33	29.06
19	31.39	25.99	28.86
20	31.31	25.64	28.65
21	31.22	25.28	28.43
22	31.13	24.91	28.20
23	31.01	24.54	27.98
24	30.90	24.16	27.73
25	30.77	23.77	27.49
Experimental
Aexp	31.62	27.32	29.61
Range	0°-22°	14°-16°	12°-17°

It was observed that in a rigid helical system, there will be concurrence of at least one range of possible helical tilt angles if the correct rotation frame is used (indicated by the α_D frame). Thus, incompatible helical tilt angle ranges provided by consecutive residues are indicative of incorrect α_D frames, and these are varied till the phase of the hyperfine wave is acceptable, as demonstrated in Table 3. Using the A_sim values for residues 14-18 from the M2δ domain, the correct α_D value (-10° at residue 18 and extrapolated to account for other residues and constitute the α_D frame) was replaced with incorrect ones ranging from -5° to 20°. Figure 5 illustrates that changing the α_D value shifts the hyperfine waves to the left or right, thus altering the ranges of tilt angles calculated for each residue. However, this frame shift also results in the proposed helical tilt ranges of consecutive residues that contradict each other, as demonstrated in Table 2. For instance, when out of phase by 30°, residue 18 resulted in a range from 25°-29°, while residue 15 had a range from 17°-19°.

Table 3.

Comparison of helical tilt ranges obtained using different α_D values at residue 18 (and extrapolated to other residues). Using the correct α_D value or one out frame by just 5°, the correct helical tilt range was found. For an α_D value that is greater than 5° out of frame, the helical tilt ranges obtained at each residue began to contradict each other and thus no overall helical tilt angle range could be determined. The gray column indicates the correct α_D frame.

Residue	αD (at residue 18)
	-10°	-5°	0°	10°	20°
14	0-22	0-25	0-27	0-32	0-36
15	14-16	14-16	15-17	16-18	17-19
16	12-17	11-16	10-14	8-12	7-11
17	10-32	10-32	10-31	11-29	13-24
18	12-17	14-19	16-21	20-25	25-29
Overall	14-16	14-16	N/A	N/A	N/A

Table 2 also demonstrates how using an α_D frame that is very close to the correct one will result not only in a helical tilt range that satisfies all the residues' ranges, but will also be very close to the actual helical tilt range obtained using the correct frame.

For instance, when the α_D frame was within 5° of the correct phase (-5° at residue 18), all the helical tilt angle ranges were compatible with each other and the resulting overall range of 14°-16° was the same as if the correct α_D frame was used.

2.7 Helical Rotation About the Long Axis of the Peptide

Dynamic properties have been observed for a wide variety of different membrane proteins and peptides in lipid bilayers [32-35]. These motions include rotational motion about the helical long axis, wobbling of the helical axis, uniaxial motion around the bilayer normal, and random isotropic motion [32-35]. For rotational motion about the long helical axis of the peptide, a rotational parameter (ρ) can be added to equation 3:

$$\begin{array}{l}{A}_{\text{exp}}=[A_{\parallel }^2{\text{cos}}^2\{{\text{cos}}^{-1}(\text{sin}\phi \text{sin}{\beta }_D\cdot \rho \cdot \text{sin}{\alpha }_D+\text{cos}\phi \text{cos}{\beta }_D)\}\\ +A_{\perp }^2{\text{sin}}^2\{{\text{cos}}^{-1}(\text{sin}\phi \text{sin}{\beta }_D\cdot \rho \cdot \text{sin}{\alpha }_D+\text{cos}\phi \text{cos}{\beta }_D)\}]\end{array}$$ (4)

The ρ parameter is similar to an order parameter that is scaled depending upon the magnitude of the rotational motion. This motion reveals an overall averaging of the amplitude of the hyperfine wave (Figure 6). Fast rotational motion exists on the ms timescale (as shown in Fig. 6) [37]. Dynamic averaging of this rotational motion will not cause convergence to isotropic hyperfine values, instead as the rotational rate increases the hyperfine values will approach the center value of the hyperfine wave (see Figure 6). This has been observed previously in NMR studies [37]. As observed in Figure 6, the helical tilt can still be easily determined with EPR spectra collected at 3 consecutive residues. The following hyperfine splittings would be observed as a function of helical tilt angle (0° = 31.2 G, 15° = 30.1 G, 30° = 27.1 G, and 90° = 9.30 G) under fast rotational motion about the helical tilt axis.

Figure 6.

Illustration of the effects of static (blue) and fast rotational dynamics (red) about the long helical axis of the peptide aligned in a membrane. Using simulated A_exp values corresponding to a tilt angle of 15°, β_D (21°), A_∥ (33.3 G), A_⊥ (5.6 G), α_D (-10). Rapid increase of axial rotation about the long helical axis of the peptide causes an averaging of the amplitude of the hyperfine waves as dictated by equation 4.

The other modes of motion will change the overall orientation of the spin-labeled peptide with respect to the membrane normal and the static magnetic field. In these cases, as the magnitude of the motions increase the EPR hyperfine values will approach isotropic values. Under these conditions, it would be difficult to determine the helical tilt of the peptide with respect to the membrane.

3. Discussion

This article describes the relationship between hyperfine waves produced by the periodicity of an α helix, and its corresponding helical tilt angle, for a TOAC spin labeled transmembrane model system. These waves also depend on the director tilt axis angle, dynamics, and experimental conditions. Due to possible variability of these factors, a range of helical tilt angles are generated and compared for consecutive residues to arrive at a final helical tilt angle.

This article successfully demonstrates the viability of using a hyperfine wave-derived method to accurately determine the helical tilt angle of the M2δ. Using this technique, a helical tilt angle range of 14°-16° was calculated from A_sim values, derived from a protein domain known to have a 15° helical tilt. Five consecutive residues from the M2δ domain were used in this simulation, due to a higher number of residues correlating to a larger probability of narrowing the range of possible tilt angles. However, three consecutive residues should be sufficient to obtain a satisfactory range, especially if the α_D value is unknown.

This simulation kept the values of A_∥, A_⊥, and β_D constant. The α_D value was extrapolated for each residue based upon the most common 3.6 residues per turn periodicity, which correlated to a change of 100° in the α_D value for consecutive residues. For helices with a different periodicity, this extrapolation of α_D can be changed to account for the difference in pitch.

When the α-helix is not held in a rigid environment, there may not be a fixed α_D frame, and therefore the α_D values would likely be averaged out. As the periodic nature of the hyperfine waves depends on these changes in α_D values between residues, the sinusoidal nature of the waves would be replaced with an increasingly linear one (depending on how much motion takes place). Interestingly, it is hypothesized that the linear nature of these “waves” would facilitate the determination of helical tilt angles because the location of the “wave” would be more indicative of a specific tilt angle (the A_exp values depending on one less factor). Furthermore, reducing the acceptable error could counteract increasing helical motion.

The use of an EPR-based hyperfine wave approach for determining the helical tilt range has several advantages when compared to the solid-state NMR technique. Due to the sensitivity of EPR spectroscopy, this technique only requires a small amount of sample (approx. 50 μg). Furthermore, only a few residues (approximately three) need to be labeled for this procedure to be successful. The use of the TOAC spin label, which is rigidly bound to the backbone of the α-helix, provides significant results that correlate to the secondary structure of a peptide. TOAC labeling also allows for specificity. Since only a few residues need to be labeled at a time, this technique lends itself well to the characterization of specific domains of a peptide of interest. It should be noted that the TOAC spin label to this point has been generally limited to solid phase peptide synthesis due to the inability to incorporate this site-specific spin label into larger membrane proteins.