Abstract
It has been documented that concurrently active motor units fire under the control of a common drive. That is, the firing rates show high correlation with near-zero time lag. This degree of correlation has been found to vary among muscles and among contractions performed at different force levels in the same muscle. This study provides an explanation indicating that motor units recruited during a contraction cause an increase in the variation (SD) and a decrease in the degree (amplitude) of the correlation of the firing rates. The degree of correlation is lower in muscles having greater spindle density. This effect appears to be mediated by the proprioceptive feedback from the spindles and possibly the Golgi tendon organs. Muscle spindles in particular respond to the mechanical excitation of the nonfused muscle fibers and provide a discordant excitation to the homonymous motoneurons, resulting in a decrease in the correlation of the firing rates of motor units. The implication of this work is that the decreased correlation of the firing rates in some muscles is not necessarily an indication of a decreased common drive from the CNS, but rather an inhibitory influence of the proprioceptive feedback from the peripheral nervous system. This explanation is useful for understanding various manifestations of the common drive reported in the literature.
INTRODUCTION
It has been shown that motor units are controlled in unison, rather than individually, indicating that they receive a common drive (De Luca and Erim 1994; De Luca et al. 1982b). This phenomenon may be seen visually by plotting the firing rates of motor units or, more analytically, by noting that the cross-correlation function of the firing rates has a maximum at a time lag of approximately zero. This observation has been confirmed independently by other researchers (Guiheneuc 1992; Iyer et al. 1994; Marsden et al. 1999; Miles 1987; Patten et al. 2000; Semmler et al. 1997; Stashuk and de Bruin 1988). The most cogent explanation for the origin of the common drive is that it is mediated centrally. Reports by Cheney and Fetz (1980), Belhaj-Saif et al. (1998), and McKiernan et al. (2000) indicate that there exist corticomotoneuronal cells in the premotor cortex and rubromotoneuronal cells whose activity is correlated with motor unit action potentials in muscles of the forearms of primates performing voluntary contractions. However, the question remains as to whether feedback from the proprioceptive and Renshaw systems affects the strength of the common drive.
It has been further reported that the degree of the common drive—that is, the amplitude of the cross-correlation function—varies among muscles (De Luca 1982a; Patten et al. 2000) and between dominant and nondominant hands (Kamen et al. 1992; Semmler and Nordstrom 1995). It is also altered by different proprioceptive conditions (Garland and Miles 1997), exercise (Semmler and Nordstrom 1997), and aging (Erim et al. 1999). It is unclear why these variations occur. This study was performed to investigate potential causes for the reported variation in the common drive.
Previous measurements of the common drive have been made over intervals of time of about 5 s. That approach is acceptable if one seeks to obtain only a single value of common drive over an interval of time. In this study, we sought to obtain a time-dependent function to estimate the common drive. This is accomplished by the use of the instantaneous cross-correlation function, which provides estimates of the cross-correlation as a function of time. Details on this approach are reported in Williams (1996) and Bonato et al. (2000).
METHODS
Four muscles—the tibialis anterior (TA), the trapezius, the first dorsal interosseous (FDI), and the vastus lateralis (VL)—were chosen for this study because they are known to have varying degrees of Renshaw recurrent inhibition (Katz and Pierrot-Deseilligny 1998), varying numbers of muscle spindles (Voss 1971), and all contain Golgi tendon organs (GTOs). All subjects volunteered for the experiments. None of the subjects had any known neuromuscular or musculoskeletal disorders or diseases. All gave an informed consent approved by the Boston University institutional review board.
Experimental protocol
Subjects were accommodated in a sitting position and the limb or digit being tested was secured so that it could produce only isometric contractions while contracting against a stiff force gauge. To compare the data from separate contractions and across subjects, the data were collected from contractions performed at the same relative force level. The normalization was performed by measuring the force of the maximal voluntary contraction (MVC), which was obtained by the following protocol. The subjects were asked to elicit and sustain the perceived maximal force for approximately 3 s. This procedure was repeated three times and the greatest value was used as the MVC for the subject. Then the subjects were asked to produce isometric forces by accurately tracking force trajectories that appeared on a computer screen. Once the subjects showed proficiency in following the target–force trajectory, a quadrifilar needle or fine-wire electrode (De Luca and Adam 1999; De Luca and Forrest 1972) was inserted into the belly of the muscle. (This electrode detects three differential channels of electromyographic [EMG] activity.) When a suitable position for the electrode was found—i.e., when the EMG signal appeared to be decomposable—the subject was asked to contract and follow a prescribed trajectory. The EMG signals were amplified, then band-pass filtered from 1 to 10 kHz. The signals were digitized at 20 kHz and decomposed into the constituent motor unit action potential trains with the use of the Precision Decomposition I algorithm (De Luca and Adam 1999; LeFever et al. 1982). Briefly, this technique uses template-matching, template-updating, and firing-rate statistics to reliably identify the occurrence of all the detected motor unit action potentials, yielding a time series representation of the motor unit firings.
TA EXPERIMENTS.
A cohort of six subjects (five males, one female), with age ranging from 23 to 39 yr (30.8 ± 7.0), participated. The subjects were seated in a chair with their dominant leg fixed in a specially designed ankle device that immobilized the ankle joint and restricted the TA to contract isometrically. They were asked to follow a force trajectory presented on a computer screen by isometrically dorsiflexing the ankle. The trapezoidal trajectory consisted of a 60-s-long plateau at 20% MVC with increasing and decreasing slopes of 10% MVC/s. See Broman et al. (1985) for additional details of the experimental setup. The constant-force segments of 10 contractions were analyzed.
TRAPEZIUS EXPERIMENTS.
A cohort of three male subjects, with age ranging from 32 to 50 yr (43.3 ± 10.0), participated. The subjects were asked to generate an isometric force by attempting to elevate the shoulder against a strap. It is difficult to construct force-measuring systems that accurately measure the force of a shrugging shoulder. Thus the contraction level was monitored by displaying the root-mean-square (RMS) value of the surface EMG signal detected from the same muscle. All RMS values were normalized by the RMS of the EMG signal detected during the MVC. The subjects generated a slowly increasing ramp contraction of 0.05% MVC/s. Contraction levels in the neighborhood of 2 to 3% MVC were investigated. For further details on the experimental protocol see Westgaard and De Luca (2001). Nine contractions were analyzed.
VL EXPERIMENTS.
Two male subjects (both 22 yr of age) participated. The subjects were seated in a chair with their dominant lower limb fixed in a specially designed ankle device that immobilized the knee joint and restricted the VL to contract isometrically. They were asked to follow a force trajectory presented on a computer screen by isometrically extending the knee joint. The trapezoidal trajectory consisted of a 50-s-long plateau at 20% MVC. See Adam and De Luca (2005) for additional details of the experimental setup. The constant-force segments of two contractions were analyzed.
FDI EXPERIMENTS.
Subjects were asked to follow a trajectory that was preset on a computer screen by abducting the index finger of their dominant hand against a force gauge. The hand and wrist were secured in a fixed position by a specially designed device that constrained the FDI to contract isometrically. See De Luca et al. (1982a) for additional details. Two different experiments were performed with this setup: 1) Isometric constant-force contraction: a cohort of seven subjects (five males, two females), with age ranging from 24 to 37 yr (30.9 ± 6.3), participated. The force trajectory consisted of a trapezoid with a 60-s-long plateau at 20% MVC and with increasing and decreasing slopes of 10% MVC/s. The constant-force segments of 15 contractions were analyzed. 2) Isometric ramp contraction: a cohort of five subjects (four males, one female), with age ranging from 26 to 50 yr (35 ± 9.4), participated. The force trajectory consisted of a ramp with a rate of 0.33% MVC/s and the contraction lasted 45 s. Eight contractions were analyzed.
Data analysis
The firing rates of motor units were calculated by taking the inverse of the interpulse interval. To better visualize the behavior of the firing rates, the time series were sampled at 100 Hz and processed with a finite-impulse-response band-pass filter with corner frequencies of 0.75 and 12 Hz. An example of the time-varying firing rates of motor units from an isometric contraction at 20% MVC from the FDI muscle is shown in Fig. 1. Visual inspection of the smoothed firing rates reveals that they are varying in unison. It is this characteristic that has been referred to as common drive and can be quantified by calculating the cross-correlation functions of motor unit pairs (De Luca et al. 1982b).
FIG. 1.
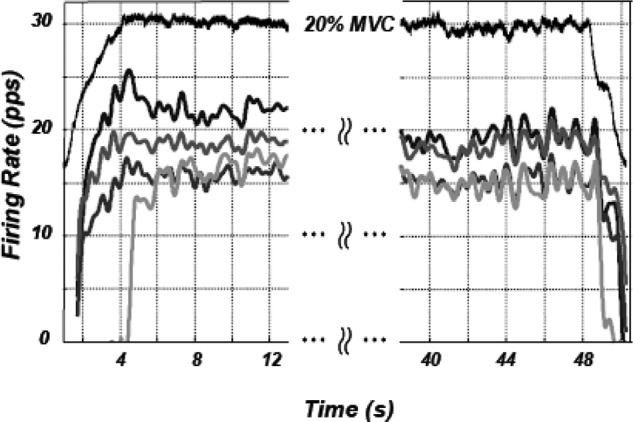
The firing rates of 4 motor units (MUs) detected from the first dorsal interosseous (FDI) muscle during an isometric constant-force contraction at the 20% MVC level performed by a 24-yr-old subject. The top trace represents the force of the contraction. The contraction lasted 50 s and the time axis is segmented. The firing rates are smoothed with a low-pass filter having a 2-Hz cutoff frequency. The smoothing was applied to provide a more distinguishable representation of the firing rates. Note that the firing rates fluctuate in unison with no apparent phase lag, indicating the presence of a “common drive.”
Only motor units that were recruited at <95% of the target force level were considered for further analysis. Motor units recruited above this level present an unstable firing rate because the suprathreshold excitation that fires the motor units may not be stable, as evidenced by the fluctuation of the attempted constant-force contraction.
To investigate the time-varying behavior of the cross-correlation of the firing rates of motor units during a contraction, we chose to estimate the instantaneous cross-correlation functions, defined as
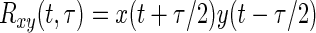 |
where x and y are the firing-rate time series of the two considered motor units, t is the time variable, and τ is the time-lag variable.
When x = y, the instantaneous cross-correlation function becomes the instantaneous autocorrelation function. The correlation between pairs of motor units may be measured by normalizing the instantaneous cross-correlation function according to the following formula
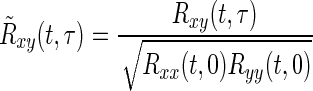 |
where R̃xy(t, τ) is the normalized instantaneous cross-correlation function [see the work of Williams (1996) and Bonato et al. (2000) for further details]. This definition is analogous to that used in the stationary case to derive the cross-correlation coefficient in our previous publications.
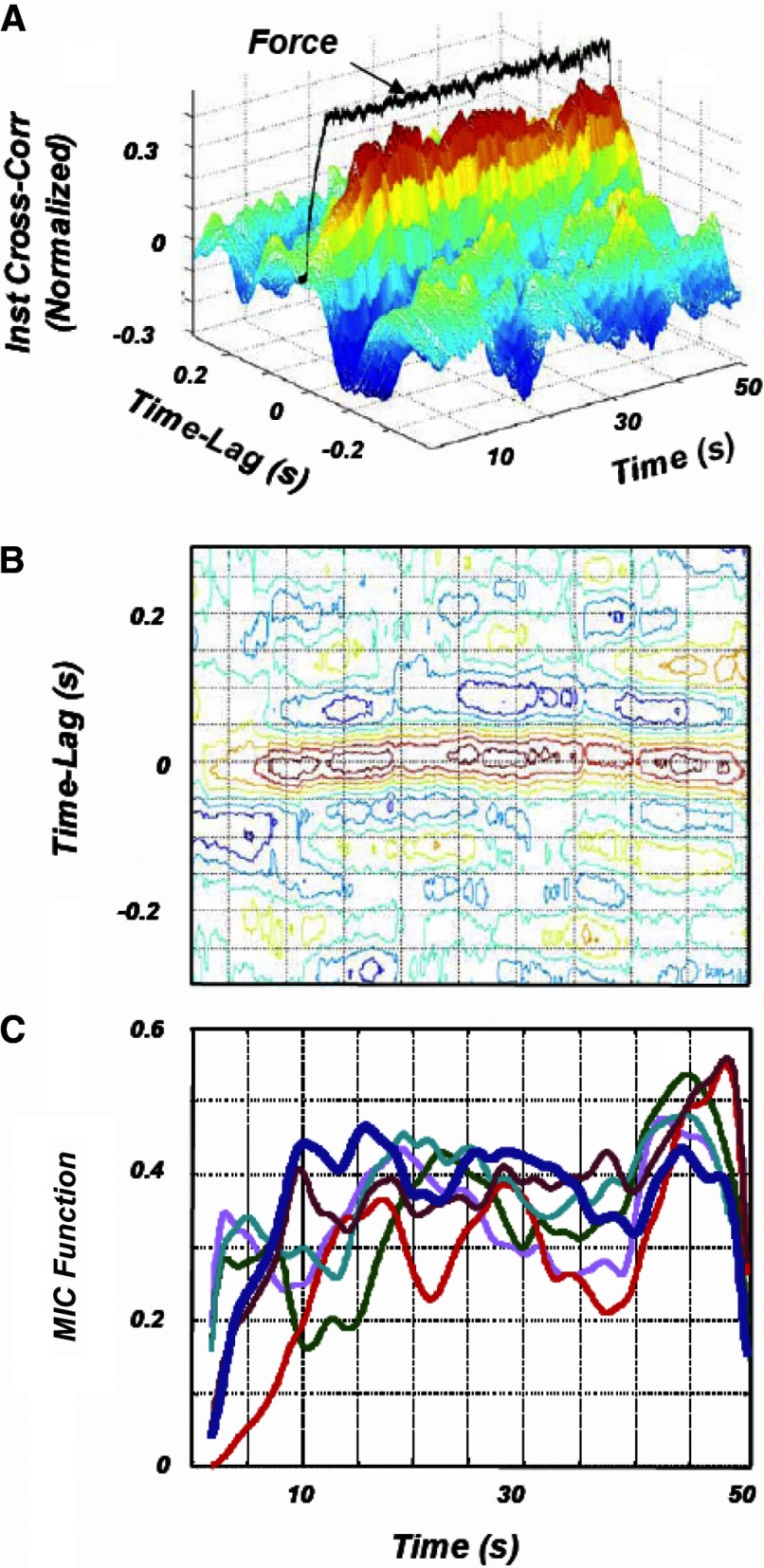
The normalized instantaneous cross-correlation function provided a representation that was associated with large variability when applied to firing rate data; consequently, it was smoothed along the time axis. A rectangular window of 8 s was found to provide satisfactory smoothing without concealing time variations of the correlation between motor unit firing rates. A typical normalized instantaneous cross-correlation function for the firing rate time series of two motor units is shown in Fig. 2A. A contour-level representation of the same function is shown in Fig. 2B. It may be seen that maxima are located in the range of −0.05 to 0.05 s, as previously reported by De Luca et al. (1982b). By plotting the maxima as a function of time, one obtains functions like those in Fig. 2C, which will be referred to as maxima instantaneous cross-correlation (MIC) functions. These functions represent the time course of the common drive throughout a contraction.
FIG. 2.
A: instantaneous cross-correlation function of the firing rates of 2 MUs from the contraction in Fig. 1. Note that the peak of this function for each time instance occurs at or near a time lag of 0 s and that the amplitude of the peak is not constant throughout the contraction. The dark line represents the isometric constant force of the FDI. B: a contour-level representation of the instantaneous cross-correlation function. The location of the peak of the instantaneous cross-correlation function is easily identified as being near 0-s time lag. Note that the amplitude of the function varies throughout the contraction. C: the ensemble of the maxima instantaneous cross-correlation (MIC) functions, representing the time course of the common drive, of all the possible MU pairs in the contraction shown in Fig. 1. Note that they all fluctuate during their time course. The MIC function shown as a blue trace was derived from the instantaneous cross-correlation function shown in the top panel.
RESULTS
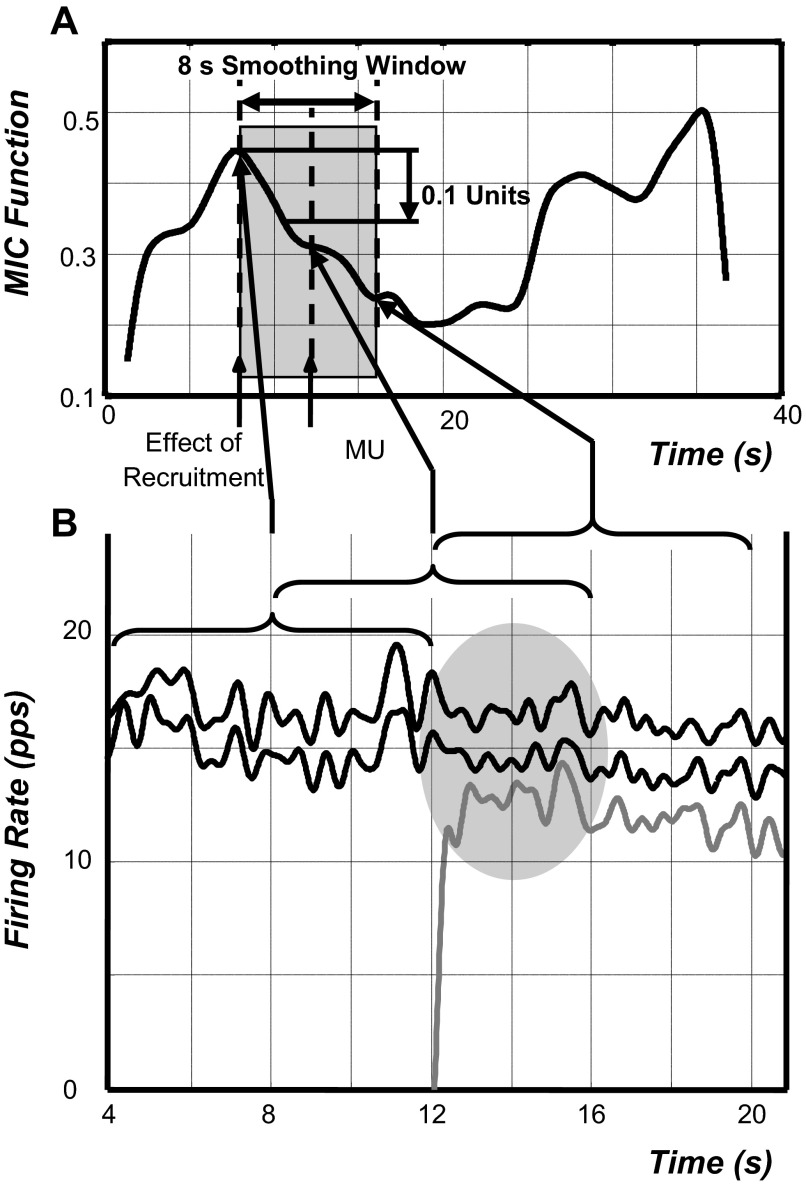
Many of the MIC functions revealed an interesting behavior when a new motor unit was recruited. That is, on recruitment of a motor unit the amplitude of the MIC function of previously active motor unit pairs decreased. This phenomenon can be seen in Fig. 2C and more clearly in Fig. 3. In Fig. 3B, a new motor unit is recruited at about 12 s. For 3 s subsequent to the recruitment, the average firing rates of the two previously active motor units decrease by two to three pulses/s. Importantly, the fluctuations of the firing rates of the previously active motor units are in unison prior to the motor unit recruitment and in discord after the recruitment, as shown in the shaded region. After the 3-s interval the fluctuations of the firing rates are once again in unison. The MIC function in Fig. 3A registers the discord in the firing rates as a decrease in the MIC function, which increases when the firing rates fluctuate in unison again. (The delay is caused by the 8-s smoothing window.)
FIG. 3.
A: an example of a MIC function containing a significant decrease (P < 0.05) of 0.1 unit (see text for details) in the neighborhood of a MU recruited at t = 12 s. The shaded area indicates the duration (8 s) of the smoothing window used to derive the MIC function. Note that the beginning of the decrease coincides with the beginning of the smoothing window, 4 s prior to the actual recruitment time. This lead effect is caused by the smoothing window applied to the instantaneous cross-correlation function from which the MIC function is derived. B: the firing rate (in pulses per second) of the 2 MUs used to calculate the above-shown MIC function and the firing rate of the newly recruited MU at t = 12 s. It can be seen that prior to the recruitment, the firing rates are fluctuating in unison with no apparent delay. However, soon after recruitment the firing rates begin to lose their well-coordinated phase and amplitude relationship and appear to be discordant. This behavior is highlighted by the shaded elliptical region and is quantified by the MIC function. The duration of the smoothing window is shown above the firing rates. It can be seen that the discordant firing rates take effect on the MIC function as soon as the leading edge of the smoothing window intersects them at the time of recruitment. The MIC function value calculated at this time is placed at the time corresponding to half of the window length, i.e., 4 s. Consequently, this is the earliest an effect can be registered on the MIC function. (However, if the discordant behavior of the firing rates is weak or is slightly delayed and the correlation of the firing rates prior to the recruitment time is progressively increasing, then the effect will be noticed later, i.e., between 4 s prior to recruitment and the time of recruitment.)
Because MIC functions are inherently noisy, the question arises as to how much of a change in the function constitutes a physiologically significant occurrence that indicates a causal relationship rather than an occurrence caused by random fluctuations.
To clarify this point, an objective method was constructed to determine the level of change of the function that could be considered as significant. This was done by synthesizing firing-rate time series and measuring the SD of the resulting normalized MIC function. Pairs of firing-rate time series were constructed by adding different samples of Gaussian uncorrelated noise to a common signal according to Erim et al. (1996). The amplitude of the noise was chosen so that the average amplitude of the MIC functions was 0.4 unit. This value corresponded to typical cross-correlation values found in real data. One hundred pairs were synthesized. The average standard deviation (SD) value was 0.05 unit. Thus a fluctuation in the MIC function was considered to be significant if it was >2SDs (0.1 unit), corresponding to P < 0.05 for a Gaussian-distributed variable. Additionally, because the functions were filtered with an 8-s smoothing window, for any fluctuation to be causally related to the recruitment of a new motor unit it had to begin about 4 s before the time of the recruitment. An example of an actual MIC function that displays all these characteristics associated with when a new motor unit is recruited is presented in Fig. 3. It is evident that prior to the recruitment of the new motor unit, the firing rates of the previously active motor units fluctuate in unison (Fig. 3B), but immediately after the recruitment at t = 12 s, the same firing rates become discordant. It is this very effect that is represented in the highlighted decrease in the MIC function in Fig. 3A.
The duration and alignment of the 8-s smoothing window used to calculate the MIC functions are shown in Fig. 3A. Note that due to the influence of this smoothing window, the effect of the motor unit recruitment is seen 4 s earlier on the MIC functions.
It was found that 96% of all the motor unit recruitments were associated with a significant deflection in the cross-correlation function that preceded the recruitment event. Having thus established a reasonable basis for causality, it was possible to proceed with regression analysis, which by itself does not establish causality.
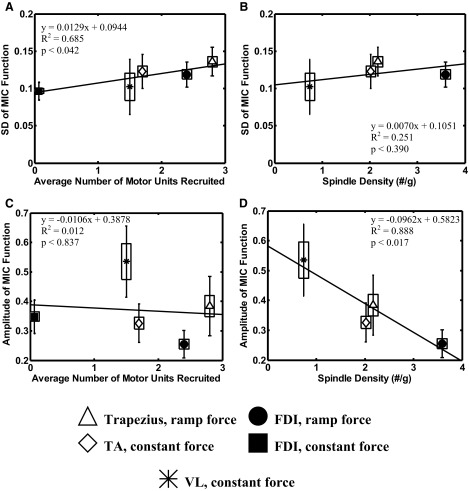
To compare the amount of variation in the common drive among the muscles studied, we calculated the mean and SD values of the MIC functions within each contraction for a particular muscle and then calculated the ensemble average across all the contractions of that muscle. For each MIC function these values were calculated for the time interval not including the ascending and descending phases of the firing rate time series that occurred due to the recruitment and derecruitment of a motor unit at the beginning and end of the contraction. These values are plotted in Fig. 4 as a function of the average number of motor units recruited in a contraction and, separately, as a function of the spindle density in the muscle. [According to the widely cited work of Voss (1971), the human VL contains 0.74 spindle/g, the trapezius contains 2.02 spindles/g, the TA contains 2.10 spindles/g, and the FDI contains 3.69 spindles/g.]
FIG. 4.
In this figure the symbol represents the mean value, the box represents the SE, and the bars represent the SD of the MIC amplitude and SD values calculated across subjects and contractions for different muscles, each of which is represented by a different symbol. A: the SD of the MIC function of the firing rates vs. the average number of MUs that are recruited during the contraction. Note that the slope of the linear regression is significantly (P < 0.042) greater than zero and has an R2 value of 0.685. The vales for the 2 FDI contractions (filled circle and square) are significantly different (P < 0.005). B: the SD of the MIC function of the firing rates vs. the spindle density in each muscle measured in number of spindles per gram of muscle. The SD values appear to be unrelated to the spindle density. C: the amplitude of the MIC function of the firing rates vs. the average number of MUs that are recruited during the contraction. Note that the regression among the muscles is poor (R2 = 0.012) and the slope is not significantly different from zero (P < 0.837). However, within the same muscle (the FDI) the amplitude of the MIC function decreases as the number of recruited MUs increases. The values for the FDI in the ramp-force contractions (filled circle) and the FDI constant-force contractions (filled square) are significantly different (P < 0.001). D: the amplitude of the MIC function of the firing rates vs. the spindle density in each muscle measured in number of spindles per gram of muscle. Note that the amplitude decreases as the spindle density increases. The slope of the linear regression is significantly (P < 0.017) greater than zero and has an R2 value of 0.888.
A linear regression analysis was performed on the data in Fig. 4, A–D. Significant regression lines were identified in Fig. 4A describing the relationship between the average number of motor units recruited and the SD of the MIC function (P < 0.042) and in Fig. 4D describing the relationship between spindle density and the amplitude of the MIC function (P < 0.017). In Fig. 4C, mean values of the amplitude of the MIC function were significantly greater for FDI constant-force contractions compared with FDI ramp-force contractions, based on a pairwise post hoc comparison (t = 4.18; P < 0.001) that was calculated following the convention (Glantz 1981) of first determining that the five mean values were significantly different using an ANOVA (F = 18.78; P < 0.001).
The data from the FDI isometric contractions were not included in the spindle density plots because, in those contractions, no motor units were recruited; thus the influence of the spindles on the MIC function could not be evaluated. A summary of the data is presented in Table 1. The spindle density was used as a parameter to describe the association between MIC functions and the influence of the feedback from the spindles. A better assessment of the spindle influence would be provided by the ratio of motor units to spindles in an average motor unit territory of a muscle. That parameter would provide a more direct relationship between the contraction of muscle fibers and the excitation of a spindle in the proximity of the muscle fibers. Unfortunately, that ratio cannot be calculated because the requisite parameters are not available from the literature. Additionally, the gain of the spindle feedback might also influence the spindle feedback. However, that parameter is difficult to obtain in the FDI and the trapezius muscles.
TABLE 1.
Details about the muscles, contractions, motor unit recruitment characteristics, and calculated parameters
| Contraction Type | Number of Subjects | Age, Mean ± SD | Number of Contractions | Total Number of MUs Analyzed | Number of MUs Analyzed per Contraction | Number of New MUs Recruited | Number of New MUs Recruited per Contraction | Spindle Density, #/g | MIC Function |
|
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | |||||||||
| FDI ramp force | 5 | 34.4 ± 9.7 | 8 | 31 | 4.4 | 17 | 2.4 | 3.59 | 0.26 | 0.12 |
| FDI const. force | 7 | 30.9 ± 6.3 | 15 | 51 | 3.4 | 0 | 0.0 | 3.59 | 0.34 | 0.10 |
| TA const. force | 6 | 30.8 ± 7.0 | 10 | 54 | 5.4 | 17 | 1.7 | 2.02 | 0.33 | 0.12 |
| Trapezius ramp force | 3 | 43.3 ± 10.0 | 9 | 46 | 5.1 | 25 | 2.8 | 2.17 | 0.38 | 0.14 |
| VL const. force | 2 | 22 | 2 | 18 | 9.0 | 3 | 1.5 | 0.74 | 0.54 | 0.10 |
Muscles: FDI, first dorsal interosseous; TA, tibialis anterior; VL, vastus lateralis, const., constant; MIC, maxima instantaneous cross-correlation; MU, motor unit.
DISCUSSION
When a newly recruited motor unit fires, there is a disruption in the cross-correlation of the firing rates of the previously recruited motor units, causing an increase in the variation of the correlation of the firing rates. The increase in variation is proportional to the number of motor units that are recruited during a contraction. This appears to be true across muscles and even within a muscle (the FDI) when the force output increases during a contraction. As may be seen in Figs. 2 and 3, the disruption to the cross-correlation function and derived MIC function caused by the newly recruited motor unit begins quickly after recruitment, if not at recruitment itself. The disruption was observed during isometric slow-ramp contractions at low levels (the 2–3% MVC in the trapezius muscle) and constant-force contractions at higher force levels (20% MVC) in the TA and FDI.
Two types of disruptions of the cross-correlation functions are evident in Figs. 2 and 3: 1) At recruitment, the cross-correlation between firing rates of the recruited motor unit and that of any of the previously recruited motor units begins at zero and increases as the firing rate of the recruited motor unit increases. This occurs only as a result of the computation of the cross-correlation function, bears no physiological relevance other than to indicate recruitment of a motor unit, and shows the time course of the firing rate increase. In the analyzed data, most of these occurrences are not captured by the calculated MIC functions because the beginning and end of the contraction were not considered in the calculation. However, the effects of those motor units that are recruited during the contraction do influence the MIC functions. This factor is evident in Fig. 4, A and C. 2) When a motor unit is recruited, the firing rates of the previously active motor units are temporarily suppressed as the firing rate of the recruited motor unit increases. The time course of the firing-rate decrease differs among the motor units. Consequently, the amplitude of the MIC functions of the firing rates of previously active motor units first decreases, then subsequently increases as the effect of the recruitment wears off, causing an increase in the SD of the MIC functions. A third observation is that the amplitude of the MIC functions varies among muscles and appears to be related to the density of muscle spindles in the muscles.
There are three systems that provide feedback to homonymous motor units that are capable of influencing the firing rates: 1) the Renshaw recurrent inhibition, 2) the muscle spindle proprioceptive afferent feedback, and 3) the nonreciprocal inhibition of Golgi tendon organs (GTOs).
The reciprocal inhibition from the Renshaw system is particularly appealing for explaining the behavior of the MIC functions because there is some evidence that it may have a graded feedback gain in different muscles, with a greater gain in proximal muscles than that in distal muscles (Katz and Pierrot-Deseilligny 1998; Rossi and Mazzocchio 1991). However, this gradation has not been well quantified in humans (Jani 1992). Nonetheless, the modeling work of Maltenfort et al. (1998) has shown that the Renshaw recurrent inhibition has the potential of reducing the correlation of motor unit firings. However, according to Katz et al. (1993) and Rossi and Mazzocchio (1991) the FDI receives no, or almost no, homonymous and heteronymous Renshaw recurrent inhibition. Yet, in Fig. 4 it is evident that in the FDI the SD of the cross-correlation increases when more motor units are recruited in the ramp contraction compared with the constant-force contraction where no motor units are recruited. Thus it appears that the Renshaw inhibition cannot explain the behavior of the MIC functions. It may participate in some capacity, but it is not a dominant or essential factor.
The proprioceptive feedback from spindles and GTOs appears to constitute a more likely candidate to explain the observation in this study. Muscle spindles and GTOs are found in most muscles in the body, with the exception of the facial muscles (Folkins et al. 1978; Lovell et al. 1977). The involvement of the proprioceptive feedback in the modulation of motor units firings was previously suggested by Garland and Miles (1997) to explain their observation that the degree of cross-correlation among firing rates in the flexor digitorum profundus muscle varied when the fourth hand digit was flexed. They suggested that the altered proprioceptive feedback was either directly or indirectly involved, but did not provide evidence to substantiate the suggestion.
It is generally accepted that the Ib fibers from the GTOs provide a negative feedback (nonreciprocal inhibition) to the homonymous motor units and that the GTOs respond to tension from the muscle fibers. Furthermore, they can respond to the tension generated by individual motor units (Binder et al. 1974). Thus as the Ib fibers increase their firing rate, the inhibition to the homonymous motor units increases. In a complementary fashion, during a contraction the muscle spindles also provide a negative feedback (disfacilitation) to the homonymous motor units. Muscle spindles that are arranged in parallel with the muscle fibers will tend to slacken when the muscle contracts and firings of the Ia fibers will decrease and consequently decrease the excitatory feedback, which amounts to a virtual negative feedback. Broman et al. (1985) suggested that these two mechanisms could be responsible for the observed decrease in the firing rates of active motor unit pairs when a new motor unit was recruited. A similar observation can be made in Fig. 3B. Moreover, it appears that the decreasing firing rate of active motor units is uncorrelated with the increasing firing rate of the recruited motor unit. This effect tends to reduce the amplitude and increase the SD of the calculated MIC functions. The communal effect of this behavior in the FDI is seen in Fig. 4, A and C. Note that the amplitude of the MIC function decreases (P < 0.001) and the SD increases (P < 0.005) in the force increasing (ramp) contractions in which motor units are recruited. However, this relationship does not hold across muscles. The reason for this discrepancy is evident in Fig. 4D, which shows that the amplitude of the MIC function is inversely proportional to the spindle density in the individual muscles (R2 = 0.888, P < 0.017).
It is apparent in Fig. 4, B and D that the amplitude of the MIC function decreases (P < 0.017) as a function of increasing spindle density, whereas the SD is not dependent (R2 = 0.251; P < 0.390) on the spindle density, which in turn varies among muscles. A mechanism for explaining this observation is found in the behavior of muscle spindles. When a motor unit is recruited the muscle fibers shorten. Spindles in the proximity of the contracting muscle fibers will be either slackened or stretched, depending on their orientation with respect to the shortening fiber. If they are in parallel with the muscle fibers they will tend to slacken and the Ia firings will decrease; if they are in series and well anchored, they will tend to stretch and the Ia firings will increase. This dual behavior was previously reported by Binder and Stuart (1980) and Edin and Vallbo (1990). As the muscle fibers relax, the opposite occurs. This vacillation of the spindle output continues until the fibers become fused or quasi-fused and the force ripple of the muscle fiber is reduced, at which time the proprioceptive feedback to the motoneuron pool is reduced and becomes more or less stable (Edin and Vallbo 1990). From the behavior of the MIC functions in Fig. 2C, this sequence of events appears to take place within 5 to 10 s of the recruitment.
It is known from the work of Henneman and Mendell (1981) that some of the Ia fibers connect with only ≤65% of the homonymous motoneurons, whereas others connect to all. This arrangement indicates that individual motoneurons receive varying degrees of feedback from the spindle population. Additionally, the extensive interneuron connections in the motoneuron pool render varying excitatory and inhibitory inputs to individual motoneurons at any instant of time. The summed effect of these explicit interconnections and inputs provides a system wherein the instantaneous net excitation to an individual motoneuron is likely to differ from that of its neighbor. Thus at any point in time during the recruitment of a motor unit, the varying degrees of excitation from the afferent feedback will facilitate some and disfacilitate other motoneurons. Consequently, the instantaneous firing rates of the motor units will vary in a discordant manner and the amplitude of their cross-correlation will decrease, although the variation (measured by the SD) remains essentially unaltered (Fig. 4B) because the feedback from the spindles activated by the currently active motor units remains essentially constant. This behavior is evident in the plots of Fig. 3B.
The findings in this work are supported by various reports in the literature. For example, the greatest measured value of the cross-correlation (0.77 over short intervals of 5 s) was reported by Kamen and De Luca (1992) in the orbicularis oris muscle, which is believed to be devoid of spindles (Folkins and Larson 1978; Stal et al. 1990) and GTOs (Falkins and Larson 1978; Lovell et al. 1977). In another study, De Luca et al. (1982a) reported that the cross-correlation value in the FDI during isometric constant-force contractions was greater for contractions performed at 60% MVC than those at 30% MVC. It is known that in the FDI all available motor units are recruited ≲50% MVC from work by De Luca et al. (1982b) who measured the MVC in a manner similar to that used in the experiments performed in this work. Even lower levels have been reported by Duchateau and Hainaut (1990). Thus at 60% MVC there would be minimal, if any, recruitment to decrease the cross-correlation of the firing rates.
Involvement of the proprioceptive feedback also explains the short (0–50 ms) latency found among the firing rates of motor units, as seen in most cross-correlation functions of motor unit pairs (De Luca et al. 1982b). The latency would be due to the delay resulting from the time required to activate a spindle, for the Ia fibers to propagate to the homonymous motoneurons in the motoneuron pool, and for the excitation to propagate via the alpha-motoneurons to the muscle fibers.
The influence of the motor unit recruitment in reducing the degree of correlation of the firing rates of motor units explains observations reported in the literature concerning the common drive (the amplitude of the cross-correlation) in contractions of increased force fluctuation. Increased force fluctuations are due, in part, to the increased recruitment and derecruitment of motor units while the production of a fixed force is attempted. For example, Erim et al. (1999) found the cross-correlation of firing rates of motor units in the FDI muscles in elderly (>65 yr) healthy subjects to be significantly (P < 0.0001) lower than that in young healthy subjects (<35 yr) for contractions performed at 20% MVC, but not for contractions at 50% MVC where there are few, if any, motor units left to recruit. They also reported that the attempted constant-force contractions in the elderly were less steady, an observation supported by the work of Vaillancourt et al. (2003). In another study Kamen et al. (1992) found that the degree of correlation of firing rates in the FDI of the dominant hand was greater than that in the nondominant hand. From the work of Adam et al. (1998) it is known that the force variability of the FDI in the dominant hand is significantly (P < 0.01) less than that of the nondominant hand. Semmler and Nordstrom (1998) found statistically significant differences in the correlation of the firing rates in untrained subjects compared with those of skill-trained subjects and strength-trained subjects. The force fluctuations were not reported, but it is known from the work of Laidlaw et al. (1999) that trained subjects produce force outputs with fewer fluctuations.
It is important to highlight the fact that the force fluctuations referred to are those that occur in the normal course of attempted constant-force contractions in neurologically healthy individuals. There is evidence that in patients with acute cerebellar stroke (Sauvage et al. 2007) the correlation of the firing rates increases as the patients generated oscillatory contractions when constant-force contractions of the FDI are attempted. Also, a recent report by Mochizuki et al. (2006) has shown that the modulation of motor unit firings in the soleus muscle is greater during postural tasks (standing quietly) than that during voluntary isometric tasks (plantarflexion). During quiet standing the soleus muscle is continuously contracted and relaxed as it participates in the postural sway. In both examples, the monitored muscle contraction fluctuated in an involuntary oscillatory manner. These fluctuations are different from the more random force fluctuations that occur during normal voluntary contractions, such as those discussed earlier. During a force oscillation, a substantial number of the motor units are continuously recruited and derecruited, causing the firing rates to oscillate in unison and consequently increasing the correlation between the firing rates. The preceding discussion refers to the influence of individual motor units recruited during a contraction.
A recent report by Sowman et al. (2007) indicates that the correlation of the motor unit firing rates decreases when the force fluctuation of the masseter muscle decreases. This muscle contains no spindles (Kubota and Masegi 1977) or Renshaw system (Katz and Pierrot-Deseilligny 1998), although it does contain GTOs. The behavior of the correlation is opposite that seen in muscles containing spindles. This result suggests that the spindles play the dominant proprioceptive role that affects the firing rates. However, it is not possible to extract clear deductions because the reduced force fluctuation was a consequence of an injection of xylocaine (2%) in the peri-incisal periodontium and it is not known what effect the anesthetic had on the GTOs in the masseter muscle.
In conclusion, the results support the notion that the proprioceptive feedback from muscle spindles and possibly GTOs initiated by motor unit recruitment decreases the amplitude and increases the variation of correlation among motor unit firing rates (common drive). This is so irrespective of whether the force is constant or linearly increasing. Consequently, contractions that have more motor unit recruitments produced either by intentional force increases or fluctuations about a constant-force mean value have decreased firing-rate correlation values. The degree of common drive is likely influenced by the ongoing activity of muscle spindles during a contraction. Thus muscles that contain greater spindle densities present smaller correlation values. These observations support the hypothesis that the common drive originates in the CNS and is diminished by the proprioceptive feedback from spindles and possibly GTOs.
GRANTS
This work was supported in part by Bioengineering Research Partnership Grants HD-38585 and HD-050111 from the National Center for Medical Rehabilitation Research of the National Institute of Child Health and Human Development.
Acknowledgments
We thank Drs. Zeynep Erim and Rolf Westgaard for contributing to the data used in the investigation reported here and D. Schatzberg and Dr. S. Roy for assisting in preparation of the manuscript.
The costs of publication of this article were defrayed in part by the payment of page charges. The article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. Section 1734 solely to indicate this fact.
REFERENCES
- Adam and De Luca 2005.Adam A, De Luca CJ. Firing rates of motor units in human vastus lateralis muscle during fatiguing isometric contractions. J Appl Physiol 99: 268–280, 2005. [DOI] [PubMed] [Google Scholar]
- Adam et al. 1998.Adam A, De Luca CJ, Erim Z. Hand dominance and motor unit firing behavior. J Neurophysiol 80: 1373–1382, 1998. [DOI] [PubMed] [Google Scholar]
- Belhaj-Saif et al. 1998.Belhaj-Saif A, Karrer JH, Cheney PD. Distribution and characteristics of poststimulus effects in proximal and distal forelimb muscles from red nucleus in the monkey. J Neurophysiol 79: 1777–1789, 1998. [DOI] [PubMed] [Google Scholar]
- Binder et al. 1974.Binder MD, Kroin JS, Moore GP, Stauffer EK, Stuart DG. The response of Golgi tendon organs to single motor unit contractions. J Physiol 271: 337–349, 1974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binder and Stuart 1980.Binder MD, Stuart DG. Response of Ia and spindle group II afferent to single motor unit contractions. J Neurophysiol 43: 621–629, 1980. [DOI] [PubMed] [Google Scholar]
- Bonato et al. 2000.Bonato P, Ceravolo R, De Stefano A, Molinari F. Use of cross-time-frequency estimators for structural identification in non-stationary conditions and under unknown excitation. J Sound Vib 237: 775–791, 2000. [Google Scholar]
- Broman et al. 1985.Broman H, De Luca CJ, Mambrito B. Motor unit recruitment and firing rate interaction in the control of human muscles. Brain Res 337: 311–319, 1985. [DOI] [PubMed] [Google Scholar]
- Cheney and Fetz 1980.Cheney PD, Fetz EE. Functional classes of primate corticomotoneuronal cells and their relation to active force. J Neurophysiol 44: 773–791, 1980. [DOI] [PubMed] [Google Scholar]
- Dawson-Saunders and Trapp 1994.Dawson-Saunders B, Trapp RG. Basic and Clinical Biostatistics (2nd ed.). East Norwalk, CT: Appleton & Lange, 1994.
- De Luca and Adam 1999.De Luca CJ, Adam A. Decomposition and analysis of intramuscular electromyographic signals. In: Modern Techniques in Neuroscience Research (1st ed.), edited by Windhorst U, Johansson H. Heidelberg, Germany: Springer-Verlag, 1999, p. 757–776.
- De Luca and Erim 1994.De Luca CJ, Erim Z. Common drive of motor units in regulation of muscle force. Trends Neurosci 17: 299–305, 1994. [DOI] [PubMed] [Google Scholar]
- De Luca and Forrest 1972.De Luca CJ, Forrest WJ. An electrode for recording single motor unit activity during strong muscle contractions. IEEE Trans Biomed Eng 19: 367–372, 1972. [DOI] [PubMed] [Google Scholar]
- De Luca et al. 1982a.De Luca CJ, LeFever RS, McCue MP, Xenakis AP. Behavior of human motor units in different muscles during linearly-varying contractions. J Physiol 329: 113–128, 1982a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Luca et al. 1982b.De Luca CJ, LeFever RS, McCue MP, Xenakis AP. Control scheme governing concurrently active human motor units during voluntary contractions. J Physiol 329: 129–142, 1982b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duchateau and Hainaut 1990.Duchateau J, Hainaut K. Effects of immobilization on contractile properties, recruitment and firing rates of human motor units. J Physiol 422: 55–65, 1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edin and Vallbo 1990.Edin BB, Vallbo AB. Muscle afferent responses to isometric contractions and relaxations in humans. J Neurophysiol 63: 1307–1313, 1990. [DOI] [PubMed] [Google Scholar]
- Erim et al. 1999.Erim Z, Beg MF, Burke DT, De Luca CJ. Effects of aging on motor unit control properties. J Neurophysiol 82: 2081–2091, 1999. [DOI] [PubMed] [Google Scholar]
- Erim et al. 1996.Erim Z, De Luca CJ, Mineo K, Aoki T. Rank-ordered regulation of motor units. Muscle Nerve 19: 563–573, 1996. [DOI] [PubMed] [Google Scholar]
- Folkins and Larson 1978.Folkins JW, Larson CR. In search of a tonic vibration reflex in the human lip. Brain Res 151: 409–412, 1978. [DOI] [PubMed] [Google Scholar]
- Garland and Miles 1997.Garland S, Miles TS. Control of motor units in human flexor digitorum profundus under different proprioceptive conditions. J Physiol 502: 693–701, 1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glantz 1981.Glantz SA Primer of Biostatistics. New York: McGraw-Hill, 1981.
- Guiheneuc 1992.Guiheneuc P Le recrutement des unités motrices: méthodologie, physiologie et pathologie. In: EMG: Actualités en Electromyographie, edited by Cadilhac J, Dapres G. Montpellier, France: Sauramps Médical, 1992, p. 35–39.
- Henneman and Mendell 1981.Henneman E, Mendell LM. Functional organization of motoneuron pool and its inputs. In: Handbook of Physiology. The Nervous System. Motor Control. Bethesda, MD: Am. Physiol. Soc., 1981, sect. 1, vol. II, pt. 1, p. 423–507.
- Iyer et al. 1994.Iyer MB, Christakos CN, Ghez C. Coherent modulations of human motor unit discharges during quasi-sinusoidal isometric muscle contractions. Neurosci Lett 170: 94–98, 1994. [DOI] [PubMed] [Google Scholar]
- Jani 1992.Jani L Golgi tendon organs in mammalian skeletal muscles: functional properties and central action. Physiol Rev 72: 623–667, 1992. [DOI] [PubMed] [Google Scholar]
- Kamen and De Luca 1992.Kamen G, De Luca CJ. Firing rate interactions among human orbicularis oris motor units. Int J Neurosci 64: 167–175, 1992. [DOI] [PubMed] [Google Scholar]
- Kamen et al. 1992.Kamen G, Greenstein-Solar S, De Luca CJ. Lateral dominance and motor unit firing behavior. Brain Res 576: 165–167, 1992. [DOI] [PubMed] [Google Scholar]
- Katz et al. 1993.Katz R, Mazzocchio R, Penicaud A, Rossi A. Distribution of recurrent inhibition in the human upper limb. Acta Physiol Scand 149: 183–198, 1993. [DOI] [PubMed] [Google Scholar]
- Katz and Pierrot-Deseilligny 1998.Katz R, Pierrot-Deseilligny E. Recurrent inhibition in humans. Prog Neurobiol 57: 325–355, 1998. [DOI] [PubMed] [Google Scholar]
- Kubota and Masegi 1977.Kubota K, Masegi T. Muscle spindle supply to the human jaw muscle. J Dent Res 56: 901–909, 1977. [DOI] [PubMed] [Google Scholar]
- Laidlaw et al. 1999.Laidlaw DH, Kornatz KW, Keen DA, Suzuki S, Enoka RM. Strength training improves the steadiness of slow lengthening contractions performed by old adults. J Appl Physiol 87: 1786–1795, 1999. [DOI] [PubMed] [Google Scholar]
- LeFever and De Luca 1982.LeFever RS, De Luca CJ. A procedure for decomposing the myoelectric signal into its constituent action potentials. Part I. Technique, theory, and implementation.IEEE Trans Biomed Eng 29: 149–157, 1982. [DOI] [PubMed] [Google Scholar]
- Lovell et al. 1977.Lovell M, Sutton D, Lindeman RC. Muscle spindles in nonhuman primate extrinsic auricular muscles. Anat Rec 189: 519–523, 1977. [DOI] [PubMed] [Google Scholar]
- Maltenfort et al. 1998.Maltenfort MG, Heckman CJ, Rymer WZ. Decorrelating actions of Renshaw interneurons on the firing of spinal motoneurons within a motor nucleus: a simulation study. J Neurophysiol 80: 309–323, 1998. [DOI] [PubMed] [Google Scholar]
- Marsden et al. 1999.Marsden J, Farmer S, Halliday D, Rosenberg J, Brown P. The unilateral and bilateral control of motor unit pairs in the first dorsal interosseous and paraspinal muscles in man. J Physiol 521: 553–564, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKiernan et al. 2000.McKiernan BJ, Marcario JK, Karrer JL. Correlations between corticomotoneuronal (CM) cell postspike effects and cell-target covariation. J Neurophysiol 83: 99–115, 2000. [DOI] [PubMed] [Google Scholar]
- Miles 1987.Miles TS The cortical control of motor neurons: some principles of operation. Med Hypotheses 23: 43–50, 1987. [DOI] [PubMed] [Google Scholar]
- Mochizuki et al. 2006.Mochizuki G, Semmler JG, Ivanova TD, Garland SJ. Low-frequency common modulation of soleus motor unit discharge is enhanced during postural control in humans. Exp Brain Res 175: 584–595, 2006. [DOI] [PubMed] [Google Scholar]
- Patten et al. 2000.Patten C, McGill KC, Lateva Z, Rose J. Common drive among concurrently active motor units in cerebral palsy and post-stroke hemiparesis. Soc Neurosci Abstr 26: 462, 2000. [Google Scholar]
- Rossi and Mazzocchio 1991.Rossi A, Mazzocchio R. Presence of homonymous recurrent inhibition in motoneurons supplying different lower limb muscles in humans. Exp Brain Res 84: 367–373, 1991. [DOI] [PubMed] [Google Scholar]
- Sauvage et al. 2006.Sauvage C, Manto M, Adam A, Roark RM, Jissendi P, De Luca CJ. Ordered motor unit firing behavior in acute cerebellar stroke. J Neurophysiol 96: 2769–2774, 2006. [DOI] [PubMed] [Google Scholar]
- Semmler and Nordstrom 1995.Semmler JG, Nordstrom MA. Influence of handedness on motor unit discharge properties and force tremor. Exp Brain Res 104: 115–125, 1995. [DOI] [PubMed] [Google Scholar]
- Semmler and Nordstrom 1998.Semmler JG, Nordstrom MA. Motor unit discharge and force tremor in skill- and strength-trained individuals. Exp Brain Res 119: 27–38, 1998. [DOI] [PubMed] [Google Scholar]
- Semmler et al. 1997.Semmler JG, Nordstrom MA, Wallace CJ. Relationship between motor unit short-term synchronization and common drive in human first dorsal interosseous muscle. Brain Res 767: 314–320, 1997. [DOI] [PubMed] [Google Scholar]
- Sowman et al. 2007.Sowman PF, Ogston KM, Turker KS. Periodontal anaesthetisation decreases rhythmic synchrony between masseteric motor units at the frequency of jaw tremor. Exp Brain Res 179: 673–682, 2007. [DOI] [PubMed] [Google Scholar]
- Stal et al. 1990.Stal P, Eriksson PO, Eriksson A, Thornell LE. Enzyme-histochemical and morphological characteristics of muscle fibre types in the human buccinator and orbicularis oris. Arch Oral Biol 35: 449–458, 1990. [DOI] [PubMed] [Google Scholar]
- Stashuk and de Bruin 1988.Stashuk D, de Bruin H. Automatic decomposition of selective needle-detected myoelectric signals. IEEE Trans Biomed Eng 35: 1–10, 1988. [DOI] [PubMed] [Google Scholar]
- Vaillancourt et al. 2003.Vaillancourt DE, Larsson L, Newell KM. Effects of aging on force variability, single motor unit discharge patterns, and the structure of 10, 20, and 40 Hz EMG activity.Neurobiol Aging 24: 25–35, 2003. [DOI] [PubMed] [Google Scholar]
- Voss 1971.Voss H Tabelle der absoluten und relativen Muskelspindelzahlen der menschlichen Skelettmuskulatur. Anat Anz 129: 562–572, 1971. [PubMed] [Google Scholar]
- Westgaard and De Luca 2001.Westgaard RH, De Luca CJ. Motor control of low-threshold motor units in the human trapezius muscle. J Neurophysiol 85: 1777–1781, 2001. [DOI] [PubMed] [Google Scholar]
- Williams 1996.Williams WJ Reduced interference distributions: biological applications and interpretations. Proc IEEE 84: 1264–1280, 1996. [Google Scholar]