Abstract
Basal dendrites of prefrontal cortical neurons receive strong synaptic drive from recurrent excitatory synaptic inputs. Synaptic integration within basal dendrites is therefore likely to play an important role in cortical information processing. Both synaptic integration and synaptic plasticity depend crucially on dendritic membrane excitability and the backpropagation of action potentials. We carried out multisite voltage-sensitive dye imaging of membrane potential transients from thin basal branches of prefrontal cortical pyramidal neurons before and after application of channel blockers. We found that backpropagating action potentials (bAPs) are predominantly controlled by voltage-gated sodium and A-type potassium channels. In contrast, pharmacologically blocking the delayed rectifier potassium, voltage-gated calcium, or Ih conductance had little effect on dendritic AP propagation. Optically recorded bAP waveforms were quantified and multicompartmental modeling was used to link the observed behavior with the underlying biophysical properties. The best-fit model included a nonuniform sodium channel distribution with decreasing conductance with distance from the soma, together with a nonuniform (increasing) A-type potassium conductance. AP amplitudes decline with distance in this model, but to a lesser extent than previously thought. We used this model to explore the mechanisms underlying two sets of published data involving high-frequency trains of APs and the local generation of sodium spikelets. We also explored the conditions under which IA down-regulation would produce branch strength potentiation in the proposed model. Finally, we discuss the hypothesis that a fraction of basal branches may have different membrane properties compared with sister branches in the same dendritic tree.
INTRODUCTION
Neuronal dendrites are responsible for combining the information carried by their synaptic inputs in a process called dendritic or synaptic integration (Gulledge et al. 2005; Spruston et al. 2001). Synaptic integration is far from independent of the generation of output action potentials (APs) since APs initiated in the axon initial segment propagate robustly back into the dendrites (Spruston et al. 1995; Stuart and Sakmann 1994) while synaptic integration is taking place (Bar-Yehuda et al. 2008; Häusser et al. 2001; Waters et al. 2003). Backpropagating action potentials (bAPs) play an important role in the induction of long-term synaptic plasticity (Bi and Poo 1998; Linden 1999; Magee and Johnston 1997; Markram et al. 1997b; Sjöstrom and Häusser 2006). To understand AP backpropagation one must understand the underlying membrane mechanisms responsible for the dendrite's intrinsic excitability (Martina et al. 2000). Voltage-gated sodium channels are distributed on many neuronal dendrites and allow for the possibility of actively propagated dendritic APs (Johnston et al. 1996; Stuart et al. 1997). Dendritic potassium channels, especially A-type potassium channels, which activate quickly, can attenuate APs in apical (Hoffman et al. 1997) and basal dendrites (Kampa and Stuart 2006). Although potassium channels always counteract sodium channels, the quantitative—not just qualitative—contribution of both channel types in all dendritic segments (proximal and distal) must be understood to properly evaluate dendritic excitability and its impact on AP backpropagation and synaptic integration (London and Häusser 2005; Spruston 2008).
Interactions between bAPs and synaptic contacts located on basal dendrites of cortical pyramidal neurons have recently been studied by several research groups (Gordon et al. 2006; Kampa et al. 2006; Nevian and Sakmann 2006; Sjöstrom and Häusser 2006). Basal dendrites are targets of dense recurrent excitation among cortical pyramidal neurons (Feldmeyer et al. 2002; Kritzer and Goldman-Rakic 1995; Larkman 1991; Markram et al. 1997a) and may therefore play an important role in the generation of sustained activity and other forms of cortical information processing (Benucci et al. 2004; Compte et al. 2003). Excitability properties of basal dendrites have seen a recent surge in research interest thanks to technical advances allowing optical recordings from thin dendrites (Schiller et al. 2000). Voltage-sensitive dyes (VSDs) have been used to record AP waveforms (Antic 2003; Kampa and Stuart 2006; Zhou et al. 2007) and initiation of sodium spikes (Milojkovic et al. 2005) in basal dendrites of neocortical pyramidal neurons, whereas sophisticated patch-clamp techniques have successfully provided direct electrical recordings (Nevian et al. 2007). These new techniques allow better access to dendritic AP initiation and propagation details, compared with using calcium signaling as an indirect reporter of dendritic voltage fluctuations.
In spite of the advancement in experimental techniques used to study properties of basal dendrites, observed dendritic AP initiation and propagation behavior in this part of the dendritic arbor have not been clearly and quantitatively linked to the underlying voltage-dependent conductances. Recent studies performed in the somatosensory cortex coincide with the amplitude decline of bAPs but propose very different biophysical models to explain this phenomenon (Kampa and Stuart 2006; Nevian et al. 2007). Sodium channel densities are proposed to be uniform and very low in one model (30 pS/μm2; Kampa and Stuart 2006) and nonuniform and nearly threefold larger in the other (Nevian et al. 2007). In addition, the proposed potassium channel distributions are very different in these two studies; rapidly inactivating A-type potassium channels are incorporated in one model (Kampa and Stuart 2006), but omitted in the other (Nevian et al. 2007).
To determine the biophysical bases for AP propagation in basal dendrites of the rat prefrontal cortex (PFC), we used VSDs to optically record the time course of bAPs before and after pharmacologically blocking several major ion channel types. AP waveforms were sampled simultaneously along the entire length of basal branches, providing an unprecedented amount of information about the spatial and temporal dynamics of basal dendritic AP propagation and its sensitivity to various channel blockers. Blocking either of the voltage-gated sodium or A-type potassium channel populations resulted in a significant decrease or increase, respectively, in bAP amplitude in PFC basal dendrites. In contrast, pharmacologically blocking the delayed rectifier potassium conductance, voltage-gated calcium conductances, or hyperpolarization-activated mixed cation conductance (Ih) had little effect on dendritic AP propagation. Experimental data in control, tetrodotoxin (TTX), and 4-aminopyridine (4-AP) conditions were used to fit a biophysical, multicompartmental model (NEURON; cf. Carnevale and Hines 2006). The resulting best-fit model had nonuniformly distributed sodium (decreasing density with distance from soma) and A-type potassium channels (increasing density with distance). Since the VSDs do not report calibrated membrane potentials, we used the AP amplitudes from our best-fit model as predictions of the actual dendritic AP amplitudes. In addition, we modeled the backpropagation of high-frequency AP triplets (Zhou et al. 2008) and the initiation of local dendritic sodium spikelets (Ariav et al. 2003; Milojkovic et al. 2005; Nevian et al. 2007). The combined results from the present study and recent experimental studies on thin dendrites (Losonczy et al. 2008; Milojkovic et al. 2005; Nevian et al. 2007; Zhou et al. 2008) suggest that all sister branches in the dendritic tree of one neuron may not have the same membrane excitability.
METHODS
Acute slice preparation
Sprague–Dawley rats (postnatal day 21 [P21] to P33) were anesthetized with halothane, decapitated, and the brain was removed with the head immersed in ice-cold, artificial cerebrospinal fluid (ACSF), according to an animal protocol approved by the Center for Laboratory Animal Care, University of Connecticut. Brain slices (300 μm) were cut from frontal lobes in the coronal plane. ACSF contained (in mM) 125 NaCl, 26 NaHCO3, 10 glucose, 2.3 KCl, 1.26 KH2PO4, 2 CaCl2, and 2 MgSO4 (pH 7.4). Whole cell recordings were made at 34–35°C (32–33°C local TTX experiments) from visually identified layer V pyramidal neurons on the medial part of the slice. Intracellular solution contained (in mM) 135 K-gluconate, 2 MgCl2, 3 Na2-ATP, 10 Na2-phosphocreatine, 0.3 Na2-GTP, and 10 HEPES (pH 7.3, adjusted with KOH). Morphological reconstructions were made from neurons filled with biocytin (0.5%) and processed with an avidin-based (Vectastain PK-6100 Standard) kit. Reconstructions were made in Neurolucida (MBF Bioscience, Williston, VT).
Voltage-sensitive dyes
Voltage-sensitive dye (VSD) injections were essentially as described previously (Antic 2003). Briefly, the VSD, either JPW1114 purchased from Molecular Probes (Eugene, OR), or JPW3028 (generously provided by J. Wuskell and L. Loew, University of Connecticut Health Center) was dissolved in the intracellular solution (0.3–0.8 mM) and loaded into neurons through whole cell pipettes (∼30 min). Loading pipettes were then pulled out (outside-out patch) and neurons were incubated at room temperature for 1–2 h. Slices were transferred to a recording microscope and neurons were repatched with dye-free electrodes.
Experimental setup for simultaneous electrical and multisite optical recordings
Electrical signals were amplified with an Axon Instruments Multiclamp 700B and digitized with a Digidata Series 1322A (Molecular Devices, Sunnyvale, CA) at 10 kHz. Fluorescence signals were recorded optically (excitation 520 ± 45 nm; dichroic 570 nm; emission >610 nm) using a 2-kHz frame-rate (80 × 80 pixels; NeuroCCD, RedShirtImaging, Decatur, GA) camera. Dendrites were illuminated with a Xenon 250W short-arc lamp (770 X W/T Opti-Quip, Highland Mills, NY). Optical AP signals with good signal-to-noise quality were obtained by averaging a small number of sweeps (see spike-triggered averaging).
In bath-applied TTX experiments, somata were repatched with two pipettes after pulling off the dye-filled pipette. The waveform command signal in pCLAMP 9.2 (Molecular Devices) was used to voltage-clamp the soma using a waveform prerecorded in current clamp in the same neuron. With a second channel in current-clamp mode, the amplitude of the somatic response was monitored (Fig. 1). In general, the amplitude fell short of the command waveform unless certain measures were taken. Series resistance compensation was first adjusted by trial and error until the desired AP amplitude was recorded on the second channel to within 10%. In some cases, with large access resistance, this was not sufficient and it was necessary to scale the command waveform in pCLAMP by a certain factor (not >1.3). When the cell was not successfully dual repatched (1/4 cells), a single channel was used to voltage-clamp the soma and signal matching was done using somatic optical waveforms (to within 10%).
FIG. 1.
Dendritic attenuation of artificially generated somatic action potentials (APs) in the presence of global tetrodotoxin (TTX). A: composite photograph of neuron filled with voltage-sensitive dye JPW1114. B: low-resolution charge-coupled device (CCD) camera was used to sample optical signal inside the box shown in A. The cell body is patched with 2 electrodes. One channel remains in current clamp to monitor membrane potential, necessary to verify the efficacy of the voltage-clamped AP waveform in TTX conditions (methods). Somatic AP amplitude is 109% of Control in TTX and 88% of Control in Washout conditions (45-min washout). Detector sets outlined correspond to 5 regions of interest (ROIs) on 2 basal branches. C: electrical (whole cell) and optical (ROIs 1–5) signals following natural (Control, Washout) or artificially generated somatic APs (block of sodium channels with TTX, 1 μM). Spike-triggered averages, n = 4 sweeps.
For calcium-sensitive dye imaging neurons were injected with Calcium Green-1 (400 μM) dissolved in intracellular solution. By 20 to 30 min following the breakthrough, dendritic calcium signals were sampled at a 200-Hz frame rate using the exact same system as described for multisite VSD imaging.
GLUTAMATE MICROIONTOPHORESIS.
Pyramidal cells were injected with a fluorescent dye Alexa Fluor 594 (50–80 μM) purchased from Invitrogen (Carlsbad, CA). Sharp glass pipettes (40 ± 10 MΩ) were filled with 200 mM sodium glutamate (pH 9), attached to the motorized micromanipulator (P-285, Sutter Instrument, Novato, CA), and positioned at <15 μm from the dendritic shafts, using alternating fluorescent and infrared videomicroscopy. An Iso-Flex (A.M.P.I., Jerusalem, Israel) stimulus isolation unit, controlled by a Master 8 programmable pulse generator (A.M.P.I.), was used to deliver (5-ms duration; 0.8- to 3.0-μA amplitude) negative current pulses. Each dendrite was stimulated with high intensities of glutamate current capable of triggering large (∼20 mV) long-lasting (>150 ms) somatic plateau depolarizations accompanied with AP firing. Glutamate intensity was varied above and below threshold in an attempt to create conditions for local sodium spike initiation. At each stimulus intensity level glutamate was applied multiple times (trains of three to eight glutamate pulses, 1- to 2-s interstimulus interval) to control for the clogging of the glutamate electrode, to monitor the reliability of the dendritic response, and to improve the chances of detecting local dendritic sodium spikes (Fig. 9, C and D shows two of the three consecutive glutamate pulses).
FIG. 9.
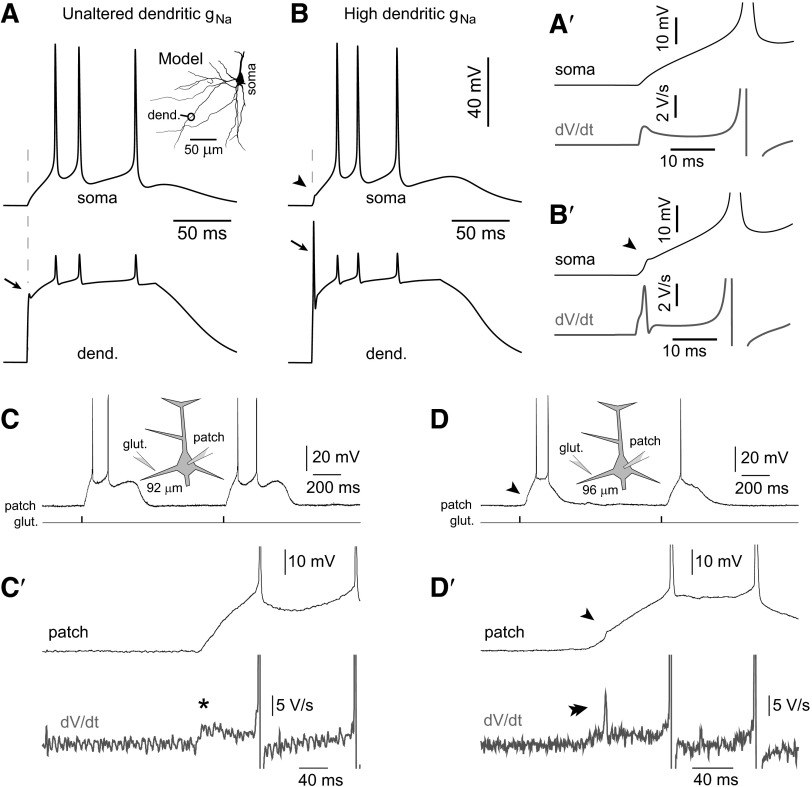
Modeling the generation of local dendritic spikelets and testing model predictions in experiment. A: response of the soma (top) and dendrite (bottom) to the stimulus (plateau-like conductance; methods) delivered at location indicated in the inset (dend.). All model parameters identical to the best-fit model are shown in Fig. 6 (Unaltered), including proximal dendritic gNa_prox = 150 and gKA_prox = 150 pS/μm2. Initial dendritic spikelet (arrow) has very small amplitude and is not detected in the somatic recording. A′: enlarged view of the somatic membrane potential response near the stimulus onset time along with the first derivative of this response. B: somatic and dendritic responses after boosting the proximal sodium conductance in the stimulating branch to 375 pS/μm2 (slope value maintained at −0.5 pS·μm−2·μm−1). The dendritic spikelet (arrow) is greatly enhanced and causes a fast deflection in the somatic recording (arrowhead), which is easily detectable in the first derivative of the somatic waveform shown in B′. C: diagram of experimental setup with glutamate iontophoresis at basal dendrites and somatic whole cell patch recording. Distance of the glutamate electrode from the center of the soma indicated below the diagram. C′: enlarged view of the somatic membrane potential response to glutamate iontophoresis, along with the first derivative of this response (asterisk). D and D′: same as in C and C′ except a different cell. An initial sharp deflection appears in the somatic recording (arrowhead), which is easily detectable in the first derivative (double arrowhead).
Signal processing and data analysis
SPIKE-TRIGGERED AVERAGING.
For each trial (which we define to be control, drug, or washout) 3 to 20 optical recording sweeps (depending on signal strength) were averaged off-line using spike-triggered averaging in MATLAB. Averaging improves signal-to-noise ratio and triggering off of spikes is necessary because the peak of AP shows a small temporal jitter from sweep to sweep. Each sweep is one repetition of the AP triggering and recording sequence and consists of 150 samples (frames). Consecutive sweeps were initiated after a time delay between 15 and 30 s. Time signals from each detector or pixel were first preconditioned and oversampled. A high-pass filter was used to remove slow, vibration-related oscillations (seventh-order Butterworth, 3-dB cutoff at 42 Hz, MATLAB: filtfilt) before low-pass filtering (3-dB cutoff at 928 Hz, second-order Chebychev II, MATLAB: filtfilt). Signals were then oversampled from 2 to 20 kHz (MATLAB: interp, l = 4, alpha = 0.5, r = 10). For each sweep, signals were spatially averaged over the pixels of a specifically chosen region-of-interest (ROI) near the cell body, with the best single-sweep signal-to-noise quality. The peaks of the first derivative of these waveforms were used to temporally align the rising edge of AP waveforms in each sweep. Once temporally aligned, all corresponding pixels from each sweep were averaged to complete the spike-triggered averaging routine.
SIGNAL ANALYSIS AND UNCERTAINTY.
Amplitudes of the spike-triggered averaged optical signals are computed for each detector set (ROI) and converted to percentage in MATLAB (Supplemental Fig. S5).1 Optically recorded half-widths (Supplemental Fig. S5) for each cell were adjusted by a factor necessary to compensate for the low optical sampling rate (2 kHz) and off-line filtering. This factor was determined by applying the same undersampling and filtering to the electrical recordings (10 kHz) and measuring the effect on half-widths. Optical half-widths were decreased by between 9.2 and 26.0%. Data preceding the AP triggering (≥40 ms) is noise, used to compute the uncertainty in the measured signals (Supplemental Fig. S5). This noise is assumed to corrupt the peak measurement and, consequently, to directly affect the amplitude measurement. Calculation of amplitude ratios involves dividing two noisy signals: z = x/y. The uncertainty in amplitude ratio (error bars, Figs. 2B and 3D) depends on amplitudes and SDs of numerator and denominator according to
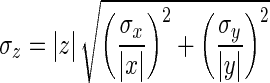 |
(1) |
Uncertainties in half-widths are determined by assuming that the signal noise affects determination of the half-width threshold. The threshold is shifted up and down by the signal noise (σnoise), to determine the upper and lower ranges of half-width that correspond to the particular noise level (error bars, Figs. 2C and 3E). In this method, upper and lower error bars can differ depending on the particular AP waveform. For example, for two points in Fig. 2C, branch 1, TTX conditions, near 200 μm, the recorded AP waveforms narrow quickly for an upward shift in the 50% threshold, which leads to a large lower error bar. At the same time, these AP waveforms widen slightly for a downward shift in the 50% threshold, and the upper error bar is small.
FIG. 2.
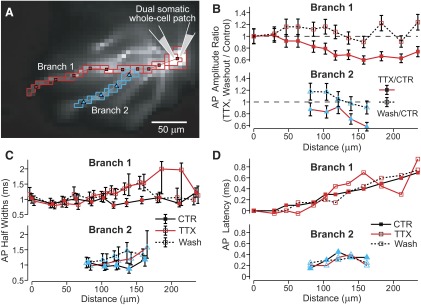
Multisite view of AP backpropagation before, during, and after the block of sodium channels with global TTX. A: same neuron as Fig. 1B with nonoverlapping ROIs. B: amplitudes of averaged AP signals in bath TTX, 1 μM (filled symbols) or Washout conditions (open symbols) divided by amplitudes in Control conditions are plotted for each ROI as a function of distance from the soma. Error bars represent SD of amplitude ratios based on SD of noise and signal amplitude in each condition (methods). C: AP half-widths in Control (filled), TTX (open), and Washout (dashed line) conditions as a function of distance from soma. Error bars reflect uncertainty due to signal noise (methods). D: AP propagation latencies relative to the somatic AP, measured at 90% AP amplitude.
FIG. 3.
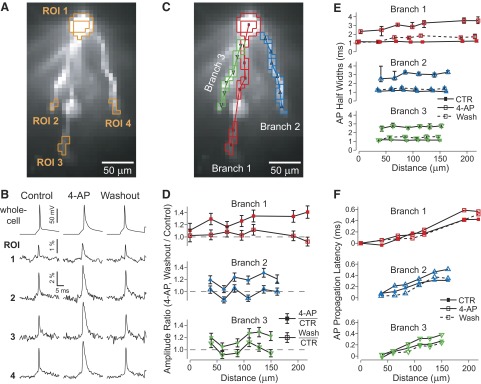
Quantifying the effect of A-type potassium channels on AP backpropagation in basal dendrites of layer V prefrontal pyramidal cells. A: CCD image of basal dendrites filled with voltage-sensitive dye (VSD) JPW3028. B: spike-triggered average (8 sweeps) of spatially averaged signals from pixels within ROIs outlined in A for Control, 4-aminopyridine (4-AP, 8 mM), and Washout (40 min) conditions. In 4-AP condition we also used synaptic blockers (see methods). C: same image as in A with nonoverlapping ROIs along length of 3 basal branches. D: amplitudes of averaged membrane potential responses in 4-AP or Washout conditions divided by amplitudes in Control conditions (closed, open symbols) are plotted for each ROI as a function of distance from the soma. Error bars as in Fig. 2B. E: AP half-widths in Control, 4-AP, and Washout conditions as a function of distance from soma. Error bars as in Fig. 2C. F: AP propagation latencies relative to the somatic AP, measured at 90% amplitude.
Propagation latencies were determined by computing the times at which the optical AP waveforms crossed a threshold at 90% of the peak amplitude (Supplemental Fig. S5). These crossing times were then referenced to the somatic 90% crossing time to convert to propagation delay or latency; 90% crossing times were used instead of peak times because 4-AP could significantly change the peak of the AP waveforms and considerably delay the peak times. Propagation latencies using the 90% crossing times were slightly smaller than if peak times had been used. AP waveforms from the computational model were analyzed (amplitudes, half-widths, latencies) using the exact same MATLAB code used to analyze the optical waveforms to directly compare experimental and computational data without the possibility of bias.
CORRECTION OF UNDERESTIMATED DENDRITIC LENGTHS.
In our optical recording environment, performed with Olympus ×40 LUMPlanFI objective, each pixel on the high-speed charge-coupled device camera covers a 6.1 × 6.1-μm area, determined using a calibration graticule; 4–8 neighboring pixels were typically grouped into ROIs and spatially averaged. The centers of these ROIs are then connected by straight lines and the distances between centers are calculated to find the path distance of each dendritic location from the soma. However, since the distance between centers of these ROIs is typically 20 μm, the dendritic structure and curvature below this resolution are lost and distances are underestimated. We estimate this underestimation using a reconstructed pyramidal neuron and correct for it (Supplemental Fig. S6). Distances between ROI centers are computed as described earlier and inflated according to Supplemental Fig. S6, before finding the cumulative path length. Typical ROI spacing requires a typical inflation of distances by about 7%.
Computational modeling of prefrontal, layer V, basal dendrites
BEST-FIT MODEL TO BASAL DENDRITIC AP PROPAGATION.
The model prefrontal pyramidal neuron was constructed using morphology from a reconstructed cortical prefrontal layer V pyramidal neuron and by incorporating voltage-gated channels from previously published studies (Mainen and Sejnowski 1996; Migliore et al. 1999; Schaefer et al. 2003). Simulations were performed in NEURON (version 5.8; Carnevale and Hines 2006) and code will be made available on ModelDB (http://senselab.med.yale.edu/senselab/modeldb/). In simulated bath TTX conditions, the sodium conductance density was set to zero everywhere. The somatic AP waveform recorded previously in control conditions was then played back using a voltage-clamp point process (SEClamp, rs = 0.01) to match the control AP waveform. Voltage-gated sodium channels were distributed on the model's soma, axon, and apical dendrites with maximal conductance densities of 900, 5,000, and 375 pS/μm2, in each region, respectively. Note that these values directly multiply the product of gating variables and do not include a temperature adjustment factor. If the original na.mod file (Mainen and Sejnowski 1996) was used without modification, as is common among previous studies, the maximal conductance parameter, gbar_na, would need to be 2.12-fold smaller as a result of the temperature-adjustment factor. Nominal temperature in the present study was 32°C. In other words, at 32°C nominal temperature a gbar_na of 100 pS/μm2 in the present study would be equal to gbar_na of 47.2 pS/μm2 in Mainen et al. (2006). The large axonal sodium conductance was used for robust axonal AP initiation. Sodium channel inactivation kinetics was modified to approximate those from Kole et al. (2008), which was necessary for AP firing to follow high-frequency stimulation without strong amplitude decline. Additionally, sodium inactivation voltage dependence was shifted in the axon to allow the model to respond appropriately to strong, sustained stimulation as in dendritic plateau stimulation. Delayed rectifier potassium channel conductance density was 40 pS/μm2 (again without the Mainen et al. temperature factor, as with sodium conductance), except in the model's axon, where it was 100 pS/μm2. In the soma, A-type potassium channels of the “proximal” type (Migliore et al. 1999) were added with a conductance density of 150 pS/μm2. In the apical dendrites the total A-type potassium conductance density was uniformly 300 pS/μm2, but this total was a mixture of “proximal” and “distal” IA channels (Migliore et al. 1999) that included a linearly increasing portion of distal channels, starting from zero at the soma and changing to purely distal channels beyond 300 μm. In the basal dendrites, the sodium and A-type potassium conductances were given linear distributions with parameters determined by fitting to the experimental data (see following text). Both sodium and A-type potassium conductances were found to equal 150 pS/μm2 proximal to the soma but had different slopes. The sodium conductance declined by 0.5 pS·μm−2·μm−1, whereas the A-type potassium conductance increased by 0.7 pS·μm−2·μm−1. If the reader seeks to compare the A-type potassium conductances here with previous studies, we point out the following: the study by Kampa and Stuart (2006) states that a 20 pS/μm2 conductance was used, whereas in the model published online a 0.02 S/cm2 was used, which is equivalent to 200 pS/μm2. This value was also multiplied by a spine factor (2), whereas ours was not.
The axon included a low-threshold–activated, slowly inactivating potassium current (IL, designed to mimic data in Shu et al. 2007) with conductance density of 50 pS/μm2 beyond a 15-μm distance from the soma. A low-threshold voltage-dependent calcium conductance was distributed on the dendrites (locations ≥30 μm from the soma) with a conductance density of 1.6 pS/μm2 along with a high-voltage–activated calcium conductance at 0.4 pS/μm2 (Kampa and Stuart 2006; Mainen and Sejnowski 1996). The soma and perisomatic regions contained 8 and 2 pS/μm2 of low-threshold and high-voltage–activated calcium conductance, respectively. Passive membrane properties were as follows: specific intracellular resistivity = 90 Ω·cm, specific membrane capacitance = 1 μF/cm2, leak conductance = 0.04 mS/cm2. To account for dendritic spines, a “spine factor” of 1.5 was used to increase capacitance and leak conductance in the dendrites beyond a distance of 50 μm.
To trigger local dendritic sodium spikes in the model (Figs. 9 and 10) a custom plateau-like conductance was delivered in a distal dendritic segment (Fig. 9A, inset). The parameters of plateau conductance were adjusted to match glutamate-evoked dendritic depolarizations (Milojkovic et al. 2004, 2005). More specifically, the plateau conductance rose exponentially with a 1-ms time constant and was allowed to saturate for 110 ms before falling exponentially to zero with a 20-ms time constant. Maximal, saturated conductance = 0.01 μS; reversal potential = 0 mV. Boosting of dendritic voltage-gated conductances (sodium or A-type, or both, Figs. 9 and 10) was modeled by increasing the proximal density, while preserving identical slopes as in best-fit model (e.g., decreasing gNa slope: 0.5 pS·μm−2·μm−1; increasing gKA slope: 0.7 pS·μm−2·μm−1).
FIG. 10.
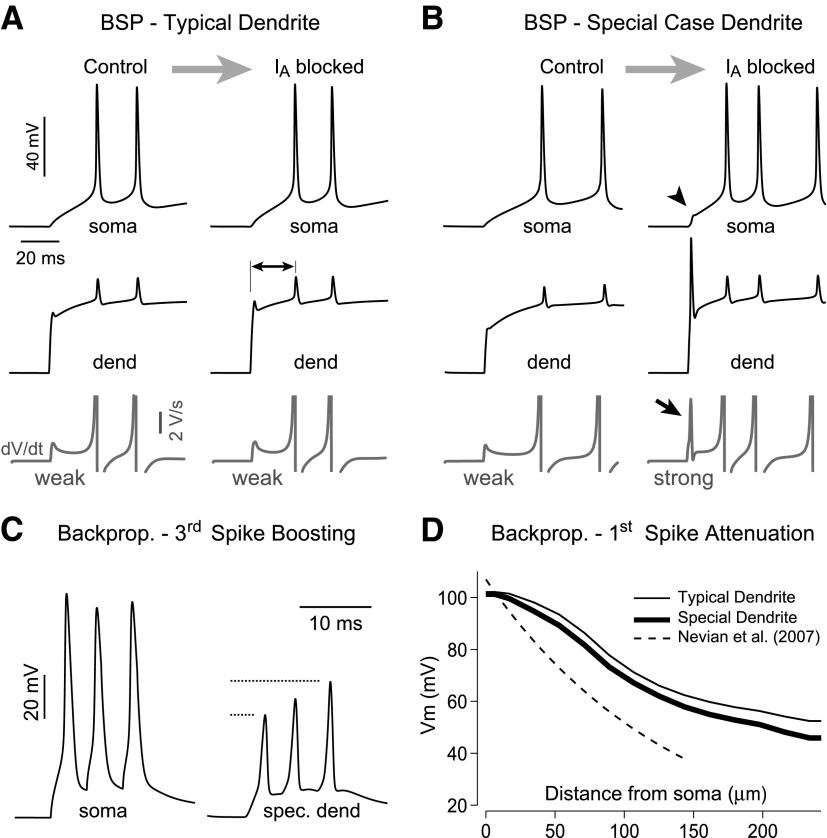
The role of IA in local dendritic spikes and the possibility for branch strength potentiation (BSP). A: control: all model parameters identical to best-fit model shown in Fig. 6 (Unaltered), including proximal dendritic gNa_prox = 150 and gKA_prox = 150 pS/μm2. Stimulus: same as in Fig. 9, A and B. IA blocked: dendritic A-type conductance set to zero in an attempt to induce BSP (Losonczy et al. 2008). Removal of IA did not result in a significant local dendritic spike potentiation, nor an increase in somatic dV/dt (bottom trace, weak), compared with Control, but it did reduce the latency of the first AP (double-headed arrow). B: proposed model of a special case basal dendrite with increased Na+ and A-type K+ conductances (375 and 1,200 pS/μm2, respectively), where blocking IA does lead to a significant local dendritic spike that is easily detectable in both the somatic waveform (arrowhead) and its first derivative (arrow, strong). C: special case dendrites show much greater “boosting” of dendritic AP amplitudes during high-frequency trains of somatically triggered APs (compared with Fig. 8); more consistent with data from Kampa and Stuart (2006). D: in spite of greatly increased gKA in special case dendrites (gKA = 1,200 pS/μm2), the dendritic amplitudes of the 1st bAP show an attenuation profile similar to that of the best-fit model (Typical Dendrite), which is more moderate than observed experimentally in somatosensory cortex by Nevian et al. (2007).
MODEL FITTING.
The model was fit to experimental data using the following approach: AP waveforms from simulations were analyzed and amplitude data were averaged over the basal dendrites (Fig. 6B). Half-widths and latencies were calculated in exactly the same way as with the optical AP waveforms (Supplemental Fig. S5) and were averaged over the model basal dendrites. The model data averaged over the basal dendrites were taken as the fit data. AP amplitude ratios TTX/Control and AP amplitude ratios 4-AP/Control were used to fit the model.
FIG. 6.
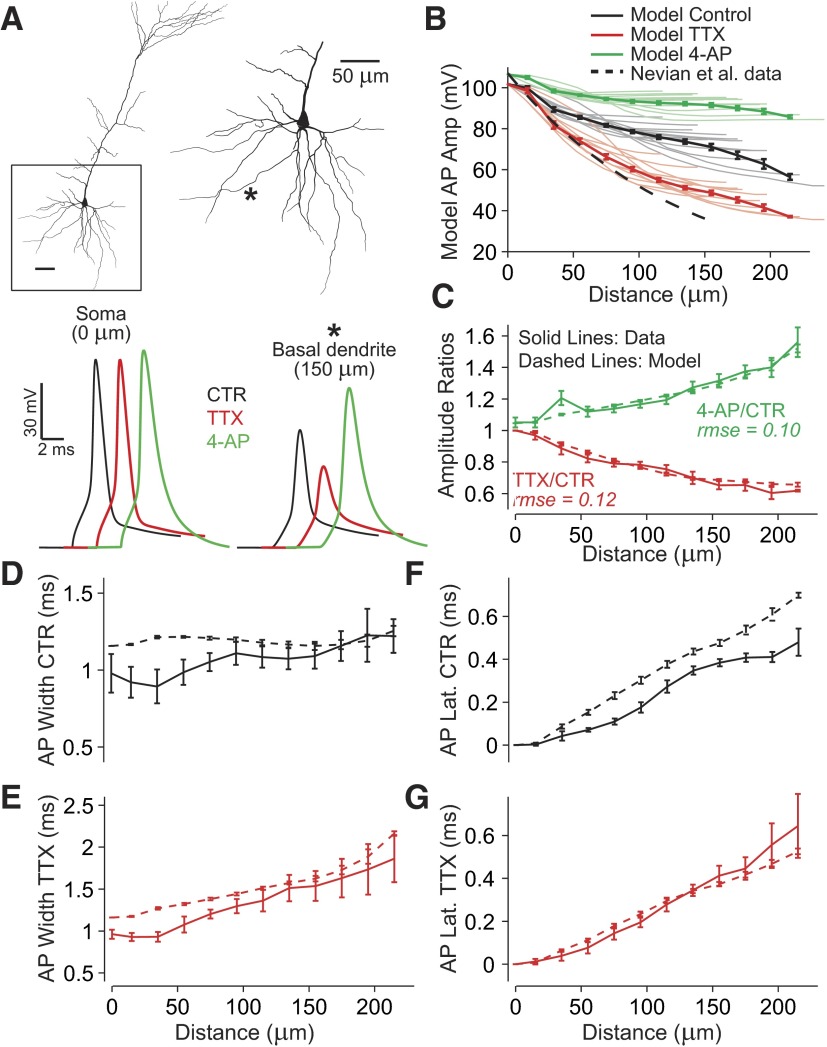
Modeling prefrontal basal dendrites to reproduce multisite AP backpropagation data obtained in Control, TTX, and 4-AP conditions. A: Neurolucida reconstructed layer V pyramidal neuron from the rat prefrontal cortex (P28). Basal arbor is enlarged at right with one example recording location indicated (*). Sample AP waveforms from the soma and * are shown below in Control (CTR, black), after simulated sodium channel block (TTX, red, somatic waveform is reproduced using voltage clamp), or A-type potassium channel block (4-AP, green). Line colors correspond to experiment type in the same way in all panels. A uniform voltage-gated Na+ conductance and a nonuniform K+ conductance (A-type) are chosen along with passive membrane properties to best-fit data (Fig. 7). B: thin lines indicate model AP amplitudes in Control (gray), simulated TTX (red), and 4-AP conditions (green) as a function of distance from soma in individual basal branches in NEURON. In all, 250 locations on 13 model basal dendrites with distinct tips beyond 115 μm are included. Superimposed are binned and averaged data (thick lines). Dashed line, indicating Control AP amplitudes from somatosensory basal dendrites, is shown for comparison [exponential fit from Nevian et al. (2007) experimental patch-clamp data]. C: dashed lines indicate model amplitude ratios TTX/Control or 4-AP/Control, whereas solid lines indicate experimental amplitude ratios. Values of rmse represent root mean squared error between mean model data and experimental data (methods) used to fit the model (Fig. 7). D and E: AP half-widths in Control and TTX conditions as a function of distance from the soma (solid lines = experiment; dashed lines = model). F and G: AP latencies using 90% of peak value crossing times.
For each of the amplitude ratios, the analyzed model data were compared with the experimental data by computing root mean squared errors (rmse). Experimental and fit data were first scaled by factors making the mean of the experimental data equal to one to avoid one fit parameter from being more important than the other. These two rmse values were averaged to assess the overall (cumulative) fit error (Fig. 7). Basal dendritic sodium and A-type potassium conductance distributions were assumed linear and were systematically varied over a wide range over a four-dimensional parameter space to determine the best-fit values of these model parameters (Supplemental Fig. S7). Other parameters, such as delayed rectifier potassium conductance, leak conductance, and somatic conductances, were manually varied to find the lowest possible overall model fit. This was done by first determining the sensitivities of AP amplitudes, half-widths, and latencies to each model parameter and using this information to modify parameters and improve fits before finally fitting the basal sodium and A-type potassium distributions. An automated optimization approach based on a genetic algorithm (Keren et al. 2005), if feasible, would allow a larger parameter space to be searched exhaustively and could potentially lead to improved overall fits, something that could be pursued in future studies.
FIG. 7.
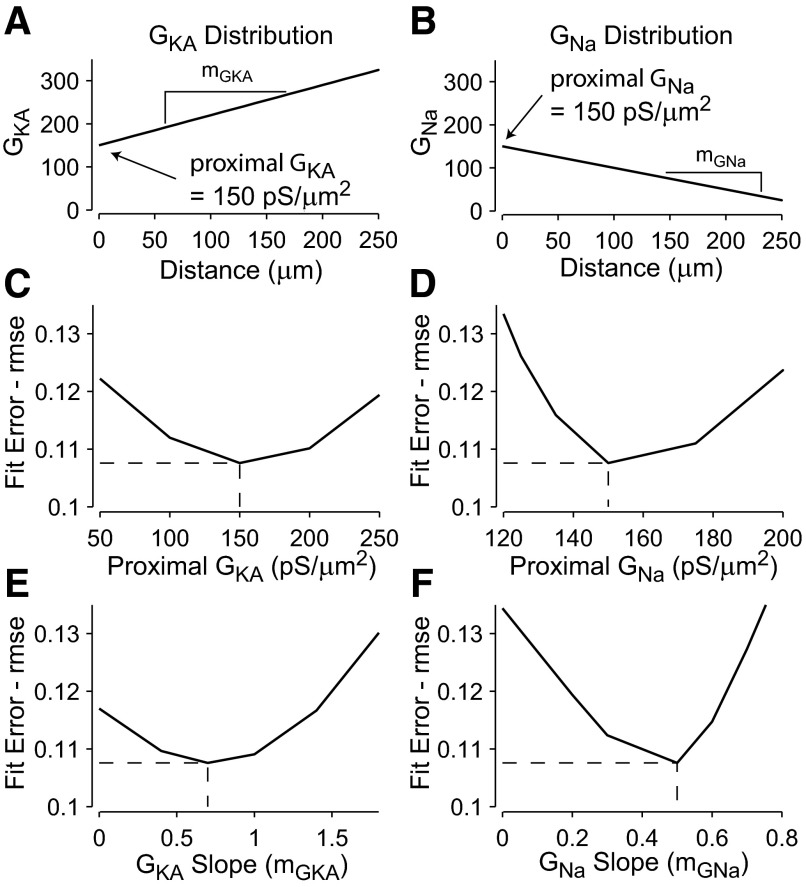
Fit errors used to simultaneously fit model INa and IA conductance distributions to experimental data. A: best-fit A-type potassium conductance rises from a proximal conductance density of 150 pS/μm2 at the interface with the soma (distance = 0 μm) with a slope of 0.7 pS·μm−2·μm−1. B: best-fit sodium conductance declines from a proximal density of 150 pS/μm2 with a slope of 0.5 pS·μm−2·μm−1. C–F: overall fit error (average rmse) between data and model is an average of 2 rmse values for amplitude ratios 4-AP/Control and TTX/Control. This overall fit error is plotted as a function of 4 model parameters: the slopes and y-intercepts (proximal to the soma) of the sodium and A-type potassium conductance distributions. The best-fit conductance distributions correspond to the local minimum in overall error values, whereby increasing or decreasing any of the 4 parameters while holding the other 3 constant leads to increased fit error. Sign of the slope of the sodium conductance distribution is reversed for convenience.
RESULTS
Role of sodium channels
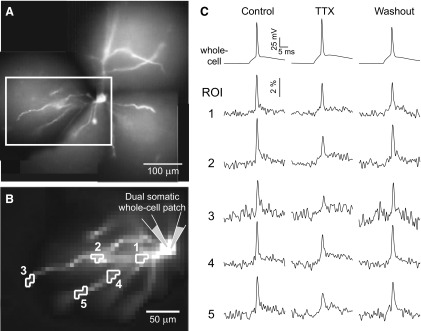
To study the role of voltage-gated sodium channels (VGSCs) in AP backpropagation, layer V pyramidal neurons in prefrontal cortex were loaded with the VSD JPW1114 (Supplemental Fig. S1A) and TTX-filled micropipettes were positioned near the middle segment of visually identified basal dendrites (Supplemental Fig. S1B). On brief (1-s), focal TTX application, AP amplitudes were clearly reduced near the application site (Supplemental Fig. S1C, TTX) compared with control measurement obtained prior to TTX puff (Supplemental Fig. S1, Control). This series of experiments established that VSD recordings can reliably detect drug-induced changes in AP amplitude. Differences in AP peak amplitude were detected between control, drug, and washout periods (Supplemental Fig. S1C), as well as between control dendrites and test dendrites (compare ROI 4 and ROI 6). Unfortunately, the fraction of blocked sodium channels and the spatial extent of this block (the membrane area affected) cannot be determined or controlled with local TTX application. This renders local TTX application unsuitable for quantitative estimates of sodium channel conductance.
To quantitatively assess the contribution of VGSCs to AP backpropagation in various segments of the basal dendritic tree, it was necessary to use a bath-applied TTX protocol. Bath-applied TTX (1 μM) ensured complete, uniform block of voltage-gated sodium channels. In bath-applied TTX, the natural AP generation was lost and voltage clamp was used to generate a somatic AP waveform (playback AP) (Spruston et al. 1995; Stuart and Sakmann 1994). To ensure that the somatic AP in TTX matched the amplitude of that in control, a second whole cell recording in current-clamp mode was used to monitor the somatic waveforms (methods).
We were able to inject the VSD, pull the loading pipettes out, repatch with two recording pipettes (dual somatic patch), match the AP waveform in voltage-clamp configuration, and complete VSD imaging in three neurons. In one additional cell we used a somatic VSD signal to match the amplitude of the playback AP. Neuron position and focus were kept fixed between subsequent recordings in control and TTX conditions, allowing relative comparisons of signals sampled from the same dendritic segment in two subsequent recording sweeps (Djurisic et al. 2004; Milojkovic et al. 2004). Action potential waveforms were recorded optically from many regions along each basal dendrite in the visual field, including both proximal (Fig. 1, ROI 1) and distal dendritic regions (Fig. 1, ROIs 3 and 5), and were analyzed to determine the relative AP amplitude, AP half-width, and AP propagation latency (Fig. 2).
After bath application of TTX, a strong reduction in AP amplitude (Fig. 2B) was observed in all basal dendrites of all neurons tested (n = 4). Reduction in amplitude was determined by computing the amplitude of optical AP waveforms (methods; Supplemental Fig. S5) in control and TTX conditions, and taking the ratio of TTX/Control (Fig. 2B). Note that AP amplitudes cannot be measured directly via imaging since the internally applied VSD cannot be calibrated (Antic 2003). However, since the dye responds linearly to changes in voltage, amplitude ratios can be quantified in spite of the lack of calibration (Djurisic et al. 2004; Milojkovic et al. 2004). Recordings from 46 regions over seven basal dendrites from four neurons exhibited consistent behavior and were combined to determine the mean characteristics of basal dendrite AP propagation (Fig. 5). Amplitudes in TTX conditions were 60 ± 8% of those in control at a distance of 195 μm (Fig. 5A). Action potential half-widths were 0.93 ± 0.03 and 0.95 ± 0.04 ms at the soma in control and TTX conditions and 1.2 ± 0.3 and 1.7 ± 0.5 ms in the dendrites (195 μm), in control and TTX conditions, respectively (Fig. 5). Binning the data according to distance from the soma into 50-μm intervals indicated that the observed half-widths in TTX conditions were greater than those in control conditions for distances >60 μm (one tailed t-test, P < 0.05). Linear regression analysis of peak latency data indicated that average propagation velocities were 0.32 and 0.31 m/s in control and TTX conditions, respectively (Fig. 5, F and G). The fact that propagation velocities were essentially unchanged in TTX is consistent with the observation in apical dendrites of cortical pyramidal neurons that AP propagation velocities are unchanged at the end of trains of action potentials that cause sodium channel inactivation in distal apical dendrites (Larkum et al. 2001).
FIG. 5.
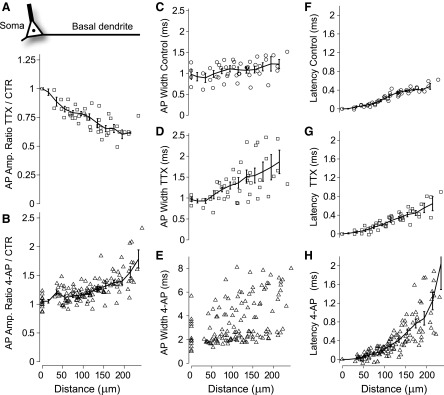
Contributions of both sodium and A-type potassium channels to AP amplitude, shape, and velocity. A: amplitude ratios of optical AP waveforms, TTX (1 μM) over Control conditions, as a function of distance from center of soma (see schematic neuron). Mean ratios found by binning data using a sliding boxcar window (error bars are ±SE). B: AP amplitude ratios, 4-AP (8 mM) over Control. C–E: AP half-widths as a function of distance from soma in Control, TTX, and 4-AP conditions, respectively. F–H: latencies calculated using 90% of peak values in Control, TTX, and 4-AP conditions, respectively. Linear regression indicated that average propagation velocities for distances <250 μm are 0.32, 0.31, and 0.15 m/s in Control, TTX, and 4-AP conditions, respectively. TTX data set (open squares) includes recordings from 46 regions over 7 basal dendritic branches from 4 neurons, whereas the 4-AP data set (open triangles) includes recordings from 179 regions over 24 basal branches from 11 neurons.
Role of A-type potassium channels
A-type potassium channels, which activate rapidly with depolarization, can severely reduce the amplitude of action potentials (Acker and White 2007; Hoffman et al. 1997). Two recent studies in layer V of somatosensory cortex have reported significantly different effects of A-type potassium channels on AP backpropagation in basal dendrites (Kampa and Stuart 2006; Nevian et al. 2007). We analyzed the effect of A-type potassium channels on AP backpropagation in basal dendrites in layer V prefrontal pyramidal cells by performing VSD imaging in control conditions and after pharmacological block of the channel. In bath-applied 4-AP [8 mM, with synaptic blockers: bicuculline (10 μM), 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX, 10 μM), 2-amino-5-phosphonovaleric acid (APV, 30 μM)], amplitudes increased very little at the soma, but significantly in the dendrites (Fig. 3B). Therefore the ratio of amplitudes in 4-AP over those in control (4AP/Control) increased with distance from the soma (Figs. 3D and 5B). At 200 μm from the soma, amplitude ratios ranged from 1.1 to 2.1 (1.5 ± 0.3, n = 12 ROIs between 185 and 215 μm) in 11 neurons tested.
Action potential widths increased in bath 4-AP conditions (Figs. 3E and 5E). Large increases in width were observed in the somatic recordings, but the increases were even greater in the dendrites. Effects on width, as with effects on amplitude, were reversible after washout of the drug (Fig. 3, B and E), confirming that effects were indeed due to the drug and not any to other artifact such as dye toxicity (Antic et al. 1999). Propagation latencies increased in 4-AP (Figs. 3F and 5H). This is a counterintuitive effect if one assumes that potassium channels slow propagation. However, the concomitant increase in AP amplitude presumably complicates this issue.
Ih has little effect on AP backpropagation in basal dendrites
The hyperpolarization-activated, mixed cation current Ih causes a rectifying “sag” in response to hyperpolarizing current steps (Supplemental Fig. S2). In prefrontal cortical pyramidal cells, blocking this ionic current with 4-(N-ethyl-N-phenylamino-1,2-dimethyl-6-methylamino)pyridinium chloride (ZD7288, 20 μM) significantly reduced the sag from 2.0 ± 0.8 mV in control conditions to 0.2 ± 0.3 mV (Supplemental Fig. S2B, both cases measured near −100 mV). In spite of the clear effects on sag, blocking Ih failed to significantly affect amplitudes of bAPs (Supplemental Fig. S2C). Amplitude ratios, ZD7288 conditions over control (ZD7288/Control), seemed to decrease slightly but were not significantly different from 1 between 0 and 100 μm (0.97 ± 0.09, P = 0.2), between 100 and 150 μm (0.96 ± 0.08, P = 0.06), or between 150 and 200 μm (1.0. ± 0.15, P = 0.8). Latencies were not significantly affected across these same regions (data not shown), whereas there was a small increase in AP half-width that reached statistical significant for distances between 100 and 150 μm (1.3 ± 0.2 ms control, 1.8 ± 0.3 ms ZD7288, P = 0.003).
Voltage-gated calcium channels and calcium-activated potassium channels have little effect on AP backpropagation in basal dendrites
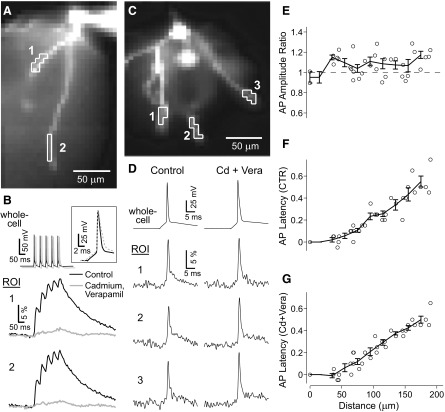
Calcium influx through voltage-gated calcium channels can depolarize the membrane and lead to broad dendritic depolarizations in some neurons (Häusser et al. 2000; Kampa and Stuart 2006; Larkum et al. 2001). Calcium influx also activates calcium-dependent potassium channels, which can hyperpolarize the membrane. We pharmacologically blocked all calcium influx to test for the effects of these two channel types on AP backpropagation in basal dendrites. Before the actual VSD measurements were done, we performed control experiments with calcium-sensitive dye Calcium Green-1 (400 μM) to determine the pharmacological potency of our VGCC blockers. Calcium imaging demonstrated that calcium influx was abolished by bath-applying CdCl2 and verapamil (200 and 20 μM, respectively, Fig. 4B). Interestingly, AP amplitude ratios, cadmium + verapamil over control, were ≳1, meaning that dendritic AP amplitudes increased slightly on block of VGCCs (Fig. 4, D and E). Thus VSD recordings could not detect any significant contribution of voltage-gated calcium channel electrogenesis to the amplitude of single bAP in basal dendrites. The small increase in AP amplitude is due either to an effect of calcium-activated potassium channels or to a nonspecific effect of cadmium ions on membrane excitability. For example, cadmium was shown to shift the voltage dependence of A-type potassium channels in neostriatal cholinergic interneurons (Song et al. 1998).
FIG. 4.
Disruption of calcium influx has a small effect on voltage waveforms of single backpropagating APs (bAPs). A: pyramidal cell filled with Calcium Green-1. Two ROIs outlined on 2 basal dendrites. B: whole cell recordings during a 20-Hz train of APs, along with optical recordings in Control (black) and after blocking calcium influx (gray) with bath applied cadmium chloride (200 μM) and verapamil (100 μM); average of 6 repetitions. Inset shows first AP in train on an extended timescale. C: image of basal dendrites of a different layer V neuron filled with JPW3028 (400 μM) with 3 ROIs outlined. D: whole cell recordings during single bAPs, along with optical recordings in Control and after blocking calcium influx as in B. All traces are spike-triggered averages of 8 repetitions. E–G: pooled data, raw and binned, from 8 dendritic branches from 2 neurons (n = 5 basal dendrites) showing peak AP amplitude ratios (Cadmium + Verapamil over Control, in E), AP propagation latencies in Control (F), and in calcium blockers (Cd + Vera, G).
Delayed rectifier potassium channels
If delayed rectifier potassium channels (IKDR) play a major role in limiting the amplitude of bAPs, like A-type potassium channels do (see Fig. 3), then blocking IKDR channels should result in a large increase in AP amplitude in basal dendrites. We bath-applied tetraethylammonium (TEA, 5 mM) and did not see a large change in AP amplitude compared with control measurements obtained on the same neuron prior to TEA bath application (Supplemental Fig. S3C). Similar results were obtained in three neurons (n = 6 dendrites). Bath TEA, however, did increase AP half-widths considerably (Supplemental Fig. S3D). This fact serves as a positive control of the drug potency and also has implications for the 4-AP results. The TEA results suggest that the enhanced propagation with 4-AP (Fig. 3) is not simply due to broader APs.
Nevian et al. (2007) also observed a significant TEA-induced increase in AP half-width in basal dendrite, but they report a small increase in dendritic AP amplitude, too. There are several possible explanations for our failure to detect a small increase in dendritic AP amplitude. One most likely explanation is poor sensitivity of voltage-imaging technique (Antic 2003). However, the bottom line is that TEA-induced changes in AP amplitude in any study (Nevian et al. 2007 and the present study, Supplemental Fig. S3) are much smaller than those obtained here with 4-AP (Fig. 3). Taken together, these data suggest that not all potassium channels equally affect AP amplitude. A-type potassium channels typically activate much faster than their noninactivating, “delayed rectifier” counterparts (Hoffman et al. 1997; Migliore et al. 1999), which allows them to potently limit AP amplitude (Acker and White 2007). Unfortunately, TEA also blocks A-type potassium channels to some degree (Hoffman et al. 1997) and it is thus not feasible for us to quantitatively determine the exact contribution of any change in dendritic AP properties to the delayed-rectifier potassium channel independent of contributions from the A-type potassium channel.
Modeling layer V prefrontal cortical basal dendrites to predict voltage-gated channel distributions
Briefly, we constructed multicompartmental models of basal dendritic trees and searched for the specific channel densities and spatial distributions that could accurately reproduce our experimental measurements in a control condition (normal ACSF), as well as the effects of TTX and 4-AP on AP backpropagation. In the following text we describe the step-by-step progression of our modeling effort and the logic behind some critical decisions.
Our starting point was a Neurolucida reconstructed layer V pyramidal neuron from the rat medial PFC (Fig. 6A) endowed with passive and active membrane mechanisms previously used in the computational models of neocortical pyramids (Mainen and Sejnowski 1996; Schaefer et al. 2003). Several important changes were made. First, the original sodium channel description (na.mod; Mainen et al. 1996) was modified to uncouple temperature from the Na+ maximal conductance density (gbar; see methods). Before the modification, setting gnabar to 40 pS/μm2 resulted in an actual maximal sodium conductance density of 84.8 pS/μm2, slightly more than double, at 32°C. In the new sodium model description changing temperature no longer alters the maximal sodium conductance. The same temperature dependence was removed from the Hodgkin–Huxley-like delayed rectifier potassium channel (kv.mod; Mainen et al. 1996). As a result of this modification, the sodium and potassium conductance levels in our model appear somewhat inflated compared with previously published studies (Mainen and Sejnowski 1996; Rapp et al. 1996; Vetter et al. 2001).
Second, additional changes were required for the model to reproduce the AP afterhyperpolarization (AHP) obtained in the somatic whole cell recordings from layer 5 pyramidal cells in the rat mPFC (Fig. 1C, whole cell), specifically to prevent a deep AHP. This required reduction of the somatic density of delayed rectifier potassium conductance to 40 pS/μm2 (Schaefer et al. 2003) and an increase in the somatic calcium channel conductance (Kampa and Stuart 2006; Schaefer et al. 2003) to 10 pS/μm2. In this configuration the model's post AP repolarization was more representative of the dynamics of the experimental somatic AP (Fig. 1C, whole cell).
Third, sodium channel inactivation properties were modified to resemble those measured recently in somatosensory cortex (Kole et al. 2008). Inactivation kinetics was faster in the new description, which allowed AP firing to follow high-frequency stimulation without rapid amplitude decay (Fig. 8, soma). In addition, the inactivation voltage dependence was shifted (depolarized) in the axon to improve the model's response to sustained stimuli such as model plateau potentials (Figs. 9 and 10).
FIG. 8.
High-frequency trains of action potentials in prefrontal basal dendrites. A1: field of basal dendrites from a layer V prefrontal cortical pyramidal neuron loaded with VSD. High-frequency triplets of APs were elicited by somatic current injection with an 8-ms interstimulus interval (ISI). VSD recordings from tips of basal branches show moderate increases in amplitudes of the 2nd and 3rd action potentials relative to the first (inset). A2: simultaneous somatic whole cell (top) and VSD recordings (bottom) from the basal tip circled in A1 show very little boosting of AP amplitude during the train. B1: neuron model from Fig. 6 with 2 inset “recordings” of AP triplets elicited with 8-ms ISI. There is an increase in amplitude of about 10% between the 1st and 3rd APs in the train at location indicated (*). B2: AP triplet waveforms from the model soma and dendrite marked “dend-1” in B1.
Next, we used VSD measurements from multiple locations along basal dendrites, in control and TTX conditions, to search for passive cable parameters that would provide the best fit for the experimentally observed AP propagation latencies. In the present model the AP latencies in the basilar dendritic tree were most sensitive to the axial resistivity and membrane capacitance and less sensitive to the membrane resistance or distributions of voltage-gated Na+ and K+ conductances. With dendritic-specific membrane capacitance (Cm) and resistance (Rm) fixed at 1.5 μF/cm2 and 16.7 kΩ/cm2, respectively, we found that specific axial resistance (Ra = 90 Ω·cm) provided the best cumulative fit of the experimentally observed AP propagation latencies in control (ACSF) and TTX conditions.
In the next stage of the model development we set out to fit the relative amplitudes of AP-associated optical signals in the basilar dendritic tree treated with sodium channel blocker (TTX) and A-type potassium channel blocker 4-AP, compared with control amplitudes. It must be stated at this point again, that VSD measurements do not report the absolute amplitude of an electrical signal, in millivolts (discussed in Antic 2003). However, the linear voltage dependence of VSDs (Ross et al. 1977) allows one to use the relative change in optical signal size obtained from the same dendritic segment, same detector pixel, in two subsequent sweeps (Djurisic et al. 2004; Milojkovic et al. 2004). We simulated our TTX and 4-AP experiments by blocking the model's sodium and A-type potassium channels, respectively, and compared the amplitude ratios TTX/Control and 4-AP/Control in the model neuron to those recorded experimentally (Fig. 5). To quantitatively evaluate and compare different versions of the model we computed error values based on the mean squared error between experimental and simulation data (see methods). Each of the two amplitude ratios was compared with the experimental data by computing a fit error value and an overall fit error value was obtained by averaging these two values. This fit error was minimized by changing model parameters systematically and running new simulations.
In the present model delayed rectifier potassium channels contribute very little to AP amplitude; blocking them increases AP amplitudes by about 1.5% in the soma and 3% in the midbasal dendrites. This is consistent with our experimental data (Supplemental Fig. S3) and thus in the remainder of the project we narrowed down our parameter search to sodium and A-type dendritic conductances.
Spatial distributions of both sodium and A-type potassium channels were assumed linear, either uniform along the dendrite, increasing (positive slope) or decreasing with distance (negative slope). Attempting to fit more elaborate channel distributions would require additional free parameters in the model, which seemed unreasonable given the significant noise in the experimental data. Assuming linear distributions for two conductances still left four free parameters to be fit: the perisomatic or proximal conductance densities of each ionic conductance (GNa_prox and GKA_prox), along with the slope in each conductance distribution (change in conductance density per unit distance from the soma: mGNa and mGKA). In the model, the exact same distribution was applied to each basal dendrite from a reconstructed pyramidal neuron (Fig. 6A). Since morphology can affect backpropagation (see amplitudes from different basal branches in Fig. 6B, thin lines; also Supplemental Fig. S4), we decided to average over all basal branches in the model to fit the mean propagation behavior rather than fitting one branch, risking that the branch's unique morphology might bias the results. This goes hand in hand with the nature of our data set, where VSD recordings were collected and pooled from several different branches in the basilar dendritic tree, all of which may have differing morphologies.
Although initial simulations were always performed using a uniform distribution of all dendritic conductances, better results of the model fitting were obtained when both sodium and A-type potassium conductances were distributed nonuniformly on basal dendrites. Fit errors with respect to the experimental data were minimized (Fig. 7) when sodium conductance densities were decreasing with distance from the soma and IA conductance densities were increasing with distance along the same dendritic branch. Finally, the best-fit model (minimum error) included Na+ conductance starting at 150 pS/μm2 at the soma (GNa_prox), decreasing linearly to 50 pS/μm2 at a distance of 200 μm; and A-type potassium conductance starting at 150 pS/μm2 at the soma (GKA_prox), increasing linearly to 290 pS/μm2 at a distance of 200 μm. Plotting the overall error in the neighborhood of these values demonstrates that these parameters led to a local minimum in error values, whereby either increasing or decreasing any of the parameters (GNa_prox, GKA_prox, mGNa, mGKA) led to an increase in the fit error (Fig. 7). As mentioned at the beginning of this paragraph, slope values of zero correspond to uniform conductance distributions and are less favored in this model, as shown by the increased fit error values (Fig. 7, E and F, zero slopes).
Action potential amplitudes in the model's basal dendrites were consistently greater than those measured in basal dendrites in somatosensory cortex using patch pipettes (Nevian et al. 2007). In the present model the dendritic AP amplitude was 71% of the somatic value at 140 μm from the soma, whereas in Nevian et al. (2007) data this value was about 37% of the somatic value. Since VSDs do not report the absolute value of membrane potential, the model's AP amplitudes constitute predictions of the actual amplitudes in the dendrites of the rat prefrontal cortex. The accuracy of these predictions depends on the accuracy of the model, discussed early, and amplitude predictions would be expected to change to some degree if model parameters that affect AP propagation were modified.
High-frequency trains of APs in prefrontal basal dendrites
Here we tested to see how well our “best-fit” model, which showed minimum error for AP amplitude ratios in control and drug conditions (Figs. 6 and 7), was able to reproduce spike amplitudes during high-frequency trains of APs. Action potential triplets were elicited experimentally and in simulations using a train of three current pulses at 125 Hz. In good agreement with experimental data (Fig. 8A), dendritic AP amplitudes in the model showed minimal increase with the temporal order of the spikes in the train (Fig. 8B). The largest relative increase in the amplitude of the third spike occurred at the distal tip of the longest basal dendrite in the model (Fig. 8B1, asterisk). At this location, there was close to a 10% increase of the third AP compared with the first. This increase was in part due to the accumulation of A-type potassium channel inactivation between APs. Removing all voltage-gated calcium channels in the model resulted in a lesser amplitude boosting of the third spike, thus indicating that calcium channels may also contribute to this behavior (Kampa and Stuart 2006). Although the small third spike boosting effect shown here is typical for prefrontal basal dendrites, much greater boosting has been observed in some prefrontal dendritic branches (Zhou et al. 2008; their Fig. 2) as well as in somatosensory basal dendrites (Kampa and Stuart 2006). Our “best-fit” model (Fig. 6) was not capable of reproducing these cases with very significant (∼100%) amplitude boosting of the third AP in the high-frequency train. Nevertheless, our present biophysical model faithfully represents >90% of VSD measurements obtained from distal ends of short- and medium-range PFC basal dendrites during 125-Hz AP firing (Zhou et al. 2008). In the next section we explore models with modified sodium and potassium conductances that have much different dendritic responses to high-frequency stimulation than the unmodified “best-fit” model.
Generation of fast sodium spikelets in PFC basal dendrites
Strong excitatory stimulation of PFC basilar dendrites sometimes, not always, produces an initial spikelet riding on the top of the glutamate-evoked plateau potential (Milojkovic et al. 2004). These initial spikelets were attributed to the activation of voltage-gated sodium conductance because they were effectively blocked by TTX (Milojkovic et al. 2005). When stimulated with an excitatory conductance change (methods), the present best-fit model produced small initial spikelets in the beginning of the dendritic plateau potential (Fig. 9A, arrow). However, this spikelet was not reflected in the somatic waveform, indicating that the present model was not able to reproduce experimental data obtained in a small fraction of basilar dendrites. More specifically, Milojkovic et al. (2005) found that only a small fraction of PFC basilar dendrites (9.6%) can generate large-amplitude initial spikes accompanied with a sharp deflection in the somatic whole cell recording. To reproduce these large sodium spikes reflected in the somatic membrane potential waveform we found that it was possible to use the same model, only with the basal dendrite endowed with a greater maximal sodium conductance [Fig. 9B, large basal spike (arrow) with somatic infliction (arrowhead)].
Recently, the first derivative of the somatic voltage waveform has been used to detect a nonlinearity in the somatic membrane response attributed to remote glutamate-induced dendritic spike initiation (Losonczy et al. 2008). We used this method to test the predictions of our biophysical model (Fig. 9, A′ and B′). We performed glutamate microinotophoresis on 37 basal dendrites in 35 PFC layer 5 pyramidal neurons, at distances in the range 69–110 μm from the soma (average distance 91 ± 12 μm). The intensity of glutamate iontophoretic current was adjusted to trigger somatic plateau depolarizations (amplitude ∼20 mV, duration >150 ms) accompanied by AP firing (Fig. 9C). In 28 of 37 basal dendrites glutamatergic stimuli produced somatic plateau depolarizations with smooth charging curves (Fig. 9C′, top trace). In this group the first derivatives of the somatic charging curve had peak amplitudes <10 V/s (mean 7.1 ± 2.3 V/s; n = 28) and broad waveforms (Fig. 9C′, asterisk). In 9 of 37 basal dendrites, on the other hand, a nearly identical glutamatergic stimulus (location, intensity, duration) triggered sharp deflections during the somatic charging curve (Fig. 9D′, arrowhead), which caused a narrow transient in the first derivative (double arrowhead), with amplitudes ranging between 12 and 80 V/s (mean amplitude 26.5 ± 23.2 V/s; n = 9). We thus concluded that the smooth voltage waveform and its spikeless first derivative (Fig. 9C′, asterisk) are characteristic of the majority of PFC basal branches (∼76%). This behavior actually characterizes basal dendrites in our best-fit model (Fig. 9, A and A′). A sharp inflection in the charging curve (Fig. 9D′, arrowhead) and a pointy transient in the first derivative (double arrowhead), on the other hand, are characteristics of a smaller number of PFC basilar dendrites (24%). Experimental measurements from spike-generating basal dendrites (Fig. 9, D and D′) were predicted by our model with enhanced dendritic sodium conductance (Fig. 9, B and B′).
In summary, our model suggested that to fully reproduce the entire spectrum of local spike generation properties found in layer 5 PFC neurons, a fraction of basilar dendrites (∼25%) must be endowed with special properties compared with the majority of other basal dendritic branches potentially within the same basal dendritic arbor. In other words, our simulations suggested that an increased density of sodium channels (∼2.5-fold compared with the best-fit model) may underlie the ability of some basal dendrites to generate local sodium spikes, manifested in the somatic voltage waveform as sharp deflections (Fig. 9D′, arrowhead). The heterogeneity in membrane excitability among small-diameter branches of the same dendritic tree has been directly or indirectly implied in several recent studies using glass electrode or optical measurements of dendritic function (Losonczy et al. 2008; Milojkovic et al. 2005; Nevian et al. 2007; Zhou et al. 2008).
Down-regulation of A-type conductance and branch strength potentiation in the best-fit model
It has been reported recently that down-regulation of A-type conductance may increase the excitability of thin dendritic branches (called branch strength potentiation [BSP]) and result in a significant increase in the nonlinearity of the somatic voltage waveform (Losonczy et al. 2008). We tested this scenario in computer simulations by comparing voltage waveforms before and after the complete block (removal) of A-type conductance from the target dendrite. We started this series of simulations using our best-fit model (endowed with gNa_prox = 150 pS/μm2 and gKA_prox = 150 pS/μm2; Control condition). We dub these dendrites “Typical” because they faithfully reproduce multisite voltage imaging data during AP backpropagation (Figs. 7 and 8) and 76% of glutamate iontophoresis data (Fig. 9, C and C′). In typical dendrites, changing gKA_prox from 150 pS/μm2 to zero produced minimal changes in the dendritic and somatic voltage waveforms (Fig. 10A, compare Control and IA blocked). The first derivative of somatic waveform showed no indication of dendritic spike initiation (Fig. 10A, bottom trace). The only effect of IA loss in typical dendrites was a decrease in the latency of the somatic AP (Fig. 10A, double-headed arrow).
Next we asked what sodium and A-type potassium channel densities are necessary such that basal dendrites are capable of exhibiting significant IA-dependent BSP. To make basal dendrites sensitive to A-type conductance down-regulation and able to produce a clear transition from WEAK to STRONG branch (see Losonczy et al. 2008 for an explanation) it was necessary to increase dendritic gNa by ≥2.5-fold and at the same time increase dendritic gKA by ≥5-fold compared with our best-fit model. We dubbed these dendrites “Special case” dendrites because they bear densities of dendritic Na+ and A-type K+ channels that are outside of the plausible range determined in Fig. 7. In the special case dendrite shown in Fig. 10B, Control dendritic gNa_prox was set to 375 pS/μm2 and gKA_prox = 1,200 pS/μm2. Down-regulation of proximal A-type conductance from 1,200 pS/μm2 to zero (IA blocked) causes a potentiation of dendritic excitability, local initiation of a sodium spike, and strong nonlinearity in the somatic waveform as determined by a sharp transient in the first derivative (Fig. 10B, bottom trace, arrow). That is, down-regulation of A-type conductance can turn WEAK basilar branches into STRONG ones, if dendrites are endowed with special properties.
The biophysical model shown in Fig. 10B is just one of several possible solutions to combine high densities of Na+ and A-type K+ channels and acquire adequate sensitivity to A-type down-regulation (conversion from WEAK to STRONG). We performed a detailed search of two parameters (dendritic gNA and gKA) required to reproduce BSP behavior by systematically changing gNA and gKA in the model. Synaptic input conductance (stimulus) and stimulus location on the dendrite were fixed in these simulations. For each combination of gNA and gKA we calculated the first derivative of the somatic voltage response during the charging phase and its peak value is plotted versus gNA (Supplemental Fig. S7). Multiple pairs of gNA_prox and gKA_prox produced a strong increase in dV/dt following the IA block, thus mimicking a successful BSP (Supplemental Fig. S7, vertical arrow). Nevertheless, in all successful BSP simulations basal dendrites had to be endowed with higher gNA and higher gKA than the best-fit model—which renders them “special case” dendrites. We tested whether such special case dendrites may explain some discrepancies between recently published data (Kampa and Stuart 2006; Nevian et al. 2007) and results published by this laboratory (Antic 2003; Zhou et al. 2007, 2008). Toward this aim we repeated our simulations of AP backpropagation using the same parameters as in Fig. 10B. Special case basal dendrites, endowed with high gNA_prox (375) and high gKA_prox (1,200 pS/μm2), showed greater boosting of the third AP in the high-frequency train (Fig. 10C), as previously described by Kampa and Stuart (2006). In spite of the high density of A-type conductance, however, Special case basal dendrites have an AP attenuation profile nearly identical to that of Typical dendrites in the best-fit model (Fig. 10D). In summary, “special case” dendrites can reproduce some previously published features of thin dendritic branches (dendritic spike initiation: Milojkovic et al. 2005; Nevian et al. 2007; somatic manifestation of dendritic spike initiation: Losonczy et al. 2008; Milojkovic et al. 2005; present study; branch strength potentiation by A-type down-regulation: Losonczy et al. 2008; and third spike boosting in high-frequency train: Kampa and Stuart 2006; Zhou et al. 2008, their Fig. 2), whereas severe AP attenuation cannot be explained by the current model.
DISCUSSION
The present study is based on a number of experimental achievements. All neurons in the data set were injected through patch electrode, pulled outside-out, and repatched with a fresh pipette after ≥1 h of incubation. The AP waveforms were simultaneously recorded from several neighboring dendrites (VSDs) in parallel with the somatic whole cell recording. Along each dendrite, AP signals were simultaneously sampled from multiple sites before and after each application of channel blockers TTX, 4-AP, TEA, cadmium, and ZD7288. In experiments using TTX, the multisite VSD imaging was combined with dual patch-clamp recording; i.e., the cell body of the dye-filled neuron was repatched with two pipettes. One patch pipette was used to voltage-clamp the membrane in the shape of an AP. The other patch pipette was used to monitor the success of this command signal. At the end, our experimental effort yielded a unique description of AP backpropagation pattern in the basilar dendritic tree. The description included: AP peak latencies, AP half-widths, and relative AP amplitudes in proximal and distal dendritic segments, before and after pharmacological manipulations (Fig. 5). The abundant amounts of data were successfully incorporated into one meaningful biophysical model (Fig. 6).
The major findings of the present study are as follows. 1) Voltage-gated sodium channels play an important role in AP backpropagation in basal dendrites of layer V, prefrontal cortical pyramidal cells, such that blocking these channel with TTX leads to a significant reduction in dendritic AP amplitude (Fig. 1; Supplemental Fig. S1). 2) Pharmacological block of the A-type K+ conductance, on the other hand, produces a significant increase in both AP amplitude and duration (Fig. 3B). 3) Delayed rectifier potassium (IKDR), voltage-gated calcium conductances, and hyperpolarization-activated mixed cation (Ih) affect AP backpropagation to a lesser extent. 4) A very large number of data points (multiple recording sites, three experimental conditions: Control, TTX, and 4-AP) point to one best model (minimum error, Fig. 7). 5) The best model of the present experimental data in basal dendrites of PFC neurons includes nonuniformly distributed voltage-gated Na+ and A-type K+ conductances. More precisely, Na+ conductance densities are estimated to be 150 pS/μm2 proximal to the soma, declining by 0.5 pS·μm−2·μm−1. The estimated A-type K+ conductance also turned out to be 150 pS/μm2 proximal to the soma, but it increased by 0.7 pS·μm−2·μm−1 along the dendrite. 6) The present model predicts lesser AP attenuation than previously reported in basal dendrites of the somatosensory cortex (Kampa and Stuart 2006; Nevian et al. 2007). 7) The present model successfully reproduced experimental measurements of the high-frequency AP triplets (Fig. 8), as well as the glutamate-evoked sodium spikelets (Fig. 9). 8) The present model successfully reproduced 76% of basal dendrites that do not make large-amplitude local dendritic sodium spikes, detectable in the somatic recording (Typical dendrites). To reproduce the other 24% of basal dendrites one must assign higher gNa densities in the model (Special case dendrites). 9) Down-regulation of IA current in Typical dendrites does not result in strong potentiation of dendritic excitability (Fig. 10A). Down-regulation of IA current in “special case” dendrites (endowed with higher gNa and gKA), on the other hand, is capable of converting WEAK into STRONG dendrites, as recently reported in thin branches of CA1 hippocampal pyramidal neurons (Losonczy et al. 2008). 10) The present study suggests that all sister branches belonging to the same dendritic tree may not necessarily have the same level of intrinsic excitability.
Previously published models of AP backpropagation in basal dendrites
Two recent studies that have examined AP backpropagation in basal dendrites have proposed computational models to explain the experimentally observed behavior (Kampa and Stuart 2006; Nevian et al. 2007). Although these two studies agree on a very rapid rate of AP attenuation, they exhibit significant discrepancies between the two data sets. Blocking sodium channels in the somatosensory cortex had no effect on AP backpropagation in basal dendrites as reported by calcium signaling (Kampa and Stuart 2006). At the same time, blocking A-type potassium channels substantially increased AP amplitude (Kampa and Stuart 2006), in contrast to a patch-clamp study in somatosensory cortex, which found small albeit statistically significant effects of blocking this channel (Nevian et al. 2007). AP peak latencies from Kampa and Stuart (2006) exhibit exponential rise with distance (their Fig. 3). AP latencies from Nevian et al. (2007; their Fig. 1) do not appear to reproduce this feature, are smaller, and actually show a propagation velocity very comparable to that observed in the present study. Finally, these two recent studies proposed very different roles for both voltage-gated sodium and potassium conductances. In the Kampa and Stuart (2006) model, sodium conductance is uniform in the basal dendrites with a conductance density of 30 pS/μm2, whereas in Nevian et al. (2007), the sodium channel distribution is nonuniform with either a single hot spot or a linear decline with distance. As a final point, Nevian et al. (2007) did not use a K+ channel with exact properties of A-type current in their model, but rather a delay-rectifier–like channel, which may or may not fully mimic the role of A-type current in the model of AP backpropagation.
The major goal of this study was not to accurately quantify the degree of AP attenuation in basal dendrites. The goal was to determine which model parameters provide the best fit of the abundant experimental data generated by multisite measurements of AP peak latencies, AP half-widths, and relative AP amplitudes in three experimental conditions (Control, TTX, and 4-AP). The AP attenuation pattern, described herein, is a consequence of that fitting process.
The quantitative difference between the present model output and that of the Kampa et al. (2006) model and Nevian et al. 2007 patch-clamp measurements, in the proximal 140 μm, could arise from the inaccuracy of the VSD method or from the specific modeling parameters used here. We were working in a different cortical area (prefrontal cortex), which could also potentially explain differences between our results and previously published results in the somatosensory cortex. Additionally, many experimental conditions (e.g., animal age, ionic composition of solutions, patch-electrode series resistance, and capacitance compensation) are potential sources of discrepancy and deserve attention (discussed in Zhou et al. 2008).
Passive parameters
Action potential propagation latencies are very sensitive to the model's specific axial resistivity Ra and less sensitive to specific membrane resistance or density of sodium and potassium channels (Antic 2003; Bar-Yehuda et al. 2008; Trevelyan and Jack 2002). With the passive parameters (Cm and Rm) set to values consistent with those published previously, we used Ra to fit the experimental latencies and arrived at 90 Ω·cm. This Ra value is in good agreement with previously published studies that attempted to fit their dual-site or multisite experimental measurements with a realistic biophysical model of a cortical pyramidal neuron (Antic 2003; Inoue et al. 2001; Nevian et al. 2007; Stuart and Spruston 1998).
Nonuniform distribution of Na+ and A-type K+ dendritic conductance
In the initial stages of the modeling project, we chose the uniform (flat) distribution of Na+ channels and a monotonic linear increase in A-type channels. In these initial simulations we varied three parameters: 1) global dendritic gnabar; 2) proximal gKA (Fig. 7A); and 3) the slope of A-type potassium conductance (mGKA). We had originally avoided fully exploring the possibility of nonuniform sodium conductance based on the lack of experimental evidence in the literature. Recall that patch-clamp measurements from the soma, dendrites, and axons indicated that sodium channels are uniformly distributed in the primary somatic processes (Colbert and Johnston 1996; Magee and Johnston 1995; Stuart and Sakmann 1994). However, eventually we expanded our search of parameter space to include both uniform and nonuniform sodium and A-type conductance distributions. Exhaustive searching was done on a four-dimensional parameter space (described in Fig. 7) and repeated many times to determine the consistency and accuracy (overall fit values) of findings, while changing other parameters such as the passive parameter Ra and the delayed rectifier potassium conductance (gKDR; kv.mod in the model). To our surprise, we found that a nonuniform sodium conductance does improve the model's ability to fit the data (Figs. 6 and 7). Nonuniform Na+ conductance has also been found by Nevian et al. (2007) to be one of the several plausible solutions for fitting the AP waveform in basal dendrites. Simple linear sodium conductance distributions were considered in Nevian et al. (2007) and in the present model. Attempting to fit more elaborate channel distributions (hot spots) would have required additional free parameters in the model, which was deemed unreasonable in this project (see methods and Limitations). Nevertheless, one must remain open to the possibility of the existence of the occasional channel clusters in basal dendrites. For example, some thin dendritic branches in the rat CNS do have the ability to cluster voltage-gated sodium channels (Kosaka and Kosaka 2007) and some small fraction of the PFC basal dendrites (∼9.6%) do have the ability to generate large-amplitude sodium spikelets (Milojkovic et al. 2005). In the present study we used the first derivative of the somatic response (dV/dt), to search for signs of remote dendritic sodium spike initiation, and found that nearly 24% of basal branches are endowed with this feature (Fig. 9, C and D).
The second voltage-gated channel, equally critical for shaping the AP backpropagation pattern in basilar dendrites, A-type K+ channel, has also been found to cluster in some CNS neurons (Kollo et al. 2006). In this scenario, dendritic branches without A-type channel clusters would exhibit greater ability to trigger sodium spikelets (Milojkovic et al. 2005; Nevian et al. 2007), whereas branches endowed with A-type channel clusters would show stronger attenuation of bAPs (Kampa and Stuart 2006; Zhou et al. 2008, their Fig. 2).
Limitations
Comparing computational models to experimental data has served a very useful purpose in exploring the biophysical mechanisms underlying experimental measurements from individual CNS neurons (Antic 2003; Schaefer et al. 2003; Stuart and Spruston 1998; Thurbon et al. 1998). However, this approach clearly has limitations and we take the opportunity here to discuss these limitations and their impact on our modeling approach. First of all, the present modeling was based on voltage-sensitive dye imaging data that, as with all experimental data, contains noise. Data from individual branches were comprised of a number of individual sweeps (temporal and spatial averaging) chosen during the experiments to attain a subjectively good quality signal in distal dendritic locations as determined by the experimenter. Noise from these averaged data sets was then quantified off-line and appears in the error bars in the plots (Figs. 2 and 3). For amplitude ratios, which are simply the division of two experimental measurements, the errors were computed according to an error-propagation formula (methods, Eq. 1).
In different dendritic branches that have different morphologies and possibly different channel distributions (Golding et al. 2001; Losonczy et al. 2008; Zhou et al. 2008, their Fig. 2) the AP backpropagation pattern may differ. To counter for this natural variability, many data points, from many dendritic branches, are combined to obtain the mean propagation behavior in our dendrites. This is plotted in Fig. 5, where error bars are SEs. Although these error bars are reasonable, they are clearly not zero, meaning there is a degree of uncertainty in what we are fitting, which affects the expected accuracy of the resulting model. Therefore the conclusions based on models of this kind cannot be categorical and unequivocal.
In spite of these limitations, the present model was successful in fitting a very large set of data points, which included multisite measurements of AP peak latencies, AP half-widths, and relative AP amplitudes before and after application of channel blockers. In addition to the current data set, the best-fit model successfully reproduced two previously observed behaviors. First, a recent study from this laboratory has shown that within the high-frequency train of APs (≤125 Hz) the relative amplitudes of backpropagating waveforms are relatively uniform in the most distal tips of short- and medium-range basal branches (Zhou et al. 2008). In the absence of any parameter modifications, the best-fit model (Fig. 6) was stimulated (somatic current injection) to fire triplets of APs. AP waveforms propagated back into the basilar dendritic tree with minimal changes in relative AP amplitude (Fig. 8B). Second, in the best-fit model the local initiation of fast sodium spikelets occurred in the dendrite on plateau-like depolarization (Fig. 9B; see also Rhodes 2006). This kind of membrane potential waveform, small sodium spikelet riding on top of glutamate-evoked dendritic plateau potential has been documented in PFC neurons using VSD recording (Milojkovic et al. 2004, 2005).
Implications
There is a misconception in the field that experimental and modeling studies from this laboratory advocate “full propagation in basal dendrites” (Kampa and Stuart 2006). In the Antic (2003; his Fig. 3) model the amplitude of the dendritic AP at only 150 μm from the soma has already suffered a loss (attenuation). Basal dendrites were always perceived and modeled as weakly excitable membranes (Antic 2003; Rapp et al. 1996; Vetter et al. 2001), so the full-size AP propagation in basal dendrites was never really an issue. All experimental and model data point to some degree of AP attenuation in this part of the dendritic tree (Antic 2003; Kampa and Stuart 2006; Nevian et al. 2007; Zhou et al. 2008; present study). The discrepancy is in the degree of attenuation. Although Kampa and Stuart (2006) and Nevian et al. (2007) argue for a very rapid and severe amplitude decline (down to 36% of the somatic value at 140 μm from the soma; their Fig. 7C1), the results of this laboratory bring several pieces of experimental evidence that are incompatible with a severe amplitude decline hypothesis (Antic 2003; Zhou et al. 2008; present study).
The present study goes beyond the competing hypotheses of modest versus severe attenuation. It points to one single biophysical model that can arguably satisfy the largest set of experimental data points obtained simultaneously from an individual neuron (Figs. 1–5). Although fitting many features of experimental data related to signaling and excitability properties in basal dendrites of the prefrontal cortex (Milojkovic et al. 2005; Zhou et al. 2008), the present model also resonates with commonalities among observations of backpropagation properties in basal as well as apical dendrites of several neuronal populations. First, backpropagation is active and supported by voltage-gated sodium channels (Stuart et al. 1997). At the same time backpropagation is decremental; the AP amplitude declines steadily with increasing distance from the soma (Nevian et al. 2007; Spruston et al. 1995; Stuart and Sakmann 1994). Second, the transient A-type K+ conductance plays an important role in limiting backpropagation (Hoffman et al. 1997; Kampa and Stuart 2006; Migliore et al. 1999).
Two interesting neurobiological concepts can be indirectly inferred from the present experiment–model merger. First, a significant increase in dendritic AP amplitude on 4-AP block suggests that modulatory signals (e.g., down-regulation of A-type conductance) may influence the AP-dependent processes in the most distal segments of PFC basal dendrites (Gordon et al. 2006; Kampa et al. 2006; Linden 1999; Sjöstrom and Häusser 2006). Second, there is a growing amount of evidence that branches of the same type exhibit heterogeneous behavior when it comes to AP backpropagation (Golding et al. 2001; Losonczy et al. 2008; Zhou et al. 2008) or local sodium spike initiation (Milojkovic et al. 2005; Nevian et al. 2007). It was determined that only a small fraction of PFC basal branches (10–24%) have the ability to generate local sodium spikelets, large enough to inflict sharp transients in the somatic voltage waveform (Milojkovic et al. 2005; present study). To model those exceptionally excitable branches (here termed “special case” dendrites) one needed to endow them with an exceptional level of voltage-gated sodium conductance: ≤2.5-fold in the current example (Fig. 9B). To model branch strength potentiation one needed to endow dendrites with additional A-type channels (Fig. 10B). If some thin dendritic branches do have anomalously high densities of sodium and potassium channels, then new experimental techniques are needed to detect and identify those branches in brain sections. At the present moment, dendritic clustering of voltage-gated channels has been documented only in the rat olfactory bulb (Kosaka and Kosaka 2007). Further advances in molecular mapping of voltage-gated channels and associated protein complexes (Ogawa and Rasband 2008), together with advances in electrical and optical recordings (Kole et al. 2008; Nevian et al. 2007), may resolve this issue in the future.
GRANTS
This work was supported by National Institute of Mental Health Grant MH-063503.
Supplementary Material
Acknowledgments
We thank A. Roth for kindly providing the model files of Schaefer and colleagues (2003), D. Oliver and D. Bishop for help with Neurolucida, and B. Kath for help with NEURON.
The costs of publication of this article were defrayed in part by the payment of page charges. The article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. Section 1734 solely to indicate this fact.
Footnotes
The online version of this article contains supplemental data.
REFERENCES
- Acker and White 2007.Acker CD, White JA. Roles of IA and morphology in action potential propagation in CA1 pyramidal cell dendrites. J Comput Neurosci 23: 201–216, 2007. [DOI] [PubMed] [Google Scholar]
- Antic et al. 1999.Antic S, Major G, Zecevic D. Fast optical recordings of membrane potential changes from dendrites of pyramidal neurons. J Neurophysiol 82: 1615–1621, 1999. [DOI] [PubMed] [Google Scholar]
- Antic 2003.Antic SD Action potentials in basal and oblique dendrites of rat neocortical pyramidal neurons. J Physiol 550: 35–50, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ariav et al. 2003.Ariav G, Polsky A, Schiller J. Submillisecond precision of the input–output transformation function mediated by fast sodium dendritic spikes in basal dendrites of CA1 pyramidal neurons. J Neurosci 23: 7750–7758, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bar-Yehuda et al. 2008.Bar-Yehuda D, Ben-Porat H, Korngreen A. Dendritic excitability during increased synaptic activity in rat neocortical L5 pyramidal neurons. Eur J Neurosci 28: 2183–2194, 2008. [DOI] [PubMed] [Google Scholar]
- Benucci et al. 2004.Benucci A, Verschure PF, Konig P. Two-state membrane potential fluctuations driven by weak pairwise correlations. Neural Comput 16: 2351–2378, 2004. [DOI] [PubMed] [Google Scholar]
- Bi and Poo 1998.Bi GQ, Poo MM. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J Neurosci 18: 10464–10472, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carnevale and Hines 2006.Carnevale NT, Hines ML. The NEURON Book. Cambridge, UK: Cambridge Univ. Press, 2006.
- Colbert and Johnston 1996.Colbert CM, Johnston D. Axonal action-potential initiation and Na+ channel densities in the soma and axon initial segment of subicular pyramidal neurons. J Neurosci 16: 6676–6686, 1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Compte et al. 2003.Compte A, Sanchez-Vives MV, McCormick DA, Wang XJ. Cellular and network mechanisms of slow oscillatory activity (<1 Hz) and wave propagations in a cortical network model. J Neurophysiol 89: 2707–2725, 2003. [DOI] [PubMed] [Google Scholar]
- Djurisic et al. 2004.Djurisic M, Antic S, Chen WR, Zecevic D. Voltage imaging from dendrites of mitral cells: EPSP attenuation and spike trigger zones. J Neurosci 24: 6703–6714, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldmeyer et al. 2002.Feldmeyer D, Lubke J, Silver RA, Sakmann B. Synaptic connections between layer 4 spiny neurone-layer 2/3 pyramidal cell pairs in juvenile rat barrel cortex: physiology and anatomy of interlaminar signalling within a cortical column. J Physiol 538: 803–822, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golding et al. 2001.Golding NL, Kath WL, Spruston N. Dichotomy of action-potential backpropagation in CA1 pyramidal neuron dendrites. J Neurophysiol 86: 2998–3010, 2001. [DOI] [PubMed] [Google Scholar]
- Gordon et al. 2006.Gordon U, Polsky A, Schiller J. Plasticity compartments in basal dendrites of neocortical pyramidal neurons. J Neurosci 26: 12717–12726, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gulledge et al. 2005.Gulledge AT, Kampa BM, Stuart GJ. Synaptic integration in dendritic trees. J Neurobiol 64: 75–90, 2005. [DOI] [PubMed] [Google Scholar]
- Häusser et al. 2001.Häusser M, Major G, Stuart GJ. Differential shunting of EPSPs by action potentials. Science 291: 138–141, 2001. [DOI] [PubMed] [Google Scholar]
- Häusser et al. 2000.Häusser M, Spruston N, Stuart GJ. Diversity and dynamics of dendritic signaling. Science 290: 739–744, 2000. [DOI] [PubMed] [Google Scholar]
- Hoffman et al. 1997.Hoffman DA, Magee JC, Colbert CM, Johnston D. K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature 387: 869–875, 1997. [DOI] [PubMed] [Google Scholar]
- Inoue et al. 2001.Inoue M, Hashimoto Y, Kudo Y, Miyakawa H. Dendritic attenuation of synaptic potentials in the CA1 region of rat hippocampal slices detected with an optical method. Eur J Neurosci 13: 1711–1721, 2001. [DOI] [PubMed] [Google Scholar]
- Johnston et al. 1996.Johnston D, Magee JC, Colbert CM, Cristie BR. Active properties of neuronal dendrites. Annu Rev Neurosci 19: 165–186, 1996. [DOI] [PubMed] [Google Scholar]
- Kampa et al. 2006.Kampa BM, Letzkus JJ, Stuart GJ. Requirement of dendritic calcium spikes for induction of spike-timing-dependent synaptic plasticity. J Physiol 574: 283–290, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kampa and Stuart 2006.Kampa BM, Stuart GJ. Calcium spikes in basal dendrites of layer 5 pyramidal neurons during action potential bursts. J Neurosci 26: 7424–7432, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keren et al. 2005.Keren N, Peled N, Korngreen A. Constraining compartmental models using multiple voltage recordings and genetic algorithms. J Neurophysiol 94: 3730–3742, 2005. [DOI] [PubMed] [Google Scholar]
- Kole et al. 2008.Kole MH, Ilschner SU, Kampa BM, Williams SR, Ruben PC, Stuart GJ. Action potential generation requires a high sodium channel density in the axon initial segment. Nat Neurosci 11: 178–186, 2008. [DOI] [PubMed] [Google Scholar]
- Kollo et al. 2006.Kollo M, Holderith NB, Nusser Z. Novel subcellular distribution pattern of A-type K+ channels on neuronal surface. J Neurosci 26: 2684–2691, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosaka and Kosaka 2007.Kosaka T, Kosaka K. Heterogeneity of nitric oxide synthase-containing neurons in the mouse main olfactory bulb. Neurosci Res 57: 165–178, 2007. [DOI] [PubMed] [Google Scholar]
- Kritzer and Goldman-Rakic 1995.Kritzer MF, Goldman-Rakic PS. Intrinsic circuit organization of the major layers and sublayers of the dorsolateral prefrontal cortex in the rhesus monkey. J Comp Neurol 359: 131–143, 1995. [DOI] [PubMed] [Google Scholar]
- Larkman 1991.Larkman AU Dendritic morphology of pyramidal neurones of the visual cortex of the rat: III. Spine distributions. J Comp Neurol 306: 332–343, 1991. [DOI] [PubMed] [Google Scholar]
- Larkum et al. 2001.Larkum ME, Zhu JJ, Sakmann B. Dendritic mechanisms underlying the coupling of the dendritic with the axonal action potential initiation zone of adult rat layer 5 pyramidal neurons. J Physiol 533: 447–466, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linden 1999.Linden DJ The return of the spike: postsynaptic action potentials and the induction of LTP and LTD. Neuron 22: 661–666, 1999. [DOI] [PubMed] [Google Scholar]
- London and Häusser 2005.London M, Häusser M. Dendritic computation. Annu Rev Neurosci 28: 503–532, 2005. [DOI] [PubMed] [Google Scholar]
- Losonczy et al. 2008.Losonczy A, Makara JK, Magee JC. Compartmentalized dendritic plasticity and input feature storage in neurons. Nature 452: 436–441, 2008. [DOI] [PubMed] [Google Scholar]
- Magee and Johnston 1995.Magee JC, Johnston D. Characterization of single voltage-gated Na+ and Ca2+ channels in apical dendrites of rat CA1 pyramidal neurons. J Physiol 487: 67–90, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magee and Johnston 1997.Magee JC, Johnston D. A synaptically controlled, associative signal for Hebbian plasticity in hippocampal neurons. Science 275: 209–213, 1997. [DOI] [PubMed] [Google Scholar]
- Mainen and Sejnowski 1996.Mainen ZF, Sejnowski TJ. Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 382: 363–366, 1996. [DOI] [PubMed] [Google Scholar]
- Markram et al. 1997a.Markram H, Lubke J, Frotscher M, Roth A, Sakmann B. Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex. J Physiol 500: 409–440, 1997a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram et al. 1997b.Markram H, Lubke J, Frotscher M, Sakmann B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275: 213–215, 1997b. [DOI] [PubMed] [Google Scholar]
- Martina et al. 2000.Martina M, Vida I, Jonas P. Distal initiation and active propagation of action potentials in interneuron dendrites. Science 287: 295–300, 2000. [DOI] [PubMed] [Google Scholar]
- Migliore et al. 1999.Migliore M, Hoffman DA, Magee JC, Johnston D. Role of an A-type K+ conductance in the back-propagation of action potentials in the dendrites of hippocampal pyramidal neurons. J Comput Neurosci 7: 5–15, 1999. [DOI] [PubMed] [Google Scholar]
- Milojkovic et al. 2004.Milojkovic BA, Radojicic MS, Goldman-Rakic PS, Antic SD. Burst generation in rat pyramidal neurones by regenerative potentials elicited in a restricted part of the basilar dendritic tree. J Physiol 558: 193–211, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milojkovic et al. 2005.Milojkovic BA, Wuskell JP, Loew LM, Antic SD. Initiation of sodium spikelets in basal dendrites of neocortical pyramidal neurons. J Membr Biol 208: 155–169, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevian et al. 2007.Nevian T, Larkum ME, Polsky A, Schiller J. Properties of basal dendrites of layer 5 pyramidal neurons: a direct patch-clamp recording study. Nat Neurosci 10: 206–214, 2007. [DOI] [PubMed] [Google Scholar]
- Nevian and Sakmann 2006.Nevian T, Sakmann B. Spine Ca2+ signaling in spike-timing-dependent plasticity. J Neurosci 26: 11001–11013, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa and Rasband 2008.Ogawa Y, Rasband MN. The functional organization and assembly of the axon initial segment. Curr Opin Neurobiol 18: 307–313, 2008. [DOI] [PubMed] [Google Scholar]
- Rapp et al. 1996.Rapp M, Yarom Y, Segev I. Modeling back propagating action potential in weakly excitable dendrites of neocortical pyramidal cells. Proc Natl Acad Sci USA 93: 11985–11990, 1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhodes 2006.Rhodes P The properties and implications of NMDA spikes in neocortical pyramidal cells. J Neurosci 26: 6704–6715, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross et al. 1977.Ross WN, Salzberg BM, Cohen LB, Grinvald A, Davila HV, Waggoner AS, Wang CH. Changes in absorption, fluorescence, dichroism, and birefringence in stained giant axons: optical measurement of membrane potential. J Membr Biol 33: 141–183, 1977. [DOI] [PubMed] [Google Scholar]
- Schaefer et al. 2003.Schaefer AT, Larkum ME, Sakmann B, Roth A. Coincidence detection in pyramidal neurons is tuned by their dendritic branching pattern. J Neurophysiol 89: 3143–3154, 2003. [DOI] [PubMed] [Google Scholar]
- Schiller et al. 2000.Schiller J, Major G, Koester HJ, Schiller Y. NMDA spikes in basal dendrites of cortical pyramidal neurons. Nature 404: 285–289, 2000. [DOI] [PubMed] [Google Scholar]
- Shu et al. 2007.Shu Y, Yu Y, Yang J, McCormick DA. Selective control of cortical axonal spikes by a slowly inactivating K+ current. Proc Natl Acad Sci USA 104: 11453–11458, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sjöstrom and Häusser 2006.Sjöstrom PJ, Häusser M. A cooperative switch determines the sign of synaptic plasticity in distal dendrites of neocortical pyramidal neurons. Neuron 51: 227–238, 2006. [DOI] [PubMed] [Google Scholar]
- Song et al. 1998.Song WJ, Tkatch T, Baranauskas G, Ichinohe N, Kitai ST, Surmeier DJ. Somatodendritic depolarization-activated potassium currents in rat neostriatal cholinergic interneurons are predominantly of the A type and attributable to coexpression of Kv4.2 and Kv4.1 subunits. J Neurosci 18: 3124–3137, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spruston 2008.Spruston N Pyramidal neurons: dendritic structure and synaptic integration. Nat Rev Neurosci 9: 206–221, 2008. [DOI] [PubMed] [Google Scholar]
- Spruston et al. 1995.Spruston N, Schiller Y, Stuart G, Sakmann B. Activity-dependent action potential invasion and calcium influx into hippocampal CA1 dendrites. Science 268: 297–300, 1995. [DOI] [PubMed] [Google Scholar]
- Spruston et al. 2001.Spruston N, Stuart G, Häusser M. Dendritic integration. In: Dendrites, edited by Spruston N, Stuart G, Häusser M. Oxford, UK: Oxford Univ. Press, 2001, p. 231–270.
- Stuart and Spruston 1998.Stuart G, Spruston N. Determinants of voltage attenuation in neocortical pyramidal neuron dendrites. J Neurosci 18: 3501–3510, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart et al. 1997.Stuart G, Spruston N, Sakmann B, Häusser M. Action potential initiation and backpropagation in neurons of the mammalian CNS. Trends Neurosci 20: 125–131, 1997. [DOI] [PubMed] [Google Scholar]
- Stuart and Sakmann 1994.Stuart GJ, Sakmann B. Active propagation of somatic action potentials into neocortical pyramidal cell dendrites. Nature 367: 69–72, 1994. [DOI] [PubMed] [Google Scholar]
- Thurbon et al. 1998.Thurbon D, Luscher HR, Hofstetter T, Redman SJ. Passive electrical properties of ventral horn neurons in rat spinal cord slices. J Neurophysiol 79: 2485–2502, 1998. [DOI] [PubMed] [Google Scholar]
- Trevelyan and Jack 2002.Trevelyan AJ, Jack JJ. Detailed passive cable models of layer 2/3 pyramidal cells in rat visual cortex at different temperatures. J Physiol 539: 623–636, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vetter et al. 2001.Vetter P, Roth A, Häusser M. Propagation of action potentials in dendrites depends on dendritic morphology. J Neurophysiol 85: 926–937, 2001. [DOI] [PubMed] [Google Scholar]
- Waters et al. 2003.Waters J, Larkum M, Sakmann B, Helmchen F. Supralinear Ca2+ influx into dendritic tufts of layer 2/3 neocortical pyramidal neurons in vitro and in vivo. J Neurosci 23: 8558–8567, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou et al. 2007.Zhou WL, Yan P, Wuskell JP, Loew LM, Antic SD. Intracellular long wavelength voltage-sensitive dyes for studying the dynamics of action potentials in axons and thin dendrites. J Neurosci Methods 164: 225–239, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou et al. 2008.Zhou WL, Yan P, Wuskell JP, Loew LM, Antic SD. Dynamics of action potential backpropagation in basal dendrites of prefrontal cortical pyramidal neurons. Eur J Neurosci 27: 1–14, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.