A Biologically Realistic Network Model of Acquisition and Extinction of Conditioned Fear Associations in Lateral Amygdala Neurons

Abstract

The basolateral amygdala plays an important role in the acquisition and expression of both fear conditioning and fear extinction. To understand how a single structure could encode these “opposite” memories, we developed a biophysical network model of the lateral amygdala (LA) neurons during auditory fear conditioning and extinction. Membrane channel properties were selected to match waveforms and firing properties of pyramidal cells and interneurons in LA, from published in vitro studies. Hebbian plasticity was implemented in excitatory AMPA and inhibitory GABA_A receptor-mediated synapses to model learning. The occurrence of synaptic potentiation versus depression was determined by intracellular calcium levels, according to the calcium control hypothesis. The model was able to replicate conditioning- and extinction-induced changes in tone responses of LA neurons in behaving rats. Our main finding is that LA activity during both acquisition and extinction can be controlled by a balance between pyramidal cell and interneuron activations. Extinction training depressed conditioned synapses and also potentiated local interneurons, thereby inhibiting the responses of pyramidal cells to auditory input. Both long-term depression and potentiation of inhibition were required to initiate and maintain extinction. The model provides insights into the sites of plasticity in conditioning and extinction, the mechanism of spontaneous recovery, and the role of amygdala NMDA receptors in extinction learning.

INTRODUCTION

It is well established that the amygdaloid complex plays an important role in the acquisition and expression of learned fear associations (Davis 2006; LeDoux 2000; Maren and Quirk 2004). Recent data indicate that it also plays a key role in extinction of those memories (Falls et al. 1992; Herry et al. 2006; Laurent et al. 2008; Sotres-Bayon et al. 2007). Given that extinction is itself a learning process, an important goal is to understand how a single structure can encode both acquisition and extinction memories. To address this, we employed a computational modeling approach, incorporating known biophysical and connectivity properties of lateral amygdala neurons, to predict learning-induced changes in the responses of single units to conditioned stimuli. Our overall goal is to bridge biophysical and network modeling approaches to gain insight into how the amygdala solves the “problem” of extinction and ultimately how it interacts with other structures to regulate fear expression.

The components of the amygdala that are critical for fear conditioning are the lateral nucleus (LA), the basal nucleus (BL), and the central nucleus (CE) (Maren 2001). LA is widely accepted to be a key site of synaptic events that contribute to fear learning (Paré et al. 2004; Sigurdsson et al. 2007). There are two main types of neurons within the LA and the BL: pyramidal-like glutamatergic projection neurons and local circuit γ-aminobutyric acid (GABA)-ergic interneurons (McDonald 1984). In auditory fear conditioning, convergence of tone (conditioned stimulus, CS) and foot-shock (unconditioned stimulus, US) inputs in LA leads to potentiation of CS inputs, resulting in larger tone responses in LA (Blair et al. 2001). Increased LA responses are relayed to the CE via the basal nuclei (Pitkanen 2000), and the intercalated (ITC) cell masses (Paré et al. 2004), eliciting fear responses via successive projections to brain stem and hypothalamic sites (LeDoux 2000). As a result, rats learn to freeze to tones that predict foot shock.

Once acquired, conditioned fear associations are not always expressed. Repeated presentation of the tone CS in the absence of the US causes conditioned fear responses to diminish rapidly, a phenomenon termed fear extinction (Myers and Davis 2007; Rescorla 2002). The neural mechanisms of fear extinction are not well understood, and a neural analysis of extinction and inhibition is still in its infancy (Delamater 2004; Quirk and Mueller 2008). Some psychological theories described extinction as an “unlearning” process due to a violation of the CS-US association established in fear acquisition (Rescorla and Wagner 1972). This unlearning view has been challenged by the observation that fear recovers spontaneously after extinction. An alternative theory proposes that extinction does not erase the CS-US association but instead forms a new memory that inhibits conditioned responding (Bouton and King 1983; Quirk 2002). Given the central role of the LA in the acquisition and expression of fear memory, it has been proposed that this structure may be a site of inhibition in extinction (Hobin et al. 2003; Myers and Davis 2002; Sotres-Bayon et al. 2004).

Computational models have long been used to understand emotional learning and memory and to explain a wide range of behavioral responses (e.g., Grossberg and Schmajuk 1987). Armony et al. (1995) developed an anatomically constrained neural network (connectionist) model of fear conditioning based on single-unit recording data. Focusing on areas of convergence of CS and US pathways, tone inputs with a specific frequency (CS) were associated with a mild foot shock (US). Using simplified computational units, a neural network model of the thalamo-cortico-amygdala circuitry was constructed and trained using a modified Hebbian-type learning rule (Armony et al. 1995). The model was able to reproduce data related to frequency-specific changes of the receptive fields known to exist in the auditory thalamus and amygdala, but extinction and other related phenomena were not simulated. Balkenius and Morén (2001) proposed a neural network model for emotional conditioning. The model focused on the amygdala and the orbitofrontal cortex and their interaction; the amygdala was the locus of acquisition and the orbitofrontal cortex was the site for extinction learning. The model simulated basic phenomena related to emotional conditioning including acquisition, extinction, blocking, and habituation. The main drawback of such connectionist models is that the elementary units for cells are not biophysically realistic and therefore cannot model the underlying neural processes responsible for learning. What is needed is a model that incorporates recent advances in cellular neurophysiology and synaptic plasticity.

The electrophysiological and morphological properties of LA/BL neurons have been characterized in a number of studies (Faber and Sah 2002, 2005; Faber et al. 2001; Lang and Paré 1998; Paré et al. 1995; Washburn and Moises 1992a,b; Womble and Moises 1993). There are several in vitro and in vivo recording studies of LA neurons during fear conditioning and extinction (McKernan and Shinnick-Gallagher 1997; Ono et al. 1995; Paré and Collins 2000; Quirk et al. 1995, 1997; Repa et al. 2001). Our goal is to integrate diverse neurophysiological data into a biophysical computational framework and analyze possible neural plasticity mechanisms from a systems perspective.

Starting with experimentally validated biophysical single-cell models, we developed an LA network consisting of eight pyramidal cells and two GABAergic interneurons. Hebbian-type plasticity was implemented in the AMPA (alpha-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid) and the GABA_A receptor synapses involved in fear learning. We showed that LA can learn both conditioning and extinction. Fear memory is not erased fully by extinction but is inhibited by interneurons that undergo synaptic plasticity during extinction training. We also evaluated the contribution of depotentiation in pyramidal excitatory synapses, and of N-methyl-d-aspartic acid (NMDA) receptors to extinction learning. The model predicts that fear memory is stored in the pyramidal cells, and extinction memory is stored in both interneurons and pyramidal cells.

METHODS

LA pyramidal cell model

Principal neurons in the LA exhibit a range of firing properties in response to prolonged current injection (Faber et al. 2001). Most of these pyramidal cells (∼60%) show full frequency adaptation, firing only a few spikes in response to a sustained depolarization. About 30% of LA pyramidal cells show clear spike frequency adaptation during the first 5–10 action potentials, and ∼10% fire repetitively with little accommodation in response to a depolarizing current step (Faber et al. 2001). This difference in firing patterns is largely due to the amplitude of the afterhyperpolarization (AHP) following spike trains (Faber et al. 2001). To represent the range of firing properties, three different types of pyramidal cells were modeled: type A with full adaptation, type B with medium adaptation, and type C with weak adaptation. All cells had the same ionic currents but differed in maximal conductance densities for some currents responsible for frequency accommodation (Table A1).

TABLE A1.

Maximal conductance densities (in ms/cm²) and Ca²⁺ time constants for the I_sAHP current (in ms)

	INa	IDR	IM	IH	ID	ICa	IC	IsAHP	τCa
Pyramid A
Soma	120	12	0.30	—	—	0.1	—	—	—
Dendrite	40	3	0.30	0.1	1.0	0.2	0.5	0.10	1000
Pyramid B
Soma	120	12	0.20	—	—	0.1	—	—	—
Dendrite	40	3	0.20	0.1	0.4	0.2	0.5	0.15	500
Pyramid C
Soma	120	12	0.25	—	—	0.1	—	—	—
Dendrite	40	3	0.25	0.1	0.1	0.2	0.5	0.50	120
Interneuron
Soma	35	8	—	—	—	—	—	—	—
Dendrite	10	3	—	—	—	—	—	—	—

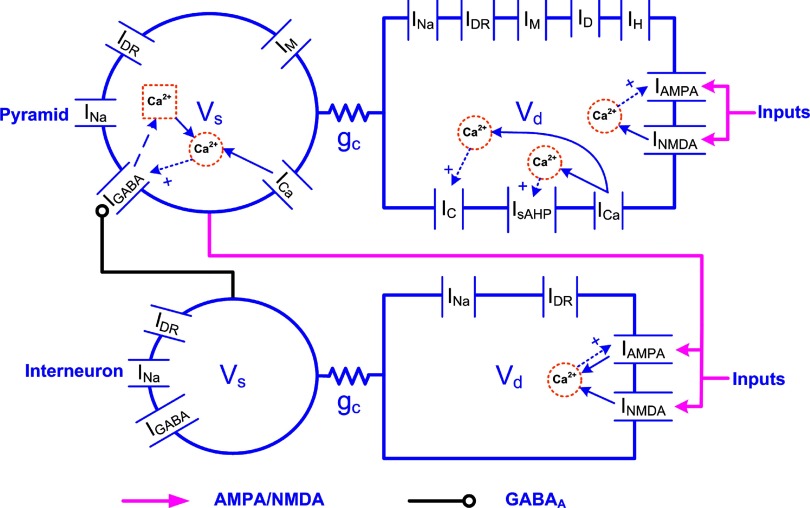
The LA pyramidal cell model had two compartments representing a soma (diameter of 15 μm; length of 15 μm) and a dominant apical dendrite (diameter of 5 μm; length of 400 μm) (Faber et al. 2001; Washburn and Moises 1992b). Both compartments had a leakage current (I_L), a spike-generating sodium current (I_Na), a potassium delayed rectifier (I_DR), and a high-voltage activated Ca²⁺ current (I_Ca). Three calcium-activated potassium currents exist in LA principal neurons: fast BK Ca²⁺- and voltage-dependent C-type current (I_C), apamin-sensitive, small-conductance (SK) current (I_AHP), and a slow apamin-insensitive, voltage-independent afterhyperpolarization current (I_sAHP), contributing to fast, medium, and slow AHP, respectively (Faber and Sah 2002). The current I_AHP is not included in this model because blocking the medium AHP current has no effect on discharge frequency or on spike frequency adaptation (Faber and Sah 2002). The slow AHP current plays a key role in spike frequency adaptation (Sah 1996) and is thought to localize to the proximal apical dendrite (within ≈200 μm of the soma) to interact with the inhibitory postsynaptic potentials (IPSPs) (Sah and Bekkers 1996). In addition, an α-dendrotoxin (α-DTX)-sensitive, slowly inactivating voltage-gated K⁺ current (I_D) mediated by Kv1.2-containing channels also controls spike frequency adaptation in LA pyramidal cells and is selectively expressed in the apical dendrite rather than the soma (Faber and Sah 2004, 2005). I_D differs from I_sAHP in that it determines the initial frequency, whereas the main effect of I_sAHP occurs only after a few action potentials (Faber and Sah 2005). Basolateral amygdala (BLA, which includes LA and BL) neurons also exhibit a pronounced and slow depolarizing sag in response to hyperpolarizing current pulses, and this is mediated by two hyperpolarization-activated currents (I_H and I_IR) (Womble and Moises 1993). Because I_IR has a threshold for activation near −85 mV, it does not contribute to the resting potential of pyramidal cells (Womble and Moises 1993) and thus is not included in the model. The I_H current is included only in the dendrite compartment because its density in the soma is much lower than in the apical dendrite (Magee 1998). Activation of muscarinic cholinergic receptors produces a long-lasting depolarization and enhanced excitability of BLA neurons, demonstrating the existence of a voltage-gated persistent muscarinic current (I_M) (Washburn and Moises 1992a). I_M also contributes to medium AHP (Storm 1989) and to spike frequency adaptation in BLA neurons (Washburn and Moises 1992a). Equations 1 and 2 represent the membrane voltage equation for the two compartments (Fig. 1)

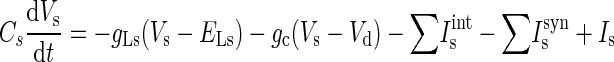(1)

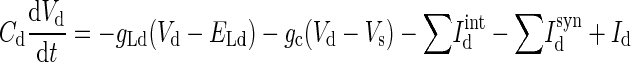(2)

where V_s and V_d are the somatic and dendritic membrane potentials (mV), I_s^int(I_d^int) and I_s^syn(I_d^syn) are the intrinsic currents and the synaptic currents in the soma/dendritic compartments, respectively, I_s (I_d) is the electrode current applied to the soma (dendrite), C is the membrane capacitance (in the model C_d = C_s, and g_Ld = g_Ls), and g_c is the coupling conductance between the soma and the dendrite. The passive properties of the model were adjusted to reproduce the input resistance (R_IN), membrane time constant (τ_m), and resting potential (V_rest) of LA pyramidal neurons recorded in vitro. The values for the specific membrane resistance, membrane capacity and cytoplasmic (axial) resistivity were, respectively, R_m = 30 KΩ-cm², C_m = 1.0 μF/cm², and R_a = 150 Ω-cm. The leakage reversal potential (E_L) was set to −75 mV. The resulting V_rest is about − 69.5 mV (empirically measured mean is − 69.5 mV) (Washburn and Moises 1992b), R_IN ∼150 MΩ (matching the empirically measured mean of ∼150 MΩ) (Faber et al. 2001), and τ_m = R_mC_m = 30 ms (∼29 ms empirically) (Faber et al. 2001).

FIG. 1.

Two-compartment pyramidal cell and interneuron models with ionic and synaptic currents. For the pyramidal cell, 2 different Ca²⁺ pools mediated by voltage-dependent calcium channels (VDCCs) regulated I_C and I_sAHP currents in the dendrite. The plasticity at AMPA receptors was a function of N-methyl-d-aspartate (NMDA) Ca²⁺, and plasticity at GABA_A synapses was a function of Ca²⁺ from 2 sources described in the text. For the interneuron, the Ca²⁺ underlying learning at the AMPA synapse came from both AMPA and NMDA receptors.

CURRENT KINETICS.

Pyramidal neurons in the BLA are remarkably similar in morphological and electrophysiological characteristics to pyramidal neurons in the hippocampus and cerebral cortex (Washburn and Moises 1992a,b). Thus most of the conductance kinetics in our model were adapted from computational studies on CA1 hippocampal neurons by Warman et al. (1994) and from prefrontal cortex (PFC) models by Durstewitz et al. (2000): I_Na, I_DR, I_Ca, and I_C kinetics were adapted from Durstewitz et al. (2000) and those for I_M and I_sAHP from Warman et al. (1994). The mathematical description of I_H was based on a study of the current in the rat BLA neurons (Womble and Moises 1993), and the current I_D was taken from Locke and Nerbonne (1997), who studied this current in rat visual cortical cells with the activation kinetics adjusted to fit LA pyramidal cells (Faber and Sah 2004). The ionic current for channel i, I_i was modeled as I_i = g_im^ph^q, where g_i was its maximal conductance, m its activation variable (with exponent p), h its inactivation variable (with exponent q), and E_i its reversal potential. The kinetic equation for each of the gating variables x (m or h) takes the form

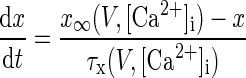(3)

where x_∞ is the voltage- and/or Ca²⁺-dependent steady state and τ_x is the voltage- and/or Ca²⁺-dependent time constant. The maximal conductances for all ionic currents and the expressions of x_∞ and τ_x for each gating variable are listed in Tables A1 and A2. The reversal potentials were: E_Na = 45 mV, E_K = −80 mV, E_Ca = 120 mV, and E_H = −43 mV (Huguenard and McCormick 1992).

TABLE A2.

Gating variables for ion channels used in the network model

Current Type	Gating Variable	α	β	x∞	τx, ms
A. LA pyramidal cell model
INa	p = 3		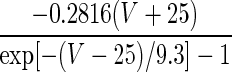	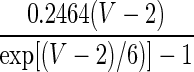α/(α + β)	1/(α + β)
	q = 1	0.098 × exp[− (V + 40.1)/20]		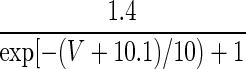α/(α + β)	1/(α − β)
IDR	p = 4		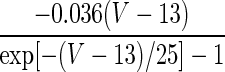	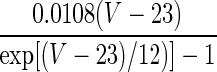α/(α + β)	1/(α + β)
IM	p = 2		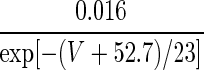	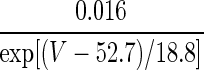α/(α + β)	1/(α + β)
IH	p = 1	—	—		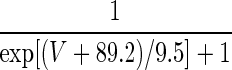1727 × exp(0.019V)
ID	p = 1	—	—		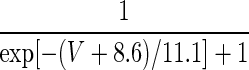1.5
	q = 1	—	—		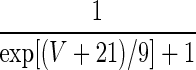569
ICa	p = 2	—	—		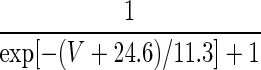1.25 × sec h[− 0.031(V + 37.1)]
	q = 1	—	—		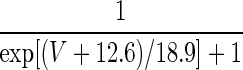420.0
IC	p = 2	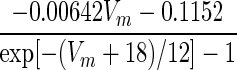withVm=V+40log10([Ca]i1)	1.7×exp[−(Vm+152)/30]	α/(α + β)	max(1/(α + β), 1.1)
IsAHP	p = 1		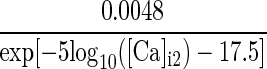	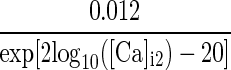α/(α + β)	48
B. LA interneuron model
INa	p = 3	2.1 × exp[(V + 18.5)/11.57]	2.1 × exp[− (V + 18.5)/27]	α/(α + β)	1/(α − β)
	q = 1	0.045 × exp[− (V + 29)/33]	0.045 × exp[(V + 29)/12.2]	α/(α + β)	1/(α + β)
IDR	p = 4	0.15 × exp[(V + 19)/10.67]	0.15 × exp[− (V − 19)/42.68]	α/(α + β)	1/(α + β)

LA, lateral amygdala.

CALCIUM DYNAMICS.

Different Ca²⁺ ionic pools (Warman et al. 1994) were modeled for ionic and synaptic currents (Fig. 1). For instance, there were two in the dendrite of the pyramidal cell for ionic currents, one mediating the activation of I_c ([Ca²⁺]₁) and the other mediating the activation of I_sAHP ([Ca²⁺]₂). This is because I_c must deactivate rapidly following an action potential to generate the fast AHP, whereas I_sAHP should activate gradually after each spike for the slow AHP. The intracellular calcium for each pool is regulated by a simple first-order differential equation (Warman et al. 1994) of the form

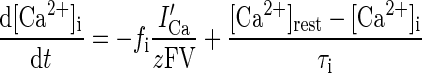(4)

where i = 1 or 2, representing the first or second calcium pool, f_i is the fraction of the Ca²⁺ influx via calcium current I_Ca(f₁ = 0.7, f₂ = 0.024, I_Cafor ionic currents), z = 2 is the valence of the Ca²⁺ ion, F is the Faraday constant; volume V = wA with w as the shell thickness (1 μm) and A the dendritic surface area, and τ_i represents the Ca²⁺ removal rate of the ith pool. The amplitude of the slow AHPs in cells showing full spike frequency adaptation is much larger than in cells that discharge tonically (Faber and Sah 2001). Also there is evidence that Ca²⁺ ions, as opposed to channel kinetics, determine the time course of AHP currents (Mainen and Sejnowski 1998). Accordingly, τ₁ = 1 ms for all three types of pyramidal cells, whereas τ₂ = 1000 ms for type A cell, 500 ms for type B cell, and 120 ms for type C cell. The resting Ca²⁺ concentration was [Ca²⁺]_rest = 50 nmol/l, which was the same as the initial concentration (Durstewitz et al. 2000). The Ca²⁺ pools for synaptic currents were involved in learning and are described later.

LA GABAergic interneuron model

A quarter of the LA neurons are inhibitory interneurons (McDonald and Augustine 1993). Recent data indicate that four subtypes of parvalbumin-positive interneurons exist in the BLA: fast spiking (FS), delayed firing (DF), accommodating (AC), and stuttering (ST) (Rainnie et al. 2006; Woodruff and Sah 2007). Our network used only the FS cell type because it is the most common cell type and the vast majority of synaptic connections between principal neurons and parvalbumin-positive interneurons are formed by the FS and DF interneuron subpopulations (Woodruff and Sah 2007). Compared with pyramidal cells, the FS interneurons have faster action potentials with a half-width of 0.76 ± 0.04 ms (1.2 ± 0.1 ms for pyramidal cells) and do not show appreciable frequency adaptation (Lang and Paré 1998; Mahanty and Sah 1998; Rainnie et al. 2006; Woodruff and Sah 2007). The resting potential is about −69.4 mV, and the steady-state firing frequency at 0.4-nA current injection is ∼80 Hz (Szinyei et at. 2003). The interneuron model also consistsed of two compartments, a soma (diameter of 15 μm; length of 15 μm) and a dendrite (diameter of 10 μm; length of 150 μm). Each compartment contained a fast Na⁺ (I_Na) and a delayed rectifier K⁺ (I_DR) currents with kinetics that reproduced the much shorter spike duration (Durstewitz et al. 2000). The passive membrane properties were as follows: R_m = 20 KΩ- cm², C_m = 1.0 μF/cm², R_a = 150 Ω-cm, and E_L = −70 mV.

Network structure and synaptic interactions

The afferent projections from the auditory thalamus and cortex to the amygdala form excitatory synapses on both principal neurons and inhibitory interneurons (Mahanty and Sah 1998; Weisskopf and LeDoux 1999). Glutamatergic synaptic transmission to pyramidal cells and interneurons is mediated by both AMPA and NMDA receptors (Szinyei et al. 2003; Weisskopf and LeDoux 1999). Excitatory AMPA- or NMDA-synaptic conductance is involved in both the pyramidal-to-pyramidal and pyramidal-to-interneuron connections (Smith et al. 2000; Szinyei et al. 2000). GABAergic interneurons send inhibitory GABA_A recurrent collaterals onto pyramidal cells and tightly control their activity (Lang and Paré 1997; Li et al. 1996). Although there are far fewer interneurons than pyramidal cells, one interneuron can inhibit many pyramidal cells through divergent projections (Mahanty and Sah 1998). The processing and transmission of excitatory inputs to the principal cells along neural pathways in the amygdala are determined by both feedback and -forward GABAergic inhibition (Wang et al. 2001).

Using the experimental information cited in the preceding text, we developed an LA network model consisting of eight pyramidal cells and two GABAergic interneurons (see Fig. 2A) with all-to-all connectivity (Durstewitz et al. 2000; Wang 1999). Among the eight pyramidal cells, five were type A (P1–P5), two were type B (P6–P7), and one was type C (P8). In the network model, we were particularly interested in information processing in the sensory-receptive region—the dorsal part of LA (LAd). Three of the pyramidal cells (P5, P7, and P8) and both the interneurons received direct tone/shock inputs; P3 received only tone input, and P1 and P4 received only shock input; and P2 and P6 received no direct afferent inputs. In this fully connected architecture, each pyramidal neuron received excitatory inputs from all other pyramidal cells (excluding itself) as well as inhibitory inputs from both the interneurons. Both interneurons received excitatory inputs from all pyramidal cells and thus provided both feedforward and -back inhibition to pyramidal cells. Also the two interneurons inhibited each other (Woodruff and Sah 2007). The synaptic delays for tone and shock inputs were set to 8 ms to represent the transmission delay between the start of tone and the arrival of information in the LA (Li et al. 1996). The synaptic delays for all intrinsic transmission were set to 2 ms.

FIG. 2.

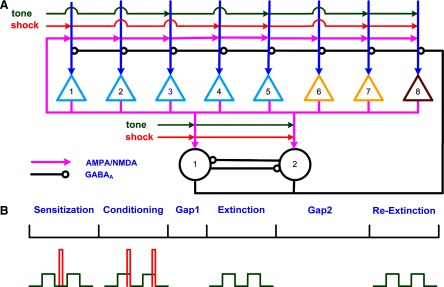
Architecture of the lateral amygdala (LA) network and conditioning protocol. A: triangles represent pyramidal cells and circles representing interneurons. Among the 8 pyramidal cells, 5 were type A (P1–P5), 2 type B (P6–P7), and 1 type C (P8). Each pyramidal cell excited all the other cells including interneurons. Each interneuron inhibited all the pyramidal cells and the other interneuron. Three pyramidal cells (P5, P7, and P8) and 2 interneurons received direct tone/shock inputs; P3 received tone input only; P1 and P4 received shock input only; and P2 and P6 did not receive direct tone/shock inputs. B: simulation schedule showing tone (green) and shock (red) inputs during sensitization, conditioning and the 2 extinction phases. There was a short gap between conditioning and extinction and a longer gap before re-extinction.

The AMPA/NMDA receptors were placed in the dendrite compartment, whereas the GABA_A receptors were located in the somata of both the pyramidal cell and interneuron models (Fig. 1). The synaptic conductance induced by the arrival of presynaptic spikes was summed at each synapse with saturation. On glutamate binding, both AMPA and NMDA receptors become permeable to a mixture of ions including Na⁺, K⁺, and Ca²⁺, and binding of GABA to GABA_A receptors leads to the opening of channels selective to chloride ions (Koch 1999). The summed response of these ionic channels to transmitter binding can be treated as a time-varying change in the membrane conductance in series with the synaptic reversal potential (Koch 1999). Accordingly, the AMPA, NMDA, and GABA_A synaptic transmission currents were all modeled by dual exponential functions as listed in Eqs. 5–7 (Durstewitz et al. 2000)

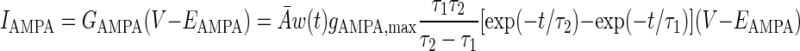(5)

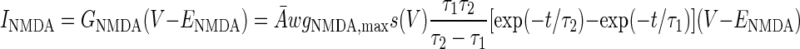(6)

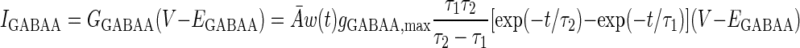(7)

where w(t) is the adjustable synaptic weight for AMPA and GABA_A synapses (w was held fixed for the NMDA synapses); Ā is a normalization constant chosen so that g_{AMPA, max}, g_{NMDA, max}, and g_{GABAA, max} assume their maximum values; and τ₁ and τ₂ are the rise and decay time constants, respectively. Spontaneous excitatory postsynaptic currents (sEPSCs) were always significantly faster in interneurons than in pyramidal cells (Mahanty and Sah 1998). So for AMPA receptor channels, τ₁ = 0.5 ms and τ₂ = 7 ms for pyramidal cells, and τ₁ = 0.3 ms and τ₂ = 2.4 ms for interneurons (Mahanty and Sah 1998). For NMDA receptor channels, τ₁ = 5 ms, τ₂ = 125.0 ms for both pyramidal cells and interneurons (Weisskopf and LeDoux 1999). The voltage-dependent variable s, which implements the Mg²⁺ block was defined as: s(V) = [1 + 0.33 exp(−0.06 V)]^-1 (Zador et al. 1990). The maximal conductances were chosen as g_{AMPA, max} = 1 nS and g_{NMDA, max} = 0.5 nS, so that the relative contributions of AMPA and NMDA components to EPSCs matched data reported by Weisskopf and LeDoux (1999) (total charge transfer is 1:4.6 at V_m = −75 and +45 mV, respectively). The synaptic reversal potentials were set as E_AMPA = E_NMDA = 0 mV (Durstewitz et al. 2000). For the GABA_A synaptic current, τ₁ = 0.25 ms, τ₂ = 3.75 ms, and g_{GABAA, max} = 0.6 nS (Wolf et al. 2005), E_GABAA = −75 mV for the pyramidal cells and E_GABAA = −60 mV for the interneurons (Martina et al. 2001).

Background inputs and specific afferent inputs

LA projection neurons show low rates of spontaneous activity in control conditions (Gaudreau and Paré 1996; Paré and Collins 2000). To achieve the low average spontaneous firing rate of ∼1 Hz in the experiments modeled (Quirk et al. 1995), independent, Poisson-distributed, random excitatory background inputs were delivered to all the pyramidal cells. These inputs represent unmodeled synaptic connections from other brain areas such as prefrontal cortex and hippocampus. Similar background inputs were provided to the interneurons to generate reported spontaneous firing rates of ∼8 Hz (Paré and Gaudreau 1996).

In fear conditioning, specific afferent excitatory (AMPA and NMDA) synapses encoding the CS (tone) and US (shock) information are delivered to LA from the auditory cortex and auditory thalamus (Bordi and LeDoux 1994; Quirk et al. 1997). The specific tone and shock inputs were represented by two separate regular spike trains delivered to the AMPA/NMDA channels in the cells. The firing frequency for the tone and shock inputs was set at 200 Hz to model the summed activity of multiple inputs in vivo. The tone inputs also included noise represented by random Poisson spikes with an average frequency of 2 Hz. Given that the tone starts out as neutral and the shock as noxious, the conductance strength encoding the shock information was set much higher than that representing the tone inputs (see Table A3).

TABLE A3.

Model parameters for network connections and inputs

Connection	Initial Weight	fmax (fmin = 0.8 for all)	Learning Factor		Ca2+ Threshold, μmol
			Scaling	Decay	Low	High
Tone to Pyr	10.0	3	15.0	0.01	0.55	0.7
Pyr to Pyr	1.5	3	2.5	0.01	0.50	0.6
Inter to Pyr	5.0	4	2.0	0.02	0.55	0.7
Tone to Inter	3.0	3	1.0	0.02	0.55	0.7
Pyr to Inter	1.0	3	2.0	0.01	0.50	0.6

The shock synapse (weight = 40 for pyramidal cell and 20 for interneuron) and the interneuron-to-interneuron synapse (weight = 3) do not potentiate. Pyr, pyramidal cell; inter, interneuron.

Hebbian learning in LA

Learning of conditioned fear is accompanied by changes in synaptic strengths in the neural circuitry of LA. Long-term potentiation (LTP) has been demonstrated in slice preparations for both cortico-amygdalar (Huang and Kandel 1998; Humeau et al. 2003, 2005; Tsvetkov et al. 2002) and thalamo-amygdalar pathways (Huang et al. 2000; Humeau et al. 2005; Tsvekov et al. 2004). Induction of LTP in both pathways depends on postsynaptic processes because postsynaptic depolarization is needed to trigger influx of Ca²⁺ ions via NMDA receptors (Bauer et al. 2002; Tsvekov et al. 2002) or voltage-dependent L-type Ca²⁺ channels (Bauer et al. 2002; Humeau et al. 2005; Weisskopf et al. 1999). In vivo, LTP can be induced in both thalamic and cortical inputs when tone and foot shock are paired (Rogan and LeDoux 1995) but not when they are unpaired (Rogan et al. 1997). Excitatory glutamatergic synapses from the thalamus or cortex onto interneurons exhibit NMDA-receptor-dependent potentiation (Bauer and LeDoux 2004). This potentiation is also AMPA-receptor-dependent because AMPA receptors on inhibitory neurons lack the GluR2 subunit, making them calcium-permeable (Mahanty and Sah 1998). It was further shown that inhibitory inputs onto pyramidal cells are modifiable via a Ca²⁺-dependent mechanism (Bauer and LeDoux 2004; Mahanty and Sah 1998). In addition to LTP, long-term depression (LTD) can be readily induced in excitatory amygdala synapses by low-frequency stimulation of the lateral nucleus at 1 Hz for 15 min (Wang and Gean 1999).

Following the experimentally determined locations for plasticity described in the preceding text, all the excitatory AMPA synapses in the model were set to be adjustable except for those delivering shock or background inputs. Similarly the inhibitory synapses from interneurons onto pyramidal cells were modifiable, but the strength of the NMDA synapses was held fixed. We used a biophysical Hebbian rule termed “calcium control hypothesis” (Gerstner and Kistler 2002; Shouval et al. 2002a,b) to implement learning by adjusting the synaptic weight w_j in Eqs. 5 and 7 as

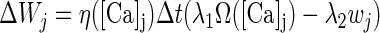(8)

where η is the Ca²⁺-dependent learning rate and Ω is a Ca²⁺-dependent function with two thresholds (θ_d and θ_p; θ_d ≤ θ_p) (see Fig. A1 ); λ₁ and λ₂ represent scaling and decay factors, respectively; the local calcium level at synapse j is denoted by [Ca]_j and Δt is the simulation time step. With this learning rule, the synaptic weight decreases when θ_d < [Ca]_j < θ_p, and increases (with modulation by the decay term λ₂w_j) when [Ca]_j > θ_p. One of the key assumptions of this learning rule is that the dominant source of calcium influx in the postsynaptic cell is through NMDA receptors. This calcium influx was calculated as I_Ca^N = P₀w⁻¹G_NMDA(V − E_Ca) (Shouval et al. 2002a) where G_NMDA is the NMDA conductance in Eq. 6 (the term w^-1 ensures that it is calculated per synapse). P₀ was selected to be 0.015 so that the fraction of the NMDA current carried by Ca²⁺ ions averaged to 7% at negative potentials (Koch 1999).

FIG. A1.

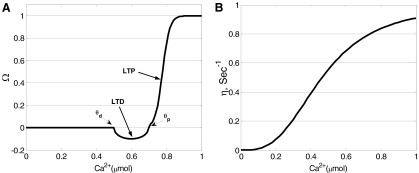
Functions used in the calcium control hypothesis of Eq. 8. A: Ω function. B: learning rate η; adapted from Shouval et al. (2002a).

As mentioned earlier, the calcium influx (used for learning) at the glutamatergic synapses on interneurons occurs through both NMDA and AMPA receptors. The calcium influx through AMPA receptors was calculated as I_Ca^A = P₀w⁻¹(0)G_AMPA(V − E_Ca) with P₀ = 0.001. G_AMPA is the AMPA conductance in Eq. 5, and w(0) is the initial AMPA synaptic weight. The Ca²⁺ current through the AMPA/NMDA receptors was separated from the total AMPA/NMDA current in this manner and used for implementation of the learning rule (Kitajima and Hara 1997; Shouval et al. 2002a).

Potentiation of the GABA synapse between the interneuron and pyramidal cell was demonstrated by directly stimulating inhibitory neurons within the LA in the presence of 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX) and (2R)-amino-5-phosphonopentanoic acid (APV), which block glutamatergic transmission (Bauer and LeDoux 2004). This potentiation was Ca²⁺-dependent and expressed postsynaptically, but the exact underlying mechanism is presently unknown (Bauer and LeDoux 2004; Sigurdsson et al. 2007). Several different mechanisms have been reported for potentiation at GABAergic synapses in other brain regions (Gaiarsa et al. 2002). In all of the mechanisms, a postsynaptic rise in intracellular Ca²⁺ concentration is required to trigger long-term plasticity. In the neonatal rat hippocampus, potentiation could be induced by Ca²⁺ influx through the voltage-dependent Ca²⁺ channels (VDCCs), whereas in the cortex and cerebellum, this process requires Ca²⁺ release from postsynaptic internal stores on GABA receptor activation (Gaiarsa et al. 2002). Thus both presynaptic activity (GABA receptor activation or interneuron firing) and postsynaptic activity (activation of VDCCs by membrane depolarization) contribute to the potentiation of GABA synapses. The process from GABA receptor stimulation to internal Ca²⁺ release involves activating a cascade of complex intracellular reactions (Komatsu 1996). Such a complex process can be simplified by assuming that the Ca²⁺ release is proportional to the stimulation frequency or GABA_A conductance. Hence we modeled this simplified process by considering Ca²⁺ release from the internal stores into a separate Ca²⁺ pool (Fig. 1), using an equation similar to that for the AMPA/NMDA case: I_Ca^G = P₀w⁻¹(t)G_GABAA(V − E_Ca) with P₀ = 0.01, and G_GABAA as the GABA_A conductance in Eq. 7. Note that I_Ca^G models the dependence of Ca²⁺ release on GABA_A stimulation frequency but not Ca²⁺ influx through the GABA_A channel. Postsynaptic activity contributed Ca²⁺ to the same pool from VDCCs (I_Ca) in the soma compartment (Fig. 1).

The concentration of the calcium pool at synapse j followed the same dynamics as in Eq. 4 with f_i = 0.024 (Warman et al. 1994), τ_i = 50 ms (Shouval et al. 2002b), V is the volume of a local Ca²⁺ pool with a diameter of 2 μm (similar to a spine; Kitajima and Hara 1997); I_Ca′ = I_Ca^N + I_Ca^A for the excitatory synapses on interneurons; I_Ca′ = I_Ca^G + kI_Ca (k = 0.01) for the inhibitory GABA_A synapses onto pyramidal cells, and I_Ca′ = I_Ca^N for all other modifiable synapses (see Fig. 1).

All the synaptic weights were constrained by upper (W_max) and lower (W_min) limits (Hasselmo and Barkai 1995). Maximum (f_max) and minimum (f_min) folds were specified for each modified synapse so that W_max = f_max × w(0) and W_min = f_min × w(0). For each adjustable synapse, the following parameters were selected iteratively (Table A3) to match the neuronal behaviors recorded in vivo for LA cells (Quirk et al. 1995): scaling factor, decay factor, two thresholds and the initial weight. It was found that the qualitative results reported were similar even with different initial weights.

Simulation design

The schedule of tone and shock inputs in the simulation was based on in vivo studies (Quirk et al. 1995, 1997). We scaled down the timing of the auditory fear conditioning protocol by approximately two orders of magnitude so that it would be suitable for computational study. The simulation included a sensitization phase, conditioning phase, and two extinction phases (Fig. 2B). Each tone lasted 500 ms and each shock lasted 100 ms, and the interval between two tones was 3.5 s. During the sensitization phase, 10 unpaired tones and shocks were presented to the network with the shocks occurring randomly between the tones. Following sensitization, 10 paired tones and shocks were provided in the conditioning phase with shock present during the last 100 ms of the tone. In extinction, 30 tones were delivered to the neurons without any shock (pure tones). The gap between conditioning and extinction phases was 40 s and the model was tested for spontaneous recovery after a delay of 840 s. The second extinction phase also used 30 pure tones. The entire schedule lasted 1,200 s. Simulations were performed on a personal computer using the software package GENESIS (Bower and Beeman 2003) with the Crank-Nicholson integration method, and a time step of 10 μs.

RESULTS

Firing properties of single neurons

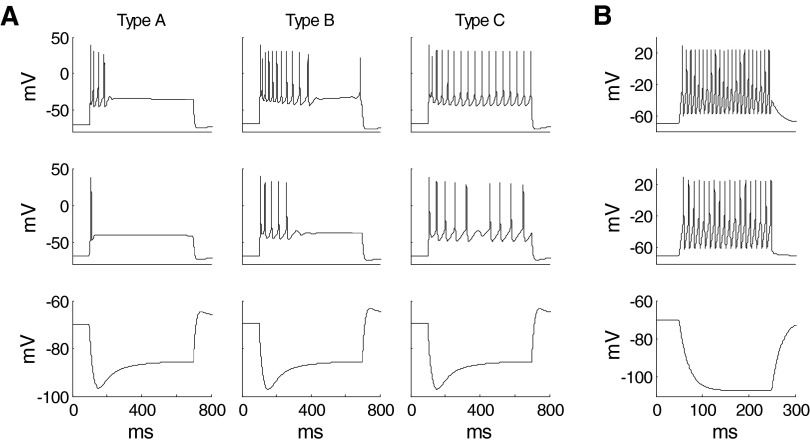
Waveforms and firing properties of model neurons closely matched data obtained from in vitro studies (Faber and Sah 2002; Faber et al. 2001). Voltage responses of three types of pyramidal cell (A–C) models in response to three different levels of current injections are shown in Fig. 3A. With a 600-ms, 400-pA depolarizing current step, cell A fired only 4 spikes, cell B showed clear frequency adaptation during the first 11 spikes, and cell C fired repetitively. A slow depolarizing sag was observed in response to a hyperpolarizing current injection (Fig. 3A, bottom), a phenomenon termed “anomalous rectification” due to the activation of the I_H current (Womble and Moises 1993). The interneuron model showed no frequency adaptation and fired at relatively high frequency in response to depolarizing current steps (Fig. 3B), consistent with experimental observations in vitro (Mahanty and Sah 1998; Martina et al. 2001; Washburn and Moises 1992b) and in vivo (Lang and Paré 1998).

FIG. 3.

Responses of units to intracellular current pulses. A: voltage responses of the 3 types of LA pyramidal cell models (A–C) to 3 600-ms current injections starting from 100 ms (top row: 400 pA; middle row: 300 pA; bottom row: −100 pA). Compare with Fig. 2 of Faber et al. (2001) (reproduced as Supplementary Fig. S1¹). B: voltage responses of the interneuron model to 200-ms current injections of the same magnitude (top row: 400 pA; middle row: 300 pA; bottom row: −100 pA).

Fear learning and extinction

FIRING RATE OF LA UNITS.

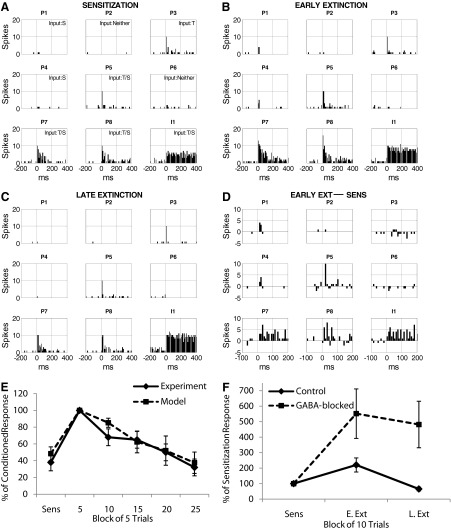
Quirk et al. (1995) described the tone responses of simultaneously recorded LA pyramidal neurons at different points during the training process. The main finding in that study was that conditioning significantly increased the number of tone-elicited spikes with the greatest effects at the shortest latency following tone onset. These conditioned responses were reversed by extinction training. The peri-event time histograms (PETHs) of all pyramidal cells and one interneuron (I1) in the LA network during sensitization are shown in Fig. 4A. All pyramidal neurons showed clear frequency adaptation with the tone responses concentrated in the first 100 ms, indicating a good match with the experimental recordings (Quirk et al. 1995). Also the tone response latency for pyramidal cells was in the 10- to 20-ms range, consistent with experimental data (Quirk et al. 1997). The magnitude of the tone responses varied across units, depending on the cell type and whether or not the unit received a direct tone input. For example, the type A neuron P1 showed little tone responsiveness because it received no direct tone input. Although both P5 and P7 received direct tone inputs, P7 was more responsive than P5 since P7 is a type B cell, while P5 is type A. The interneuron (I1) fired continuously in response to tone input with an average firing frequency of ∼50 Hz.

FIG. 4.

The effects of training on the tone responses of individual neurons. Tone responses of pyramidal cells (P1–P8) and 1 interneuron (I1) during sensitization (A), early extinction (B), and late extinction phases (C). D: differences in tone responses between early extinction and sensitization. Tone started at t = 0; bin width was 10 ms and spike counts during 10 trials were summed together. In the top right of each box in the sensitization phase, “T” indicates direct tone input and “S” indicates direct shock input. Compare with Fig. 2 of Quirk et al. (1995) (reproduced as Supplementary Fig. S2). E: comparison of the experimental data (Fig. 4, Quirk et al. 1997) and the model tone responses for the last block of 5 trials in sensitization and successive 5-trial blocks during extinction. The total spikes (0–50 ms) in each block of 5 trials were normalized to the responses in the 1st block of extinction for each cell and the mean ratio (with SE) among 4 significant conditioned pyramidal cells calculated. F: comparison of the tone responses in conditioned pyramidal neurons (n = 5) for the control and GABA-block cases. The tone responses (total spikes in 0–200 ms) for each cell in each phase were normalized to the responses during sensitization and the mean ratio (with SE) among all cells calculated. Same for Figs. 6E and Fig. 7E.

The PETHs of LA cells during early extinction (tones 1–10) and late extinction (tones 20–30) are shown in Fig. 4, B and C. Conditioning significantly increased the magnitude of tone responses of all the cells receiving direct shock input (Fig. 4D). The effects of conditioning were most pronounced at the shortest response latencies. The latency of the earliest significant plasticity (the 1st bin showing an increase of ≥2 spikes with conditioning) was 10–20 ms for P1, P4, P7, and P8, and 20–30 ms for P5. Extinction training brought the tone responses of the conditioned pyramidal cells back to preconditioning levels or even lower (Fig. 4C). All these results were consistent with experimental findings for LA pyramidal cells (Quirk et al. 1995). Although conditioning also enhanced the interneuron tone responses, extinction further increased its responding (Fig. 4C). Figure 4E shows a very good match between experimental (Fig. 4) (Quirk et al. 1997) and model conditioned tone responses for the last block of five trials in sensitization and successive five-trial blocks during extinction.

To test the importance of GABAergic inhibition on extinction, we blocked GABA transmission by setting g_{GABAA, max} = 0 immediately before extinction training. Figure 4F shows the average change in pyramidal tone responses across the experiment, relative to the sensitization phase, for both control and GABA-blocked cases. In the control case, the average tone response increased by 120% after conditioning and returned to sensitization levels in late extinction. However, when GABA receptors were blocked, tone responses were greatly augmented and could not be extinguished. Thus similar to experimental reports (Chhatwal et al. 2005; Harris and Westbrook 1998), GABA transmission in LA is essential for extinction learning.

SYNAPTIC WEIGHTS.

An examination of synaptic weights provides insights into the functioning of the model. Figure 5A shows the time courses of synaptic weights for the tone-to-pyramidal (tone-pyr) and tone-to-interneuron (tone-inter) synapses. All tone synaptic weights decreased slightly during the sensitization phase when tone and foot shock were unpaired and increased during conditioning (except P3). The synapses showing greater potentiation (e.g., tone-P8) underwent greater depression in extinction. This is because the synapse with greater potentiation has a relatively high level of Ca²⁺ for faster and larger plasticity. In contrast to the tone-pyr weights, the tone-inter weights continued to increase as extinction proceeded. Three factors account for this extinction-induced increase: first, interneurons have no frequency adaptation and so continued to fire at high rates during extinction, allowing more Ca²⁺ influx via removal of the Mg⁺ block from NMDA receptors; second, the AMPA receptors on interneurons are Ca²⁺-permeable (Mahanty and Sah 1998); third, the shock inputs to interneurons have been effectively replaced in extinction by the excitatory drive from pyramidal cells which were potentiated during conditioning. Representative pyramidal-to-pyramidal (pyr-pyr) coupling strengths are shown in Fig. 5B. The strength between two pyramidal cells depended on whether one or both cells received direct shock input. If the postsynaptic neuron did not receive direct shock input, the connection remained unchanged throughout training (e.g., P5–P6). If the postsynaptic neuron received direct shock input and the presynaptic neuron received direct tone input (no shock), then the connection strength potentiated more during conditioning than sensitization (e.g., P3–P4). If both pre- and postsynaptic neurons received direct shock input, the connection potentiated during both sensitization and conditioning phases to a larger degree than when only the postsynaptic neuron received direct shock input, (e.g., P1–P4 vs. P3–P4). Similar to the tone-pyr synapses, the pyr-pyr synapse that showed greater potentiation also showed deeper depotentiation during the extinction phase (e.g., P7–P8).

FIG. 5.

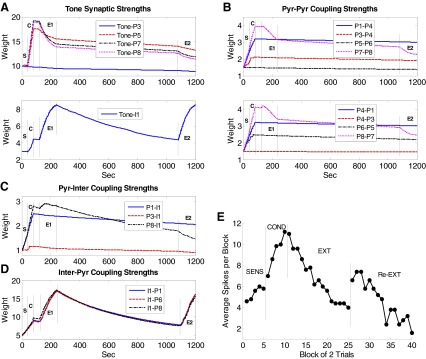
Time courses of representative synaptic strengths in the LA network during acquisition and extinction of fear. A: tone synapses; B: pyr-pyr synapses; C: pyr-inter synapses; and D: inter-pyr synapses. S, sensitization; C, conditioning; E1, 1st extinction; E2, 2nd extinction. E: spontaneous recovery of fear and re-extinction. Average tone responses (spikes in 0–200 ms) by block of 2 trials of conditioned pyramidal cells (n = 5) for the entire schedule.

As with tone synapses onto interneurons, potentiation of pyramidal-to-interneuron (pyr-inter) synapses depends on both AMPA and NMDA receptors. Figure 5C shows the time courses of synaptic strengths for the P1-I1, P3-I1, and P8-I1 synapses. The potentiation of the P1-I1 and P8-I1 synapses was much larger than that of the P3-I1 synapse during sensitization and conditioning phases because P3 received no direct shock input. During extinction, the P8-I1 synapse potentiated to the maximum level and then decreased slightly, while the P1-I1 strength showed a slow but consistent decay because P8 had a higher firing rate compared with P1. Time courses of the inhibitory synaptic strengths from I1 to each of P1, P6, and P8 are shown in Fig. 5D. These interneuron-to-pyramidal (inter-pyr) connections are important in that they control both feedforward and -back inhibition on the pyramidal cells. All the inter-pyr synaptic strengths had very similar time courses: they potentiated in sensitization, conditioning, and extinction phases and showed appreciable decay during the two gaps. Plasticity at this GABAergic synapse depends on the interneuron firing rate. As cited in methods (Hebbian learning in LA), GABA receptor stimulation is hypothesized to trigger internal Ca²⁺ release proportionally to the GABA_A conductance. Furthermore, this has been modeled using an equation similar to that for the AMPA/NMDA receptors with the Ca²⁺ release from internal stores replacing Ca²⁺ through the receptor model. The postsynaptic Ca²⁺ also comes from VDCCs. After conditioning, the interneuron firing increased significantly (Fig. 4B), enabling the inhibitory synapse to continue to strengthen in extinction. This plasticity also depends on Ca²⁺ influx through voltage-gated calcium channels (on pyramidal cells), explaining why the synapse with more postsynaptic activity (e.g., I1-P8) showed stronger strengthening. Even though P3 and P6 did not show conditioned responses, they received increasing inhibition from the interneurons. Thus our model predicts that a neuron can show the effects of extinction even if it does not exhibit a conditioned response.

To summarize, this model provides insights into the mechanisms of fear acquisition and extinction. The large increase in tone synaptic strengths of pyramidal cells, together with the potentiation of pyr-pyr synapses, resulted in elevated tone responses in early extinction. Although the inhibition from interneurons also increased with conditioning, it was overcome by potentiated excitation at this stage. During extinction, the excitatory inputs to pyramidal cells (tone-pyr and pyr-pyr inputs) underwent differing degrees of depression with the more active synapses losing a greater percentage of the strength gained in conditioning. At the same time, excitatory inputs to interneurons (tone-inter and some pyr-inter synapses) continued to strengthen in extinction, leading to stronger potentiation of the inhibitory GABA synapses onto pyramidal cells. The model showed that this increase in inhibition, combined with LTD at the excitatory pyramidal synapses, ultimately caused tone responses of pyramidal cells to decrease to preconditioning levels. This predicts that LTD at excitatory synapses serves to accelerate and/or strengthen extinction.

Persistence of fear memory and spontaneous recovery

Although extinction training reversed some of the conditioning-induced increases in tone-pyr and pyr-pyr synapses, the strengths of these synapses were still well above preconditioning levels at the end of extinction, indicating a persistence of fear memory. Following extinction, we inserted a long gap (840 s) followed by re-extinction, to model spontaneous recovery of fear. During the gap, tone inputs were never activated, however, activity fluctuated randomly with the noise present. Accordingly, the strengths of tone-inter and some pyr-inter synapses (e.g., P8-I1) decayed considerably (Fig. 5, A and C) during the gap due to Hebbian weakening, whereas little decay was seen in the tone-pyr and pyr-pyr synapses (A and B). This was due to the fact that, with only background inputs, pyramidal cells fire at much lower frequencies compared with the interneurons, limiting Ca²⁺ influx and resulting plasticity. Ca²⁺ entry into pyramidal cells was also limited by the fact that AMPA receptors on pyramidal cells are not Ca²⁺ permeable, whereas, as cited earlier, those in interneurons are (Bauer and LeDoux 2004; Mahanty and Sah 1998). Thus the model predicts that the low spontaneous firing rate of pyramidal cells acts to preserve the original fear memory.

The strength of inter-pyr synapses also decreased considerably during the long gap due to relative high spontaneous firing rates of interneurons (Fig. 5D), causing extinguished tone responses in pyramidal neurons to recover spontaneously (Fig. 5E). During subsequent re-extinction, excitatory synapses onto pyramidal cells were again depressed (Fig. 5, A and B), and the tone synapses onto interneurons exhibited potentiation (A). As in initial extinction, the inhibitory synapses onto pyramidal cells potentiated (Fig. 5D), permitting re-extinction (E). Figure 5E shows the modulation of tone responses by trials in conditioned pyramidal cells (n = 5) during the entire training course. The recovered response of the units was higher than that in sensitization or late extinction but was lower than that in early extinction consistent with some loss of conditioning memory during both the first extinction and the gap. Following re-extinction, the response was the lowest among all phases.

Some other observations with respect to the long gap can be made. First, the decay in the excitatory synapses onto pyramidal cells in re-extinction was smaller than that during the first extinction (compare phases E2 and E1 in Fig. 5, A and B) due to a decrease in the pyramidal cell firing rate in re-extinction. Second, during re-extinction, some pyr-inter coupling strengths (see black line in Fig. 5C) were depressed. Thus the inhibition on pyramidal cells could be relieved briefly at the beginning of re-extinction, before the tone-inter and inter-pyr synapses re-strengthened. This may cause tone responses to increase slightly during the early re-extinction trials (Fig. 5E) and may explain the paradoxical increase in conditioned freezing observed in experiments at the start of extinction (see Mueller et al. 2008, Fig. 1C; Quirk 2002, Fig. 2B). This provides additional confirmation for the model. Last, the amount of decay at interneuron and inter-pyr synapses was proportional to the duration of the gap between the two extinction sessions: a longer gap would imply stronger recovery of fear as has been observed experimentally (Quirk 2002).

Some predictions from the model

IMPORTANCE OF LOW SPONTANEOUS FIRING RATE FOR MAINTAINING PLASTICITY.

Pyramidal cells in LA have very low spontaneous firing rates (Gaudreau and Paré 1996; Likhtik et al. 2006; Paré and Collins 2000), but the implications of this low firing rate for learning are not clear. Our model predicts that a low rate of spontaneous firing in LA may act to preserve the fear memory (due to decreased incidence of Hebbian weakening). To test this, we increased the spontaneous firing rate of pyramidal cells by a factor of 4.7 (from 1.5 to 7 Hz, by increasing both the strength and firing frequency of background inputs) during the gap between extinction and re-extinction. This led to a corresponding increase in the spontaneous firing rates of the interneurons. The time courses of representative synaptic weights are shown in Fig. 6, A–D. Tone inputs to pyramidal cells and interneurons showed a small increase in their rate of decay across the gap (Fig. 6A). In contrast, the internal synaptic connections showed much faster decay. This was true for excitatory (pyr-pyr) as well as inhibitory (pyr-inter and inter-pyr) connections (Fig. 6, B–D) consistent with our prediction that increased spontaneous firing results in faster decay of plasticity. In fact, the strength of inhibitory connections (but not tone-inputs) decayed to presensitization levels. The loss of inhibitory plasticity apparently compensated for the loss of excitatory plasticity because conditioned tone responses were still apparent during recovery (Fig. 6E). Thus increasing the spontaneous activity of cells during the long gap did cause faster decay of both excitatory and inhibitory plasticity but did not alter the expression of either conditioning or extinction memory. This suggests a degree of robustness in the network: despite large fluctuations in spontaneous firing rates, the output of tone responses is preserved.

FIG. 6.

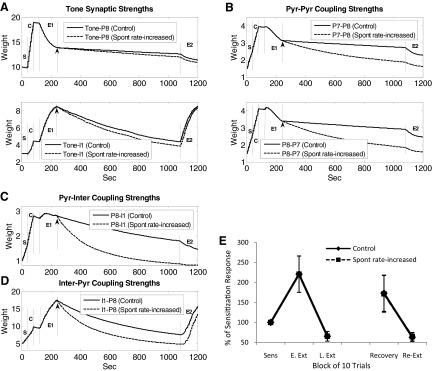
Effect of increasing spontaneous firing rate on memory storage. Fear memory stored in the tone-pyr and pyr-pyr synapses decayed faster when the spontaneous firing rate of pyramidal cells was increased near fivefold during the long recovery gap; extinction memory stored in the tone-inter, pyr-inter and inter-pyr synapses also decayed faster. Time courses of A: representative tone synaptic strengths; B: representative pyr-pyr synaptic strengths; C: representative pyr-inter synaptic strengths; and D: representative inter-pyr synaptic strengths. ↑, time when the spontaneous rate was increased. E: comparison of the tone responses in conditioned pyramidal neurons (n = 5) in the control and spontaneous rate-increased cases.

NMDA CURRENTS ARE REQUIRED FOR EXTINCTION LEARNING.

Consistent evidence shows that NMDA-type glutamate receptors are required for the formation of extinction memory (Falls et al. 1992; Santini et al. 2001; Sotres-Bayon et al. 2007; Suzuki et al. 2004). To test the effect of blocking NMDA receptors on the acquisition of extinction, we reduced g_NMDA,max from 0.5 to 0 nS for all the NMDA channels in the model, just prior to extinction training. The time courses of representative synaptic strengths in the network are shown in Fig. 7, A–D. Both potentiation and depression require adequate postsynaptic Ca²⁺ concentration. Depending on the synapse, this comes from NMDA, AMPA, internal Ca²⁺ stores or VDCC channels (Fig. 1) as cited earlier. With NMDA receptors blocked, LTD was blocked at the excitatory synapses onto pyramidal cells (Fig. 7, A and B), and potentiation was blocked at the tone-inter, pyr-inter, and inter-pyr synapses (Fig. 7, A, C, and D) due to low Ca²⁺ levels. Although the Ca²⁺ level at the inter-pyr synapse was not NMDA-dependent, it was dependent on the presynaptic firing and went down as the interneuron firing rate decreased due to NMDA blockade (results not shown). As shown in Fig. 7E, the loss of NMDA-mediated inhibitory plasticity completely prevented extinction of tone responses. However, if NMDA receptors were blocked only in pyramidal cells, extinction proceeded normally (dash-dot line in Fig. 7E) because NMDA-mediated inhibition in interneurons continued to potentiate. Thus this suggests that LA interneurons may be a critical site of NMDA-mediated plasticity in extinction.

FIG. 7.

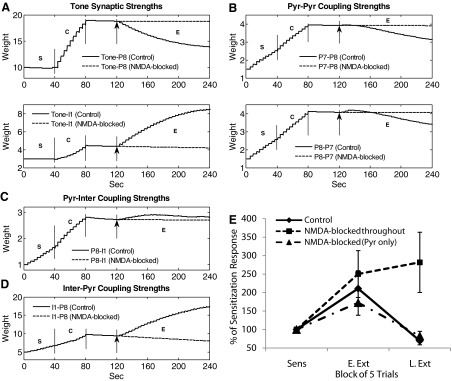
Effect of blocking all NMDA receptors. Extinction failed when NMDA receptors were blocked immediately before extinction. Time courses of A: representative tone synaptic strengths; B: representative pyr-pyr synaptic strengths; C: representative pyr-inter synaptic strengths; and D: representative inter-pyr synaptic strengths.↑, the instant when the block was implemented. E: comparison of the tone responses in conditioned pyramidal neurons (n = 5) for 3 cases: control, NMDA-blocked in all synapses, and NMDA-blocked in pyramidal cells. Pyramidal cells continued to have significantly elevated responses in late extinction when all NMDA receptors were blocked, but the tone responses decreased if NMDA receptors were blocked only in the pyramidal synapses. Sens, last 5 trials in sensitization; E. Ext, first 5 trials in extinction; L. Ext, last 5 trials in extinction.

LTD IS NECESSARY FOR COMPLETE EXTINCTION.

As shown in the preceding text, blocking NMDA receptors prevented depotentiation of the excitatory synapses onto pyramidal cells but at the same time blocked potentiation of inhibitory connections. To evaluate the contribution of LTD, independent of potentiation of inhibition, we selectively blocked LTD only at the tone-pyr and pyr-pyr synapses by preventing Ca²⁺ influx via the NMDA channels. This blockade of LTD was induced during the two extinction sessions. The time courses of representative synaptic weights are shown in Fig. 8, A–D. During extinction, the decay of weights at the tone-pyr and pyr-pyr synapses was blocked as expected, but potentiation of tone-inter, pyr-inter, and inter-pyr connections was maintained. Under these conditions, tone responses still extinguished, but more slowly than controls as evidenced by higher tone responses in late-extinction and re-extinction (Fig. 8E). In addition to being slower, extinction in the absence of LTD was not as complete as controls (note that tone responses reached a “floor” of 6 spikes during extinction in Fig. 8E). This is because the extinction-induced decrease in pyramidal cell firing rate reduced the excitatory drive onto the interneurons. As a result, the degree of inhibition of pyramidal cells reached a steady value. Thus LTD allows for faster and deeper extinction.

FIG. 8.

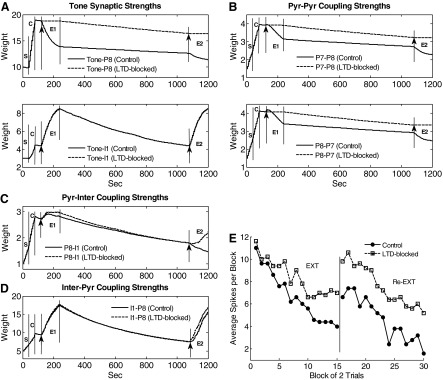
Effect of blocking LTD. Extinction slowed down when long-term depression (LTD) at the excitatory synapses on pyramidal cells was blocked during extinction. Shown are time courses of A: representative tone synaptic strengths; B: representative pyr-pyr synaptic strengths; C: representative pyr-inter synaptic strengths; and D: representative inter-pyr synaptic strengths. ↑, the time when LTD blockade was implemented. E: comparison of tone responses (0–200 ms) in the control and LTD-blocked cases by block of 2 trials for conditioned pyramidal cells (n = 5) during extinction and re-extinction.

DISCUSSION

Our network represents a first attempt to incorporate cellular neurophysiology and synaptic plasticity mechanisms into a biophysical model to investigate the underlying mechanisms of fear learning. The model provides a plausible mechanism as to how memory for conditioning and extinction develop and co-exist in LA and how they can regulate fear expression.

Both acquisition and extinction can be learned within the LA

Our model predicts that fear expression is determined by a balance between pyramidal cell and interneuron excitations and that cells in LA can learn both conditioning and extinction. The large potentiation of the excitatory inputs onto pyramidal cells caused by conditioning leads to elevated responses in early extinction. As extinction progresses, increasing feedforward and -back inhibition from the interneurons, combined with depotentiation at excitatory synapses onto pyramidal cells, ultimately bring the responses of the pyramidal cells back to preconditioning levels or even lower.

The key to extinction in this model is that tone-inter and inter-pyr synapses exhibit strengthening during extinction even in the absence of shock. This occurs because the shock-induced excitation of the interneurons is replaced by pyramidal cell inputs that have been potentiated during conditioning. Thus in the absence of pyramidal to interneuron connections, there would be no strengthening of the tone-inter and inter-pyr inputs and therefore no extinction. From a functional point of view, this suggests that the foundation for extinction is laid in conditioning and that strong conditioning enables strong extinction (homeostatic control). Because the excitatory inputs to interneurons exhibit potentiation during extinction, our model predicts that the interneurons within LA may increase their tone responses as extinction progresses. A recent experimental finding indicated the presence of such “extinction cells” within the basal amygdala (Herry et al. 2008), but the particular neuron type has yet to be determined. Nevertheless an appreciable increase in interneuron firing rate across extinction training is not necessary for extinction learning. This is because the conditioning-induced increase in interneuron firing rate was sufficiently high to enable potentiation at the inhibitory GABA synapses onto pyramidal cells. Indeed, Fig. 4, A–C, shows that there was a significant increase in the interneuron firing rate immediately after conditioning but little further increase as extinction progressed.

Both LTD and potentiation of inhibition contribute to extinction

The cellular mechanism of fear extinction has long been an issue of debate. An early hypothesis was that extinction could result from a depression of potentiated synapses and depotentiation may be the cellular mechanism for extinction (Goldman et al. 1990; Teyler and Discenna 1984). However, this was challenged when spontaneous recovery of fear was demonstrated, implying the persistence of fear memory after extinction (Bouton and King 1983; Pavlov 1927). This led to an alternative hypothesis where extinction does not erase the fear memory but instead creates a new memory that inhibits the fear response (Bouton and King 1983; Quirk 2002). Such an inhibitory memory could reside in excitatory neurons in the vicinity of the amygdala that inhibit the principal cells in LA via an extra-amygdaloid circuit or in the inhibitory interneurons in the LA (Falls et al. 1992).

Our model suggests a co-existence of these two mechanisms. Extinction did cause depression in potentiated synapses but did not completely reverse conditioning-induced changes. Furthermore, the degree of depotentiation varied from synapse to synapse. Even if potentiation at one synapse (such as the tone-pyr synapse) is completely reversed by extinction, fear could still be stored at other synapses (such as the pyr-pyr synapse). Thus a proportion of the fear memory is erased by extinction, while the rest is inhibited by potentiation at local GABAergic synapses. This agrees with previous findings supporting extinction-induced depotentiation (Lin et al. 2003) and augmentation of inhibition (Chhatwal et al. 2005) in the BLA. A recent study (Kim et al. 2007) reported a unique form of depotentiation during extinction that reversed conditioning-induced potentiation at thalamic input synapses onto the LA ex vivo. Moreover extinction reversed conditioning-induced enhancement of surface expression of AMPA receptor subunits in LA synaptosomal preparations (Kim et al. 2007). This new experimental finding supports our prediction that multiple mechanisms underlie extinction of consolidated memory (also see Myers et al. 2006). Indeed our simulation shows that potentiation of inhibition alone is not sufficient for complete extinction.

Location of storage sites within LA

There are two possible sites for fear memory storage in LA: the tone synapses from the auditory thalamus (or cortex) onto the pyramidal cells or the synapses between pyramidal cells. While both are capable of storing fear memory, there is an important difference. The synaptic coupling between two pyramidal cells will be strengthened as long as both receive strong inputs such as shocks. In contrast, the tone synaptic weight increases only when tone and shock are paired and deceases when tone and shock are unpaired. Hence the model predicts that tone synapses will only store specific tone-shock associations, while the pyr-pyr synapses can store a generalized fear memory related to the occurrence of shock (which could be related to contextual fear conditioning). Also the pyr-pyr synapses decayed less on average in extinction compared with the tone-pyr synapses as a result of frequency adaptation of pyramidal cells (Fig. 5, A and B). Together these findings suggest that the pyr-pyr synapse is well suited to encode long-term fear memory. In support of this, Repa et al. (2001) showed that neurons in the ventral part of LA (which receive input from the dorsal part) serve to store extinction-resistant long-term fear memories.

LA contains different types of principal neurons which have different degrees of frequency adaptation (Faber et al. 2001). The model suggests that these have different functional roles. The cells with stronger adaptation are slower to learn fear but are able to maintain fear memory for a long time, whereas the cells with weaker adaptation learn fear faster, but also extinguish faster (Fig. 5, A and B). Therefore pyramidal cells with weaker adaptation are important for fear expression, whereas those with stronger adaptation are important for long-term storage of fear associations. Because the majority of pyramidal cells in LA are strongly adapting, LA is well suited for storing long-term fear memory.

For extinction memory, there are three possible sites of plasticity: the tone synapse at the interneuron, the inhibitory synapse from interneuron to pyramidal cell, and the excitatory synapse from pyramidal cell to interneuron. A comparison of the decay rates of these three synapses (Fig. 5) suggests that the first two may mediate short-term extinction memory (large and uniform decay rates during the gap), while the last could store long-term extinction memory (e.g., P1-I1 in Fig. 5C). Nevertheless the tone-inter and inter-pyr synapses exhibited substantial potentiation during both extinction sessions, whereas the pyr-inter synapses did not. Long-term storage of extinction in LA pyramidal cells suggests that many of the molecular mechanisms of extinction storage in the LA are similar to storage of conditioning, as has been observed (Myers and Davis 2007; Quirk and Mueller 2008).

Maintenance of conditioning and extinction memories

Our model suggests that with a sufficiently long gap after conditioning, conditioned fear memory would be lost due to Hebbian weakening. This suggests the necessity of some active process that maintains fear memory through rehearsal or replay. In support of this, NMDA receptors are needed days and weeks after training to maintain conditioned fear memory (Wang et al. 2006), and reactivation of memory triggers an NMDA-dependent reconsolidation processes within the amygdala (Nader et al. 2000; Tronson and Taylor 2007). Thus long-term consolidation and reconsolidation processes may serve to counteract depotentiation of synapses that would occur over an extended period of time. With respect to extinction memory, high spontaneous activity during the long gap was sufficient to completely eliminate inhibitory plasticity at the inter-pyr and pyr-inter connections, but re-extinction was not impaired. Interneuron activity depends on the pyramidal cell firing rate and the strength of the pyr-inter connection. Although the pyr-inter plasticity vanished, the pyramidal cell firing was high at the start of re-extinction (recovery), causing the interneuron to re-establish the inhibition plasticity. However, if the pyr-inter connection is removed (no pyramidal input to the interneuron), extinction will fail. This underscores an important insight from this model, namely, that a critical amount of the plasticity necessary for extinction is accrued during conditioning.

Limitations

There are a number of limitations of our model which should be acknowledged: 1). The size of this LA network was intentionally small to facilitate the study of the underlying neural plasticity in detail and is typical of previous biophysical modeling studies (Durstewitz et al. 2000). It remains to be determined whether the qualitative conclusions and predictions from the model will hold for a larger network. 2) The model parameters in Table A3 were selected to match experimental data as closely as possible. Improved understanding of connectivity and learning mechanisms in LA will help refine these estimates. 3) As mentioned earlier, there is considerable heterogeneity in the firing properties of GABAergic interneurons in BLA (Rainnie et al. 2006; Woodruff and Sah 2007). We only modeled the most common cell type—fast spiking (FS) interneurons. This is justifiable because the second most common cell type—delay firing (DF) cells also fire nonaccommodating trains of high-frequency spikes after an initial delay in response to depolarizing current injection, and FS and DF cells together account for 70% of the parvalbumin-positive interneurons in BLA (Woodruff and Sah 2007). 4) Although potentiation of inhibitory synapses in LA is dependent on postsynaptic calcium, the molecular induction and expression mechanisms are currently unknown (Bauer and LeDoux 2004; Sigurdsson et al. 2007). We modeled this plasticity based on inhibitory LTP mechanisms reported in the rat hippocampus, cortex and cerebellum (Gaiarsa et al. 2002). Specifically, we used an equation similar to that for the AMPA/NMDA receptors with the Ca²⁺ release from internal stores replacing the Ca²⁺ through the receptor model. A better understanding of the Ca²⁺ mechanisms underlying potentiation of inhibitory synapses in LA will help improve this model. 5) As mentioned earlier, the present model investigates information processing primarily in LAd neurons receiving direct thalamic inputs. Extensions to include neurons showing persistence of potentiated tone responses observed in the ventral part of LA (LAv) (Repa et al. 2001) will be the topic of a separate study. 6) Our model focused only on plasticity in the LA. Recent physiological studies have shown that, in addition to LA, plasticity is also seen in other amygdaloid nuclei (ITC and CE) (Royer and Paré 2002; Samson and Paré 2005; Wilesky et al. 2006). Also expression of fear and extinction are regulated by contextual and temporal factors that are processed by other structures that influence the amygdala, such as the hippocampus and medial prefrontal cortex (Corcoran and Maren 2004; Milad and Quirk 2002). Thus additional modules will be needed to model the processes that regulate fear expression in real-life conditions.

In conclusion, we have shown that realistic LA neurons, incorporating known conductances, connectivity, and synaptic plasticity mechanisms, can learn fear conditioning and extinction. The biophysical realism of the model allowed us to test the importance of basal firing rates, NMDA receptors and depotentiation. Furthermore, our results suggest specific storage sites within the LA for conditioning versus extinction, and factors that can affect the persistence of these memories. The ultimate goal of this computational study is to model pathologies associated with the fear circuit (e.g., post traumatic stress disorder) and assist in the development of new treatments.

GRANTS

This research was supported in part by the National Science Foundation Grant DGE-0440524 to S. S. Nair and National Institutes of Mental Health Grant MH-058883 to G. J. Quirk.