Left ventricle segmentation using Graph searching on Intensity and Gradient and A priori knowledge (lvGIGA) for short axis cardiac MRI

Abstract

Purpose

To develop and evaluate an automated left ventricle (LV) segmentation algorithm using Graph searching based on Intensity information, Gradient information, and A priori knowledge (lvGIGA).

Material and Methods

The lvGIGA algorithm was implemented with coil sensitivity correction and polar coordinate transformation. Graph searching and expansion were applied to extract myocardial endocardial and epicardial borders. LV blood and myocardial signal intensities were iteratively estimated for accurate calculations of LV blood volume and myocardial mass, including compensation for partial volume effects. The lvGIGA algorithm was used to measure blood volume, myocardial mass, and ejection fraction, and compared with clinical manual tracing and the commercial MASS software on cardiac cine SSFP images from 38 patients.

Results

The success rate for segmenting both endocardial and epicardial borders was 95.6% of slices for lvGIGA compared to 37.8% for MASS (excluding basal slices that required manual enclosure of ventricle blood). The lvGIGA segmentation result agreed well with manual tracing, within -2.9±4.4mL, 2.1±2.2%, and -9.6±13.0g for blood volume, ejection fraction, and myocardial mass, respectively.

Conclusion

The lvGIGA algorithm substantially improves the robustness of LV segmentation automation over the commercial MASS software, agrees well with clinical manual tracing, and may be a useful tool for clinical practice.

Introduction

Quantification of cardiac function can be performed by calculating cardiac chamber volumes and ejection fraction from diastolic and systolic phases of cardiac MRI. Manual tracing has been considered the gold-standard for cardiac output quantification in clinical practice. However, manual tracing is a labor-intensive and time consuming process that is subject to inter- and intra-observer variability. Additionally, complex cardiac structures such as papillary muscles and trabeculations make it difficult to accurately trace the left ventricle (LV) margins in detail. Many algorithms have been introduced to remove observer variation and improve time efficiency, but full automation in segmenting the LV with sufficient accuracy has yet to be achieved.

Traditional segmentation algorithms use thresholding, region-growing, edge-detection, and clustering (1-8). Since these algorithms each require significant user interaction to segment the LV, they have been combined with other segmentation techniques in hybrid schemes to minimize user intervention. Such hybrid algorithms, however, have several limitations: 1) They are reliable for mid-ventricular slices, but they generally fail at the basal and apical slices; 2) They do not accurately segment the detailed structure of papillary muscles and trabeculations; and 3) They do not account for partial volume effects.

Graph-based segmentation algorithms generate a graph by calculating a cost in each pixel or node and finding the minimum cost path (9-11). However, these algorithms cannot segment complex cardiac structures and fail when the myocardial margins are ill-defined or at the basal and apical slices.

Active contour models (ACM) segment objects through energy minimization of internal forces such as rigidity and elasticity, and external forces such as edges (12-14). Locating initial contours near the object is critical to the success of ACM segmentation. ACM is also ineffective with low contrast images and is inefficient with regard to computational costs. Active shape model (ASM) segmentation depends on a statistical shape model that is built using prior knowledge represented by hand-annotated segmentation from a training data set. The active appearance model (AAM) is an extension of ASM that uses the shape and texture variation of objects (15, 16). Using a manual training data set, the model is generated using principal component analysis. The model is then deformed according to statistical variation to fit new data sets. Both ASM and AAM are limited by the variation and the creation of training sets. Both also require expensive computational costs for iterative procedures. Moreover, variably complex cardiac structures make ACM, ASM, and AAM ineffective in extracting the detailed margins of the LV.

Level-set segmentation is a more recent, yet well established, method to segment objects in noisy data (17-19). However, level-set methods have difficulties in determining the stopping terms, require good initialization of segmenting objects, are prone to settling in local minima, and have expensive computational costs. To avoid some of these issues, a prior model is built by manually segmenting training data and determining the stopping criteria. However, dependency on prior models results in the loss of segmentation detail, potentially concealing cardiac abnormalities, while retaining expensive computational costs.

In this paper, we propose a left ventricle segmentation algorithm based on Graph searching of both Intensity and Gradient information and A prior knowledge of the myocardium that surrounds and differs from blood (lvGIGA). This lvGIGA algorithm is capable of estimating detailed LV structures and a partial volume mixture of blood and myocardium. Initial evaluation of lvGIGA on 38 patients demonstrated a very high degree of automation far superior than the commercial MASS software.

Materials and Methods

lvGIGA algorithm

The proposed LV segmentation algorithm of short-axis cardiac cine MRI is based on graph searching using a mixed intensity and gradient criterion in addition to a priori knowledge. The following assumptions regarding short-axis cardiac MRI are used in lvGIGA: the LV is roughly cylindrical and circular on each short axis cross-sectional image, blood is surrounded by myocardium, and the signal intensity of blood is different from that of myocardium. Using this knowledge, the lvGIGA algorithm is performed on each short axis image with the following steps (Figure 1):

Figure 1.

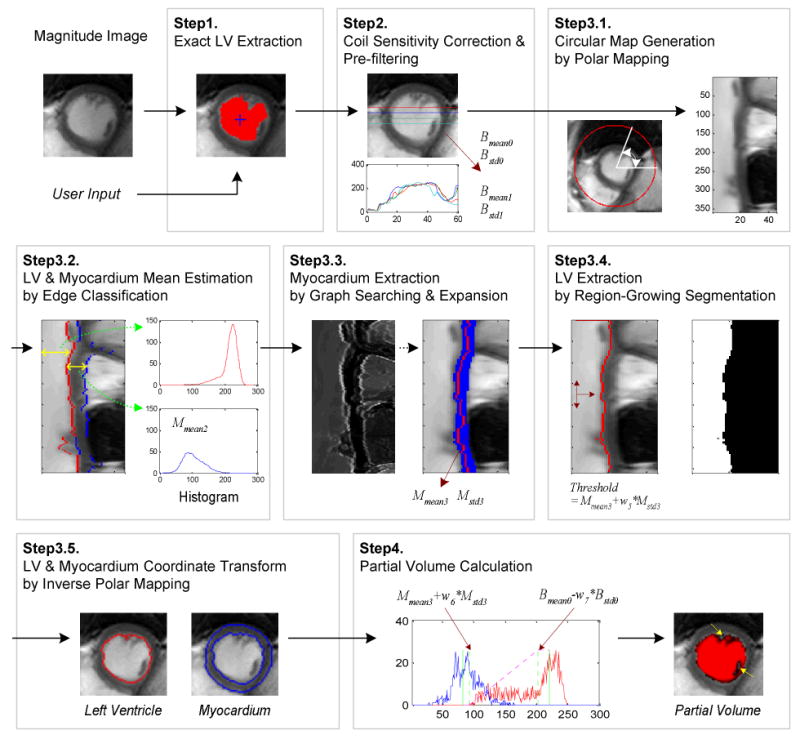
Cardiac left ventricle and myocardial segmentation and partial volume calculation algorithm.

• Step1 Extract an initial LV using edge-based region growth

• Step2 Correct for coil sensitivity variation and filter out the signal noise

• Step3 Segment the LV and myocardium

• Step3.1 Generate a circular map from the corrected image

• Step3.2 Estimate the intensity statistics of the LV and myocardium using edge classification

• Step3.3 Extract the myocardium using graph searching and expansion

• Step3.4 Detect the LV by using threshold-based region-growth

• Step3.5 Transform the coordinates from the circular map to a Cartesian image

• Step4 Calculate the LV volume in that image while accounting for partial voxels

• Step5 Repeat the algorithm on the next image.

Step1. Extract an initial LV

An initial LV segmentation is performed using edge-based region-growing from a user-selected seed point (edge constraint of less than 5% intensity difference among neighboring pixels).

Step2. Coil sensitivity correction and noise filtering

Image intensity variation due to coil sensitivity non-uniformity is corrected based upon the assumption that the LV cavity signal should be homogeneous: a planar equation F(X,Y) is fit to a least-squares solution using LV pixels identified from Step1; the image intensity is then multiplied by a factor F(C_x,C_y)/ F(X,Y), where C_x and C_y represent the center-of-mass coordinates of the initial LV. Figure 2 shows coil sensitivity correction results. Residual images represent the intensity difference between before and after coil sensitivity correction. For increasing the robustness of edge detection in later steps, a noise filter (19) is applied. Blood signal intensity mean and standard deviation are then calculated from coil sensitivity corrected images before and after noise filtering as (B_mean0, B_std0) and (B_mean1, B_std1), respectively.

Figure 2.

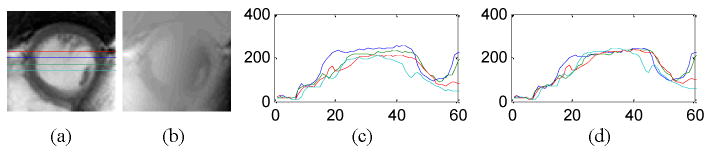
Coil sensitivity correction. (a) Magnitude images, (b) residual images, (c) intensity profiles before correction, and (d) intensity profiles after correction.

Step3. Left ventricle and myocardium segmentation

Step3.1. Circular map generation

Since the LV has a roughly circular shape, a circular polar map is generated, using the center-of-gravity from the initial LV extracted in Step1 as the polar center. A Cartesian coordinate (x, y) is converted to a polar coordinate (radius r, angle θ). The size of the circle is selected to cover all possible cardiac areas.

Step3.2. Estimation of LV blood and myocardium statistics using edge classification

Edge information is extracted using the Canny detector on the circular map of the noise-filtered coil-corrected image of Step2. The sensitivity threshold and sigma of the Canny detector in this study were set to 0.3 and 1.0, respectively. Two edges are identified as follows: Points for the 1^st edge are identified by searching in the radial r direction from the center using the constraint that intensity at the inner radial side of the edge is larger than intensity at the outer radial side of the edge by B_std1 or more. Points for the 2^nd edge are identified by searching further in the radius r direction from the 1^st edge using the constraint that intensity at the inner radial side of the edge is less than B_mean1 + B_std1. Figure 3a-b show the Canny edge detection and the 1^st and 2^nd edge classification. Subsequently, an intensity histogram is calculated in the radial direction between the LV center (the 1^st point) and points identified on the 1^st edge as the histogram of LV blood signal. Similarly, we calculate a histogram between the 1^st edge and 2^nd edge as the histogram of myocardial signal. An averaging filter with a width of 60 bins is used to smooth the histograms. The blood mean intensity, B_mean2, and the myocardial mean intensity, M_mean2, are set to the values of the peak locations in the smoothed blood and myocardial histogram.

Figure 3.

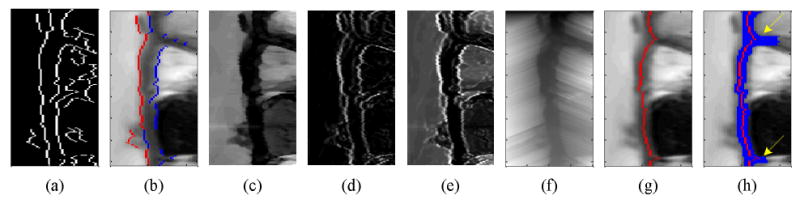
Edge classification and myocardium extraction by graph searching and expansion. (a) Canny edge detection, (b) edge classification of 1st edge (in red) and 2nd edge (in blue), (c) intensity difference, (d) gradient, (e) cost in each node of graph, (f) accumulated cost, (g) myocardial center axis by graph searching, and (h) myocardial segmentation by expansion.

Step3.3. Myocardium extraction by graph searching and expansion

The center axis of the myocardium is detected using a graph searching technique and myocardial thickness is extracted by expanding outward from the center axis using constraints based on the myocardial intensity statistics. A graph is then constructed with the assumption that each pixel is connected with its neighboring pixels in the anglular direction on the circular map. In other words, pixel (r, θ) is connected with pixel (r+n, θ-1) and pixel (r+n, θ+1), where n is an integer. The cost in each node of the graph is computed by combining the normalized intensity difference and the gradient image as follows:

$$\text{Cost}(r,\theta )=w_1|\text{I}(r,\theta )-M_{\text{mean}2}|/\text{max}(I(\text{r},\theta ))+w_{2}G(r,\theta )/\text{max}(G(r,\theta ))$$ (1)

where I is the image output from Step2, G is its corresponding gradient magnitude image from Step3.2, and M_mean2 is also from the above Step3.2. The variable r and θ refer to the radial direction and the angular direction on circular map, respectively. Cost is low when intensity is similar to M_mean2 and the gradient is small (locations far from edges). w₁ and w₂ are weighting constants to control dependency on image content. We set both to 1.0 to equally weight image intensity and gradient information. This procedure is illustrated in Figs.3c-e. Figure 3e shows the cost function in each pixel of the graph with brightness representing cost.

The graph searching technique is applied to find the minimal cost path in the angular direction (9-11, 20). The accumulated cost in each pixel is calculated by adding the minimum cost in previous pixels, θ-1, and a weighted distance to its own cost as follows:

$$\text{AccCost}(r,\theta )=\text{Cost}(r,\theta )+{\text{min}}_k(\text{Cost}(r+k,\theta -1))+w_3\text{dist}(k_{\text{min}})$$ (2)

where k is a searching range of previous pixels, w₃ is a weighting constant to convert pixel distance to cost which is empirically set as 0.01 for cine SSFP images. dist(k_min) represents a distance from the previous minimum cost pixel. After calculating the accumulated cost from the beginning (θ =1) to the end (θ =N), pixels are searched in reverse to find the pixel with the minimal accumulated cost in each angular direction. During this search, edge information is used to block a search beyond the edge. The minimum cost path is defined as the myocardial center axis.

The mean and standard deviation, M_mean3 and M_std3, of the myocardial center axis are calculated and expanded to detect the myocardial thickness. Expansion is performed in the radial and angular directions by comparing intensity. When I(r, θ) − I(r_c, θ_c) < w₄×MC_Std3 is satisfied, we continue expanding, otherwise, expansion stops in that direction. Here (r_c, θ_c) represents the pixel in the myocardial center axis. w₄ is a weighting constant that is empirically set to 1.2 and 2.0 for endocardial and epicardial contour detection, respectively, roughly accounting for Gaussian noise effects. Figure 3g-3h show the myocardial center axis and the myocardial thickness by graph searching and expansion.

The epicardial contour in MRI may not be well defined when the intensity differences between myocardium and other tissues are small. Figure 4a shows a case where arrows point to locations with ill-defined epicardial contours. As a result, myocardial region expansion in the radial direction (searching for epicardial contour) has a leakage problem shown in Figure 3h and Figure 4b. This leakage is addressed in the following manner: first, the average distance between the endocardial contour and myocardial center axis (half thickness, th), and the average distance between the endocardial contour and epicardial contour (full thickness, tf) are calculated. As shown in Figure 4b, exact epicardial contour points are retrieved by searching points with myocardial thickness in the range (tf − th, tf + th). Then, the epicardial contour is traced along the θ-direction forward and backward. If a consecutive change in myocardial thickness is larger than th, the epicardial radial location at that point is set to the radial location of its preceding contour point (see Figure 4c and Figure 4d). Finally, the epicardial contour's radial position is updated with the minimum among the forward and backward contour tracings (see Figure 4e). To filter noise, low-pass filtering is applied to the epicardial contour (see Figure 4f and Figure 4g).

Figure 4.

Myocardial segmentation update applying distance constraints. (a) Circular map, (b) exact epicardial range, (c) forward contour tracing, (d) backward contour tracing, (e) updated epicardial contour, (f) epicardial contour after low-pass filtering, and (g) updated myocardial segmentation.

Step3.4. LV detection by region-growing segmentation

On the circular map, region-growing starts from the initial LV from Step1. The region grows if the signal intensity of each pixel is larger than region-growing threshold M_mean3+w₅×M_std3 with w₅ = 2.0 (capturing 99.4% of all full myocardial voxels of Gaussian noise). The region-growing stops if it meets myocardium extracted in Step3.3. Thus, myocardium is a constraint used to block region-growing in the radial direction.

Step3.5. Coordinate transform of LV and myocardium

Segmented LV blood and myocardium are converted from polar coordinates to Cartesian coordinates, using the inverse calculation of polar mapping in Step3.1.

Step4. Partial volume calculation

By the end of Step3, the LV has been segmented and intensity statistics of the LV and myocardium have been calculated: B_mean0, B_std0, M_mean3, and M_std3. In order to design an intensity weighting function for calculating LV partial volumes within voxels at the edge of myocardium, two constants, M_right and B_left, are defined as follows:

$$\begin{array}{ll}{M}_{\text{right}}\hfill & =M_{\text{mean}3}+w_6\times M_{\text{std}3}\hfill \\ B_{\text{left}}\hfill & =B_{\text{mean}0}-w_7\times B_{\text{std}0}\hfill \end{array}(3)$$ (3)

where w₆ and w₇ are constants to control volume calculation set at 2.0 and 2.0, respectively. Accounting for Gaussian noise, the assignments ensure that at least 99.4% of full-blood and full-myocardial voxels will be weighted correctly, while maintaining the proportionality of partial-voxel interpolation. Using these values, the intensity weight function is designed as follows:

$$\begin{array}{lll}PV=1\hfill & \text{if}\hfill & I_c(r,\theta )\ge B_{\text{left}}\hfill \\ PV=0\hfill & \text{if}\hfill & I_c(r,\theta )\le M_{\text{right}}\hfill \\ PV=(I_c\text{(}r,\theta \text{)}-M_{\text{right}})/(B_{\text{left}}-M_{\text{right}})\hfill & \text{if}\hfill & M_{\text{right}}<I_c(r,\theta )<B_{\text{left}}\hfill \end{array}$$ (4)

Here I_c, image intensity with only coil sensitivity correction, is used to avoid noise filtering that destroys the fine details of papillary muscles and trabeculations (PMT). The intensity weighting function for partial volume calculation is shown in Figure 1, where the histogram of LV blood is in red, the histogram of myocardium is in blue, and the PMTs are pointed out in the image in Step4 by arrows.

Experimental evaluation

Our Institutional Review Board approved this retrospective image analysis. No informed consent was required. Cardiac cine SSFP images were acquired from 38 patients using a GE Signa 1.5T scanner (15 male, mean age 52.4 ± 15.1years). The most common clinical indications for referral were the assessment of presence or pattern of myocardial scar. Imaging parameters were TR 3.3-4.5ms, TE 1.1-2.0ms, flip angle 55-60, matrix size 192×192 – 256×256, image dimensions 256×256, receiver bandwidth 125kHz, FOV 290-400×240-360, slice thickness 6-8mm, and slice gap 2-4mm. The LV in each subject was imaged in 6-10 slices, 20-28 cardiac phases. 635 total images (two cardiac phases, systole and diastole, from all patients) were segmented by manual tracing, our lvGIGA segmentation, and the MASS commercial software. Manual tracing was performed by two physicians who routinely perform clinical cardiac MRI with 8 years and 3 years experience. Papillary muscles and trabeculations were excluded from the blood volume as specified in our clinical analysis protocol. Trabeculations were defined as myocardium protruding > 1.5 mm from the circumferential contour of the LV cavity, with equivalent signal intensity to the adjacent LV wall (21, 22). Basal image positions were defined by the most basal image encompassing at least 50% of circumferential myocardium (21). All tracings were performed blinded to other results.

Endocardial volume in diastolic and systolic phases, epicardial volume, and ejection fraction were measured using lvGIGA segmentation and compared with manual tracing and the commercial MASS software (MASS Analysis on GE Advantage Workstation, Medis Medical Imaging Systems, Leiden, The Netherlands). Both full volume (FV, without partial volume consideration) and partial volume (PV) for LV endocardial volume were calculated at both diastole and systole. Diastolic epicardial volume (including both LV blood and myocardium) was calculated and myocardial mass was derived from the epicardial volume and endocardial volume difference multiplied by the density of myocardium (1.05g/mL). Linear regression and Bland-Altman analysis were performed to assess the correlation between manual tracing with the MASS software and lvGIGA segmentation.

Performance of the automated algorithms lvGIGA and MASS was evaluated by visually identifying contour deviations from the LV border by more than 10% in area. These were recorded as algorithm failures, and the improper contour segmentation was corrected by user intervention. The number of user interventions was recorded for each algorithm.

Results

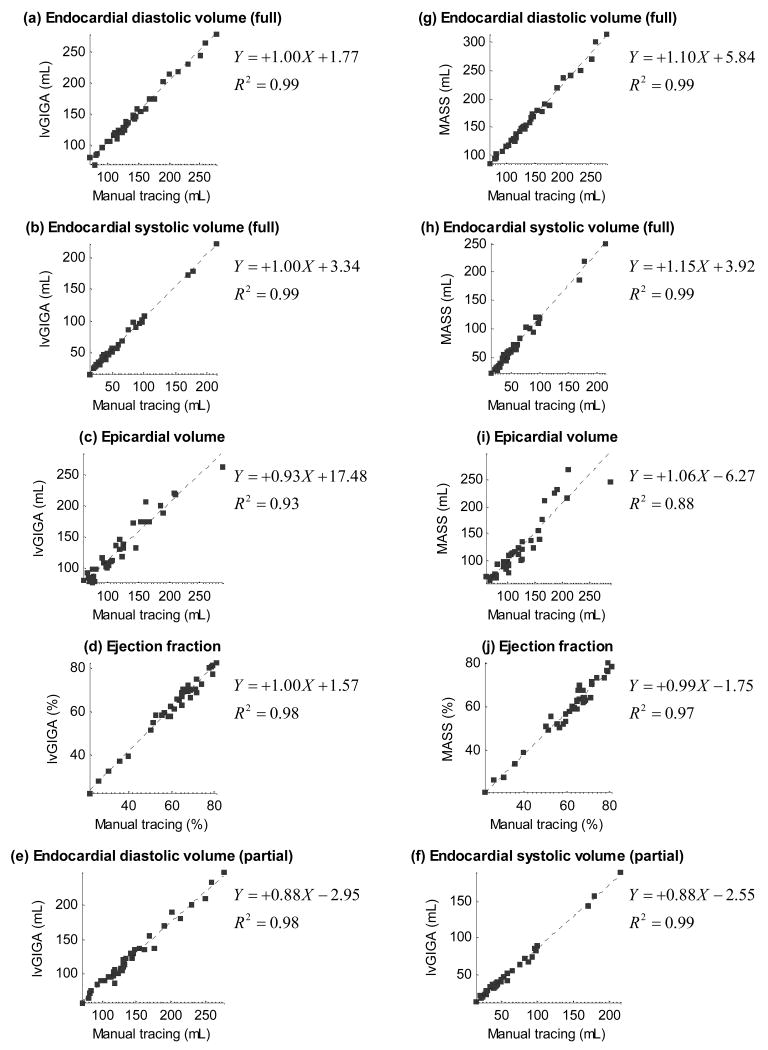
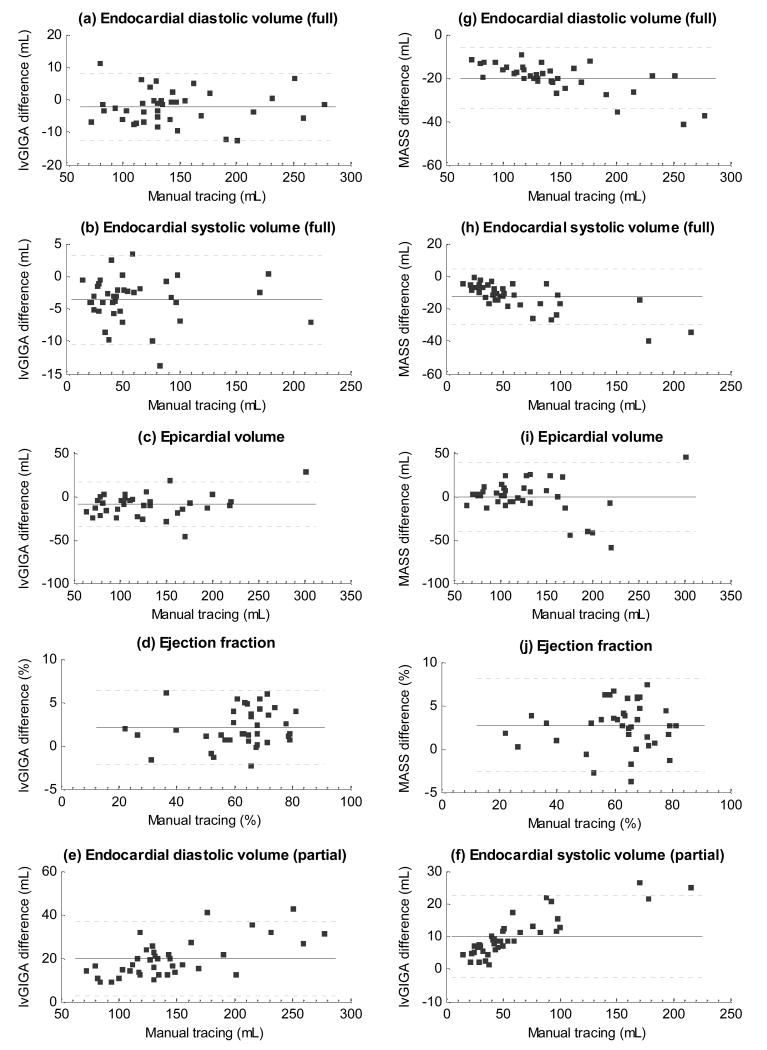
The left ventricular blood volume at end diastole and end systole, the ejection fraction, the epicardial volume in diastole, and the myocardial mass are shown in Table 1 and Figure 5 for manual tracing, lvGIGA and MASS software. While blood volume measurements from the lvGIGA algorithm without partial voxel interpolation were similar to that of manual tracing, corresponding lvGIGA blood volume measurements with partial voxel interpolation were smaller than manual tracing, and MASS blood volume measurements were larger than manual tracing because papillary muscles and trabeculations were not excluded. Ejection fraction measurements were similar for all three measurement methods. Both lvGIGA and MASS showed slightly less correlation with manual tracing for myocardial mass measurements than for blood volume measurements, possibly due to additional discordance in epicardial contour segmentation. However, lvGIGA consistently showed smaller standard deviations than MASS (Table 1) indicating it is a more robust technique. Comparisons among manual tracing, lvGIGA, and MASS are illustrated in the Bland-Altman plots in Figure 6.

Table 1.

Performance of lvGIGA and MASS software compared to manual tracing in 38 patients.

	Manual tracing – lvGIGA (Full volume)			Manual tracing – lvGIGA (Partial volume)			Manual tracing – MASS software
	Absolute	Relative	Corr.	Absolute	Relative	Corr.	Absolute	Relative	Corr.
End diastolic volume	-2.3±5.2 (mL)	-1.7±4.3 (%)	R2=0.99	19.6±8.7 (mL)	13.8±4.5 (%)	R2=0.98	-20.0±6.9 (mL)	-14.3±3.3 (%)	R2=0.99
End systolic volume	-3.6±3.4 (mL)	-8.1±7.8 (%)	R2=0.99	10.0±6.3 (mL)	17.7±6.2 (%)	R2=0.99	-12.7±8.5 (mL)	-23.1±10.1 (%)	R2=0.99
Ejection fraction	2.1±2.2 (%)	3.5±4.1 (%)	R2=0.98	3.5±4.1 (%)	-2.7±3.5 (%)	R2=0.98	2.6±2.7 (%)	4.5±4.5 (%)	R2=0.97
Epicardial volume	-11.4±10.8 (mL)	-4.8±3.7 (%)	R2=0.99	-	-	-	-21.0±20.8 (mL)	-7.7±5.6 (%)	R2=0.96
Myocardial mass	-9.6±13.0 (g)	-9.2±10.8 (%)	R2=0.93	-	-	-	-1.0±20.2 (g)	0.0±12.3 (%)	R2=0.88

Figure 5.

Endocardial volume in diastolic and systolic phases, epicardial volume, and ejection fraction plots of the presented lvGIGA algorithm and the MASS software against manual tracing. Endocardial volume of the lvGIGA algorithm with partial volume compensation is also shown.

Figure 6.

Bland-Altman plots of the presented lvGIGA algorithm (a-f) and the MASS software (g-j) against manual tracing, where endocardial volume in diastolic and systolic phases, epicardial volume, and ejection fraction. Endocardial volume of the lvGIGA algorithm with partial volume compensation is also shown.

Table 2 summarizes the number of user interventions necessary to correct for improper segmentations in both lvGIGA and MASS software. While basal slices were problematic for both lvGIGA and MASS because of the LV outflow tract disruption of the circular myocardial border, the lvGIGA drastically reduced the number of intervention needed by MASS for both endocardial (from 10.6% to 0.6% slices) and epicardial (from 51.6% to 3.8% slices) contour segmentation. Excluding the basal slices, lvGIGA had a success rate of 95.6% while MASS had a success rate of only 37.8% for LV segmentation. Fig. 7 shows an example of LV segmentation using the three methods, illustrating the quality in defining endocardial and epicardial contours, and partial volume. The substantial inclusion of lung tissue (Fig.7f vs Fig.7g) was found to be an major error in the MASS software, which was nearly completely eliminated by lvGIGA.

Table 2.

User-intervention comparison between our lvGIGA segmentation and the MASS software in 38 patients (numbers in parenthesis are based on patients)

		lvGIGA algorithm	MASS software
Endocardial	Basal slices	22/635, 3.5%	32/635, 5.0%
		(17/38, 44.7%)	(24/38, 63.2%)
	Other slices	4/635, 0.6%	67/635, 10.6%
		(3/38, 7.9%)	(28/38, 73.7%)
Epicardial	Additional slices	13/339, 3.8%	175/339, 51.6%
		(8/38, 21.1%)	(38/38, 100.0%)

Figure 7.

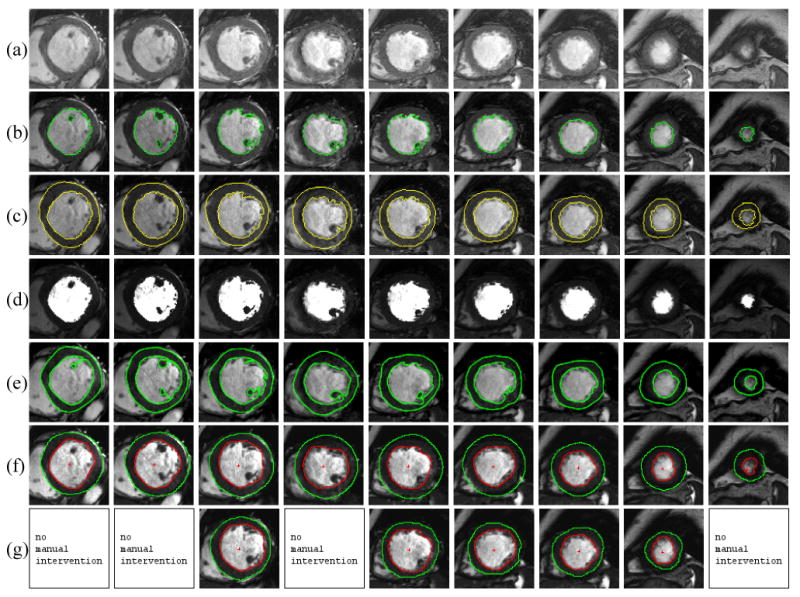
lvGIGA segmentation results. (a) original magnitude images. (b) left ventricle blood at end diastole, (c) myocardium and (d) partial volumes. (e) left ventricle blood and myocardium by manual tracing. MASS segmented left ventricle and myocardium (f) before and (g) after manual intervention.

Discussion

Preliminary data demonstrate that our proposed lvGIGA algorithm provides LV segmentation that is in good agreement with clinical manual tracings and substantially improves the robustness of accurate automation over the commercial MASS software. Additionally, the lvGIGA algorithm is capable of separating blood and myocardium within the same voxel.

lvGIGA assumes that myocardium surrounds homogeneous blood and that the myocardial and blood signal intensities differ by ≫ 5%. These minimal assumptions (a priori knowledge) allow for the correction of coil sensitivity variations, the identification of the inner endocardial border as the first significant gradient line, and the identification of the outer epicardial border as the second significant gradient line in the polar coordinate. Blood and myocardial intensity statistics are iteratively estimated as endocardial and epicardial border definitions improve during the segmentation. The intensity and gradient information are combined to determine the cost function for graph searching and expansion, which is further constrained by smoothing. In this manner, the lvGIGA algorithm accurately identifies endocardial and epicardial borders and blood and myocardial signal statistics for blood volume and myocardial mass measurements.

The non-uniformity of coil sensitivity is corrected using a least-squares fitted plane on LV blood signal. This coil sensitivity correction works well on patients with ischemia but it may be affected by high flow jets in patients with cardiac valve disease. When the myocardial contour is disrupted by the LV outflow tract in the basal-most slice, lvGIGA requires manual intervention, though less frequently than with the commercial MASS software. Excluding the basal-most slice, lvGIGA almost eliminates the need for manual intervention, while the MASS software requires manual intervention in about half of the slices. With regard to automation robustness, lvGIGA offers a substantial improvement over MASS. In 4 non-basal slices where lvGIGA failed to identify the endocardial border, two were apical slices where lvGIGA was unable to define the LV gravity center due to irregular blood and myocardial distributions. The other two slices had very bright areas within the myocardium. In slices where lvGIGA failed to accurately identify the epicardial border, there was an insufficient difference in signal intensity between myocardium and adjacent organs such as the lungs, causing the segmented myocardium to include these tissues. In addition, smoothing the epicardial contour tends to ignore possible complex myocardial texture. These factors may contribute to an “over-segmentation” in epicardial border and corresponding epicardial volume (Table 1). In comparison, the endocardial border has a clear boundary and can be reliably detected without smoothing. This may explain why the lvGIGA epicardial volume difference with manual tracing was found to be larger than the lvGIGA endocardial volume difference, and that the lvGIGA myocardial mass was slightly larger than that by manual tracing. This over-segmentation problem may be addressed by integrating the lvGIGA output into active contour model or level-set methods.

Noise filtering is necessary for reliable estimation of edges in the lvGIGA algorithm, but this also smoothes out fine muscular structures, resulting in apparent “over-segmentation” of blood. The partial volume calculation of blood volume and myocardial mass compensates for this noise filtering problem. Partial volume calculation may be important for the accurate volume determination from cine cardiac MR images, which are typically acquired using 6-8mm thick slices and consequently have substantial voxels that contain a mixture of blood and myocardium. The validity of the partial volume interpretation remains to be evaluated. Neither manual tracing nor MASS software can be considered as a true reference standard for blood volume and myocardial mass.

In conclusion, we demonstrate a left ventricle segmentation algorithm that extracts endocardial and epicardial borders and enables partial volume calculations for accurate and automated determination of the LV blood volume and myocardial mass. Graph searching based on combined intensity and gradient information is effective for myocardial contour detection. The a priori knowledge that myocardium surrounds blood and differs in signal intensity from blood by ≫5% is sufficient for the contour extraction process. Accordingly this algorithm is referred to as lvGIGA, left ventricle segmentation using Graph search based on Intensity and Gradient information and A priori knowledge.