The Role of Nucleotide Cofactor Binding in Cooperativity and Specificity of MutS Recognition

Abstract

Mismatch repair (MMR) is essential for eliminating biosynthetic errors generated during replication or genetic recombination in virtually all organisms. The critical first step in Escherichia coli MMR is the specific recognition and binding of MutS to a heteroduplex, either containing a mismatch or an insertion/deletion loop of up to four nucleotides. All known MutS homologs recognize a similar broad spectrum of substrates. Binding and hydrolysis of nucleotide cofactors by the MutS-heteroduplex complex is required for downstream MMR activity, although the exact role of the nucleotide cofactors is less clear. Here we showed that MutS bound to a 30-bp heteroduplex containing an unpaired-T with a binding affinity ≈ 400-fold stronger than to a 30-bp homoduplex, a much higher specificity than previously reported. The binding of nucleotide cofactors decreased both MutS specific and non-specific binding affinity, with the later marked by a larger drop, further increasing MutS specificity by ≈ 3-fold. Kinetic studies showed that the difference in MutS K_D for various heteroduplexes was attributable to the difference in intrinsic dissociation rate of a particular MutS-heteroduplex complex. Furthermore, the kinetic association event of MutS binding to heteroduplexes was marked by positive cooperativity. Our studies showed that the positive cooperativity in MutS binding was modulated by the binding of nucleotide cofactors. The binding of nucleotide cofactors transformed E. coli MutS tetramers, the functional unit in E. coli MMR, from a cooperative to a non-cooperative binding form. Finally, we found that E. coli MutS bound to single-strand DNA with significant affinity, which could have important implication for strand discrimination in eukaryotic MMR mechanism.

1. Introduction

Mismatch repair (MMR) is a critical cellular pathway for virtually all organisms. It is responsible for removing replication errors that have escaped proofreading as well as for correcting mismatches stemming from genetic recombination (see reviews ^{1; 2; 3}). Early genetic studies show that MMR depresses mutation rates by 100–1000-fold in Escherichia coli (E. coli) ⁴. MMR deficiencies in humans are implicated in hereditary non-polyposis colorectal carcinomas (HNPCC, also termed Lynch syndrome), one of the most widespread genetic disorders ^{5; 6}. People with HNPCC are at greatly enhanced risk to a host of cancers compared to the general population ⁵. MMR is also crucial in maintaining the stability of repeated sequences of 1- to 6- nucleotides naturally occurring in human genomes ^{7; 8; 9; 10}. Instability of the repeated sequences in human genomes can lead to many other genetic disorders including the fragile X syndrome, Kennedy’s disease, and Huntington’s disease ^{7; 8; 9; 10}. In addition to DNA repair, eukaryotic MMR has been found to play a role in a wide array of important cell functions, ranging from regulation of genetic recombination ¹¹ to diversification of antibodies ¹². MMR is also involved in surveillance of DNA damage ¹³, where cells with irreparable DNA damage are targeted by MMR-dependent apoptosis ¹⁴.

Studies on the E. coli MMR pathway provide much valuable insight into its eukaryotic and mammalian counterparts. The critical first step in E. coli MMR is the recognition and binding of MutS to its specific substrates, which in turn signals for the downstream repair activity. Nearly all DNA repair pathways target very specific DNA errors, typically nucleotides modified in a particular way. However, MutS mainly recognizes regular nucleotides that pair with anything other than their Watson-Crick pairing partner in a double-strand context ¹. All signals for repair become lost as soon as the two strands dissociate. Indeed, it is a remarkable feat that E. coli MutS recognizes all eight possible mismatch combinations, as well as insertion/deletion loop (IDL) of up to four nucleotides ^{15; 16}. As the best conserved component in MMR systems, bacterial, eukaryotic, and mammalian MutS homologs all share similar affinities for various substrates ^{15; 17; 18}.

Several crystal structures of bacterial and human MutS homologs complexed with a variety of heteroduplexes all show strikingly similar characteristics ^{19; 20; 21; 22}. The first prominent feature shared by all structures of the complex is a 45~60°-kink in DNA ^{19; 20; 21; 22}, a feature also observed in atomic force microscopy (AFM) studies ²³. Base pairing at the mismatch site undergoes significant reorganization upon MutS binding in order to accommodate the 45~60°-kink in the DNA helix ^{20; 21}. While the flanking sequences adopt a mostly canonical B-DNA form, the major groove narrows and deepens as the minor groove broadens and becomes shallower immediately around the mismatch site ^{20; 21}. When superimposed on the MutS-heteroduplex structure, a straight DNA helix would severely clash with parts of MutS and significantly reduce the protein-DNA interface ²¹.

The second prominent feature shared by all crystal structures of the MutS-heteroduplex complex is an unusually limited number of specific interactions. For E. coli MutS, there are only two protein-DNA interactions involving the DNA base. MutS Phe-36 stacks onto one of the DNA bases at the mismatch site, and MutS Glu-38 forms a hydrogen-bond with the same DNA base, giving rise to the highly-conserved Phe-X-Glu motif^{19; 20; 21}. All other protein-DNA interactions in MutS-heteroduplex complex involve solely the DNA backbone, thus imposing no direct sequence readout for mismatch recognition ^{19; 20; 21}.

Another feature revealed by the structural studies is a common “induced-fit” binding mechanism ^{19; 20; 21}. The binding of a heteroduplex stabilizes the otherwise disordered DNA-binding domains of Taq MutS through extensive protein-DNA interactions ¹⁹. In the crystal structure of the human MutS homolog, hMutSα, complexed with different types of DNA substrates, hMutSα shows coordinated rearrangement to accommodate the different surface contours of particular substrates ²². This “induced-fit” binding mechanism may also help explain the conserved broad spectrum of substrates for the MutS proteins.

MMR is disrupted without a fully functional MutS ATPase domain, the best conserved region in MutS apart from the Phe-X-Glu motif ^{1; 2; 19; 22}. The helix-turn-helix motif in the MutS ATPase domain is crucial for MutS dimer formation, without which MutS cannot bind to its substrates ^{24; 25}. The precise role of ATP binding and hydrolysis by MutS in mismatch recognition is not well-known. Biochemical studies suggest that they might be important in activating interactions between MutS and downstream proteins in MMR ²⁶. Other lines of evidence suggest that ATP binding to MutS acts as a “conformational switch,” which is transmitted via a connector domain to generate conformational changes in the DNA-binding domain ³. Paradoxically, binding of ATP or ATP analogs to MutS decreases the binding affinity of MutS for mismatch sites, with the complex rapidly dissociating upon ATP binding ^{27; 28}. Consequently, ATP binding and hydrolysis by MutS remains an area of active research and intense interest.

In addition, the structural studies show that MutS dimers bind to mismatch sites as asymmetric units ^{19; 20; 21}. For the prokaryotic MutS homodimers, only one monomer interacts specifically with the DNA base via the Phe-X-Glu motif ^{19; 20; 21}. Furthermore, the two ATP binding sites in MutS dimers show considerably different binding affinities for nucleotides ^{29; 30; 31}. These observations are consistent with the fact that eukaryotic MutS homologs generally evolved into heterodimers ³². At a higher organizational level, prokaryotic MutS dimers can further self-associate to form tetramers in equilibrium. However, while MutS tetramers have been reported to interact with the heteroduplex, only one dimer in the tetramer directly interacts with the mismatch ^{33; 34}. A binding model based on the crystal structure of the MutS C-terminal domain (tetramerization domain) also predicts that only one dimer in the E. coli tetramer would directly interact with the mismatch ³⁵. Although MutS single-point mutants deficient in tetramer formation do not completely abolish MMR activity, they give rise to enhanced mutation rates in E. coli³⁵. Furthermore, MutS mutant lacking the C-terminal domain leads to compromised downstream MMR activation in vitro ³⁴ and shows the MutS null phenotype in vivo ³⁶, all pointing towards a crucial biological role for MutS tetramers. However, the precise role of MutS tetramers in mismatch recognition remains under debate.

In this study, we developed a system based on fluorescence resonance energy transfer (FRET) to investigate MutS binding to various mismatch sites and the effect of nucleotide cofactors on binding behavior. The advantage of such a system was that it could unambiguously differentiate between specific and non-specific binding. We measured the equilibrium specific and non-specific binding constants of MutS for various mismatch sites, as well as their respective kinetic association and dissociation rates. We also investigated the stoichiometry of the MutS-heteroduplex complex. Finally, we investigated the impact of nucleotide cofactors in general by examining each MutS binding parameter mentioned above in the presence of nucleotide cofactors. The results in this study provided further clarification of the role of nucleotide cofactors in mismatch recognition by MutS.

2. Results

2.1 Positive Cooperativity in Equilibrium Binding of MutS

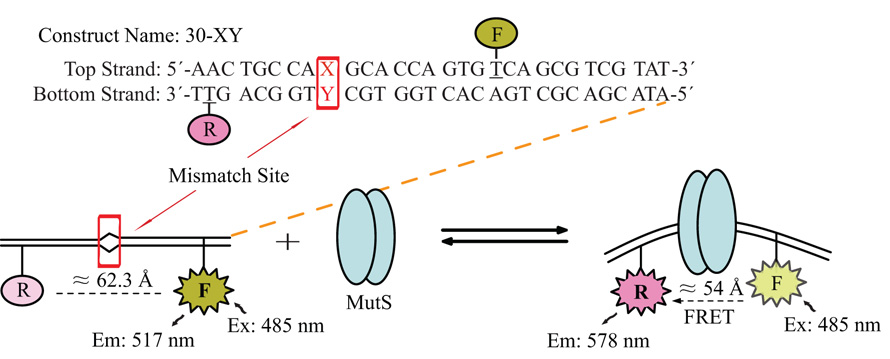
To investigate the binding of MutS to mismatch sites in solution, we used a heteroduplex construct strategically-labeled with a donor and an acceptor on the opposite sides of the mismatch site. The binding of MutS to the heteroduplex induced a kink in the DNA duplex at the mismatch site. This kink led to a change in the distance between the donor and the acceptor, which was in turn monitored by FRET signals. Different combinations of donor and acceptor positions were empirically tested initially and the one that gave rise to the strongest FRET signal was adopted in this study. The basic sequence of the heteroduplex construct and a representation of the experimental scheme in our study are shown in Figure 1. Apart from the mismatch site, denoted by the box, the rest of the sequence was kept identical for all constructs. Changing the nucleotide at the mismatch site allowed us to test all possible mismatch combinations (see Table 1 for the naming of various constructs).

Figure 1. Construct Sequence and Experimental Scheme.

Shown here is the basic sequence of the 30-bp construct, kept identical throughout this study. The box denotes the position of the mismatch site X-Y, which can be configured to produce any mismatch combination. The top strand was labeled with fluorescein, the donor, while the bottom strand was labeled with TAMRA, the acceptor, at the underlined positions. The schematic representation shows that the distance between the donor and acceptor shortened upon MutS binding, giving rise to FRET signals.

Table 1. MutS K_D and K_D-NSP.

Construct Names: the number at the beginning of the construct name indicates the total number of base-pairs in the duplex; while the first and second letter represent the nucleotide at the mismatch site in the top- and bottom-strand respectively. The rest of the sequence was kept identical, as shown in Figure 1. The construct with unpaired-T(s) contained the G-C pair at the mismatch site, with one or two extra deoxythymidines immediately 3′ to the C at the mismatch site in the bottom strand. All MutS concentrations are expressed in monomers. The literature KD values were from

Construct Names	Type of Mismatch	KD or (KD-NSP) at 21°C (nM)	KD or (KD-NSP) at 10°C (nM)	KD or (KD-NSP) from Previous Studies (nM)
30-1ΔT	Unpaired-T	56	62	35 ± 1.6a
30-2ΔT	2 Unpaired-T	74	89	N/A
30-GT	G-T	69	74	39 ± 4b
30-TG	T-G	70	80	39 ± 4b
30-AC	A-C	97	154	53 ± 4b
30-AA	A-A	108	214	110 ± 7b
30-GG	G-G	137	168	150 ± 10b
30-AG	A-G	251	319	270 ± 30b
30-TT	T-T	321	291	140 ± 9b
30-CT	C-T	331	324	370 ± 40b
30-CC	C-C	410	300	480 ± 50b
30-GC	Homoduplex	(23111)	(30499)	(390 ± 64)a

^aIAsys biosensor binding studies ³⁷ and from

^bfoot-printing binding studies ¹⁶.

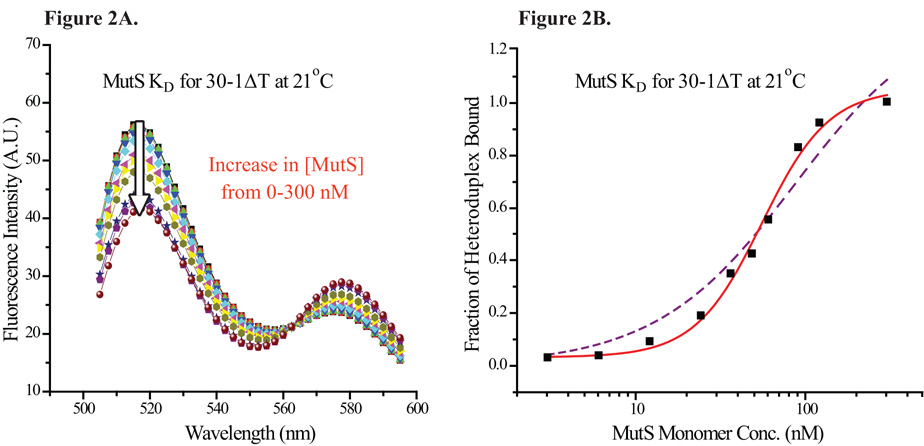
A titration of the heteroduplex with increasing MutS concentration led to a decrease in the donor peak emission and an increase in the acceptor peak emission, as shown in Figure 2A. Control experiments with singly-labeled single-strand DNA (ssDNA) or singly-labeled heteroduplexes (labeled with only the donor or the acceptor) all showed a small decrease in the emission when titrated with MutS (data not shown). The precise reason for the relatively small reduction in signal (5~8% at saturation) was unknown (see discussion). Nevertheless, for the data obtained with the doubly-labeled heteroduplex, analysis of either the donor or the acceptor emission yielded comparable results (data not shown). These results indicated that the small reduction in signal likely had little effect on data analysis.

Figure 2. Equilibrium Titration of Heteroduplexes with MutS.

(2A) Equilibrium titration scan of 30-1ΔT with increasing MutS concentration; excitation wavelength = 485 nm. The arrow points in the direction of increasing MutS monomer concentration, from 0 to 300 nM. As the MutS concentration rose, the fluorescein emission peak decreased and the TAMRA peak emission increased. (2B) The intensity of fluorescein peak (517 nm) was taken from each trace and normalized to represent the fraction of heteroduplexes bound by MutS. The binding profile of 30-1ΔT by MutS was fitted to a sigmoidal function, shown by the solid line. The fit provided by a 1:1 binding isotherm, shown by the dashed line, did not describe the data as closely as the fit provided by a sigmoidal function.

As the donor gave rise to greater signal change than the acceptor, the data here draw on the donor peak emission normalized using Equation 1. The normalized signal was then plotted against the protein concentration in log scale (Figure 2B). The binding profile was fitted to a sigmoidal function (Equation 2, solid line in Figure 2B), which provided a better fit for the observed data than a 1:1 binding isotherm (dashed line in Figure 2B). Interestingly, MutS binding profiles to other mismatches all showed similar characteristics (Supplementary Figure S1), suggestive of positive cooperativity in MutS binding. Furthermore, compiled MutS-heteroduplex binding curves yielded a Hill coefficient of 2.4 ± 0.4, a characteristic of positive cooperativity. While a large Hill coefficient by itself is not always a dependable indicator for positive cooperativity, several other findings (see below) supported the view that E. coli MutS bound to heteroduplexes with positive cooperativity.

The MutS K_D measured in this manner for all eight mismatch combinations as well as IDL of 1–2 nucleotides ranged from 56 to 410 nM (Table 1). The K_D obtained in the equilibrium titrations showed the order of MutS affinity for different types of mismatch to be 1ΔT > 2ΔT ≈ G-T > A-C ≈ A-A > G-G > A-G > T-T ≈ C-T > C-C, in good agreement with previous studies ^{16; 37}. We carried out the equilibrium titrations at two different temperatures, 10°C and 21°C. With the exception of the three weakest substrates for MutS (T-T, C-T, and C-C), MutS generally showed stronger affinity to its specific substrates at the higher temperature (Table 1). These results indicated that the specific binding reaction of MutS was endothermic in most cases, while the binding reaction appeared to be exothermic when interacting with the weakest substrates.

2.2 Positive Cooperativity in Kinetic Association of MutS

We used stopped-flow fluorometry to probe the kinetics of MutS binding to the heteroduplex. As in equilibrium binding experiments, the change in distance between the donor and the acceptor gave rise to FRET signals. Rapid mixing of labeled heteroduplexes and MutS protein in large excess produced a decrease in the donor emission that was observed in real time. Under the assumption of pseudo-first-order reaction, four or more kinetic traces of MutS associating with the heteroduplex were averaged and fit to a single-exponential function, yielding the apparent association rate (k_obs).

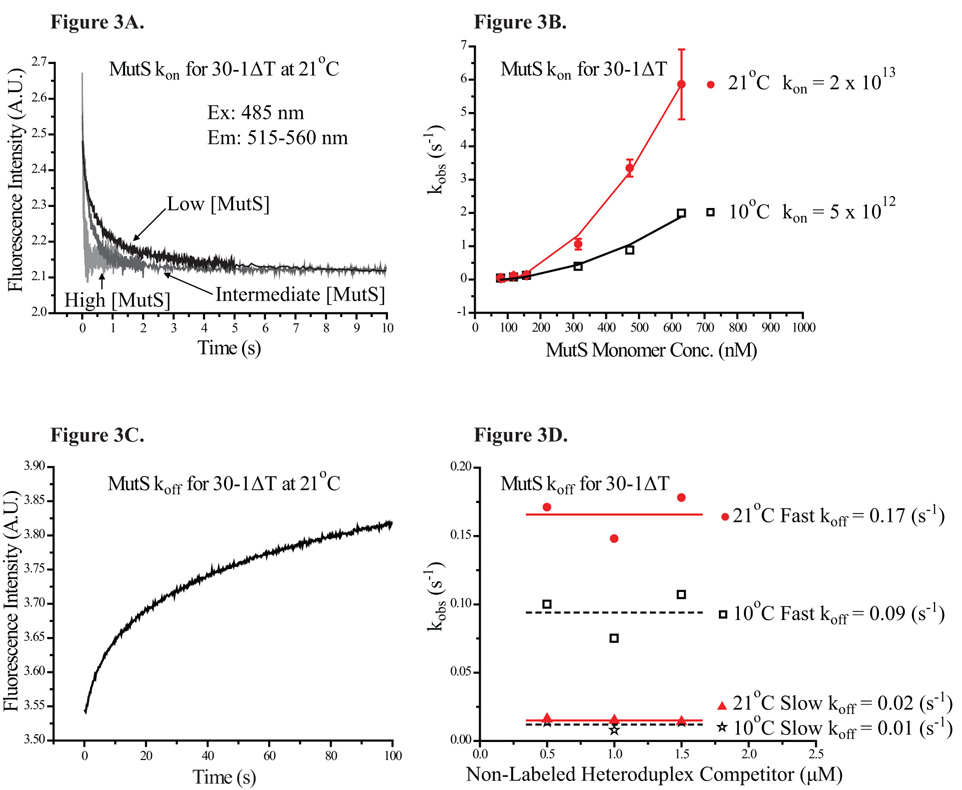
The kinetic association traces of 30-1ΔT with MutS at three different concentrations are shown in Figure 3A, where the rate of association visibly increased with rising MutS concentration. The k_obs of MutS with 30-1ΔT was plotted against the MutS concentration (Figure 3B). The binding profile was then fitted to a simple quadratic function (Equation 6), giving rise to a third-order association rate constant (k_on). The lack of linearity in the k_obs profile was once again indicative of positive cooperativity. Interestingly, the k_obs profiles of MutS for two additional constructs, 30-GT and 30-AA, both showed the same characteristics of positive cooperativity as 30-1ΔT. Furthermore, the MutS k_on value for all three constructs tested were essentially identical (Table 2), while the MutS K_D for 30-AA and 30-1ΔT showed a 2-fold difference (Table 1). This result suggested that k_on was not responsible for the change in MutS K_D for different mismatch sites. Kinetic association measurements at different temperature showed that the k_on of MutS for 30-1ΔT was 2 × 10¹³ (s⁻¹M⁻²) at 21°C and 5 × 10¹² (s⁻¹M⁻²) at 10°C (Figure 3B, Table 2). While the k_on was significantly slower at the lower temperature, the kinetic traces retained the characteristics of positive cooperativity.

Figure 3. Kinetic Association and Dissociation Profiles of MutS.

(3A) Kinetic association traces of MutS at three different concentrations with 30-1ΔT are shown here. The intensity of the fluorescein peak decreases at different rates depending on the final concentration of MutS. (3B) The apparent kinetic association rates for two different temperatures are plotted against concentration of MutS. The resulting kinetic association profiles were fitted with a simple quadratic function, indicative of positive cooperativity. (3C) Shown here, kinetic dissociation trace of MutS-30-1ΔT complex was fitted to a double-exponential function, yielding two rates. (3D) The apparent kinetic dissociation rates for two different temperatures are plotted against concentration of non-labeled heteroduplex competitors. The kinetic dissociation rates remained constant regardless of the concentration of competitors.

Table 2. Effect of Different Heteroduplex Constructs, Temperature, and Nucleotide Cofactors on MutS Kinetic Association and Dissociation Rates.

Construct	Temp. (°C)	kon (s−1M−2)	Fast koff (s−1)	$K_D=\sqrt{\frac{k_{\mathit{\text{off}}}}{k_{\mathit{\text{on}}}}}$ (nM)	Slow koff (s−1)	$K_D=\sqrt{\frac{k_{\mathit{\text{off}}}}{k_{\mathit{\text{on}}}}}$ (nM)	KD (Equi.) (nM)
30-1ΔT	21	2 × 1013	0.17	91	0.02	27	56
30-GT	21	2 × 1013	0.17	91	0.01	26	64
30-AA	21	2 × 1013	0.47	153	0.08	63	108
30-1ΔT	10	5 × 1012	0.09	137	0.01	50	62
30-1ΔTa (AMPPNP)	21	6 × 105 a; b (AMPPNP)	0.19 a (AMPPNP)	321 c	0.02 a (AMPPNP)	39 c	123 a (AMPPNP)

^aThe kinetic association and dissociation rates as well as equilibrium K_D, were measured in the presence of 1 mM AMPPNP.

^bThe MutS k_on for 30-1ΔT was obtained through a linear function, bearing the unit of s⁻¹M⁻¹.

^cIn the presence of 1 mM AMPPNP, K_D = k_off/k_on. All MutS concentrations are expressed in monomers.

2.3 Kinetic Dissociation Rates of MutS-Heteroduplex Complex

We employed stopped-flow fluorometry to probe the dissociation kinetics of MutS from the heteroduplex. By rapid mixing of the preformed specific complex with non-labeled heteroduplexes in great excess, MutS dissociating from the specific complex would predominately re-associate with the non-labeled heteroduplexes. The rate of signal increase of donor emission in real-time was indicative of the MutS dissociation rate (k_off). A representative kinetic dissociation trace of MutS-30-1ΔT complex is shown in Figure 3C. Alternatively, by rapid mixing labeled heteroduplexes with preformed non-labeled-heteroduplex-MutS complex, the rate-limiting dissociation reaction could be derived from the rate of MutS binding to the labeled heteroduplex. The two experimental methods yielded very similar results as expected; the data we present here were collected via the first experimental method. Interestingly, the kinetic dissociation traces of MutS-heteroduplex for both experimental methods displayed two phases and could only be adequately described by a double-exponential function.

The biphasic quality in the kinetic dissociation traces of MutS-heteroduplex suggested that there were two processes in the dissociation reaction. To determine whether there were two distinct processes taking place, we carried out sequential-flow fluorometry experiments and found that these two processes progressed concurrently (see Supplementary Figure S2). To further evaluate the possibility of a FRET kinetic component due to DNA strand exchange, competitors of different sequences were employed to challenge the pre-formed complex in the dissociation reactions. In one instance the competitor and the heteroduplex in the pre-formed complexes shared the same sequence; in the other instance they did not. The resulting dissociation traces in either case appeared similarly biphasic (data not shown), ruling out the possibility of interference contributed by DNA strand exchange.

Here, we reported both k_off values (a fast k_off and a slow k_off) associated with each heteroduplex tested (Table 2). While both the fast and slow k_off appeared to remain constant regardless of the competitor concentrations (Figure 3D), MutS complexed with different mismatch sites showed noticeably different k_off values (Table 2). The fast and slow k_off of MutS-30-1ΔT was ≈ 0.17 (s⁻¹) and ≈ 0.02 (s⁻¹) respectively. MutS K^D values for 30-1ΔT could be derived from the k_on and k_off values ($K_D=\sqrt{\frac{k_{\mathit{\text{off}}}}{k_{\mathit{\text{on}}}}}$, Equation 7).

Considering either the fast k_off or the slow k_off, the MutS K_D for 30-1ΔT was calculated to be 91 nM and 27 nM respectively, roughly in agreement with the K_D of 56 nM from equilibrium measurements. Similarly, the k_off of MutS-30-GT complex was ≈ 0.17 (s⁻¹) and ≈ 0.01 (s⁻¹), yielding K_D values of 91 nM and 26 nM respectively, again roughly agreeing with the equilibrium K_D of 64 nM. For a weaker MutS substrate, the k_off of MutS-30-AA complex was ≈ 0.47 (s⁻¹) and ≈ 0.08 (s⁻¹), 3- to 4-fold faster than that of either MutS-30-1ΔT or MutS-30-GT complex. The calculated K_D values for 30-AA was 163 nM and 63 nM, similar to the equilibrium K_D of 108 nM (Table 2). The K_D values calculated from k_on and the fast k_off were roughly 2- to 3-fold higher than the equilibrium K_D values, whereas the K_D values calculated from k_on and the slow k_off were roughly 1- to 3-fold lower than the equilibrium K_D values (Table 2). More importantly, the K_D values for different heteroduplexes calculated from the kinetic rate constants clearly showed a consistent trend with their respective K_D value obtained from the equilibrium studies. The kinetic association and dissociation studies together suggested that the k_off values of the specific complex were the determining factor in MutS affinity for various mismatch sites.

To probe the effect of temperature on the dissociation kinetics of MutS specific complex, we measured the k_off of MutS-30-1ΔT complex at 10°C, which were ≈ 0.09 (s⁻¹) and ≈ 0.01 (s⁻¹) (Figure 3D). From these k_off values, the K_D values were estimated to be 137 nM and 50 nM respectively, comparable to the equilibrium K_D of 62 nM at 10°C (Table 2). Analysis of the kinetic association and dissociation of MutS-30-1ΔT complex at two different temperatures revealed that the cause for the decreased MutS affinity at the lower temperature was the much smaller k_on in this case.

2.4 MutS Non-Specific Binding Constants: Competition Assays

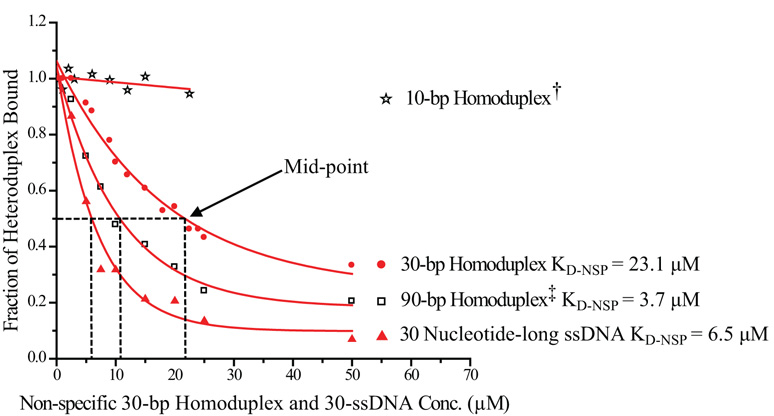
We employed competition assays to probe the non-specific binding of MutS in solution. When encountering a mixed population of heteroduplex and homoduplex in solution, the extent of MutS binding to either substrate depended on the relative strength of MutS affinities for the two substrates. Since the equilibrium between free MutS and MutS-heteroduplex complex was linked to the equilibrium between free MutS and MutS-homoduplex complex, the non-specific binding constant (K_D-NSP) of MutS could be extracted from the competition assays. In these competition assays, MutS was combined with a DNA solution containing a fixed concentration of labeled heteroduplex and an increasing concentration of non-labeled homoduplex. Each sample was incubated a minimum of 5 minutes before recording the fluorescence spectrum, or at least 6-fold the relaxation time for dissociation of the slowly dissociating complex (1/0.02 s⁻¹ = 50 s, Table 2), thus assuring equilibration of the system. The change in the FRET signal correlated with change in the amount of specific complex. As the concentration of homoduplex in the sample increased, the extent of specific binding of heteroduplex by MutS decreased. Titration profiles of MutS-30-1ΔT complex by various homoduplex competitors are shown in Figure 4.

Figure 4. Non-Specific Binding of MutS: Competitions Assays.

Titration of a preformed MutS-30-1ΔT complex with non-labeled non-specific competitors at 21°C: 10-bp homoduplex^† (star), 30-bp homoduplex (filled circle), 90-bp homoduplex^‡ (open box) and 30 nucleotide-long single-strand DNA (filled triangle). For ease of comparison, the 10-bp homoduplex^† is plotted as 1/3 of its actual molar concentration and the 90-bp homoduplex^‡ is plotted as 3 times its actual molar concentration. Thus at any given concentration, the molar concentration of DNA base-pairs would be kept equal across different samples (see text for details). The dashed line indicates the concentration of competitors required to cause half of the preformed specific complex to dissociate. For 30-bp homoduplex, ≈ 21.8 µM was required; for 90-bp homoduplex, ≈ 3.6 µM was required; for 30-ssDNA, ≈ 6.2 µM was required. For 10-bp homoduplex, even at the highest concentration tested, at 67.5 µM, only ≈ 5% of the specific complex became dissociated. The calculated KD-NSP was ≈ 23.1 µM for 30-bp homoduplex, ≈ 3.7 µM for 90-bp homoduplex, and ≈ 6.5 µM for 30-ssDNA.

Note that the presence of some MutS-heteroduplex complex even in the sample with the highest concentration of homoduplex was consistent with expectations: The slowly dissociating MutS-30-1ΔT complex had a kinetically-estimated K_D of 27 nM (Table 2), whereas the homoduplex had an estimated K_D-NSP of 23 µM, or 1000 times weaker binding than the heteroduplex. At the highest concentration, homoduplex exceeded heteroduplex by 2500-fold, which was equivalent to only 2.5-fold in binding capacity. Thus it was expected that ≈ 30% of the MutS-heteroduplex complex would remain.

Our binding model (Equation 3) assumed that MutS bound as a tetramer to each mismatch site, as demonstrated experimentally below. Since we were unable to directly determine the stoichiometry of non-specific complexes, the binding model assumed that MutS bound non-specifically to DNA as a dimer. Here we reported the K_D-NSP values that represented a relatively conservative estimate, as the assumption of MutS tetramer binding in non-specific complexes would produce values of K_D-NSP that are roughly twice as large. However, the net non-specific binding was unaffected by the assumption, since tetramer binding involves four monomers instead of two, but with half the affinity.

We determined the concentration of competitors required to cause 50% of the preformed specific complex to dissociate, represented by the dashed line in Figure 4. With the exception of the mismatch site, all 30-bp homoduplex and 30-bp heteroduplex constructs shared identical sequences (Figure 1). The 30-bp homoduplex constructs had G-C Watson-Crick pairs instead of a mismatch. From the relationship defined by Equation 3, we were able to determine the specificity S of MutS (S = K_D-NSP/K_D). From the predetermined value of K_D of the specific complex, we then calculated the K_D-NSP of MutS for a 30-bp homoduplex to be ≈ 23.1 µM, which was 413-fold weaker than the binding of 30-1ΔT (S = 413, Table 1). We note that under the assumption of MutS tetramer binding to homoduplexes, the S values would be roughly twice as large. Therefore the S value of 413 for E. coli MutS reported in this study represented a relatively conservative estimate.

To assess the role of end-binding in non-specific binding by MutS, we carried out the same competition assay with a 10-bp homoduplex and a 90-bp homoduplex in addition to the 30-bp homoduplex. To minimize the impact of sequence variance on MutS affinity, the sequence of the 10-bp, 30-bp, and 90-bp homoduplex were carefully kept comparable to each other, while all constructs had blunt DNA ends. Specifically, dividing the sequence of 30-bp homoduplex into three 10-bp-long pieces, we mixed equal amounts of all three pieces to generate the final 10-bp homoduplex sample. The sequence of the 90-bp homoduplex also contained the 30-bp homoduplex sequence internally. For ease of comparison, the 10-bp homoduplex is plotted as 1/3 of its actual concentration while the 90-bp homoduplex is plotted as 3 times its actual concentration in Figure 4. Thus at a given concentration, the molar concentration of DNA base-pairs would be kept equal for the three non-specific competitors even though they differ in concentration of DNA molecules. Nevertheless, compared to the 30-bp homoduplex, the 10-bp homoduplex would have 3 times as many DNA ends while the 90-bp homoduplex would have only 1/3 as many DNA ends. If MutS has significant affinity for the DNA ends, the order of MutS affinity for different non-specific competitors from high to low would be 10-bp > 30-bp > 90-bp homoduplex. However, we observed the opposite results: the order of MutS affinity from high to low was 90-bp > 30-bp > 10-bp homoduplex (Figure 4). Our results suggested that E. coli MutS did not have a significant affinity for DNA ends.

The calculated K_D-NSP was ≈ 23.1 µM for 30-bp homoduplex and ≈ 3.7 µM for 90-bp homoduplex, a 6-fold difference, while there was only a 3-fold difference in the molar concentration of DNA base-pairs. Whereas other explanations remained possible, our results suggested that MutS had low or no affinity for the region near DNA ends. Indeed, MutS failed to bind to the 10-bp homoduplex with appreciable affinity. Even with the highest concentration of 10-bp homoduplex competitor present (67.5 µM), ≈ 95% of the preformed MutS-heteroduplex complex remained bound. Thus, the K_D-NSP of MutS for 10-bp homoduplex was too weak to be measured via our competition assays. Furthermore, the approximate length of DNA region near the DNA ends with no detectable MutS affinity could be estimated from the MutS affinities for homoduplexes of difference lengths (Equation 4). Taken together, the MutS affinities for 90-bp, 30-bp, and 10-bp homoduplex suggested that MutS did not have detectable affinity for up to ≈ 9-bp at the end region of DNA constructs.

We carried out the same competition assay with a 30-nucleotide-long ssDNA (30-ssDNA), in this case either the top or the bottom strand of the 30-bp homoduplex. The calculated K_D-NSP was ≈ 6.5 µM for 30-ssDNA. Comparison of MutS K_D-NSP for 30-bp homoduplex and 30-ssDNA (Figure 4) revealed that MutS had nearly 4-fold higher affinity for ssDNA than for double-strand DNA, a result that might have significant implication in eukaryotic MMR mechanism. Lastly, to test the effect of temperature on MutS non-specific binding, we also compared the competition assays carried out at both 21°C and 10°C. The calculated K_D-NSP for 30-bp homoduplex was ≈ 30.5 µM at 10°C, higher than the K_D-NSP of ≈ 23.1 µM for the same construct at 21°C (Table 1), indicating weaker MutS non-specific binding at the lower temperature.

2.5 The Effect of Nucleotide Cofactors on Cooperativity of MutS Binding

Functional ATPase domains in MutS, which bind and hydrolyze ATP at a moderate rate, are required for triggering downstream activity in MMR ^{1; 2}. While ATP binding by MutS has been shown to decrease its binding affinity for the heteroduplex ^{27; 28}, the precise role of ATP in the MMR mechanism is not well understood. In this study, we used a non-hydrolysable ATP analog, 5′-adenylyl-imidodiphosphate (AMPPNP), to probe the effect of ATP binding on the kinetics and specificity of MutS binding. Equilibrium titrations of the labeled heteroduplex with increasing MutS concentration were carried out in the presence of AMPPNP. The fraction of heteroduplexes bound by MutS in the presence of AMPPNP of various concentrations was plotted against MutS concentration in log scale (Figure 5A).

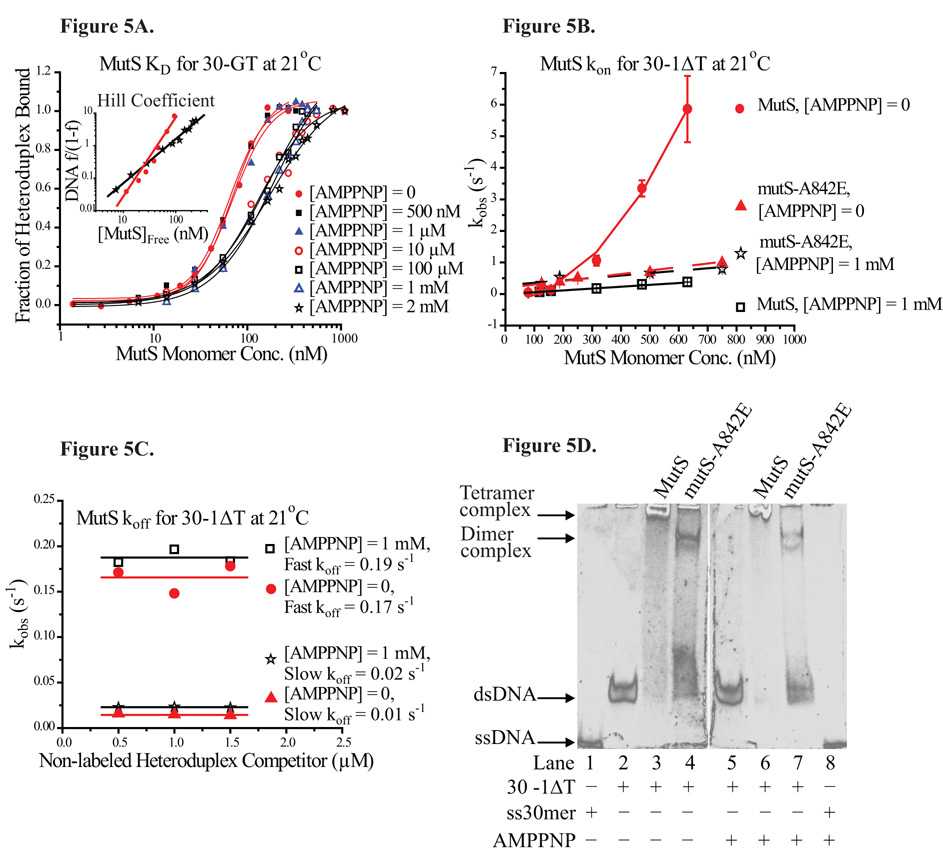
Figure 5. Effect of AMPPNP on Specific Binding of MutS.

(5A) Equilibrium titration of 30-GT by increasing MutS in the presence of different amounts of AMPPNP, ranging from 0 to 2 mM. The Hill plot representing binding profiles of MutS for 30-GT in the absence and in the presence of 2 mM AMPPNP is shown in the inset. The Hill coefficient decreased from 2.4 to 1.4. (5B) The apparent kinetic association rates of MutS for 30-1ΔT in the absence of AMPPNP (filled circle) and in the presence of 1 mM AMPPNP (open box). The apparent kinetic association rates of mutS-A842E in the absence of AMPPNP (filled triangle) and in the presence of 1 mM AMPPNP (star). (5C) The apparent kinetic dissociation rates of MutS-30-1ΔT complex in the absence and in the presence of 1 mM AMPPNP. (5D) EMSA: Lane 1: 30-ssDNA, Lane 2: 30-1ΔT, Lane 3: 30-1ΔT complexed with 1µM MutS, Lane 4, 30-1ΔT complexed with 1 µM mutS-A842E, (Lane 5~8: with 1 mM AMPPNP) Lane 5: 30-1ΔT, Lane 6: 30-1ΔT complexed with 1µM MutS, Lane 7, 30-1ΔT complexed with 1 µM mutS-A842E, Lane 8: 30-ssDNA.

The equilibrium titrations showed that in the presence of less than 1 µM AMPPNP, the value of MutS K_D for 30-GT was essentially unaffected. However, in the presence of more than 10 µM (up to 2 mM) AMPPNP, the value of MutS K_D increased from ≈ 69 nM to 176 nM, a more than 2-fold increase. In the presence of more than 10 µM AMPPNP, the shape of the equilibrium titration profiles also changed appreciably, signifying some loss of positive cooperativity. A comparison of MutS binding profiles for different heteroduplexes showed that all 11 constructs used in this study gave rise to very similar Hill coefficient values (2.4 ± 0.4 on average). Meanwhile, the MutS binding profiles of constructs tested in the presence of more than 10 µM AMPPNP gave rise to markedly lower Hill coefficient values (1.6 ± 0.2 on average). As shown in the inset of Figure 5A, the Hill coefficient of MutS binding to 30-GT decreased from ≈ 2.4 (no AMPPNP) to ≈ 1.4 (2 mM AMPPNP), indicative of loss of positive cooperativity.

To investigate the effect of AMPPNP on the kinetic binding of MutS, we measured the k_on and k_off of MutS for 30-1ΔT in the presence of 1 mM AMPPNP. The k_obs profiles of MutS binding to 30-1ΔT both in the absence and in the presence of 1 mM AMPPNP are shown in Figure 5B (filled circle and open box, respectively). The two k_obs profiles showed significantly different characteristics. While the values of k_obs were very similar at lower MutS concentrations (< 200 nM), the k_obs values of MutS were much lower in the presence of AMPPNP at higher MutS concentrations. In fact, the k_obs values in the presence of AMPPNP displayed a linear relationship with MutS concentration instead of the cooperative quality defined by the simple quadratic function (Equation 6) in the absence of AMPPNP. The kinetic association profile of MutS with 30-1ΔT in the absence of AMPPNP was fit to a simple quadratic function, yielding a k_on of 2 × 10¹³ (s⁻¹M⁻²) at 21°C. However, the same kinetic association profile in the presence of 1 mM AMPPNP was fit to a linear function, yielding a k_on of 6 × 10⁵ (s⁻¹M⁻¹) (Table 2). Another common ATP analog, adenosine 5′-(γ-thio) triphosphate (ATPγS), is hydrolysable albeit at a very slow rate. To ensure that AMPPNP was not unique in its ability to instigate the observed changes in MutS binding behavior, we also determined the kinetic association profile of MutS with 30-1ΔT in the presence of ATPγS, which yielded a comparable k_on of ≈ 4 × 10⁵ (s⁻¹M⁻¹) (Supplementary Figure S3).

In contrast, the presence of 1 mM AMPPNP did not appear to affect the kinetic dissociation profile of MutS-heteroduplex complexes. Similar to the earlier results in the absence of AMPPNP, the kinetic dissociation traces of the MutS-30-1ΔT continued to display two phases in the presence of AMPPNP. These traces were fit to a double-exponential function, yielding two k_off values (a fast k_off and a slow k_off). Both the fast and slow k_off values remained constant regardless of the competitor concentrations (Figure 5C). The k_off values of MutS-30-1ΔT in the absence and in the presence of 1 mM AMPPNP were comparable to each other. The fast and slow k_off was 0.17 s⁻¹ and 0.02 s⁻¹ respectively in the absence of AMPPNP, while the fast and slow k_off was 0.19 s⁻¹ and 0.02 s⁻¹ respectively in the presence of AMPPNP (Figure 5C, Table 2). These results suggested that AMPPNP-binding did not affect the dissociation process of MutS-heteroduplex complexes. Kinetic dissociation experiments in the presence of ATPγS yielded similar results as AMPPNP (Supplementary Figure S3). In summary, when bound by AMPPNP, MutS did not bind to heteroduplexes with appreciable cooperativity, resulting in a significantly decreased k_on value. Conversely, the k_off of MutS from the specific complex was unaffected by AMPPNP binding. In the presence of AMPPNP, the decrease in MutS specific affinity could be attributed mainly to the decrease in k_on values due to loss of positive cooperativity.

2.6 Tetramer Formation Required for MutS Binding Cooperativity

The ability of MutS dimers to form oligomers of higher orders in solution (e.g. tetramers or hexamers) is a probable source of positive cooperativity in MutS binding. To further evaluate whether the loss of tetramer formation would lead to loss of positive cooperativity, we tested a MutS mutant deficient in tetramer formation, mutS-A842E. In mutS-A842E, the single-point mutation is located on the C-terminal domain that has been shown to be critical for MutS tetramer formation. Another example is the truncated MutS variant used in crystal structural studies that lacks the C-terminal domain (residues 801~853), rendering it incapable of forming tetramers ^{34; 38}.

In electrophoresis mobility shift assay (EMSA), the mutS-A842E-30-1ΔT complex traveled much faster than the MutS-30-1ΔT complex (Figure 5D). From this result we inferred that MutS likely interacted as tetramers with heteroduplexes and that mutS-A842E likely interacted as dimers with heteroduplexes. Interestingly, the kinetic association profile of mutS-A842E with 30-1ΔT (filled triangle in Figure 5B) also lacked the cooperative quality defined by the simple quadratic function in the kinetic association profile of MutS (filled circle in Figure 5B). The presence of AMPPNP did not significantly alter the kinetic association profile of mutS-A842E with 30-1ΔT (star in Figure 5B). Furthermore, the kinetic association profile of mutS-A842E was remarkably similar to that of AMPPNP-bound MutS (Figure 5B). Indeed, the similarity in the kinetic association behaviors of mutS-A842E and AMPPNP-bound MutS suggested that AMPPNP binding might be involved in signaling against cooperative tetramerization.

2.7 The Effect of Nucleotide Cofactors on MutS Non-Specific Binding

To investigate the effect of AMPPNP on MutS non-specific binding, we carried out the competition assays described in section 2.4 in the presence of 1 mM AMPPNP. The calculated K_D-NSP changed from ≈ 23.1 µM to ≈ 169.2 µM for 30-bp homoduplex upon addition of AMPPNP (Table 3); whereas the specific K_D only changed from 56 nM to 123 nM for 30-1ΔT upon addition of AMPPNP (Table 3). Both MutS specific affinity and non-specific affinity decreased in the presence of AMPPNP; however, the MutS non-specific affinity decreased much more drastically than MutS specific affinity. As a result, the relative S value between 30-bp homoduplex and 30-1ΔT increased from 413 to 1376, a 3-fold increase upon addition of AMPPNP. For 30-ssDNA, the calculated K_D-NSP changed from ≈ 6.5 µM to ≈ 27.3 µM upon addition of AMPPNP. The relative S between 30-1ΔT and 30-ssDNA increased from 116 to 222 upon addition of AMPPNP, a nearly 2-fold increase.

Table 3. Effect of Nucleotide Cofactors on MutS Non-specific Binding.

Non-specific Construct	AMPPNP Conc. (mM)	MutS KD-NSP (µM)	MutS KD for 30-1ΔT (nM)	S = KD-NSP/KD.
30-bp Homoduplex	0	23.1	56	413
	1	169.2	123	1376
30-ssDNA	0	6.5	56	116
	1	27.3	123	222

All competition assays as well as the equilibrium titration of MuS for 30-1ΔT were carried out at 21°C. Relative specificity, S = K_D-NSP/K_D.

2.8 The Effect of Nucleotide Cofactors on Stoichiometry of the MutS-Heteroduplex Complex

To distinguish dimer from tetramer stoichiometry in the MutS-heteroduplex complex, we carried out a titration of 600 nM heteroduplex (≈ 10-fold K_D) with increasing MutS concentration. The high concentration of heteroduplex in the sample ensured that nearly all MutS in the sample would be in the bound state prior to saturation. As seen in Figure 6, the fraction of bound heteroduplexes increased linearly with the MutS concentration in the initial stage of the titration (250~1000 nM MutS). As the MutS concentration rose close to the saturation point, the linearity became lost. Eventually the number of MutS molecules exceeded the number needed to fully complex all available heteroduplexes. Additional MutS molecules did not instigate additional change in the FRET signals, reaching a plateau. To obtain the stoichiometry of the MutS-heteroduplex complex, the slope of the initial linear phase was determined for each series of data points. A minor correction term involving the K_D of the specific complex was then applied to the slope to account for the non-stoichiometric binding behavior (Equation 5). The stoichiometry for MutS-30-1ΔT determined this way was 3.6 : 1 (n = the number of MutS monomer in complex with one heteroduplex, n ≈ 3.6 in this case). Thus, the stoichiometry value of MutS-30-1ΔT revealed that MutS bound to each heteroduplex predominantly as tetramers, in good agreement with our EMSA results (Figure 5D).

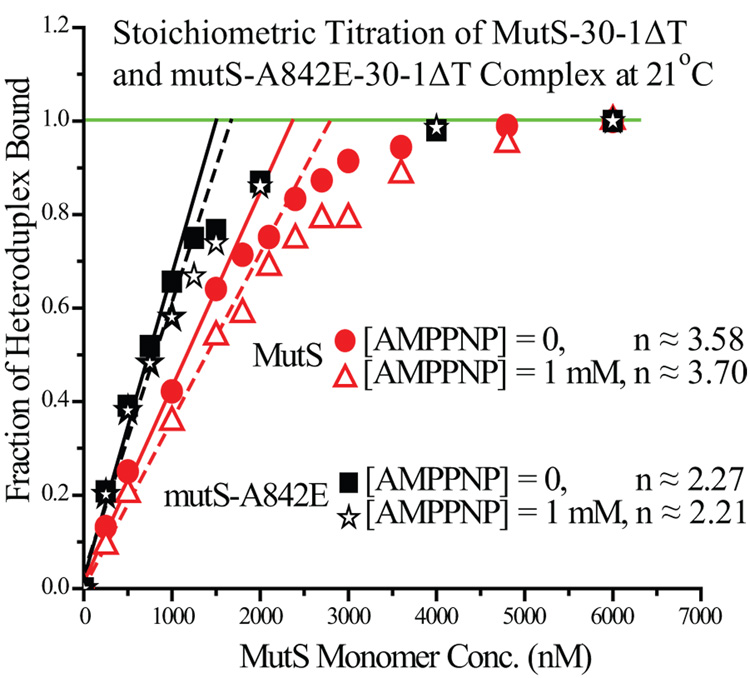
Figure 6. Effect of AMPPNP on Stoichiometric Titration of Heteroduplexes by MutS and mutS-A842E.

High concentrations of heteroduplex (600 nM ≈ 10-fold KD) was titrated by increasing concentrations of either MutS or mutS-A842E, a single-point mutation deficient in tetramer formation. The titrations were carried out both in the absence and in the presence of 1mM AMPPNP. The initial linear phase is evident for both sets of titration data, as is the plateau region near the end. A correction term was applied to the slope of the initial data points (MutS ≤ 1000 nM) to calculate the value of stoichiometry of MutS-heteroduplex complex (see Materials and Methods). The stoichiometry of MutS-30-1ΔT was determined to be 3.58 in the absence of nucleotide cofactors, and 3.7 in the presence of 1 mM AMPPNP. Whereas the stoichiometry of mutS-A842E-30-1ΔT was determined to be 2.27 in the absence of nucleotide cofactors, and 2.21 in the presence of 1 mM AMPPNP.

We also carried out the same stoichiometric titration with mutS-A842E, the mutant deficient in tetramer-formation. The stoichiometric titration with mutS-A842E showed that this mutant variant bound to heteroduplexes primarily as dimers (n ≈ 2.3) (Figure 6), again in good agreement with our EMSA results (Figure 5D). Furthermore, stoichiometric titration in the presence of 1 mM AMPPNP was carried out to investigate the effect of AMPPNP on stoichiometry of MutS-heteroduplex complex. Interestingly, the presence of AMPPNP did not change the extent of MutS tetramer formation, with MutS binding to each specific heteroduplex predominantly as tetramers (n ≈ 3.7) (Figure 6). Similarly, mutS-A842E bound to each heteroduplex predominately as dimers in the presence of AMPPNP (n ≈ 2.2) (Figure 6).

In addition, we employed EMSA to compare the MutS specific complex samples in the presence of AMPPNP (Figure 5D, Lane 5~8) to the ones in the absence of AMPPNP (Figure 5D, Lane 1~4). The results showed no change in mobility of the complexes upon addition of AMPPNP. The stoichiometric titrations and the EMSA findings all lent supports to the model that MutS bound to heteroduplexes as tetramers at saturating concentrations, while mutS-A842E bound as dimers. The presence of AMPPNP did not affect the stoichiometry of either MutS-heteroduplex or mutS-A842E-heteroduplex complex. The point mutation in mutS-A842E presumably blocked tetramer formation by repulsive interaction or steric clash. It appeared that AMPPNP eliminated or sharply reduced the cooperative interaction between dimers, but did not prevent tetramer formation in the complex.

3. Discussion

One of the central questions concerning the mechanism of MMR pathway is how MutS recognizes its uniquely broad spectrum of specific substrates. Among the vast amount of DNA materials in the genome, the task of MutS to efficiently locate a mismatch, either produced by the replication machinery or the process of recombination, is a challenging one. Indeed, roughly half of the reported mutations contributing to HNPCC are mapped to the genes of human MutS homologs, underlining the significance of their proper function ^{39; 40}. Mismatch sites, lacking the modified chemical groups generally prevalent in other types of DNA damage, would be nearly undistinguishable from most normal DNA base-pairs from a chemical structural point of view. Yet remarkably, MutS achieves specificity without forming an extensive network of specific interactions with the mismatch site in the complex. Currently, much less is known about the non-specific binding than the specific binding of MutS. Moreover, since a fully functional ATPase domain in MutS is required for downstream MMR activities ^{1; 2}, the role of nucleotide cofactors in MutS binding mechanism is a point of intense interest and debate.

We exploited the 45~60° kink in the DNA helix upon MutS binding and developed a FRET-based system to study the equilibrium and kinetic binding of MutS in solution. The construct shared the same sequence as the one used in the structural studies of E.coli MutS ¹⁹, with minor changes to accommodate the strategically-placed fluorophores. (Figure 1). Such a system could unambiguously distinguish between MutS specific binding to mismatch sites and MutS non-specific binding to homoduplexes, since the FRET signal would only arise from the former. We note that a small reduction in intensity of fluorophore emission was observed in singly-labeled heteroduplexes (donor or acceptor only) when bound by MutS. To further evaluate whether the fluorophores were specific binding substrates for MutS, a competition assay was carried out. When challenged by competitors labeled with either one or both or no fluorophores, MutS showed comparable affinities for the heteroduplex in each case, indicating that the fluorophores were not specific binding substrates for MutS (Supplementary Figure S4).

While we were unable to rule out other possibilities, inspection of the crystal structure suggested that MutS binding to nearby mismatch sites could lead to change in local environment of the fluorophores. Such changes could give rise to additional change in fluorescence intensity that is strongly coupled with nearby MutS binding. Future binding studies might benefit from employing a donor-acceptor pair with a longer Förster distance that would allow the fluorophores to be further separated from the binding site. Although this small reduction in intensity of fluorophore emission complicated the data analysis of the kinetic dissociation rates (see below), its impact on the data analysis of all other experiments was negligible. All E. coli MutS protein used in this study included a His-tag on the N-terminal. The attached His-tag was not removed since past studies have shown that the His-tag does not alter the binding behavior of MutS ^{41; 42}.

The equilibrium K_D and the order of MutS affinity for various heteroduplexes obtained in this study were all in good agreement with earlier studies (Table 1) ^{16; 37}. The equilibrium binding studies at two different temperatures revealed that the binding reaction of MutS to heteroduplexes is endothermic in most cases. However, when the binding reaction involved the three pyrimidine-pyrimidine mismatch sites (C-T, T-T, and C-C), the MutS binding reaction appeared to be exothermic (Table 1). Crystal structures of MutS complexed with various mismatch sites (ΔT, G-T, A-C, A-A, G-G) suggest that the different mismatch sites are recognized by MutS in a similar way via a common binding mode. However, no crystal structure of MutS complexed with a pyrimidine-pyrimidine mismatch has been solved. It is possible that MutS binds to the pyrimidine-pyrimidine mismatch sites through a different set of protein-DNA interactions, which might help explain the weak MutS binding affinities for them.

In addition to corroborating an earlier study on Taq MutS ⁴³ (see below), our kinetic studies further revealed that the dissociation rates of various complexes predominantly governed the strength of MutS binding affinity for various heteroduplexes (Table 2). In other words, while MutS associated with various heteroduplexes at similar rates, it dissociated from the complexes at very different rates for different heteroduplexes. Although the crystal studies point to a common “induced-fit” binding mechanism, the results from this study revealed that MutS likely employed different recognition modes with subtle variations for different mismatch sites. These subtle variations contributed to different dissociation rates of MutS-heteroduplex complex, ultimately leading to different binding affinities for various mismatch sites. In the cases of pyrimidine-pyrimidine mismatch sites, the recognition mode differed sufficiently that the binding reaction changed from endothermic to exothermic.

Consistent with previous MutS equilibrium binding studies ^{34; 44}, positive cooperativity was clearly observed and further characterized in this study. The equilibrium profiles of MutS binding to various heteroduplexes were fitted to a sigmoidal function (Figure 2B and Supplementary Figure S1). In addition, the binding profiles yielded a Hill coefficient of 2.4 ± 0.4 on average, further indication of positive cooperativity in MutS binding. In the kinetic studies, the k_on profiles were fit to a simple quadratic function (Equation 6), indicative of positive cooperativity as well.

Using the simple quadratic function, the k_on of MutS for 30-1ΔT was determined to be 2 × 10¹³ (s⁻¹M⁻²) at 21°C and 5 × 10¹² (s⁻¹M⁻²) at 10°C (Figure 3B, Table 2). The slower k_on at lower temperature was the basis for the decrease in MutS affinity, which was only slightly offset by a marginally slower k_off (Table 2). The activation energy of the MutS binding was estimated using Arrhenius equation to be ≈ 20 kcal·mole⁻¹, a rather high value partially due to the third-order nature of k_on obtained in our analysis. However, we also calculated the linear slope of the initial phase of the kinetic association profile ([MutS] < 160 nM) where the binding cooperativity was not significant (Figure 3B). This way, the kinetic association profile of MutS with 30-1ΔT yielded a k_on-dimer of 1.2 × 10⁶ (s⁻¹M⁻¹) at 21°C and 9.9 × 10⁵ (s⁻¹M⁻¹) at 10°C. The corresponding activation energy of MutS binding was estimated to be only ≈ 2.3 kcal·mole⁻¹, a nearly 9-fold difference. Clearly marked by positive cooperative characteristics, the activation energy for the binding reaction carried out at higher MutS concentrations (≈ 20 kcal/mol) was significantly larger than the value estimated in the lower concentration limit (≈ 2.3 kcal/mol). The larger activation energy at high MutS concentrations indicated that there was a significant energy barrier to the cooperative association process, which presumably involved tetramer formation.

However, a recent kinetic binding study of Taq MutS does not exhibit binding cooperativity at 40°C ⁴³, corroborating the finding that Taq MutS exists in solution and binds to mismatch sites predominately as dimers at concentration smaller than 10 µM ³³. Nevertheless, we note that for E. coli MutS, the positive cooperativity in binding was more pronounced at higher temperatures (Figure 3B). It remains a possibility that at higher temperatures Taq MutS could bind heteroduplexes in a cooperative manner, since some similarity exists in the C-terminal domain of E. coli and Taq MutS at the sequence level. Furthermore, when we considered the slope of the initial linear phase of the kinetic association profile ([MutS] < 160 nM), the k_on-dimer of MutS to 30-1ΔT was 1.2 × 10⁶ (s⁻¹M⁻¹) at 21°C. The binding cooperativity was not significant in the kinetic association rate estimated this way, and the value of k_on-dimer was comparable to the reported k_on of 3 × 10⁶ (s⁻¹M⁻¹) for Taq MutS associating with an unpaired-T at 40°C ⁴³. In addition, the kinetic dissociation measurements showed that the k_off values of MutS-30-1ΔT complex were 0.17 (s⁻¹) and 0.02 (s⁻¹) respectively at 21°C, comparable to the k_off of 0.07 (s⁻¹) reported for Taq MutS complexed with an unpaired-T at 40°C ⁴³.

Interestingly, while the kinetic dissociation rates appeared unaffected by the presence of AMPPNP, the positive cooperativity for MutS binding to the heteroduplex was greatly reduced. The Hill coefficient of MutS binding profile to heteroduplexes decreased from 2.4 ± 0.4 to 1.6 ± 0.2 on average, suggesting a reduction or loss of positive cooperativity in the presence of AMPPNP (Figure 5A). The presence of AMPPNP also reduced the MutS affinity for heteroduplexes by 2- to 3-fold (Table 2), although previous studies report as high as 4- to 30-fold decrease depending on salt concentration ²⁸. The k_obs of MutS association with 30-1ΔT was significantly depressed at high MutS concentrations in the presence of AMPPNP, leading to an essentially linear concentration dependence (Figure 5B). These findings led us to attribute the decrease in MutS affinity in the presence of AMPPNP to the loss of positive cooperativity in kinetic association, which directly contributed to a much slower k_on and a decreased binding affinity. Unlike AMPPNP, ATPγS is hydrolysable albeit at a very slow rate; therefore it could serve as a more suitable ATP analog in certain instances. However, substituting AMPPNP with ATPγS in these experiments yielded very similar results (Supplementary Figure S3), demonstrating that either ATP analog could instigate the observed changes in MutS binding behavior.

The kinetic association profile of 30-1ΔT with mutS-A842E, a mutant deficient in tetramer formation, was also linear (Figure 5B). In EMS A, mutS-A842E formed a complex with 30-1ΔT that traveled much faster than the MutS-30-1ΔT complex (Figure 5D), suggesting that this mutant formed predominately dimers while MutS predominately formed oligomers of higher orders. Stoichiometric titration of 30-1ΔT also indicated that mutS-A842E bound to heteroduplexes as dimers, whereas MutS bound to heteroduplexes as tetramers (Figure 6). Earlier studies show that MutS exists in an equilibrium between dimers and tetramers; however, these studies reported very different K_{D-Dimer-Tetramer} values of 95 nM and 2.2 µM (in monomer terms) ^{34; 38}. Nevertheless, the results presented in this study suggested that the ability of MutS to form tetramers served as the basis of the positive binding cooperativity, which in turn was modulated by the binding of nucleotide cofactors. However, the loss of positive cooperativity in the presence of AMPPNP did not result from any change in the stoichiometry of the final complex. Stoichiometric titrations in the absence and the presence of AMPPNP yielded closely comparable results (Figure 6), a result supported by EMS A as well (Figure 5D).

Interestingly, previous studies suggest that the presence of nucleotide cofactors or heteroduplexes promoted MutS tetramer formation ^{34; 45}. To accurately assess the stoichiometry of the complex, we only took into consideration the stoichiometric titrations carried out with MutS concentration between 250 and 1500 nM, where stoichiometric binding was ensured. It is difficult to determine whether free MutS exists predominately as dimers or tetramers within this concentration range due to the considerable difference between the previously reported K_{D-Dimer-Tetramer} values ^{34; 38}. Nevertheless, we note that at 250 nM, MutS bound to heteroduplexes as tetramers even though some MutS would most likely exists as dimers at this concentration in the absence of heteroduplexes. These results therefore provided support to the previous finding that heteroduplexes promoted MutS tetramer formation. MutS tetramers have been suggested by an electron microscopy study to mediate the DNA loop structure post mismatch recognition ^{34; 46}, however, the functional role of higher MutS oligomeric states remains a subject of active debate. Evidence from this study clearly pointed to MutS tetramers as the functional unit in mismatch binding, while the nucleotide cofactors modulated the cooperative binding property of MutS tetramers. The positive cooperativity intrinsic to MutS tetramers most likely played a key role in enhancing the efficiency in specific recognition. Mutagenesis studies have shown that E. coli cells carrying a MutS mutation deficient in tetramer formation display between 4- to 40- fold higher mutation rates ^{35; 36}, reinforcing our view. Although our studies did not determine whether nucleotide cofactors also promoted MutS tetramer formation, we showed that the binding of nucleotide cofactors changed the cooperative binding energy but not the stoichiometry of the MutS-heteroduplex complex.

A previous surface plasmon resonance study shows the difference between E. coli MutS K_D and K_D-NSP is less than 50-fold (S ≈ 4 to 47 depending on the salt concentration) ²⁸. A separate IAsys biosensor binding study shows a specificity of 11 (S ≈ 11) ³⁷, while another EMSA study reports a specificity of 24 (S ≈ 24) ⁴⁷. Much higher S values have been reported for Taq MutS (S ≈ 1700) ^{47; 48}. For E. coli MutS to efficiently survey the entire genome and successfully locate any newly generated mismatch sites, a significantly higher S value seems essential. In this study, competition assays were employed to measure the MutS K_D-NSP to homoduplexes in solution. Under the assumption of MutS binding to heteroduplexes as tetramers and to homoduplexes as dimers, the K_D-NSP of MutS for a 30-bp homoduplex was ≈ 23.1 µM, ≈ 413-fold weaker than the binding of 30-1ΔT (Figure 4, Table 1). In fact, the S value of 413 for E. coli MutS represented a relatively conservative estimate, since the S values would be roughly twice as large under the assumption of MutS binding to homoduplexes as tetramers. We also found that E. coli MutS maintained this high specificity at different temperatures (S ≈ 413 at 21°C, S ≈ 492 at 10°C) (Table 1). Since the FRET-based system in our study unambiguously distinguished between specific and non-specific interactions, the relative strength of K_D and K_D-NSP was directly assessed side by side in the same sample. The strength of non-specific binding was determined in the absence of specific binding targets in the prior studies. While any discrepancy with the previous results most likely arose from the different experimental methods and conditions, the MutS specificity reported in this study could better account for the high MMR efficiency in vivo. We further note that since the tetramer formation in E. coli MutS played an important role in specificity (see below), the apparent lack of tetramer formation in Taq MutS would suggest a different means of achieving specificity. The substantially higher specificity reported for Taq MutS (S ≈ 1700) ^{47; 48} supports this view.

Taq MutS has been reported to have significant affinity for both blunt and sticky DNA ends ⁴⁸. To probe possible E. coli MutS interactions with DNA ends, we carried out the competition assays using homoduplexes of different lengths as competitors. Interestingly, the calculated K_D-NSP of 3.7 µM for 90-bp homoduplex suggested much stronger binding than the K_D-NSP of 23.1 µM for 30-bp homoduplex (Figure 4). While there was only a 3-fold difference in the molar concentration of DNA base-pairs, the difference in binding affinity was 6-fold. Based on these findings, we estimated that E. coli MutS did not have noticeable binding affinity for regions spanning up to 9-bp at the DNA ends (Equation 4). Consistent with the idea, E. coli MutS showed no detectable affinity for the 10-bp homoduplex (Figure 4). Indeed, about 95% of the preformed MutS-heteroduplex complex remained bound after being challenged with 67.5 µM of 10-bp homoduplex competitor, the highest concentration tested. Even though the 10-bp homoduplex appeared to be completely annealed when analyzed by electrophoresis, we note that some local melting remained possible due to its low melting temperature (30°C). Such local melting of DNA duplex could potentially decrease MutS binding. Furthermore, since the homoduplexes examined in this study all had blunt ends, it remains to be tested whether E. coli MutS binds to sticky DNA ends with higher affinity. Nevertheless, the weak binding of MutS to 10-bp homoduplex was consistent with the general trend of MutS affinity observed in this study. Moreover, the potential different means of achieving specificity between E. coli and Taq MutS might contribute to the different DNA end-binding behavior exhibited by the two MutS homologs.

One major difference between the E. coli and the eukaryotic MMR pathways is that while the endonuclease MutH directs MMR to the daughter strand in E. coli, eukaryotic MMR systems lack MutH homologs to carry out this particular task. Currently, it is unknown how eukaryotic MMR systems achieve strand discrimination. One proposal is that transient nicks and gaps that appear in the nascent strand during replication could assist in guiding MMR to the nascent strand. From competition assays with ssDNA, we found that E. coli MutS had nearly 4-fold stronger affinity for ssDNA than for double-strand DNA, consistent with the proposal. Indeed, the hypothesis that the different sets of interactions between the nicks/gaps and each of the two MutS monomers could guide the MMR to the nascent strand is an attractive one. To test this hypothesis, it will be worthwhile to investigate the affinity and mechanism of various MutS homologs binding to nicked DNA duplexes in future studies as well.

Our studies further showed that in the presence of AMPPNP, the non-specific binding affinity of E. coli MutS decreased much more significantly than the specific binding affinity. As a result, E. coli MutS benefited from a 3-fold increase in S value between 30-1ΔT and 30-bp homoduplex and a 2-fold increase in S value between 30-1ΔT and 30-ssDNA upon addition of AMPPNP (Table 3). A previous IAsys biosensor binding study on effect of ATP reports a similar trend ³⁷. These results directly supported the hypothesis put forth by Yang et al. that binding of ATP by MutS serves as verification of mismatch recognition at the cost of reduced affinity for both specific and non-specific binding targets ⁴⁹. However, new findings in this study led us to propose the following modifications to the working hypothesis: 1. The functional unit for E. coli MutS is a tetramer (dimer of dimers) rather than a single dimer. 2. Upon finding a mismatch site in the genome, the MutS tetramer binds to the mismatch site with positive cooperativity. 3. Subsequent binding of ATP causes the loss of positive cooperativity between the two MutS dimers, effectively reducing the significant energy barrier associated with the positive cooperativity. Despite losing the positive cooperativity, the stoichiometry of the MutS-heteroduplex complex remains unchanged. 4. Although the loss of positive cooperativity leads to reduced specific affinity for MutS, its non-specific affinity decreases significantly more, so a MutS-homoduplex complex will dissociate before downstream MMR can be initiated. It is our view that the positive cooperativity of E. coli MutS tetramers, modulated by ATP and DNA, plays a key role in maintaining high specificity and preventing futile mismatch repairs. Furthermore, E. coli MutS displayed high affinity for ssDNA, which could have important implication in how MutS coordinates with other downstream components to achieve strand-specificity in eukaryotic MMR pathways.

4. Materials and Methods

Protein Purification

E. coli His₆-MutS was purified from E. coli HMS174(DE3)pLysS competent cells (Novagen) transformed with pTX412 ⁴¹. Single-point mutant E. coli His₆-mutS-A842E was purified from the same competent cells transformed with pMQ448. The overexpression and purification of protein were essentially as described by the laboratory of Dr. Hsieh with some modifications ⁵⁰. Briefly, transformed cells were grown at 37°C in LB with 100 µg/mL ampicillin and 34 µg/mL chloramphenicol until the culture has an optical density of ≈ 0.5, at which point the cells were induced by 100 µM of isopropyl β-D-1-thiogalactopyranoside and were allowed to grow for 3 more hours. Harvested cell pellets were flash frozen in liquid nitrogen and could be stored at −80°C for up to a year. Once the cell pellet was thawed, all subsequent purification steps were carried out without interruption. Thawed pellet re-suspended in Lysis Buffer (20 mM HEPES, pH = 7.8, 500 mM NaCl, 1 mM β-mercaptoethanol) with the addition of Complete, EDTA-free Protease Inhibitor Cocktail Tablets (Roche Applied Science) was lysed using a Microfludizer. After ultra-centrifugation at 39 krpm for 30 minutes, the supernate of cell lysate was loaded onto a 5-mL HiTrap Chelating HP column (GE Healthcare) pre-charged with nickel ions and pre-equilibrated with buffer B (20 mM HEPES, pH=7.8, 500 mM NaCl, 1 mM β-mercaptoethanol, 5 mM imidazole). The column was then washed and eluted with a gradient of 60 mM – 300 mM imidazole, with the protein peak eluting starting at ≈ 115 mM imidazole. The eluted protein was then concentrated and loaded onto a HiPrep Sephacryl S-300 HR desalting column (GE Healthcare) pre-equilibrated with buffer A (20 mM HEPES, pH = 7.8, 150 mM NaCl, 1 mM EDTA, 1 mM dithiothreitol). The eluted protein was brought to a final glycerol concentration of 30% (v/v), and was flash-frozen in liquid nitrogen in a drop-wise fashion and stored at −80°C for up to 90 days. Eletrophoretic analysis of the resulting protein in a Coomassie-stained SDS-gel revealed the purity of the protein to be greater than 95%. Protein concentration was determined by amino acid analysis carried out by the W.M. Keck Facility at Yale (New Haven, CT). All concentrations of MutS in this communication are expressed in terms of monomers.

Oligonucleotides

All deoxyoligonucleotides were synthesized by the W.M. Keck Facility at Yale (New Haven, CT). Fluorescein and tetramethylrhodamine (TAMRA) were incorporated at positions indicated in the sequence (Figure 1) via Fluorescein-dT and TAMRA-dT (Glen Research, Sterling, VA). The basic sequence of the 30-bp construct was as follows (Top Strand): 5′-AAC TGC CAX GCA CCA GTG TCA GCG TCG TAT-3′ (X = any of the four nucleotides, T = Fluorescein-dT). The Bottom Strand sequence was as follows: 5′-ATA CGA CGC TGA CAC TGG TGC YTG GCA GTT-3′ (Y = any of the four nucleotides, T = TAMRA-dT). By altering X and Y, homoduplexes or heteroduplexes containing different kinds of mismatch were produced in either a non-labeled, singly-labeled, or doubly-labeled form. The 90-bp homoduplex sequence d(CGC AGT GCT AAG ACG TAC CAT GCA ACC GTA GAT TCT AAC TGC CAG GCA CCA GTG TCA GCG TCG TAT AGT CGT GTA TAG ATC GTT ATC TGC) contained the same 30-bp basic sequence internally (italicized). Non-labeled and Fluorescein-labeled deoxyoligonucleotides were purified in a denaturing gel (10%), while TAMRA-labeled deoxyoligonucleotides were purified in a native gel (10%). The concentration of each deoxyoligonucleotide was determined using the theoretical extinction coefficient at A₂₆₀ calculated by the Oligonucleotide Properties Calculator published by Northwestern University (http://www.basic.northwestern.edu/biotools/oligocalc.html). DNA duplexes were produced by annealing equal molar amounts of matching top and bottom DNA strands in 5 mM NaCl. Duplex formation was verified by 10% polyacrylamide native gels that were stained with 1× SYBR Gold (Invitrogen, Molecular Probes, Carlsbad, CA).

Equilibrium Binding Measurements

All equilibrium measurements were done on a Cary-Eclipse fluorescence spectrometer (Varian, Palo Alto, CA) equipped with a 4-Position Peltier Thermostattable cell holder. All samples were excited at 485 nm and scanned from 500 to 600 nm with both slit widths set to 5 nm. All experiments were carried out at either 10 or 21°C. The incubation time for all samples was a minimum of 5 minutes prior to data collection. Experiments at 37°C showed that MutS was not sufficiently stable at this temperature to yield meaningful results.

1. Specific Binding Affinity

K_D values of MutS were determined by titrating 20 nM doubly-labeled heteroduplexes with increasing concentrations of MutS in 1× Binding Buffer (20 mM HEPES, pH = 7.8, 50 mM NaCl, 5 mM MgCl₂, 1 mM dithiothreitol, 100 µg/mL BSA) in the presence of specified concentration of AMPPNP (Roche Diagnostics Corp., Indianapolis, IN). All scans were normalized at the isosbestic point, empirically determined to be 562 nm. The intensity of the fluorescein peak (517 nm) was then taken to calculate the FRET efficiency:

$$\text{FRET Efficiency}=1-\frac{\mathit{\text{FI}}-{\mathit{\text{FI}}}_{\text{min}}}{{\mathit{\text{FI}}}_{\text{max}}-{\mathit{\text{FI}}}_{\text{min}}}$$ Equation 1

where FI was the fluorescence intensity at 517 nm, FI_max was the maximum intensity observed, and FI_min was the minimum intensity observed. The FRET efficiency thus obtained was plotted against the MutS concentration on a log scale, and then fitted to a sigmoidal model, Logistic, in Microcal Origin (OriginLab, Northampton, MA).

$$y=\frac{A_1-A_2}{1+{(x/K_D)}^P}+A_2$$ Equation 2

2. Non-specific Binding Affinity

K_D-NSP values of MutS were determined using a competition assay. First, varying amount of non-labeled homoduplex was mixed with doubly-labeled heteroduplex. The DNA solution was then combined with a MutS solution to achieve a final concentration of 20 nM heteroduplex and 180 nM MutS. The experiments were performed either in the absence or in the presence of 1 mM AMPPNP. The fraction of remaining specific complexes was monitored at the fluorescein peak and was plotted against competitor concentration. The corresponding K_D-NSP was extracted from the binding profile following the relationship below, assuming that MutS bound to heteroduplexes as a tetramer and to homoduplexes as a dimer:

$$\begin{array}{c}[{{\mathrm{D}}_{\text{SP}}}^{*}{\mathrm{P}}_4]=[{{\mathrm{D}}_{\text{SP}}}^{*}],\text{and}{[\mathrm{P}]}_{\text{Free}}={\mathrm{K}}_{\mathrm{D}}(\text{at the}50\%\text{point})\hfill \\ {[\mathrm{P}]}_{\text{Total}}=4[{{\mathrm{D}}_{\text{SP}}}^{*}{\mathrm{D}}_4]+2[{\mathrm{D}}_{\text{NSP}}{\mathrm{P}}_2]+{[\mathrm{P}]}_{\text{Free}}\hfill \\ K_{D-\mathit{\text{NSP}}}=\frac{K_D\times [D_{\mathit{\text{NSP}}}]}{[{\mathit{D}}_{\mathit{\text{NSP}}}{\mathit{P}}_2]}\hfill \end{array}$$ Equation 3

where D_SP* was labeled heteroduplexes and D_NSP was non-labeled homoduplexes. Note that the assumption of MutS binding to homoduplexes as dimers would not affect the total non-specific binding. Under the alternative assumption of MutS binding to homoduplexes as tetramers, the binding affinity would be half as large, but each binding event would contribute twice as many bound proteins.

3. MutS Affinity for DNA Ends

The difference in values of K_D-NSP for homoduplexes of various lengths reflected the extent of DNA end-binding by MutS. Assuming that MutS is excluded from interacting with a region of x-bp near the DNA ends, then the different K_D-NSP values for homoduplexes of different lengths would follow this relationship:

$$\frac{n_1-2x}{n_2-2x}=\frac{K_{D-\mathit{\text{NSP}}-2}}{K_{D-\mathit{\text{NSP}}-1}}$$ Equation 4

where n was the number of base-pairs in each homoduplex competitor.

4. Stoichiometry

of the protein-DNA complex was determined by titrating 600 nM heteroduplex (20 nM doubly-labeled + 580 nM non-labeled) with increasing concentrations of MutS. The experiments were performed either in the absence or in the presence of 1 mM AMPPNP. Similarly normalized fluorescein peak intensity was plotted against MutS concentration. The initial data points (MutS concentration ≤ 1 µM) were fitted to a linear function (y = ax) and the data points with higher MutS concentration reaches a plateau (y = 1). The slope of the initial linear phase contained information on stoichiometry of the heteroduplex-MutS complex. A correction term was also applied to the slope due to non-stoichiometric binding behavior (expressed in the bracket).

$$n=\frac{\mathrm{\Delta }[\mathit{\text{MutS}}]}{{[\mathit{\text{Heteroduplex}}]}_{\mathit{\text{Total}}}\times \mathrm{\Delta }{f}_B}(1-\frac{K_D}{{[\mathit{\text{Heteroduplex}}]}_{\mathit{\text{Total}}}})$$ Equation 5

where n was the number of MutS monomer in each complex and f_B was the fraction of heteroduplexes bound.

Stopped-flow Experiments

Kinetic measurements were carried out on a DX.18MV stopped-flow Spectrometer (Applied Photophysics, Leatherhead, Surrey, UK) with an excitation wavelength of 485 nm (± 5 nm) for fluorescein excitation and 520 nm (± 5 nm) for TAMRA excitation. For evaluating fluorescein intensity change, the detection system was fitted with a 495 nm cut-on optical filter (Oriel Corporation, Stratford, CT) coupled with a ultra thin bandpass filter IF585 (Applied Photophysics, Leatherhead, Surrey, UK). For evaluating TAMRA intensity change, a single 550 nm cut-on optical filter was used (Oriel Corporation, Stratford, CT). All reactions were carried out in 1× binding buffer (20 mM HEPES, pH = 7.8, 50 mM NaCl, 5 mM MgCl₂, 1 mM dithiothreitol, 100 µg/mL BSA), either in the absence or in the presence of 1 mM AMPPNP at either 10 or 21°C. Baselines of labeled heteroduplexes rapidly mixed with buffer or with unlabeled heteroduplexes were always taken prior to each set of experiments. The experiments only proceed when the slope of the baselines were in the order of ± 10⁻⁶ FI(A.U.)/s, which was an order of 10 to 100 times smaller than the rate of amplitude change for the slow and fast dissociation rate respectively. All data were analyzed by first averaging four or more traces of each mixing reaction and then fitting to a single-exponential or a double-exponential function using Microcal Origin (OriginLab, Northampton, MA).

1. Kinetic Association

a solution of 10 nM heteroduplex and a solution of MutS ranging from 100–1000 nM in concentration were thermally pre-equilibrated for 5 minutes prior to rapid mixing. The association traces were fit to a single-exponential function, yielding k_obs. The k_obs was then plotted against increasing MutS concentration and fitted to a simple quadratic function:

$${\mathrm{k}}_{\text{obs}}=\mathrm{a}+{\mathrm{k}}_{\text{on}}{[\text{MutS}]}^2$$ Equation 6

2. Kinetic Dissociation

a solution of preformed heteroduplex-MutS complex (20nM heteroduplex + 315 nM MutS) and a non-labeled heteroduplexes in great excess (0.5~1.5 µM) were thermally pre-equilibrated for 5 minutes prior to rapid mixing. For all kinetic dissociation measurements, 100 second-long traces were collected and analyzed. The dissociation traces were fit to a double-exponential function, yielding two k_off values.

3. Calculated K_D from k_on and k_off Values

A tri-molecular reaction involving a heteroduplex and two MutS dimers follows the expression:

$$\begin{array}{cc}\frac{k_{\mathit{\text{off}}}}{k_{\mathit{\text{on}}}}=\frac{[D]{[P]}^2}{[{\mathit{\text{DP}}}_2]}\hfill & \text{When}[\mathrm{D}]=[{\text{DP}}_2],\text{then}\\ [P]=\sqrt{\frac{k_{\mathit{\text{off}}}}{k_{\mathit{\text{on}}}}}=K_{D-\mathit{\text{Apparent}}}& \hfill \end{array}$$ Equation 7

Electrophoretic Mobility Shift Assay

All samples contain either 200 nM of 30-1ΔT or 30-ssDNA in 1× Binding Buffer (20 mM HEPES, pH = 7.8, 50 mM NaCl, 5 mM MgCl₂, 1 mM dithiothreitol, 100 µg/mL BSA) with 10% glycerol. Samples contained 1 mM AMPPNP when specified. 10 µL of each sample was loaded on to a native 8% polyacrylamide gel and run at 4 W for 35 minutes. The gel was then stained with 1× SYBR Gold (Invitrogen, Molecular Probes, Carlsbad, CA) and imaged.

Supplementary Material

01. Supplementary Figure S1.

Equilibrium Titration of Heteroduplexes with MutS. Equilibrium titration profiles of all 8 possible mismatches by increasing MutS concentration are shown here. Excited at wavelength = 485 nm, the intensity of fluorescein peak (517 nm) of each titration scan was taken from each trace and normalized to represent the fraction of heteroduplexes bound by MutS. Each binding profile was fitted to a sigmoidal function, shown by the solid line. Each binding profile was also fitted to a 1:1 binding isotherm, shown by the dashed line, which provided a poorer fit for the observed data than the sigmoidal function.

02. Supplementary Figure S2.

Sequential-flow Measurements. Sequential-flow measurements were carried out to probe any intermediate states. To that end, doubly-labeled heteroduplexes (30-GT) was rapidly mixed with MutS, and the complexes were allowed to age for a specific amount of time. If the complex formation was a multi-step reaction, the complex would reach different stages of the reaction following its own time line. By reversing the reaction at different time points in the course of the binding reaction, the kinetic dissociation rates of complexes at any given age or in any given stages of formation can be directly measured. Here, the complex was rapidly mixed with non-labeled heteroduplexes in great excess at various aging time points ranging from 0.5 to 14 seconds, driving the reaction in the reverse direction. The increase in fluorescein intensity directly revealed the kinetic dissociation rate of the complex in its particular stage of formation.

The kinetic dissociation traces of complexes of different ages were all fit to a double-exponential function as before, yielding two rates. As shown in Figure S2A, the kinetic dissociation rates of complexes remained constant within experimental errors regardless of the age of the complex. The fast and the slow kinetic dissociation rates obtained this way were 0.17 and 0.02 (s⁻¹) respectively, identical to the rates measured directly (Table 2 of the main article). Furthermore, the change in fluorescein intensity depended on the age of the complexes; the longer the complexes were allowed to age, the larger the total change in fluorescein intensity (filled boxes in Figure S2B). Interestingly, the magnitude of change in fluorescein intensity for complexes of different ages was in excellent agreement with the kinetic association trace obtained by rapidly mixing MutS and doubly-labeled heteroduplexes (red line in Figure S2B). The excellent agreement between the resulting fluorescein intensity from two methods reaffirmed that our sequential-flow measurements could effectively construct the entire course of the dissociation event segment by segment. Furthermore, sequential-flow measurements conducted in the presence of AMPPNP yielded comparable results. Taken together, these results suggested that whether AMPPNP was present or not, the two dissociation rates observed in this study arose from two concurrent processes and not two separate steps in sequence.

03. Supplementary Figure S3.

Effect of Different ATP Analogs on Kinetic Properties of MutS-Heteroduplex Complexes. Different ATP analogs were independently tested to determine their effects on the kinetic association and dissociation rates of MutS-heteroduplex complex. AMPPNP was tested at two different concentrations while ATPγS was tested at one concentration. (Figure S3A) All three data sets showed that the presence of either ATP analog was sufficient to abolish the positive cooperativity and to depress the values of k_on. The kinetic association profiles of MutS for 30-1ΔT at 21°C showed very similar slopes in the presence of 1 mM AMPPNP, 50 µM AMPPNP, or 50 µM ATPγS, ranging from 4 to 6 × 10⁵ s⁻¹M⁻¹. (Figure S3B) The kinetic dissociation scans of MutS-30-1ΔT complex in the presence of either ATP analogs were all fit to a double-exponential function, yielding a fast and a slow k_off value. Within experimental errors, the k_off values of MutS-30-1ΔT complex in the presence of either ATP analog were essentially identical.

04. Supplementary Figure S4.

Electrophoretic Mobility Shift Assay. Competition assays resolved by electrophoretic methods were employed to determine whether E. coli MutS had significant affinity for the fluorophores used in this study. The experimental conditions were as described in the Materials and Methods section, except that instead of being stained with 1× SYBR Gold, the gel was dried, exposed overnight, and then imaged. Concentration of MutS in each sample is as indicated above each lane. Samples in lane 8, 16, and 24 contained 10 pM of 30-ssDNA labeled with ³³P (30-ssDNA^#), while samples in all other lanes contained 10 pM of 30-GT labeled with ³³P but not with fluorophores (30-GT^#). In addition, samples in lane 1~7 contained 120 nM cold 30-GT doubly-labeled with fluorescein and TAMRA (30-GT(FR)); samples in lane 9~15 contained 120 nM cold 30-GT singly-labeled with fluorescein (30-GT(F)); samples in lane 17~23 contained 120 nM cold 30-GT singly-labeled with TAMRA (30-GT(R)); while samples in lane 25~31 contained 120 nM cold 30-GT not labeled with any fluorophores (30-GT). MutS showed comparable affinities for 30-GT^# regardless of whether the cold competitors present in the samples were labeled with one, both, or no fluorophores at all. This result indicated that MutS did not have significant affinity for the fluorophores used in this study.