Abstract
For many bacteriophages (phages), the proteins responsible for host lysis and virion morphogenesis are expressed from the same polycistronic transcript. Such an expression pattern can potentially have a pleiotropic effect on the assembly rate and lysis time, thus affecting phage fitness. To study the effects of late promoter activity on phage life history traits and fitness, we constructed a series of isogenic phage λ strains that differ only in their late promoter pR′ sequences. The resulting late promoter activities ranged from 6 to 100% of the wild type's. The lysis times, burst sizes, and relative fitness were empirically determined for these strains. Our results showed that the lysis time is more sensitive than the assembly rate to variation in pR′ activity. However, except for the strain with the lowest activity, the relative fitnesses of all the other strains are not significantly different from each other. Ad hoc models describing the effects of the late promoter activity on lysis time and assembly rate were constructed. The expected phage burst size and fitness curve were predicted from these models. Evolution of the late promoter activity was discussed in the context of phage life history trait evolution.
BACTERIOPHAGE (phage) genes that participate in the same function or a specific stage of phage life cycle are usually clustered in a polycistronic unit to achieve functional and temporal control of the infection process (Calendar 2006 and references therein). For many phages, one such example is the clustering and coexpression of genes needed for the production of the progeny virion and the lysis of the infected host cell. However, such a genome organization and gene expression pattern can potentially pose a dilemma for the evolution of the activity of the promoter that regulates the polycistronic unit. This would be the case especially if these coexpressed genes are responsible for different phage life history traits and the effects of these traits on phage fitness are antagonistic to each other. Consequently, natural selection for higher phage fitness may result in the evolution of an optimal promoter activity.
During the lytic cycle of phage λ infection, the start of the late stage is marked by the accumulation of the antiterminator protein Q and subsequent expression of late genes from the late promoter pR′ (Herskowitz and Signer 1970 and references therein; Friedman and Gottesman 1983). The resulting single mRNA transcript contains all the lysis genes and morphogenesis genes needed for making head and tail structures (Friedman and Gottesman 1983 and references therein). That is, proteins for two important phage life history traits—host lysis and progeny production—are expressed from this single transcript. Since the phage burst size (fecundity) depends not only on how fast, but also on how long before cell lysis, the virion can be assembled, it is possible that changes in the late promoter activity would affect the expression of both traits, potentially creating an antagonistic relationship. That is, under certain conditions, there may exist an optimal promoter activity that would maximize the phage fitness.
Mechanistically, the timing of lysis can be changed by two means: with different sequences of the holin protein or different concentrations of the same holin protein. The effect of different allelic versions of the holin protein on lysis timing has been documented extensively (Raab et al. 1988; Gründling et al. 2000) and is the main focus when discussing the evolution of phage lysis timing (Wang 2006; Shao and Wang 2008). The effect of holin protein concentrations on lysis timing has also been demonstrated; generally the more the holin protein is expressed, the shorter the lysis time would be, and vice versa (Chang et al. 1995). However, at this point, the exact relationship between the lysis time and the concentration of the holin protein has not been explored systematically.
The assembly of a phage virion is formally similar to the production of intermediate metabolites (Hendrix et al. 1983; Karam 1994); both are series of sequential biochemical reactions with many intervening steps that culminate in the production of a final product. Therefore, it can be argued that the phage assembly rate can be analyzed as a metabolic flux (Kacser and Burns 1973; Savageau 1976). One way to increase the metabolic flux is the simultaneous and coordinated increase of all the enzyme concentrations involved in the pathway (Fell 1998). Even though not all phage components involved in virion assembly are enzymatic in nature, it is not an unreasonable first approximation to assume that by increasing the concentrations of all phage components needed for virion assembly, the rate of assembly would also be increased.
In this study, we hypothesized that a higher promoter activity would result in more transcription of phage λ's late mRNAs, which would in turn result in more production of the holin proteins and phage virion components; each would further result in a shortened lysis time and increased assembly rate, respectively. The same argument would also apply to the situation of a lower promoter activity, with the concomitant longer lysis time and lower assembly rate. Whether it is beneficial to evolve to a higher or a lower promoter activity would clearly depend on the effects of the late promoter activity on the length of lysis time and the magnitude of assembly rate.
For this study, we have constructed a series of isogenic λ-strains that differ only in the pR′ sequences to study the effect of late promoter activity on phage life history traits and fitness. We found that both the lysis time and the assembly rate are affected by the late promoter activity, although the lysis time is more sensitive to the effect. However, the relative fitnesses for most phage strains are similar to each other, except for the one with the lowest late promoter activity. The potential for the evolution of the late promoter activity is discussed in the context of phage life history trait evolution.
MATERIALS AND METHODS
Bacterial and phage strains, plasmids, primers, and culture conditions:
All bacterial and phage strains, plasmids, and primers used in this work are listed in Table 1. Bacteria cultures were grown in Luria–Bertani media with various antibiotics when appropriate. The concentrations of antibiotics were as follows: 100 μg/ml for ampicillin and 10 μg/ml for chloramphenicol.
TABLE 1.
Bacterial and phage strains, plasmids, and primers
| Names | Relevant genotype and feature | Source |
|---|---|---|
| Bacterial strains | ||
| XL1 Blue | recA1endA1 gyrA96 thi-1 hsdR17 supE44 relA1 lac [F′ proAB lacIqZDM15 Tn10 (Tetr)] | Stratagene |
| IN25 | Originally MC4100 | Wang (2006) |
| IN56 | MC4100 (λ cI857), with wt pR′ sequence | Wang (2006) |
| IN158 | MC4100 (λ cI857 Sam7) | Wang (2006) |
| SYP021 | MC4100 (λ cI857 pR′∷cam) | This study |
| SYP026 | MC4100 (λ cI857 pR′-M2) | This study |
| SYP027 | MC4100 (λ cI857 pR′-M1) | This study |
| SYP028 | MC4100 (λ cI857 pR′-M5) | This study |
| SYP029 | IN158 with pZS*1-pR′M1-lacZ | This study |
| SYP030 | IN158 with pZS*1-pR′M2-lacZ | This study |
| SYP032 | IN158 with pZS*1-pR′WT-lacZ | This study |
| SYP033 | IN158 with pZS*1-pR′M5-lacZ | This study |
| SYP037 | IN158 with pZS*1-pR′M3-lacZ | This study |
| SYP041 | IN158 with pZS*1-pR′M4-lacZ | This study |
| SYP043 | MC4100 (λ cI857 pR′-M4) | This study |
| SYP044 | MC4100 (λ cI857 pR′-M3) | This study |
| SYP049 | MC4100(λ cI857 R∷lacZα−) | Shao and Wang (2008) |
| SYP097 | MC4100(λ cI857 pR′-M1 R∷lacZα+) | This study |
| SYP098 | MC4100(λ cI857 pR′-M2 R∷lacZα+) | This study |
| SYP099 | MC4100(λ cI857 pR′-M3 R∷lacZα+) | This study |
| SYP100 | MC4100(λ cI857 pR′-M4 R∷lacZα+) | This study |
| SYP101 | MC4100(λ cI857 pR′-M5 R∷lacZα+) | This study |
| Phages | ||
| All phage strains were thermally induced (see materialsandmethods) from the lysogens above | ||
| Plasmids | ||
| pZS*12-lac | lacZ replacement of luc in pZS*12-luc; the ori gene is derived from low-copy-number pSC101 | This study |
| pS105cmycRφlacZ | With wild-type pR′ | Wang et al. (2003) |
| pZS*1-Cam-lacZ | Cam replacement of pR′ in pZS*1-pR′WT-lacZ | This study |
| pZS*1-pR′WT-lacZ | pZS*12-lacZ with lac operator replaced with wt λ pR′ | This study |
| pZS*1-pR′M1-lacZ | pZS*1-pR′WT-lacZ with wt pR′ replaced with M1 sequence | This study |
| pZS*1-pR′M2-lacZ | pZS*1-pR′WT-lacZ with wt pR′ replaced with M2 sequence | This study |
| pZS*1-pR′M3-lacZ | pZS*1-pR′WT-lacZ with wt pR′ replaced with M3 sequence | This study |
| pZS*1-pR′M4-lacZ | pZS*1-pR′WT-lacZ with wt pR′ replaced with M4 sequence | This study |
| pZS*1-pR′M5-lacZ | pZS*1-pR′WT-lacZ with wt pR′ replaced with M5 sequence | This study |
| pSwtRlacZαblueRz | Insertion of lacZα at the end of phage λ R | Shao and Wang (2008) |
| pSwtRlacZαwhiteRz | LacZα− mutant of pSwtRlacZαblueRz | Shao and Wang (2008) |
| Primers | ||
| See supplemental materials for sequences | ||
Standard PCR and DNA sequencing:
Unless stated otherwise, all protocols for PCR cloning and DNA sequencing are the same as described previously (Shao and Wang 2008).
Construction of isogenic reporter plasmids and phage λ-strains with mutant pR′:
To determine the late promoter activity, plasmids were constructed by placing the reporter gene lacZ from Escherichia coli under the control of various mutant pR′'s that were introduced to the plasmids by site-directed mutagenesis. Isogenic λ-strains that differ only in their late promoter pR′ sequences were also constructed for the purposes of determining the effects of late promoter activity on phage lysis time, on burst size, and for pairwise competition experiments. See supplemental materials for details of phage strain construction and the construction flowchart.
Figure 1shows the mutations introduced into λ's pR′ region. Since high-fidelity PCR was used for most of the strain construction, DNA sequencing was performed to ensure the identity of PCR-cloned genes.
Figure 1.—
Sequences of wt and mutant λ pR′ regions used in this study. Boldface sequences show the −35 and −10 regions of the λ pR′ promoter. Underlines show the mutated positions in either the −35 or the −10 regions. Mismatches on the right tabulate the number of mutations that are different from the consensus sequence.
Determination of the pR′ promoter activity:
Overnight cultures of lysogen strains (see supplemental materials for strain names) were diluted 100-fold in two sets of 3 ml fresh LB media and incubated at 30° until the cultures reached an early exponential phase of A550 ∼ 0.2. One set of the cultures was thermally induced at 42° for 20 min and then shifted to 37° for another 30 min. The other set was left at 30° to grow for 50 min. The β-galactosidase activities of both sets of cultures were then determined (Miller 1992) as measurements of the late promoter activity under induced (Q-dependent) and uninduced (Q-independent) conditions.
Lysis time and burst size determinations:
The lysis times and burst sizes of λ-phages were determined as described previously (Wang 2006). Briefly, the lysis time was determined by subjecting the lysogen culture to a temperature-shift regimen of 30°–42° and then finally 37° to thermally induce the excision of prophage from the bacterial chromosome. The time of initial decline of the culture turbidity (A550) was recorded as the lysis time. For burst size determination, exponentially grown bacterial culture, after preadsorption of the phages at a low multiplicity of infection (m.o.i.) of ∼0.01, was immediately diluted and incubated at 37° for a certain period, depending on the lysis time. The fold of increase of phage concentration is used as the average burst size.
Phage competition experiments and determination of relative fitness:
The detailed conditions for the competition experiment (Shao and Wang 2008) and phage plating (Wang 2006) have been described previously. Briefly, for the competition experiments, equal proportions of lacZα-marked wild type (wt) and pR′mutant phage strain were used to infect ∼106 cells/ml of exponentially grown cells at an m.o.i. of ∼0.02. After incubation at 37° for 4 hr, a portion of the culture was withdrawn and mixed with IPTG and X-gal-impregnated molten top agar and plated on an LB agar plate. Each phage strain was differentiated by the color of emergent plaques (blue or colorless) and counted to determine its concentration. The relative fitness was calculated as ln(Rmt)/ln(Rwt), where R is the ratio of phage concentrations at time 0 and hour 4 (i.e., P4/P0,where P is the phage concentration) and the subscripts of mt and wt represent the mutant strain and the wt, respectively.
Statistical analyses:
The Tukey–Kramer honestly significant difference (HSD) test at the α = 0.05 level, as implemented in JMP (v. 5.0.1a for MacOS), was used to test for the equality of means. Since most data were collected with few replicate experiments (between three and six), the calculated standard errors have all been corrected for small sample sizes according to Sokal and Rohlf (1995, p. 53). The correction results in a larger standard deviation and standard error than the typically calculated one.
RESULTS
Construction of isogenic λ-phages with different pR′sequences:
To examine the impact of pR′ promoter activity on phage lysis time, burst size, and relative fitness, we constructed five λ-phage mutants with different pR′ sequences (see Figure 1). To avoid destroying the Q binding site (Guo and Roberts 2004), we mutated sequences only within the −35 and/or −10 regions so that the interaction between Q and pR′ was maintained. We hypothesized that the pR′ activity would be strengthened or weakened by decreasing or increasing the number of mismatches, respectively, to the consensus σ70 promoter sequence (Harley and Reynolds 1987; Lisser and Margalit 1993) (see Figure 1). The number of mismatches is, in increasing order, 0 (M1), 1 (M2), 3 (wt), 2 (M5), 5 (M3), and 6 (M4). While M5 has only two mismatches (both at the −35 region), one of the mutations is located within the first three nucleotides of the hexamer sequence (the G to A change), which has been shown to be critical for promoter activity (Lisser and Margalit 1993). Therefore, we expect the ranking of the promoter activity to be M1 > M2 > wt > M3 > M4 > M5.
Determining the promoter activity of pR′ mutants:
The promoter activity was determined with or without thermal induction of the Q protein. The uninduced condition (i.e., Q independent) is used as a gauge of the intrinsic pR′ promoter activity, while the induced condition (i.e., Q dependent) is to assess the promoter activity experienced during phage lytic infection. Table 2 shows the results.
TABLE 2.
Late promoter activity, lysis time, burst size, assembly rate, and growth rate of phage λ pR′ mutants
| Late promoter activitya
|
Burst size (phages/cell) | Assembly rateb (phages/min) | Growth rate (hr−1)
|
||||
|---|---|---|---|---|---|---|---|
| Name | Uninduced | Induced | Lysis time (min) | Competing | Standard | ||
| wt | 6.9 ± 0.6 (B)c | 247.0 ± 17.8 (100%)d (A)c | 52.8 ± 1.1 (D)c | 153.9 ± 7.2 (A, B)c | 6.21 | 2.72 ± 0.090 (A)c | 2.68 ± 0.097 (A)c |
| M1 | 9.6 ± 0.5 (A) | 208.4 ± 6.5 (84%) (B) | 52.5 ± 1.0 (D) | 157.0 ± 11.5 (A, B) | 6.41 | 2.69 ± 0.093 (A) | 2.67 ± 0.072 (A) |
| M2 | 10.2 ± 0.5 (A) | 216.0 ± 4.8 (87%) (B) | 52.8 ± 1.7 (D) | 151.0 ± 27.1 (B) | 6.09 | 2.67 ± 0.142 (A) | 2.66 ± 0.083 (A) |
| M3 | 4.5 ± 0.3 (C) | 149.4 ± 2.2 (60%) (C) | 56.5 ± 1.0 (C) | 163.1 ± 19.7 (A, B) | 5.72 | 2.77 ± 0.062 (A) | 2.68 ± 0.091 (A) |
| M4 | 3.0 ± 0.5 (D) | 75.9 ± 3.6 (31%) (D) | 61.5 ± 1.0 (B) | 186.1 ± 6.8 (A) | 5.56 | 2.60 ± 0.071 (A) | 2.75 ± 0.060 (A) |
| M5 | 3.4 ± 0.2 (C, D) | 14.6 ± 0.4 (6%) (E) | 103.3 ± 2.8 (A) | 104.2 ± 1.7 (C) | 1.38 | 1.28 ± 0.209 (B) | 2.73 ± 0.119 (A) |
All values, if possible, are shown with mean and 95% confidence intervals, which are calculated with standard errors corrected for small sample sizes (see materials and methods).
β-Galactosidase activity in Miller units.
The assembly rate is estimated using b/(tL − e), where b is the burst size, tL is the lysis time, and e is the eclipse period, which is set to 28 min (Wang 2006).
Different letters in the same column show means that are significantly different from each other, using the Tukey–Kramer HSD test at the α = 0.05 level, as implemented in JMP (v. 5.0.1a for MacOS).
Percentages inside the parentheses denote the promoter activities relative to that of the wt.
As expected, under the uninduced condition, all promoter activities were very low. Presumably the uninduced activities were the result of tR′ (terminator) leakage. However, these low values can still be considered as an indicator of the true activity of these mutant pR′'s because they are independent of the Q function. By using the Tukey–Kramer HSD test (unplanned comparisons of means), the ranking of the uninduced promoter activity is shown to be M1 ≈ M2 > wt > M3 ≈ M5 ≈ M4, somewhat conforming to our expectation described above.
Table 2 also shows the promoter activities after Q induction, not surprisingly, with much higher values. However, unplanned comparisons among these induced promoter activities showed the ranking of promoter activities to be wt > M1 ≈ M2 > M3 > M4 > M5. This is an unexpected result, with the wt promoter having the highest activity.
Effect of promoter activity on lysis time:
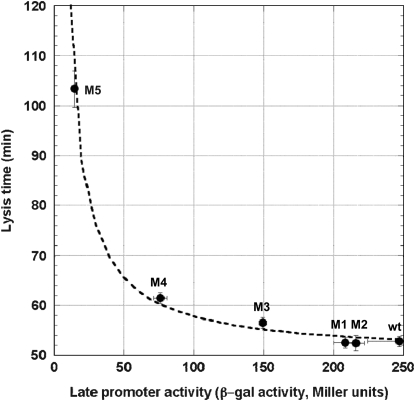
We postulated that a stronger pR′ promoter would transcribe the late mRNA transcript more frequently and accumulate the S holin protein more rapidly, thus causing a reduction in lysis time; while a weaker pR′ would have the opposite effect (Chang et al. 1995). Figure 2 shows the general negative relationship between the promoter activity and lysis time. As expected, as the promoter activity becomes higher, the lysis time becomes shorter, but only to a certain extent. Once the promoter activity is >84% of the wt's (i.e., M1 and M2; see Table 2), the lysis times are virtually the same. Figure 2 also shows the ad hoc relationship obtained by fitting the data to the model of tL = tMIN(t1/2 + a)/a, where both tMIN and t1/2 are the parameters to be estimated and a is the late promoter activity. Even though this is an arbitrary function, it nevertheless fulfills the basic requirement: namely when a → 0, tL →  , and when a →
, and when a →  , tL → tMIN. The estimated parameters are tMIN = 50.0 and t1/2 = 15.7.
, tL → tMIN. The estimated parameters are tMIN = 50.0 and t1/2 = 15.7.
Figure 2.—
Effect of the late promoter activity on lysis time. Solid symbols represent the empirically determined lysis times. Error bars denote the 95% confidence intervals. Some of the intervals are too small to show. The dashed curve represents the fitted model of tL = 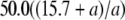 , where tL is the lysis time and a is the late promoter activity.
, where tL is the lysis time and a is the late promoter activity.
Our result suggests that, when the late promoter activity is low, the “limiting step” in determining the lysis time is the amount of the holin protein being produced. However, once enough holin proteins are produced, factors other than the amount of the S holin proteins, for example, the rate of holin insertion onto the membrane or the rate of oligomerization, etc., become limiting in determining the lysis time.
Effect of promoter activity on assembly rate and burst size:
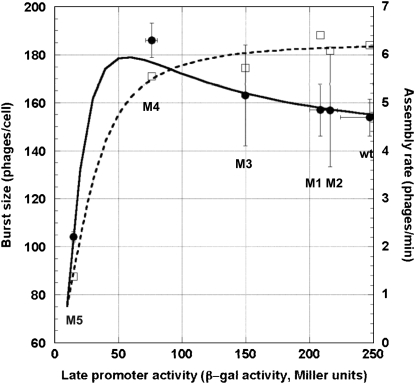
The effect of late promoter activity on burst size is shown in Figure 3. The burst size actually increased even as the promoter activity declined to only ∼31% of the wt's (i.e., M4; see Table 2). Within this range of the promoter activity, the lysis time lengthened from ∼53 to ∼62 min (see Table 2). However, once the promoter activity is only ∼6% of the wt's, the burst size is reduced as well, even though the lysis time has now increased to ∼103 min.
Figure 3.—
Effects of the late promoter activity on assembly rate and burst size. Open squares denote the estimated assembly rates and solid circles show the empirically determined burst sizes. Error bars denote the 95% confidence intervals. The dashed curve shows the fitted model of m = 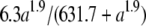 , where m is the assembly rate and a is the late promoter activity. The solid line shows the predicted burst size based on the equation of b = m(tL − e), where b is the burst size, tL is the lysis time (see Figure 3), m is the assembly rate (see above), and e is the eclipse period of 28 min (see text).
, where m is the assembly rate and a is the late promoter activity. The solid line shows the predicted burst size based on the equation of b = m(tL − e), where b is the burst size, tL is the lysis time (see Figure 3), m is the assembly rate (see above), and e is the eclipse period of 28 min (see text).
Table 2 shows the estimated assembly rates using m = b/(tL − e), where m is the assembly rate, b is the burst size, tL is the lysis time, and e is the eclipse period, which has been estimated to be 28 min (Wang 2006). A simple Hill equation of m = mMAXan/(an + m1/2), where mMAX, m1/2, and n are the parameters to be estimated, is arbitrarily chosen to describe the relationship between the late promoter activity a and the assembly rate m. Again, this equation fulfills two requirements: namely, when a → 0, m → 0, and when a → 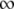 , m → mMAX. Figure 3 (dashed curve) shows the relationship using the estimated parameter values of mMAX = 6.3, m1/2 = 631.7, and n = 1.9.
, m → mMAX. Figure 3 (dashed curve) shows the relationship using the estimated parameter values of mMAX = 6.3, m1/2 = 631.7, and n = 1.9.
Figure 3 (solid curve) also shows the predicted burst size based on the predicted assembly rate and predicted lysis time (see above). So far, our results suggest that, within a certain range of the late promoter activity (say, >31% of the wt's), the capacity to assemble phage progeny does not decline discernibly with decreasing late promoter activity. The consequence of this relatively well-buffered assembly capacity is that the phage with a weaker late promoter activity is actually producing a larger burst size because of a lengthened lysis time. However, once the late promoter activity is declined to such an extent (say, <6% of the wt's), the capacity to assemble deteriorates sharply, such that even a very much lengthened lysis time could not increase the burst size.
Effect of promoter activity on phage relative fitness:
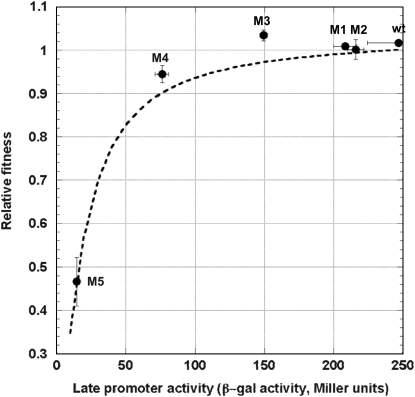
The effect of late promoter activity on phage relative fitness was determined by pairwise competition experiments. In this study the λ-strain carrying the wt pR′ promoter sequence was used as the standard strain and the others as the competing strains. Table 2 and Figure 4 show the results.
Figure 4.—
 |
Since the same λ-strain was used as the standard strain in each pairwise competition, its growth rate in each competition can be used as an internal control for the culture environment (Shao and Wang 2008). As shown in Table 2, the growth rates for the standard strain are not significantly differently from each other, indicating that the culture environment for competition is similar across all experiments.
The effect of the late promoter activity on phage relative fitness is shown in Figure 4. On the surface, it seems that mutant M3, which has ∼60% activity of that of the wt (see Table 2), has the highest relative fitness. However, unplanned comparisons using the Tukey–Kramer HSD test showed that there is no significant difference among the growth rates of the competing strains, except for mutant M5, which has the lowest late promoter activity (see Table 2).
Since the phage growth rate (fitness) is calculated as μ = ln(b)/(tS + tL), where b is the burst size, tS is the search time for the host, and tL is the lysis time (Shao and Wang 2008), we would also be able to describe the relationship between the late promoter activity and phage relative fitness if tS is known. For each phage strain, the tS was estimated by tS = (ln(b)/μ) − tL, using data presented in Table 2. With nonlinear regression, the relationship between tS and the late promoter activity a was further described as 52.5(a + 17.0)/a (results not shown). The phage relative fitness was then calculated as μCOM/μSTD, where the subscripts COM and STD denote the competing and the standard strains, respectively. In this case, the growth rate μ is treated as a function of the late promoter activity a and is expressed as
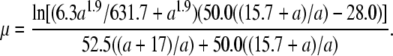 |
Figure 4 shows the result of this calculated relative fitness in relation to the late promoter activity. Our result indicates that the current wt late promoter activity is very close to, if not already on, the plateau of the fitness curve.
DISCUSSION
Effect of λ late promoter activity on lysis time:
At present, there is no systematic study on the relationship between the late promoter activity and lysis time. Our result indicates an asymptotic relationship of tL = 50.0(15.7 + a)/a between the lysis time tL and the late promoter activity a (see results and Figure 2). However, we note that this equation is simply the result of curve fitting on the basis of the pattern of available data points. It is not intended to represent the true relationship. Nevertheless, this phenomenological relationship is likely to be valid when the late promoter activity a is smaller than the wt's. On the other hand, it is not clear if the relationship would still hold if a is much larger. According to this equation, the shortest lysis time the phage can achieve by increasing the late promoter activity is 50 min when a → 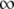 . But circumstantial evidence seems to suggest that this may not be a valid relationship when a is large. While studying the molecular mechanism of host lysis, the wt S gene of phage λ has been expressed from various backgrounds, from the single-copy and double-copy prophages in a lysogen (Raab et al. 1988), from medium- and high-copy-number plasmids (Chang et al. 1995; Gründling et al. 2000), up to the very active phage T7 promoter (Smith et al. 1998). The lysis time resulting from these various expression systems can be used as a gauge on what the lysis time would be like if phage λ has a late promoter activity that is higher than the wt's. The general trend is that there is a progressive shortening of the lysis time as more holin proteins are expressed. In fact, the lysis time is ∼20 min when the amount of holin is overexpressed to >100-fold that of the wt level (Smith et al. 1998, Figure 2). Clearly, more empirical studies are needed to accurately evaluate the impact the late promoter activity has on lysis time.
. But circumstantial evidence seems to suggest that this may not be a valid relationship when a is large. While studying the molecular mechanism of host lysis, the wt S gene of phage λ has been expressed from various backgrounds, from the single-copy and double-copy prophages in a lysogen (Raab et al. 1988), from medium- and high-copy-number plasmids (Chang et al. 1995; Gründling et al. 2000), up to the very active phage T7 promoter (Smith et al. 1998). The lysis time resulting from these various expression systems can be used as a gauge on what the lysis time would be like if phage λ has a late promoter activity that is higher than the wt's. The general trend is that there is a progressive shortening of the lysis time as more holin proteins are expressed. In fact, the lysis time is ∼20 min when the amount of holin is overexpressed to >100-fold that of the wt level (Smith et al. 1998, Figure 2). Clearly, more empirical studies are needed to accurately evaluate the impact the late promoter activity has on lysis time.
Effect of λ late promoter activity on assembly rate and burst size:
The observed relationship between the late promoter activity and the assembly rate was initially fitted through the simple Michaelis–Menten equation. However, the resulting model, when combined with the above promoter activity–lysis time model, did not yield burst sizes that resemble the empirically estimated ones. Therefore, the Hill equation, a similarly asymptotic model, was used to fit the data points; this resulted in a much smaller mean squared error than that of the Michaelis–Menten equation (result not shown). On the basis of this model, the maximum assembly rate mMAX is estimated to be 6.3 phages/min. This value is smaller than a previous estimate of 7.7 phages/min (Wang 2006). It is not clear why these two estimates are different. One possibility is simply how these two assembly rates were estimated: one estimate used linear regression on data obtained from phage strains carrying different S alleles that resulted in a different lysis time (Wang 2006) and the other used nonlinear regression with indirectly obtained assembly rate data (this study). Also, in this study, the estimation of the assembly rate assumed that the eclipse period (the time period within which no phage progeny is assembled yet) was not a function of the late promoter activity and remained at 28 min. This assumption of 28 min is likely to be violated, particularly in the case of M5 (the mutant with the lowest late promoter activity, ∼6% of the wt's, see Table 2). It is possible that lower concentrations of virion components may also delay the assembly of the first progeny virion, thus lengthening the eclipse period. If indeed the M5′s eclipse period is >28 min, then the estimated assembly rate for M5 would be an underestimate. That is, under such a scenario, all the estimated assembly rates would be similar to each.
Whether M5′s eclipse period is 28 min or not, it is evident from our result (see Figure 3) that the relationship between the late promoter activity and virion assembly rate is not linear, as we expected on the basis of the assumption that coordinated and simultaneous increase or decrease of all virion components would respectively increase or decrease the assembly rate accordingly. Our result suggests that either our assumption of linearity is not correct or the rate-liming step of virion assembly is not at the steps regulated by the late promoter, e.g., genomic DNA replication, etc., and thus not influenced by variation in the late promoter activity. However, a recent study of phage λ assembly showed that, at least under the in vitro condition, the rate-limiting step of phage assembly, when compared to the genomic DNA packaging, is at the step of head–tail joining (Gaussier et al. 2006), a step in which the component concentrations would certainly be influenced by the late promoter activity. To complicate matters further, in the same study, the authors also showed that not all the relationships between component concentrations and virion assembly are as straightforward as the Michelis–Menten kind. In fact, some components are actually inhibitory to the process of virion assembly at elevated concentrations (e.g., gpFI, gpD, and tails; see Gaussier et al. 2006, Figure 4). Therefore, the coordinated and simultaneous increase or decrease of component concentrations, as effected by changing the late promoter activity, may not be directly translated into increase or decrease of the assembly rate.
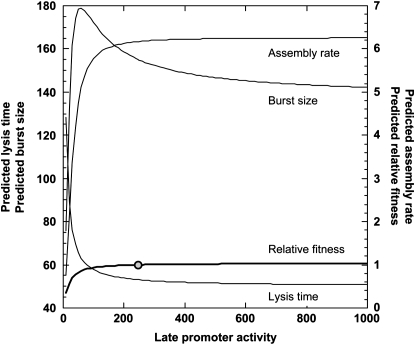
Whether our assumption on the relationship between the late promoter activity and the assembly rate is correct or not, the observation that there is a maximum burst size indicates that the assembly rate is much less sensitive to the variation in late promoter activity when compared to the lysis time. Our results indicate that a relatively large buffering capacity is maintained during the late stage of the infection cycle to sustain a somewhat constant assembly rate. Furthermore, our results also suggest that further increase of the late promoter activity would not have much effect on increasing the virion assembly rate (see Figure 5). However, as in the case with the lysis time, we need to be aware that this extrapolation has no empirical support for it yet. Experiments with late promoter activities higher than the wt's, for example by transplanting the entire late regulatory circuit from other phages, are needed to establish the conclusion that phage λ's assembly rate is at the maximum with respect to the late promoter activity.
Figure 5.—
The extrapolated relationships between the late promoter activity and assembly rate, lysis time, burst size, and relative fitness. Equations in Figures 2–4 were used to show these relationships when the late promoter activity is higher than that of the wt. The wt promoter activity is shown as a solid circle.
Effect of λ late promoter activity on phage fitness:
Whether phage λ's late promoter activity can readily evolve or not would have to be evaluated in terms of its effect on phage fitness. Our fitness model is actually a composite of several equations derived from various model fittings. As discussed above, all these component equations are asymptotic in nature. The choices of these equations are mainly dictated by data patterns. Nonetheless, we can justify the overall asymptotic relationship between the late promoter activity and lysis time or assembly rate. However, to derive the fitness model, we also introduced a fitted equation describing the relationship between the late promoter activity and the search time tS. At first glance, there is no a priori reason to believe that the late promoter activity would directly affect the search time. This equation is simply describing a phenomenological relationship. With that caveat in mind, we can nonetheless extrapolate this fitness model to explore the conditions when the late promoter activity is much higher than the current wt level. Figure 5 shows the extrapolated relationships between the late promoter activity and lysis time, burst size, and relative fitness. Not surprisingly, the current model shows that the wt's late promoter activity is already on top of the fitness plateau, suggesting that even further increase of the late promoter activity would not improve the phage fitness much. Since this is an extrapolation, empirical tests are still needed to confirm such a prediction.
Evolution of the optimal late promoter activity in a broader context:
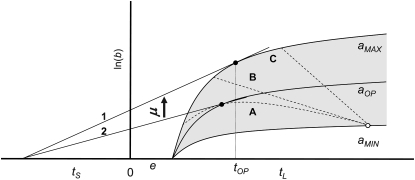
For any phage, there would always exist a possibility of an optimal promoter activity if the lysis genes (mainly the holing genes) and morphogenesis genes are regulated by the same said promoter. But the condition for the existence of an optimal late promoter activity would depend on how the assembly rate and the lysis time are affected by the activity. As shown in Figure 6, the assembly rate and the lysis time can be affected in such ways that the relationship between these two traits could be described as curve A, B, or C. In all three scenarios, the lysis time becomes shorter and the assembly rate higher (i.e., steeper rise of the burst size curve) to a varying degree in relation to each other as the late promoter activity becomes higher. If the relationship between these two traits follows curve A, then we would expect that the evolution of the late promoter activity be dictated by the need to balance the cost and benefit of having too high (resulting in a higher assembly rate and a shorter lysis time) or too low (resulting in a lower assembly rate and a longer lysis time) an activity, thus leading to an optimal activity that maximizes the phage fitness (i.e., the slope of the tangent line 2). On the other hand, if the relationship follows curve B or C, then the cost of having a “wrong” lysis time would be more than compensated by having a high assembly rate (as a consequence of high promoter activity). That is, with such relationships, the evolution of the late promoter activity would be driven toward as high an activity as possible. We note, however, that the global maximum fitness (i.e., slope of the tangent line 1) in this case would be achieved by the phage strain having the highest possible assembly rate (as a result of highest possible late promoter activity) and the optimal lysis time tOP. That is, evolution of the late promoter activity alone would, in most cases, result in suboptimal strains. Even under the condition of constant host density, subsequent evolution would involve the inexorable climb of the late promoter activity and fine tuning of the lysis time via mutation(s) at the holin gene.
Figure 6.—
Graphical representation of phage long-term fitness (growth rate) under the environment of constant host density. This representation follows the convention of Wang et al. (1996). In this representation, the evolution of phage fitness is to result in a higher growth rate μ, which is defined as 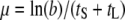 , where b is the burst size at lysis time tL, and tS is the average search time for a given host density. Solid curves represent the accumulation of progeny of phage strains with different late promoter activities, from the lowest of aMIN to the highest of aMAX. The gray area represents all possible values in between these two extremes. Dashed curves A, B, and C represent the possible relationships between lysis time (tL) and assembly rate for a given late promoter activity. For example, the open circle shows that the strain with the lowest late promoter activity would have the longest lysis time and lowest assembly rate (i.e., the steepness of the curves represented by the solid curves). Tangent line 1 shows the global fitness maximum in this representation, i.e., the strain with the highest assembly rate and the optimal lysis time tOP. Tangent line 2 shows the condition where the optimal late promoter activity is possible. In this case, the slope of the tangent line 2 (the long-term phage fitness) would be the largest when compared to other possible late promoter activity with different combinations of lysis time and assembly rate constrained by curve A.
, where b is the burst size at lysis time tL, and tS is the average search time for a given host density. Solid curves represent the accumulation of progeny of phage strains with different late promoter activities, from the lowest of aMIN to the highest of aMAX. The gray area represents all possible values in between these two extremes. Dashed curves A, B, and C represent the possible relationships between lysis time (tL) and assembly rate for a given late promoter activity. For example, the open circle shows that the strain with the lowest late promoter activity would have the longest lysis time and lowest assembly rate (i.e., the steepness of the curves represented by the solid curves). Tangent line 1 shows the global fitness maximum in this representation, i.e., the strain with the highest assembly rate and the optimal lysis time tOP. Tangent line 2 shows the condition where the optimal late promoter activity is possible. In this case, the slope of the tangent line 2 (the long-term phage fitness) would be the largest when compared to other possible late promoter activity with different combinations of lysis time and assembly rate constrained by curve A.
Acknowledgments
The authors thank the anonymous reviewers for their careful reading and thoughtful comments on this manuscript. This study is sponsored by National Institutes of Health grant GM 072815.
References
- Calendar, R. (Editor), 2006. The Bacteriophages. Oxford University Press, New York.
- Chang, C. Y., K. Nam and R. Young, 1995. S gene expression and the timing of lysis by bacteriophage λ. J. Bacteriol. 177 3283–3294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fell, D. A., 1998. Increasing the flux in metabolic pathways: a metabolic control analysis perspective. Biotechnol. Bioeng. 58 121–124. [DOI] [PubMed] [Google Scholar]
- Friedman, D. I., and M. Gottesman, 1983. Lytic mode of lambda development, pp. 21–51 in Lambda II, edited by R. W. Hendrix, J. W. Roberts, F. W. Stahl and R. A. Weisberg. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY.
- Gaussier, H., Q. Yang and C. E. Catalano, 2006. Building a virus from scratch: assembly of an infectious virus using purified components in a rigorously defined biochemical assay system. J. Mol. Biol. 357 1154–1166. [DOI] [PubMed] [Google Scholar]
- Gründling, A., U. Bläsi and R. Young, 2000. Genetic and biochemical analysis of dimer and oligomer interactions of the lambda S holin. J. Bacteriol. 182 6082–6090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo, J., and J. W. Roberts, 2004. DNA binding regions of Q proteins of phages λ and ϕ80. J. Bacteriol. 186 3599–3608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harley, C. B., and R. P. Reynolds, 1987. Analysis of E. coli promoter sequences. Nucleic Acids Res. 15 2343–2361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hendrix, R. W., J. W. Roberts, F. W. Stahl and R. A. Weisberg (Editors), 1983. Lambda II. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY.
- Herskowitz, I., and E. R. Signer, 1970. A site essential for expression of all late genes in bacteriophage λ. J. Mol. Biol. 47 545–556. [DOI] [PubMed] [Google Scholar]
- Kacser, H., and J. A. Burns, 1973. The control of flux. Symp. Soc. Exp. Biol. 27 65–104. [PubMed] [Google Scholar]
- Karam, J. D. (Editor), 1994. Molecular Biology of Bacteriophage T4. American Society for Microbiology, Washington, DC.
- Lisser, S., and H. Margalit, 1993. Compilation of E. coli mRNA promoter sequences. Nucleic Acids Res. 21 1507–1516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller, J. H., 1992. A Short Course in Bacterial Genetics. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY.
- Raab, R., G. Neal, C. Sohaskey, J. Smith and R. Young, 1988. Dominance in lambda S mutations and evidence for translational control. J. Mol. Biol. 199 95–105. [DOI] [PubMed] [Google Scholar]
- Savageau, M. A., 1976. Biochemical Systems Analysis: A Study of Function and Design in Molecular Biology. Addison-Wesley, Reading, MA.
- Shao, Y., and I. N. Wang, 2008. Bacteriophage adsorption rate and optimal lysis time. Genetics 180 471–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, D. L., C.-Y. Chang and R. Young, 1998. The λ holin accumulates beyond the lethal triggering concentration under hyperexpression conditions. Gene Exp. 7 39–52. [PMC free article] [PubMed] [Google Scholar]
- Sokal, R. R., and F. J. Rohlf, 1995. Biometry. W. H. Freeman, New York.
- Wang, I. N., 2006. Lysis timing and bacteriophage fitness. Genetics 172 17–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, I.-N., D. E. Dykhuizen and L. B. Slobodkin, 1996. The evolution of phage lysis timing. Evol. Ecol. 10 545–558. [Google Scholar]
- Wang, I.-N., J. Deaton and R. Young, 2003. Sizing the holin lesion with an endolysin-β-galactosidase fusion. J. Bacteriol. 185 779–787. [DOI] [PMC free article] [PubMed] [Google Scholar]