Linkage Disequilibrium and Demographic History of Wild and Domestic Canids

Abstract

Assessing the extent of linkage disequilibrium (LD) in natural populations of a nonmodel species has been difficult due to the lack of available genomic markers. However, with advances in genotyping and genome sequencing, genomic characterization of natural populations has become feasible. Using sequence data and SNP genotypes, we measured LD and modeled the demographic history of wild canid populations and domestic dog breeds. In 11 gray wolf populations and one coyote population, we find that the extent of LD as measured by the distance at which r² = 0.2 extends <10 kb in outbred populations to >1.7 Mb in populations that have experienced significant founder events and bottlenecks. This large range in the extent of LD parallels that observed in 18 dog breeds where the r² value varies from ∼20 kb to >5 Mb. Furthermore, in modeling demographic history under a composite-likelihood framework, we find that two of five wild canid populations exhibit evidence of a historical population contraction. Five domestic dog breeds display evidence for a minor population contraction during domestication and a more severe contraction during breed formation. Only a 5% reduction in nucleotide diversity was observed as a result of domestication, whereas the loss of nucleotide diversity with breed formation averaged 35%.

RECOMBINATION, recurrent mutation, selection, admixture, and mate choice are factors that influence the extent of linkage disequilibrium (LD) within a species (Gaut and Long 2003; Mueller 2004; Deonier et al. 2005). The extent of LD is one of several attributes that affects how readily phenotypic traits in natural populations can be mapped using whole-genome association studies. Extensive LD allows associations to be detected more readily using a small number of distantly placed informative markers, whereas low LD necessitates fine-scale mapping (Slate 2005; Kohn et al. 2006; Steiner et al. 2007). Several studies have measured the extent of LD in plant, invertebrate, and domestic vertebrate species (Farnir et al. 2000; Remington et al. 2001; McRae et al. 2002; Haddrill et al. 2005; Ingvarsson 2005; Cutter et al. 2006; Harmegnies et al. 2006); however, little is known about the extent of LD in wild populations of nonhuman vertebrates.

Among populations of the same species that share similar rates of recombination and mutation and where selection is weak, a critical variable for determining the extent of LD is demographic history. In general, populations that have remained large for a substantial period of time or have rapidly expanded demonstrate lower levels of LD than those that are small or have experienced recent population bottlenecks (Pritchard and Przeworski 2001; Reich et al. 2001; Gaut and Long 2003; Mueller 2004). Therefore, the extent of LD can be used as a tool to infer demographic history. With the exception of a few model species, the extent of LD has not been used to explore population history primarily because large numbers of markers need to be typed in a substantial number of samples. To date, there have been only a few wild vertebrate species for which the extent of LD has been carefully documented: the collared flycatcher (Ficedula albicollis) (Backstrom et al. 2006), red deer (Cervus elaphus) (Slate and Pemberton 2007), and wild mice (Mus musculus domesticus) (Laurie et al. 2007). Additionally, LD was modeled in a wild Soay sheep population using simulations that included parameters of population history (McRae et al. 2005).

The domestic dog (Canis familiaris) is emerging as an important model for understanding the genetic basis of morphology, behavior, and disease in mammals (Sutter and Ostrander 2004; Ostrander and Wayne 2005; Parker and Ostrander 2005; Wayne and Ostrander 2007). In 2005, a 7.8× whole-genome shotgun sequence and assembly of the boxer was completed (Lindblad-Toh et al. 2005). In addition, a 1.5× survey sequence of the Standard poodle became publicly available in 2003 (Kirkness et al. 2003). These two resources, together with 100,000 random sequence reads from nine other dogs of unrelated breeds and 20,000 sequence reads from each of four gray wolves (C. lupus) and one coyote (C. latrans) (Lindblad-Toh et al. 2005), provide extensive resources for identifying markers for large-scale genetic analysis of wild canid species.

In this article, we utilize dog-derived single-nucleotide polymorphisms (SNPs) as well as extensive resequencing to obtain estimates of LD in wild and domestic canids. Sutter et al. (2004) first characterized the extent of LD in 5 dog breeds across five 1-Mb regions, followed by Lindblad-Toh et al. (2005), who examined the extent of LD within 10 dog breeds across a 15-Mb region. We expand the number of domestic dog breeds for which the extent of LD is estimated (12 new breeds), although our primary goal is to determine the range that LD extends in a large panel of wild canid populations, including gray wolves and coyotes, and compare these estimates to those from domestic dog breeds. Furthermore, we explore the relationship of LD and demographic history by comparing estimates of LD to known population histories. We also model population histories using the site frequency spectra (SFS) of each population based on origination from an ancestral wolf population followed by specific demographic scenarios. These predicted SFS are then compared to those observed.

MATERIALS AND METHODS

Blood, tissue, or buccal swab samples were collected from 908 individuals: 18 dog breeds, n = 546 (unrelated at the grandparent level); 14 gray wolf populations, n = 344; and one coyote population, n = 18 (Table 1). To determine the rate of successful amplification of dog-derived molecular markers in distant relatives of the domestic dog, an additional 93 samples were typed from golden jackal (C. aureus), bat-eared fox (Otocyon megalotis), gray fox (Urocyon cinareoargenteus), and Channel Island fox (Urocyon littoralis). For samples with low DNA concentrations, whole-genome amplification was performed according to manufacturer guidelines [QIAGEN (Valencia, CA) REPLI-g kit].

TABLE 1.

Samples genotyped and sequenced

Genotyping (106 SNP loci)			Sequencing (18 amplicons)a
No. of populations	No. of individuals	Species	No. of populations	No. of individuals	Species
14	344	Gray wolf	4	73	Gray wolf
1	18	Coyote	1	17	Coyote
18	546	Domestic dog breeds	5	97	Domestic dog breedsb
1	18	Golden jackal	1	1	Golden jackal
1	20	Bat-eared fox
1	29	Gray fox
1	26	Channel Island fox
	1001			188

^aSubset of samples that were SNP genotyped.

^bSame sample set used in Sutter et al. (2004).

Gray wolf populations sampled varied in demographic history and include individuals from large outbred populations and from smaller inbred or recently bottlenecked populations (supplemental Table S1). Furthermore, the populations chosen here have been the focus of previous genetic research (Lehman and Wayne 1991; Lehman et al. 1992; Roy et al. 1994, 1996; Vilà et al. 1999a; Leonard et al. 2005; Ramirez et al. 2006; Musiani et al. 2007 ) such that demographic and population genetic conclusions from LD patterns can be independently verified.

The domestic dog breeds included in this study also vary in relatedness and demographic history; thus, they provide a test of the use of LD to assess population demography across a variety of timescales and population sizes. American Kennel Club (AKC) registration statistics (AKC website: http://www.akc.org/reg/dogreg_stats.cfm) were used as a proxy for effective population size and recent demographic history. Kendall's τ and a Mantel's test were performed to determine the significance of association between LD and the log of the number of registered individuals.

All 1001 samples were genotyped on an ABI 3730 (Applied Biosystems, Foster City, CA) for 106 SNP loci (Table 1; supplemental Figure S1), using a custom set of primers designed for the SNPlex genotyping system (Applied Biosystems). The 106 SNPs genotyped were chosen as a representative subset of the 200 SNPs described previously in Sutter et al. (2004), which were ascertained by direct resequencing of 5 loci on 5 chromosomes, each spanning a noncontiguous 5-Mb region. Genemapper 4.0 was used to make genotype calls for each SNP locus (Applied Biosystems).

To determine the effect of ascertainment bias on LD estimates from genotype data and to model demographic history (see below), sequencing of 18 amplicons spaced across a noncontiguous 5-Mb region of chromosome 1 (similar to Sutter et al. 2004) was performed on 188 individuals (a subset of genotyped individuals): five breeds of dog, n = 97 (same as Sutter et al. 2004); four gray wolf populations, n = 73; a coyote population, n = 17; and one golden jackal (supplemental Table S2 and supplemental Figure S2). Eleven of the 18 amplicons were reported previously in Sutter et al. (2004). The 11 amplicons were chosen to minimize the amount of sequencing but still measure low- to medium-range LD (i.e., 10–100 kb). We designed and sequenced an additional 7 amplicons, spaced at 50-kb intervals from the central region on chromosome 1, to enhance this latter goal (supplemental Figure S2 and supplemental Table S2). Sequences were run on an ABI 3730 and polymorphisms were identified and viewed using Phred/Phrap/Consed/Polyphred (Nickerson et al. 1997; Ewing and Green 1998; Ewing et al. 1998; Gordon et al. 1998). All data will be made available on upon request.

Analysis:

Genepop (Raymond and Rousset 1995) was used to calculate levels of heterozygosity and Hardy–Weinberg equilibrium. Estimates of nucleotide diversity were calculated from sequence data representing a sampling of one chromosome per individual for 2000 iterations. This was done to account for inbreeding within breeds and potential sampling of closely related individuals in wild populations. To determine if and to what degree there was a loss of diversity during the domestication of dogs, we sampled one chromosome from each of five domestic dog breeds and four wild canid populations and calculated loss of diversity as 1 − (π in dogs)/(π in wolves). Additionally, the loss of nucleotide diversity at breed formation (1 − (π in breed)/(π in dogs)) was calculated by sampling one chromosome from each individual of each breed of dog and one chromosome from each individual across all breeds. Haplotypes were inferred across each population using the software program PHASE (Stephens et al. 2001; Stephens and Donnelly 2003). The percentages of haplotypes within and among breeds/populations were calculated as in Sutter et al. (2004). The software program Haploview (Barrett et al. 2005) was used to calculate r² and D′, which were plotted by matching allele frequencies between pairs of SNPs with an allele frequency difference of <10% (Eberle et al. 2006). Median values for each distance category were calculated and a logarithmic curve was fitted to the data. An r² of 0.2 was arbitrarily chosen as the value for which the extent of LD was compared between populations and species.

Ascertainment bias:

The discovery panel for genotyped loci contained five breeds of dog: one breed from each of five distinct phylogenetic groupings (Parker et al. 2004, 2007; Sutter et al. 2004). Genotyping these loci in populations outside the discovery panel will likely result in ascertainment bias because SNPs at high frequency in one population/breed may be rare or absent in others. Thus, the level of ascertainment bias present in this study was assessed by performing simulations that replicated the ascertainment scheme (supplemental Figure S3). This scheme utilized the original sequence data (Sutter et al. 2004) in the following procedure:

1. One breed of dog was randomly chosen as the focus breed and individuals from the four other breeds were designated as the ascertainment panel.

2. For each amplicon, two individuals were randomly selected from the ascertainment panel and compared. If any marker was segregating, it was flagged as a SNP and “genotyped” in the focus breed. This sampling was repeated for 2000 bootstraps.

3. The extent of LD was calculated for the focus breed and compared to the extent of LD based on the observed sequence data.

This sampling increased the diversity of sequence comparisons used and accounted for possible unobserved sequences due to recombination among amplicons. Also, we wanted to reduce the bias caused by using a limited set of starting points.

Population structure:

Principal component analysis (PCA) using the program Eigenstrat (Price et al. 2006) was performed on genotyped loci to determine if the 106-SNP data set identified population substructure. Twstats (Patterson et al. 2006) in Eigenstrat was used to determine the number of significant principal components. As “a rule of thumb,” one plus the number of significant principal components is considered the number of groups identified by the PCA.

Demographic modeling:

To explore the demographic history of wild canid populations and domestic dog breeds, we used the program PRFREQ (Williamson et al. 2005; Boyko et al. 2008) to estimate demographic parameters under a composite-likelihood framework. The program utilizes the Poisson random field (PRF) approach (Sawyer and Hartl 1992), which predicts the distribution of allele frequencies across sites on the basis of single-locus diffusion theory. Demographic parameters are then estimated by maximum likelihood using the SFS. Assumptions of the program are the Wright–Fisher model of mutation and independence among sites. However, the majority of loci utilized in this study were in linkage disequilibrium. Therefore, the likelihoods should be interpreted as a “composite-likelihood” function, an approximation of the true likelihood (Caicedo et al. 2007), as the assumption of independence between sites is violated. Because of the violation of linkage equilibrium, simulations of linked sites within amplicons were performed to verify our P-values (see supplemental text). Two likelihood functions were used to make inferences. The first is based on the number of SNPs in each frequency class (denoted “Poisson”), and the second is based on the proportion of SNPs in each class (denoted “multinomial”). The Poisson likelihood function is much more powerful for inference of bottlenecks, since it takes into account the degree of reduction in diversity as well as the skew in allele frequency distribution. The multinomial-likelihood function captures only the latter, but has the advantage of not requiring a priori assumptions regarding the population-scaled mutation rate, θ. Across models, the significance of incorporating additional demographic parameters was assessed by using the likelihood-ratio test (2 log[L(model 1)/L(model 2)]).

Domestication model:

To model the initial domestication event in dogs (Figure 1a), sequence data from Sutter et al. (2004) derived from 5 breeds of dog were combined with genotype data from this study, producing a combined data set containing 22 dog breeds. Loci common to both data sets and not segregating in the outgroup (golden jackal) were retained for further analysis (82 SNPs). To generate an unfolded site frequency spectrum representative of the ancestral domesticated dog population to estimate demographic parameters, we randomly selected one chromosome from each breed for 2000 iterations and constructed a SFS averaged across iterations. SNPs with sample sizes <14 (due to missing data) were excluded, leaving a total of 76 SNPs. SNPs with sample sizes >14 were “projected” to a sample size of 14. This involved using the hypergeometric distribution to calculate the probability of the latter falling into each frequency class of a SFS with sample size 14 and summing over all SNPs in each frequency class to create the final SFS (Clark et al. 2005).

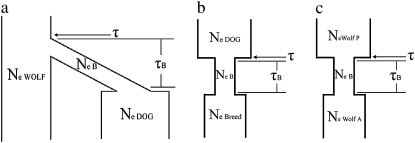
Figure 1.—

Demographic model of (a) dog domestication, (b) dog breed formation, and (c) wolf population size change. N_eWOLF, N_eB, N_eDOG, N_eBreed, N_eWOLFP, and N_eWOLFA are the effective population sizes of the gray wolf (constant over time), of the population during the bottleneck, the effective population size of dogs, the effective population size of breeds, the effective population size of gray wolves prior to a population size change, and the effective population size of wolves after a population size change, respectively. τ is the time of the domestication event from the present, and τ_B is the bottleneck duration.

To control for the effect of ascertainment bias on our observed SFS, we chose to create a corrected site frequency spectrum as outlined in Nielsen et al. (2004). Corrections were made under the basic model, assuming all SNPs were ascertained at a discovery panel depth of five (for the five initial dog breeds in the ascertainment panel). We found the maximum likelihood of the true probabilities of each entry in the site frequency spectrum given our observed values of entries.

PRFREQ was then used to estimate demographic parameters based on two site frequency spectra (corrected for ascertainment bias and uncorrected). We estimated the following parameters: length of the domestication event (τ_B), the bottleneck population size (ω_B), and the domesticated dog population size after the bottleneck (ω) (Figure 1a and Table 2). The model that best fit the observed data was determined by comparing the likelihoods of the nested models. A constant population size of 21,591 in gray wolf (N_ewolf) was assumed over time, estimated from Watterson's θ (θ = 4N_eμ) calculated from pairwise estimates between all wolves and using a mutation rate (μ) of 1 × 10⁻⁸ per generation (Lindblad-Toh et al. 2005). This value was reevaluated excluding populations found later to exhibit some evidence of a past contraction event (see results) but was minimally different (22,600). The initiation of the domestication of domestic dogs (τ) was assumed to be 15,000 years before present (Olsen 1985; Savolainen et al. 2002).

TABLE 2.

Parameters and demographic models tested

	Parameters				Domestic dog		Wild canids:
Nested likelihood models	τ	ω	τB	ωB	Domestication	Breed formation	Wild population history
Constant population size	—	—	—	—	X	X	X
Contraction at fixed time	Fixed	Varied	—	—	X	X	—
Contraction at unknown time	Varied	Varied	—	—	X	X	X
Bottleneck of fixed size	Fixed	Varied	Varied	Fixed	X	—	—
Bottleneck of unknown size	Fixed	Varied	Varied	Varied	X	—	—
Bottleneck of fixed length	Varied	Varied	Fixed	Varied	—	X	—
Bottleneck of unknown length	Varied	Varied	Varied	Varied	—	X	X

—, not applicable or not tested; τ, time of contraction event in number of generations; τ_B, length of time the contraction occurred in number of generations; ω, effective population size following the contraction scaled in terms of the ancestral wolf/dog effective population size; ω_B, effective population size during the contraction scaled in terms of the ancestral wolf/dog effective population size.

Breed formation model:

To further model the formation of breeds (Figure 1b), we used the complete sequence data from Sutter et al. (2004) from five chromosomes in five dog breeds. However, as a result of breeding programs, dog breeds are highly inbred, and an individual's chromosomes are more similar than expected under random mating. Since this could potentially affect our demographic inferences, we attempted to reduce the effects of inbreeding within breeds by sampling one chromosome per individual per breed, creating a site frequency spectrum for each of 2000 iterations, and averaging across iterations. Because the data were generated by sequencing and sample sizes of SNPs were consistent across loci, corrections for sample size and ascertainment bias were not necessary as with modeling the domestication event. Likelihoods between several nested models were compared to determine which model best fit the observed data (Figure 1b and Table 2).

Wild canid model:

To model the formation of wild canid populations (Figure 1c), we used chromosome 1 sequence data generated in this study across four gray wolf populations and one coyote population. To account for potential inbreeding in wild canid populations, and to ensure that unknown closely related individuals did not bias our estimates, we chose to perform the same chromosome sampling done for dog breeds. As in the breed formation models, corrections for sample size and ascertainment bias were not necessary.

Nested models identical to those examined for breed formation were used to model the wild canid populations (Figure 1c and Table 2). However, models fixing the time of contraction were not tested, as we did not know a priori whether we should expect to see a population contraction or expansion nor the timing of such an event. For those populations with evidence for a population decline, we tested models varying the contraction event.

RESULTS

Genetic diversity:

To study the effects of demographic history on LD in wild canids and domestic dogs, we sequenced 11,279 bp spanning ∼5.2 Mb on dog chromosome 1 (supplemental Figure S2 and supplemental Table S2). A total of 92 SNP loci (supplemental Tables S2 and S3) were identified of which 54 were polymorphic across four gray wolf populations, 48 were polymorphic in one coyote population, and 43 were polymorphic across five breeds of dog.

Eighteen percent of SNPs on average were shared within and between canid species with gray wolf populations exhibiting the highest sharing (27%; supplemental Table S4). Interestingly, 24 loci (26%) were observed to have the derived allele fixed in domestic dogs but polymorphic in gray wolves, which likely reflects the bottlenecks associated with domestication or breed formation. The average proportion of shared haplotypes within and between species was 74%. Wolf populations had the highest average percentage of haplotype sharing (90%; supplemental Table S4). Average nucleotide diversity among dog breeds was significantly different from that within dog breeds (t-test P-value <0.001; supplemental Table S5) and among wolf populations (P-value <0.001). Furthermore, examination of the ratio of nucleotide diversity suggests a minimal loss of diversity as a result of the domestication event (0.05) whereas the average loss of diversity due to breed formation was much larger (0.35).

Using data from five chromosomes (1, 2, 3, 34, and 37), 105 of 106 loci were successfully genotyped in 18 dog breeds and a variety of wild canid species (supplemental Table S6). In the most distantly related species, ∼93% of loci in golden jackals and 80% of loci in bat-eared fox, gray fox, and island fox were successfully amplified. Observed heterozygosity values ranged from 0.24 in golden jackals to 0.31, 0.29, and 0.33 in the bat-eared, gray, and island fox, respectively.

Population structure:

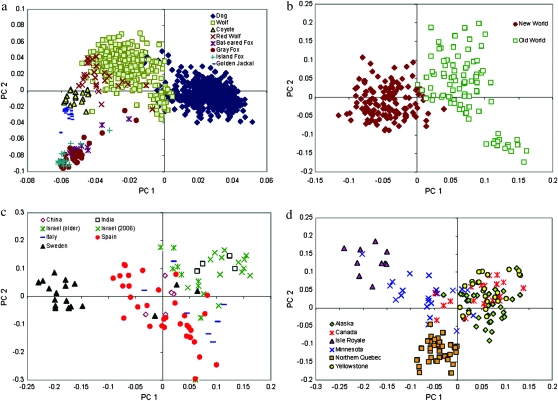
Population structure across a variety of wild canid species and domestic dog breeds was explored through PCA of the genotype data (Figure 2, a–d). Fourteen principal components (PCs) were found to be significant for the seven canid species analyzed (Figure 2a). Domestic dog, gray wolf, coyote, golden jackal, and fox were found to separate along principal component axes 1 and 2. Red wolf was found to overlap both coyote and gray wolf but more so with the latter species.

Figure 2.—

Principal component analysis of SNP genotype data within and across species: (a) all species, (b) gray wolves, (c) Old World wolves, and (d) New World wolves.

PCA of 13 gray wolf populations revealed 11 significant principal components (Figure 2b). The most distinct pattern was observed along the first axis of variation separating Old World and New World wolf populations. Minimal overlap between the two groups was evident. PCA was then performed separately on Old and New World populations (Figure 2, c and d). Seven Old World gray wolf populations were found to have 7 significant principal components. The first axis of variation visibly separated the majority of the populations with a distinct separation of Swedish gray wolves. Six New World gray wolf populations were found to have 6 significant principal components. Isle Royale, Minnesota, and northern Quebec defined distinct clusters, and Alaska, Canada, and Yellowstone formed a fourth cluster.

PCA of 18 domestic dog breeds exhibited 15 significant principal components (data not shown). There was considerable overlap between breeds. However, Akita displayed virtually no overlap with any other domestic dog breed while Pekingese exhibited slight separation along the first axis of variation. Along the second axis of variation, mastiffs and, to a lesser extent, Portuguese water dogs exhibited separation from the main cluster of breeds.

Ascertainment bias:

Ascertainment bias typically produces a pattern characterized by a decrease in low-frequency alleles and an increase in higher-frequency alleles (Clark et al. 2005; Rosenblum and Novembre 2007). A shift in allele frequencies was observed between the sequence and the genotype data; however, there was no discernible pattern (supplemental Figure S4). Simulations showed that the degree to which the difference in allele frequency affects estimates of LD varies for each breed (supplemental Figure S5). Ascertainment bias in Labrador retriever was observed to have minimal effects; however, in golden retriever the effect was large. Despite the variance in estimates, the rank order of breeds based on estimates of LD remained the same.

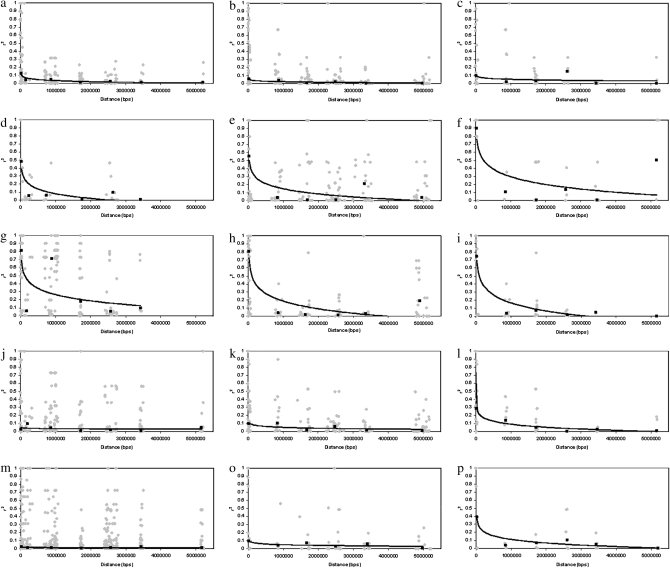
Site frequency spectra generated from sequence and genotype data for gray wolf and coyote populations were similar to those for the domestic dog in showing no distinguishable patterns (supplemental Figure S4). When LD estimates from sequence data were compared with LD estimates from genotype data, sequence data generally gave lower estimates of LD (Figure 3). The Spanish gray wolf was the exception with an increase in LD measured from genotyped data to sequenced data. Despite the shift in LD estimates from sequence to genotype data, the rank order of LD estimates of each population remained the same.

Figure 3.—

Decay plots of LD (r²) estimates from sequence data and genotype data in (a–c) Alaskan gray wolf, (d–f) Israeli gray wolf, (g–i) Spanish gray wolf, (j–l) Yellowstone gray wolf, and (m–o) coyote. The first column of data represents decay plots from chromosome 1 sequence data. The second column of data represents data from SNP genotypes on all five chromosomes, and the third column of data represents decay plots from SNP genotypes just on chromosome 1. Shaded diamonds are pairwise r². Solid squares are average r² for each distance group for which a logarithmic trend line was fitted to the data (solid line).

Given that ascertainment bias is present within the genotype data set, we proceeded with caution by focusing on general trends (e.g., strong association between the extent of LD and demographic history). Additionally, we relied on estimates from resequencing to make unbiased estimates and comparisons of genetic diversity and extent of LD between domestic and wild canids.

Linkage disequilibrium:

The extent of LD estimated from genotyped data in gray wolf populations ranged from <10 kb in Alaskan gray wolves to >5 Mb in gray wolves from Isle Royale (; Table 3; see supplemental Figure S6 for D′ estimates). The extent of LD was consistent with the known demographic history of each population. Large outbreeding populations such as Alaska, Minnesota, Canada, Yellowstone, and northern Quebec exhibited such low levels of LD that the decay curves did not extend to an r² value of 0.2 (Figure 3 and Table 3). Therefore, we take a conservative approach and consider these populations to generally have LD levels <10 kb. However, small/bottlenecked populations such as Isle Royale, Spanish, Italian, and Swedish gray wolves exhibited high levels of LD (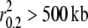). Finally, coyotes exhibited levels of LD below an r² value of 0.2 (Figure 3), consistent with their large population size in southern California (Vilà et al. 1999a; Fedriani et al. 2001).

TABLE 3.

Estimated extent of linkage disequilibrium measured as the distance at which r² decays to 0.2

Domestic dog				Wild canid
Breed	Genotype data	Sequence data	2006 AKC registration	Populations	Genotype data	Sequence data
Labrador retriever	20 kb	785 kb	123,760	Alaska	<10 kb	<10 kb
Saint Bernard	83 kb		3,828	Canada	<10 kb
Pomeranian	200 kb		18,218	Yellowstone	<10 kb	<10 kb
Poodle	250 kb		29,939	Minnesota	<10 kb
Standard poodle	318 kb			Israel (older)	<10 kb
Toy poodle	415 kb			Northern Quebec	<10 kb
Dachshund	427 kb		36,033	Israel (2006)	564 kb	241 kb
Whippet	500 kb		1,836	Spain	906 kb	1.7 Mb
Pembroke Welsh corgi	639 kb		10,250	Sweden	1 Mb
Old English sheepdog	672 kb		1,403	Italy	3.2 Mb
Miniature poodle	672 kb			Isle Royale	a
Scottish terrier	716 kb		3,545
Doberman pinscher	826 kb		11,546	Coyote	<10 kb	<10 kb
Portuguese water dog	846 kb		1,454
Golden retriever		1.4 Mb	42,962
Akita	1.3 Mb	1.4 kb	2,457
Border terrier	1.3 Mb		873
Briard	2 Mb		284
Irish wolfhound	2.2 Mb		1,016
Basset hound	2.4 Mb		7,844
Pekingese	4.2 Mb	a	3,155
Mastiff	a		6,913
Bernese mountain dog		a	3,714

^aThe decay curve did not reach an r² of 0.2.

Estimates of LD from genotyped data in dog breeds ranged from 20 kb to >5 Mb (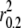; Table 3). The extent of LD was found to be significantly correlated to the log of registered individuals for both Kendal's τ rank correlation (P-value = 0.02) and Mantel's test (P-value = 0.0001). However, 3 breeds had sample numbers below the minimum cutoff (n < 17) used by Sutter et al. (2004), introducing potentially greater bias into our measures of LD. When these breeds were excluded from the analysis, the correlation statistics for the remaining 14 breeds were still significant (Kendal's τ, P-value = 0.003; Mantel's test, P-value = 0.0002). Thus, the level of LD within dog breeds was found to be well correlated with 2006 registration numbers (supplemental Figure S7).

Values of LD based on sequence data were highly correlated with those based on SNP genotypes (Kendal's τ, P-value = 0.02; Mantel's test, P-value = 0.0001). The extent of LD between species based on sequence data demonstrated that gray wolves and coyotes have less LD (<10 kb–1.7 Mb) than the domestic dog (785 kb– >5 Mb; Table 3). The extent of LD seen in the Spanish gray wolf population was much higher than that in any other sequenced gray wolf population (1.7 Mb). We explored the possibility of relatedness among the samples by eliminating individuals with high levels of allele sharing based on 11 microsatellite loci (vonHoldt et al. 2008) and confirmed that high levels of LD are still present in a sample set of reduced allele sharing ().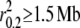

Domestication modeling:

Parameter estimates were scaled in terms of the estimated gray wolf effective population size (i.e., ω = N_eDOG/N_eWOLF) and multinomial calculations were found to be qualitatively similar to Poisson calculations (see supplemental Tables S7 and S8 and supplemental Figures S8–S10). The contraction at fixed time model, with a single contraction event fixed at 15,000 years ago, explained the data significantly better than the null model of constant population size (Table 4). This applied for both the ascertainment bias corrected (P-value = 2.27 × 10⁻⁶) and uncorrected data sets (P-value = 4.01 × 10⁻⁸). The corrected Poisson calculations suggest that this contraction was followed by a population expansion (bottleneck of fixed size, Table 4), although the improvement in the model fit is slight (P-value = 0.033) and unlikely to be significant after correcting for linkage in the data set. Therefore, we focus on the contraction at fixed time model findings. The estimate of ω for the Poisson calculation of the contraction at fixed time model was 0.23 for the uncorrected data, indicating the dog ancestral population size was 0.23 times the size of the wolf ancestral population and 0.25 for the corrected data. Therefore, results suggest a single minor contraction event was associated with domestication of the dog.

TABLE 4.

Poisson-calculated parameter estimates under nested likelihood models of domestication

	Contraction at fixed time (d.f. = 1)			Contraction at unknown time (d.f. = 2)			Bottleneck of fixed size (d.f. = 2)					Bottleneck of unknown size (d.f. = 3)
Models	τ = fixed	ω = varied	P-value	τ = varied	ω = varied	P-value	τ = fixed	ω = varied	τB = varied	ωB = 0.1	P-value	τ = fixed	ω = varied	τB = varied	ωB = varied	P-value
Uncorrected	5,000	0.23	4.01 × 10−8	2,245	0.12	0.51	5,000	64.5	1,835	0.1	0.51	5,000	0.11	3,023	0.9	0.8
Corrected	5,000	0.25	2.27 × 10−5	16,193	0.38	0.11	5,000	2.5	2,591	0.1	0.03	5,000	1.8	2,159	0.08	0.1

See Table 2 for description of parameters. P-values were calculated from a likelihood-ratio test, where a P-value <0.05 indicates the alternative model fits the data better than the previous model. Null model: τ = ∞ and ω =1.

Breed formation modeling:

Demographic parameters based on the discussed model of breed formation were estimated for each of five breeds from the averaged sampled site frequency spectra. Across all breeds and calculations, no models had a higher likelihood than the contraction at fixed time model (Table 5), which indicates a contraction without a subsequent increase in population size. Under the contraction at fixed time model, Bernese mountain dog and Pekingese were observed to have the largest bottleneck with a current effective population size ∼0.0055 and 0.0056 that of the ancestral dog effective population (assumed to be equal to the gray wolf effective population size). Labrador retriever, golden retriever, and Akita exhibited a weaker reduction in population size with values of 0.0095, 0.011, and 0.012, respectively.

TABLE 5.

Poisson-calculated parameter estimates under nested likelihood models of breed formation and wild canid population history

	Contraction at fixed time (d.f. = 1)			Contraction at unknown time (d.f. = 2)
Breed/wild canid population	τ = fixed	ω = varied	P-value	τ = varied	ω = varied	P-value
Akita	100	0.012	6.74 × 10−8	92	0.011	0.96
Bernese mountain dog	100	0.006	0	756	0.039	0.77
Golden retriever	100	0.011	4.72 × 10−10	92	0.01	0.99
Labrador retriever	100	0.01	1.03 × 10−10	367	0.035	0.83
Pekingese	100	0.006	0	65	0.004	0.87
Alaskan wolf	—	—	—	97	0.053	0.61
Israeli wolf	—	—	—	10,796	0.25	0.002
Spanish wolf	—	—	—	227	0.028	0.014
Yellowstone wolf	—	—	—	16	0.045	0.99
Coyote	—	—	—	20,512	1.63	0.26

See Table 2 for description of parameters. P-values were calculated from a likelihood-ratio test, where a P-value <0.05 indicates the alternative model fits the data better than the previous model. Null model: τ = ∞ and ω =1.

Although not significantly better than the contraction at fixed time model, both ω and τ were optimized under the contraction at unknown time model, allowing examination of the timing of breed contractions. Under this model, Pekingese was observed to have a severe reduction in population size ∼65 generations ago (ω = 0.0035), while Akita and golden retriever were observed to have similar contraction times at ∼92 generations (ω = 0.0113 and 0.0100). It is important to note that when estimating both ω and τ, timing estimates may not be entirely realistic, as there is a trade-off between having a recent τ and a severe population decline and having a more distant τ but less severe decline. For example, the founding prediction of 755 generations ago for Bernese mountain dog, originating from a small number of individuals and maintained as a small population, is likely an overestimate. Regardless, the bottleneck at breed formation across breeds is orders of magnitude more severe, and more recent, than an ancient domestication event and more likely to influence differences in LD among breeds (see below).

Wild canid modeling:

As with the inference of breed formation, we used Poisson calculations to determine the presence and severity of a bottleneck within gray wolf and coyote populations. Only the contraction at unknown time model of the Spanish and Israeli gray wolf populations was found to be significantly different from the null model (Table 5). The Spanish gray wolf was observed to have undergone a contraction (ω = 0.028) ∼226 generations ago (∼700 years ago) and the Israeli wolf population was observed to have undergone a more mild population decline (ω = 0.25) >10,000 generations ago (30,000 years ago). Again, these estimates may not be entirely accurate as they may represent the trade-off between ω and τ (see above). Finally, no significant evidence was found to support a change in population size in Alaskan and Yellowstone gray wolf or coyote populations.

DISCUSSION

The extent of LD and its relationship to demographic history has been well documented in domesticated and model organisms (Dunning et al. 2000; Pritchard and Przeworski 2001; Ardlie et al. 2002; Laurie et al. 2007). However, little research has been done to explore the extent of LD in wild populations, particularly vertebrate species. As mentioned previously, only a few studies to date have measured the extent of LD in naturally occurring vertebrate populations. Utilizing SNP markers developed in the domestic dog and extensive resequencing, we explored the extent of LD and modeled demographic history in several populations of wild canids. Additionally, we calculated the same measures in the domestic dog for comparison.

Five domestic dog breeds, four gray wolf populations, and one coyote population were sequenced for 11,279 bp on chromosome 1. Levels of LD in domestic dogs were consistent with previous studies (Sutter et al. 2004; Lindblad-Toh et al. 2005) and, in general, we found that gray wolf and coyote populations exhibited lower levels of LD (<10 kb–1.4 Mb) than domestic dog breeds (785 kb– >5 Mb; Table 3). Barley (Caldwell et al. 2006), soybean (Hyten et al. 2007), sheep (McRae et al. 2002, 2005), and house mice (Laurie et al. 2007) display a consistent pattern of reduced levels of LD in wild populations compared to their domesticates. This is expected since domestication likely results in a bottleneck event. However, across wild populations, demographic history can still be observed to strongly influence levels of LD. For example, the Spanish wolf population had LD levels higher than some domestic dog breeds (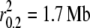). In the past century, gray wolves from Spain were hunted to near extinction, but have steadily risen in numbers since the enactment of hunting restrictions (Ramirez et al. 2006). In contrast, Labrador retrievers exhibited levels of LD similar to wild gray wolf populations (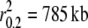) as they are the most popular breed in the United States today with ∼150,000 new registrations per year (www.AKC.org). Finally, coyotes were found to display the lowest levels of LD (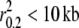) relative to all domestic dog breeds and gray wolf populations. Consistent with low levels of LD, coyote population sizes are reportedly an order of magnitude greater than those of the gray wolf (Vilà et al. 1999a).

As seen with the sequence data, LD levels from SNP genotype data were found to correspond with known demographic history for the 11 gray wolf populations. For example, the Isle Royale gray wolf population is a small population of wolves that inhabits an island in Lake Superior off the shore of Minnesota. The population was founded by a single breeding pair in 1950 (Peterson et al. 1998). Previous genetic research found population heterozygosity levels half that observed in the mainland progenitor (Wayne et al. 1991). The extent of LD in the Isle Royale population (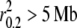) is consistent with that expected in small and/or severely bottlenecked populations (Pritchard and Przeworski 2001; Gaut and Long 2003; Mueller 2004). Other populations that are known to have undergone a contraction or have a history of small population size had high levels of LD (Spanish, Swedish, and Italian gray wolves) (for supporting demographic and genetic research see Lehman et al. 1992; Wayne et al. 1992; Vilà et al. 1999a; Ramirez et al. 2006; Fabbri et al. 2007). At the other end of the spectrum, populations of Alaskan, Canadian, and northern Quebec gray wolves have been large and of constant size for a long time and exhibit low levels of LD (Weckworth et al. 2005; Musiani et al. 2007). Supporting this finding, genetic studies (Wayne et al. 1992; Roy et al. 1994; Vilà et al. 1999b) of Alaskan and northern Canadian gray wolf populations found high variability and reduced population differentiation, suggesting a large population size and higher levels of gene flow than among European wolf populations that were more structured. Similarly, LD estimates in dog breeds from SNP genotype data corroborate findings from sequence data as exemplified by a significant correlation to popularity of the breed based on registration numbers (supplemental Figure S7). Thus, the extent of LD measured from the SNP genotype data also supports the correlation between LD and demographic history in wild and domestic populations.

Demographic modeling:

Previous studies based on mtDNA analysis (Vilà et al. 1997; Savolainen et al. 2002) have indicated that four to six matrilines of gray wolf were involved in the founding of the domestic dog. In contrast, analysis of major histocompatability (MHC) loci suggested several hundred founders or extensive backcrossing with wild canids is needed to explain present-day diversity in domestic dogs (Vilà et al. 2005). Lindblad-Toh et al. (2005) found evidence for two major bottlenecks in modern dog breeds, the first occurring as a result of domestication from wolves, supported by short-range LD estimates, and the second occurring as a result of breed formation, supported by long-range LD. Lindblad-Toh et al. (2005) simulated the demographic history of domestic dogs over a coarse grid of demographic parameter values and compared the observed and simulated rates of pairwise polymorphism across 10 15-Mb regions. They then selected the domestication parameters for which the simulations resulted in polymorphism values that were the closest to observed values. Although they did find evidence for two major bottlenecks, they did not use a rigorous likelihood framework and thus are not able to perform any hypothesis testing or formal model selection. For our analysis, we searched a denser grid of domestication parameter values and examined the site frequency spectra of dogs rather than pairwise polymorphism. For domestication events with parameters that were searched over this grid, we calculated the likelihood of the observed domesticated dog site frequency spectrum. In this likelihood framework, we were able to perform nested likelihood-ratio tests to test the null hypothesis of constant population size and make meaningful comparisons between models.

From our demographic modeling, we found evidence for a modest population contraction ∼15,000 years ago (5000 generations ago) and severe contractions at breed formation. The contractions due to breed formation were found to be an order of magnitude greater than the domestication contraction on the basis of analysis of the site frequency spectra. From nucleotide diversity estimates, only a 5% reduction in diversity was observed as a result of domestication whereas an average of 35% of nucleotide diversity was lost due to breed formation. This severe contraction at breed formation was expected, as continued inbreeding within a given breed may act to maintain a small effective population size even if the census population size has actually increased since breed formation. The absence of a strong signal for a contraction at domestication may reflect continued interbreeding between early dogs and wolves or multiple domestication events (Tsuda et al. 1997; Vilà et al. 1997; Randi and Lucchini 2002). Indeed, high levels of diversity observed in domestic dogs may have been maintained through a modest population bottleneck, backcrossing with wolf populations, and rapid population expansion (Vilà et al. 2005; Wayne and Ostrander 2007).

Finally, demographic modeling of the site frequency spectra of wild canid populations and dog breeds was found to be concordant with estimates of LD and known population history. In wild canid populations, a significant population decline was observed for the Spanish gray wolf and to a lesser extent the Israeli gray wolf population, which was expected from known historical data. Furthermore, neither coyote nor Alaskan and Yellowstone gray wolf populations showed significant evidence of a population size change. In modeling the demographic history of domestic dog breeds, Pekingese and Bernese mountain dog exhibited the greatest population contraction and more modest contractions were observed in golden retriever and Labrador retriever. The strong concordance observed in this study between the extent of LD, demographic modeling, and known demographic history supports the use of LD to infer population history not only in model organisms but also in wild populations.

Population structure:

Eighty percent or greater of SNPs that were discovered in dogs successfully amplified in the most distantly related species and polymorphism levels ranged from 25 to 40%. Genetic isolation and/or admixture revealed in the PCA was consistent with previous studies (Wayne et al. 1991, 1992; Lehman et al. 1992; Roy et al. 1994; Vilà et al. 1999a; Leonard et al. 2005). Within gray wolves, PCA identified strong geographic differentiation between Old and New World populations as well as between populations within each continent. Similar relationships have been observed in mtDNA studies of gray wolves (Wayne et al. 1992; Roy et al. 1994; Vilà et al. 1999a). Patterns in the PCA plots were consistent with previous phylogenetic studies (Roy et al. 1996; Vilà et al. 1999a; Leonard et al. 2005; Lindblad-Toh et al. 2005). For example, PC one supports the fundamental genetic distance between wild canids and domestic dogs. PC two distinguishes wild canids from each other with coyotes and golden jackals positioned nearest to the gray wolves and red wolves overlapping coyotes and gray wolves. The overlap of red wolves with both species is consistent with extensive hybridization in the past (Wayne and Jenks 1991). The high degree of SNP amplification success between species suggests that dog-derived SNP markers may be useful in mapping phenotypic traits in wild canid species. To support this conclusion, Kukekova et al. (2007) used dog-derived microsatellite markers to develop a genetic map for the silver fox and Sacks and Louie (2008) and Seddon et al. (2005) sequenced SNP loci from the dog genome to develop new SNPs for genetic studies in gray wolf, coyote, red fox, and gray fox.

Conclusions:

The extent of LD in natural vertebrate populations has been difficult to assess in the past because large-scale genomic surveys were possible only in model species. However, with the availability of high-throughput genotyping and information from genome sequencing projects, a new era has emerged in the genetic characterization of natural populations. Utilizing these resources, we have estimated LD in 11 natural populations of gray wolf, one population of coyote, and 18 dog breeds. Additionally, because a causal relationship exists between LD and population history, we have made inferences about the demographic and evolutionary processes in wild and domestic canids. Our results suggest that a relatively minor population contraction was associated with domestication in dogs and that genetic variation was preserved in the rapid expansion that followed. However, this variation is now partitioned in dog breeds that generally have high and variable amounts of LD. The high level of LD in some wolf populations further suggests the possibility of trait mapping in natural populations. For example, in North America, approximately half of wolves are dark colored (Musiani et al. 2007; Anderson et al. 2009), and given the recent identification of coat color mutants in dogs associated with black color (Caldwell et al. 2006), similar mutants may now be identified through association studies in wild wolves. Finally, we demonstrate how statistical models in general can be used to make inferences about population demography and show that predictions generally fit with observed levels of LD and known population history. Consequently, our approach may have wide applicability to other species with extensive genomic resources and their close relatives.