The Impact of Environmental Heterogeneity on Genetic Architecture in a Wild Population of Soay Sheep

Abstract

This work demonstrates that environmental conditions experienced by individuals can shape their development and affect the stability of genetic associations. The implication of this observation is that the environmental response may influence the evolution of traits in the wild. Here, we examined how the genetic architecture of a suite of sexually dimorphic traits changed as a function of environmental conditions in an unmanaged population of Soay sheep (Ovis aries) on the island of Hirta, St. Kilda, northwest Scotland. We examined the stability of phenotypic, genetic, and environmental (residual) covariance in males during the first year of life between horn length, body weight, and parasite load in environments of different quality. We then examined the same covariance structures across environments within and between the adult sexes. We found significant genotype-by-environment interactions for lamb male body weight and parasite load, leading to a change in the genetic correlation among environments. Horn length was genetically correlated with body weight in males but not females and the genetic correlation among traits within and between the sexes was dependent upon the environmental conditions experienced during adulthood. Genetic correlations were smaller in more favorable environmental conditions, suggesting that in good environments, loci are expressed that have sex-specific effects. The reduction in genetic correlation between the sexes may allow independent evolutionary trajectories for each sex. This study demonstrates that the genetic architecture of traits is not stable under temporally varying environments and highlights the fact that evolutionary processes may depend largely upon ecological conditions.

ENVIRONMENTAL heterogeneity has long been recognized as an important factor influencing the evolution of fitness-related traits in the wild (Roff 2002). The evolution of a trait depends upon the selection upon it, underlying genetic variation, and to a large degree the genetic relationships with other traits (Lynch and Walsh 1998). There is evidence that selection can vary considerably from year to year (Price et al. 1984; Robinson et al. 2008) and genetic variability in quantitative traits can change in response to environmental conditions (Hoffmann and Merilä 1999; Charmantier and Garant 2005). However, we know surprisingly little about the influence of environmental conditions on genetic correlations between traits in wild populations. Laboratory evidence suggests that the environment may influence genetic relationships between traits (Sgrò and Hoffmann 2004), but estimates obtained in a controlled or in an arbitrary range of conditions show a lack of concordance with those obtained in wild habitats (Conner et al. 2003). As a result, laboratory and environment-specific estimates of genetic correlations can make predictions for a trait's evolution, but these are valid only for the environment in which they were measured. Therefore, at present, it is difficult to generalize about the evolution of a trait that is expressed in populations that experience variable environmental conditions (Steppan et al. 2002).

The influence of changing environmental conditions on the G matrix (the matrix of additive genetic variance and covariances corresponding to a set of traits) has been the focus of theoretical quantitative genetic studies (e.g., Jones et al. 2003). There is evidence of genotype-by-environment interaction for many traits expressed in wild populations (Charmantier and Garant 2005) and thus we may also expect that associations between traits may depend upon the environmental conditions encountered by an individual. Genetic correlations among traits may arise from pleiotropy, where a given locus affects more than one trait (Cheverud 1988; Lynch and Walsh 1998), which may limit the potential for those traits to evolve independently. There has recently been much interest in assessing genetic correlations between the sexes (Rice and Chippindale 2001; Foerster et al. 2007; Poissant et al. 2008), but all of these predictions have also been made in average environmental conditions. For sexually dimorphic traits, expectations of between-sex genetic correlations are unclear (Lande 1980; Badyaev 2002). We might expect that the genetic determination of a trait and the patterns of genetic covariance between traits may differ both within and between the sexes, producing the differences in trait growth that are commonly observed (Lande 1980; Badyaev 2002; Roff 2002), but so far evidence suggests that genetic expression in both sexes is influenced by the same developmental pathway (Roff 2002; Jensen et al. 2003; Parker and Garant 2005). However, to our knowledge, no study has yet determined whether genetic correlations, both within and between the sexes, vary across gradients of the environmental conditions encountered by individuals in the wild (Garant et al. 2008).

This study aims to assess the stability of phenotypic, genetic, and environmental (residual) associations between traits, within and between the sexes, across a range of environmental conditions experienced by a wild population. We focus on the traits of horn length, body weight, and parasite load in a feral population of Soay sheep (Ovis aries) from the island of Hirta, St. Kilda, United Kingdom. Weather conditions, population density, and consequently resource availability fluctuate from year to year, providing substantial differences between individuals in the environments they experience and thus their survival rates (Clutton-Brock and Pemberton 2004). These varying conditions, combined with a large pedigree and extensive repeated morphological measures, provide an excellent opportunity to assess the potential effects of environmental heterogeneity on genetic architecture of traits. Previous studies on this population have shown additive genetic variance for many morphological traits (Milner et al. 2000; Coltman et al. 2001; Wilson et al. 2005), genetic correlations between traits (Coltman et al. 2001), and genotype-by-environment interactions for birth weight (Wilson et al. 2006). Here we apply a random regression animal model approach to assess the extent to which quantitative genetic parameters of a range of morphological traits measured during life vary as a function of environmental conditions. We then extend this methodology to the multivariate case, testing whether the phenotypic covariance structure, and the underlying G matrix, depends on the environmental conditions experienced. Since the traits considered here are known to be sexually dimorphic and there are differences in trait growth and survival across ages, we look at sex-specific traits in lambs and then across all ages.

METHODS

Study species and data collection:

Soay sheep (O. aries) were introduced onto the island archipelago of St. Kilda, northwest Scotland in the North Atlantic (57°49′N, 08°34′W), during the Bronze Age (Clutton-Brock and Pemberton 2004). The unmanaged study population of Village Bay, Hirta, was founded in 1932 with the introduction of 107 sheep from neighboring Soay and currently fluctuates from 211 to 671 individuals, with an average of 432 due to periodic overwinter crashes following years of high population density and poor weather conditions (Clutton-Brock and Pemberton 2004). The population has been the subject of intensive individual-level study since 1985, yielding morphological and life-history data for 6387 pedigreed individuals, including 3626 maternal links and 1699 paternal links (from 807 distinct dams and 495 distinct sires). Maternal identity is known from field observations and paternity is inferred by microsatellite-based paternity analysis at a pedigreewide confidence level of ≥80%, allowing no more than one allelic mismatch between offspring and putative sire, using maximum likelihood implemented in CERVUS (Marshall et al. 1998).

We considered the following phenotypic traits:

• Horn length: Soay sheep have a distinct polymorphism for horn type, producing a full horn (males, 86%; females, 32%), a reduced horn (or “scur”: males, 14%; females, 28%), or no horn at all (“poll”: 40% of females only). We use only horn length measures of full (normal-horned) individuals, as sufficient, reliable estimates of size could only be obtained for this group. The horns of sheep grow cumulatively over life, with horn increments formed when growth stops over winter, forming an annulus. This provides an annual measure (in millimeters) of horn growth at each age, which can be measured at any point of an individual's life and after death (Robinson et al. 2006). We used cumulative horn measures in our analyses (the sum of the incremental growth). We did not use horn measures that were recorded in August of the first year of life as they were poorly associated with measurements recorded after the increment had stopped growing.

• Body weight: Measurements of live weight (measured to the nearest 0.1 kg) and parasite load were made during a 2-week period in August, in which 49–67% of the study area population are rounded up each year, and during late autumn when free-ranging males are sampled during the rut.

• Parasite load: As a measure of parasite load, we used measures of fecal egg counts of five nematode gut parasites collectively termed strongyles (Clutton-Brock and Pemberton 2004). These counts represent a measure of nematode parasite infection as they are correlated with worm burden in Soay sheep (Grenfell et al. 1995), they are associated with other immune measures in domestic sheep (Shaw et al. 1999), and they are associated with overwinter survival in Soay sheep (Illius et al. 1995). Previous work has shown a negative genetic correlation between parasite load and weight within this population (Coltman et al. 2001). Fecal egg counts showed high positive skew and were therefore log_e transformed for analyses (Coltman et al. 2001).

For males, a total of 2876 body weight and 2881 parasite measures from 1685 males and 2679 horn length measures from 1449 normal-horned males were available. For females, a total of 3270 body weight and 4891 parasite measures from 1335 females and 661 horn length measures from 428 normal-horned females were available. All individuals were born between 1985 and 2005.

Quantitative genetic analyses:

Quantitative genetic parameters were estimated using an animal model, which combines pedigree and phenotypic data to partition the phenotypic variance of each trait into additive genetic, maternal, and environmental components (Kruuk 2004). Animal models are a form of linear mixed model that we implemented in ASReml (Gilmour et al. 2002) using restricted maximum likelihood, which are able to accommodate unbalanced data sets and complex pedigrees (Kruuk 2004). Here, we used random regression animal models (Wilson et al. 2006; Robinson et al. 2008) to model the additive genetic effects of each trait as a polynomial function of an environmental covariate, testing whether genetic effects are influenced by environmental variation. We used the described environmental quality of a given year, using the proportion of live-born lambs that survived the first winter that followed their birth year (E: values ranged from 5 to 86% and were then standardized to the interval −1 ≤ E ≤ 1), with low survival indicating poor conditions in any given year.

(Co)variance among first-year lamb traits:

First, we conducted random regression animal models for first-year lamb traits, where genetic and residual (environmental) effects are modeled as a function of the environment. We first analyzed lamb traits because they may show different patterns of trait growth and survival than those of adult sheep (Clutton-Brock and Pemberton 2004) and the models were not complicated by having to account for repeated measures on individuals. We present our analysis of first-year male traits only, as model convergence was suboptimal when first-year female horn length was included, probably due to low sample sizes. Also, our estimates of additive genetic variance for first-year female body weight and parasite load were similar to those for males, but not significantly different from zero. Fixed effects included year of birth (BYR) (BYR 1985–2005, fitted as a factor), which was fitted for all three traits to remove effects of conditions at birth on mean trait values and to remove temporal trends in the mean. For body weight and parasite load, month of measurement (MONTH: factor) was fitted to account for the fact that measures were taken at different times of year.

Thus for each trait y and individual i we fitted the random regression model

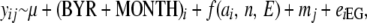(1)

where y is one of the three traits measured on individual i with mother j; μ is the mean of each trait; f(a_i, n, E) is the random regression function of an orthogonal polynomial of the additive genetic merit values a_i as a function of E, with order n; m_j is the maternal random effect of mother j that has a population-level variance V_M; and e_iEG is the environment-specific residual error for individual i grouped by environment group EG, which is a four-level factor (1, very poor; 2, poor; 3, good; 4, very good) produced by grouping birth years on the basis of the 25% quartile of the distribution of E (see below).

Each individual is represented only once within the data set, as individuals are only ever born into one environment. However, as related individuals are born into different environments, the genetic effects for each trait can be estimated as a function of environmental quality. However, estimates of residual covariance between environments could not be made as multiple records for individuals across environments were not possible and thus we partitioned the residual error structure into four levels of EG, defined by the four quartiles of E. We began by fitting the model without any additive or maternal effects such that all the phenotypic variance, after conditioning on the fixed effects, was allocated to this residual structure. We tested for significant differences in phenotypic variance over E by rerunning the model with a single constant error structure and comparing models using log-likelihood-ratio tests. Subsequently, we added the additive genetic and maternal effects and, using a forward selection procedure (while keeping the residual structure divided), compared a series of successively more complex random regression models that differed in the order of polynomial function of the additive effects from n = 0 (a_i as constant) to n = 2 (a_i as a quadratic function of E). Models were compared using log-likelihood-ratio tests, with degrees of freedom as the added number of variance and covariance components estimated with increasing function (for example, a comparison of zero- to first-order models requires 2 d.f., to account for the two additional parameters of variance in slope and covariance between slope and intercept). A second-order function did not provide a better fit in any model; therefore only zero- to first-order comparisons are shown. Once the final model was selected it was rerun with a single constant error structure and models were compared using log-likelihood-ratio tests to test for environmental heterogeneity in residual (environmental) effects. The estimated variance–covariance matrix of random regression coefficients {matrix Q with dimensions [(n + 1) × (n +1)]} was transformed to a corresponding G matrix for environment-specific traits according to the relationship G = ZQZ′, where Z is the vector of orthogonal polynomials evaluated at the values of standardized environmental quality (Z′ is the transpose of Z).

We then formulated a multivariate (in the sense of multiple traits) version of model 1 to model genetic covariance among the three lamb traits (horns, parasite load, weight) as functions of E. Thus, for example, choosing n = 1 fitted a first-order random regression function for each trait, producing a single 6 × 6 variance–covariance matrix {Q with dimensions [(3 × (n + 1)) × (3 × (n + 1))], where n = 1}. This resulted in estimates of the variance in intercept and slope and their covariance for each trait and the covariance between traits in intercept and slope. For each pair of traits in turn, we reran the model estimating the covariance in intercept and constraining the three-slope covariance components to zero and compared models using log-likelihood-ratio tests with 3 d.f., testing against the null hypothesis that there is no change in covariance over E. For some traits, there was no evidence of a significant change in genetic effects across environment and so in the multivariate model we fitted a zero-order random regression function for that trait. We then examined the changing covariance across environments between traits of first- and zero-order function by estimating the covariance between the intercept of the zero-order trait and the slope of the first-order trait. We then reran the model with the covariance between intercept and slope constrained to be zero and compared models using log-likelihood-ratio tests with 1 d.f. We also tested for significant residual covariance, using log-likelihood-ratio tests.

Results of the multivariate models are presented as above using G = ZQZ′, where Z is the vector of orthogonal polynomials evaluated at the values of standardized environmental quality (Z′ is the transpose of Z), to gain an additive genetic variance–covariance matrix of environment-specific (co)variance estimates for all traits. The diagonal of the covariance matrices between the additive genetic variance estimates of the traits provides estimates of the genetic covariance between traits across E. All covariance estimates were rescaled to give the genetic correlations, providing a dimensionless estimate of the association between both traits. Both the covariance and correlations produced the same patterns. An analogous method was used to estimate the approximate standard errors, which were converted into ∼95% confidence intervals (Fischer et al. 2004).

(Co)variance among traits across life:

Second, we then used the same multivariate random regression framework to investigate the influence of later life environments on genetic covariance between traits in both males and females, and across the sexes, accounting for repeated measures taken on individuals over their lifetime. To do this, we used repeated measures on each trait collected at different ages over the life span of individuals. We standardized each measure at each age (1–7+) to a zero mean and unit variance, thus placing all trait measures on the same scale with the same mean and removing any effects of increased variance with age. Thus for each individual i we extended the multivariate version of model 1 to a multivariate random regression accounting for repeated measures,

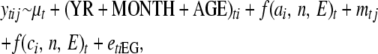(2)

where combinations of traits t of individual i and mother j were included as response variables; f(a_i, n, E) is the random regression function on an orthogonal polynomial of E, with order n, of the additive genetic merit values a_i of individuals; f(c_i, n, E)_t is the random regression function on an orthogonal polynomial of E, with order n, of the permanent environment effect c_i that accounts for the nonindependence of repeated measures on an individual; m_j is the maternal random effect of mother j that has a population-level variance V_M; and e_iEG is the environment-specific residual error for individual i grouped by EG. In this case, individuals are measured repeatedly across different environments and thus we were able to estimate residual covariance across environments.

We began by using a zero-order random regression function, which estimated the covariance between traits assuming no change across E. Using this model structure, we tested whether the additive genetic (co)variance matrix differed generally between males and females by comparing it to a model where we fixed all the (co)variance estimates of the random effects for all three traits to be consistent between the sexes. In both models the residual (co)variances were allowed to vary between the sexes and we used log-likelihood-ratio tests to compare the models. Our results are unbiased by scale effects as phenotypic data were scaled to unit variance prior to analysis (Hadfield et al. 2007).

We then increased the order of the random regression function in a stepwise manner, using the same methodology as described above to assess the significance of the estimates gained, to test against a null hypothesis that there is no change in covariance over E, and to present the results. In model 1, we were assessing genotype-by-environment effects by examining the relationship between relatives born into different environments. However, model 2 differs in the fact that we were assessing an individual's response to the multiple environments it experiences over its lifetime. Individuals may differ in their response to the environment because of their genotype (genotype-by-environment interaction) or because they vary in their allocation to a given trait (an environmentally driven response indicated by changing permanent environmental effects across environments). Therefore for each trait, we increased the order of both the additive genetic and the permanent environmental effects simultaneously and used log-likelihood-ratio tests with 4 d.f. (as the model estimates both slope and slope–intercept covariance, for both G and PE effects) to assess whether this produced a significantly improved model fit and thus whether there was changing individual-level variance across environments. We did not have the power to determine whether changing individual-level variance was exclusively reflected by a change in G or a change in PE for each trait and thus our estimates should be treated with some caution. However, we assumed that changing individual-level variance was reflected to some degree by changes in G and we assessed the significance of the genetic covariance between traits in the same way as for model 1, by constraining the elements of the covariance matrix and comparing models using log-likelihood-ratio tests.

RESULTS

Effect of environment on components of variance of lamb male traits:

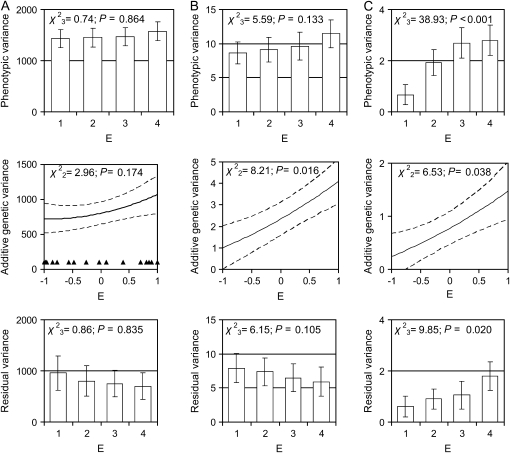
We first examined how the phenotypic, genetic, and residual components of variance in each trait in the first year of life varied across a range of environmental conditions in males (model 1). For lamb horn length, there was no evidence for a change in additive genetic variance with environmental quality, indicating that the same phenotype is expressed by a given genotype across different environmental conditions, and there was no evidence for any change in residual variance, resulting in no change in total phenotypic variance across environments (Figure 1A). For male lamb weight, additive genetic variance significantly increased with increasing environmental quality and there was a trend for reduced residual variance, resulting in no change in total phenotypic variance (Figure 1B). There was evidence that the total phenotypic variance of male lamb parasite burden increased with increasing environmental quality, which was driven by increasing additive genetic variance and residual variance (Figure 1C).

Figure 1.—

Phenotypic, additive genetic, and residual variance for lamb male traits of (A) horn length, (B) body weight, and (C) parasite load as a function of the environmental quality of their first year (E: distribution shown by solid triangles). Results were obtained from model 1 (see methods), where phenotypic and residual variance was estimated by grouping years on the basis of the quartiles of the distribution of E (1, very poor; 2, poor; 3, good; 4, very good), and error bars show the 95% confidence intervals of the estimates. Additive genetic effects were estimated as a linear function of E and are shown by a solid line, with dashed lines indicating the 95% confidence intervals of the estimates. Significance testing was conducted using a log-likelihood-ratio comparison of model 1 with a model with constant variance across all environments.

We also examined the additive genetic correlation surfaces for each trait across first-year environments. For first-year male horn length and parasite load, genetic correlations between environments were close to +1 and relatively stable. However, for body weight, there were only very weak genetic correlations across different environmental conditions (test for difference from +1: χ²₁ = 5.56, P = 0.018). These results suggest that for body weight, different loci may be involved across environments.

Effect of environment on covariance of lamb male traits:

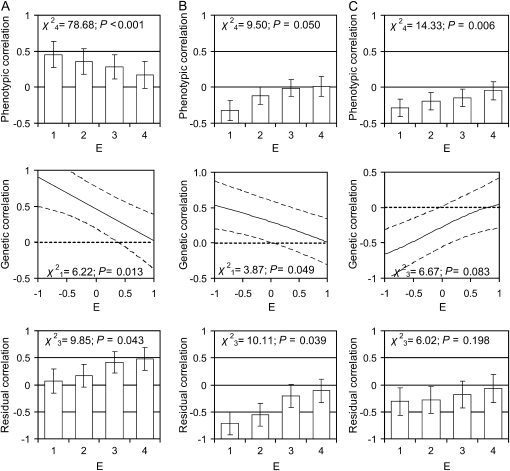
We then tested whether the phenotypic, genetic, and environmental covariances between first-year male horn length, body weight, and parasite load varied depending upon the environmental quality experienced during development (multivariate extension of model 1). We found significant phenotypic correlations between all first-year male traits, which generally reduced in magnitude as environmental quality increased (Figure 2). Genetic correlations between lamb male horn length and both body weight and parasite load were positive and decreased in magnitude with increasing environmental quality (Figure 2, A and B). Residual correlations between horn length and body weight were positive, implying that resource allocation to body weight was positively associated with allocation to horn growth and increased in magnitude with increasing environmental quality (Figure 2B). Residual correlations between horn length and parasite load were negative, implying resource allocation to reducing parasite load was associated with allocation to increased horn length (Figure 2B). Although we observed a significant phenotypic relationship between body weight and parasite load, which appeared to decrease with increasing environmental quality, we could not significantly demonstrate that this effect was due to changing genetic or residual covariance, although the trend in genetic correlation was only marginally nonsignificant (Figure 2C). This was most likely the result of the large standard errors, coupled with smaller covariance estimates for this comparison.

Figure 2.—

Phenotypic, genetic, and residual (environmental) correlations between lamb male traits of (A) horn length and body weight, (B) horn length and parasite load, and (C) body weight and parasite load as a function of environmental quality (E) of the first year of life. Results were obtained from a multivariate version of model 1 (see methods), where phenotypic and residual correlations were calculated within each quartile of the distribution of E (1, very poor; 2, poor; 3, good; 4, very good), with error bars representing the 95% confidence intervals of the estimates. The genetic correlations were estimated as linear functions of E and are shown by solid lines, with dashed lines indicating the 95% confidence intervals of the estimates. Significance testing was conducted using log-likelihood-ratio tests, against a null hypothesis of no change in covariance over E.

(Co)variance between traits across life:

Second, we then used repeated trait measures recorded over the life span of individuals to first examine the relationships between traits assuming no genotype-by-environment interactions (model 2 with zero-order polynomial function). Males were generally larger than females, with larger parasite burdens and larger horns (Table 1). We found significant additive genetic variance for all traits with similar coefficients of additive genetic variance and heritability values between the sexes (Table 1). There was evidence of different genetic relationships between traits within each sex (general comparison of male and female matrices: χ²₆ = 14.82, P = 0.022). In males, we found significant genetic correlations between horn length and body weight and between body weight and parasite load (Table 2). Contrary to the evidence suggesting a genetic correlation between first-year male parasite load and male horn length (Figure 2), there was no evidence of a significant correlation across all ages (Table 2). In females, there was no evidence of a genetic correlation between horn length and any other trait (Table 2). The genetic correlation between female body weight and parasite load was relatively strong, but remained marginally nonsignificant (−0.278 ± 0.169; χ²₁ = 3.23, P = 0.072).

TABLE 1.

Means, standard deviations, sample sizes, and variance components (± standard error) across all ages, for traits measured in adult males and females

Trait	Mean	SD	N	VA	VPE	VM	VR	CVA	h2
Males
Horn length (mm)	265.29	108.45	2679/1449	811.70 ± 176.30***	892.20 ± 159.20***	14.71 ± 29.57	479.30 ± 18.71***	10.74	0.37 ± 0.08
Body weight (kg)	21.22	8.08	2032/1685	0.67 ± 0.32*	4.30 ± 0.76***	0.57 ± 0.32	7.38 ± 0.40***	3.86	0.05 ± 0.02
Parasite load (loge FEC)	5.69	1.75	1730/1685	0.30 ± 0.07***	0.00 ± 0.00	0.00 ± 0.00	2.12 ± 0.09***	9.63	0.12 ± 0.03
Females
Horn length (mm)	116.90	41.22	661/428	269.40 ± 114.30*	307.30 ± 114.30**	5.56 ± 25.82	95.13 ± 7.95***	14.04	0.40 ± 0.15
Body weight (kg)	18.97	5.20	2882/1335	1.52 ± 0.36**	1.98 ± 0.32***	0.20 ± 0.16	1.92 ± 0.07***	6.50	0.27 ± 0.06
Parasite load (loge FEC)	4.39	2.64	3131/1335	0.26 ± 0.07***	0.08 ± 0.12	0.03 ± 0.04	4.99 ± 0.14***	11.62	0.05 ± 0.02

Estimates were obtained from multivariate animal models (see methods, model 2). Significance of the estimates was assessed using log-likelihood-ratio tests: *P < 0.05; **P < 0.01; ***P < 0.001. N, number of observations/individuals; V_A, additive genetic variance; V_PE, permanent environment effects; V_M, maternal variance; V_R, residual (environmental) variance; CV_A, coefficient of additive genetic variance; h², heritability.

TABLE 2.

Genetic correlations between males and females (diagonal), between traits in males (above diagonal), and between traits in females (below diagonal), across all ages assuming no genotype-by-environment interaction

	Horn length	Body weight	Parasite load
Horn length	0.223 ± 0.201	0.541 ± 0.143**	0.151 ± 0.178
Body weight	0.097 ± 0.168	0.793 ± 0.246**	−0.530 ± 0.210**
Parasite load	0.093 ± 0.202	−0.278 ± 0.169	0.838 ± 0.273***

Estimates and standard error (± SE) were obtained from multivariate animal models (see methods, model 2). Significance from zero was assessed using log-likelihood-ratio tests: *P < 0.050; **P < 0.010; *** P < 0.001.

Across sexes positive genetic correlations were found for body weight and parasite load (model 2; Table 2). In both cases, estimates were significantly greater than zero, but not significantly less than +1 (tested against the alternate hypothesis of r_G = +1: body weight χ²₁ = 1.60, P = 0.206, parasite resistance χ²₁ = 0.11, P = 0.740). Interestingly, the cross-sex correlation for horn length was significantly less than one (log-likelihood-ratio test against a model where correlation was fixed to one: χ²₁ = 7.60, P = 0.006).

Finally, we then extended the analysis of repeated trait measures to examine the effects of environmental conditions on genetic covariance between adult traits (multivariate version of model 2 with increasing order of polynomial function). There was no evidence that the individual-level variance of horn length varied as a function of the environment in either sex (male horn length, χ²₄ = 4.74, P = 0.315; female horn length, χ²₄ = 3.54, P = 0.472). There was evidence that individual-level variance of male (χ²₄ = 18.98, P = 0.001) and female (χ²₄ = 16.08, P = 0.003) parasite load and male (χ²₄ = 21.06, P < 0.001) and female (χ²₄ = 18.96, P = 0.001) body weight varied as a function of the environment.

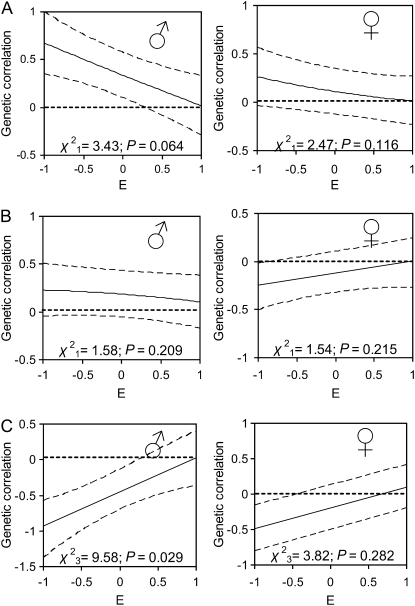
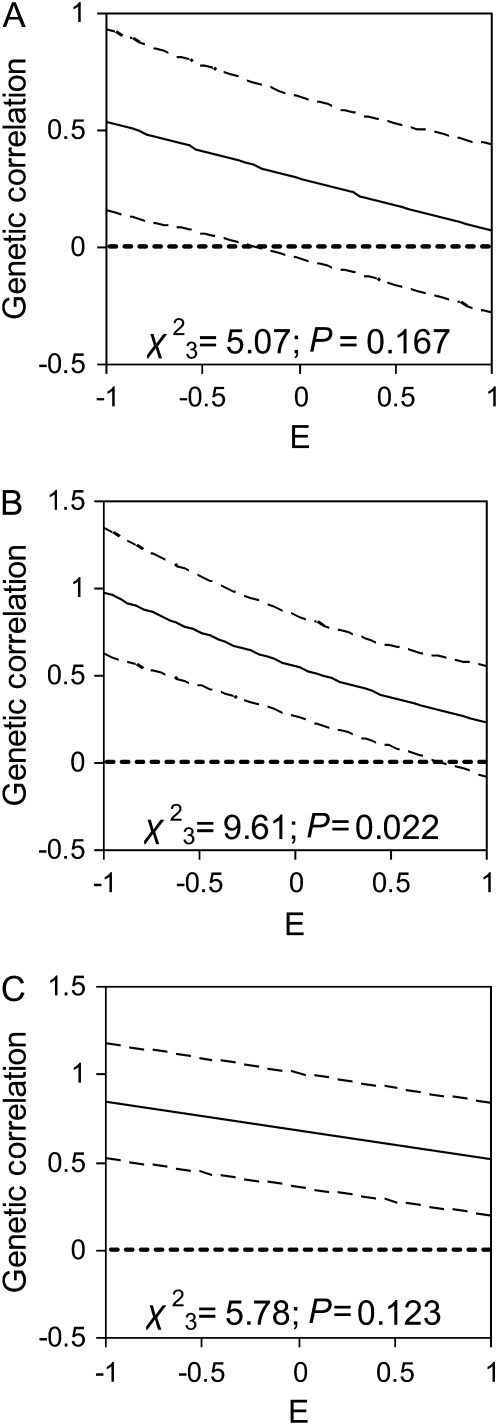
Genetic correlations between traits in males (Figure 3) and between the sexes (Figure 4) may be dependent upon environmental conditions experienced by an individual over the course of its life. The genetic correlations among all traits tended toward zero when environmental quality increased (Figure 3), although this pattern was significant only for the correlation between male body weight and parasite load and was marginally significant for male body weight and horn length probably due to the strength of the relationships in poor conditions. Genetic correlations between the sexes in body weight decreased with increasing environmental quality (Figure 4). There was no evidence that the genetic correlation between the sexes in parasite load or horn length was dependent upon the environmental conditions experienced during the first year of life (Figure 4).

Figure 3.—

Genetic correlation between traits measured across all ages: (A) horn length and body weight, (B) horn length and parasite load, and (C) body weight and parasite load in (♂) males and (♀) females across all ages, as a function of the environmental conditions experienced during each year of life (E). Results were obtained from model 2 (see methods), where the genetic correlations were estimated as linear functions of E and are shown by solid lines, with dashed lines indicating the 95% confidence intervals of the estimates. The significance of the trends shown was assessed using log-likelihood-ratio tests, against a null hypothesis of no change in covariance over E.

Figure 4.—

Genetic correlations in (A) horn length, (B) body weight, and (C) parasite load between males and females averaged across ages, as a function of the environmental conditions experienced during each year of life (E). Results were obtained from a multivariate version of model 2 (see methods), where the genetic correlations were estimated as linear functions of E and are shown by solid lines, with dashed lines indicating the 95% confidence intervals of the estimates. The significance of the trends shown was assessed using log-likelihood-ratio tests, against a null hypothesis of no change in covariance over E.

DISCUSSION

We have shown that genetic relationships between traits both within and across the sexes can differ depending upon the environmental conditions an individual experiences. Our results are consistent with previous work, which has shown that G has the potential to vary across environments (Roff 2002; Steppan et al. 2002; Sgrò and Hoffmann 2004). The environmental conditions experienced during development resulted in genotype-by-environment interactions for weight, which in turn resulted in changing genetic correlations between traits within males and between the sexes. By assessing the relationships between traits as a function of the environmental conditions in which they were expressed, we were able to show that when environmental conditions are relatively poor there were strong genetic relationships between all traits. However, if environmental conditions are relatively good, these correlations tended toward zero both within males and across the sexes. If we had assumed that genetic covariances were constant across environments, we would have concluded that highly positive genetic correlations would constrain the evolution of the sexually dimorphic traits of weight within this population (Coltman et al. 2001) and supported previous studies that have suggested genetic constraint on sexually dimorphic traits (Badyaev 2002; Jensen et al. 2003). Our results suggest that in good environments, loci are expressed that have sex-specific effects and as a result, if environmental conditions on St. Kilda were consistently good, we can predict that both horn length and body weight may be free to move along independent evolutionary trajectories in males. This study highlights the fact that evolutionary processes can be fully understood only with both phenotypic and genetic data (Roff 2002) and that these processes may depend largely upon ecological conditions.

The environment can have a direct influence on quantitative genetic parameters (Hoffmann and Parsons 1991; Hoffmann and Merilä 1999) and numerous studies have shown that the environment can directly influence the genetic determination of a suite of traits (Via and Lande 1985; Hoffmann and Merilä 1999; Charmantier and Garant 2005; Nussey et al. 2007) and thus the genetic correlations between them under laboratory conditions (Simmons and Roff 1996; Norry and Loeschcke 2002; Cano et al. 2004). In this study, additive genetic variance of both male body weight and parasite load increased with increasingly favorable environmental conditions, supporting previous studies of natural populations (Merilä 1997; Garant et al. 2004; Charmantier and Garant 2005). These genotype-by-environment interactions resulted in changing genetic correlations among male traits across environmental conditions, which also resulted in changing genetic correlations between the sexes. The genetic correlation across environments for both male and female body weight was low, suggesting environment-specific expression, whereas the genetic correlation for male parasite load was high across environments, suggesting environmentally sensitive allelic effects.

Previous studies on this population have found significant additive genetic variance for parasite load (Smith et al. 1999; Coltman et al. 2001) and for morphometric traits (Milner et al. 2000) in the average environment. We found a positive genetic correlation between first-year horn length and parasite load in poor environments, but this was not evident when we examined the trait across all ages. This result implies a genetic trade-off between the two traits in early life and may help to explain the negative association between horn growth and survival previously reported in this population (Robinson et al. 2008). Further extension of these models to allow genetic effects to (co)vary as a function of both age and environment may shed more light on this issue and enable the testing of the influence of environmental conditions on genetic architecture at each age. We found negative genetic correlations between body weight and parasite load across most environments, in both sexes, supporting previous results and suggesting that individuals with genetically low parasite burdens are likely to experience superior growth (Coltman et al. 2001).

We found evidence for sex differences in the genetic architecture of traits that we examined. Currently, very few studies have demonstrated sex differences in the genetic architecture of sexually dimorphic traits (Merilä et al. 1998; Coltman et al. 2001; Jensen et al. 2003; Parker and Garant 2004; Poissant et al. 2008), with many studies concluding high genetic constraint between the sexes (Merilä et al. 1998; Coltman et al. 2001; Parker and Garant 2004). In females, there was no evidence of a genetic correlation between horn length and any other trait, while in males horn length was correlated with both body weight over life and parasite load within the first year of life, in poor environments. Genetic correlations between the sexes in body weight decreased as environmental conditions improved, indicating reduced potential for genetic constraint between the sexes under these conditions. In contrast, there was no significant change in the cross-sex genetic correlation in parasite resistance across environments, suggesting no differences in genetic expression between males and females for parasite resistance. These results suggest that to understand the evolution of sexually dimorphic traits we must consider all environments in which they are expressed.

This is the first evidence that in a wild population, genetic covariances between a suite of traits may not be stable under temporally fluctuating environmental conditions. We need to consider the effects of genotype-by-environment interactions at all stages of analysis: from single traits, to multivariate phenotypes, to sexual antagonism studies. This study demonstrates the complexities of the relationships between traits both within and between the sexes and provides a way in which these relationships can be modeled for populations experiencing temporally fluctuating environmental conditions.