Abstract
In the language of mathematics, one needs minimally two interacting variables (two dimensions) to describe repeatable periodic behaviour, and in the language of density dependence, one needs delayed, not immediate, density dependence to produce cyclicity. Neither language specifies the causal mechanism. There are two major potential mechanisms: exogenous mechanisms involving species interactions as in predator–prey or host–parasite, and endogenous mechanisms such as maternal effects where population growth results from the cross-generational transmission of individual quality. The species interactions view stemming from a major observation of Elton and a simultaneous independent theory by Lotka and Volterra is currently dominant. Most ecologists, when faced with cyclic phenomena, automatically look for an interacting species one step below or above in a food chain in order to find an explanation. Maternal effects hypothesis, verbally suggested in the 1950s, had only found its theoretical implementation in the 1990s. In a relatively short time, the degree of acceptance of this view grew to the level of a ‘minority opinion’ as evidenced by the widely used textbook of Begon et al. This short review attempts to describe the arguments for and against this internal two-dimensional approach.
Keywords: maternal effects, reproductive allocation, population cycles, delayed density dependence, individual quality, predator–prey dynamics
1. Introduction
The rich diversity of dynamic patterns and the magnitude of temporal fluctuations in the abundance of wild animal populations have long fascinated ecologists. Central among the observed dynamic patterns are population cycles, whose repetitive, clock-like variation in density can sometimes reach spectacular amplitudes of eight orders of magnitude (Baltensweiller & Fischlin 1989). While only a minority of populations and species undergo cyclic dynamics (Kendall et al. 1998), understanding this noteworthy minority case can shed light to infer the mechanisms underlying the dynamics of the larger share of non-cyclic, but highly fluctuating, natural populations. Just as the understanding of planetary orbits shed light on the general movements of earthily bodies, understanding of cycling populations may help us clarify more general cases (Ginzburg & Colyvan 2004).
The relative novelty, and perhaps the reason for its controversial character, of the maternal effects hypothesis (Ginzburg & Taneyhill 1994; Ginzburg 1998; Inchausti & Ginzburg 1998) was precisely that it articulated in a simple mathematical model how the transmission of individual quality can induce cyclic population dynamics in two well-studied cases: forest Lepidoptera and northern cyclic voles. Moreover, the dynamics predicted by these models having a rather small number of parameters that could be fitted from the commonly available time-series counts agreed well with the observed data (Ginzburg & Taneyhill 1994; Inchausti & Ginzburg 1998), both for the cycle periods and their geographical variation, and for the shapes of population cycles. Moreover, the maternal effects hypothesis implies that populations have a tendency to oscillate in abundance with an intrinsic period necessarily exceeding six generations (Ginzburg & Taneyhill 1994, but see Berryman 1995; Ginzburg & Taneyhill 1995). The minimum period of six generations arises from the changes in individual quality declining for larger concurrent population abundance (Nt+1 in equation (2.1)), and thus it stems from the biological assumption that individual quality changes quickly in response to the environmental changes, but its effect on population growth would span at least one generation. The minimum period is a qualitatively important prediction that can help test the maternal effects hypothesis against data, since other mechanisms proposed to explain cyclicity such as predation only approximately predict the cycle periods in terms of complex combination of several parameters that are difficult to estimate precisely in the field (e.g. Weitz & Levin 2006).
Uncovering the ecological causes of complex population dynamics has proved to be a difficult empirical issue despite all the effort devoted to it (Murdoch et al. 2002; Turchin 2003; Begon et al. 2006). Cyclic populations, which have attracted much attention in the ecological literature, have shown an extreme resilience to verification with experimental manipulations, which generally failed to prevent the occurrence of the cycles (e.g. Krebs et al. 1995; Norrdhal & Korpimäki 1995, but see Moss et al. 1996 for an exception). In the language of mathematics, generating cyclic dynamics needs minimally two interacting variables (two dimensions) to induce a delayed, not immediate, density-dependent feedback on the population growth rate (Begon et al. 2006). Two main classes of mechanisms have been traditionally proposed to explain this delayed feedback on the population growth rate: exogenous mechanisms involving species interactions with specialist predators (Turchin & Hanski 1997; Kendall et al. 1999; Murdoch et al. 2002; Turchin 2003), parasites (Redpath et al. 2006) and food resources (both quantity and quality; Keith 1990; Turchin & Batzli 2001), and endogenous mechanisms including changes in individual quality transmitted by maternal effects (Ginzburg & Taneyhill 1994), territoriality (Matthiopolous et al. 2002) and genetics (Chitty 1960). The overriding historical influence of the Lotka–Volterra predator–prey equations has contributed to the notion that complex dynamics may only result from interspecific interactions. While non-trophic hypotheses for cyclic behaviour have been proposed before (e.g. Chitty 1960; Wellington 1960), only recently have they gained wider acceptance (e.g. Ginzburg & Taneyhill 1994; Moss et al. 1996; Ginzburg 1998; Inchausti & Ginzburg 1998; Benton et al. 2001; Beckerman et al. 2002). We have proposed (Ginzburg & Taneyhill 1994; Ginzburg 1998; Inchausti & Ginzburg 1998) maternal effects to be a general mechanism capable of inducing a delayed density-dependent feedback and cyclic population dynamics in northern voles and forest Lepidoptera. These are two of the main cyclic taxa whose extreme resilience to verification with experimental manipulations has made them classical study cases appearing in main textbooks (Begon et al. 2006). The maternal effects hypothesis has both been controversial (Berryman 1995; Hanski et al. 2001; Turchin & Hanski 2002; Turchin 2003) and stimulated field, experimental and theoretical works. In this paper, we will review the current status of the maternal effects hypothesis in population ecology and assess the criticisms it has raised over the last 10 years.
2. Maternal effects: explaining cyclic population dynamics
(a) The effect
Noticing the heterogeneity among the individuals of the same species requires no more than a casual observation. Besides the differences related to individual (st)age, size and sex sometimes considered in population models (Leslie 1948), phenotypic differences among individuals belonging to the same ‘homogeneous’ class leads to variation in their realized vital rates above and beyond what can be expected by chance (Conner & White 1999). The unequal contribution of the individuals of the same (st)age and sex to population growth and fitness has been well documented for many taxa (review in Brommer 2000). Inter-individual variation in demographic performance reflects in part their contingent exposure to the current and previous environments and can have considerable consequences for population dynamics (e.g. Bjornstad & Hansen 1994; Benton et al. 2001, 2006). Below, we argue that considering individual quality as a dynamic variable both being affected by and determined through changes in population abundance turns out to be an ‘economical’ (in the sense of employing a small number of parameters) way of portraying the qualitative effect of inter-individual variation in demographic performance.
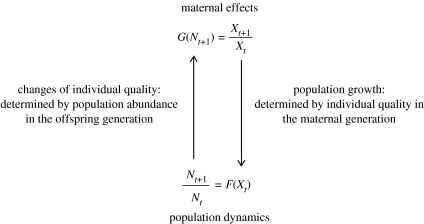
Maternal (or more generally parental) effects denote the effects of the maternal phenotype on her offspring in addition to her direct genetic effects (Räsänen & Kruuk 2007). They are ubiquitous in nature as they have been shown for many traits and taxa, and their role as important evolutionary force has been well established (Rossiter 1996; Mousseau & Fox 1998; Räsänen & Kruuk 2007). Whether maternal effects can be adaptive has been a matter of debate and the current consensus (Marshall & Uller 2007; Uller 2008) views maternal effects as transgenerational phenotypic plasticity (i.e. the parental environment affects or modulates the fitness of the offspring) whose adaptive value depends on the environmental variation encountered by the offspring, and on the fitness currency considered. A key feature of the maternal effects hypothesis is that the average individual quality is influenced by the population density in the current generation (Ginzburg & Taneyhill 1994). This amounts to assuming that individual quality is a dynamic variable both capable of responding relatively quickly to environmental changes and capable of having prolonged (of at least one generation) effects on population growth (figure 1).
Figure 1.
Feedbacks between population growth and changes in individual quality implied in the maternal effects hypothesis. In contrast to traditional kinetic approaches in population ecology where , population abundance affects the growth rate through changes in individual quality, which in turn determines the abundance of offspring generation. These dependencies induce an inertial effect (equation (2.2)), whereby the current population growth rate depends on the growth rate at the previous generation . Cycles require two interacting variables; it is either two species or quantity and quality, as in the maternal effects case.
(b) The model
The simplest model of maternal effects involves two linked dynamic variables
| (2.1) |
where Nt and Xt are the population abundance and the average individual quality, respectively, at time t, and F and G are the nonlinear, monotonically increasing functions describing the saturating effects of individual quality on population growth, and of concurrent population abundance on the temporal changes in individual quality. Being a reflection of the amount of energy stored by individuals, individual quality Xt is both the result of the interactions between individuals and their environment and a constraint on their reaction to changes in resource abundance and predators. By transmitting individual life-history responses to the environment across generations, maternal effects effectively modify the demographic performance (survival, growth, reproduction) of the progeny depending on the environmental conditions that faced the parental generation, thus introducing a delayed density-dependent response in population growth. This can readily be shown by rewriting equation (2.1) as
| (2.2) |
where Rmax is the maximum growth rate and F−1(Nt+1/Nt) is the inverse of the function denoting the effects of the average individual quality on the population growth rate. The important point to note in equation (2.2) is that the cross-generational transmission of maternal effects induces a delayed density-dependent effect manifested as a ‘memory’ of the previous population growth rate (Nt/Nt−1). In the absence of maternal effects, equation (2.2) is simply a model of direct density dependence. While individual quality typically refers to the energetic state or energy reserves, other measures of quality (parasite or viral load, nutritional quality of the food consumed, disease resistance, etc.) can be pertinent as long as they reflect the non-lethal effects of the environment (Peckarsky et al. 2008 and references therein) and affect the demographic rates of the next generation. The cross-generational transmission of individual quality can generate delayed density dependence that can destabilize population dynamics and, under some circumstances, generate population cycles. ‘Under some circumstances’ simply means that strong direct density-dependent effects due to resource shortage at currently high population densities can override the delayed density-dependent effects induced by the maternal effects and lead to non-cyclic dynamics (e.g. Ergon et al. 2001; Banks & Powell 2004). This is by no means peculiar to the maternal effects hypothesis, but common to all ecological processes proposed to explain cyclic dynamics. That it is the balance between the relative strengths of direct and delayed density-dependent forces is what determines the observed dynamics is not a new idea (Murdoch et al. 2002; Turchin 2003).
(c) Comparison with predator–prey views
Predator–prey or, more generally, victim–enemy interactions have been proposed to be the main and only possible explanation for cyclic population dynamics, achieving at times a paradigmatic status in the minds of their main proponents (Turchin & Hanski 1997; Kendall et al. 1999; Murdoch et al. 2002; Turchin 2003). While it is indisputable that the models showing the action of specialist predators can, in principle, generate delayed density dependence through a steep reduction in prey numbers leading to the subsequent demise of the predator population owing to intense resource shortage, it is by no means clear that this must be so in nature. Even in the famous and widely cited examples of lynx–hare interactions in northern Canada (Krebs et al. 1995) and of northern European voles (Turchin & Hanski 1997, 2002), long, careful and painstaking field experiments have failed to yield conclusive evidence in support of predation by specialists being the cause of cycles. Permanently excluding the lynx from a large permanent plot in Kluane (Yukon, Canada) during 10 years did not prevent hares from cycling with the same 10-year period, though it certainly changed their amplitude compared with natural conditions (Krebs et al. 1995). A 16-year breeding experiment with hares from the same location showed the existence of intrinsic differences in the annual breeding performances similar in magnitude and in timing to those observed in the field (Sinclair et al. 2003), thus highlighting the importance of changes in individual quality during the hare cycle (see Boonstra et al. (1998) for details). The widely underestimated non-consumptive effects often involved in predator–prey interactions (Krebs 1996; Boonstra et al. 1998; Peckarsky et al. 2008) could induce the changes in individual quality (as indicated by overwinter changes in body weight) that are associated with the decline in juvenile survival that initiates and seals hare crashes (Keith 1990) well before lynx predation becomes an important source of mortality (Royama 1992). It is also known that hares maintain a 10-year cycle even when foxes are their main predator and in the absence of lynx in several areas of southern Canada (Elton & Nicholson 1942; Keith 1963). Similarly, the predation exclusion experiments with northern cyclic voles have failed to provide conclusive evidence about the decisive role of least weasel, the specialist predator allegedly causing vole cycles (see Begon et al. (2006), pp. 432–435 for a summary). Interestingly enough, vole cycles have tended to fade and disappear across Fennoscandia, despite there being no clear signs of either reduction in the density of specialist predators or increases in generalist predators (Hörnfeldt 2004). The number of parameters used in common predator–prey models is comparable with the number Ptolemaeus used when fitting the planet trajectories from the Earth-centred view (Ginzburg & Jensen 2004). These models remain unreliable owing to ‘overfitting’ and over-abundance of the parameters, which is an unfortunately common sin in ecological modelling. The explanation of why the period has to be longer than six generations is a little technical. Interested readers are referred to p. 54 of Ginzburg & Colyvan (2004).
The importance of individual quality in population dynamics is by no means a recent idea. Leslie (1959) appears to be the first to suggest that differences between cohorts can destabilize population dynamics and generate dampening oscillations. Cohort effects describe the situation when cohorts of a population differ from each other because individuals belonging to one of them share an average property (Lindström & Kokko 2002). They typically portray the effects induced by the conditions in early development in birds and mammals (Lindström 1999). While similar to the maternal effects, in that they represent the effect of individual quality, cohort effects do not necessarily imply that individuals subject to varying external conditions pass on their quality to their progeny, but merely that their demographic performance be distinguished from other cohorts (Beckerman et al. 2002; Lindström & Kokko 2002). McNamara & Houston (1996) have championed the notion of state-dependent life histories whereby the individuals' physiological state and diversity of experience (e.g. their individual quality) to environmental circumstances can explain the observed variation in the life-history responses of many taxa in a common environment. The explanatory power of a life-history theory could benefit from accounting for the influence of past environmental effects on current and future fitness (Beckermann et al. 2002). However, the cross-generational transmission of maternal effects is certainly modulated by the specific environmental context wherein they are assessed (Plaistow et al. 2006, 2007).
3. Consequences of a maternal effects view of population dynamics
One interesting consequence of the maternal effects hypothesis (equation (2.1)) is the focus on generations as the biological scale for viewing population dynamics phenomena. This view effectively proposes a ‘specio-centric’ temporal scale that is defined by each species' demography, rather than the annual or semi-annual scale that is often dictated or constrained by the sampling schemes chosen for human convenience. While changes in a species' environment can occur at several absolute temporal scales (i.e. daily, seasonal, annual), the demographic significance of these changes is better characterized at the generation time scale at which reproduction takes place. Generation time is certainly an abstract construct for age(stage)-structured populations. Potential definitions (see Leslie 1966) include the mean age of childbearing, the average time between the birth of parents and the birth of the offspring, and the effective time period to which lifetime reproduction can be attributed in order to obtain the observed per capita growth rate. Considering the units of variables is curiously far from being a moot issue. Classical models (i.e. Lotka–Volterra competition equations, MacArthur–Rosenzweig predation model) were formulated as instantaneous models aiming at capturing essential qualitative features of population dynamics, not as equations aiming to yield precise quantitative predictions. It was never clear what it stands for in the differential equations. Having a specio-centric temporal scale for formulating population dynamic models seems to be a step in the right direction.
The maternal effects hypothesis entails an inertial view of population dynamics according to which the cross-generational transmission of individual quality gives to every natural population an intrinsic tendency to oscillate with a period greater than six generations (Ginzburg 1998). In an analogy with the physical world, it is the common knowledge that an appropriately disturbed guitar string or suspension bridge will oscillate with a natural period determined by the internal properties of the object, not by the origin of the disturbance. Both the amplitude and the shape of the oscillations do depend on the force of the disturbance; it is only the period that does not. The eigenperiod is an intrinsic property of the species: its tendency when appropriately disturbed to oscillate at a specific period (Ginzburg & Colyvan 2004). It has not escaped the ecologists' note that the ensemble of oscillating populations show a relatively narrow set of cycle periods (4-year cycles, 10-year cycles) that have been used to almost classify cycle syndromes (e.g. Finnerty 1980). Interestingly enough, why the periods are actually those observed and why the populations of the similar species rarely cycle with different periods are the two features rarely addressed in most accounts of cyclic population dynamics (Murdoch et al. 2002; Turchin 2003). Murdoch et al. (2002), in competition with a very simple maternal model, had formulated a more complex argument based on predation attempting to explain the gap in the observed periods. According to this view, long periods are characteristic to specialist predator–prey pairs. This contradicts Calder's (1983) earlier finding that the periods of cycling relate clearly to the generation time of the prey, but not of the predator. Confirmation of the latter finding by Krukonis & Schaffer (1991) makes a strong case for the eigenperiod residing in the prey and propagating up the food chain. While the inertial view of population dynamics stemming from the maternal effects hypothesis does not entirely solve this issue, it provides an explanation for why similar species cycle with similar periods by separating the nature of extrinsic perturbation from the period of the realized population dynamics. In the words of Krebs (1996, p. 10): ‘Every naturalist can show differences between every cycle of every population. In my view, these differences will be interesting and explicable once we understand the underlying similarities’. The eigenperiod hypothesis can help ecologists to see the commonalities in the forest despite the moderate differences among the trees.
4. The current status of the maternal effects hypothesis
The maternal effects hypothesis generated interest among population ecologists and it has also been questioned and subjected to debate. The main points of contention have been the failure to detect the changes in individual quality in the field experiments (Ergon et al. 2001; Banks & Powell 2004) and the simplistic structure of the initial models (Benton et al. 2001; Turchin & Hanski 2002; Plaistow et al. 2006). The initial models of the maternal effects hypothesis postulated that mothers experiencing lower density had higher individual quality and gave rise to higher quality offspring than those living at high population densities (Ginzburg & Taneyhill 1994; Inchausti & Ginzburg 1998; Ginzburg 1998). These early models ignored (st)age population structure, and implicitly assumed that maternal effects would only last one generation. The empirical interest motivated by these models has yielded a richer and more complex view of maternal effects in the context of population dynamics. For instance, maternal effects can modulate the investment of mothers through the trade-off between offspring size and number (e.g. Beckerman et al. 2002, 2006), they can last more than one generation (e.g. Fox & Savalli 1998; Hercus & Hoffmann 2000) and their expression can be contingent depending on specific environmental circumstances (e.g. Räsänen et al. 2005; Beckerman et al. 2006; Plaistow et al. 2006). Good theories, including these more complex scenarios, would require further theoretical developments.
The original maternal effects model were deterministic and hence ignored the rich array of interactive effects between age structure and environmental variability (Benton et al. 2001, 2008) and, at best, only considered the year as divided into breeding and non-breeding seasons (Inchausti & Ginzburg 1998; Turchin & Hanski 2002). While relaxing these simplifying assumptions may warrant reformulating the key aspects of the initial maternal models in specific circumstances, the inescapable price to be paid for including greater detail will be a steep increase in complexity and in the number of parameters (see Benton et al. 2001; Beckerman et al. 2003), which will generally hinder their reliable parametrization and comparison with field data.
A currently weak feature of the maternal effects hypothesis concerns the empirical measurement of individual quality. The maternal transmission of individual quality can involve the endowment at birth of energy (proteins or lipids; Plaistow et al. 2006), nutrients (Giron & Casas 2003), antibodies (Martinez-Padilla 2006), hormones (Grooothius et al. 2005), parasites (Demastes et al. 2003), etc. or the modification of offspring early environment through the schedule of provisioning of the offspring and their competitive environment (Beckerman et al. 2006). All these features of individual quality reflecting the mothers' environment can affect the growth trajectory and demographic performance of their offspring. We think that it is unlikely that a single variable can portray individual quality for all species and habitats or even for the main groups of taxa (Rossiter 1996). It is then not particularly surprising that the current environmental conditions could override the effects of the specific maternal effects sought in each experimental design (Ergon et al. 2001; see Beckerman et al. 2006). Moreover, Plaistow et al. (2006) have suggested that because maternal effects may influence different traits according to the environmental context, multivariate studies are needed to detect maternal effects in the field. As with any hypothesis, this should not be construed to imply that neither the prevalence of maternal effects nor their determining effects on population dynamics are true by default. Admittedly, there is currently limited guidance applicable to most species and habitats for demonstrating empirically the action of maternal effects as a means of cross-generational transmission of individual quality regardless of the underlying mechanism(s) generating variation in parental quality. The development of standardized protocols and experimental approaches probably applicable for separate taxa to measure the occurrence, magnitude and importance of maternal effects remains a research priority for the coming years (Rossiter 1996; Räsänen & Kruuk 2007). It is likely that the direct detection of maternal effects through experimental manipulations will remain possible only for small-sized species of short generation times and limited mobility and having a reasonably high recapture rate in the field. Detecting maternal effects in (semi-)natural populations requires disentangling mother–offspring covariance for a set of phenotypic traits from the effects of their sharing of a common environment (Kruuk & Hadfield 2007). Assuming that parent–offspring relationships can be established through either direct observation or paternity inference (Marshall et al. 2002), cross-fostering designs involving the partial exchange of offspring between parents could help discerning true maternal effects from the sharing of a common environment (Kruuk & Hadfield 2007). However, for species with long generation times that typically have high recapture rates, recent advances based on the ‘animal model’ would permit partitioning the phenotypic variation and estimating the magnitude of maternal effects based on the use of pedigrees denoting the degree of kinship between individuals (Kruuk & Hadfield 2007 and references therein). The use of these promising new statistical methods based on generalized mixed-effects models will undoubtedly widen our perspective on the prevalence and importance of maternal effects in nature.
5. Conclusion
The routes converting an environmental effect (predation, parasites, endogenous factors, etc.) into a population response depend on whether the effects translate into direct lethal effects leading to delayed effects through the overshooting of equilibrium density. Ecologists have traditionally employed three main approaches (and combinations thereof) to describe and explain population dynamics: statistical models stemming from time-series analysis; phenomenological models involving implicit mechanisms; and explicitly mechanistic models. At one extreme, models inspired in time-series and econometric literature typically aim to describe, analyse and extrapolate data while rarely needing to hypothesize the ecological processes that could account for the observed dynamics (Royama 1992). At the other extreme lies the ecologists' dream of fleshing into a model the explicit mechanisms responsible for the observed dynamics. All population dynamics models can be seen as a practical compromise between our current knowledge about the ecological causes of the dynamics, limited ability to estimate population parameters from field data at the relevant spatial and temporal scales and ultimate goal of expressing these interactions in terms of ecological mechanisms. Mechanistic and phenomenological are the terms describing the two ends of the spectrum of ecological models. Every population model has, to an extent, elements of both, since they result from mixtures of the partial understanding of biological mechanisms and curve-fitting decisions, and ours is not an exception.
All of the above does not mean that the traditional trophic mechanism of predation does not function in nature. There is simply no reason to believe, as most ecologists do, that it deserves the paradigmatic status that it has acquired. There is indeed a large literature showing multispecific trophic interactions as complex food web diagrams of interacting species in every textbook (e.g. Begon et al. 2006). In a paradoxical contrast to this bewildering multidimensional complexity of trophic interactions in natural communities, when ecologists have attempted to estimate the number of dynamic variables affecting the long-term changes in the abundance of natural populations, they have consistently found that they can be embedded in low-dimensional attractors, with two dimensions being the minimally sufficient space in which the dynamics of most ecological time series can be described (e.g. Murdoch et al. 2002; Turchin 2003). A viable proximate explanation of population dynamics must not only be consistent with the estimated dimension of the observed dynamics, but also postulate a mechanism that can parsimoniously account for the delayed density dependence causing the cyclic behaviour. The maternal effects hypothesis is not only plausible and consistent with the low dimensionality found in the ecological data but also quite likely in many of the famous cases of voles, lynx–hares and forest insects. The eigenperiod hypothesis (Ginzburg & Colyvan 2004) distinguishing the period of cycling from the cause of cyclicity, in particular, stresses the role of internal mechanisms by expressing the cycle period in units of generation time. We are looking forward to the times when the two views on causality of cycles will be weighted fairly equally and the main message will be: you have to have at least two dimensions to cycle, whether it is an external or internal mechanism that is responsible.
Footnotes
One contribution of 12 to a Theme Issue ‘Evolution of parental effects: conceptual issues and empirical patterns’.
References
- Baltensweiler W., Fischlin A. The larch budmoth in the Alps. In: Berryman A., editor. Dynamics of forest insect populations, patterns, causes, implications. Plenum Press; New York, NY: 1989. pp. 331–351. [Google Scholar]
- Banks P., Powell F. Does maternal condition or predation risk influence small mammal population dynamics? Oikos. 2004;106:176–184. doi:10.1111/j.0030-1299.2004.12679.x [Google Scholar]
- Beckerman A., Benton T.G., Ranta E., Kaitala V., Lundberg P. Population dynamic consequences of delayed life history effects? Trends Ecol. Evol. 2002;17:263–270. doi:10.1016/S0169-5347(02)02469-2 [Google Scholar]
- Beckerman A., Benton T., Lapsley C., Koesters N. Talkin' ‘bout my generation: environmental variability and cohort effects. Am. Nat. 2003;162:754–767. doi: 10.1086/381056. doi:10.1086/381056 [DOI] [PubMed] [Google Scholar]
- Beckerman A.P., Benton T.G., Lapsley C.T., Koesters N. How effective are maternal effects at having effects? Proc. R. Soc. B. 2006;273:485–493. doi: 10.1098/rspb.2005.3315. doi:10.1098/rspb.2005.3315 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Begon M.J., Harper L., Townsend C.R. 3rd edn. Blackwell; London, UK: 2006. Ecology. [Google Scholar]
- Benton T.G., Ranta E., Kaitala V., Beckerman A.P. Maternal effects and the stability of population dynamics in noisy environments. J. Anim. Ecol. 2001;70:590–599. doi:10.1046/j.1365-2656.2001.00527.x [Google Scholar]
- Benton T.G., Plaistow S.G., Coulson T.N. Complex population dynamics and complex causation, devils, details and demography. Proc. R. Soc. B. 2006;273:1173–1181. doi: 10.1098/rspb.2006.3495. doi:10.1098/rspb.2006.3495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benton T.G., St Clair J.J.H., Plaistow S.J. Maternal effects mediated by maternal age, from life histories to population dynamics. J. Anim. Ecol. 2008;77:1038–1046. doi: 10.1111/j.1365-2656.2008.01434.x. doi:10.1111/j.1365-2656.2008.01434.x [DOI] [PubMed] [Google Scholar]
- Berryman A. Population cycles, a critique of the maternal and allometric hypothesis. J. Anim. Ecol. 1995;64:290–293. doi:10.2307/5763 [Google Scholar]
- Bjornstad O., Hansen T. Individual variation and population dynamics. Oikos. 1994;69:167–171. doi:10.2307/3545298 [Google Scholar]
- Boonstra R., Hik D., Singleton G.R., Tinnikov A. The impact of predator-induced stress on the snowshoe hare cycle. Ecol. Monog. 1998;68:371–394. doi:10.1890/0012-9615(1998)068[0371:TIOPIS]2.0.CO;2 [Google Scholar]
- Brommer J. The evolution of fitness in life-history theory. Biol. Rev. 2000;75:377–404. doi: 10.1017/s000632310000551x. doi:10.1017/S000632310000551X [DOI] [PubMed] [Google Scholar]
- Calder W. Dover; Mineola, NY: 1983. Size, function and life history. [Google Scholar]
- Chitty D. Population processes in the vole and their relevance to general theory. Can. J. Zool. 1960;38:98–113. doi:10.1139/z60-011 [Google Scholar]
- Conner M., White G. Effects of individual heterogeneity in estimating the persistence of small populations. Nat. Res. Modelling. 1999;12:109–127. [Google Scholar]
- Demastes J., Hafner M.S., Hafner D.J., Spradling T.A. Pocket gophers and chewing lice, a test of the maternal transmission hypothesis. Mol. Ecol. 2003;7:1065–1069. doi: 10.1046/j.1365-294x.1998.00383.x. doi:10.1046/j.1365-294x.1998.00383.x [DOI] [PubMed] [Google Scholar]
- Elton C., Nicholson M. The ten-year cycles in numbers of the lynx in Canada. J. Anim. Ecol. 1942;11:215–244. doi:10.2307/1358 [Google Scholar]
- Ergon T., MacKinnon J.L., Stenseth N.C., Boonstra R., Lambin X. Mechanisms for delayed density dependent reproductive traits in field voles, Microtus agrestis, the importance of inherited environmental effects. Oikos. 2001;95:185–197. doi:10.1034/j.1600-0706.2001.950201.x [Google Scholar]
- Finnerty J. Yale University Press; New Haven, CT: 1980. The population cycles of small mammals. [Google Scholar]
- Fox C., Savalli U. Inheritance of environmental variation in body size, superparasititsm of seeds affects progeny and grandprogeny body size via a monogenetic maternal effect. Evolution. 1998;52:172–182. doi: 10.1111/j.1558-5646.1998.tb05150.x. doi:10.2307/2410932 [DOI] [PubMed] [Google Scholar]
- Ginzburg L. Inertial growth, population dynamics based on maternal effects. In: Mousseau T., Fox C., editors. Maternal effects as adaptations. Oxford University Press; New York, NY: 1998. pp. 42–53. [Google Scholar]
- Ginzburg L., Colyvan M. Oxford University Press; New York, NY: 2004. Ecological orbits. [Google Scholar]
- Ginzburg L., Jensen C. Rules of thumb for judging ecological theories. Trends Ecol. Evol. 2004;19:121–126. doi: 10.1016/j.tree.2003.11.004. doi:10.1016/j.tree.2003.11.004 [DOI] [PubMed] [Google Scholar]
- Ginzburg L., Taneyhill D. Population cycles of forest Lepidoptera, a maternal effects hypothesis. J. Anim. Ecol. 1994;63:79–92. doi:10.2307/5585 [Google Scholar]
- Ginzburg L., Taneyhill D. Higher growth rate implies shorter cycle, whatever the cause. J. Anim. Ecol. 1995;64:294–295. doi:10.2307/5764 [Google Scholar]
- Giron D., Casas J. Mothers reduce egg provisioning with age. Ecol. Lett. 2003;6:273–277. doi:10.1046/j.1461-0248.2003.00429.x [Google Scholar]
- Groothuis T.G.G., Müller W., von Engelhardt N., Carere C., Eising C.M. Maternal hormones as tool to adjust offspring phenotype in avian species. Neurosci. Biobehav. Rev. 2005;29:329–352. doi: 10.1016/j.neubiorev.2004.12.002. doi:10.1016/j.neubiorev.2004.12.002 [DOI] [PubMed] [Google Scholar]
- Hanski I., Henttonen H., Korpimäki E., Oksanen L., Turchin P. Small rodent dynamics and predation. Ecology. 2001;82:1505–1520. doi:10.1890/0012-9658(2001)082[1505:SRDAP]2.0.CO;2 [Google Scholar]
- Hercus M., Hoffmann A. Maternal and grandmaternal age influence offspring fitness in Drosophila. Proc. R. Soc. B. 2000;267:2105–2110. doi: 10.1098/rspb.2000.1256. doi:10.1098/rspb.2000.1256 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hörnfeldt B. Long-term decline in numbers of cyclic voles in boreal Sweden, analysis and presentation of hypotheses. Oikos. 2004;107:376–392. doi:10.1111/j.0030-1299.2004.13348.x [Google Scholar]
- Inchausti P., Ginzburg L. Small mammals cycles in Northern Europe, patterns and evidence for a maternal effects hypothesis. J. Anim. Ecol. 1998;67:180–194. doi:10.1046/j.1365-2656.1998.00189.x [Google Scholar]
- Keith L. University of Wisconsin Press; Madison, WI: 1963. Wildlife's ten year cycle. [Google Scholar]
- Keith L. Dynamics of snowshoe hare populations. In: Genoways H., editor. Current mammalogy. vol. 2. Plenum Press; New York, NY: 1990. pp. 119–195. [Google Scholar]
- Kendall B.E., Prendergast J., Bjørnstad O.N. The macroecology of population dynamics, taxonomic and biogeographic patterns in population cycles. Ecol. Lett. 1998;1:160–164. doi:10.1046/j.1461-0248.1998.00037.x [Google Scholar]
- Kendall W., Briggs C.J., Murdocb W.W., Turchin P., Ellner S.P., Mccauley E., Nisbet R.M., Wood S.N. Why do populations cycle? A synthesis of statistical and mechanistic modeling approaches. Ecology. 1999;80:1789–1805. [Google Scholar]
- Krebs C. Population cycles revisited. J. Mammal. 1996;77:8–24. doi:10.2307/1382705 [Google Scholar]
- Krebs C.J., Boutin S., Boonstra R., Sinclair A.R.E., Smith J.N.M., Dale M.R.T., Martin K., Turkington R. Impact of food and predation on the snowshoe hare cycle. Science. 1995;269:1112–1115. doi: 10.1126/science.269.5227.1112. doi:10.1126/science.269.5227.1112 [DOI] [PubMed] [Google Scholar]
- Krukonis G., Schaffer W. Population cycles in mammals and birds, does periodicity scale with body size? J. Theor. Biol. 1991;148:469–493. doi:10.1016/S0022-5193(05)80232-2 [Google Scholar]
- Kruuk L., Hadfield J. How to separate genetic and environmental causes of similarity between relatives. J. Evol. Biol. 2007;20:1890–1903. doi: 10.1111/j.1420-9101.2007.01377.x. doi:10.1111/j.1420-9101.2007.01377.x [DOI] [PubMed] [Google Scholar]
- Leslie P. Some further notes on the use of matrices in population dynamics. Biometrika. 1948;35:213–245. [Google Scholar]
- Leslie P. The properties of a certain lag of population growth and the influence of an external random factor on a number of such population. Physiol. Zool. 1959;32:151–159. [Google Scholar]
- Leslie P. The intrinsic rate of increase and overlap of successive generations in a population of guillemots Uria aalge Pont. J. Anim. Ecol. 1966;35:291–301. doi:10.2307/2396 [Google Scholar]
- Lindstrom J. Early development and fitness in birds and mammals. Trends Ecol. Evol. 1999;14:343–348. doi: 10.1016/s0169-5347(99)01639-0. doi:10.1016/S0169-5347(99)01639-0 [DOI] [PubMed] [Google Scholar]
- Lindström J., Kokko H. Cohort effects and population dynamics. Ecol. Lett. 2002;5:338–344. doi:10.1046/j.1461-0248.2002.00317.x [Google Scholar]
- Marshall D., Uller T. When is a maternal effect adaptive? Oikos. 2007;116:1957–1963. doi:10.1111/j.2007.0030-1299.16203.x [Google Scholar]
- Marshall T.C., Slate J., Kruuk L., Pemberton J.M. Statistical confidence for likelihood-based paternity inference in natural populations. Mol. Ecol. 2002;7:639–655. doi: 10.1046/j.1365-294x.1998.00374.x. doi:10.1046/j.1365-294x.1998.00374.x [DOI] [PubMed] [Google Scholar]
- Martinez-Padilla J. Prelaying maternal condition modifies the association between egg mass and T cell-mediated immunity in kestrels. Behav. Ecol. Sociol. 2006;60:510–515. doi:10.1007/s00265-006-0193-1 [Google Scholar]
- Matthiopolous J., Moss R., Lambin X. The kin facilitation hypothesis for red grouse population cycles, territorial dynamics of the family cluster. Ecol. Model. 2002;47:291–307. doi:10.1016/S0304-3800(01)00420-3 [Google Scholar]
- McNamara J., Houston A. State-dependent life histories. Nature. 1996;380:215–221. doi: 10.1038/380215a0. doi:10.1038/380215a0 [DOI] [PubMed] [Google Scholar]
- Moss R., Watson A., Parr R. Experimental prevention of a population cycle in red grouse. Ecology. 1996;77:1512–1530. doi:10.2307/2265548 [Google Scholar]
- Mousseau T.A., Fox C.W. Oxford University Press; Oxford, UK: 1998. Maternal effects as adaptations. [Google Scholar]
- Murdoch W.W., Briggs C.J., Nisbet R.M. Princeton University Press; Princeton, NJ: 2002. Consumer resource dynamics. [Google Scholar]
- Norrdahl K., Korpimäki E. Effects of predator removal on vertebrate prey populations, birds of prey and small mammals. Oecologia. 1995;103:241–248. doi: 10.1007/BF00329086. doi:10.1007/BF00329086 [DOI] [PubMed] [Google Scholar]
- Peckarsky B., et al. Revisiting the classics, considering nonconsumptive effects in textbook examples of predator–prey interactions. Ecology. 2008;89:2416–2425. doi: 10.1890/07-1131.1. doi:10.1890/07-1131.1 [DOI] [PubMed] [Google Scholar]
- Plaistow S.J., Lapsley C.T., Benton T.G. Context-dependent intergenerational effects, the interaction between past and present environments and its effect on population dynamics. Am. Nat. 2006;167:206–215. doi: 10.1086/499380. doi:10.1086/499380 [DOI] [PubMed] [Google Scholar]
- Plaistow S.J., St Clair J.J., Grant J., Benton T.G. How to put all your eggs in one basket, empirical patterns of offspring provisioning throughout mother's lifetime. Am. Nat. 2007;170:520–529. doi: 10.1086/521238. doi:10.1086/521238 [DOI] [PubMed] [Google Scholar]
- Räsänen K., Kruuk L. Maternal effects and evolution at ecological time scales. Func. Ecol. 2007;21:408–421. doi:10.1111/j.1365-2435.2007.01246.x [Google Scholar]
- Räsänen K., Laurila A., Merilä J. Maternal investment in egg size: environment-and-population-specific effects on offspring performance. Oecologia. 2005;4:546–553. doi: 10.1007/s00442-004-1762-5. doi:10.1007/s00442-004-1762-5 [DOI] [PubMed] [Google Scholar]
- Redpath S.M., Mougeot F., Leckie F., Hudson P.J. Testing the role of parasites in driving the cyclic population dynamics of a gamebird. Ecol. Lett. 2006;9:410–441. doi: 10.1111/j.1461-0248.2006.00895.x. doi:10.1111/j.1461-0248.2006.00895.x [DOI] [PubMed] [Google Scholar]
- Rossiter M. Incidence and consequences of inherited environmental effects. Annu. Rev. Ecol. Syst. 1996;27:451–476. doi:10.1146/annurev.ecolsys.27.1.451 [Google Scholar]
- Royama T. Chapman and Hall; New York, NY: 1992. Analytical population dynamics. [Google Scholar]
- Sinclair A.R.E., Chitty D., Stefan C.I., Krebs C.J. Mammal population cycles, evidence for intrinsic differences during snowshoe hare cycles. Can. J. Zool. 2003;81:216–220. doi:10.1139/z03-006 [Google Scholar]
- Turchin P. Princeton University Press; Princeton, NJ: 2003. Complex population dynamics. [Google Scholar]
- Turchin P., Batzli G. Availability of food and the population dynamics of arvicoline rodents. Ecology. 2001;82:1521–1534. doi:10.2307/2679797 [Google Scholar]
- Turchin P., Hanski I. An empirically-based model for the latitudinal gradient in vole population dynamics. Am. Nat. 1997;149:842–874. doi: 10.1086/286027. doi:10.1086/286027 [DOI] [PubMed] [Google Scholar]
- Turchin P., Hanski I. Contrasting alternative hypotheses about rodent cycles by translating them into parameterized models. Ecol. Lett. 2002;4:267–276. doi:10.1046/j.1461-0248.2001.00204.x [Google Scholar]
- Uller T. Developmental plasticity and the evolution of parental effects. Trends Ecol. Evol. 2008;23:432–436. doi: 10.1016/j.tree.2008.04.005. doi:10.1016/j.tree.2008.04.005 [DOI] [PubMed] [Google Scholar]
- Weitz J., Levin S. Size and scaling of predator prey dynamics. Ecol. Lett. 2006;9:548–557. doi: 10.1111/j.1461-0248.2006.00900.x. doi:10.1111/j.1461-0248.2006.00900.x [DOI] [PubMed] [Google Scholar]
- Wellington W. Qualitative changes in natural populations during changes in abundance. Can. J. Zool. 1960;38:290–314. doi:10.1139/z60-036 [Google Scholar]