Sequence memory for prediction, inference and behaviour

Abstract

In this paper, we propose a mechanism which the neocortex may use to store sequences of patterns. Storing and recalling sequences are necessary for making predictions, recognizing time-based patterns and generating behaviour. Since these tasks are major functions of the neocortex, the ability to store and recall time-based sequences is probably a key attribute of many, if not all, cortical areas. Previously, we have proposed that the neocortex can be modelled as a hierarchy of memory regions, each of which learns and recalls sequences. This paper proposes how each region of neocortex might learn the sequences necessary for this theory. The basis of the proposal is that all the cells in a cortical column share bottom-up receptive field properties, but individual cells in a column learn to represent unique incidences of the bottom-up receptive field property within different sequences. We discuss the proposal, the biological constraints that led to it and some results modelling it.

1. Prediction and sequence memory

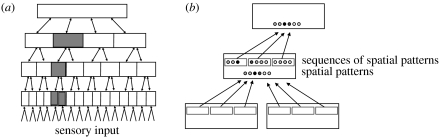
Prediction is a ubiquitous function of the brain. During every moment of our waking life, our brains are trying to predict what sights, sounds and tactile sensations will be experienced next. Previously, we have proposed a theory for how the neocortex learns a model of the world from sensory data, and how it uses this model to make predictions and infer causes (Hawkins & Blakeslee 2004; George & Hawkins 2005; Hawkins & George 2006). We refer to this theory as ‘hierarchical temporal memory’ (HTM). HTM models the neocortex as a tree-shaped hierarchy of memory regions, in which each memory region learns common sequences of patterns (figure 1). Representations of sequences are passed up the hierarchy, forming the elements of sequences in upper regions, and predictions of the next elements in sequences are passed down the hierarchy. By training on time-varying sensory patterns, an HTM builds a spatial and temporal model of the world. HTMs are modelled as a form of Bayesian network, where sequence memory forms the core learning method for each region in the network. When sequence memory is implemented in a probabilistic way, it naturally leads to probabilistic predictions at every level of the hierarchy.

Figure 1.

(a) A conceptual diagram of an HTM model of neocortex. Models such as this replicate the hierarchical connectivity of neocortical regions, and treat the entire system as a Bayesian network. (b) Four connected regions from (a), illustrating the feed-forward pathway. Circles indicate spatial patterns that form the elements of learned sequences. Small rectangles indicate learned sequences of patterns. Relatively constant representations of sequences are passed up the hierarchy, where they combine to form the individual elements of sequences in parent regions. The feedback pathway is not shown. Each region uses its sequence memory to predict what elements will probably occur next and passes this prediction down the hierarchy. The unfolding of learned sequences is the foundation of prediction.

HTM is just one example of a class of hierarchical learning models designed to mimic how the neocortex learns, infers and predicts. Similar models include Hierarchical Model and X, or HMAX (Riesenhuber & Poggio 1999) and convolutional neural networks (LeCun & Bengio 1995). Both these models use hierarchical representations and form groups of spatial patterns at each level in the hierarchy. In both cases, no temporal order is maintained within these groups. Thus, the models are most suitable for spatial pattern recognition, as they cannot recognize time-based patterns or make predictions. Another model similar to HTM is the hierarchical hidden Markov model (HHMM; Fine et al. 1998). HHMMs learn sequences at each level of a hierarchy, as do HTMs, and therefore are able to recognize temporal patterns and make predictions. However, HHMMs are strictly temporal—they do not have the ability to infer spatial patterns.

HTM combines the best of all these models. It is a self-learning model that is inherently temporal, and it can infer and make predictions about spatial and temporal patterns.

HTMs learn by storing sequences of patterns in each memory region. The basic idea is that the patterns that frequently occur together in time share a common cause and can be grouped together. Time acts as a teacher, indicating which patterns mean the same thing even though they may be spatially dissimilar. When implemented in a hierarchy, the net result is that fast changing sensory inputs result in slower changing patterns as one ascends the hierarchy. Relatively stable patterns at the top of the hierarchy can unfold in time to produce faster changing patterns at the bottom of the hierarchy. This theory postulates that recall of sequences leads to prediction, thought and motor behaviour.

In this paper, we will not fully review HTM or exhaustively contrast it to other hierarchical memory models. Instead, we focus on a core feature of HTM (and HHMM), which is intimately tied to prediction; specifically, how might sequences be stored in the neocortex?

2. Constraints on sequence memory

Using a computer and linear computer memory, it is easy to store sequences. Every time one makes an audio recording or saves a text file, one is storing a sequence of patterns. However, this kind of memory is not sufficient for the kind of learning and recall that brains need to do. Real-world sensory data are never exactly the same, are noisy and do not come with markers indicating when sequences begin and end. The simple approach of storing every pattern that occurs will consume too much memory and be unmanageable.

The following is a set of requirements or ‘constraints’ that a biological sequence memory must meet, which are different from linear computer memory.

(a) Probabilistic prediction

Our sequence memory must make probabilistic predictions of future events from noisy inputs. The data sensed from the world are ambiguous at any time instant. Therefore, what is available to the sequence memory at any instance is a distribution of the likely states of the sequence. Similarly, our predictions must be distributions over possible next states. This is a strong constraint and eliminates many possible memory mechanisms. For example, when we listen to someone speaking, the words we hear are often ambiguous in isolation. From this ambiguous input, we anticipate what words will be said next. We usually cannot predict exactly, but some words are more likely than others. Our memory system must be able to handle ambiguity in its input, and all predictions should be distributions—sometimes over large numbers of possible elements.

(b) Simultaneous learning and recall

We cannot make a clear distinction between when our memory system is learning and when it is recalling. It must be able to learn or extend learned sequences, while simultaneously recalling and predicting what is likely to occur next.

(c) Auto-associative recall

Learned sequences are recalled auto-associatively. This is similar to the game of ‘name that tune’. As inputs arrive, the memory has to decide which learned sequences best match the input. An input may match multiple learned sequences or none. Our memory system must be able to recognize sequences even if it is presented with a partial sequence from the middle of a previously learned sequence. In a computer, it is possible to implement auto-associative recall using repetitive search algorithms, but brains do not work this way. We desire a memory mechanism that is naturally auto-associative.

(d) Variable-order memory

To correctly predict what is likely to happen next, it is often necessary to use knowledge of events that occurred some time in the past. Imagine we have two sequences of letters, ‘ABCDE’ and ‘YBCDZ’. Both sequences contain the same three-element sequence ‘BCD’ but vary in the first and last elements. Our memory system must be able to correctly predict the last element of the sequence based on an input that occurred many time steps earlier, a situation that is sometimes referred to as the ‘branching problem’.

The branching problem forces upon us an important constraint: the internal representation of an afferent pattern must change depending on the temporal context in which it occurs. In the example above, the representation for the elements ‘B’, ‘C’ and ‘D’ must be somehow different when preceded by ‘A’ than by ‘Y’.

In mathematical terms, the number of previous inputs required to predict the next input is known as Markov order. When only one previous input is necessary, the model is first order. Let X_t represent the input at time t. In a first-order model, X_t+1 does not depend on any input besides the previous input, X_t. If we want to know the distribution over what might occur next, P(X_t+1), we do not need to know anything that happened in the past (X_t−1 to X₀); we need only to know the current input, X_t. Specifically,

$$P(X_{t+1}|X_t,X_{t-1},X_{t-2},\dots ,X_0)=P(X_{t+1}|X_t).$$

But in our example with the letter sequences above, if we see ‘ABCD’ or ‘YBCD’, we need to go all the way back to the first letter to predict the one that comes next. This requires a fourth-order model,

$$P(X_{t+1}|X_t,X_{t-1},X_{t-2},\dots ,X_0)=P(X_{t+1}|X_t,X_{t-1},X_{t-2},X_{t-3}).$$

Keeping track of these long dependencies allows us to use the initial letter, ‘A’ or ‘Y’, in order to predict the final letter, ‘E’ or ‘Z’. However, the amount of memory required to keep track of long dependencies grows exponentially with the order of the model, quickly becoming infeasible to store and to learn. Therefore, we desire a variable-order Markov model. Variable-order models learn long sequences (high order) as necessary, but use short sequences (low order) for other parts of the data. They allow us to learn complex sequences with manageable amounts of resources.

(e) Biological constraints

We propose that a sequence memory mechanism that meets these theoretical constraints must exist in all regions of neocortex, in all sensory modalities. Given our belief of the central importance of sequence memory for neocortical function, whatever mechanism the brain uses for sequence memory should be prevalent throughout the neocortex. Therefore, any proposed mechanism should map to one or more prominent features of neocortical anatomy.

3. Sequence memory in the neocortex

Our theory of biological sequence memory is inspired by the previous work of Rodriguez et al. (2004), although they used it in a different functional context and with a different biological mapping. We feel it is important to reintroduce this memory technique in the current context of hierarchical neocortical models and give it an expanded biological and mathematical foundation.

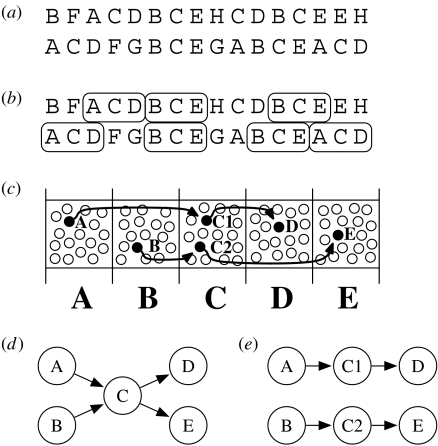
The basics of this idea are fairly simple, and are explained in figure 2a–c. In biological terms, we can think of the cells in a neocortical column as having the same bottom-up receptive field properties. This is a well-known phenomenon believed to occur throughout the neocortex. Within a particular cortical column, there might be dozens of cells within a layer all exhibiting similar or identical feed-forward receptive field properties. Although these cells exhibit similar responses to a purely feed-forward input, in our model, these cells learn to form different responses in the context of natural sequences. Only some of these cells will be active when that feed-forward pattern occurs within a learned sequence.

Figure 2.

(a) Hypothetical sequence of inputs. Letters A to H represent bottom-up input patterns to five columns of cells. Within this sequence of inputs are repeating subsequences intermixed with non-repeating elements. (b) Sequence (a) in which two common subsequences, ACD and BCE, are highlighted. A second-order Markov model is necessary to differentiate these sequences. In general, we require a memory mechanism that can learn and represent sequences of arbitrarily high order. (c) Proposed manner in which the neocortex represents the sequences highlighted in (b). The five columns each respond to a different bottom-up input. One layer of cells is shown, representing neurons which all respond to their column's bottom-up inputs. After training, individual neurons become part of a particular temporal sequence. Filled circles indicate neurons, which participate in the two sequences highlighted in (b). Arrows illustrate lateral excitatory connections. Two neurons, C1 and C2, are used in column C because input C occurs in both sequences. This permits the memory to correctly predict ‘D’ after the input sequence AC and ‘E’ after the input sequence BC. The length and Markov order of the memory is limited by the number of cells in a particular layer within a column. Required inhibitory pathways are not shown. (d) First-order Markov model of transitions learned from (a). Correct prediction from state C is not possible because the input that preceded C is not captured. (e) Result of applying the state-splitting algorithm first proposed by Cormack & Horspool (1987) to (d). Both C1 and C2 respond to a purely bottom-up pattern C, but C1 uniquely responds if A occurs before C, and C2 uniquely responds if B occurs before C. Accurate prediction after input C is possible because C1 will be active if A occurred previously, while C2 will be active if B occurred previously. These states map directly onto the cortical model in (c). Unlike the biological equivalent, the state-splitting technique has no a priori limit to the length of sequences or the number of sequences in which a bottom-up input can appear.

Consider an analogy; imagine we have a column of cells that respond to the sound made when we say the word ‘to’. Because, in English, the words ‘to’, ‘two’ and ‘too’ are homonyms, each of these words spoken in isolation will invoke the same response among these co-columnar cells. However, these words are not interchangeable in context. Imagine we hear the phrases ‘I sat next to’, ‘can I come too?’ and ‘the number after one is two’. In these three phrases, the final words have different meanings, and we perceive them as different. For us to perceive these homonyms as different, our brains must use different neural activations for them.

We propose that through the course of training, individual cells form horizontal connections to previously active cells in nearby columns (figure 2c). These horizontal connections form the basis of sequence memory. When a cell is activated by a horizontal connection prior to receiving its feed-forward activation, it will inhibit its co-columnar cells, thus guaranteeing a unique representation for the feed-forward pattern in the context of a previously learned sequence.

4. Biological implications of a sequence memory model

The proposed model for sequence memory provides a theoretical basis for the columnar organization and horizontal connections observed throughout the neocortex. It also provides a simple mechanism for what we believe is a ubiquitous need for prediction and learning in hierarchical learning models in general.

As a biological model, it is speculative and has numerous requirements for it to work. We now discuss some of these implications before describing how we implemented a software algorithm to mimic the biological theory and tested it within our HTM models.

(a) Sparsification of response

A prediction of this proposal is that general cell activity in the neocortex should become more sparse and selective when receiving input in naturally occurring sequences versus receiving spatial inputs in temporal isolation or random order. A more specific variation of this prediction is that co-columnar cells should exhibit similar responses to simple stimuli, but they should become more sparse and selective when presented with natural sequences. Several studies have observed such behaviour. Yen et al. (2007) reported that in cat striate cortex, classical columnar organization (which is usually determined via simple stimuli such as bars and gratings) changes dramatically and becomes sparser when the animal is subjected to complex time-varying natural images. Similar results were shown by Vinje & Gallant (2000) in macaque V1. Here, they found that input from outside a cell's classical receptive field increased sparseness. This result was observed when the animal was subjected to a time-varying simulated natural viewing stimulus, and the effect was somewhat increased under free natural viewing. Machens et al. (2004) found that the rat auditory cortex exhibited increased sparseness when subjected to complex natural sounds. They report that only 11 per cent of the responses to natural sounds could be attributed to the classical receptive field property of the cells, and suggested the remainder was due to the interactions between frequencies and the time-varying properties of the neural encoding.

These and similar studies have been largely or partially motivated by demonstrating the existence of sparse encoding, which is an efficient method of representation in neural tissue (Olshausen & Field 1996). Our HTM models similarly employ sparse encoding, but here we suggest that our sequence memory model is one means, and perhaps a primary one, to achieve it.

(b) Inhibitory requirements

A specific inhibitory effect is required for our proposal to work in neocortical tissue. When a column of cells is activated primarily from a feed-forward input, all or a majority of the excitatory cells within a layer of a column should be active together. However, if that same feed-forward pattern occurs within a learned sequence, we want only one or a few cells to be active. This requires that an excitatory lateral input to one or a few cells inhibits all the other cells in the near proximity. This laterally induced inhibition must be stronger and faster than the feed-forward excitation.

(c) Distributed representations

We assume that the neocortex uses distributed representations in two ways. First, we do not assume that individual cells are sufficient to represent anything. Although our figures show individual cells representing patterns within sequences, this is only a convenience. We assume that, in almost all cases, multiple cells are simultaneously active, although the pattern of activation will always be sparse.

Representations are also distributed in a second sense. Like Bayesian networks, HTM models assume that activations are distributed. Every region of the hierarchy passes a distribution of potentially active sequences to its parent regions. Again, the figures in this paper do not show this, but our software models are implemented this way. The neocortex works with probabilistic inputs and makes probabilistic predictions.

(d) Efficient computation

The memory system must use information from previous inputs when making predictions, and both the history of inputs and the forward predictions are distributions over many states. Performing this calculation in a brute-force manner is not biologically realistic in terms of capacity or speed. Our biological model performs the calculation using dynamic programming, a mechanism first described by Bellman (1957). Refer to George (2008, §4.6.2) for a detailed mapping of the biological theory to dynamic programming equations.

(e) Cortical layers

We believe that the sequence model we have described occurs among pools of neurons within the same layer of neocortex, using lateral connections to cells in the same layer of other columns. We do not believe that the effect is likely to occur across cortical layers unless evidence exists for strong interlaminar lateral connections.

Previously, we have proposed why the different cell layers observed in the neocortex might exist (Hawkins 2007). It is not our intention to review these proposals in this paper, but a brief overview might be useful. Cellular layers 2–6 all exhibit lateral connections, although there are differences. In our view, these differences reflect the kind of sequences that can be learned, and sequence learning is occurring in some form in layers 2–6.

Hierarchical memory models need to make a distinction between information flowing up the hierarchy and information flowing down the hierarchy. In a crude way, one can think of downward flowing information as expectation and upward flowing information as reality. Bayesian theory tells us that these two streams of information must remain segregated, but that they must also be combined to form a local belief at each level of the hierarchy (Pearl 1988). Because sequence memory is required in both the feed-forward path and the feedback path, we believe that some cell layers are learning feed-forward sequences (layers 4 and 3) and other layers are learning feedback sequences (layers 2 and 6). Layer 5 is where they are combined to form a belief. Here, the main point is that we believe that sequence memory is occurring in multiple cell layers and that there are theoretical reasons why this should be so.

(f) Sequence timing

When we learn a melody, part of the memory of the melody is the duration of each note, which varies from note to note. Similarly, when we memorize a poem or a dance step, we remember the duration for each element in the sequence. We can speed up or slow down a recalled sequence, but the absolute duration of the sequence elements is stored and can be recalled.

As described so far, our sequence memory model has no means of storing the duration of sequence elements, and it has no means of changing the rate at which a sequence is recalled. Our sequence memory mechanism therefore needs a neural mechanism that can encode the durations of sequence elements. This neural mechanism should exist in all regions of the neocortex and should be tightly coupled with the sequence memory mechanism proposed in this paper. Previously (Hawkins & Blakeslee 2004), we have proposed such a duration mechanism involving layer 5 pyramidal cells, which project to non-specific thalamic nuclei, which project to neocortical layer 1, which form synapses with apical dendrites of pyramidal cells in layers 2, 3 and 5. It is beyond the scope of this paper to describe this mechanism further.

When a human learns a melody, there is an upper limit to the duration of individual notes that can be learned of approximately one second. This is why musicians need to count for notes or rests that are longer than a second. Assuming that a similar limit exists in other modalities, the sequence memory proposed in this paper can learn arbitrarily long sequences of elements where the duration of each element is between a few tens of milliseconds and approximately one second. In a software implementation, the duration limits need not be fixed, but could depend on the parameters of the model and the resources allocated to it.

(g) Memory capacity

Our proposed biological model tells us something about the capacity of sequence memory. Consider an analogy to music. Imagine we have 12 columns each with 50 cells, where each column represents one of the 12 musical tones in Western music. Such a memory can learn melodies and melodic phrases, but there is a limit to the number and length of the sequences that can be stored. At one extreme, it could learn a single sequence of 600 notes using exactly 50 of each of the 12 tones. If the memory were allocated this way, the system could only recognize the single melody, but it could do so auto-associatively when presented with any portion of the melody, or even a partially garbled portion of the melody. In addition, it would be able to predict the next note or the entire remaining portion of the melody. At another extreme, the memory could learn 100 sequences of six notes each. The point is that there are a fixed number of states that can be allocated to a few long sequences or many short sequences or any combination in between.

It might appear that such a memory system is too limited to store all the information we have in our brains. A human can memorize a tremendous amount of temporally associated information, including long speeches, long pieces of music, lengthy journeys, etc. The answer to this objection is that capacity of HTM derives primarily from the hierarchy, not the sequence memory in each node (George 2008). The hierarchy allows learned sequences to be used repeatedly in different combinations. When memorizing a speech with a hierarchy of sequence memories, the speech is stored as a series of phrases at one level of the hierarchy, the phrases are decomposed into a series of words at the next lower level and each word is decomposed into a series of phonemes at the next lower level.

5. The state-splitting algorithm

Over the past 3 years, we have been creating and testing models of HTM in software. During this time, we have tried several different sequence memory techniques, starting with the simplest method of storing all afferent sequences, and progressing to complex methods such as prediction suffix trees (Ron et al. 1996; Seldin et al. 2001). In the end, we have settled on a sequence memory model we call ‘state-splitting’, depicted in figure 2d,e. State-splitting was inspired by and maps closely to our proposed biological sequence memory mechanism. As with other techniques, state-splitting generates variable-order Markov models, which can capture complex dependencies within sequences. However, state-splitting is the only sequence memory model we have found that meets all of the above constraints and maps well to neocortical anatomy. In addition, we have found state-splitting to be simpler to implement than some other methods.

The state-splitting technique was first described by Cormack & Horspool (1987), although they used the algorithm for data compression and in a non-biological context. We borrow their technique and apply it to prediction and inference in an HTM setting.

(a) Splitting states

State-splitting deviates from our proposed biological sequence memory in one significant way. In the biological model, we start with a column of cells that share bottom-up receptive field properties and then assign the cells to unique sequences. By contrast, in the state-splitting model, we start with a single state and then split the state as we learn sequences (similar to adding neurons, as we need them). State-splitting accomplishes the same goal as the biological model, but there is no limit on the number of assignable elements for each column, and no resources are wasted over-representing inputs which appear only in a few sequences.

The state-splitting algorithm begins with one state per input pattern. During learning, it observes the activation of states, and counts a transition between state i and state j if input j is active immediately after input i is active. The mechanism also works if more than one state is active at a particular point in time. The sequence of activations are tracked in a Markov chain T, a matrix in which T_i,j contains the number of transitions from state i to state j. Periodically, we examine T to determine whether some states belong to multiple sequences. Any such state is split to create one or more new copies.

Intuitively, we wish to split a state when we believe that it reliably participates in more than one sequence. To test this, we check whether a state frequently follows a particular state (i.e. it clearly participates in a sequence), and we also check whether it follows other states as well (i.e. it may appear in other sequences). From Cormack & Horspool (1987), we borrow the two parameters min_cnt1 and min_cnt2. We split state t into two states when there exists a state s for which the two conditions hold,

$$\begin{array}{c}{T}_{s,t}\ge \text{min}\_\text{cnt}1,\\ \sum _{i,i\ne s}{T}_{i,t}\ge \text{min}\_\text{cnt}2.\end{array}$$

After the split, we consider the system to be in the new state t′ if s is active previously; otherwise, the system is in the original state t. Thus, by construction, the states automatically participate in separate sequences. Through multiple splits, states may participate in many sequences.

We continue learning transitions in the new Markov chain T, which now has an expanded set of states. But even though we still treat the model as first order, it is now implicitly higher order. States which have been split are constructed to activate after a specific predecessor; thus, some states contain higher order information by bundling together inputs from multiple time steps. Figure 2d shows the initial first-order model built from the frequent sequences highlighted in figure 2b. The algorithm chooses to split state C into C1 and C2, where C1 originates from A and C2 originates from B. The new model is shown in figure 2e. Although only first-order transitions are maintained, splitting C allows the model to capture the second-order information necessary to recognize the two sequences and form correct predictions.

(b) Identifying sequences

We have described the algorithm used to build the variable-order memory necessary for modelling sequences and making predictions. HTM requires another component of sequence memory, which identifies individual sequences in order to communicate with the parent regions in the hierarchy. We believe that there are biological equivalents, but they are beyond the scope of this paper.

6. Experimental results

We wish to verify that the state-splitting algorithm can be used to model the statistics of real-world sensory data. In this section, we demonstrate the performance of the algorithm on motion capture data of human subjects.

Motion capture data are recorded with a camera that measures the position and joint angles of an actor in a special suit. We obtained data from the Carnegie Mellon Graphics Laboratory Motion Capture Database, available at http://mocap.cs.cmu.edu. Data are recorded from 32 joints at each point in time. We use sequences of these joint angles for training and testing our model.

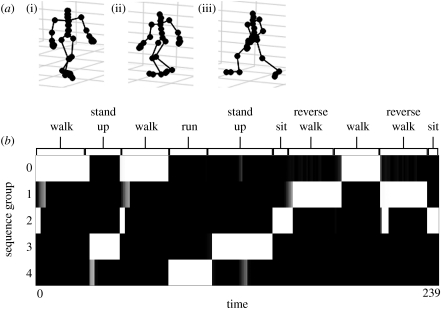
The data are also sufficient for us to render stick-figure representations of the actors. Figure 3a shows three example poses. When the poses do not appear in a sequence, it is difficult to recognize which action the subject is performing, and it would not be possible to predict next likely poses.

Figure 3.

(a) Three separate motion capture inputs from a human subject. Each input is a set of angles from 32 joints. When shown a sequence of such poses, humans have no difficulty recognizing activities such as running, walking and sitting. However, actions are difficult or impossible to recognize from static poses such as these (i)–(iii), because many poses could be part of several different actions. (b) Unsupervised classification of motion capture sequences. The state-splitting algorithm described in this paper was shown a sequence of 239 poses in which the subject repeatedly performed four different actions (‘walk’, ‘run’, ‘sit’ and ‘stand up’). As an extra test, the ‘walk’ sequences were also played backwards as a fifth action (‘reverse walk’), guaranteeing that the exact same poses were used but in a different temporal order. The vertical axis represents the five sequences groups, learned without supervision. The horizontal axis shows the time progression of the 239 poses. The labels at the top of the chart indicate what action the subject was performing at that time. The learned sequences closely match the subject's performed actions, demonstrating that the state-splitting method was able to learn the sequences.

We train on a file of many sequences, with 239 poses in total. Before building the temporal model, we quantize the poses to 66 quantization points. Each input to the state-splitting algorithm is the index of the quantization point with the lowest Euclidean distance to the original input. Using this quantization, we transform each input from a dense vector to a single index. We then learn the Markov chain with these indices and apply the state-splitting algorithm. We pass over the same data five times in total, in order to produce more splits and create a higher order model.

To ascertain whether the resultant Markov chain accurately models the data, we apply an unsupervised sequence-identification algorithm to discover five sequence groups. Figure 3b shows the result of playing a long segment of the training data and tracking the activation of the five groups. Although the groups were labelled without supervision, each one clearly corresponds to a particular action. We observe that the group activations switch appropriately when the subject switches actions, with only occasional errors at the intersections. We happily note that the ‘walk’ and ‘reverse-walk’ sequences are correctly distinguished, proving that temporal order is being used.

The results in figure 3b demonstrate learning and inference with higher order sequences, using the state-splitting algorithm. It is a straightforward matter to generate predictions from the temporal models within individual nodes in an HTM. Generating predictions using the entire hierarchy together is one of our current areas of research.

Source code for the state-splitting algorithm and the motion capture example is available from http://www.numenta.com/for-developers/software.php.

7. Conclusion

The neocortex can be viewed as a memory system that builds a model of the world for inference, prediction and behaviour. We claim that all these goals can be achieved using a hierarchically organized memory system, in which each node in the hierarchy uses probabilistic sequence memory to group patterns together. The hierarchical organization of the neocortex is well documented, and Bayesian theory provides a basis for understanding how hierarchies can infer causes in the face of ambiguity. In this paper, we have proposed a simple yet powerful technique for how regions of neocortex might learn probabilistic sequences. The technique relies on columnar organization of cells that share bottom-up receptive field properties. Through lateral connections, individual cells learn to represent bottom-up patterns within specific sequences. Although simple, the proposed sequence memory technique solves the difficult tasks of learning sequences of arbitrarily high order from distributed inputs, recognizing time-based patterns and making distributed predictions.