Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2009 Feb 25;25(8):996–1003. doi: 10.1093/bioinformatics/btp114

Predicting helix–helix interactions from residue contacts in membrane proteins

Allan Lo 1,2, Yi-Yuan Chiu 3, Einar Andreas Rødland 4,5, Ping-Chiang Lyu 2, Ting-Yi Sung 3,*, Wen-Lian Hsu 3,*
PMCID: PMC2666818  PMID: 19244388

Abstract

Motivation: Helix–helix interactions play a critical role in the structure assembly, stability and function of membrane proteins. On the molecular level, the interactions are mediated by one or more residue contacts. Although previous studies focused on helix-packing patterns and sequence motifs, few of them developed methods specifically for contact prediction.

Results: We present a new hierarchical framework for contact prediction, with an application in membrane proteins. The hierarchical scheme consists of two levels: in the first level, contact residues are predicted from the sequence and their pairing relationships are further predicted in the second level. Statistical analyses on contact propensities are combined with other sequence and structural information for training the support vector machine classifiers. Evaluated on 52 protein chains using leave-one-out cross validation (LOOCV) and an independent test set of 14 protein chains, the two-level approach consistently improves the conventional direct approach in prediction accuracy, with 80% reduction of input for prediction. Furthermore, the predicted contacts are then used to infer interactions between pairs of helices. When at least three predicted contacts are required for an inferred interaction, the accuracy, sensitivity and specificity are 56%, 40% and 89%, respectively. Our results demonstrate that a hierarchical framework can be applied to eliminate false positives (FP) while reducing computational complexity in predicting contacts. Together with the estimated contact propensities, this method can be used to gain insights into helix-packing in membrane proteins.

Availability: http://bio-cluster.iis.sinica.edu.tw/TMhit/

Contact: tsung@iis.sinica.edu.tw

Supplementary information:Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Integral membrane proteins play an important role in many critical life processes such as signal transductions, bioenergetics, ion transport and cell adhesions. Although the transmembrane (TM) region of a helical-bundle protein can be predicted reliably using first principles or machine-learning methods (Bernsel et al., 2008; Jones 2007; Lo et al., 2008), the mechanisms by which TM proteins fold into native structures remain poorly understood due to the paucity of solved structures. The fold of a helical membrane protein can be dissected into pairs of interacting TM helices, connecting loops and extramembraneous domains. Some previous studies have focused on the TM regions, and found that interactions between TM helices are important determinants of folding and stabilization (DeGrado et al., 2003; Popot and Engelman, 2000). In order to gain insights into helix–helix interactions in membrane proteins, it is critical to assimilate information from helix-packing geometries, sequence motifs and structural contacts. Canonical models describing the geometries of helix-packing such as ‘knob-into-hole’ and ‘ridge-into-groove’ have been proposed (Chothia et al., 1981; Langosch and Heringa, 1998). Several groups have also focused on the occurrence of motifs that mediate helical associations (Russ and Engelman, 2000; Sal-Man et al., 2007; Walters and DeGrado, 2006). However, studies aiming at delineating residue contacts between TM helices have not been extensively examined. In contrast, contact prediction is an active research area for soluble proteins, as seen in the case of the Critical Assessment of Structure Prediction experiments (Izarzugaza et al., 2007). It has been shown that predicted contact maps can serve as spatial constraints for ranking structural models (Miller and Eisenberg, 2008), inference for folding rates and pathways (Ouyang and Liang, 2008) and estimation of disordered regions (Schlessinger et al., 2007). Therefore, methods that predict structural contacts may be valuable for the purpose of structure prediction in membrane proteins, whose available structures are limited.

Several works related to TM helical contacts included a comparison of helix-packing modes between soluble and TM proteins (Eilers et al., 2002). Another approach examined the burial status of residues in interacting helices, but did not directly predict contact pairs (Park et al., 2007). A recent work employed correlated mutation analysis (CMA) and consensus approaches to predict contact pairs and interacting helices (Fuchs et al., 2007). Interestingly, several existing sequence-based contact prediction methods for soluble proteins directly predict the contact map (Punta and Rost, 2005; Shackelford and Karplus, 2007). Such a process requires a high computational cost incurred by a quadratic growth of residue pairs for prediction. In addition, the contact map space is dominated by non-contact pairs, which are generally of little interest for structural modeling. From the above considerations, contact prediction methods may benefit from a hierarchical approach, in which non-contact residues are eliminated in the first level, followed by predicting the pairing relationships of contact residues in the second level.

Here, we present a two-level hierarchical approach using support vector machines (SVMs) to predict residue structural contacts and helix–helix interactions in membrane proteins. Residue and residue pair contact propensities are estimated and they capture important information about helix–helix interactions. The proposed hierarchical framework starts at the first level, in which contacts and non-contacts are predicted on a per residue basis. The second level further predicts the structure of the contact map from all possible pairs of predicted contact residues. We evaluate the accuracy of contact pair prediction using the conventional direct and the proposed two-level schemes on a development set of 52 protein chains and an independent test set of 14 protein chains. Based on the experimentally determined topology, the two-level method consistently improves the direct method in overall contact pair prediction accuracy in both datasets, while reducing a significant fraction of contact pairs for prediction. Our method also compares favorably with the state-of-the-art contact predictors based on CMA. The predicted contacts are then used to infer helix–helix interactions. Given a threshold (T) of at least five pairs of predicted contacts, helix–helix interactions can be predicted with an accuracy of 67% and a specificity of 95%. Our results demonstrate that the incorporation of contact propensities with other sequence and structural features into a novel two-level prediction framework improves residue contact prediction in membrane proteins.

2 METHODS

2.1 Datasets

We obtained the non-redundant set of α-helical TM proteins from the PDBTM database (Tusnady et al., 2005), a collection of automatically identified membrane proteins from the Protein Data Bank (PDB) (Berman et al., 2000). The initial list as of October 2008 contained 252 protein chains and we removed those of (i) theoretical models; (ii) NMR structures; (iii) single-pass TM helices; (iv) low-resolution structures (>4Å); and (v) no contacts after applying our contact selection criteria defined in Section 2.3. The remaining 150 protein chains were reduced at mutual sequence identity of <30% using Cd-hit (Li and Godzick, 2006). To this end, we obtained 66 polytopic protein chains containing at least two TM helices for training and testing. Since the number of TM helices varied drastically in all proteins, we divided the data into four groups based on the number of TM helices (2–4, 5–6, 7–9 and ≥10). For a proper assessment of performance, we partitioned the data into a development set of 52 protein chains for training and LOOCV and an independent test set of 14 proteins for external validation while also observing that both sets contained roughly the same distribution of TM helices in each group. The development set was used for estimating the contact propensities, SVM model training and parameter-tuning in LOOCV for both Levels 1 and 2. The development set is listed in Table 1S and the independent test set is listed in Table 2S of Supplementary Material.

2.2 System architecture and model training

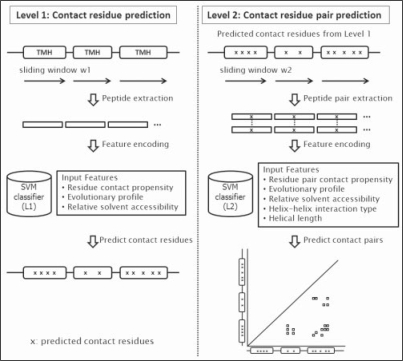
To predict TM interhelical residue contacts, we developed TMhit (TM helix–helix interaction prediction) based on a hierarchical architecture with two levels via SVM classifiers. Within each level, we trained and tested a different SVM model for discrimination between contact and non-contact residues or pairs. In Figure 1, we describe the flow of prediction given a tested protein. In the first level, contact residues are predicted and marked by an ‘x’. In the second level, all possible pairs of predicted contact residues, called contact pair candidates, are further classified into contact and non-contact pairs. For training the SVM models, each Level 1 or Level 2 classifier was trained independently using the radial basis function kernel with probability option in the LIBSVM package (Chang and Lin, 2001). We performed LOOCV in each level to assess prediction accuracy and optimize the training parameters, C and γ. In LOOCV, each time one protein chain is withheld for testing, and Levels 1 and 2 SVM models are trained on the remaining proteins. The above process is repeated N times, where N is the number of total protein chains. In order to further reduce sequence and structural similarity not detected by Cd-hit, we removed protein chains from the training set if significant BLAST hits were found [E-value<1e-4; equivalent to the superfamily level in the ASTRAL database (Chandonia et al., 2004)] for the tested protein during LOOCV and the independent test. For estimating the performance of the two-level model, the tested protein was then run through the combined Levels 1 and 2. Through this procedure, C and γ were selected as 1.0 and 0.12 for Level 1, respectively, and 3.0 and 0.06 for Level 2.

Fig. 1.

Fig. 1.

Open in a new tab

Overview of TMhit methodology. In the left panel, the first level of TMhit is described. Contact residue prediction is performed in the following order: peptide extraction using sliding windows, feature encoding and prediction by SVM in Level 1. The ‘x’ marks the predicted contact residues in the first level. In the right panel, the second level of TMhit predicts the contact pair candidates based on the output of the first level (i.e. only the residues predicted in the first level as marked by an ‘x’ are considered). Contact pair prediction is performed in the following order: peptide pair extraction using sliding windows, feature encoding and prediction by SVM in Level 2. The final output is a contact map comprised of all predicted contact pairs.

2.3 Definition of interacting TM helices

The structures of the proteins in both development and independent test sets were downloaded from PDB and we used STRIDE to extract the location of TM helices (Frishman and Argos, 1995). We also used a TM topology predictor, SVMtop, to simulate the case when the structure is not available (Lo et al., 2008). Only TM-spanning helices of length at least 17 residues were kept for further analysis. We followed the same definition for interacting helices used by Walters and DeGrado (2006). First, the distance between any two atoms from an interacting helical pair was less than the sum of their van der Waals (VDW) radii plus a threshold of 0.6Å. The VDW radii were taken from Li and Nussinov (1998). Second, at least one pair of residues, one from each helix, had a distance <6.0Å between their Cß atoms. The distribution of contact and non-contact pairs as a function of the two distance criteria is shown in Figure 1S of Supplementary Material. Third, at least three pairs of VDW contacts must be found between a pair of interacting TM helices. Applying all three criteria to the development set of 52 protein chains with observed topology, we obtained 321 interacting TM helical pairs and 2693 contact pairs for training the Level 2 SVM model. These contact pairs were made up from 3348 contact residues out of a total of 8813 residues, which were used for developing the Level 1 SVM model. For the independent test set of 14 protein chains, we obtained 85 interacting helical pairs, 768 contact pairs and 939 contact residues out of a total of 2399 residues.

We also calculated the contact density (Cd), which is defined as the ratio between the total observed contact pairs and all possible residue pairs (Punta and Rost, 2005). Using the above criteria, observed Cd values for the development set and the independent test set were 0.34% and 0.37%, respectively. Therefore, <99% of all possible contact pairs were non-contact pairs in our datasets. To avoid imbalanced training for SVM in Level 2, we defined the ratio of contact to non-contact pairs as 1:4, such that the total number of all non-contact pairs was equal to four times the number of contact pairs. From this ratio, we randomly selected non-contact pairs according to its frequency in each distance bin separated by the Cß−Cß distance of 4Å beyond the 6Å cut-off into four groups (i.e. 6–10, 10–14, 14–18 and >18Å).

2.4 Estimation of contact propensities

2.4.1 Residue contact propensities

To quantify the relative preference of amino acids participating in interhelical contacts, we first estimated residue contact propensities. Since some amino acids have relatively small sample sizes and might be heavily influenced by statistical errors, we used an empirical Bayes method in order to account for the variation. The details as well as the applications of this method have been described previously (Casella, 1985). Two important parameters, the shrinkage factors, μr and Mr, were added into the calculation. Here, μr corresponds to the a priori expected probability of any residue forming contacts and Mr is the weight given on this estimate. We derived μr and Mr using a beta-binomial model. For each residue type, we assumed a random contact probability from a beta distribution with parameters Mr(1 − μr) and Mrμr. We used a maximum likelihood estimator for μr and Mr, and the estimates were 0.36 and 28.69, respectively. The details of derivation and estimation of the shrinkage factors are described in the Supplementary Material. 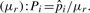The estimated residue contact propensity of amino acid type i is given by Inline graphic where ni is the number of amino acid type i occurring in residue pair contacts and Ni is the total number of amino acid type i in the helical domain. Residue contact propensity (Pi) for amino acid type i is calculated as the corresponding estimated contact propensity Inline graphic divided by the a priori expected residue contact probability Inline graphic

2.4.2 Residue pair contact propensities

The residue pair contact propensities represent the general preference for pairs of amino acids forming contacts. Similar to the calculation for residue contact propensities, we added the two shrinkage parameters: a priori expected contact pair probability μp, and also the weight for the probability Mp, in the estimation of residue pair contact propensities of amino acid type 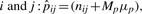Inline graphic where nij is the number of observed contact pairs of amino acid type i and j, and Nij is the number of possible contact pairs between contact residues of amino acid type i and j (residues counted in ni) from the same set of interacting helices. Using a beta-binomial model and a maximum likelihood estimator, μp and Mp were estimated at 0.02 and 2432.63, respectively. The residue pair contact propensities (Pij) of amino acid type i and j is simply the ratio between the estimated residue pair contact propensities 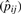Inline graphic and the expected contact pair probability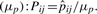 Inline graphic

2.5 Input features for prediction

For training the SVM classifiers, we selected and integrated five different types of information including contact propensities, evolutionary profile, relative solvent accessibility (RSA), helix–helix interaction type, and helical length. We encoded these features using sliding windows in order to capture the information contained in the immediate neighbors of the central residues. In the first level, positions of i ± n with respect to each central residue i in the sliding window were included. For the second level, the sliding windows included positions from i ± n and j ± n for central residues i and j in the helical pair. We set n = 4 (window size of 9) for both Levels 1 and 2. The total dimension of each peptide encoded by a feature was the length of the vector multiplied by the window size. Each input feature is described in detail below:

2.5.1 Contact propensities

Residue and residue pair contact propensities calculated in Section 2.4 were incorporated in Levels 1 and 2 predictions, respectively. Both types of contact propensities were encoded using sliding windows as described above. Specifically, each central pair (i, j) in Level 2 was encoded by a total of 17 pair contact propensities taken from the central residues of each window (i or j) against all other residues in the oppositely aligned window (i ± 4 or j ± 4). The values were scaled in the range of [0, 1] using a sigmoid function (Mitchell, 1997).

2.5.2 Evolutionary profile

The evolutionary profile of each protein chain was obtained by running PSI-BLAST (Altschul et al., 1997) on the NCBI non-redundant database with three iterations and the E-value set to 1e-3. Each residue of a peptide was represented by a vector composed of 20 log-odds scores indicated by the position specific scoring matrix (PSSM). This feature was encoded using sliding windows in both Levels 1 and 2, and normalized in the range of [0, 1] using a sigmoid function.

2.5.3 RSA

The RSA values were obtained by first calculating the solvent accessibility and then normalized by the reference values in Samanta et al. (2002). To estimate the experimentally calculated RSA, we used a probe radius of 2Å, as also used by Beuming and Weinstein (2004) to emulate the -CH2- group in the lipid environment. We also used predicted RSA by ASAP (Yuan et al., 2006) to consider the situation without a structure. This feature was used in both Levels 1 and 2 and encoded using sliding windows.

2.5.4 Helix–helix interaction type

Helix–helix interaction types capture the information of interactions on the site of contact and helical orientations. We divided a TM helix into capping and core regions. The capping regions included the first and last five residues or first and last 25% of total helical length, respectively, whichever was larger. Additionally, we also considered the orientation of helical pairs to be either anti-parallel or parallel by observing the topological information. An anti-parallel pair is defined as the N-term of each helix facing a different localization, otherwise it is a parallel pair. We obtained the above information using TOPDB, a recently published database containing experimentally verified topologies (Tusnady et al., 2008). In order to mirror the case without a structure, SVMtop was used. For each contact residue pair, we examined if residue i and j was located in TM capping or TM core regions plus the helical orientation as described above. There were six interaction types in total by combining three types of pair contact sites (‘cap-core’, ‘cap-cap’ and ‘core-core’) with two types of helical orientations. This feature was represented by a 6-bit vector of binary values in Level 2 only.

2.5.5 Helical length

The use of global information of a protein can provide information about helical contacts. For example, helical length and crossing angles were found to be strongly correlated with helix-packing motifs (Walters and DeGrado, 2006). Here, we used the helical length as global information and scaled it in the range of [0, 1] by minimum–maximum normalization with specified lower and upper bounds. The lower bound was set at 17, the minimum length defined for a fully membrane-spanning helix in Section 2.3. The maximum length was set at 51, three times of the minimum length. For helices of length over 51, a value of 1.0 was assigned. For any pair of residue contacts, two values for helical length, one from each helix, were calculated. This feature was encoded as input in Level 2 only.

2.6 Evaluation measures

For contact residue prediction in Level 1, we evaluated the performance in terms of accuracy, sensitivity and Matthews correlation coefficient (MCC) (Matthews, 1975). For prediction of contact pairs in Level 2, we assessed the predictions by accuracy, which was the total number of correctly predicted contact pairs divided by all predicted pairs. We ranked the predicted contact pairs according to the probabilities generated by LIBSVM and included the top L/5 as the final prediction. Here, L is the total length of helical segments within each protein chain. Improvement over random (IMP) (Grana et al., 2005) is defined as the ratio between prediction accuracy and the expected accuracy of a random prediction, which follows the same definition as Cd in Section 2.3. To estimate the statistical significance of the prediction, P-values were calculated from one-sided Fisher's exact tests (Mehta and Patel, 1997). We also evaluated contact pairs by δ-analysis, which represents the percentage of correctly predicted contacts within a sequence separation of δ around the observed contacts (Ortiz et al., 1999). We set δ = 4, and therefore the intervals for predicted contacts were (i − 4, i + 4) and (j − 4, j + 4), about one turn around the observed contact pair (i, j) on the TM helices. Helix–helix interaction predictions were evaluated based on accuracy, sensitivity (Sn), and specificity (Sp). Here, Sn = TP/(TP + FN) and Sp = TN/(TN + FP), where TP, TN and FN are true positives, true negatives and false negatives, respectively. Standard errors (SEboot) of evaluation measures were estimated using a bootstrapping method with 1000 replicates. Details of the bootstrapping procedure are described in Supplementary Material.

3 RESULTS

3.1 Statistical analysis of contact propensities

3.1.1 Residue contact propensity

The residue contact propensities and their values on a logarithmic scale are shown in Table 3S and Figure 2S, respectively, of Supplementary Material. A value above 1.00 indicates that the particular residue is more overrepresented in residue contact pairs and otherwise for an underrepresented amino acid. The five most overrepresented amino acids in descending order include polar and small types: Cys (1.43), Met (1.27), Ala (1.25), Ser (1.19) and Gly (1.19). In contrast, low contact propensities were observed for charged amino acids: Lys (0.49), Arg (0.68), Asp (0.68) and Glu (0.72), in ascending order. All observations reported above significantly differ from 1.00 with P-values < 0.05. Among the aromatic residues, Tyr is slightly favored (1.17) while Phe and Trp have propensities values close to 1.00, indicating a neutral preference for residue contact.

3.1.2 Residue pair contact propensities

The counts of residue pairs involved in interhelical contacts and their propensities are listed in Tables 4S and 5S of Supplementary Material. We show the residue pair contact propensities in Figure 3S of Supplementary Material on a color-coded log2 scale. For brevity, we only report the statistically significant pairs (P-value < 0.05). The first group with overrepresented contact pairs belongs to the polar residues, namely Asn, His, Ser and Thr in pairs of NS (1.15), ST (1.13) and HT (1.10). We also observe high propensities for pairs mediated by small residues such as Ala and Gly (FG: 1.14, GH: 1.14, AV: 1.13 and AM: 1.11). In contrast, low contact propensities are represented by some non-polar pairs involving Leu and Ile (LL: 0.84 and LI: 0.87) and small–small pairs (AA: 0.88). Ionic pairs of oppositely charged residues have propensities near 1.00, indicating a neutral preference for contact. Aromatic pairs have propensity values close to or slightly below 1.00.

3.2 Feature set selection and cross validation accuracy of the development set

3.2.1 Feature set selection

To gain insight into the relative importance of input features to contact pair prediction, we trained Level 2 models based on combinations of input features from observed information and evaluated them by LOOCV on the development set. The combinations included five feature sets of increasing complexities: (i) profile-only; (ii) profile + RSA; (iii) profile + propensity; (iv) profile + propensity + RSA; and lastly (iv) all five features as described in Section 2.5. Their relative strengths in discriminating power are compared in receiver operating characteristic (ROC) curves shown in Figure 4 of Supplementary Material. In ROC plots, models better than a random prediction yield curves above the diagonal line. Interestingly, the prediction is improved incrementally by feature sets of increasing complexities. Most notably, the addition of features specific to TM helices such as contact propensities, helix–helix interaction type and helical length further improves those using profile and RSA. The optimal feature set includes all features with an area under curve of 0.75.

3.2.2 LOOCV accuracy

We used the LOOCV procedure to estimate the accuracy of individually trained Levels 1 and 2 SVM models on the development set of 52 protein chains. All models were trained based on the observed information as feature inputs. The selected Level 1 model attains an accuracy of 66%, sensitivity of 67% and MCC of 0.45. We computed the Cd after applying Level 1 and found an approximately 3-fold increase from 0.4% to 1.1%, which was also equivalent to 79% reduction of contact pair candidates for Level 2 prediction. This Level 1 model was then combined with a Level 2 model to form a two-level system for comparison with direct prediction (L2 only). Contact pair prediction accuracies of direct and two-level systems estimated by LOOCV are shown in Table 6S of Supplementary Material. The contact prediction accuracy by direct prediction is 10%; and 33% if one turn around actual contacts is allowed (δ = 4). This is outperformed by two-level prediction at 13% and 38%. The improvement in contact pair prediction by the two-level method is around 3% (P-value = 2.4e-6).

We also compared contact prediction accuracy across different groups containing protein chains of varied TMH number as listed in Table 7S of Supplementary Material. Generally, contact prediction accuracy diminishes as the number of TMH increases by comparing the four groups, with an exception of Group 3 (7–9 TMHs) which has an accuracy of 31%. Furthermore, the contact prediction accuracy for proteins of seven TMHs is 38%. Since we reduced redundant or close homologs during LOOCV as described in Section 2, our results suggest that these proteins may have structurally conserved features that can be predicted more reliably.

3.3 Prediction accuracy of the independent test set

For an external validation and a second comparison of direct and two-level models trained on parameters optimized by LOOCV, we evaluated contact prediction accuracy on the independent test set. To avoid overestimation of accuracy, we removed protein chains from training if they appeared to be close homologs to the tested protein after BLAST alignment (E-value < 1e-4). In Table 1, we show contact residue prediction accuracy of Level 1 using predicted or observed information from TM topology and RSA. This comparison serves to illustrate the difference in prediction accuracy between a real and an idealized case. Evaluated on the independent test set, using both types of information resulted in a similar level of sensitivity around 70%, but a higher accuracy of 67% and MCC of 0.47 if observed information was used. This comparison implies that better TM topology and RSA prediction methods will contribute to contact prediction. In both cases, by adding a Level 1 model which filtered out predicted non-contact residues, a large fraction contact pair candidates (∼80%) was reduced for subsequent Level 2 prediction and Cd was also increased by 3-fold.

Table 1.

Contact residue prediction accuracy of the independent test set

Methods Accuracy (%) Sensitivity (%) MCC L2 input (%)
TMhitL1Pred 44.8 (±6.4) 68.9 (±3.2) 0.23 (±0.05) 19.2
TMhitL1Obs 66.5 (±5.5) 70.6 (±2.1) 0.47 (±0.03) 21.2
Open in a new tab

The standard error (SEboot) estimated by bootstrapping follows the ‘±’ sign.

L2 Input (%) denotes the remaining contact pair candidates as input for prediction in L2.

In Table 2, we compare contact pair prediction using two-level TMhit and the direct prediction method (L2 only). As expected, using observed information improves the accuracy compared with those obtained from predicted information. A large improvement (6–8%) can be seen using observed information in both direct and two-level methods when one turn around the contacts is allowed. Among all models, best contact prediction accuracy (16%) is obtained using observed information by the two-level TMhit. The IMP prediction is ∼43-fold. Consistent with the results from LOOCV on the development set, the two-level method improves the direct method with predicted or observed information by ∼3% with P-values of 3.9e-3 and 6.9e-3, respectively. Through our evaluations, the results from both LOOCV and independent test show that using the two-level model leads to not only a substantial reduction of contact pair candidates for prediction, but also higher accuracy independent of the source of information.

Table 2.

Contact pair prediction accuracy of direct prediction and two-level models on the independent test set

Methods Contact pair prediction
 δ-analysis (|δ| = 4)
Accuracy (%)
 IMP P-value Accuracy (%)
Direct prediction
    TMhitL2 onlyPred 9.8 (±4.0) 47/480 26.4 1.2e-57 30.6 (±7.8)
    TMhitL2 onlyObs 12.7 (±4.9) 61/480 34.2 1.6e-72 38.5 (±7.3)
Two-level model
    TMhit Pred 12.5 (±4.8) 60/481 33.7 5.4e-80 34.8 (±6.5)
    TMhit Obs 16.0 (±4.5) 77/481 43.1 1.1e-99 41.2 (±7.2)
Open in a new tab

The standard error (SEboot) estimated by bootstrapping follows the ‘±’ sign.

3.4 Comparison of contact pair prediction accuracy with existing methods

We further compare contact pair prediction accuracy using direct and two-level TMhit with existing methods based on CMA. In Table 3, we compare with the best three single representatives, namely, McBASC-McLachlan (Olmea and Valencia, 1997), OMES KASS (Kass and Horovitz, 2002) and ELSC (Dekker et al., 2004), plus two consensus methods implemented by HelixCorr (Fuchs et al., 2007). We evaluated our method on the same dataset with identical helical assignment from structures and contact definition as in HelixCorr. Specifically, HelixCorr employed only one side-chain distance constraint of 5.5Å between any two heavy atoms. Using the above definition, the Cd is 2.0%, about four times of that (0.5%) by our criteria. In order to remove bias, we discarded redundant proteins from the development set and retrained the Levels 1 and 2 predictors. Two-level TMhit obtains an overall accuracy of 31% in contact pair prediction while direct prediction (L2 only) attains an accuracy of 24%. Compared with the CMA-based methods in HelixCorr, direct or two-level TMhit outperforms the single methods by at least 2-folds, which is ∼14% and 21% in contact pair prediction, respectively. TMhit also compares favorably with the best consensus methods, with a difference of 19% in predicting inter-helical contacts. When up to one turn is allowed from the observed contact (δ = 4), TMhit achieves 57% in accuracy which is comparable with the consensus methods by HelixCorr. From this comparison, not only two-level TMhit compares favorably against several CMA-based methods, it also improves the direct method by an even larger margin given a more relaxed contact definition.

Table 3.

Comparison of contact pair prediction accuracy with CMA methods using observed information and contact definitions in HelixCorr

Methods Contact pair prediction
 δ-analysis (|δ| = 4)
Accuracy (%) P-value Accuracy (%)
TMhit 31.0 (±7.0) 2.2e-109 56.8(±7.5)
TMhitL2 only 23.6 (±7.5) 3.2e-71 48.6(±8.0)
McBASC McLachlan 10.0 6.5e-17 46.0
OMES KASS 9.0 1.2e-14 50.0
ELSC 10.0 6.5e-17 41.0
CONSENSUS-14 12.0 1.4e-53 55.0
CONSENSUS-R-5 11.0 3.6e-42 56.0
Open in a new tab

The standard error (SEboot) estimated by bootstrapping follows the ‘±’ sign.

3.5 Predicting helix–helix interactions from contacts

Inter-residue contacts when examined collectively between secondary structure elements provide the basis of molecular interactions. Here, the contacts predicted between TM helices can be used to predict helix–helix interactions. Using our definition of helix–helix interactions and observed topology, there are totally 85 interacting helical pairs from 14 polytopic protein chains in the independent test set. In Table 4, we calculate the accuracy of helix–helix interactions using the predicted contacts by TMhit. The prediction accuracy, sensitivity and specificity reflect how much contact prediction can influence helix–helix interaction prediction based on the threshold. T denotes the minimum number of predicted contact pairs required to classify any helical pair as interacting partners. For example, when T=3, at least three unique contact pairs must be predicted on an interacting helical pairs. At this cut-off, the accuracy, sensitivity and specificity rates are 56%, 40% and 89%, respectively. As the threshold for contact pairs increases, the accuracy and specificity of helix–helix interaction also increases, at the expense of sensitivity. Depending on the threshold chosen, best accuracy and sensitivity can be achieved around 82% and 72%, respectively.

Table 4.

Prediction performance in helix–helix interaction using TMhit on the independent test set

Thresholds (T) Accuracy (%) Sensitivity (%) Specificity (%)
1 contact pair 39.1 (±5.0) 71.8 (±4.1) 59.4 (±4.1)
2 contact pairs 45.4 (±6.1) 51.8 (±7.1) 77.4 (±3.2)
3 contact pairs 55.7 (±7.3) 40.0 (±8.2) 88.5 (±1.8)
4 contact pairs 61.4 (±6.8) 31.8 (±6.7) 92.7 (±1.2)
5 contact pairs 66.7 (±6.4) 25.9 (±6.6) 95.3 (±1.2)
6 contact pairs 76.0 (±7.2) 22.4 (±5.4) 97.4 (±1.1)
7 contact pairs 77.3 (±6.9) 20.0 (±4.8) 97.9 (±1.2)
8 contact pairs 82.4 (±8.3) 16.5 (±4.3) 98.7 (±1.0)
Open in a new tab

The standard error (SEboot) estimated by bootstrapping follows the ‘±’ sign.

3.6 Effect of hierarchical framework on contact density and prediction accuracy

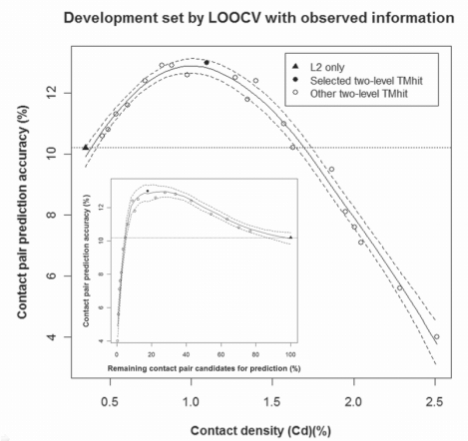
As described in Sections 3.2 and 3.3, the two-level architecture evaluated by LOOCV and independent test reveals that higher contact prediction accuracy can be achieved by eliminating a large fraction of contact pair candidates for prediction in Level 2. Here, we further characterize the relationship between Cd and prediction accuracy under the two-level framework. In Figure 2, we compare contact prediction accuracy as a function of Cd obtained from direct prediction and twenty two-level prediction models based on the LOOCV results from the development set. All two-level models were constructed by combining the identical direct method with a chosen Level 1 model of different sensitivity or reduction rate for contact pair candidates. Clearly, a higher reduction rate in Level 1 leads to screening out more non-contact residues while preserving observed contacts among contact pair candidates for prediction and Cd is increased accordingly. To gain insight into the relationship, we performed non-linear local regression to obtain the estimated regression curve. The accuracy of the direct method is shown as a dotted horizontal line for comparison. Most notably, many two-level models attain equal or higher accuracy than the direct method with up to a 5-fold increase in Cd, from 0.34% to 1.62%. Figure 2 inset shows a similar trend when we examine prediction accuracy as a function of remaining contact pair candidates. Two-level models improve the direct method with at most 95% reduction (or 5% remaining) of contact pair candidates. However, beyond this point, the accuracy of two-level models falls quickly because too many contact residues have been filtered out. We also observe the same trend in the independent test set using predicted or observed information as shown in Figures 5S and 6S of Supplementary Material. Thus, our analysis shows that given a properly trained Level 1 classifier and a suitable choice of reduction rate by enriching the proportion of observed contacts, the proposed two-level framework may very likely improve prediction accuracy compared to the direct method.

Fig. 2.

Fig. 2.

Open in a new tab

Comparison of contact pair prediction accuracy as a function of Cd by direct and two-level models on the development set using observed information (topology and RSA). Direct prediction (L2 only) is shown in filled triangle and its accuracy is shown in a dotted horizontal line. Two-level models are shown in filled (selected) or empty circles (others). The regression curve was estimated from all models (smoothing parameter α = 0.8) using the LOCFIT package (Loader, 2004) and the dashed line indicates the confidence band at 95% confidence limits. Inset: comparison of prediction accuracy as a function of percent remaining contact pair candidates for prediction by Level 2.

4 DISCUSSION

In this work, we introduce a novel two-level framework based on machine learning to predict residue contacts and infer interactions between TM helices. First, we estimate the propensities of residues or pairs in contact and incorporate them as input features for prediction. One notable feature in our calculation is the introduction of empirical Bayes shrinkage estimation which accounts for randomness due to the scarcity of data. Essentially, the shrinkage estimators provide more adjustment for residues or pairs with low counts, and otherwise for high counts. Our estimation of residue contact propensities carries a medium to high level of correlation (Pearson's r = 0.48 and Spearman's ρ = 0.65) with that by Eilers et al. (2002). In particular, high correspondence is found for small, polar and charged residues. Recent works by Gimpelev et al. (2004) and Walters and DeGrado (2006) also found a preference of Ala and Gly in helix-packing sequence motifs. Another confirmation by our work also includes several overrepresented contacts pairs between polar–polar residues. The role of polar residues in a membrane milieu has been found to be of particular importance to folding of TM domains via networks of hydrogen bonds (Zhou et al., 2001). These polar–polar residue contacts do not only contribute to stability in TM helix–helix interactions but may also confer to functionally important sites in the protein interior.

Through extensive benchmarks using cross validation, independent testing and comparison with existing methods, we establish that the proposed two-level architecture has an advantage over direct prediction of contact pairs in both computational complexity and accuracy. Combined with a Level 1 predictor that effectively screens out non-contacts on a per residue basis, the subsequent prediction in Level 2 is enriched in Cd. Punta and Rost (2005) have reported that contact prediction becomes more difficult with decreasing Cd. Therefore, from this perspective, two-level predictions may improve direct predictions. As an example shown in Figure 7S of Supplementary Material, we compare the predicted contact maps of a cytochrome c oxidase (PDB ID: 1qleC) (Harrenga and Michel, 1999) obtained from direct and two-level prediction. Clearly, the two-level prediction captures most of the helix–helix interactions while the direct prediction fails in doing so. In addition, the two-level prediction produces a reduced number of falsely predicted contacts. Overall, the prediction by the two-level method more closely resembles the observed contact map.

Furthermore, the two-level framework is also attractive from the perspective of implementation. By separating the prediction into two levels, relevant input features can be applied in each level, thus the accuracy of each level can be improved more effectively. Since we trained each level separately, existing direct prediction methods can be easily extended by adding a Level 1 predictor to mimic the hierarchical system.

As observed in Figure 2, the prediction accuracy suffers when too many contacts have been filtered out, which is not desirable for length-based contact prediction. Thus, there is a trade-off between the reduction rate and sensitivity with respect to Level 1. Interestingly, it has been suggested that roughly one contact for every eight residues is sufficient to reconstruct tertiary structures close to native folds in soluble proteins (Li et al., 2004). Although at present this number is unclear for membrane proteins, this estimate provides a clue to adjusting the level of reduction rate in Level 1.

Due to the experimental difficulties in solving membrane protein structures, the available data accumulate at a slow pace. Hence, computational prediction and modeling play an important role in elucidating the structure genomics of membrane proteins. To gain insights into membrane protein folding, interactions between TM helices must be correctly predicted. This work may complement previous helix-packing studies and facilitate structure prediction. A recent work by Yin et al. (2007) has shown that novel membrane-spanning peptides targeted to TM helices can be designed in silico. In relation to the above work, TMhit may be applied to select potentially interacting peptides and key residues for improving the binding specificity by protein engineering.

Funding: Thematic Program of Academia Sinica (grant number AS95ASIA03); National Science Council (grant number NSC 97-2627-P-001-004, in part).

Conflict of Interest: none declared.

Supplementary Material

[Supplementary Data]
btp114_index.html (655B, html)

REFERENCES

  1. Altschul SF, et al. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Berman HM, et al. The protein data bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bernsel A, et al. Prediction of membrane-protein topology from first principles. Proc. Natl Acad. Sci. USA. 2008;105:7177–7181. doi: 10.1073/pnas.0711151105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Beuming T, Weinstein H. A knowledge-based scale for the analysis and prediction of buried and exposed faces of transmembrane domain proteins. Bioinformatics. 2004;20:1822–1835. doi: 10.1093/bioinformatics/bth143. [DOI] [PubMed] [Google Scholar]
  5. Casella G. An introduction to empirical bayes data analysis. Am. Stat. 1985;39:83–87. [Google Scholar]
  6. Chandonia JM, et al. The ASTRAL Compendium in 2004. Nucleic Acids Res. 2004;32:D189–D192. doi: 10.1093/nar/gkh034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chang CC, Lin CJ. LIBSVM: a library for support vector machines, 2001. 2001 Available at http://www.csie.ntu.edu.tw/∼cjlin/libsvm(last accessed date January 19, 2009) [Google Scholar]
  8. Chothia C, et al. Helix to helix packing in proteins. J. Mol. Biol. 1981;145:215–250. doi: 10.1016/0022-2836(81)90341-7. [DOI] [PubMed] [Google Scholar]
  9. DeGrado WF, et al. How do helix–helix interactions help determine the folds of membrane proteins? Perspectives from the study of homo-oligomeric helical bundles. Protein Sci. 2003;12:647–665. doi: 10.1110/ps.0236503. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Dekker JP, et al. A perturbation-based method for calculating explicit likelihood of evolutionary co-variance in multiple sequence alignments. Bioinformatics. 2004;20:1565–1572. doi: 10.1093/bioinformatics/bth128. [DOI] [PubMed] [Google Scholar]
  11. Eilers M, et al. Comparison of helix interactions in membrane and soluble alpha-bundle proteins. Biophys. J. 2002;82:2720–2736. doi: 10.1016/S0006-3495(02)75613-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Frishman D, Argos P. Knowledge-based protein secondary structure assignment. Proteins. 1995;23:566–579. doi: 10.1002/prot.340230412. [DOI] [PubMed] [Google Scholar]
  13. Fuchs A, et al. Co-evolving residues in membrane proteins. Bioinformatics. 2007;23:3312–3319. doi: 10.1093/bioinformatics/btm515. [DOI] [PubMed] [Google Scholar]
  14. Grana , et al. CASP6 assessment of contact prediction. Proteins. 2005;61:214–224. doi: 10.1002/prot.20739. [DOI] [PubMed] [Google Scholar]
  15. Gimpelev M, et al. Helical packing patterns in membrane and soluble proteins. Biophys. J. 2004;87:4075–4086. doi: 10.1529/biophysj.104.049288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Harrenga A, Michel H. The cytochrome c oxidase from Paracoccus denitrificans does not change the metal center ligation upon reduction. J. Biol. Chem. 1999;274:33296–33299. doi: 10.1074/jbc.274.47.33296. [DOI] [PubMed] [Google Scholar]
  17. Izarzugaza JM, et al. Assessment of intramolecular contact predictions for CASP7. Proteins. 2007;69(Suppl 8):152–158. doi: 10.1002/prot.21637. [DOI] [PubMed] [Google Scholar]
  18. Jones DT. Improving the accuracy of transmembrane protein topology prediction using evolutionary information. Bioinformatics. 2007;23:538–544. doi: 10.1093/bioinformatics/btl677. [DOI] [PubMed] [Google Scholar]
  19. Kass I, Horovitz A. Mapping pathways of allosteric communication in GroEL by analysis of correlated mutations. Proteins. 2002;48:611–617. doi: 10.1002/prot.10180. [DOI] [PubMed] [Google Scholar]
  20. Langosch D, Heringa J. Interaction of transmembrane helices by a knobs-into-holes packing characteristic of soluble coiled coils. Proteins. 1998;31:150–159. doi: 10.1002/(sici)1097-0134(19980501)31:2<150::aid-prot5>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
  21. Li AJ, Nussinov R. A set of van der Waals and coulombic radii of protein atoms for molecular and solvent-accessible surface calculation, packing evaluation, and docking. Proteins. 1998;32:111–127. [PubMed] [Google Scholar]
  22. Li W, Godzick A. Cd-hit: a fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics. 2006;22:1658–1659. doi: 10.1093/bioinformatics/btl158. [DOI] [PubMed] [Google Scholar]
  23. Li W, et al. Application of sparse NMR restraints to large-scale protein structure prediction. Biophys. J. 2004;87:1241–1248. doi: 10.1529/biophysj.104.044750. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lo A, et al. Enhanced membrane protein topology prediction using a hierarchical classification method and a new scoring function. J. Proteome Res. 2008;7:487–496. doi: 10.1021/pr0702058. [DOI] [PubMed] [Google Scholar]
  25. Loader C. Smoothing: local regression techniques. In: Gentle J, editor. Handbook of Computational Statistics. Heidelberg: Springer-Verlag; 2004. pp. 540–560. [Google Scholar]
  26. Matthews BW. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. Biophys. Acta. 1975;405:442–451. doi: 10.1016/0005-2795(75)90109-9. [DOI] [PubMed] [Google Scholar]
  27. Mehta CR, Patel NR. Exact inference in categorical data. Biometrics. 1997;53:112–117. [Google Scholar]
  28. Miller CS, Eisenberg D. Using inferred residue contacts to distinguish between correct and incorrect protein models. Bioinformatics. 2008;24:1575–1582. doi: 10.1093/bioinformatics/btn248. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Mitchell TM. Machine Learning. Boston, MA: WCB-McGraw-Hill; 1997. pp. 96–97. [Google Scholar]
  30. Olmea O, Valencia A. Improving contact predictions by the combination of correlated mutations and other sources of sequence information. Fold Des. 1997;2:S25–S32. doi: 10.1016/s1359-0278(97)00060-6. [DOI] [PubMed] [Google Scholar]
  31. Ortiz AR, et al. Ab initiofolding of proteins using restraints derived from evolutionary information. Proteins. 1999;(Suppl 3):177–185. doi: 10.1002/(sici)1097-0134(1999)37:3+<177::aid-prot22>3.3.co;2-5. [DOI] [PubMed] [Google Scholar]
  32. Ouyang Z, Liang J. Predicting protein folding rates from geometric contact and amino acid sequence. Protein Sci. 2008;17:1256–1263. doi: 10.1110/ps.034660.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Park Y, et al. Prediction of the burial status of transmembrane residues of helical membrane proteins. BMC Bioinformatics. 2007;8:302. doi: 10.1186/1471-2105-8-302. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Popot JL, Engelman DM. Helical membrane protein folding, stability, and evolution. Annu. Rev. Biochem. 2000;69:881–922. doi: 10.1146/annurev.biochem.69.1.881. [DOI] [PubMed] [Google Scholar]
  35. Punta M, Rost B. PROFcon: novel prediction of long-range contacts. Bioinformatics. 2005;21:2960–2968. doi: 10.1093/bioinformatics/bti454. [DOI] [PubMed] [Google Scholar]
  36. Russ WP, Engelman DM. The GxxxG motif: a framework for transmembrane helix-helix association. J. Mol. Biol. 2000;296:911–919. doi: 10.1006/jmbi.1999.3489. [DOI] [PubMed] [Google Scholar]
  37. Sal-Man N, et al. Specificity in transmembrane helix-helix interactions mediated by aromatic residues. J. Biol. Chem. 2007;282:19753–19761. doi: 10.1074/jbc.M610368200. [DOI] [PubMed] [Google Scholar]
  38. Samanta U, et al. Quantifying the accessible surface area of protein residues in their local environment. Protein Eng. 2002;15:659–667. doi: 10.1093/protein/15.8.659. [DOI] [PubMed] [Google Scholar]
  39. Schlessinger A, et al. Natively unstructured regions in proteins identified from contact predictions. Bioinformatics. 2007;23:2376–2384. doi: 10.1093/bioinformatics/btm349. [DOI] [PubMed] [Google Scholar]
  40. Shackelford G, Karplus K. Contact prediction using mutual information and neural nets. Proteins. 2007;69(Suppl 8):159–164. doi: 10.1002/prot.21791. [DOI] [PubMed] [Google Scholar]
  41. Tusnady GE, et al. PDB_TM: selection and membrane localization of transmembrane proteins in the protein data bank. Nucleic Acids Res. 2005;33:D275–D278. doi: 10.1093/nar/gki002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Tusnady GE, et al. TOPDB: topology data bank of transmembrane proteins. Nucleic Acids Res. 2008;36:D234–D239. doi: 10.1093/nar/gkm751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Walters RF, DeGrado WF. Helix-packing motifs in membrane proteins. Proc. Natl Acad. Sci. USA. 2006;103:13658–13663. doi: 10.1073/pnas.0605878103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Yin H, et al. Computational design of peptides that target transmembrane helices. Science. 2007;315:1817–1822. doi: 10.1126/science.1136782. [DOI] [PubMed] [Google Scholar]
  45. Yuan Z, et al. Predicting the solvent accessibility of transmembrane residues from protein sequence. J. Proteome Res. 2006;5:1063–1070. doi: 10.1021/pr050397b. [DOI] [PubMed] [Google Scholar]
  46. Zhou FX, et al. Polar residues drive association of polyleucine transmembrane helices. Proc. Natl Acad. Sci. USA. 2001;98:2250–2255. doi: 10.1073/pnas.041593698. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
btp114_index.html (655B, html)
btp114_1.pdf (779.7KB, pdf)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES