Folding kinetics of the human prion protein probed by temperature jump

Abstract

Temperature-jump perturbation was used to examine the relaxation kinetics of folding of the human prion protein. Measured rates were very fast (≈3,000 s⁻¹), with the extrapolated folding rate constant at ≈20 °C in physiological conditions reaching 20,000 s⁻¹. By a mutational analysis of core residues, we found that only 2, on the interface of helices 2 and 3, have significant ϕ-values in the transition state. Interestingly, a mutation sandwiched between the above 2 residues on the helix–helix contact interface had very little effect on the overall free energy of folding but led to the formation of a monomeric misfolded state, which had to unfold to acquire the native PrP^C conformation. Another mutation that led to a marked destabilization of the native fold also formed a misfolded intermediate, but this was aggregation-prone despite the native state of this mutant being soluble. Taken together, the data imply that this fast-folding protein has a transition state that is not compact (m value analysis gives a β_t value of only 0.3) but contains a developing nucleus between helices 2 and 3. The fact that a mutation in this nucleus had a negligible effect on stability but still led to formation of aberrant conformations during folding implies an easily perturbed folding mechanism. It is notable that in inherited forms of human prion disease, where point mutations produce a lethal dominant condition, 20 of the 33 amino acid replacements occur in the helix-2/3 sequence.

To date, ≈25 human diseases have been described that are characterized by the deposition of denatured proteins within animal tissues (1). However, among these, only the prion diseases produce self-propagating infectious material. The common theme of prion diseases, as exemplified by bovine spongiform encephalopathy in cattle and Creutzfeldt–Jakob Disease, Gerstmann-Sträussler-Scheinker Syndrome, and fatal familial insomnia in humans, is their association with a slow buildup of a misfolded protein (PrP^Sc) in the brain (2, 3). This deposition is accompanied by a loss of neuronal cells and the characteristic spongiform change. The result of this neurodegenerative process is a debilitating, dementing, and invariably fatal disease.

The prion protein in its normal or cellular form (PrP^C) is ubiquitously expressed, with the highest levels in the central nervous system, in lymphatic tissue, and at neuromuscular junctions. It is a glycosylated, cell-surface protein held in situ by a glyco-lipid anchor (4). The misfolded, pathogenic or “scrapie” form (PrP^Sc) is covalently identical to PrP^C (4, 5) but has a radically different conformation that renders it susceptible to aggregation (6). Although PrP^Sc has never been purified to homogeneity, fractions enriched for infectivity contain a high proportion of PrP (7). It is well established that prion diseases arise by 1 of 3 processes (2, 3, 8). In outline, all 3 etiological routes can be described with reference to a single, general model in which the native PrP^C molecule is in equilibrium with the rare PrP^Sc-like conformational isoform. PrP^Sc can then be stabilized by complimentary association with a like molecule or can actively convert PrP chains to a like conformation. Assembly then continues until a stable seed is formed. Such structures can continue to grow by accretion and can divide by breakage into smaller, infectious units. This gross mechanism explains the observation that prion diseases occur by inherited mutations that destabilize the cellular form and therefore predispose it to conversion to PrP^Sc or by iatrogenic or dietary infection with PrP^Sc. Sporadic cases, in which the cause is unknown, can be explained within the above paradigm either by somatic mutation or by a rare, stochastic conversion of the wild-type protein to the PrP^Sc conformation.

The involvement of a conformational shift away from the PrP^C conformation in prion pathogenesis, emphasizes the need to understand the structure and dynamic behavior of the cellular form and the factors that influence the conversion process. We have previously expressed and purified recombinant forms of human PrP to study in vitro processes that might lead to the formation of PrP^Sc-like structures (9–11), and we have investigated the conformational plasticity of the PrP^C structure by equilibrium hydrogen–deuterium exchange kinetics (12).

In the study we describe here, we wished to measure the kinetics of folding and unfolding of human PrP^C. In particular, we wanted to elucidate the effects of conservative core truncation mutations on these processes and so produce a classical ϕ-value analysis. Initially, we attempted stopped-flow rapid-mixing techniques to capture the rates of reaction but found that the transients were too fast. However, by poising the equilibrium between the folded and unfolded states, at a range of denaturant concentrations, we were able to measure relaxation rate constants accurately using temperature perturbation.

Results

Thermodynamic Properties of PrP.

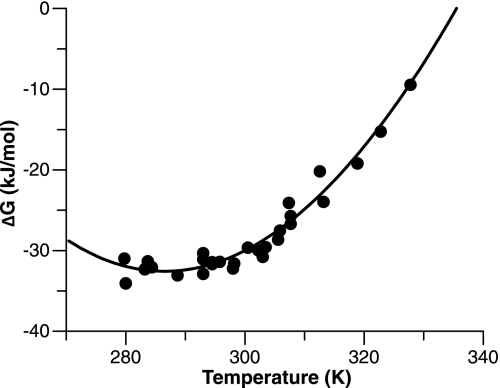
The sensitivity to temperature of the reversible folding equilibrium of wild-type human PrP^C (91–231) was determined by guanidinium hydrochloride (GuHCl) denaturation at temperatures between 5 °C and 55 °C. The resultant free energies of folding were plotted against temperature, as shown in Fig. 1 and the classical thermodynamic parameters of ΔH, ΔS, and ΔC_P extracted by fitting the data to an integrated form of the van't Hoff equation (see Eq. 2 in Materials and Methods). Importantly, this information can be used to approximate the extent of the equilibrium shift when the temperature is jumped. For instance, if the system is poised at 15 °C, a jump of 6 °C will shift the system toward the unfolded state by ≈1 kJ/mol. In practice, this means that at a denaturant concentration that balances the concentrations of the folded and unfolded states (i.e., K_(F/U) = 1.0), an increase of ≈10% in the population of the unfolded state would be expected.

Fig. 1.

Temperature dependence of PrP stability. The free energy (ΔG) of PrP folding was calculated from equilibrium unfolding transitions monitored by the CD signal, as described in Materials and Methods. Error bars are omitted for clarity, however, all errors in the ΔG values are in the range 1.0–1.3 kJ/mol. The curve represents a fit to Eq. 2 (see Materials and Methods), which generates estimates of the enthalpy (ΔH), entropy (ΔS), and heat capacity (ΔC_P) changes of folding. Calculated values at 25 °C are: ΔH = −124.8 ± 6.4 kJ mol⁻¹, ΔS = −0.32 ± 0.02 kJ mol⁻¹, ΔC_P = −8.21 ± 0.79 kJ K⁻¹ mol. According to the formula of Robertson and Murphy (25), who used a dataset of 49 proteins, the expected heat capacity change upon unfolding for a protein of given length can be estimated by the formula: ΔC_P = ((No. of residues × 0.062) − 0.53) measured in units of kJ/K/mol. There are 104 residues in the structured domain of PrP^C; hence, the expected change is 5.9 kJ/K/mol.

Generating an Optical Signal.

Such a perturbation would be sufficient to measure the temperature-jump kinetics of the system, as long as there is a strong signal change in the folding/unfolding transition. Unfortunately, wild-type human PrP (91–231) showed little signal change, and, in addition, its indole fluorescence was weak. However, when we replaced phenylalanine-198 by tryptophan, to give PrP F198W (91–231), and truncated the unstructured N terminus to give PrP F198W (119–231), the resultant species showed excellent optical properties. The former modification introduced an indole group, the fluorescence of which was enhanced by a factor of 4 upon folding, and the truncation of the unfolded terminus removed the unresponsive tryptophan-99. Neither of these modifications alters the stability of the molecule to a measurable extent [see supporting information (SI) Text and Table S1], and the resultant molecule has exactly coincident and reversible CD and fluorescence signals in denaturation experiments (see SI Text and Fig. S1), showing the 2-state nature of the folded-to-unfolded equilibrium. Interestingly, the probe mutation that was used by Glockshuber and colleagues to provide a folding signal for the mouse protein (F175W) (13) was found to block folding when introduced into human PrP (see SI Text).

Core Mutants and Their Stability.

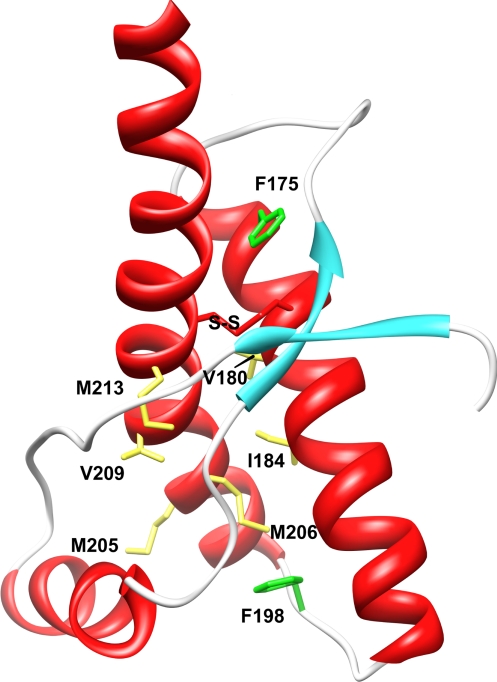
A series of hydrophobic truncation mutations were introduced into human PrP to probe the folding reaction by ϕ-value analysis, as illustrated in Fig. 2. The amino acids chosen have buried hydrocarbon side chains, they are widely spread through the protein, and, between them, probe local environments covering all of the major structural elements of PrP. Residues F175, V180, and I184 are all located on helix 2. F175 is close to the β-sheet region, whereas V180 and I184 make extensive contacts with helix 3. M205, M206, V209, and M213 are all on helix 3. M206 is in contact with several helix 2 residues, and M205, V209, and M213 make interactions with helix 1 and adjoining loop regions. The effect of these mutations on protein stability is summarized in Table 1.

Fig. 2.

Position of PrP hydrophobic core mutations and native disulfide bond. Schematic representation of the human PrP (121–231) peptide backbone, showing the location of the residues that were truncated for ϕ-analysis and the position of phenylalanine residues mutated to provide tryptophan probes.

Table 1.

Thermodynamic parameters of mutant PrPs

Core mutation	ΔG, kJ mol−1	ΔΔG, kJ mol−1	m, kJ mol−1 M−1	Midpoint molar activity
WT	−30.99 ± 0.85		−6.32 ± 0.16	2.00 ± 0.01
F175A	−28.51 ± 0.70	2.48 ± 1.10	−6.12 ± 0.16	1.91 ± 0.09
V180A	−26.10 ± 0.93	4.89 ± 1.26	−6.70 ± 0.27	1.59 ± 0.01
I184V	−30.12 ± 0.46	0.87 ± 0.97	−6.58 ± 0.09	1.87 ± 0.003
M205A	−18.06 ± 0.80	12.92 ± 1.17	−4.43 ± 0.19	1.67 ± 0.01
M206A	−24.72 ± 1.12	6.27 ± 1.41	−6.33 ± 0.24	1.59 ± 0.01
V209A	−29.74 ± 0.53	1.25 ± 1.01	−6.02 ± 0.10	2.02 ± 0.004
M213A	−17.94 ± 0.70	13.05 ± 1.11	−5.13 ± 0.23	1.43 ± 0.02

The free energy change (ΔG), degree of destabilization (ΔΔG), cooperativity (m) and midpoint (T_m) of the equilibrium unfolding transition for each protein were calculated by using a 2-state model of folding. Unfolding was induced by GuHCl and monitored by CD at 222 nm, at 21.5 °C and pH 8.0. The folding midpoint is expressed as molar denaturant activity, derived from GuHCl concentration as described in SI Text.

Temperature-Jump Relaxation Kinetics.

For PrP F198W (119–231) and for most of the truncation mutants, the fluorescence transients observed are well described by single-exponential processes (see Fig. S2). There are 2 exceptions: M205A and V209A. The former mutant is described in detail below. The latter was omitted from the kinetic study because of the consistent and repeatable lack of a signal change when the equilibrated protein was temperature-jumped despite the fact that it showed a freely reversible equilibrium folding transition (see Table 1).

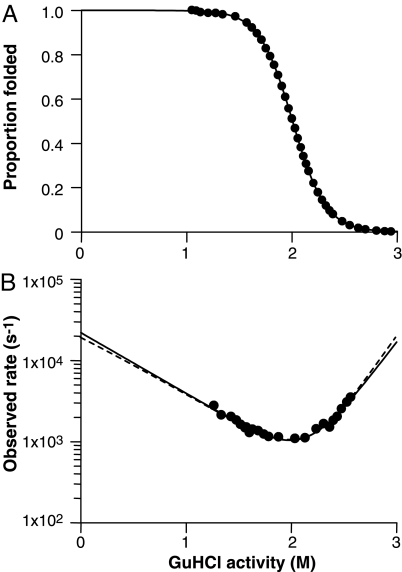
There was a limit to the range of denaturant activities (see SI Text for the conversion to denaturant activity) within which we could record a measurable change in signal in response to the temperature jump. For the wild-type molecule, this was 1.3–2.6 M activity (1.6–3.8 M concentration). Outside this window, the equilibrium was either too far toward the folded or too far toward the unfolded state to lead to a perceptible change in concentrations as the equilibrium was perturbed (see Fig. 3). This inevitable limitation meant that we could not look for transient intermediates in the system that are populated at denaturant activities <1.3 M. Superimposed on the rate plot shown in Fig. 3B are 2 analytical fits. The continuous line is a constrained fit using the values of K_F/U and m_U-F from the equilibrium data shown in Fig. 3A (i.e., the fit must fulfil the criteria k_f = k_u·K_F/U and −m_t = m_U-F − m_U). In this latter fit, the kinetic data are used to define only 2 parameters with the well-defined equilibrium unfolding curve supplying the other 2. Across the whole dataset, this was considered to provide better estimates of the kinetic constants, hence the values shown in Table 2 are calculated in this way.

Fig. 3.

Folding kinetics of human PrP F198W (119–231). Equilibrium unfolding (A) and folding kinetics (B) of human PrP F198W (119–231), recorded at pH 8 and 21.5 °C and fitted to a 2-state model of folding (solid line). The dashed line represents a fit constrained by using the value for K_W obtained from equilibrium experiments.

Table 2.

Kinetic folding parameters of wild-type and mutant PrPs

PrP mutant	kF, s−1 (× 103)	kU, s−1	KW (× 103)	mF	mU	βt	ϕ
WT	22.1 ± 6.0	0.14 ± 0.05	158 ± 12	−1.7 ± 0.2	3.9 ± 0.4	0.30 ± 0.06
F175A	17.8 ± 1.6	0.11 ± 0.07	161 ± 10	−2.1 ± 0.1	4.0 ± 0.1	0.34 ± 0.03	–
V180A	10.3 ± 0.8	0.32 ± 0.10	32.4 ± 0.4	−2.3 ± 0.1	3.6 ± 0.1	0.39 ± 0.03	0.48
I184V*	17.3 ± 1.7	0.13 ± 0.02	133 ± 6	−1.6 ± 0.3	3.9 ± 0.5	0.29 ± 0.10	–
M205A*	13.5 ± 3.7	8.6 ± 0.03	1.57 ± 0.20	−1.5 ± 0.1	2.9 ± 0.2	0.34 ± 0.04	0.11
M206A	4.1 ± 0.4	0.31 ± 0.13	13.2 ± 1.1	−1.3 ± 0.1	2.8 ± 0.1	0.32 ± 0.03	0.68
M213A	10.7 ± 1.0	20.5 ± 2.53	0.52 ± 0.03	−1.6 ± 0.1	2.7 ± 0.1	0.37 ± 0.03	0.13

Folding kinetics of human PrP F198W (119–231) and 7 of the truncation mutants were measured at pH 8.0 after a 12-kV jump to 21.5 °C. Note that the parameters for m_F and m_U were not calculated for PrP I184V as for the other mutants because of the different analytical methods used for the 3-state kinetics (see Eqs. 3 and 4 in Materials and Methods). The equilibrium constants (K_W) are taken from equilibrium denaturation curves and were used as constraints in fitting rate plots. Similarly the equilibrium m values were used as constraints in fitting the kinetic constants m_F and m_U.

*The I184V mutant folded through an intermediate state that was more compact than the rate-limiting transition state. In these cases, the value for k_F is virtual and given by the product of the real folding rate and the equilibrium constant K_I/U. For the M205A mutation, the folding limb, the data below a denaturant activity of 1.5 M was removed from the fitting procedure because of the appearance of a precipitate in these conditions.

ϕ-Values.

Table 2 shows that there are 2 residues with large ϕ-values (V180 and M206), both of which are squarely on the interface between helix 2 and helix 3. These residues form the majority of the contact area in the central region of this interaction, and this result implies that this substructure is well developed in the transition state for folding. Residues 205 and 213 have much less significant ϕ-values; the former reports interaction between helix 2 and helix 1, whereas the latter forms an extensive contact with a long surface loop that connects helix 1 with the small β-sheet structure. The data imply that these structures form later in the folding trajectory.

Unorthodox Behavior.

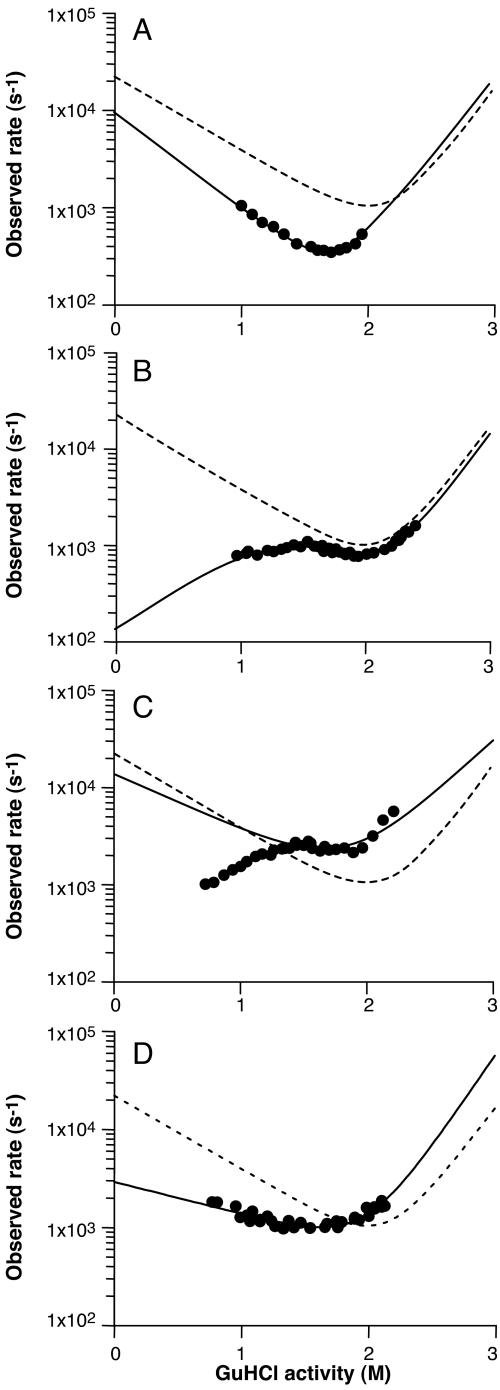
Representative rate plots for 4 core mutants are shown in Fig. 4. The V180A mutant (Fig. 4A) behaved much like the wild type and gave an orthodox chevron plot with a slightly slower folding rate and faster unfolding. However, this plot stands in stark contrast to those representing data from I184V and M205A (Fig. 4 B and C), where there was a clear nonlinearity in the folding limb. For both proteins, the rate of folding began to decrease at denaturant activities less than ≈1.5 M to produce a downwardly curved plot.

Fig. 4.

Comparison of rate plots for parent and representative mutants. Shown are V180A (A), I184V (B), M205A (C), and M206A (D). The dashed line shows the folding of the “wild-type” F198W construct for comparison, with the solid line showing the equilibrium-constrained kinetic fit.

Such downward curvatures can arise by 1 of 2 processes. There might be an inhibitory and rapid interaction of protein chains in the unfolded state that detracts from the proportion of molecules that can undergo the unimolecular folding transition from unfolded to folded. In these circumstances, as the denaturant concentration is reduced, the tendency for chains to interact in the unfolded state is increased, thus incrementally diminishing the folding-competent population. Alternatively, there may be a misfolded, monomeric intermediate state that is in rapid equilibrium with the unfolded ensemble. If this misfolded conformation or collection of conformations is more compact than the productive transition state, then it must unfold before it can pass across this barrier. In these circumstances, the slope of the chevron plot becomes positive at low denaturant activities to give the unorthodox patterns seen in Fig. 4 B and C. The analytical solution to the relaxation behavior of the latter misfolding mechanism is given in Eq. 4 in Materials and Methods.

In the case of the M205A mutant, there was a distinct tendency to form turbid aggregates during temperature-perturbation experiments performed at denaturant activities <1.5 M, and the individual transients in this region were not perfectly exponential. However, in the graph shown in Fig. 4C, the dominant exponential phase is plotted to give an idea of the time scale over which the relaxation occurred. In view of these complicating factors, it seemed inadvisable to analyze the M205A data in terms of Eq. 4. For the M205A data, measurements made below a denaturant activity of 1.5 M were removed from the fitting procedure because of the appearance of a precipitate in these conditions.

The case is quite different for I184V (see Fig. 4B), where there is no turbidity in any of the equilibrated solutions after the perturbation experiments. Also, the possibility that the inhibitory phase of the chevron plot was due to nonnative interactions between unfolded chains was tested by examining the kinetics at a range of protein concentrations, however, we found no concentration dependence of the relaxation rate constants (see SI Text and Fig. S3). In this case, it is valid to use the model that includes the overcompact intermediate, and analysis by this method yields an extrapolated true folding rate of ≈120 s⁻¹ and an equilibrium constant K_I/U of ≈130. In the case of the data reported for the I184V mutant in Table 2, the value for k_F is virtual and given by the product of the real folding rate and the equilibrium constant K_I/U (i.e., k_F = 15,600 s⁻¹). In effect this would be the folding rate if the overcompact intermediate were not populated and the protein folded directly from the unfolded state. The m value of the folding slope for the mechanism that includes the misfolded state is 2.0 (±0.1) rather than the value of −1.6 for the virtual chevron plot shown in Table 2.

Discussion

Previous kinetic studies of PrP folding have shown that at low temperature (5 °C), the human protein folds by way of a populated intermediate (14–16). The rate-limiting conversion of this species into the native state occurs at ≈1,400 s⁻¹, some 14-fold slower than the rate-limiting step at 25 °C measured in our current study. Because we cannot perform perturbation experiments at low denaturant concentrations, it is not possible to detect the presence of such an unstable intermediate by using our higher-temperature data. A major objective of the work of Surewicz and colleagues was to investigate the effects of naturally occurring mutations in PrP that lead to inherited prion disease (15). The broad conclusion was that 2/3 of these stabilized the intermediate, but folding rates were essentially the same.

In contrast, the purpose of the experiments described here was to probe the folding nucleus of PrP by classical ϕ-value analysis, and the results have provided several surprises with respect to the effects of amino acid substitutions on the folding of human PrP. First, we tried to use the F175W mutation that had previously been used in the murine PrP to provide a folding signal (13). The fact that there is 90% identity between the human and mouse sequences led us to expect that this mutation would be nondisruptive, as it was shown to be in the mouse protein. However, the F175W version of the human protein did not fold to a soluble native state. The residue is on helix 2 and makes close contact with I215 on helix 3 and M166, which resides on the turn between the second β-strand and helix 2 (Fig. 2). Inspection of the context of F175 in the mouse structure shows it to make contact with V215 and V166, both of which are less bulky than their human counterparts. Perhaps the most likely reason for the inability of the human F175W mutant to fold is that the extra bulk of the indole group, compared with the phenyl, prevents the formation of the 179–214 cystine (disulfide) bridge by steric interference, but in the case of the mouse protein, the increase in bulk can be accommodated and the disulfide bond made. Irrespective of the explanation, the result illustrates the pitfalls of drawing parallels between mutations on different wild-type frameworks in PrP, e.g., interpreting human mutations on the basis of their effects on the mouse protein.

Second, the V209A mutant, although expressible, was highly destabilized according to equilibrium measurements. Despite showing a normal unfolding transition in these experiments, it was not amenable to temperature-jump perturbation analysis because it showed no signal change in the relaxation measurements. It seems likely that when equilibrated in the t-jump apparatus, this mutant formed some kinetically locked, misfolded (perhaps oligomeric) state that was not in rapid equilibrium with either the unfolded or folded states.

Of the remaining 6 core mutants, 2 (F175A and I184V) have very little effect on the free energy of folding. The former result is somewhat surprising because the residue occupies a buried site in the protein, and its substitution by tryptophan, as described above, is highly destabilizing. One would expect the burial and consequent dehydration of a phenylalanine rather than an alanine side chain would be more favorable by a little >10 kJ/mol. In other words the F-to-A mutation should lead to a destabilization of approximately 2 orders of magnitude in K_F/U; this is without including the effects of losing potential van der Waals interactions. Perhaps the explanation is related to that offered for the effect of the F175W mutation described earlier, i.e., if this region of human PrP is sterically strained because of the presence of over-bulky side chains, then the F175A mutation might relieve this.

Only residues V180 and M206 on helices 2 and 3 have significant ϕ-values in the transition state of the folding reaction. The side chains of these residues mediate interactions between the 2 major helices in the structured core of PrP^C, helices that are linked by a disulfide bond across residues 179 and 214. In general, the data imply that this fast-folding protein has a transition state that is not compact (m value analysis gives a β_t value of only 0.3) but contains the developing nucleus around the disulfide bond between helices 2 and 3. Interestingly, previous hydrogen-exchange analysis of human PrP shows that ≈8 residues clustered around the 179–214 bridge have exchange rates that are sufficiently slow to imply their protection in the unfolded state (12). Indeed, the comparatively low value of β_t is possibly because this region has native-like structure in the unfolded state, thereby producing a localized nucleated mechanism in which the transition state is early in the pathway.

The most arresting result of this study was the strong influence of the I184V mutation on the kinetics of folding as compared with its immeasurably small effect on the stability of the native state and on the kinetic barrier to unfolding. The I184V mutation might be acting through increasing the propensity to form intermolecular interactions in the unfolded state, so that the normal folding energetics are perturbed by the need to break such interactions before the native state can be acquired. This possibility can be ruled out, however, by the fact that the observed folding rate constant is insensitive to protein concentration (Fig. S3). A further possibility is that the mutation leads to a significant distortion of the folded-state structure. In these circumstances, one might see that the equilibrium transitions between the unfolded and native states are isoenergetic, as indeed might be the unfolding barrier, but because the native states are different, there could be quite different folding trajectories. The possibility that the native state was structurally perturbed was tested by measuring diagnostic NMR parameters, such as ¹H and ¹⁵N chemical shifts, hydrogen exchange protection, and NMR relaxation dynamics.

The NMR 1D and 2D ¹H-¹⁵N-HSQC spectra of both the F198W and I184V/F198W constructs were found to be very similar to those of the wild-type protein, with only limited and localized chemical shift changes surrounding the sites of the mutations, caused in part by the changes associated with the change in chemical composition (Figs. S4 and S5). An even more sensitive measure of local stability is hydrogen/deuterium exchange of backbone amides. The observed rates of hydrogen/deuterium exchange (Fig. S6) reveal that the I184V mutant shows no significant difference in the global and local fluctuations that permit the exchange process, i.e., they display identical (within error) hydrogen exchange protection factors to those of “wild-type” protein (12). However, an inherent limitation of the hydrogen-exchange technique is that it provides information only for those regions that display measurable protection in the folded state. To extend our analysis, we compared the conformational dynamics of both mutants through the use of ¹⁵N spin relaxation measurements, which provide information on the flexibility within the protein. The longitudinal and transverse relaxation times [T₁ (¹⁵N) and T₂ (¹⁵N)] were identical (within error) (Fig. S7) to those values observed for the wild-type protein, showing there is no change in the conformational mobility of the protein, either surrounding the mutation or, indeed, further away.

The NMR data thus indicate that the I184V mutation has no effect on the native state. We are therefore left with the conclusion that the polypeptide has 2 potential trajectories along which it can fold. For the wild-type sequence, the chain folds to the native state by traversing a relatively low-energy (but measurable) transition state barrier. Replacing the isoleucine with a valine, however, makes available an alternative and faster path to a highly compact state that is not native and is kinetically trapped. The data show that this state is ≈12 kJ/mol more stable than the unfolded state (U) in physiological conditions but 18 kJ/mol less stable than the native state. From this compact nonnative state, the fastest route to the native conformation—which is ≈30 kJ/mol more stable than U—is by unfolding and passing through the conventional, wild-type transition state.

This type of behavior is reminiscent of that shown by the bacterial immunity protein Im7 (17). The folding intermediate populated by this 4-helix protein has been probed by measuring the kinetic properties of an extensive series of point mutants. It was concluded that the intermediate contains 3 of the 4 helices that appear in the native structure, packed around a defined hydrophobic core. However, this intermediate was shown to contain many nonnative interactions, and, as a consequence, to progress to the native state, hydrophobic contacts needed to be broken to attain the rate-limiting transition state before the final helix docks onto the developing structure. In the context of the prion protein, the data described here indicate that the folding pathway is very sensitive even to minor modifications of the contact surface between helix 2 and helix 3. Interestingly, in the inherited forms of human prion disease, where point mutations produce a lethal dominant condition, 20 of the 33 amino acid replacements occur in the helix 2/helix 3 region (18). Indeed, truncation experiments (19) show that a protein consisting only of residues 89–140 and of helices 2 and 3 (residues 177–231) is capable of propagating the scrapie agent, whereas spin-labeling of PrP shows that residues 160–220 are converted from helix to a parallel, in-register β-structure when PrP^C is converted to amyloid (20).

Materials and Methods

CD, Fluorescence, and Temperature-Jump Experiments.

Details of the CD and fluorescence measurements and of the equipment used in the temperature-jump kinetics, and also its calibration, are described in the SI Text.

Measurement of Protein Folding Kinetics.

For kinetic experiments, an initial protein concentration of 30 μM was used, in a sample volume of 2 mL, with 20 mM Na₂HPO₄ and varying concentrations of GuHCl. The sample was gently mixed between jumps to reduce the effect of photobleaching. In accordance with the calibration, at least 15 seconds was left between each jump to ensure complete sample cooling.

Analytical Methods: Equilibrium Unfolding.

For equilibrium unfolding transitions, data were fitted to the following equation, where K_F/U and K_F/U(W) are equilibrium constants at a given denaturant activity (D) and in water, respectively, and m_U-F describes the sensitivity of the equilibrium to denaturant activity:

Calculation of Thermodynamic Parameters: ΔH, ΔS, and ΔC_p.

The enthalpy (ΔH), entropy (ΔS) and heat capacity (ΔC_P) changes for PrP folding at a reference temperature (T₀) of 298 K/25 °C were calculated from the free energy change of folding (ΔG_(T)) at each temperature (T) as follows (21).

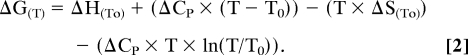Analytical Methods: Kinetics.

Calculating the folding and unfolding rates.

For kinetic plots representing 2-state kinetics (all proteins except PrP I184V), the PrP folding and unfolding rates in the absence of denaturant (k_F(W) and k_U(W), respectively) were calculated from the observed relaxation rate (k_obs) as follows:

where D is molar denaturant activity (see SI Text), and m_F and m_U represent the linear dependence of k_F and k_U on denaturant activity (22). The continuous lines shown in Fig. 3B are constrained fits using the values of K_F/U and m_U-F from the equilibrium data shown in Fig. 3A (i.e., the fits fulfilled the criteria k_f = k_u·K_F/U and −m_t = m_U-F − m_U). In this latter fit, the kinetic data are used to define only 2 parameters with the well-defined equilibrium unfolding curve supplying the other 2. Across the whole dataset, this was considered to provide better estimates of the kinetic constants; hence, the values shown in Table 2 are calculated in this way.

For PrP I184V, which did not fit to a 2-state model, the following 3-state model was used to calculate the folding and unfolding rates (21), where k_F-I(W) and k_I-F(W) are the folding and unfolding rates in water associated with the misfolded state (M) to folded state (F) transition, and K_I/U(W) is the equilibrium constant in water for the unfolded state (U) to intermediate transition. The m values describe how the free energies of the states vary with denaturant activity, D (m_t is the m value of the I–F transition state).

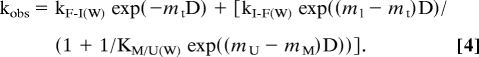NMR spectroscopy, amide exchange-protection, and spin relaxation experiments.

The details of protein sample preparation for NMR, the assignment methodology for PrP F198W and PrP I184V/F198W, calculation of chemical shift differences, spin relaxation rates, and the measurement of hydrogen–deuterium exchange rates/protection factors are described in the SI Text. Fig. 2 and Fig. S5, displaying the NMR structure of Human PrP^C (23), were prepared by using University of California, San Francisco (UCSF) Chimera (24).