Fermi surface nesting induced strong pairing in iron-based superconductors

Abstract

The discovery of high-temperature superconductivity in iron pnictides raised the possibility of an unconventional superconducting mechanism in multiband materials. The observation of Fermi-surface (FS)-dependent nodeless superconducting gaps suggested that inter-FS interactions may play a crucial role in superconducting pairing. In the optimally hole-doped Ba_0.6K_0.4Fe₂As₂, the pairing strength is enhanced simultaneously (2Δ/T_c≈7) on the nearly nested FS pockets, i.e., the inner hole-like (α) FS and the 2 hybridized electron-like FSs, whereas the pairing remains weak (2Δ/T_c≈3.6) in the poorly nested outer hole-like (β) FS. Here, we report that in the electron-doped BaFe_1.85Co_0.15As₂, the FS nesting condition switches from the α to the β FS due to the opposite size changes for hole- and electron-like FSs upon electron doping. The strong pairing strength (2Δ/T_c≈6) is also found to switch to the nested β FS, indicating an intimate connection between FS nesting and superconducting pairing, and strongly supporting the inter-FS pairing mechanism in the iron-based superconductors.

In charge-doped superconductors, such as copper oxides (cuprates), electron or hole doping may influence the superconducting (SC) properties differently (1, 2). As an example, angle-resolved photoemission spectroscopy (3) (ARPES) and Raman scattering (4) revealed a nonmonotonic behavior in the SC gap function of the electron-doped cuprates that is different from the simple dx²-y²-wave function observed in the hole-doped cuprates (5). On the other hand, in the new Fe-based superconductors (6–9), no direct comparison of the SC order parameter has been made between hole- and electron-doped systems. ARPES studies on hole-doped Ba_1-xK_xFe₂As₂ have observed isotropic gaps that have different values on different Fermi surfaces (FSs) with strong pairing occurring on the nearly nested FS pockets (10–13). Thus, it is particularly important to conduct a comparison of the SC gaps and their FS dependence of an electron-doped pnictide. We have chosen BaFe_1.85Co_0.15As₂, which is optimally electron doped (14) with the same crystal structure as the Ba_1-xK_xFe₂As₂ system (9).

Results

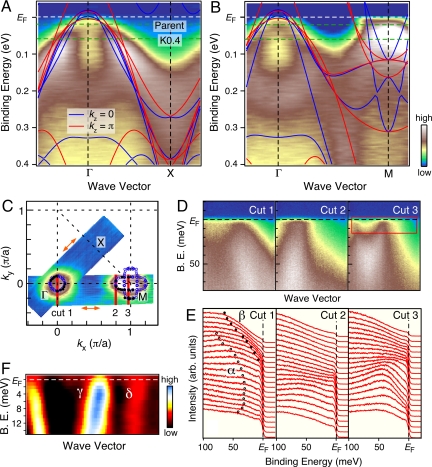
Fig. 1 A and B show ARPES intensity plots of BaFe_1.85Co_0.15As₂ (T_c = 25.5 K) as a function of binding energy and momentum (k) along 2 high-symmetry lines in the Brillouin zone (BZ). We observe a hole-like dispersion centered at the Γ point and 2 electron-like FSs near the M point. Even though a reasonable agreement is found between experiment and renormalized band calculations (15), some experimental features such as the energy position of the 0.2 eV band at the Γ point and the bottom of the electron band at the M point, are not well reproduced by band calculations. This suggests a possible orbital and k dependence of the mass-renormalization factor. Fig. 1C shows the ARPES intensity at the Fermi level (E_F) plotted as a function of the in-plane wave vector. A circular and an elongated intensity pattern centered at the Γ and M points are clearly visible, and they are attributed to the hole- and electron-like bands in Fig. 1 A and B. In Fig. 1 D and E, we show ARPES intensity plots near E_F and the corresponding energy distribution curves (EDCs) measured at 3 representative cuts indicated in Fig. 1C. In cut 1 of Fig. 1E, 2 hole-like bands are clearly visible. The inner band, which is assigned to the likely degenerate α band (10, 16), sinks significantly (≈30 meV) and does not create a small FS pocket as observed in the hole-doped samples (10), confirming the electron doping by the Co substitution. The outer band (the β band) crosses E_F creating a hole pocket at the Γ point. We also notice that the number of hole-like bands crossing E_F in the present ARPES experiment is different from the band calculations (1 and 3, respectively). Along cut 3, which is close to M, we can distinguish an electron-like band crossing E_F with a bottom at ≈40 meV creating an elongated FS pocket shown in Fig. 1C. A closer look at the second derivative of momentum distribution curves (MDCs) in Fig. 1F reveals the presence of an additional band whose dispersion near E_F is nearly parallel to the main band. This suggests that the electron-like FSs consist of the inner (γ) and outer (δ) pockets resulting from the hybridization of 2 ellipsoidal pockets elongated along the k_x and k_y directions (see Fig. 1C), as in the case of hole-doped Ba_0.6K_0.4Fe₂As₂ (16). We remark here that the topology of the FS near the M point in hole-doped Ba_1-xK_xFe₂As₂ is controversial among several ARPES groups. This controversy is closely related to the presence of a hole-like band around the M point that intersects the electron-like bands in the vicinity of E_F, producing a complicated intensity distribution pattern around E_F. It is thus important to follow carefully the band dispersion with high-energy and momentum resolutions when determining the FS topology (10, 11). As clearly seen in Fig. 1C, the β-hole pocket is nearly nested with the electron pockets, in sharp contrast to the observation of a good FS nesting between the α-hole pocket and the electron pockets in the hole-doped Ba_0.6K_0.4Fe₂As₂.

Fig. 1.

Fermi surface and band structure of electron-doped BaFe_1.85Co_0.15As₂. (A and B) ARPES intensity plots of BaFe_1.85Co_0.15As₂ (T_c = 25.5 K) as a function of wave vector and binding energy measured at 8 K along the ΓX (A) and the ΓM (B) lines with the He Iα (hν = 21.218 eV) resonance line, together with the band dispersion from the first-principle calculations for k_z = 0 and π (blue and red curves, respectively). Calculated bands for BaFe₂As₂ (15) were shifted downward by 40 meV and then renormalized by the factor of 2. Green broken lines denote the expected E_F positions of BaFe₂As₂ and Ba_0.6K_0.4Fe₂As₂. (C) FS contour determined by plotting the ARPES spectral intensity integrated within ± 5meV with respect to E_F. Black filled circles show the k_F positions determined by tracing the experimental band dispersion, whereas blue open circles are symmetrized k_F points obtained by assuming a 4-fold symmetry with respect to the Γ and M point, respectively. The symmetrized k_F points (blue open circles) coincide well with the original ones (black filled circles), confirming the validity of this symmetry operation. Orange arrows show the polarization vector of the incident light for each cut. (D) ARPES spectral intensity at 8 K as a function of wave vector and binding energy. (E) Corresponding EDCs measured along 3 representative cuts 1–3 shown in C. Circles in E traces the energy dispersion of the α and β bands. (F) Second derivative plot of MDCs along cut 3 to highlight the presence of another weaker electron-like band (δ).

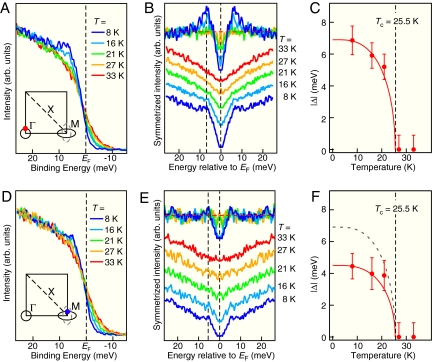
We now illustrate how the SC gap evolves below T_c on each FS. Fig. 2A displays the temperature (T) dependence of the EDCs at a Fermi vector (k_F) on the β-hole pocket measured across T_c. At 8 K, the midpoint of the leading edge below T_c is shifted toward higher binding energy by ≈4 meV with a pileup of spectral weight at ≈7 meV, indicating the opening of a SC gap. A similar gap value has been observed in the density of states (DOS) by scanning tunneling spectroscopy on a same type of sample (17). We have eliminated the effect of the Fermi–Dirac distribution function by symmetrizing the EDCs at each temperature (18) (Fig. 2B). To cancel out the influence of the V-shaped spectral DOS, which originates from the tail of the α-band, we divided each symmetrized spectrum by the 33-K normal state spectrum (see top of Fig. 2B). As one easily notices, a sharp coherence peak emerges below T_c at 7 meV. Interestingly, the spectral weight at E_F displays a small depression even at T = 27 K, indicating a possible weak pseudogap just above T_c. We have estimated the size of the SC gaps and plotted them in Fig. 2C. It is found that a simple Bardeen–Cooper–Schrieffer mean-field T dependence with Δ(0) = 7 meV reproduces satisfactorily the extracted gap amplitudes. In Fig. 2 D and E, we plot the T dependence of raw and symmetrized EDCs measured on the ellipsoidal electron pocket. Although the overall T dependence of the leading-edge shift and the spectral weight suppression below T_c on the electron pockets are qualitatively similar to those of the β FS, there are some differences: A weaker coherence-peak weight accompanied with a reduction of spectral weight at E_F, and a smaller SC-gap size (4.5 vs. 6.7 meV, see Fig. 2F) are observed. These results demonstrate the FS-sheet dependence of the SC gap. We also noticed that the weight of the coherence peak is much weaker than that of hole-doped Ba_0.6K_0.4Fe₂As₂ (10), possibly owing to a lower superfluid density due to a lower T_c value (25.5 vs. 37 K) and disorder scattering induced by in-plane Co substitution.

Fig. 2.

Temperature dependence of the superconducting gap. (A) T dependence of EDC measured at a k_F point on the β FS (red dot in Inset). (B) Symmetrized EDCs and the same but divided by the spectra at T = 33 K. Dashed line denotes the position of SC coherence peak. (C) T dependence of the SC gap size. Solid line is the BCS mean-field gap with T_c = 25.5 K and Δ(0) = 7 meV. (D–F) same as A–C but measured on the k_F point of the ellipsoidal electron pocket. Dashed line in F is the same as the solid line in C.

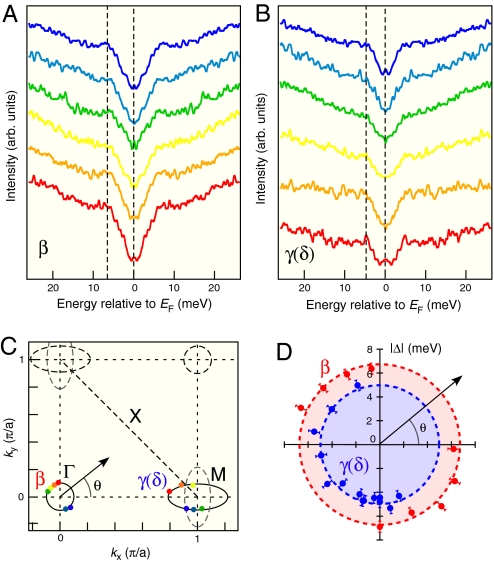
Next we turn our attention to the k dependence of the SC gaps. Fig. 3 A and B show the symmetrized EDCs measured at 8 K at various k_F points on the β-hole pocket (Fig. 3A) and the ellipsoidal electron pocket (Fig. 3B). As shown in Fig. 3D, the SC gap of each FS is nearly constant, indicating an isotropic s-wave nature. On the other hand, the average gap values of the hole and electron pockets are different (6.6 and 5.0 meV, respectively), establishing unambiguously the FS-dependent nature of the SC gap.

Fig. 3.

Momentum dependence of the superconducting gap. (A and B) Symmetrized EDCs at 8 K measured at various k_F points on the β and electron-like FS, labeled by respective colored symbols correspondingly. (C) Extracted FS from the ARPES measurements together with the definition of FS angle (θ). (D) SC gap values at 8 K as a function of θ extracted from the EDCs shown on the polar plot, for the β and electron-like FSs (red and blue dots, respectively). Dashed circles represent the averaged gap value.

Discussion

A direct comparison of the ARPES data on the electron- and hole-doped SC pnictides allows us to conclude that: (i) the SC gap opens on multiple FSs centered at the Γ and M points, (ii) the SC gap is nodeless and exhibits nearly isotropic behavior on each FS, and (iii) the pairing strength, as reflected by the ratio of 2Δ/k_BT_c, is related to the FS nesting condition between the electron and hole pockets. In hole-doped Ba_0.6K_0.4Fe₂As₂ (10, 11), the interband scattering via the wave vector Q∼(π,0) (as defined in the unreconstructed BZ) has been suggested to enhance the pairing amplitude of the α and γ(δ) FSs (19–22), resulting in large 2Δ/k_BT_c values of 7.2–7.7, whereas the poorly nested β FS has a value of 3.6, close to the weak-coupling regime. Remarkably, in electron-doped BaFe_1.85Co_0.15As₂, the β (but not α) is connected to the γ(δ) FSs by the same Q∼(π,0) and possess strong-coupling 2Δ/k_BT_c values of 5.9, suggesting an enhancement of the pairing amplitude due to interpocket scattering on the nearly nested FSs. The observation that the pairing strength in the β band increases from 3.6 in the optimally hole-doped sample to 5.9 in the optimally electron-doped sample strongly suggests that the SC coupling strength is more related to the nesting condition among the FSs than to the orbital characters themselves. All these experimental observations suggest that the interpocket scattering and FS nesting are critical aspects of the pairing mechanism of the pnictides.

At this point, a few essential issues regarding the nature of the unconventional pairing mechanism need to be addressed. The first one is the cause of a small difference in the SC gap size of the observed FSs in the electron-doped system. This may be related to the difference in the partial DOS between electron and hole pockets. The existence of 2 electron pockets would give rise to a larger DOS at E_F in the electron pockets than in the hole pocket. This leads to a relative enhancement of the pairing amplitude in the hole pocket due to stronger Q∼(π,0) scattering from the electron pockets (23). The second issue concerns the smaller 2Δ(0)/k_BT_c values obtained on the well nested FSs in the electron-doped BaFe_1.85Co_0.15As₂ (4.5–5.9) as compared with the hole-doped Ba_0.6K_0.4Fe₂As₂ [7.2–7.7 (10)]. This might be linked to the larger pairing-breaking disorder scattering caused by the in-plane Co substitution as compared with the off-plane K substitution in Ba_0.6K_0.4Fe₂As₂. The last issue, which might be the most unusual, is the lack of anisotropy in the gap function on a given FS, in contrast to a theoretical prediction of anisotropic extended s-wave gaps based on renormalization group calculation (24). Strictly speaking, the interband scattering condition via Q = (π,0) is not perfect in either the hole or the electron-doped systems because the shape of the hole and electron pockets does not match completely (e.g., see Fig. 1C). One might therefore expect a large anisotropy in the SC gap size near the M point, whereas the observed SC gap size merely depends on the FS sheet. This implies that there might be a mechanism that keeps the intraband SC gap constant. Our observation of isotropic SC gaps that depend on FS nesting conditions is an important step toward a full understanding of high-temperature superconductivity in iron pnictides.

Materials and Methods

Samples Preparation.

High-quality single crystals of BaFe_1.85Co_0.15As₂ were grown by the self-flux method, the same growth method as for BaFe_2-xNi_xAs₂ (25). From electrical resistivity measurements, T_c of the sample has been estimated to be T_c^mid = 25.5 K. The starting material (nominal composition) was BaFe_1.8Co_0.2>As₂, whereas the actual Co content was determined by energy-dispersive X-ray spectroscopy. The low-energy electron diffraction (LEED) patterns indicate that the sample surface has a 4-fold symmetry with no signature of surface reconstruction.

ARPES Experiments.

ARPES measurements were performed by using a VG-SCIENTA SES2002 spectrometer with a high-flux discharge lamp and a toroidal grating monochromator. We used the He Iα resonance line (21.218 eV) with a partially linear polarization parallel to the ΓM (ΓX) direction for measurements of the ΓM (ΓX) cut, as shown in Fig. 1C (orange arrows). The energy resolution was set at 4 and 15 meV for the measurement of the SC gap and the valence band dispersion, respectively. The angular resolution was set to 0.2°. Clean surfaces for ARPES measurements were obtained by in situ cleaving of crystals at 8 K in a working vacuum < 5 × 10⁻¹¹ Torr and then measured immediately without annealing. Mirror-like sample surfaces were found to be stable without obvious degradation for the measurement period of 3 days. The Fermi level of the samples was referenced to that of a gold film evaporated onto the sample holder. We observed that the SC gap closes around the bulk T_c (see Fig. 2), which suggests that the present ARPES results reflect the bulk properties. We found that the periodicity of the experimental band dispersions matches well with that of the bulk crystal, suggesting that no surface relaxation or reconstruction takes place, as also supported by the measured LEED patterns. We have confirmed the reproducibility of the ARPES data on >5 sample surfaces and through thermal cycles across T_c. To extract the carrier number from the ARPES measurement, we have estimated the FS volume of the β-pocket and the ellipsoidal electron pocket to be 1.6% and 3.2% of the unfolded first BZ, respectively. The deduced total carrier number of 0.05 electrons per Fe is close to but slightly lower than the expected value of 0.075 electrons per Fe in BaFe_1.85Co_0.15As₂. The small difference may suggest a possible deviation of the Co valence from 3⁺ and the finite 3 dimensionality of the band structure (19, 26–28).