Geometry of the semicircular canals and extraocular muscles in rodents, lagomorphs, felids and modern humans

Abstract

The vestibulo-ocular reflex (VOR) exacts compensatory movements of the extraocular muscles in response to stimulation of the semicircular canals to allow gaze fixation during head movements. In this study, the spatial relationships of these muscles and canals were investigated to assess their relative alignments in mammalian species commonly used in studies of the VOR. The head region of each specimen was scanned using magnetic resonance imaging and 28 anatomical landmarks were recorded from the images to define the six extraocular muscles and the anatomical planes of the three semicircular canals. The vector rotation of a semicircular canal that does not stimulate either of its two sister canals, referred to as the prime direction, was also calculated as an estimate of the maximal response plane. Significant misalignments were found between the extraocular muscles and the canals by which they are principally stimulated in most of the species under study. The deviations from parallel orientation were most pronounced in the human and rabbit samples. There were also significant departures from orthogonality between the semicircular canals in most species. Only the guinea pig displayed no significant difference from 90° in any of its three inter-canal angles, although humans and rabbits deviated from orthogonality in just one semicircular canal pair – the anterior and posterior canals. The prime directions were found to deviate considerably from the anatomical canal planes (by over 20° in rats). However, these deviations were not always compensatory, i.e. prime planes were not always more closely aligned with the muscle planes. Results support the view that the vestibular frame remains relatively stable and that the spatial mismatch with the extraocular co-ordinate frame is principally driven by realignment of the muscles as a result of changes in the position of the orbits within the skull (orbital convergence and frontation).

Introduction

The vestibulo-ocular reflex (VOR) enables the gaze to be focused on one point whilst the head is moving. The functional components of the VOR are the semicircular canals of the inner ears, which sense angular accelerations and decelerations of the head, and the extraocular muscles, which produce appropriate compensatory movements of the eyeballs (Cohen et al. 1964; Suzuki et al. 1964). Each semicircular canal principally activates one extraocular muscle in each eye (Szentágothai, 1950; summarized in Fig. 1, Cox & Jeffery, 2007), although other extraocular muscles are also stimulated to lesser degrees. The spatial orientations of these primary functional couplings are of key interest to investigations of the organization and function of the VOR. This study examines the relative orientations of the muscles and canals in seven mammalian species, many of which are commonly used in VOR studies.

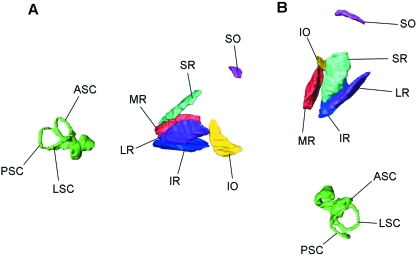
Fig. 1.

Three-dimensional representation of the extraocular muscles and semicircular canals of a cat (specimen Cat3). Surface rendering performed using Amira 4.1 (Mercury Inc., USA). (A) Lateral view. (B) Dorsal view. SO, superior oblique; IO, inferior oblique; SR, superior rectus; IR, inferior rectus; MR, medial rectus; LR, lateral rectus; ASC, anterior canal; PSC, posterior canal; LSC, lateral canal.

The orientations of the planes of the semicircular canals, both to each other and to standard stereotaxic planes, have been measured in a number of different vertebrate species. Early work in this area examined the inner ears of rabbits (de Burlet & Koster, 1916) and rats (Cummins, 1925). Due to the inaccessible nature of the inner ears, the canals were studied using wax or plaster of Paris reconstructions modelled from serial sections. Angles between the three canals and standard reference planes were calculated visually using a protractor (Cummins, 1925), or mathematically by determining the three-dimensional co-ordinates of three points on each canal in order to define a plane (de Burlet & Koster, 1916).

Later work tended to favour a technique in which the semicircular canals were surgically exposed in a skull through careful removal of portions of the temporal bone, occipital bone and tympanic bulla. The skull was then securely mounted in a stereotaxic plane, and the X, Y and Zco-ordinates of a number of points along each canal were recorded using a curved needle attached to a micromanipulator. Using this method, the semicircular canals were mapped in cats (Blanks et al. 1972; Ezure & Graf, 1984), guinea pigs (Curthoys et al. 1975), humans (Blanks et al. 1975), rabbits (Ezure & Graf, 1984; Mazza & Winterson, 1984), monkeys (Blanks et al. 1985), rats (Daunicht & Pellionisz, 1987), pigeons (Dickman, 1996), turtles (Brichta et al. 1988) and toadfish (Ghanem et al. 1998). Reisine et al. (1988) used a similar protocol on their study of rhesus monkeys, but determined the X, Y and Zco-ordinates from a resin cast of the vestibular apparatus rather than directly from the skull. Having obtained three-dimensional co-ordinate data for each canal, a plane of best fit can be calculated using either a least-squares technique or a principal components analysis in which the values of the eigenvectors corresponding to the smallest eigenvalue give the directional cosines of the normal vector to the plane. In a number of the above studies (Blanks et al. 1972, 1975, 1985; Curthoys et al. 1975; Ezure & Graf, 1984), both plane-fitting techniques were applied and were found to give virtually identical results. An alternative indirect method is the null point technique employed by Blanks & Torigoe (1989) and Haque et al. (2004) to determine the planes of the semicircular canals in the rat and rhesus monkey, respectively. In this method, the experimental animal is mounted in a three-axis rotator system, and is subjected to various angular accelerations whilst the afferent responses at the vestibular nerve root are recorded. The ‘null point’ is the orientation which produces no response, and indicates that the semicircular canal is perpendicular to the plane of angular acceleration. Once the null points have been found for each canal, the anatomical planes of the semicircular canals can be approximated in the form aX + bY + cZ = 0, referenced in the stereotaxic co-ordinate system.

With the development of more sophisticated imaging techniques, recent investigations have utilized computer reconstructions of the labyrinth to analyse the planar relationships of the semicircular canals. Reconstructions of the human labyrinth have been generated from serial sections (Takagi et al. 1989; Sato et al. 1993; Hashimoto et al. 2005), magnetic resonance images (Ichijo, 2002), and computed tomography (CT) scans (Spoor & Zonneveld, 1998; Della Santina et al. 2005). CT data have also been used to study the canals in mice (Calabrese & Hullar, 2006) and chinchillas (Hullar & Williams, 2006). As in earlier studies, planes of best fit were calculated using a least-squares technique or a principal components analysis, except for Della Santina et al. (2005), who fitted the planes visually using multi-slice planar reconstructions.

Many of the studies mentioned above have noted that the semicircular canals are not precisely orthogonal, and in some cases depart widely from orthogonality (e.g. Curthoys et al. 1975; Ezure & Graf, 1984; Mazza & Winterson, 1984). In such specimens, rotation of the head in the anatomical plane of a semicircular canal will necessarily stimulate at least one of the other two ipsilateral canals. It was thus proposed by Rabbitt (1999) that a more useful measurement to derive would be the vector of rotation of a canal that does not stimulate either of the other two canals. This is termed the ‘prime direction’ of a canal. Prime directions have been derived for rhesus monkeys (Haque et al. 2004), mice (Calabrese & Hullar, 2006) and chinchillas (Hullar & Williams, 2006). Haque et al. (2004) suggested that the oculomotor system uses the prime co-ordinate frame to encode vestibular signals. However, this hypothesis is difficult to test in rhesus monkeys due to the near-orthogonality of their semicircular canals and, therefore, the close alignment of the anatomical and the prime reference frames. Deviations of up to 15° and 21° between the two co-ordinate systems were found in mice (Calabrese & Hullar, 2006) and chinchillas (Hullar & Williams, 2006), respectively. This is due to the greater departure from orthogonality in the labyrinths of these species. The orientations of the extraocular muscles were not measured in these studies and so it is unknown if the muscles align more closely with the canal planes or the prime directions in mice and chinchillas.

Studies in which the orientations of the extraocular muscles are also included are sparse. Simpson & Graf (1981) derived the orientations of the superior oblique and superior rectus muscles from direct measurements in situ and from photographs. They compared the orientations of these two muscles with the orientations of the anterior and posterior semicircular canals to the midsagittal line in humans, cats, guinea pigs and rabbits. However, all the angles were projected on to the dorsal plane, thus losing accuracy in the reduction from three to two dimensions. Subsequently, Ezure & Graf (1984) employed a more sophisticated approach and determined the orientations of all six extraocular muscles and canals in cats and rabbits. The three-dimensional co-ordinates of the muscular origins and insertions were taken using a three-axis micromanipulator, allowing a three-dimensional vector to be calculated for each muscle. The muscle vectors were also combined into three muscle planes – the vertical recti, horizontal recti and oblique muscles. Angles were then calculated between the canal planes and both the individual muscle vectors and the combined muscle planes. Daunicht & Pellionisz (1987) conducted a similar experiment on rats, but rejected the concept of combining the six extraocular muscles into three planes.

The present study proposes to use recent advances in non-invasive image acquisition and analyses to build on the work of Simpson & Graf (1981), Ezure & Graf (1984) and latterly Daunicht & Pellionisz (1987). As such this paper is primarily concerned with the extent of the spatial mismatch between the vestibular and extraocular co-ordinate systems rather than the compensatory systems. Specific aims include (1) to measure canal–muscle orientations that represent the VOR function as described by Szentágothai (1950) and to include prime anatomical directions (e.g. Rabbitt, 1999); (2) to report on these measurement data for large samples of species commonly used in research; and (3) to provide researchers with co-registered X, Y, Zco-ordinates for the normals of the canal planes and the vectors of the extraocular muscles.

Materials and methods

Sample and imaging

The sample consists of 53 adult mammalian heads from seven species. These comprise five grey squirrels (Sciurus carolinensis, three male/two female), nine house mice (Mus musculus, five male/four female), eight brown rats (Rattus norvegicus, four male/four female), eight domestic guinea pigs (Cavia porcellus, five male/ three female), nine European rabbits (Oryctolagus cuniculus, four male/ five female), eight domestic cats (Felis catus, five male/three female), and six humans (Homo sapiens, three male/three female). Specimens of Sciurus, Mus and Rattus were imaged on a 7.0-Tesla magnetic resonance imaging system (Magnex-SMIS, UK) at the University of Manchester with a T2-weighted spin-echo multi-slice sequence (TE = 55 ms; TR = 6000–7000 ms). After acquisition the data were zero-filled to 512 × 512 data points, Fourier transformed and exported as raw binary files. The field of view (FOV) varied from 27 to 64 mm and slice thickness was 0.32 mm. The Cavia, Oryctolagus and Felis specimens were imaged on a 4.7-Tesla imaging and spectroscopy unit (Sisco-Varian, USA) at Queen Mary, University of London, with a T2-weighted spin-echo multi-slice sequence (TE = 20–50 ms; TR = 8000–16 000 ms). Data were zero-filled to 256 × 256 data points, representing FOV from 67 to 115.2 mm. Slice thickness ranged from 0.30 to 0.90 mm. For comparison we collated existing image datasets representing six Homo specimens. Data for one adult female and one adult male were kindly provided by Jim Rilling (Emory University, USA). Images were acquired from volunteers on a 1.5 T Phillips NT system (Phillips Medical, Netherlands) with a T2-weighted inversion recovery sequence (TR = 3000 ms; TE = 40 ms; TI = 200 ms). Field of view was 260 mm represented by a zero-filled matrix of 512 × 512. Slices were 2 mm thick. Another two image sets (one male and one female) were kindly provided by Dirk Bartz (University of Tübingen, Germany). Volunteers were imaged on a 1.5 T Sonata System (Siemens, Germany) with a T2-weighted 3D Constructive Interference in Steady State (CISS) sequence (TR = 13 ms; TE = 5.9 ms). The image matrices were 256 × 256, representing FOV of 230 mm and slice thickness was 0.9 mm. Finally, we studied datasets from two cryosectioned subjects (one male and one female) published by the Visible Human Project (http://www.nlm.nih.gov/research/visible/visible_human.html). Image matrices were optimized for multi-planar reformatting with 648 × 740 pixels representing FOV of 207 × 234 mm and an effective slice thickness of 1 mm. Slices for all 53 specimens were interpolated to form isometric voxels (vertices ranging from 0.05 to 0.9 mm) with the bicubic spline function in ImageJ (W. Rasband, NIH of Mental Health, Bethesda).

Measurements

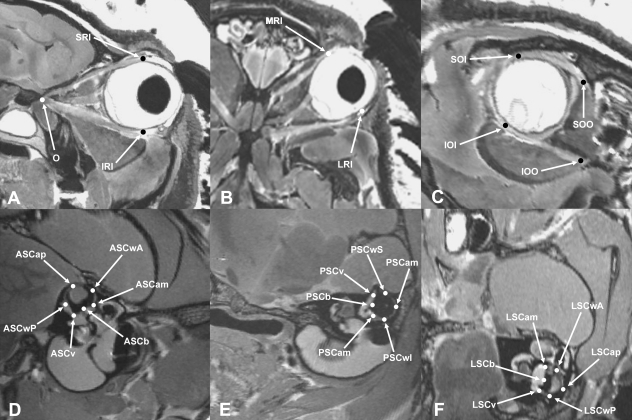
To capture the extraocular muscles and semicircular canals, a number of anatomical landmarks were taken from images using Amira 4.1 (Mercury Inc., USA). A three-dimensional reconstruction of the semicircular canals and extraocular muscles of one of the Felis specimens (Cat3) is shown in Fig. 1. This was generated from the magnetic resonance (MR) images using the surface-rendering function in Amira. Overall, 28 landmarks were recorded from reformatted planar MR images (illustrated in Fig. 2). Each extraocular muscle was represented by two landmarks: the origin and the insertion of that muscle. For the ipsilateral superior and medial rectus muscles, the same landmark was used for the origin (iO) – the centroid of the optic foramen – whereas the origin of the ipsilateral superior oblique (iSOO) was taken where the muscle runs through the trochlea and abruptly changes direction, as this was deemed to be the functional origin of this muscle. The centroid of the optic foramen on the opposite side of the head was used as the landmark for the origin of the contralateral inferior and medial rectus muscles (cO), whilst the origin of the contralateral inferior oblique (cIOO) was recorded on the medial orbital wall. The point at which each muscle inserts on the eyeball was also landmarked (iSRI, iMRI, iSOI, cIRI, cLRI and cIOI, respectively). The membranous labyrinth is not seen consistently within and between image sets. Hence, the vestibular system was represented by 18 landmarks taken from the bony labyrinth, six per semicircular canal. According to Ifediba et al. (2007) the bony canals give a reasonable estimation of membranous labyrinth orientations in humans. It seems unlikely that any difference in the orientations of the bony and membranous planes in the other species studied here will be of any great significance in comparison with the interspecific variances. One landmark was taken from each semicircular canal at its apex, i.e. the point of its curve furthest from the vestibule (ASCap, PSCap, LSCap); two mark the greatest radius of curvature of each canal (ASCwA, ASCwP, PSCwS, PSCwI, LSCwA, LSCwP); one was recorded on the margin of the vestibule diametrically opposite the apex (ASCb, PSCb, LSCb); one was taken at the canal's inferiormost arc diameter, as the canal duct enters the vestibule (ASCv, PSCv, LSCv); and one landmark was taken from the centroid of the ampulla (ASCam, PSCam, LSCam). All landmarks were recorded on the right-hand side of the specimen except those representing the contralateral extraocular muscles. Measurements were only taken from one side of the skull as there is no evidence for any significant left–right asymmetry of the semicircular canals. Furthermore, any asymmetry is likely to be insignificant compared with the noise due to intraspecific variation.

Fig. 2.

MR images of guinea pig (A–C; specimen Cavia7) and cat head (D–F; specimen Cat3) illustrating landmarks (Table 1). (A) Lateral slice through optic axis showing vertical rectus muscles. (B) Transverse slice through optic axis showing horizontal rectus muscles. (C) Cross-sectional slice through optic axis showing oblique muscles. (D) Longitudinal section through plane of anterior semicircular canal. (E) Longitudinal section through plane of posterior semicircular canal. (F) Longitudinal section through plane of lateral semicircular canal. See Table 1 for abbreviations.

Co-registration

For each individual, the co-ordinates for muscle and canal landmarks exist within the same spatial reference frame. However, the frame differs between individuals according to the position and orientation of the specimen during image acquisition. Landmark co-ordinates from individual specimens were co-registered into the same space using the generalized least-squares Procrustes superimposition (Rohlf & Slice, 1990) method as implemented in the software programme Morphologika (P. O’Higgins, Hull York Medical School, UK). The co-registered landmark co-ordinates were then used to calculate vectors and planes. This approach is preferred to registration to planes defined arbitrarily or by a few anatomical landmarks that could themselves vary between species and thereby bias findings.

Calculations

Vectors were calculated from the origin to the insertion of the six extraocular muscles: the ipsilateral superior rectus, superior oblique and medial rectus (iSR, iSO, iMR) and the contralateral inferior rectus, inferior oblique and lateral rectus (cIR, cIO, cLR). Planes of best fit for the anterior, posterior and lateral semicircular canals (ASC, PSC, LSC) were calculated from the six landmarks taken from each canal using a principal components analysis (Blanks et al. 1972; Ezure & Graf, 1984). In this technique, the values of the eigenvectors corresponding to the smallest eigenvalue gave the directional cosines of the normal vector to the plane of best fit. The landmarks, vectors and planes are summarized in Table 1. Following Rabbitt (1999) and Calabrese & Hullar (2006), the prime directions of each canal (ASC′, PSC′, LSC′) were obtained by calculating the cross product of the other two ipsilateral semicircular canals.

Table 1.

Abbreviations and descriptions of landmarks, muscle vectors and canal planes

Abbreviation	Description
Landmarks
ASCam	Centroid of the ampulla of the anterior semicircular canal
ASCap	Centroid of anterior canal at point most distant from vestibule
ASCb	Point on margin of vestibule diametrically opposite the apex of the anterior semicircular canal
ASCv	Centroid of the anterior part of the anterior semicircular canal at its inferiormost diameter as it enters the vestibule
ASCwA	Centroid of the anterior part of the anterior semicircular canal at its greatest width in the transverse plane
ASCwP	Centroid of the posterior part of the anterior semicircular canal at its greatest width in the transverse plane
cIOI	Centroid of the inferior oblique muscle as it inserts on the eyeball on the contralateral side
cIOO	Centroid of the inferior oblique muscle near its origin on the orbital wall on the contralateral side
cIRI	Centroid of the inferior rectus muscle as it inserts on the eyeball on the contralateral side
cLRI	Centroid of the lateral rectus muscle as it inserts on the eyeball on the contralateral side
cO	Centroid of the optic nerve as it passes through the optic foramen on the contralateral side
iMRI	Centroid of the medial rectus muscle as it inserts on the eyeball
iO	Centroid of the optic nerve as it passes through the optic foramen
iSOI	Centroid of the superior oblique muscle as it inserts on the eyeball
iSOO	Point on the medial orbital wall at which the superior oblique muscle abruptly changes direction (trochlea)
iSRI	Centroid of the superior rectus muscle as it inserts on the eyeball
LSCam	Centroid of the ampulla of the lateral semicircular canal
LSCap	Centroid of lateral canal at point most distant from vestibule
LSCb	Point on margin of vestibule diametrically opposite the apex of the lateral semicircular canal
LSCv	Centroid of the anterior part of the lateral semicircular canal at its medialmost diameter as it enters the vestibule
LSCwA	Centroid of the anterior part of the lateral semicircular canal at its greatest width in the sagittal plane
LSCwP	Centroid of the posterior part of the lateral semicircular canal at its greatest width in the sagittal plane
PSCam	Centroid of the ampulla of the posterior semicircular canal
PSCap	Centroid of posterior canal at point most distant from vestibule
PSCb	Point on margin of vestibule diametrically opposite the apex of the posterior semicircular canal
PSCv	Centroid of the superior part of the posterior semicircular canal at its medialmost diameter as it enters the vestibule
PSCwI	Centroid of the inferior part of the posterior semicircular canal at its greatest width in the coronal plane
PSCwS	Centroid of the superior part of the posterior semicircular canal at its greatest width in the coronal plane
Muscle vectors
cIO	Contralateral inferior oblique muscle: cIOO to cIOI
cIR	Contralateral inferior rectus muscle: cO to cIRI
cLR	Contralateral lateral rectus muscle: cO to cLRI
iMR	Ipsilateral medial rectus muscle: iO to iMRI
iSO	Ipsilateral superior oblique muscle: iSOO to iSOI
iSR	Ipsilateral superior rectus muscle: iO to iSRI
Semicircular canal planes
ASC	Anterior semicircular canal: plane of best fit of ASCam, ASCap, ASCb, ASCv, ASCwA, ASCwP
LSC	Lateral semicircular canal: plane of best fit of LSCam, LSCap, LSCb, LSCv, LSCwA, LSCwP
PSC	Posterior semicircular canal: plane of best fit of PSCam, PSCap, PSCb, PSCv, PSCwI, PSCwS

Angles between planes were calculated using the dot product:

θ = arccos(n.m/|n||m|)

where nand m are the normal vectors of the two planes and θ is the angle between them.

Angles between the muscle vectors and the canal and prime planes were calculated using the following formula:

ϕ = arcsin(n.b/|n||b|)

where n is the normal vector of the plane, b is the muscle vector and ϕ is the angle between them.

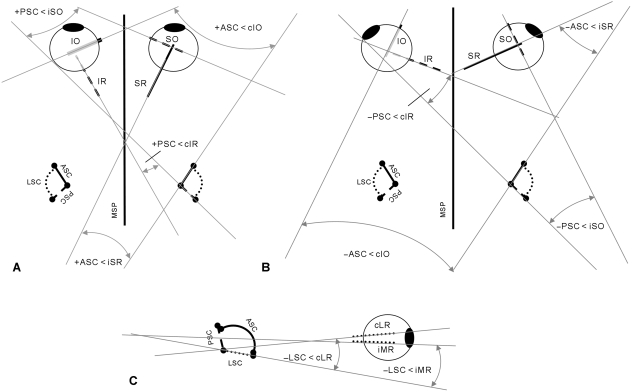
Angles were calculated between each canal plane or prime direction and the vectors of the two muscles principally activated by that canal (Szentágothai, 1950). Inter-canal angles were also calculated for each specimen, as well as the deviation between the unit normal for each canal plane and its prime direction. Following the convention used by Spoor & Zonneveld (1998) and Jeffery & Spoor (2004), angles are denoted by the abbreviations of the two planes or vectors on which they are based, separated by the < symbol. For example, ASC < iSR is the angle between the anterior semicircular canal and the ipsilateral superior rectus muscle.

As the principal components method can produce a normal vector in either direction, where necessary the X, Y and Z components for the normal vectors were multiplied by −1 so that the direction of each normal corresponded to the excitatory direction of rotation of the canal via the right-hand rule (Calabrese & Hullar, 2006; Hullar & Williams, 2006). Thus, the normal unit vector given for the anterior semicircular canal is the one that is directed anteromedially, the normal vector of the posterior canal plane points anterolaterally, and the normal to the lateral canal is ventrally oriented. Therefore, angles between the vertical semicircular canals and the vertical rectus muscles (ASC < iSR, PSC < cIR) are positive when the muscle makes a more acute angle with the midline than the canal, and negative when the canal makes a more acute angle with the midline than the muscle (Fig. 3A,B). This situation is reversed between vertical canals and oblique muscles (ASC < cIO, PSC < iSO) in which positive angles indicate that the muscle is less closely aligned to the midline than the canal and vice versa (Fig. 3A,B). Angles between the lateral semicircular canal and the extraocular muscles that it primarily activates (LSC < iMR, LSC < cLR) are positive when the muscle vector is ventral and negative when it is dorsal to the canal plane (Fig. 3C). Following Ezure & Graf (1984), angles between ipsilateral semicircular canals have been converted into internal angles; that is, the angles visible from a dorsolateral view of the labyrinth. To achieve this, the value of the angle between the anterior and lateral semicircular canals (ASC < LSC) obtained from the dot product of their normal vectors was subtracted from 180°.

Fig. 3.

Extraocular muscles and semicircular canals in dorsal view. (A) Frontal-eyed mammal. (B) Lateral-eyed mammal. The change in sign of the angles between frontal- and lateral-eyed mammals indicates that the muscles and canals have converged beyond parallel and begun to diverge in the opposite direction. (C) Extraocular muscles and semicircular canals of mammal, lateral view. Ipsilateral and contralateral muscles have been superimposed onto the same eye for ease of representation. Abbreviations as in Table 1 and Fig. 1.

Results

Angles between muscles and canals

The X, Y and Z components for the mean unit vectors representing the muscles and the mean normal unit vectors of the semicircular canal planes of each species are given in Table 2. The angles between the extraocular muscles and the semicircular canal by which they are principally activated vary widely across the species under study. The results given in Table 3 show ranges of between 50° and 62° for the canal–muscle angles. As also noted in previous work (Ezure & Graf, 1984), the extraocular muscles and semicircular canals deviate significantly from parallel orientation among species, with misalignments of almost 40° being measured between the posterior canal and the contralateral inferior rectus muscle. The mean values and standard deviations for each species are given in Table 4a–f. Again, it can be seen that even within species there is frequent non-alignment between the muscles and canals. With the exception of the rat, orientations of the posterior and anterior canals to the oblique muscles are always significantly misaligned. There are also significant deviations for orientations involving the lateral canal. Interestingly, the angle of the posterior canal to the contralateral inferior rectus lies close to spatial alignment for all but two species (rabbits and humans). Results from an analysis of variance indicate that there are highly significant differences (P < 0.001) in the orientations of the muscles to the canals between the seven species studied here. Further analysis of these results using a post-hoc Duncan test (Table 4a–f) elucidates precisely which species are differing from which. The only primate in the analysis, Homo, generally forms a group on its own, indicating that the degree of misalignment between the canals and muscles in humans is significantly different from that measured in the other species analysed here. For two angles (ASC < iSR, PSC < iSO; Table 4a,c), there is no difference between the mean value measured in the cats and that calculated for the humans, and hence they group together. In four of the six angles measured here (ASC < iSR, ASC < cIO, PSC < cIR, LSC < cLR; Table 4a,b,d,f), the rabbit was determined to be significantly different from every other species in the analysis, and thus formed a group on its own. The four rodents in the analysis (rat, mouse, squirrel, guinea pig) show few consistent trends. Despite their close phylogenetic relationship, the rats and the mice are only grouped together by the orientations of the posterior canal to the ipsilateral superior oblique muscle and the lateral canal to the medial and lateral rectus muscles (Table 4c,e,f). There are significant differences between their mean values of the other three angles (ASC < iSR, ASC < cIO, PSC < cIR; Table 4a,b,d). Indeed, when considering these angles, the rats often group with the guinea pigs, and the mice are frequently associated with the squirrels. The angle of the posterior semicircular canal to the ipsilateral superior oblique muscle (Table 4c) is notable because, for this measurement, the Duncan test splits the species into just three groups – humans and cats, and two overlapping groups of rodents and rabbits – whereas four to six groups are needed to capture the variation seen in the other five canal–muscle angles.

Table 2.

X, Y and Z components of mean values (± SD) of muscle unit vectors and normal unit vectors of semicircular canal planes

	iSR			cIO
Species	X	Y	Z	X	Y	Z
Homo	−0.342 ± 0.051	−0.242 ± 0.071	−0.904 ± 0.028	0.807 ± 0.076	−0.360 ± 0.118	0.438 ± 0.116
Felis	−0.373 ± 0.088	−0.498 ± 0.046	−0.776 ± 0.048	0.601 ± 0.087	−0.288 ± 0.142	0.728 ± 0.042
Cavia	−0.533 ± 0.064	−0.633 ± 0.041	−0.555 ± 0.046	0.349 ± 0.067	−0.322 ± 0.070	0.875 ± 0.040
Rattus	−0.437 ± 0.031	−0.595 ± 0.041	−0.672 ± 0.034	0.335 ± 0.093	−0.125 ± 0.097	0.925 ± 0.039
Mus	−0.520 ± 0.088	0.640 ± 0.051	−0.554 ± 0.060	0.443 ± 0.110	0.001 ± 0.116	0.882 ± 0.052
Sciurus	−0.678 ± 0.028	−0.490 ± 0.051	−0.543 ± 0.053	0.561 ± 0.052	0.005 ± 0.140	0.816 ± 0.038
Oryctolagus	−0.657 ± 0.099	−0.585 ± 0.038	−0.444 ± 0.145	0.140 ± 0.114	−0.199 ± 0.182	0.947 ± 0.054

	iSO			cIR
Species	X	Y	Z	X	Y	Z
Homo	−0.817 ± 0.073	−0.373 ± 0.056	0.410 ± 0.149	0.400 ± 0.052	0.417 ± 0.045	−0.813 ± 0.042
Felis	−0.833 ± 0.097	−0.200 ± 0.188	0.444 ± 0.187	0.625 ± 0.091	0.064 ± 0.102	−0.763 ± 0.088
Cavia	−0.622 ± 0.050	−0.341 ± 0.119	0.691 ± 0.077	0.859 ± 0.027	−0.106 ± 0.024	−0.497 ± 0.051
Rattus	−0.726 ± 0.093	−0.131 ± 0.124	0.651 ± 0.113	0.894 ± 0.044	−0.096 ± 0.042	−0.427 ± 0.086
Mus	−0.634 ± 0.052	−0.140 ± 0.117	0.749 ± 0.065	0.828 ± 0.028	−0.223 ± 0.041	−0.510 ± 0.051
Sciurus	−0.726 ± 0.056	−0.007 ± 0.157	0.669 ± 0.061	0.900 ± 0.017	0.054 ± 0.026	−0.431 ± 0.035
Oryctolagus	−0.423 ± 0.133	−0.587 ± 0.162	0.657 ± 0.082	0.982 ± 0.009	0.115 ± 0.118	−0.056 ± 0.090

	iMR			cLR
Species	X	Y	Z	X	Y	Z
Homo	−0.052 ± 0.062	0.104 ± 0.082	−0.989 ± 0.010	0.714 ± 0.042	0.098 ± 0.049	−0.689 ± 0.047
Felis	0.021 ± 0.059	−0.211 ± 0.099	−0.971 ± 0.014	0.792 ± 0.080	−0.292 ± 0.098	−0.512 ± 0.113
Cavia	−0.204 ± 0.043	−0.361 ± 0.043	−0.908 ± 0.018	0.950 ± 0.021	−0.299 ± 0.069	−0.025 ± 0.047
Rattus	−0.252 ± 0.030	−0.381 ± 0.045	−0.888 ± 0.018	0.945 ± 0.030	−0.281 ± 0.076	−0.130 ± 0.078
Mus	−0.339 ± 0.067	−0.496 ± 0.056	−0.794 ± 0.032	0.905 ± 0.030	−0.402 ± 0.062	−0.110 ± 0.060
Sciurus	−0.353 ± 0.034	−0.274 ± 0.087	−0.891 ± 0.021	0.966 ± 0.015	−0.208 ± 0.030	0.146 ± 0.050
Oryctolagus	−0.476 ± 0.055	−0.146 ± 0.118	−0.858 ± 0.032	0.839 ± 0.043	−0.389 ± 0.084	0.361 ± 0.087

	ASC			PSC
Species	X	Y	Z	X	Y	Z
Homo	0.829 ± 0.037	−0.201 ± 0.081	−0.512 ± 0.063	−0.647 ± 0.064	−0.159 ± 0.127	−0.734 ± 0.027
Felis	0.824 ± 0.061	−0.369 ± 0.138	−0.394 ± 0.101	−0.668 ± 0.060	−0.111 ± 0.122	−0.724 ± 0.043
Cavia	0.849 ± 0.040	−0.357 ± 0.079	−0.370 ± 0.095	−0.497 ± 0.051	−0.274 ± 0.111	−0.815 ± 0.029
Rattus	0.889 ± 0.024	−0.322 ± 0.095	−0.310 ± 0.046	−0.530 ± 0.075	−0.282 ± 0.121	−0.786 ± 0.073
Mus	0.905 ± 0.039	−0.34 ± 0.098	−0.194 ± 0.138	−0.519 ± 0.067	−0.364 ± 0.046	−0.769 ± 0.047
Sciurus	0.865 ± 0.012	−0.364 ± 0.058	−0.337 ± 0.049	−0.463 ± 0.087	−0.391 ± 0.092	−0.785 ± 0.067
Oryctolagus	0.894 ± 0.045	−0.090 ± 0.150	−0.405 ± 0.084	−0.526 ± 0.043	−0.149 ± 0.135	−0.826 ± 0.039

	LSC
Species	X	Y	Z
Homo	−0.003 ± 0.065	0.969 ± 0.016	−0.228 ± 0.077
Felis	0.073 ± 0.046	0.956 ± 0.044	−0.219 ± 0.185
Cavia	0.170 ± 0.059	0.853 ± 0.025	−0.487 ± 0.050
Rattus	−0.019 ± 0.064	0.982 ± 0.020	−0.159 ± 0.086
Mus	0.035 ± 0.037	0.940 ± 0.024	−0.331 ± 0.068
Sciurus	0.096 ± 0.032	0.961 ± 0.030	−0.226 ± 0.135
Oryctolagus	−0.050 ± 0.088	0.978 ± 0.034	0.010 ± 0.190

Table 3.

Minimum and maximum values, ranges, mean values and SD of muscle–canal and inter-canal angles for whole dataset

	ASC < iSR	ASC < cIO	PSC < iSO	PSC < cIR	LSC < iMR	LSC < cLR	ASC < PSC	ASC < LSC	PSC < LSC
Minimum	−36.31	−19.67	−21.16	−39.27	−22.01	−31.31	83.17	63.43	75.35
Maximum	24.15	36.84	30.12	22.86	28.12	24.04	115.97	102.12	116.41
Range	60.46	56.51	51.28	62.13	50.13	55.35	32.80	38.69	41.06
Mean	−3.21	8.74	−3.13	−3.18	−2.74	−10.53	97.26	80.67	94.03
SD	13.07	14.12	13.31	14.88	12.33	12.43	7.36	9.32	9.44

Table 4.

Mean values (± SD), and significance of deviation from 0° or 90°, of angles between extraocular muscles and semicircular canals, and angles between semicircular canals. Groups indicate those species which show no significant differences between means, as determined by Duncan's test

A
Species	ASC < iSR	P(x = 0°)	Groups
Homo	13.20 ± 5.52	**	A
Felis	10.75 ± 9.66	*	A
Rattus	0.62 ± 3.53	ns		B
Cavia	−1.13 ± 5.89	ns		B
Mus	−8.60 ± 4.77	***			C
Sciurus	−13.07 ± 1.91	***			C
Oryctolagus	−20.93 ± 10.14	***				D

B
Species	ASC < cIO	P (x = 0°)	Groups
Homo	31.25 ± 7.29	***	A
Felis	19.44 ± 4.35	***		B
Mus	13.82 ± 6.74	***			C
Sciurus	12.01 ± 2.79	***			C
Cavia	5.03 ± 5.02	*				D
Rattus	3.03 ± 3.89	ns				D
Oryctolagus	−14.27 ± 3.88	***					E

C
Species	PSC < iSO	P(x = 0°)	Groups
Homo	16.64 ± 8.07	**	A
Felis	15.36 ± 12.5	*	A
Rattus	−4.78 ± 4.39	*		B
Cavia	−9.44 ± 6.01	**		B	C
Sciurus	−11.32 ± 4.83	***		B	C
Mus	−11.40 ± 4.87	**		B	C
Oryctolagus	−12.82 ± 3.40	***			C

D
Species	PSC < cIR	P (x = 0°)	Groups
Homo	15.61 ± 4.66	***	A
Felis	7.48 ± 9.35	ns		B
Mus	2.55 ± 3.30	ns		B	C
Cavia	0.42 ± 3.73	ns			C	D
Sciurus	−5.70 ± 4.77	ns				D	E
Rattus	−6.32 ± 8.42	ns					E
Oryctolagus	−29.92 ± 5.72	***						F

E
Species	LSC < iMR	P (x = 0°)	Groups
Homo	19.20 ± 5.79	***	A
Cavia	5.69 ± 3.57	**		B
Felis	0.78 ± 11.24	ns		B	C
Sciurus	−5.63 ± 9.25	ns			C	D
Oryctolagus	−7.36 ± 7.62	*				D
Mus	−12.49 ± 5.32	***				D
Rattus	−13.19 ± 7.09	**				D

F
Species	LSC < cLR	P(x = 0°)	Groups
Homo	14.64 ± 6.60	**	A
Cavia	−4.77 ± 3.12	**		B
Felis	−6.63 ± 7.92	*		B
Sciurus	−8.20 ± 4.22	*		B
Rattus	−15.95 ± 6.24	***			C
Mus	−18.13 ± 4.13	***			C
Oryctolagus	−24.78 ± 4.82	***				D

G
Species	ASC < PSC	P(x = 90°)	Groups
Felis	103.34 ± 9.70	**	A
Mus	101.54 ± 6.32	***	A
Rattus	97.57 ± 4.80	**	A	B
Homo	97.14 ± 4.82	*	A	B	C
Oryctolagus	97.05 ± 5.60	**	A	B	C
Cavia	91.20 ± 5.78	ns		B	C
Sciurus	89.52 ± 4.40	ns			C

H
Species	ASC < LSC	P (x = 90°)	Groups
Cavia	91.22 ± 6.97	ns	A
Homo	85.30 ± 5.81	ns	A	B
Oryctolagus	81.73 ± 11.00	ns		B	C
Sciurus	78.97 ± 6.61	*		B	C
Felis	78.36 ± 10.05	*		B	C
Mus	76.63 ± 6.02	***		B	C
Rattus	73.35 ± 6.37	***			C

I
Species	PSC < LSC	P (x = 90°)	Groups
Sciurus	104.41 ± 9.64	*	A
Rattus	98.12 ± 10.89	ns	A	B
Oryctolagus	97.52 ± 9.82	ns	A	B
Mus	96.08 ± 6.06	*	A	B
Felis	89.49 ± 6.94	ns		B	C
Homo	88.96 ± 6.33	ns		B	C
Cavia	85.58 ± 5.39	ns			C

^***P < 0.001;

^**P < 0.01;

^*P < 0.05; ns, not significant

Angles between semicircular canals

Across all species, the variation in the angles between the three semicircular canals is relatively small compared to the variation seen in the angles between the canals and the extraocular muscles. The range across the whole dataset is 32.8° for ASC < PSC, 38.7° for ASC < LSC, and 41.1° for PSC < LSC (see Table 3), whereas ranges of up to 62° are measured in the canal–muscle angles, as noted above. This suggests that the morphology of the labyrinth varies relatively little across the mammals. The mean angles between the three semicircular canals for each species are given in Table 4g–i. As with the canal–muscle angles, an analysis of variance showed the intraspecific variation to be significantly less (P < 0.001) than the interspecific variation. However, it can be seen from the Duncan tests that the interspecific variation is less than that seen for the canal–muscle angles. These post-hoc tests split the species into only three groups with a great deal of overlap, suggesting that the species means are clustered close together. There are few discernible trends within the groupings, and there is no separation of the human sample from the other species, as seen in the canal–muscle angles. Previous work (Haque et al. 2004; Hullar & Williams, 2006) has suggested that the semicircular canals of primates more closely approximate orthogonality than those of other mammalian species such as rodents, but this was not found to be true here. Although the humans were shown to deviate from orthogonality in just one semicircular canal pair – the anterior and posterior canals – this was also the case for the rabbits, and the guinea pigs showed no significant deviations from 90° between any of the three semicircular canals. Overall, the posterior and lateral canals were most often measured to be orthogonal, the angle between them departing significantly from 90° in only the mouse and squirrel samples.

Prime directions

The X, Y and Z components for the mean unit prime directions of each species are given in Table 5. It should be noted that these are prime directions of the anatomical planes, not of the afferent sensitivity planes. It can be seen that the prime directions deviate from the unit normal vectors of the canals quite considerably – from 7.5° in guinea pigs to over 20° in rats (Table 6). In general, the prime directions are not orthogonal. Species that depart the furthest from orthogonality show the greatest deviations between prime directions and normal vectors. The orientations of the prime directions to each other, as well as to the extraocular muscles, are given in Table 7. The orientations of the extraocular muscles with the anatomical canal planes and with the prime directions were compared using Student's t-test. The results (Table 8) show that, of the 42 mean muscle vectors under study (six mean vectors in seven species), 14 are significantly more aligned with the relevant prime direction than with the anatomical canal plane – both oblique muscles of the humans and cats, as well as the lateral rectus of the cat; the inferior rectus and both horizontal recti in the rat; the superior rectus, inferior oblique and both horizontal recti in the mouse; and the inferior and medial recti of the rabbit. However, 11 mean muscle vectors are significantly less aligned with the prime direction, and the remaining 17 vectors show no significant change either way. Thus there is not a consistent trend for the extraocular muscles to be more closely aligned to the prime directions.

Table 5.

X, Y and Z components of mean values of (± SD) of unit prime directions

	ASC′			PSC′
Species	X	Y	Z	X	Y	Z
Homo	0.755 ± 0.054	−0.144 ± 0.076	−0.630 ± 0.074	−0.546 ± 0.055	−0.190 ± 0.064	−0.812 ± 0.032
Felis	0.730 ± 0.060	−0.197 ± 0.139	−0.634 ± 0.083	−0.469 ± 0.118	−0.148 ± 0.144	−0.850 ± 0.081
Cavia	0.834 ± 0.052	−0.385 ± 0.062	−0.383 ± 0.055	−0.491 ± 0.074	−0.353 ± 0.054	−0.790 ± 0.049
Rattus	0.833 ± 0.051	−0.069 ± 0.051	−0.539 ± 0.086	−0.370 ± 0.039	−0.154 ± 0.091	−0.911 ± 0.025
Mus	0.850 ± 0.045	−0.198 ± 0.045	−0.481 ± 0.066	−0.307 ± 0.112	−0.306 ± 0.078	−0.892 ± 0.026
Sciurus	0.879 ± 0.046	−0.186 ± 0.075	−0.426 ± 0.078	−0.412 ± 0.051	−0.165 ± 0.120	−0.888 ± 0.039
Oryctolagus	0.822 ± 0.062	0.048 ± 0.180	−0.537 ± 0.044	−0.415 ± 0.078	−0.010 ± 0.145	−0.896 ± 0.037

	LSC′
Species	X	Y	Z
Homo	−0.071 ± 0.056	−0.953 ± 0.033	0.263 ± 0.131
Felis	−0.228 ± 0.132	−0.894 ± 0.056	0.352 ± 0.095
Cavia	−0.194 ± 0.082	−0.882 ± 0.049	0.410 ± 0.103
Rattus	−0.168 ± 0.085	−0.873 ± 0.061	0.425 ± 0.152
Mus	−0.194 ± 0.116	−0.819 ± 0.053	0.523 ± 0.060
Sciurus	−0.155 ± 0.068	−0.840 ± 0.058	0.507 ± 0.097
Oryctolagus	−0.010 ± 0.140	−0.964 ± 0.029	0.186 ± 0.144

Table 6.

Mean values (± SD), and significance of deviation from 0°, of angles between canal normals and prime directions

Species	ASC < ASC′	P (x = 0°)	PSC < PSC′	P (x = 0°)	LSC < LSC′	P (x = 0°)
Homo	9.94 ± 5.27	**	9.34 ± 4.83	**	8.79 ± 3.37	***
Felis	19.19 ± 12.73	**	16.07 ± 9.56	**	14.82 ± 9.71	**
Cavia	7.58 ± 5.17	**	7.74 ± 5.00	**	7.93 ± 6.07	**
Rattus	20.89 ± 6.44	***	16.90 ± 7.28	***	22.94 ± 6.33	***
Mus	19.25 ± 8.03	***	16.35 ± 5.14	***	17.45 ± 5.66	***
Sciurus	12.51 ± 5.91	**	15.80 ± 8.58	*	18.78 ± 10.63	*
Oryctolagus	15.32 ± 8.19	***	14.08 ± 8.34	***	15.86 ± 10.74	**

^***P < 0.001;

^**P < 0.01;

^*P < 0.05; ns, not significant.

Table 7.

Mean values (± SD) and significance of deviation from 90° or 0°, of angles between prime directions, and between extraocular muscles and prime directions

Species	ASC′ < PSC′	P(x = 90°)	ASC′ < LSC′	P(x = 90°)	PSC′ < LSC′	P(x = 90°)
Homo	82.59 ± 4.61	*	94.39 ± 6.31	ns	89.68 ± 6.62	ns
Felis	75.66 ± 10.20	**	102.2 ± 11.28	*	93.43 ± 8.89	ns
Cavia	88.34 ± 6.28	ns	88.5 ± 7.44	ns	85.38 ± 5.88	ns
Rattus	78.75 ± 6.71	**	108.71 ± 7.44	***	101.10 ± 12.38	*
Mus	76.54 ± 6.82	***	104.94 ± 6.83	***	99.53 ± 6.19	**
Sciurus	86.95 ± 4.77	ns	101.55 ± 6.65	*	104.59 ± 10.00	*
Oryctolagus	80.65 ± 6.14	**	99.31 ± 12.15	ns	98.72 ± 11.00	*

Species	ASC′ < iSR	P(x = 0°)	ASC′ < cIO	P(x = 0°)	PSC′ < iSO	P(x = 0°)
Homo	20.26 ± 5.42	***	22.51 ± 6.85	***	10.79 ± 10.04	*
Felis	18.87 ± 5.78	***	2.36 ± 8.98	ns	3.09 ± 16.93	ns
Cavia	0.72 ± 5.15	ns	4.54 ± 4.92	*	−7.16 ± 7.13	*
Rattus	2.22 ± 4.55	ns	−12.21 ± 10.76	*	−17.94 ± 8.31	***
Mus	−2.75 ± 5.31	ns	−2.82 ± 9.80	ns	−25.68 ± 7.36	***
Sciurus	−15.98 ± 7.32	**	8.81 ± 2.91	**	−16.87 ± 6.03	**
Oryctolagus	−19.8 ± 7.16	***	−23.30 ± 6.40	***	−25.08 ± 7.21	***

Species	PSC′ < cIR	P(x = 0°)	LSC′ < iMR	P(x = 0°)	LSC′ < cLR	P(x = 0°)
Homo	21.25 ± 4.08	***	−20.91 ± 9.61	**	−18.95 ± 7.80	**
Felis	20.35 ± 10.60	**	− 9.09 ± 9.55	*	−5.62 ± 8.51	ns
Cavia	0.53 ± 5.74	ns	−0.84 ± 5.78	ns	4.12 ± 6.45	ns
Rattus	4.18 ± 6.25	ns	−0.12 ± 8.74	ns	1.69 ± 6.75	ns
Mus	15.79 ± 6.19	***	3.33 ± 5.19	ns	5.64 ± 9.20	ns
Sciurus	0.06 ± 3.93	ns	−9.64 ± 7.79	ns	5.66 ± 4.56	ns
Oryctolagus	−21.24 ± 6.07	***	−1.05 ± 12.34	ns	26.12 ± 10.52	***

^***P < 0.001;

^**P < 0.01;

^*P < 0.05; ns, not significant.

Table 8.

Probabilities that the mean orientations of the extraocular muscles to the semicircular canals and to the prime directions are equal

Species	ASC/ASC′ < iSR		ASC/ASC′ < cIO		PSC/PSC′ < iSO		PSC/PSC′ < cIR		LSC/LSC′ < iMR		LSC/LSC′ < cLR
Homo	**	(a)	*	(p)	*	(p)	*	(a)	ns		ns
Felis	*	(a)	**	(p)	*	(p)	*	(a)	ns		*	(p)
Cavia	ns		ns		ns		ns		ns		ns
Rattus	ns		**	(a)	**	(a)	**	(p)	*	(p)	**	(p)
Mus	*	(p)	***	(p)	***	(a)	***	(a)	**	(p)	***	(p)
Sciurus	ns		ns		ns		ns		*	(a)	ns
Oryctolagus	ns		***	(a)	**	(a)	***	(p)	*	(p)	ns

^***P < 0.001;

^**P < 0.01;

^*P < 0.05; ns, not significant; a, anatomical plane more closely aligned with muscle; p, prime direction more closely aligned with muscle.

Discussion

The angles between each extraocular muscle and the semicircular canal by which it is principally activated were calculated from three-dimensional co-ordinate data. It was determined that the muscles and canals are frequently not in alignment, and vary widely in their relative orientations between mammalian species commonly used in research. Similar patterns of variation have also been observed during human development (Cox & Jeffery, 2007). Across all seven species studied, the rat and the guinea pig show the closest spatial alignment between the vertical canals and the extraocular muscles, particularly with regard to the superior and inferior recti. The least aligned axes were found among the rabbits and modern humans. Proposed compensatory mechanisms for the spatial integration of vestibular signals with the activation of the extraocular muscles include changes in the maximal response planes (e.g. Estes et al. 1975; Reisine et al. 1988; Haque et al. 2004). These studies demonstrate that the plane of rotation that produces the maximum response of the ampullary nerve in the cat and rhesus monkey only differs by about 10° from the anatomical plane. In the present study, estimations of these maximal response planes using prime directions (see Rabbitt, 1999) revealed differences of about 7–23° relative to the anatomical planes. Although some of these differences were compensatory in that the prime planes were closer than the anatomical planes to the muscle orientations, the findings were inconsistent. Indeed, in a number of cases, a muscle was found to be less closely aligned to the prime direction than to the semicircular canal by which it is primarily activated (see Table 8). These findings would appear to favour the idea that the spatial mismatch is corrected for elsewhere, probably along the three-neuron arc and most likely involving signal transformations within the vestibular nuclei with reference to the flocculus (Ito, 1982; Ito et al. 1982; Brettler & Baker, 2001; Billig & Balaban, 2005). Nevertheless, there remain several other structural possibilities for helping to resolve differences between the vestibular and extraocular spatial frameworks among mammals. These include canal shape, canal torsion and fluid coupling, particularly in the common crus (Oman et al. 1987; Hullar, 2006).

Comparing values of optic divergence from Hughes (1977) with the muscle–canal angles reported here, it can be seen that the two broadly correlate. Table 4a–f show that, for each angle, the species tend to be arranged with the highly optically convergent humans (binocular vision) at one extreme, and the very optically divergent rabbits (optic axis approximately 85° from midline) at the other. This suggests that it is realignment of the extraocular muscles, rather than of the semicircular canals, that is driving the variation in their relative orientations. This is indicated by Simpson & Graf (1981) who found a range of just 4° in the angle of the anterior semicircular canal to the midline in a sample of humans, cats, guinea pigs and rabbits, but measured a range of 42° in the angle of the superior rectus muscle to the midline. Similarly, the superior oblique varied over 39° in its orientation to the midline, whereas the posterior canal had a much more restricted range of just 14°. Mediolateral realignment of the optic axes only accounts for variation in the orientation of the vertical semicircular canals to the relevant extraocular muscles (Table 4a–d). Angles measured between the lateral canal and the horizontal muscles indicate misalignment in the dorsoventral direction, which is not affected by the divergence of the eyes. This can be seen in the results for LSC < iMR and LSC < cLR (Table 4e,f), which differ from those of the other four angles. For instance, the lateral-eyed guinea pigs are more similar to the cats in these angles but tend to group with the other rodents when considering angles involving the vertical canals. However, angles of the lateral canal to the medial and lateral recti could be influenced by dorsoventral realignment of the optic axes, a process referred to as frontation (see Noble et al. 2000). For example, in humans the eyes face forwards relative to the cranium, whereas in rabbits the eyes are tilted upwards.

Changes in the relative positions of the muscles could also be influenced by changes in eye size. Increasing or decreasing the size of the eye will tend to displace the insertion points of the extraocular muscles, changing their orientations relative to the semicircular canals. Eye size does not have a simple linear relationship with body size across all mammals. At small size (< 1 kg), eye mass scales hyperallometrically with body mass, at medium size (1–79 kg) the two masses are related isometrically, and at large size (> 80 kg) they are relatively independent (Hughes, 1977; Kiltie, 2000). Similarly, Burton (2006) found an isometric relationship between eye size and brain size up to approximately 200 g brain mass, but evidence of independence between the two variables beyond this size. Hence, the difference in eye size in the rabbits, cats and humans is proportional to their difference in body size, but the four rodents in the analysis have smaller eyes than might be expected for their size, which may account for some of the variation seen in the relative orientations of the extraocular muscles.

Despite showing a great deal of variation in their orientation relative to the extraocular muscles, the semicircular canals do not vary as much in their orientations to each other. The canals are rarely perpendicular, with deviations of almost 30° from orthogonality being measured in some individuals. The one exception here is the guinea pig, in which all three inter-canal angles show no significant difference from 90°. This is in direct contradiction to Curthoys et al. (1975), who calculated mean deviations from 90° of at least 8° in all three angles in the guinea pig, and a mean angle of 58° between the anterior and lateral canals [actually reported as 122° because Curthoys et al. (1975) were measuring the supplementary angle ventral to the lateral canal]. Similarly, Blanks et al. (1975) measured a mean angle of 68° (reported as 112°) between the same two canals in humans, whereas the mean value calculated here was just over 85°. The lack of correspondence between these results may possibly be attributed to differences in the method of mapping the semicircular canals. Blanks et al. (1972, 1975) and Curthoys et al. (1975) exclude points from the common crus and ampullae from their measurements, whereas this study follows the more recent work of Calabrese & Hullar (2006) and Hullar & Williams (2006) and includes them. Also, older studies that employed a micromanipulator to map the canals (Blanks et al. 1972, 1975; Curthoys et al. 1975) tend to use three-dimensional co-ordinates from the medial-most wall of the osseous canals. In contrast, this study based on MR images was able to use the co-ordinates of centroids of each semicircular canal lumen.

To summarize, the present study finds significant variations in the spatial arrangement of the semicircular canals and the extraocular muscles both within and between species commonly used as experimental models of the vestibulo-ocular reflexes. The spatial arrangement of the canals and muscles in the cat and the arrangement among the canals in the guinea pig most closely resemble the conditions found in modern humans. The rabbit closely matches humans in terms of the severity of the functional challenge of integrating different extraocular and vestibular co-ordinate frames. However, it is important to note that humans are distinct from all the other species studied in terms of the angles between vertical canals and contralateral muscles (i.e. PSC < cIR & ASC < cIO) and the angles between the lateral canal and horizontal muscles (LSC < iMR & LSC < cLR). These angles may have some deeper functional or structural significance. For example, Spoor et al. (2007) have recently demonstrated a strong statistical link between lateral canal arc size and agility among a large sample of mammals, based on the presumed importance of arc size to calibrate mechanical sensitivity levels. Yang & Hullar (2007) report that canal orientation may also have a substantial impact on sensitivity, and varying canal angles may thus be linked with locomotor agility.

Our findings support the view that the vestibular reference frame remains relatively stable and that spatial disparities with the extraocular co-ordinate system arise due to changes of orbit position. However, the exact nature of the variation remains unclear and important questions have yet to be answered. For instance, does the extraocular frame move with the orbit as one rigid unit, or are there perhaps significant changes within the extraocular frame such as a convergence in the line of action of the superior oblique and superior rectus muscles (see Simpson & Graf, 1981)? Also, in species with extreme spatial mismatching does the functional capacity of the three-neuron arc impede the high frequency and irregular head movements normally used during agile forms of locomotion (see Spoor et al. 2007)? At present we can only surmise the answers, as the limited range of species studied to date do not give sufficient data resolution to map out statistically meaningful interspecific trends. Other possible constraints or perturbations to the extraocular co-ordinate frame and to its links with the vestibular frame include changes of basicranial architecture (Ross & Ravosa, 1993), orbital frontation (Noble et al. 2000) as well as phylogeny (Garland et al. 2005) and body size scaling. We are currently repeating the current study with a broader range of over 40 mammalian species to clarify the above questions.