Human cancellous bone from T12-L1 vertebrae has unique microstructural and trabecular shear stress properties

Abstract

Increase of trabecular stress variability with loss of bone mass has been implicated as a mechanism for increased cancellous bone fragility with age and disease. In the current study, a previous observation that trabecular shear stress estimates vary along the human spine such that the cancellous tissue from the thoracic 12 (T12)-lumbar 1 (L1) junction experiences the highest trabecular stresses for a given load was tested as a formal hypothesis using multiple human spines.

Thoracic 4, T5, T7, T9, T10, T12, L1, L2, L4 and L5 vertebrae from 10 human cadaver spines were examined. One specimen in the central anterior region was cored in the supero-inferior (SI) direction and another in the postero-lateral region was cored in the transverse (TR) direction from each vertebra. Micro-CT-based large-scale finite element models were constructed for each specimen and compression in the long axis of the cylindrical specimens was simulated. Cancellous bone modulus and the mean, the standard deviation, variability and amplification of trabecular von Mises stresses were computed. Bone volume fraction, trabecular number, trabecular thickness, trabecular separation, connectivity density and degree of anisotropy were calculated using 3D stereology. The results were analyzed using a mixed model in which spine level was modeled using a quadratic polynomial.

The maximum of trabecular shear stress amplification and minimum of bone volume fraction were found in the cancellous tissue from the T12-L1 location when results from the samples of the same vertebra were averaged. When groups were separated, microstructure and trabecular stresses varied with spine level, extrema being at the T12-L1 levels, for the TR specimens only. SI/TR ratio of measured parameters also had quadratic relationships with spine level, the extrema being located at T12-L1 levels for most parameters. For microstructural parameters, these ratios approached to a value of one at the T12-L1 level, suggesting that T12-L1 vertebrae have more uniform cancellous tissue properties than other levels. The mean intercept length in the secondary principal direction of trabecular orientation could account for the variation of all mechanical parameters with spine level.

Our results support that cancellous tissue from T12-L1 levels is unique and may explain, in part, the higher incidence of vertebral fractures at these levels.

INTRODUCTION

It is estimated that more than 2 million people experience fractures attributable to osteoporosis every year in the United States. There are approximately 8 million women currently diagnosed with osteoporosis and there is an additional 22 million with low bone mass with the potential to develop osteoporosis [6, 47]. Men are also considered at significant risk [49]. The hip, spine and the distal forearm are the most common sites of fractures but fractures of skeletal sites other than these can make up to 40% of total fractures [6, 10]. Although much of the mortality and morbidity due to osteoporosis-related fractures are associated with those of the hip [9, 18], pain and disability associated with fracture of the spine is no less of a problem, especially when the fact that 50% of the elderly female population is expected to have at least one vertebral fracture is considered [40, 41, 46]. Thoracic 12 and lumbar 1 together have the highest incidence of vertebral collapse and account for 24.2–60.6% of all vertebral fractures among T3 to L5 levels [2, 4, 16, 19, 34, 48], followed by a second peak at T7-T8 [41]. Overall, the junction of the thoracic and lumbar spine (T12-L1 vertebrae) is a critical site as far as vertebral fractures are concerned.

One of the possibilities that can explain the greater fragility of the vertebrae at the T12-L1 levels is that they have some inherent properties that are substantially different from those of other vertebrae. A number of studies investigated the variation of vertebral properties with spine level in the human spine. The results of previous work collectively indicate that there is a general tendency of vertebral strength and size to increase from superior to inferior vertebrae [8, 14, 39, 43, 44, 51, 55]. (This list is not exhaustive; see [51] for a compilation of such results.) Isolated measurements of vertebral cancellous bone did not reveal a difference in density or strength between different thoracic and lumbar levels in some studies [14, 21] while a decrease in cancellous bone density from superior to inferior vertebrae was reported in others [50, 51]. These studies greatly varied in their methods and scope, and although they reached somewhat different conclusions, none reported a minimum or maximum property that could be distinctly associated with T12 or L1 levels.

Due to advances in the imaging and computer technologies, it is possible to examine detailed 3D microstructural properties of cancellous bone. Using microcomputed tomography and large-scale finite element modeling, we previously made an observation that bone volume fraction and estimates of trabecular shear stresses in human vertebral cancellous bone vary with spine level such that the cancellous tissue from the T12 and L1 levels experiences the highest trabecular shear stresses for a given apparent compressive stress [59]. Increase of trabecular stress magnitude and variability with loss of bone mass has been implicated as a mechanism for increased cancellous bone fragility with age and disease [17, 59]. Evidence also exists that trabecular shear stress distribution parameters (trabecular shear stress per apparent uniaxial stress and coefficient of variation of trabecular shear stress) as estimated from large scale finite element analyses are associated with age [61], cancellous bone compressive strength [17] and with the amount of in vivo microdamage [58] in human vertebral bone. The variation of microstructural and stress distribution parameters with spine level could provide insight into the understanding of vertebral fractures at specific levels, however, our observation from a single spine, a 63 year-old male, has not been confirmed with a larger sample size. Therefore, our primary objective was to test, as a formal hypothesis, the observation that trabecular shear stress distribution parameters have maximum or minimum at T12-L1 levels. In addition, we sought to determine the relationship between cancellous tissue stress distribution properties and spine level for a loading direction other than the supero-inferior direction. Finally, we examined which microstructural properties could explain the variation of stress distribution properties with spine level.

METHODS

Thoracic 4, T5, T7, T9, T10, T12, L1, L2, L4 and L5 vertebrae were collected from 10 human cadaver spines (5 males, 5 females; Age=79.3±9.1 Yrs). Thoracic 6, T8, T11 and L3 vertebrae from each spine were saved for another experiment. From the central anterior region of each vertebra, a cylindrical core was cut out in the nominal supero-inferior (SI) direction using an 8 mm diameter diamond abrasive coring tool (Felker, Cerritos, CA) [57]. The ends of the bone cores were removed using a low speed saw (Model 660, South Bay Technology, Inc., Temple City, CA) resulting in cylindrical cancellous bone specimens with a nominal diameter of 8 mm and a height of 10 mm. A second core (TR) aligned with a direction perpendicular to the SI specimen was also prepared from the left or right postero-lateral region of the same vertebra (Figure 1). Out of 200 targeted specimens, 171 were successfully machined without apparent artifacts such as breakage of the specimen during coring or containing cortical shell and/or very large pores that required substantial reduction in size of the specimen in order to get a cylinder.

Figure 1.

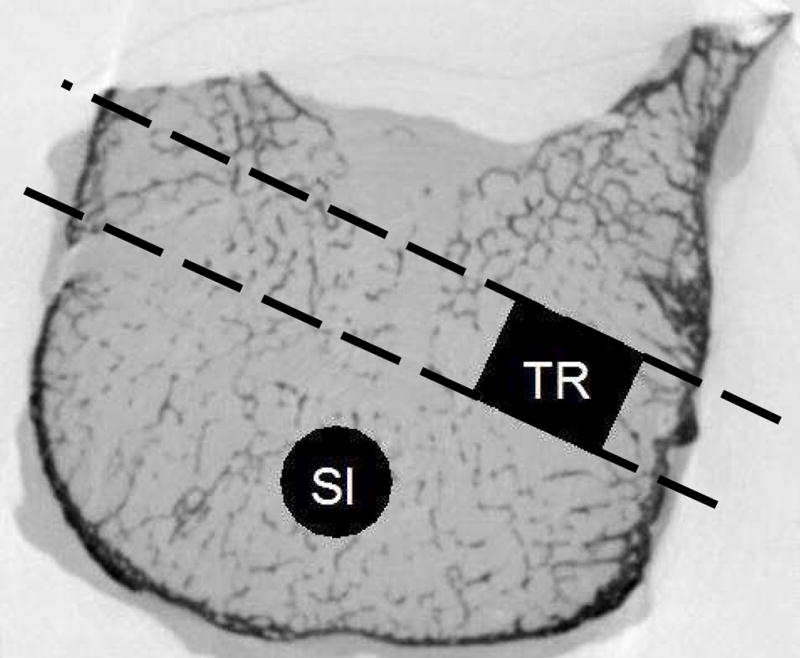
The location and direction of cores. The SI specimen was cored out first. The TR specimen was cored out second, from either the left or the right side of the vertebral body. Cylindrical cancellous bone specimens were machined by trimming the ends of these cores. The TR specimen was located approximately at the location shown in black.

No effort was made to align the specimens with principal texture directions as done in some studies focused on on-axis and off-axis material behavior of cancellous bone [53] because this would require an assumption that the anatomic directions would exactly coincide with the principal texture directions. Nonetheless, a posteriori analyses confirmed that the nominal SI and TR directions corresponded to principal texture directions (see below).

Specimens were scanned at a voxel size of 28 μm, using a microcomputed tomography (μCT) scanner (Healthcare Explore Locus, GE Medical Systems, London Ontario). μCT attenuation values (gray levels, μCT-GL) were scaled with a calibrated solid phantom and recorded in Hounsfield Units. The bone voxels in the 3D μCT images were segmented using a global threshold method based on matching the bone volumes of segmented images with those obtained using Archimedes’ principle [12]. The average, standard deviation and coefficient of variation of gray levels from bone voxels were computed.

Large-scale finite element (FE) models were constructed for each specimen and compression to 0.005 strain was simulated using fixed-end boundary conditions [25, 56, 57, 59]. A homogeneous hard tissue modulus of 5 GPa and a Poisson’s ratio of 0.3 were assigned to each element. Modulus of cancellous cylinders (E_FE) was recorded as the apparent stress (σ_app) calculated from the FE analysis divided by the simulated strain. The mean (VMExp) and the standard deviation (VMSD) of trabecular von Mises stresses were computed by fitting a three-parameter Weibull cumulative probability function to the stress distribution for each specimen [17, 58, 59]. The shear stress amplification was calculated as VMExp/σ_app and coefficient of variation (VMCV) as VMSD/VMExp.

Microstructural parameters, namely, bone volume fraction (BV/TV), bone surface-to-volume ratio (BS/BV), trabecular number (Tb.N), trabecular thickness (Tb.Th), trabecular separation (Tb.Sp), connectivity based on Euler number (Eu.N), mean intercept length in the primary, secondary and tertiary principal directions (MIL1, MIL2 and MIL3, respectively) and degree of anisotropy (DA=MIL1/MIL3) were calculated from the μCT images using 3D stereology [20, 30].

The results were analyzed using a mixed model with one of the FE or microstructural parameters as the dependent variable and spine levels and donors as the independent variables. Spine levels (SL) from T4 through L5 were numbered from four to 17 and modeled using a quadratic polynomial. Donors were introduced as a random variable. If the quadratic spine-level variable was significant, then the SL value corresponding to the maximum or the minimum of the dependent variable was recorded. If it was closer to T12 or L1 than any other vertebra, the hypothesis (that the property has an extremum at T12-L1) deemed proven.

In order to determine if microstructural parameters might account for spine-level dependence of mechanical parameters, further mixed models similar to those described above were used. For each mechanical parameter (VMExp, VMSD, VMCV, VMExp/σ_app and E_FE) found to be significantly dependent upon the quadratic spine-level variable in the mixed model described above, one or more additional models were fit with the addition of one microstructural parameter (BV/TV, BS/BV, Tb.N, Tb.Sp, Tb.Th, Eu.N, MIL1, MIL2, MIL3 or DA), if that microstructural parameter also had a significant association with quadratic representation of spine level. That is, the mechanical parameter was modeled as a function of donor, spine level and one microstructural parameter. If the microstructural parameter was significant and the coefficients of the quadratic spine-level variable for the mechanical parameter became non-significant, it was concluded that the association of the mechanical parameter with spine level was not independent of the variation in the microstructual parameter.

JMP (SAS Institute, Cary, NC) was used for the analyses and statistical significance was set at p<0.05.

RESULTS

The mean intercept length in the direction of coring strongly correlated with the mean intercept length in the primary MIL direction for the SI group specimens (r²_adj=0.99, p<0.001, slope of regression=1.011) indicating that the SI specimens were consistently machined in the primary principal MIL direction (r²_adj=0.46, p<0.001, slope=0.454; r²_adj=0.33, p<0.001, slope=0.379; for MIL2 and MIL3, respectively). The mean intercept length in the direction of coring strongly correlated with the mean intercept length in the secondary MIL direction for the TR group specimens (r²_adj=0.89, p<0.001, slope of regression=0.981) indicating that the TR specimens were consistently machined in the secondary principal MIL direction (r²_adj=0.61, p<0.001, slope=0.949; r²_adj=0.84, p<0.001, slope=0.840; for MIL1 and MIL3, respectively).

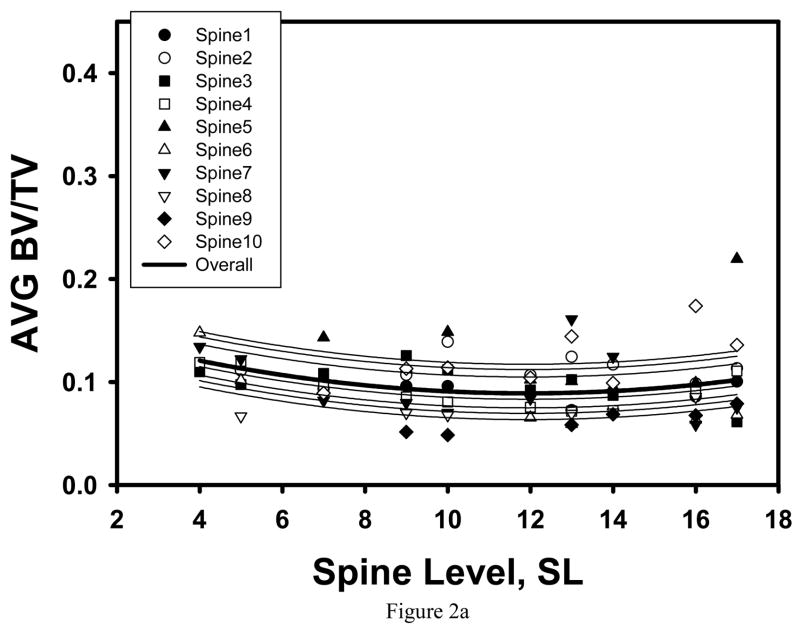
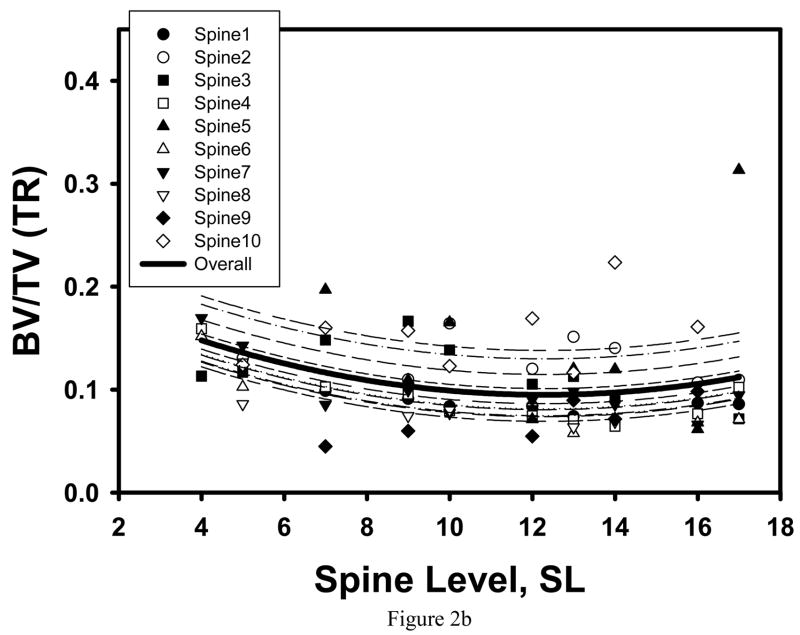
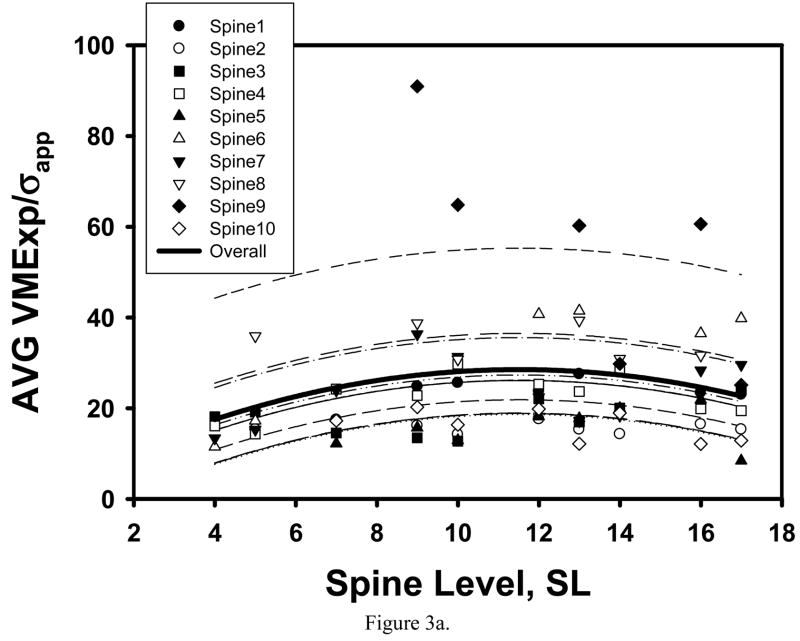
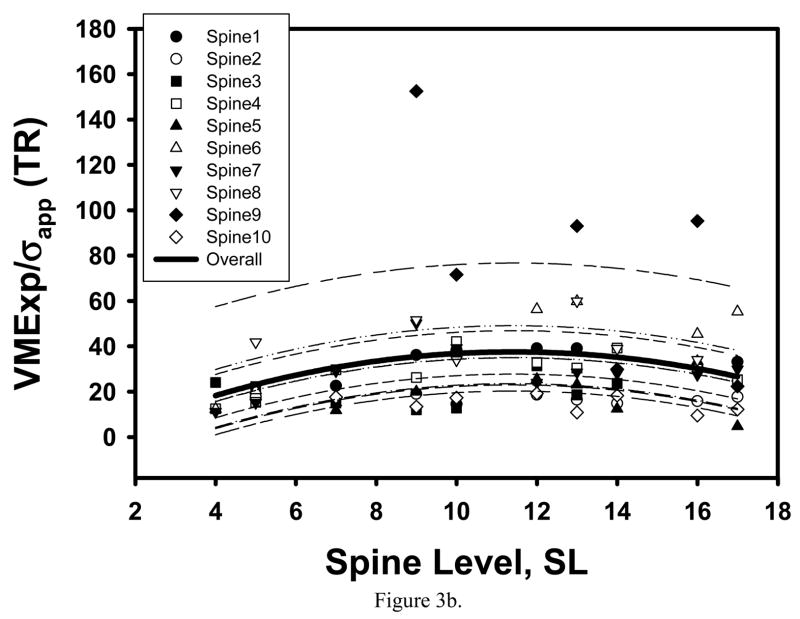
Consistent with our preliminary observation [59], the maximum of average trabecular shear stress amplification and minimum of average BV/TV were found in the cancellous tissue from the T12-L1 location (Table 1, Figure 2a, 3a). However, microstructural and trabecular stress parameters both significantly varied with spine level and had an extremum at the T12-L1 levels for the TR specimens only (Figure 2b, 3b).

Table 1.

Summary of results showing whether a given microstructural property of human vertebral cancellous bone has a significant quadratic relationship with spine level (p), at which spine level the extremum value occurs (SL) and whether the extremum is a maximum or a minimum (Ext). Results have been analyzed for the supero-inferior (SI) and transverse (TR) specimens separately as well as for their within-vertebra average (AVG) and ratio (SI/TR). The T12-L1 column indicates the value of a ratio at an SL value of 12.5, which corresponds to T12-L1 levels on a continuous scale shown on the left of the table.

Vertebra	SL	Parameter	p	SI SL	Ext	p	TR SL	Ext	p	AVG SL	Ext	p	SI/TR SL	Ext	T12-L1
T4	4	BV/TV	0.285			0.004	12.3	Min	0.007	11.9	Min	0.302
T5	5	BS/BV	0.427			0.001	11.1	Max	0.009	10.8	Max	0.065	11.7	Min	1.02
T6	6	Tb.N	0.161			0.010	14.6	Min	0.008	12.8	Min	0.837
T7	7	Tb.Sp	0.198			0.019	16.4	Max	0.016	13.0	Max	0.463
T8	8	Tb.Th	0.522			0.002	10.9	Min	0.012	11.0	Min	0.045	11.7	Max	1.01
T9	9	Eu.N	0.869			0.427			0.885			0.394
T10	10	MIL1	0.405			0.096			0.314			0.221
T11	11	MIL2	0.259			0.001	10.6	Min	0.001	10.3	Min	0.017	11.6	Max	0.98
T12	12	MIL3	0.451			0.006	11.6	Min	0.055	11.5	Min	0.052	12.0	Max	0.98
L1	13	DA	0.103			0.204			0.306			0.599
L2	14	μCT-GL	0.095			0.447			0.078			0.353
L3	15	VMExp	0.013	9.6	Max	0.001	11.1	Min	0.033	13.2	Min	0.003	10.7	Max	2.50
L4	16	VMSD	0.003	10.0	Max	0.003	10.9	Min	0.084	12.4	Min	0.004	10.7	Max	2.09
L5	17	VMCV	0.093			0.188			0.135			0.805
		VMExp/σapp	0.908			0.003	11.9	Max	0.003	11.5	Max	0.006	11.1	Min	0.65
		EFE	0.433			0.004	10.7	Min	0.039	11.9	Min	0.010	11.5	Max	5.59

Figure 2.

Mixed model fit to the BV/TV averaged over the SI and TR specimens of the same vertebra indicated a significant quadratic trend with spine level, with minimum AVG BV/TV corresponding to the T12 level (a). When separately fit to the SI and TR specimens, a significant quadratic trend with SL was found for the TR specimens only (b).

Figure 3.

Mixed model fit to the VMExp/σ_app averaged over the SI and TR specimens of the same vertebra indicated a significant quadratic trend with spine level, with minimum AVG VMExp/σ_app corresponding to the T12 level (a). When separately fit to the SI and TR specimens, a significant quadratic trend with SL was found for the TR specimens only (b).

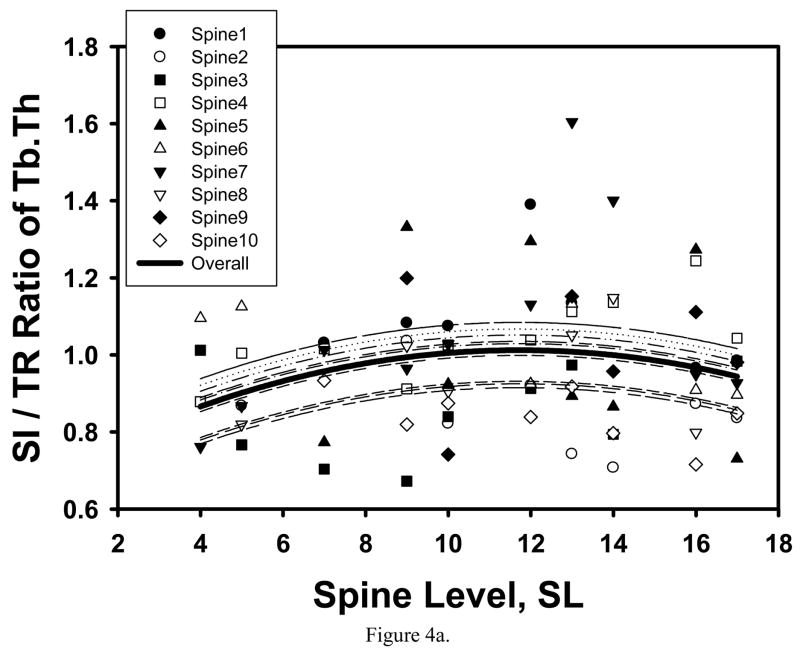
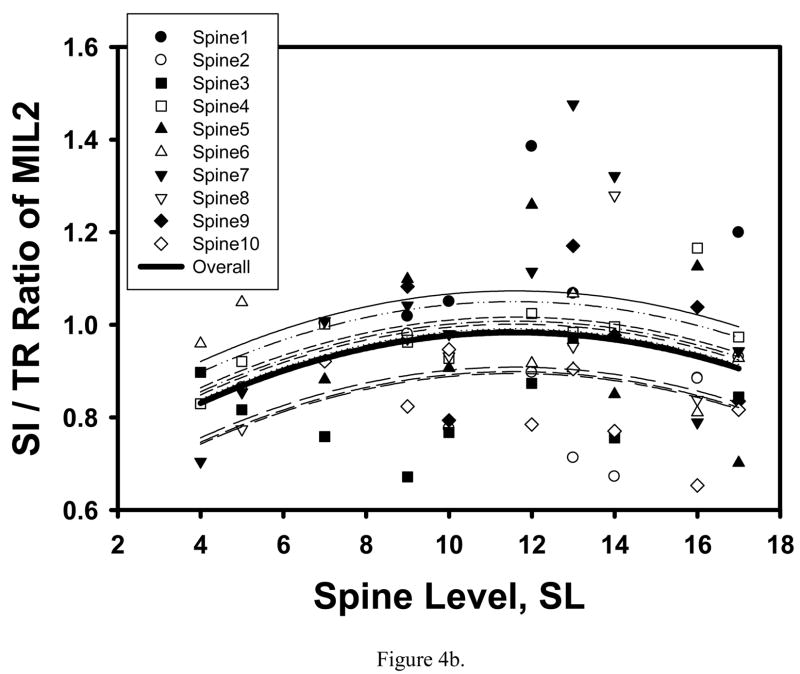
SI/TR ratio of Tb.Th, MIL2, MIL3, VMExp, VMSD, VMExp/σ_app and E_FE also had significant or marginally significant quadratic relationships with spine level, the extrema being located at the T12 level for Tb.Th, MIL2, MIL3 and E_FE (Table 1, Figure 4). Interestingly, while these ratios varied significantly along the spine, their values approached to 1 (0.980–1.023) at the T12-L1 level (SL=12.5) for Tb.Th, MIL2 and MIL3, suggesting that the cancellous tissue has more uniform properties in T12-L1 vertebrae.

Figure 4.

Mixed model fit to the SI to TR ratio of Tb.Th (a) and MIL2 (b) indicated a significant quadratic trend with spine level with maximum ratios corresponding to the T12 level.

Additional tests for interaction between gender and spine level-related terms (SL and SL²) in our models revealed no evidence of gender dependence in a relationship between spine level and one of FE/microstructure parameters (0.086<p<0.993) Therefore, gender effects were not pursued further.

Because none of the microstructural parameters significantly varied with spine level in the SI group (Table 1), models including both mechanical and microstructural parameters were not run for this group. In the TR group, all microstructural parameters were significant (Table 2) when added to the mixed models in which spine level (SL) was modeled as a quadratic polynomial. While the linear or quadratic variation of at least one mechanical parameter with spine level was independent of each microstructural parameter, none of the mechanical parameters varied with SL independently from the mean intercept length in the secondary principal direction of trabecular orientation (MIL2).

Table 2.

p-values for the main microstructural variable and the linear (SL) and quadratic terms (SL²) of spine level in the mixed models of mechanical parameters (left column). The SL terms remained significant in the model were deemed unexplained by the microstructural parameter.

Model	BV/TV SL SL2	Tb.N SL SL2	BS/BV SL SL2	Tb.Th SL SL2	Tb.Sp SL SL2	MIL2 SL SL2	MIL3 SL SL2
VMExp/σapp	<.001 0.509 0.112	<.001 0.086 0.111	<.001 0.826 0.246	0.001 0.860 0.109	<.001 0.018 0.078	<.001 0.416 0.314	0.001 0.902 0.067
EFE	<.001 0.001 0.173	<.001 <.001 0.073	<.001 0.435 0.158	<.001 0.460 0.189	<.001 0.002 0.034	<.001 0.695 0.759	<.001 0.235 0.090
VMExp	<.001 0.026 0.093	<.001 0.001 0.029	<.001 0.643 0.056	<.001 0.683 0.052	<.001 0.003 0.013	<.001 0.422 0.392	<.001 0.399 0.023
VMSD	<.001 0.092 0.157	<.001 0.013 0.075	<.001 0.514 0.139	<.001 0.543 0.117	<.001 0.009 0.045	<.001 0.780 0.533	<.001 0.357 0.070

The variation of μCT-attenuation parameters with spine level was not significant (Table 1). The coefficient of variation of bone gray levels within a specimen was 21.1±3.6%. The between-specimen variability of within-specimen variability was less (17.2%). The variability of average gray levels was less than 10% (2070±199 units) among all specimens.

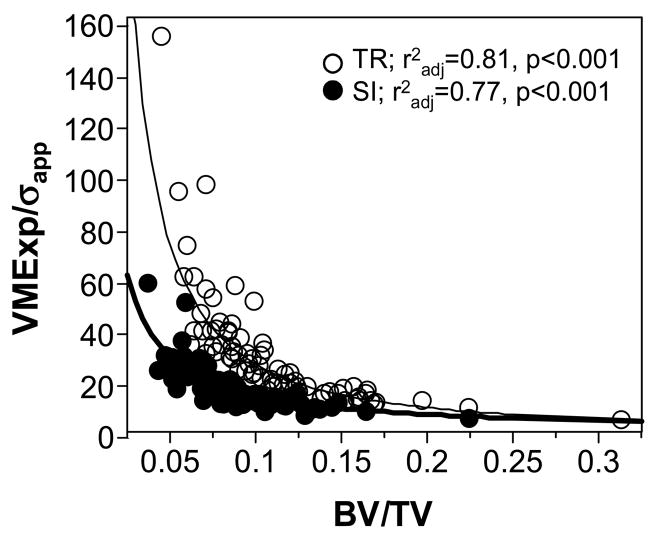
A strong negative nonlinear (log-log) relationship was found between VMExp/σ_app and BV/TV for both TR and SI specimens (Figure 5).

Figure 5.

Negative log-log relationship between VMExp/σ_app and BV/TV showing that VMExp/σ_app decreased nonlinearly with increasing BV/TV.

DISCUSSION

In support of the idea that trabecular stress distribution properties of cancellous bone explain the fragility of the T12-L1 vertebrae, we investigated the variation of trabecular stress magnitude and variability (as well as the architectural parameters) in the cancellous bone along the same spine. We have demonstrated that trabecular stress distributions caused by a uniform compression of the cancellous tissue and cancellous microstructural parameters are associated with the spine level in human vertebral bone, the results being significant for the transverse specimens only. Consistent with our preliminary observation [59], when averaged over two samples from the same vertebra, the maximum of average trabecular shear stress amplification and minimum of average BV/TV were found in the cancellous tissue from the T12 location (Table 1). The minimum BV/TV and maximum trabecular shear stress amplification in the tissue from the T12 vertebrae are consistent with reports that highest incidence of vertebral fractures is observed in the T12 and L1 vertebrae [27] and suggest that the cancellous bone from the critical T12-L1 locations is inherently weak compared to cancellous bone from other vertebrae.

When SI and TR specimens were analyzed separately, we did not find, in contrast to our initial hypothesis, that the cancellous bone structure from the central anterior location of vertebral bodies was different between spine levels. However, we did find that the architecture of the cancellous bone from the postero-lateral parts of the vertebral body varies with spine level such that the minimum values of BV/TV and MIL3 (mean intercept length in the tertiary direction) and the maximum value of shear amplification correspond to the T12 level. Because the SI specimens were cored from the anterior location in the supero-inferior direction and the TR specimens were cored from the postero-lateral locations in a transverse direction, the differences between the SI and TR specimens could be due to the anisotropy of the cancellous bone or due to anatomic site differences within the vertebra. However, the microstructural parameters are independent of the orientation of the specimen, indicating that the spine level-dependence of microstructure found for the TR specimens is due to the within-vertebra variability of cancellous tissue properties. Strong relationships found between stress amplification and BV/TV (Figure 5) for both SI and TR specimens suggest that stress amplification would follow trends similar to that of BV/TV for other combinations of specimen orientation and within-vertebra location. Thus we suspect that stress amplification in the supero-inferior direction would follow trends similar to that in the transverse direction for the postero-lateral locations in the vertebra. Therefore, while the values of modulus and stresses would be different between supero-inferior and transverse loading of a specimen from the same location, valid discussions regarding relative differences between within-vertebra and between-vertebra locations can be made. The explanatory capability of MIL2 for the significant dependence of stress and stiffness properties on spine level suggests that processes affecting trabecular thickness and spacing in the secondary structural direction are important in determining the structural organization of vertebrae at each level. Conversion of trabecular geometry from plate-like to rod-like would be one of these processes. Plate-like to rod-like transition has been noted in other high fracture-risk situations such as in the aging proximal tibia [11], in the iliac crest of women during the transmenopausal period [1] and in the iliac crest of women with prevalent vertebral fractures and continued to lose bone for three years [3]. Because resorbing trabeculae in their thinnest direction (i.e., resorbing in the MIL3 direction) can result in disconnection of the trabecular network, it seems a better adaptational strategy to remove material from the thick directions. However, reduction in MIL2 could eventually reduce the resistance of the structure to buckling as well to off-axis loads. In addition, plate-like structures have more predictable buckling directions. Changes in the secondary thickness direction of the cancellous bone would make buckling of the structure more probable in directions that would normally be prevented. Further studies on this topic should focus on parameters that quantify anisotropic geometry of single trabeculae such as structure model index which was introduced to quantitate how plate- or rod-like the trabeculae are in a volume of cancellous bone [23].

Interestingly, when the SI to TR ratio of parameters is considered for a given vertebra, the variation of trabecular architecture and stresses with spine-level were such that cancellous tissue properties become more homogeneous within the centrum of the T12-L1 than in other vertebrae. A clinical study reported that the scatter of CT-gray level values from L3-L4 vertebrae could separate females with fracture from those without fracture better than the average bone mineral density (BMD) [13]. Consistent with our finding that vertebrae from more fragile locations (T12-L1) have more homogenous cancellous tissue, the variability of CT values (for a given BMD) in the Dougherty study was lower in the group with fracture than that without fracture. However, together with our recent findings that the increased within-vertebra variability of cancellous tissue properties is associated with decreased whole vertebra strength [32, 62], these data indicate, consistent with previous reports [8, 14, 39, 51, 55], that T12-L1 vertebrae do not have less strength than other vertebrae and further suggest that mechanical factors other than uniaxial strength are involved in the greater fragility of T12-L1 vertebrae.

Finite element calculations in other studies estimated that cancellous bone from osteoporotics was stiffer than in non-osteoporotics in the predominant loading direction for a given bone mass [24, 54]. The increased homogeneity of the cancellous bone in T12-L1 may be due to an increased effort to maintain whole bone stiffness in the predominant loading direction. The donors in the current study were old and, although were not examined for osteoporosis, likely had low bone mass compared to younger individuals. In the case of bone loss, an effort to maintain bone stiffness in a given loading direction would require reorganization of the bone structure. This can have several consequences concerning bone fractures. Maintaining stiffness in the (nominal) primary loading direction would come at a cost of reduced stiffness in other loading directions and “error” loads in non-frequent load directions would be a potential source of fragility as suggested before [24, 52]. These error loads might include the infrequent but large bending loads, particularly those associated with lifting heavy objects [26].

Alternatively, an overadaptation for whole bone stiffness by homogenization of cancellous bone properties could cause an increase in the structural brittleness of T12-L1 levels which reduces their tolerance to progressive damage, even for the same loading direction. Literature data are consistent with the idea that vertebral strength and fatigue life (related to tolerance for progressive damage) are distinctly different and competing properties [22, 37, 39]. A progressive damage-related failure is especially relevant to vertebral fractures in that i) vertebrae lose a portion of their stiffness and strength when loaded beyond their ultimate load but still maintain substantial stiffness and strength when loaded a second time in laboratory experiments [35, 60], ii) clinical vertebral fractures appear to be slowly progressing, often not noticed until accidentally observed in x-ray radiograms taken for purposes other than a fracture [33, 38, 45]. If the bone is not brittle, biological processes can repair the damage caused by an overload and delay the development of a clinically observable fracture whereas an overly stiff, strong but also brittle vertebra will quickly develop a severe clinical fracture if overloaded. We propose that homogeneity of the material at the intermediate level (i.e., apparent properties of cancellous bone) and, consequently, structural brittleness of vertebrae is a potentially important factor in spinal fragility.

Some limitations should be noted. The FE models utilized homogeneous and isotropic material properties. The apparent modulus calculated from FE models is affected by the hard tissue (element) modulus distributions determined by gray level distributions [5] and expected to affect the calculation of trabecular stress distributions. However, there is currently no established method of converting gray-level values to hard tissue moduli and the variability of hard tissue moduli depends on the formulae used in the conversion. Our analyses suggest that the change in apparent modulus due to modulus variability only is small in human vertebral cancellous bone when up to a third order relationship is used to convert gray levels to element moduli [29]. Furthermore, the variation of gray levels between specimens was low and a significant dependence of gray level parameters on spine level was not observed in the current study. The value of the homogenous hard tissue modulus has no effect on the conclusions because the models are linearly scaled with this value. These are the same conditions used in studies where our observations that motivated this study were made [59]. Using homogenous properties is expected to have minor effects on our results but not affect our conclusions about cancellous bone.

This study was also limited to an investigation of the cancellous tissue that was physically cored out of vertebrae from selected regions. There were several reasons for doing this as opposed to analyzing a whole vertebral body or centrum. Firstly, our initial observation and hypothesis involved tissue quality rather than whole bone quality. Secondly, we did not wish to compromise image resolution by broadening the scope of the work. Although some studies considered μCT-based FE analysis of human vertebral bodies, the image resolution had to be less than optimal [7, 30, 36, 42, 56] and analyses were limited to a few vertebrae, probably due to computational costs [24, 31]. Micro-CT-based FE analyses of human whole vertebral bodies using sufficiently small voxels (~30μm) started to appear in more recent work [15], however, these studies are limited to spine levels that have relatively small vertebrae. Including largest vertebrae in the study would require substantially higher voxel sizes in a cone-beam system to keep image quality consistent between specimens from different spine levels in the current work. With the advances in imaging technologies, it will be possible to extend the current work to include whole vertebral bodies in future studies. A third reason for physically coring out the cancellous bone specimens was our intent to examine the experimental mechanical properties of these specimens in relationship with spine level. These studies are underway.

The specimens cored from the anterior region were in the supero-inferior direction while the specimens cored from postero-lateral regions were in the transverse direction. The original reason for doing this was to study the anisotropy of cancellous bone strength and stress distributions in relationship with spine level. Because of planned mechanical testing, the specimens were cylindrical [28] and the radial directions could not be recorded accurately. This allowed for the FE analysis of each region in one direction only. Some generalizations could be made based on the relationships found between the microstructure and FE parameters for both the superoinferior and transverse loading. However, further investigation of vertebral regional properties is necessary to gain insight into the nature of the anisotropy-anatomic site interaction.

In summary, we demonstrated that the T12-L1 cancellous tissue have unique properties which supports the most general form of our hypothesis. We further found that the variation of cancellous bone properties with spine level is dependent on the site within a vertebra, resulting in more homogenous cancellous tissue properties for T12-L1 vertebrae than other vertebrae. Taken together, the regional differences in trabecular microstructure and stress amplification between vertebra levels may explain, in part, the higher incidence of vertebral collapse at the critical T12-L1 levels.