Cyclin Aggregation and Robustness of Bio-switching

Abstract

During the cell cycle, Cdc2-cyclin B kinase abruptly becomes active and triggers the entry into mitosis/meiosis. Recently, it was found that inactive Cdc2-cyclin B is present in aggregates in immature starfish oocytes and becomes disaggregated at the time of its activation during maturation. We discuss a possible scenario in which aggregation of Cdc2-cyclin B dramatically enhances robustness of this activation. In this scenario, only inactive Cdc2-cyclin B can form aggregates, and the aggregates are in equilibrium with inactive Cdc2-cyclin B in solution. During maturation, the hormone-triggered inactivation of Myt1 depletes the soluble inactive Cdc2-cyclin B and the turnover leads to dissolution of the aggregates. This phase change, when coupled with the instability of the signaling network, provides a robust bio-switch.

INTRODUCTION

Cells enter M phase decisively and irreversibly. At the molecular level, the decisive event for entry into M phase is the activation of Cdc2 kinase (also known as cyclin-dependent kinase 1) (Nurse, 1990; Murray and Hunt, 1993). Cdc2 has an obligatory requirement for cyclin B binding (Cdc2-cyclin B is also known as M phase promoting factor or MPF). Cdc2-cyclin B activity is regulated by the activating phosphatase Cdc25 and the inactivating Wee1 family kinases, which act on two key phosphorylation sites (Solomon, 1993; Figure 1). In cells, Cdc2 activation is initiated either by changing the balance in favor of Cdc25 over Wee1 or by increasing the total Cdc2-cyclin B. The first way is thought to be more common. The second method has been demonstrated in experimental situations where exogenous cyclin B is added and binds to endogenous Cdc2, which is in excess (Swenson et al., 1986; Murray and Kirschner, 1989); it may also occur during rapid early embryonic divisions. A crucial feature of the Cdc2 activation pathway is that active Cdc2-cyclin B activates its activator Cdc25 and inactivates its inactivator Wee1 (Figure 1). This positive feedback is thought to result in all or none activation that does not flicker on and off once it is turned on.

Figure 1.

A diagram of the MPF activation pathway (adapted from Tyson et al. 2001). Note that the active MPF can in turn activate its activator Cdc25 and inactivate its inhibitor Wee1.

Theoretically, the irreversible character of Cdc2 activation can be described in terms of bistability (Tyson et al., 2001). The fact that cells can be arrested in the inactive state and when activated remain in the active state even after the stimulus is removed implies that the system can be in at least two different stable states separated by some kind of a “barrier.” Recently, experimental evidence for bistable behavior in Xenopus laevis egg extracts has been reported (Pomerening et al., 2003; Sha et al., 2003). This type of behavior can be elegantly explained by the possible bistability of a biochemical network (Thron, 1997; Ferrell and Xiong, 2001) illustrated qualitatively in Figure 2A for a hypothetical one-variable model. Usually, autoregulation implies a negative slope in the rate dependence (AB and CD portions of the graph in Figure 2A) that leads to a stable steady state, but the positive feedback mentioned above can change the sign of the slope in a certain concentration range (portion BC). As a result, the system may acquire two stable steady states, ss1 and ss3, separated by the unstable steady state ss2 (hence the term bistability). The system behavior in this case will be exactly like that in the cell cycle: if unperturbed, the system can stay infinitely long in the inactive steady state but “thrown over the unstable state” by a stimulus, it will be in the domain of attraction of the active steady state (interval [ss2, ss3] in Figure 2A) and will never return to the inactive state by itself.

Figure 2.

(A) Typical rate dependence of a one-variable bistable system. The system steady states, zero-rate points, are stable, ss1 and ss3, if the slope of the graph at the point is negative, and unstable, ss2, if it is positive. The portion of the graph with the positive slope is due to the positive feedback of active MPF on its activator and inhibitor. (B) Typical response of a bistable system to strong activation (a nonspatial simulation of the system described in Appendix 1). Note that after the stimulus is removed, the system does not return to the initial steady state. Instead, it is “attracted” to the active steady state.

Novak and Tyson (1993) have developed a detailed model of Cdc2 activation based on bistability of a biochemical pathway. An example of a switch-like behavior of the model triggered by inactivation of Wee1 is shown in Figure 2B. They found that an increase in total Cdc2-cyclin B could also trigger Cdc2 activation. The model thus reproduces key features of Cdc2 activation.

However, there are uncertainties, primarily due to the lack of experimental data necessary to make a complete model. The kinetic rate constants for the reactions shown in Figure 1 are not known, and the total concentrations (inactive plus active) of Cdc25, Wee1 and Cdc2-cyclin B are not established. These quantities, also known as parameter values, determine whether a biochemical network model is bistable.

There is another difficulty associated with parameter values. The total concentration is actually not a constant in cells, because the concentration can vary with time or in different regions. Likewise, the kinetic rate “constants” can vary due to differences in chemical potential. This leads us to the issue of robustness of the system: will the system behavior be retained in the face of biological variability? In the specific case of Cdc2 activation, over what range of total concentrations or rate constants will there be an irreversible activation of Cdc2? The two stable states of a bistable system are usually “antagonistic” in the sense that they can coexist only in a limited parameter range, whereas outside of this range only one of them prevails. This raises a concern whether bistability of a given biochemical pathway is robust enough to be the sole mechanism behind bio-switching.

Robustness of bistability has been discussed earlier in the context of cell-cycle models (Borisuk and Tyson, 1998) as well as in other contexts (Gardner et al., 2000). It has been recognized that mechanisms that result in steeply sigmoidal responses help expand parameter range where the model is bistable (Ferrell and Xiong, 2001). These mechanisms can be enzyme saturation or multistep phosphorylation in the positive feedback reactions [the former is suggested in Novak and Tyson (1993), the latter is assumed in Pomerening et al. (2003)], or cooperative binding in one or more steps of the loop (Gardner et al., 2000). It has also been noted that the presence of a buffer for MPF can, to an extent, improve robustness of bistability (Thron, 1997; see also “Analysis of the Effect of Independent Multiple Binding Sites” below). In this article, we demonstrate that bistability of a system can become essentially independent of kinetic parameters if multistability of a biochemical network couples with a phase equilibrium in the cell, so that the bio-switch involves a phase transition such as dissolution of precipitates.

The work presented here was stimulated by the discovery of aggregates of Cdc2-cyclin B in starfish oocytes (see Terasaki et al., in this issue). After applying the maturation-inducing hormone, the aggregates disappear at the time of MPF activation in a wave-like manner. In addition, experiments with fluorescence recovery after photobleaching (FRAP) indicate turnover of MPF between the aggregates and the cytoplasm.

We show how the Cdc2-cyclin B aggregates could have a central role in providing a decisive and irreversible transition. We first use a simplified model to find limits for bistability in the Cdc2 activation system in the absence of aggregates and then show that the robustness of a bio-switch can enhance significantly if the biochemical instability is coupled with a phase change in which the aggregates dissolve in the cytoplasm. Also, a simple spatial model is used to study the directionality of the Cdc2 activation wave.

RESULTS

Bistability Conditions for Activation of Cdc2 Where All Components Are Soluble

In our initial spatial simulations of Cdc2 activation (see Appendix 1 for model description), we found that it was relatively easy to destroy the bistability of the system, i.e., the system seemed to be sensitive to the choice of parameters. This is not characteristic of a robust switch and seems unlikely to be the situation inside the cell. We therefore undertook an investigation into the conditions for bistability (also known as bifurcation analysis).

To facilitate the analysis, we describe the pathway presented in Figure 1 with a simplified compartmental (nonspatial) model that can be solved analytically. Introducing notations as follows: m is the concentration of active MPF, c is the concentration of active Cdc25, and w is the concentration of active Myt1 (Myt1 is a representative of the “Wee1” family of proteins, hence the origin of the notation), and assuming, for simplicity, that the enzymes are unsaturated, the equations corresponding to the scheme of Figure 1 in the absence of aggregates can be written as

1

where m_t, c_t, and w_t are total amounts in solution of MPF, Cdc25, and Myt1, respectively, which are constant in the absence of aggregates. Each of Eqs. (1) contains a pair of kinetic parameters [the notation is similar to Novak and Tyson (1993)]. These parameters are rates of activation and inactivation of MPF (k and p), Cdc25 (k_a and k_b), and Myt1 (k_e and k_f), respectively. It is convenient for bistability analysis to introduce a nondimensional parameter α = pw_t/(kc_t), measuring the relative strengths of inhibitor versus activator, and two concentration-type parameters: m_c = k_b/k_a, m_w = k_e/k_f. The latter have the meaning of EC₅₀ values, the equivalent concentrations of active MPF that under steady-state conditions would activate half of the total amounts of Cdc25 and Myt1, respectively. One side effect of the simplification made in system 1, compared with the original Tyson model (see Appendix 1 for comparison), is that the inactive state (m = 0, c = 0, w = w_t) always exists, whereas in more realistic approaches, m and c are small but nonzero in the inactive state and this state does not exist beyond the stability threshold. However, our numerical tests show that this artifact does not significantly affect results of stability analysis, so the estimates of bistability constrains obtained below for the system 1 provide an accurate approximation for the systems with small nonzero m and c in the inactive state.1

It can be shown (for details of stability analysis, see Appendix 2), that the system described by Equation 1 may be bistable only under following condition:

2

which means that the feedback of active MPF on its inhibitor should be stronger than on the activator.

Moreover, given Eq. 2, the bistability exists only for the particular interval of m_t:

3

With , only the inactive steady state is stable, whereas for the only stable state is the active one. The bistability constraints 2 and 3 are, in fact, more restrictive than may seem. For example, in the case of the equal inhibitor/activator “strengths”, α = 1, it follows from Eq. 2 that the system would be bistable only if the effect of MPF on its inhibitor were at least twice as strong as on its activator. If we further assume (for illustration only) that m_c = 10 nM and m_w = 2.5 nM, then the bistability exists only for m_t between 8.7 and 10 nM (see Eqs. 3) (the Web site http://terasaki.uchc.edu/cdc2/provides an opportunity for numerical experimentation with this model). In general, as is shown in Figure 3, A and B, to obtain an “all or none” switch within a relatively large interval of m_t, the inequality 2 should be replaced with (α + 1)m_w << αm_c. Indeed, the width of the bistability interval, , is a decreasing function of (α +1)m_w/αm_c and drops to less than half-maximum at (α + 1)m_w/αm_c = 0.5 (Figure 3A). Also, tightening the interval 3 is accompanied by deviating from the all or none response (Figure 3B).

Figure 3.

Bistability constraints for the system 1: an all or none bistability is achieved when (α + 1)m_w is far below than, whereas m_t is close to, αm_c. (A) The width of bistability interval, (see Eqs. 3), decreases as (α + 1)m_w → αm_c. (B) As the bistability interval decreases, so does the fraction of active MPF in the active state.

This analysis demonstrates that there is a relatively narrow range of parameters in which the Cdc2 activation system is bistable with all or none response. One could argue that the evolution process might tune a system to satisfy restrictive constraints; however, given the variability in biochemical kinetic parameters, it seems unlikely that the system would rely on fine-tuning in such a fundamental process as cell cycle regulation.

Total Cdc2-Cyclin B Can Act as an Effective Switch

In mathematical terms, there is an intrinsic, parameter-independent property of the system 1. This is the instability of the inactive state (with respect to activation) above a certain parameter threshold. The stability condition with respect to the total MPF reads as m_t = αm_c (see Eq. 2.5 in Appendix 2). This implies that varying the total amount of Cdc2-cyclin B is an effective switch.

That total Cdc2-cyclin B can be an effective switch was shown by numerical simulations in the original Novak and Tyson (1993) model. In the cell, one way that total Cdc2-cyclin B could exceed a threshold is by synthesis of cyclin B. Cdc2 is usually present in excess, so that synthesis of cyclin B and its tight binding to Cdc2 will result in increasing total Cdc2-cyclin B. The rapid divisions of early embryonic development may be driven by synthesis of cyclin B rather than by regulation of Cdc2 activity by Cdc25 and Wee1 family kinases. There are also classic experiments in which increasing cyclin alone causes entry into M phase. In this work, expression of cyclin B by mRNA injection into frog oocytes caused maturation (Swenson et al., 1986), and in frog extracts depleted of endogenous mRNA, addition of cyclin mRNA can drive the extract through several cell cycles (Murray and Kirschner, 1989).

How Aggregates of Cdc2-Cyclin B Could Cause a Robust Switch

In starfish oocytes, protein synthesis inhibitors do not block maturation (Houk and Epel, 1974); this eliminates the possibility of increasing total Cdc2-cyclin B by synthesis. In this case, however, the aggregates of inactive MPF, being in equilibrium with inactive MPF in solution, can play a role of “stores,” where inactive MPF is inaccessible to the activator but ready to be released into the cytosol after the hormone is applied. Because the hormone-triggered inactivation of Myt1 depletes the soluble inactive MPF, the turnover will lead to dissolution of the aggregates, thus increasing the total amount of MPF accessible for activation. To test this idea, we extend the compartmental model discussed in the previous section.

In the presence of the aggregates, the total amount of MPF in the solution, m_t, becomes a variable, and our interpretation of the aggregates will determine the form of a governing equation for this variable. If the aggregates are the new insoluble phase of inactive MPF similar to a precipitate in a saturated solution, this equation comes from the kinetic theory of the first order phase transitions (Landau and Lifshitz, 1979). As shown in Appendix 3, the equation for m_t in this case takes the form

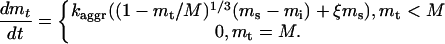4

In Eqs. 4, two new parameters are introduced: M is the “gross” MPF concentration in the cell, including aggregates, and m_s is the saturated concentration of the soluble MPF. Also, m_i is the concentration of the soluble inactive MPF, m_i ≡ m_t - m. The second term of the upper line originates from the energy cost of creating an interface between the phases and depends on the surface tension of an aggregate, so ξ is a positive constant: ξ = a_c/a_m where a_c is a critical size of nuclei at supersaturation of the order of saturation (Landau and Lifshitz, 1979) and a_m is the average size of the aggregate in the absence of the soluble phase (see Appendix 3). The kinetic constant k_aggr is mainly determined by the diffusion coefficient of the soluble MPF and the number of aggregates per unit volume.

The system is now described by Eqs. 1 and 4. It follows from Eq. 4 that there are two families of the system steady states independent of each other: one, with m_i ∼ m_s, relates to the aggregates being in equilibrium with the solution, and the other, with m_t = M, corresponds to the situation where the aggregates are dissolved. The overall system 1, 4 will be bistable if the inactive steady state is stable in the first family and there is a stable active steady state in the second family, whereas the bistability of the subsystem 1 is no longer required. As a consequence, constraints 2 and 3 are lifted. Instead, we get much more accommodating conditions, m_s < αm_c and M > αm_c, which require that the concentration of the saturated soluble inactive MPF is below a certain threshold, whereas the concentration of all MPF is above it. Indeed, as shown in Appendix 3, the analysis of bistability of the full system can be reduced to that of stability of the inactive steady state in the subsystem 1, first for m_t = m_i ∼ m_s (because m = 0 in the inactive state) and then for m_t = M, and the constraints on m_s and M shown above then follow from the stability threshold m_t = αm_c. The fact that switching the system from inactive to active is no longer constrained by the requirements 2 and 3 indicates that robustness of bio-switching is enhanced dramatically when instability in the biochemical pathway is accompanied by the dissolution of the aggregates. This is illustrated in Figure 4 by results of numerical simulations based on Eqs. 1 and 4.

Figure 4.

Dynamics of active MPF in response to activation in the systems with and without aggregation. The results of nonspatial simulations have been obtained with the parameters α = 2.0, m_w = m_c = 0.1 (relative concentration units as fraction of the maximum total MPF). (A) Results for the system described in Eqs. 1, no clumping: because the parameter values violate the condition of Eq. 2, there is no bistability on either side of the threshold, αm_c. (B) With aggregation, the system defined by Eqs. 1, 4 exhibits bistability even though both constraints, Eqs. 2 and 3, are violated.

What will happen in the model developed above if cyclin B is overexpressed? It might seem that the system will remain bistable at arbitrary large M because the bistability constraints 3 are lifted. Indeed, in the pure saturated solutions, the level of saturation, m_s, would remain independent of M and all the extra MPF would go to precipitates, so the system would never activate by overexpression.

However, in such a complex system as the cell, the additional MPF will likely be redistributed among its soluble and insoluble forms. In other words, m_s may grow with M and at some point overcome the activation threshold. Also, it was implied that MPF in aggregates is inaccessible for the activator, which in reality might be true only to a certain degree. As aggregates grow, more MPF could be activated directly from them and enter the cytoplasm thus also contributing to the increase of the total concentration of the soluble MPF to the point where it exceeds the threshold. Therefore, the enhanced robustness of bistability does not necessarily rule out activation at sufficient overexpression of MPF.

Overall, we have shown that total Cdc2-cyclin B can act as a switch during starfish oocyte maturation. In this scenario, the aggregates behave like a precipitate, and their dissolution increases the total soluble Cdc2-cyclin B beyond a threshold, thereby activating the Cdc2 system. The robustness of the switch is enhanced significantly over the situation where all of the components are soluble.

Analysis of the Effect of Multiple Independent Binding Sites

In the previous section, we showed that if the aggregates behave like a precipitate, then there is robust switching. However, the aggregates could instead consist of a scaffold which has multiple independent binding sites for inactive Cdc2-cyclin B. We investigated how well this type of aggregate would act as a switch.

In this case, because the inactive MPF is partly immobilized due to binding to some kind of existing binding sites (an immobile buffer), Eq. 4 should be replaced with

5

where b_t is the total buffer concentration, K is the dissociation constant, and k_on is the binding on-rate (see Appendix 4 for derivation of Eq. 5). The system is then described by Eqs. 1 and 5. 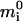In contrast with the previous case, this system has only one set of solutions with m_t = m - b_tm_i/(K + m_i) and therefore is bistable only within the parameter constraints similar to 2 and 3: according to the analysis in Appendix 4, the necessary conditions for bistability in this case are: m_w < m_c and M ∈ (M⁽¹⁾, M⁽²⁾) where M⁽²⁾ = αm_c(1 + b_t/(K + αm_c)) and where is the root of the equation 1 + b_tK/(K + x)² = αm_w(m_c - m_w)/(x - αm_w)² lying between αm_w and αm_c.

Thus, the existing binding sites for inactive MPF do not enhance robustness of switching from the perspective of parameter independence, although because of binding to the buffer, the bistability interval for the full MPF concentration M shifts to larger values and expands. Also, because of that, the amount of active MPF in the activated state can increase significantly. However, in this scenario, the clumps of inactive MPF will never disappear entirely. The simulation results in Figure 5 illustrate activation of the system 1, 5 under various conditions. In particular, switching the system state from inactive to active fails if the bistability conditions are violated.

Figure 5.

Dynamics of active MPF in response to activation in the system with MPF buffering (Eqs. 1, 5). Parameter values used in simulations: b_t = 3.6, K = 1.0, α = 2.0, m_c = 0.1 (relative concentration units as fraction of the maximum total MPF). (A) m_w = 0.02 < m_c, there exists a bistability interval for M, [2(αm_c), 4(αm_c)]. (B) m_w = m_c: no bistability exists on either side of the threshold, 4(αm_c).

Other Characteristics of the Aggregates

In both of the aggregate models presented above, it is implied that activation occurs in solution, not in the aggregates. One alternative would be that all inactive MPF is immobilized, whereas the active MPF is soluble. We explored whether under these conditions, a simple spatial model described in the subsequent section (see also Appendix 1) can account for the observed Cdc2-cyclin B clumping.

Numerical simulations of the model run under the assumptions specified above immediately show that, to obtain the stable inactive steady state in this model, it is absolutely necessary that Myt1 colocalizes with inactive Cdc2-cyclin B. In fact, Cdc2-cyclin B clumps would be the consequence of Myt1 spatial aggregation. The problem with this explanation is that a turnover observed in FRAP experiments, in this interpretation, is the turnover between inactive and active forms of Cdc2-cyclin B governed by the same processes that activate Cdc2-cyclin B after applying the maturation-inducing hormone. Because the amount of active Cdc2-cyclin B in the inactive steady state should be very low, the clump turnover in the model is much slower compared with the activation time in contrast with the experimental findings that the time scale of turnover is comparable to that of activation (see Terasaki et al., in this issue). This suggests that the turnover, observed in FRAP experiments, is the exchange of inactive Cdc2-cyclin B between its soluble and insoluble forms, the assumption used in the preceding sections.

Another implication of both aggregate models is that of the total cellular Cdc2-cyclin B, a large fraction should be in the aggregates compared with in solution.

The results of FRAP experiments can be used to estimate the ratio of the amounts of Cdc2-cyclin B immobilized in the clumps and soluble in the cytoplasm. In those experiments, the characteristic time for recovery was ∼30 s. As shown in Appendix 3, this ratio can be evaluated as 3.33NDa_avτ/R³ where N is the number of the aggregates in the cell, D is the Cdc2-cyclin B diffusion coefficient, a_av is the average radius of an aggregate, and R is the radius of the cell. With the parameter values determined from the experiments as N ≥ 2000, D ∼ 10 μm²/s, a_av ≈ 1 μm, R ≈ 90 μm, and τ as above, the estimate yields the value of ∼2.7, which means that the amount of Cdc2-cyclin B immobilized in clumps is at least equal to if not greater than that of soluble in the cytoplasm and therefore significant.

Directionality of the MPF Activation Wave

Imaging of cyclin B-GFP in starfish oocytes (see Terasaki et al., in this issue) provides evidence that MPF activation occurs as a wave originating at the animal pole. Because it is well known that the activation of bistable reaction-diffusion systems can occur in the form of a “tidal wave” (Grindrod, 1996), we combine the kinetics of the system MPF-Cdc25-Myt1 (see diagram in Figure 1) with diffusion to analyze the spatial pattern of MPF activation. For this purpose, we use spatially uniform initial distributions for all molecular species involved in the model.

Mathematically, the system is described by a set of partial and ordinary differential equations (see Appendix 1). Using the Virtual Cell modeling framework (Schaff et al., 2000), we set up a model and solved it on the two-dimensional geometry mimicking the morphology of the cell. Because the maturation of the starfish oocytes is initiated by a maturation-inducing hormone that binds to the oocyte plasma membrane and enables a signaling cascade resulting, according to (Okumura et al., 2002), in production of the kinase Akt, we model this production as a flux originating from the membrane, by using an appropriate boundary condition. A set of parameters used in the simulations is close to the one suggested in Novak and Tyson (1993) and provides system bistability (see Appendix 1 for the model description and computation details).

Simulation results are presented in Figure 6. Interestingly, even with all the initial conditions and applied membrane flux of Akt being uniform, the wave of Cdc2-cyclin B activation (disappearance of inactive Cdc2-cyclin B in Figure 6A) initiates at the animal pole and propagates in the direction of the cell axis. Why it is so becomes clear from Figure 6B showing the Akt dynamics. Even though the flux of Akt production is uniform across the plasma membrane, the accumulation of Akt in the region of animal pole is initially much higher because of enhanced “local surface-to-volume ratio.” Thus, our results indicate that the asymmetry in positioning of the nucleus inside the cell can be among the factors determining initiation and directionality of the Cdc2-cyclin B activation wave.

Figure 6.

Results of a spatial simulation of the system described in Appendix 1. (A) MPF activation wave (disappearance of inactive MPF) initiates at the left pole of the oocyte and propagates around the nucleus in the direction of the cell axis. (B) Akt dynamics as a result of the 3-min uniform influx.

DISCUSSION

A relatively simple mathematical formulation has been used to demonstrate a possible robust way of activating Cdc2-cyclin B, a classic example of a bio-switch. The main idea is that the robustness of switching in a biochemical network can be significantly enhanced if it also involves a phase transition in the cytosol such as formation or dissolution of aggregates. We came to this idea in light of the new experiments that revealed some aspects of spatial organization of the maturation process in starfish oocytes.

Because the key enzymatic interactions that govern Cdc2-cyclin B activation have an intrinsic threshold depending on the total amount of soluble Cdc2-cyclin B, the most convenient way of switching is to somehow regulate this amount, therefore the inactive MPF caged in aggregates is ideal for this purpose. At the same time, the stored MPF must “know” when it should be released, and the turnover between the aggregates and the soluble inactive MPF being in equilibrium with each other seems to be a perfect sensor for that: when, as a result of the hormone application, the cytoplasmic inactive MPF goes below saturation, the aggregates will dissolve thus increasing the total amount of MPF in the cytoplasm.

Finally, the new state must not be readily reversible, and here lies the difference between aggregation and buffering, which otherwise might look similar. In the scenario with the phase change, the new state with no aggregates is separated from the initial one by an energy barrier and, therefore, is at least metastable (characterized by the local minimum of free energy), the energy barrier being a cost of creating an interface between soluble and insoluble phases. In other words, to reverse the transition in this scenario, “binding sites” (the stable nuclei of the insoluble phase of sufficient size) must be created first, before binding could occur, whereas in the case of buffering the binding sites are readily available. Mathematically, this difference manifests itself in opposite signs of dm_t/dt in Eqs. 4 and 5 as m_t → M.

The existence of two states with local minima of free energy (in one state, aggregates are in equilibrium with soluble MPF, in the other, aggregates are dissolved) separated by the energy barrier can also be interpreted in terms of bistability. Therefore, in this scenario, the system can be bistable even if the subsystem 1 is not and the parameter constraints 2 and 3 are not met. This significantly contributes to robustness of switching, because bistability of the system becomes largely insensitive to kinetic parameters as long as the saturating concentration of the soluble MPF, m_s, is relatively low, whereas the total amount of MPF (soluble plus insoluble), M, is relatively high. However, in the case of overexpression, the additional MPF will likely be redistributed among its soluble and insoluble forms that eventually would lead to spontaneous activation.

In light of the hypotheses presented in this article, the most interesting issues that can be addressed experimentally concern Cdc2-cyclin B associations in the aggregates: are there other molecules present within the aggregates? What features of Cdc2-cyclin B could promote aggregation when inactive and prevent aggregation when active? Do the aggregates behave like a precipitate or a multiple binding site? On the theoretical side, the next obvious step for future development is the full spatial model that would include Cdc2-cyclin B aggregation.

It is possible that this analysis has more general relevance. There must be complex cellular mechanisms to regulate the amounts of all the different proteins, but it seems likely that these amounts fluctuate significantly over time and in different regions. In the Cdc2 activation pathway, we are proposing that aggregates of Cdc2-cyclin B relieve the cell of controlling amounts of the pathway components precisely. Perhaps aggregates or other mechanisms have the same role in other pathways whose response characteristics have a similar dependence on protein amounts.

APPENDIX 1

When the existing kinetic model of the reaction scheme in Figure 1 (Novak and Tyson, 1993) is combined with diffusion, it gives rise to a reaction-diffusion system that was used in spatial computer simulations of MPF activation. The model is a set of the parabolic-type partial differential equations,

1.1

where [X] is the concentration of the molecular species X, D_X is its diffusion coefficient, and the reaction term f_X includes the rates of all reactions affecting the species X. The model includes seven molecular species: active and inactive forms of MPF, Cdc25, and Myt1 and Akt. The number of variables can, however, be reduced by taking into account that uniform initial conditions and zero-flux boundary conditions for all species except Akt will be used, and the diffusion coefficients of active and inactive forms are the same. In addition, because Myt1 is believed to be associated with the endoplasmic reticulum, its diffusion can be ignored. As a result, the equations for inactive forms of MPF, Cdc25, and Myt1 can be dropped due to the conservation of mass at each spatial point, and Myt1 is described by the ordinary differential equation. The reaction terms f_X in 1.1 include the rates of activation and inactivation approximated by the Michaelis-Menten kinetics (Novak and Tyson, 1993) and Cdc25, Myt1, and Akt act as unsaturated enzymes:

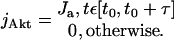1.2

where m, c, w, and a are the current concentrations of MPF, Cdc25, Myt1, and Akt, respectively, and m_t, c_t, and w_t are the corresponding total (active plus inactive) concentrations. The flux density of Akt production, j_Akt is modeled as uniform across the plasma membrane and constant within a certain characteristic time, τ:

1.3

Equations 1.1–1.3 contain a set of parameters. The parameter values used in simulations (Table 1) are close to those suggested in Novak and Tyson (1993) and provide system bistability. The initial conditions are uniform and correspond to the inactive steady state in the absence of Akt. The values of cytoplasmic diffusion coefficients of MPF, Cdc25, and Akt have been reduced to 3 μm²/s to account for the hindering effect of yolk platelets, which are abundant in the cytoplasm (Terasaki et al., 2001).

Table 1.

Parameter values used in the spatial simulations^a

Name	Symbol	Value	Units
Initial active MPF	minit	0.0114 mt	concentration
Initial active cdc25	cinit	0.0090 ct	concentration
Initial active Myt1	winit	0.9374 wt	concentration
Initial Akt	ainit	0.0	concentration
MPF activation rate	k25	1.0/ ct	1/(min·concentration)
MPF activation rate	k25	0.1/ ct	1/(min·concentration)
MPF inactivation rate	kw	10.0/ wt	1/(min·concentration)
MPF inactivation rate	kw	0.1/ ct	1/(min·concentration)
Cdc25 activation rate	kMPFc	1.0/ mt	1/(min·concentration)
Cdc25 inactivation rate	vc	0.125	1/min
Cdc25 activation Michaelis-Menten constant	KMPFc	0.1 ct	concentration
Cdc25 inactivation Michaelis-Menten constant	Kc	0.1 ct	concentration
Myt1 activation rate	vw	0.1	1/min
Myt1 inactivation rate	kMPFw	2.0/ mt	1/(min·concentration)
Akt-dependent Myt1 inactivation rate	k	1.0	1/(min·concentration)
Myt1 activation Michaelis-Menten constant	KMPFw	0.3 wt	concentration
Myt1 inactivation Michaelis-Menten constant	Kw	0.3 wt	concentration
Akt flux density	Ja	50.0	concentration·μm/s
Akt flux duration	τ	3	min
MPF diffusion coefficient	Dm	180	μm2/min
Cdc25 diffusion coefficient	Dc	180	μm2/min
Akt diffusion coefficient	Da	180	μm2/min

^aAs in Novak & Tyson (1993), parameters are normalized to the total concentrations of MPF, Cdc25, and Myt1 (m_t, c_t, w_t, respectively), which were given the value of 1 in the simulations

Using the Virtual Cell computational framework (Schaff et al., 2000), the system 1.1–1.3 has been simulated numerically on two-dimensional geometry mimicking the morphology of a starfish oocyte (Figure 6). The computational domain has been reduced in half to 190 × 95 μm due to axial symmetry and contained 5000 mesh points. The simulated time is 25 min with the integration being performed with 0.05-min time step. The numerical error is estimated to be <1.5%.

APPENDIX 2

The system 1 of the text can be easily solved for steady states. First, the steady-state values of c and w can be expressed in terms of the steady-state value of m through

2.1

Equation 2.1 follows from the last two equations of the system 1. It then follows from the first equation that the system 1 can generally have three steady states: one is the inactive one, m = 0, c = 0, w = w_t, and the other two are derived from the roots

2.2

of the equation

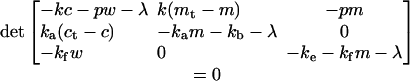2.3

It is necessary for bistability that the solutions 2.2 exist and are both positive, and these requirements lead to the conditions 2 and 3 of the text. We now show that the conditions 2 and 3 are also sufficient for bistability. The steady state is locally stable if all the eigenvalues λ of the Jacobian of the system 1 evaluated at a steady state are negative. In other words, all of the roots λ of the equation

2.4

are negative at the stable steady state. Equation 2.4 is cubic but can be easily solved for the inactive steady state. In this case,

Thus, the inactive state is stable only if

2.5

For bistability, the solutions 2.2 must exist under the condition 2.5 (the expression under the square root must be nonnegative; this, in combination with 2.5, leads to the constraint 3 of the text and stability. To check stability of the larger steady state in 2.2, we rewrite Eq. 2.4 in the form φ₁(λ) = φ₂(λ) with

It is easy to see from schematic plots of the functions φ₁ and φ₂ that two lesser roots, λ_1,2, of the equation φ₁(λ) = φ₂(λ) satisfy inequalities λ₁ < -k_e -k_fm < 0, λ₂ < -k_am - k_b < 0, whereas λ₃ is negative if φ₁(0) > φ₂(0). Using 2.1 and 2.3, one can show that the latter condition is equivalent to m² > m_w(αm_c - m_t), which, with m from 2.2 and under the condition 2.5, yields

2.6

Combining 2.5 and 2.6 brings us to the constraint 2 of the text.

APPENDIX 3

In deriving Eq. 4 of the text, we follow Landau and Lifshitz (1979). Consider a spherical aggregate with the radius of a, immersed in the solution of inactive MPF with concentration m_i. The turnover between the aggregate and the solution is due to diffusion and the concentration of the soluble inactive MPF near the aggregate is that of saturation. This concentration, m_sa, is however different from the bulk saturation concentration, m_s, because of the surface tension effects (Landau and Lifshitz, 1980):

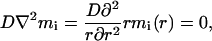3.1

where σ is the aggregate surface tension, v is the specific volume (the volume per molecule) in the aggregate, T is absolute temperature, and k_B is the Boltzmann constant. The spatial distribution around the aggregate can be estimated from the diffusion equation under steady-state conditions,

where D is the diffusion coefficient of the soluble MPF and r is the distance from the center of the aggregate. The solution of this equation with the boundary conditions, m_i(∞) = m_i, m_i(a) = m_sa has the form

and the rate of change of the amount of soluble MPF due to turnover with one aggregate can now be determined as

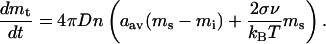3.2

In the second step of 3.2, we have used 3.1. We now introduce the number of aggregates per unit volume, n, to obtain the rate of change of the concentration of soluble MPF by using 3.2:

3.3

According to Marchenko (1996), the size distribution right after nucleation is linear and later tends to a Dirac delta-function: all aggregates gradually acquire approximately same size. In any case, and

3.4

where a_m is the average size of an aggregate if all MPF is insoluble: 4πa_m³n/3 = Mv.

The second term in 3.3 is associated with the energy cost of creating an interface between the aggregate and solution (Landau and Lifshitz, 1980). Introducing the following notation: a_c = 2σv/(k_BT), ξ = a_c/a_m, and k_aggr = 4πDna_m, we obtain from 3.3 and 3.4

3.5

Note that Eq. 3.5 holds only for m_t < M because at m_t = M all aggregates are dissolved and dm_t/dt = 0. We thus arrive at Eq. 4 of the text.

Based on the idea of diffusion-limited turnover, it is possible to estimate from the FRAP experiments the ratio of the amounts of MPF immobilized in the aggregates and soluble MPF in the cytoplasm. This ratio is 1.11N(a_av/R)³(m_a/m_i) where N is the total number of aggregates in the cell, the concentration of MPF in the aggregate, 1/v, is denoted as m_a, R is the cell radius, and we took into account that the nucleus takes ∼10% of the cell volume. The ratio of concentrations can be evaluated from the balance of fluxes in turnover; at steady state, the incoming flux from the solution, 4πDa_avm_i, is balanced by the outgoing flux , where τ is the characteristic time of fluorescence recovery: . Substituting this back in the expression above, we obtain the result used in the main text.

Finally, we perform the steady-state stability analysis for the system defined by Eqs. 1 and 4 of the text. The eigenvalue equation for this system,

reduces both in the case of the inactive steady state, m = c = 0, w = w_t, and at m_t → M, to

3.6

This means that in these cases, the stability of the full system is determined by stability of two separate subsystems: the subsystem 1 and the total soluble MPF, m_t. In the first family of steady states (see text), with sufficiently large M, M > ξm_s, m_t is stable with λ ∼ -k_aggr < 0, and the problem reduces to the stability of the subsystem 1. For the steady states with m_t = M, stability of m_t follows directly from Eq. 4 rather than from Eq. 3.6 because of discontinuity of dm_t/dt at m_t = M, and the problem again reduces to the stability of the subsystem 1.

APPENDIX 4

In the case of buffering, let b and b_t be the concentration of MPF bound to the buffer and the total buffer concentration, respectively. Then, assuming mass action kinetics with on and off rates, k_on and k_off = k_onK, we obtain

4.1

Taking into account that b = M - m_t, Eq 4.1 is equivalent to Eq. 5 of the text.

It is easy to verify that the stability condition of the inactive state of the system 1, 5, m = c = 0, w = w_t, m_t = (1/2)(M - K - b_t + ((M - K - b_t)² + 4KM)^1/2, as in the case of aggregation (Appendix 3), reduces to that of stability of the subsystem 1, m_t < αm_c. This gives us the upper bound of the bistability interval for M:

4.2

For bistability, it is necessary that the inactive steady state coexist with the active one, which comes as the simultaneous solution of Eq. 2.3 and dm_t/dt = 0. It is convenient to rewrite the system of these equations in terms of m_i ≡ m_t - m: m = Ψ₁(m_i) = Ψ₂(m_i) with Ψ₁(x) = M - x - b_tx/(x + K) and Ψ₂(x) = m_w(αm_c - x)/(x - αm_w). Schematic plots of these functions indicate that the solutions for the active state compatible with 4.2 are possible only if m_w < m_c. With decreasing M, the plot of Ψ₁(x) shifts down, and the solutions exist until the functions Ψ₁(x) and Ψ₂(x) become tangent to each other: dΨ₁(x)/dx = dΨ₂(x)/dx. This determines the lower bound of the bistability interval for ,, where is the root of the equation

such that x ∈ (αm_w,αm_c).