Abstract
How can a task-appropriate response be selected for an ambiguous target stimulus in task-switching situations? One answer is to use compound cue retrieval, whereby stimuli serve as joint retrieval cues to select a response from long-term memory. In the present study, the authors tested how well a model of compound cue retrieval could account for a complex pattern of congruency effects arising from a procedure in which a cue, prime, and target were presented on each trial. A comparison of alternative models of prime-based effects revealed that the best model was one in which all stimuli participated directly in the process of retrieving a response, validating previous modeling efforts. Relations to current theorizing about response congruency effects and models of response selection in task switching are discussed.
Keywords: task switching, response selection, cuing, priming, memory retrieval
People live in a world of ambiguity where the same stimulus can evoke different responses in a variety of contexts. A stimulus such as the number 42 might be responded to as even, lower than 50, the product of 6 and 7, a double-digit number, or possibly the answer to life, the universe, and everything (Adams, 1979). Yet when people are instructed to perform a specific task on an ambiguous stimulus (e.g., is 42 an odd or even number?), it is often trivial for them to come up with a task-appropriate response (“even”) in a second or two, even if they had just performed a different task on the same stimulus a moment ago (e.g., is 42 lower or higher than 50?). This flexibility over thought and action is considered to be a core element of cognitive control, but one that is still something of a mystery (Monsell, 1996). The mystery is most evident in task-switching situations, where a target stimulus is typically ambiguous and may require different responses for different tasks performed in rapid succession, raising the issue of how a task-appropriate response is selected. The purpose of the present study was to test a model of how this occurs (Schneider & Logan, 2005).
Compound Cue Retrieval
In many task-switching experiments, the relevant task to perform on a target stimulus is indicated by a cue. For example, for tasks involving target digits, the cue Parity might indicate an odd or even judgment and the cue Magnitude might indicate a lower or higher than 5 judgment (what we will refer to as parity and magnitude tasks, respectively). Logan and Bundesen (2003, 2004; see also Arrington & Logan, 2004) proposed a mechanism for response selection under these circumstances—later formalized in a mathematical model by Schneider and Logan (2005)—called compound cue retrieval. The basic idea behind compound cue retrieval is that the cue and the target are used as joint retrieval cues to select a unique response from long-term memory. Each stimulus provides evidence for one or more response categories (e.g., the cue Parity provides evidence for odd and even; the target 3 provides evidence for odd and low) and it is the multiplicative combination of evidence in the retrieval process that leads to selection of the response category for which there is the most evidence (e.g., odd).
Compound cue retrieval was one part of a larger model of task switching proposed by Schneider and Logan (2005). The other part was priming of cue encoding, which is the idea that the process of encoding the cue can be primed by residual activation in short-term memory of identical or associated cues across trials. Priming of cue encoding was used to account for transition effects such as switch costs (impaired performance for task switches compared with task repetitions) and cue-repetition benefits (facilitated performance for cue repetitions compared with task repetitions), as well as their reduction across preparation intervals. Since the publication of the 2005 article, the model or the conclusions drawn from it have been the target of several investigations conducted by ourselves (Arrington, Logan, & Schneider, 2007; Logan & Schneider, 2006b; Logan, Schneider, & Bundesen, 2007; Schneider & Logan, 2006, 2007) and by others (Altmann, 2006, 2007; Forstmann, Brass, & Koch, 2007; Jost, Mayr, & Rösler, 2008; Mayr, 2006; Monsell & Mizon, 2006; Travers & West, 2008). However, all of these investigations focused on priming of cue encoding and the distinction between task switching and cue switching. None of them evaluated compound cue retrieval, despite references to the “compound-cue model” (Altmann, 2006, 2007). The present investigation focuses on compound cue retrieval instead of differences between task switching and cue switching.
The only test of compound cue retrieval was in Schneider and Logan (2005), where we examined its ability to account for cue–target congruency effects. In those experiments, parity and magnitude tasks were cued by category labels (Odd and Even cued the parity task, Low and High cued the magnitude task), which introduced congruency relations between cues and targets. For example, while either Odd or Even could cue a parity judgment of the target 3, the cue Odd was congruent with the correct categorization of the target (odd) whereas the cue Even was incongruent. In three experiments, incongruent trials were slower and more error-prone than congruent trials. These response time (RT) and error rate (ER) effects were successfully modeled using compound cue retrieval, whereby the difference in evidence favoring a correct response over an incorrect response was greater on congruent trials compared with incongruent trials, resulting in faster and more accurate response selection. Subsequent studies explored the cue–target congruency effect in different contexts (Arrington et al., 2007; Logan & Schneider, 2006a), but those studies focused on using the effect as a diagnostic for different types of cue representations rather than as a test of compound cue retrieval. Thus, in contrast to priming of cue encoding, there is a paucity of research on compound cue retrieval as a mechanism for response selection in task-switching situations.
Cues versus Primes
As noted above, compound cue retrieval has only been tested with category labels as cues (Schneider & Logan, 2005). A methodological issue with the use of category-label cues is that they are atypical of the cues used in most task-switching experiments, which tend to be neutral with respect to specific response categories (e.g., using Parity and Magnitude as cues). A more theoretical issue with category-label cues is that they integrate two elements: a cue that indicates the task and a prime that suggests a specific response category. Kantowitz and Sanders (1972) and Sudevan and Taylor (1987) made an important distinction between cues and primes, noting that cues were useful and necessary for task performance whereas primes were potentially useful (if valid) but not necessary. Given this distinction, one might argue that cues should be critical for compound cue retrieval whereas primes should be less important and serve as contextual elements that modulate response selection. A major aim of the present study was to test whether compound cue retrieval could accommodate this distinction between cues and primes.
A second, related aim was to isolate the locus of prime-based effects in cognitive processing. In Schneider and Logan (2005), the cue and prime elements of the category-label cues were incorporated in compound cue retrieval in the same way (because they were one and the same entity). They were directly involved in the retrieval process, altering the rate at which evidence accumulated toward selecting one response over the other. For example, while the cue Odd indicated that a parity judgment had to be made in Schneider and Logan’s (2005) experiments, it was not predictive of an odd or an even response. Yet in compound cue retrieval, there was a priming effect whereby the rate of evidence accumulation toward an odd response was slightly boosted. When the cue and the target were congruent (e.g., Odd and 3), this facilitated response selection, but when they were incongruent (e.g., Odd and 4), this impaired response selection. The result was a cue–target congruency effect.
However, prime-based effects could have occurred in other ways without directly affecting the retrieval process. In the model, a response has been selected when the evidence in favor of that response reaches a boundary or criterion relative to the alternative response. The prime element of a category-label cue may affect the response boundaries such that less evidence is required to reach a primed boundary relative to an unprimed boundary. For example, the cue Odd might lower the boundary for an odd response and possibly raise the boundary for an even response. The correct boundary would be reached faster on cue–target congruent trials than on incongruent trials, resulting in a cue–target congruency effect. This is a different conception of prime-based effects that challenges the way they were modeled in Schneider and Logan (2005).
A more severe challenge would involve having prime-based effects occur outside of compound cue retrieval altogether. Instead of affecting response selection, the prime element of a category-label cue could affect response execution. For example, the cue Odd might partially activate the manual response associated with odd, analogous to how irrelevant flanker stimuli can partially activate their associated responses (e.g., Coles, Gratton, Bashore, Eriksen, & Donchin, 1985; Gratton, Coles, Sirevaag, Eriksen, & Donchin, 1988). This would speed responding on cue–target congruent trials relative to incongruent trials, resulting in a cue–target congruency effect (though it would likely be restricted to RT).
In summary, the locus of the prime-based component of the cue–target congruency effect in Schneider and Logan’s (2005) experiments is unclear. We had modeled the effect by assuming that it influenced the retrieval process, but as noted above, a cue–target congruency effect could just as easily have been produced by changing response boundaries or priming response execution. Category-label cues do not allow us to disentangle these possibilities or to make a clear distinction between the roles of cues and primes in cognitive processing. In the present study, we addressed these issues by testing how our model of compound cue retrieval could account for data from a task-switching procedure in which the cue and the prime were separate stimuli, comparing the fits of models in which there was no priming or priming by changes to retrieval, response boundaries, or response execution.
The Present Study
In the experiment reported below, subjects performed parity and magnitude tasks on single-digit targets. There were three stimuli on each trial: cue, prime, and target. The cue was Parity or Magnitude and it indicated the task to perform, making it both useful and necessary (Kantowitz & Sanders, 1972; Sudevan & Taylor, 1987). The prime was a randomly selected category label—Odd, Even, Low, or High—that was potentially useful (if valid) but not necessary. The target was a digit from 1–9, excluding 5. On each trial the cue was presented first, followed by the prime after a cue–prime interval (CPI), then the target after a prime–target interval (PTI), after which time a response was made. Instead of cue–target congruency, the experiment allowed us to focus on four other types of congruency (examples of each type are given in Table 1):
Table 1.
Examples of cues, primes, and targets for each type of cue–prime congruency, prime–target congruency, prime–response congruency, and response congruency
| Example Stimuli |
|||||||
|---|---|---|---|---|---|---|---|
| Cue–Prime Congruency | Prime–Target Congruency | Prime–Response Congruency | Response Congruency | Cue | Prime | Target | Correct Response |
| Incongruent | Incongruent | Incongruent | Congruent | Parity | Low | 8 | / |
| Congruent | Incongruent | Parity | Low | 7 | Z | ||
| Congruent | Incongruent | Incongruent | Parity | Low | 4 | / | |
| Congruent | Congruent | Parity | Low | 3 | Z | ||
| Congruent | Incongruent | Incongruent | Incongruent | Parity | Odd | 4 | / |
| Congruent | Parity | Odd | 8 | / | |||
| Congruent | Congruent | Incongruent | Parity | Odd | 7 | Z | |
| Congruent | Parity | Odd | 3 | Z | |||
Note. These examples are based on having the response categories odd and low mapped onto the Z key and the response categories even and high mapped onto the / key.
Cue–prime congruency
Whether the cue and the prime refer to the same task (congruent; e.g., Parity and Odd) or to different tasks (incongruent; e.g., Parity and Low).
Prime–target congruency
Whether the prime indicates one of the target’s categories (congruent; e.g., Odd and 3) or an alternative category (incongruent; e.g., Even and 3).
Prime–response congruency
Whether the prime is associated with the same manual response as required for the target (congruent) or a different response (incongruent; see Table 1 for examples).
Response congruency
Whether the target requires the same manual response for both tasks (congruent) or different responses (incongruent).
The first three types of congruency are novel aspects of our cue–prime–target procedure, whereas response congruency has been examined in several studies (e.g., Brown, Reynolds, & Braver, 2007; Kiesel, Wendt, & Peters, 2007; Meiran, 2005; Meiran, Chorev, & Sapir, 2000; Meiran & Kessler, 2008; Monsell, Sumner, & Waters, 2003; Sudevan & Taylor, 1987). The typical finding is that response incongruent trials are slower and more error-prone than congruent trials. This effect was addressed briefly in Schneider and Logan (2005, p. 362), where we noted that it was present in our experiments and our model of compound cue retrieval could produce it (though we did not explicitly model the response congruency effects in our data).
Perhaps more important is whether and how compound cue retrieval can account for the other types of congruency involving primes. As noted above, primes could affect the retrieval process, response boundaries, or response execution. Given that the primes in the present procedure are not necessary for accurate task performance (unlike in Schneider & Logan, 2005), a fourth alternative is that the primes may have no effect on performance. In what follows, we report the results of the experiment and then describe a basic framework for modeling the data. We assess the ability of four different models—representing no priming or priming of retrieval, boundaries, or execution—to account for a relatively complex pattern of congruency effects in both the RT and ER data. If our past modeling of cue–target congruency effects in compound cue retrieval was valid, then the retrieval model should provide a better account of the data than the alternative models.
Experiment
Method
Subjects
Thirty-six students from Vanderbilt University completed the experiment for course credit or $12.
Apparatus, tasks, and stimuli
The experiment was conducted using E-Prime software (Psychology Software Tools, Pittsburgh, PA) running on computers that displayed stimuli on monitors and registered responses from keyboards. The tasks were parity and magnitude judgments cued by the words Parity and Magnitude (5 mm high × 30–45 mm wide), respectively. The primes were the words Odd, Even, Low, and High (5 mm high × 15–20 mm wide). The targets were the digits 1–9 (5 mm high × 4 mm wide), excluding 5. All stimuli were displayed in white on a black background and viewed at a distance of about 50 cm.
Procedure
Instructions were presented onscreen and explained by the experimenter. Each trial began with the presentation of a cue slightly above the midpoint of the screen, centered horizontally. After the CPI (100 or 800 ms), a prime was presented 12 mm below the cue. After the PTI (100 or 800 ms), a target was presented 12 mm below the prime. Cue, prime, and target remained onscreen until a response was made, after which time the screen was cleared for 500 ms and the next trial commenced thereafter. Responses were made with the Z and/keys on the keyboard, with same-task categories assigned to different keys and all possible category–response mappings counterbalanced across subjects. Reminders of the mappings appeared in the bottom corners of the screen during the experiment.
On each trial, the cue, prime, target, CPI, and PTI were randomly selected from a table with all 256 combinations of these design elements. There were 1,024 trials, with every 256 trials including all combinations in the design. Breaks were allowed after every block of 64 trials. Subjects were instructed to respond quickly and accurately and they were informed that the prime may or may not be congruent with the cue or the target on each trial.
Results
The first block, the first trial of each block, and trials with RT exceeding 3,000 ms (1.4% of trials) were excluded from analysis. Only correct trials were included in the RT analyses.
Transitions
Although our focus will be on congruency effects, we first report transition analyses to show that our cue–prime–target procedure yielded typical task-switching data. Trials were coded for transition, CPI, and PTI, and mean RTs and ERs were each submitted to a repeated-measures analysis of variance (ANOVA) with those variables.
The RT data are shown in Figure 1. All effects except for the three-way interaction (p =.101) were highly significant (smallest F = 21.16, all ps <.001, smallest ηp2 =.38). Task switches (816 ms) were slower than task repetitions (708 ms) and this switch cost decreased from 130 to 86 ms as CPI increased and it decreased from 139 to 77 ms as PTI increased, indicating that both intervals were effective. In terms of the combined cue–target interval (CTI), switch cost decreased from 168 to 60 ms as CTI increased from 200 ms (CPI = 100 ms, PTI = 100 ms) to 1,600 ms (CPI = 800 ms, PTI = 800 ms). Besides the reductions in switch cost, there were reductions in overall RT for both CPI (34 ms) and PTI (130 ms).
Figure 1.
Transition data for response time as a function of cue–prime interval and prime–target interval. Error bars represent standard errors of the means. TS = task switch, TR = task repetition.
Mean ER was 4.3%. Task switches (5.6%) were more error-prone than task repetitions (2.9%), F(1,35) = 65.16, MSE = 7.56, p <.001, ηp2 =.65, and this switch cost decreased from 3.2% to 2.0% as PTI increased, F(1,35) = 5.33, MSE = 4.25, p <.05, ηp2 =.13. No other effects were significant (all ps >.17).
Congruency
For the congruency analyses, trials were coded for cue–prime, prime–target, prime–response, and response congruency (see Table 1 for examples). Given that the four types of congruency do not enable a complete factorial design, mean RTs and ERs were each submitted to two repeated-measures ANOVAs: a 2 (cue–prime congruency) × 2 (prime–target congruency) × 2 (response congruency) ANOVA and a 2 (cue–prime congruency) × 2 (prime–response congruency) × 2 (response congruency) ANOVA. We collapsed over transition, CPI, and PTI because preliminary analyses including those variables revealed that neither CPI nor PTI interacted with any type of congruency in RT or yielded uninterpretable four-way interactions in ER. Null interactions with CPI and PTI can be attributed to the fact that most of the congruency relations do not exist until the target has been presented, by which time both intervals have elapsed. Transition only had the effect of increasing the response congruency effect by 17 ms in RT and 3.0% in ER on task-switch trials compared with task-repetition trials. It turned out that the prime–target and prime–response congruency effects were largely restricted to cue–prime congruent trials, for which both variables are perfectly correlated (see Table 1), leading to similar results. Therefore, we include the prime–response congruency data for completeness, but we focus on the results from the first ANOVA and only refer to the results from the second ANOVA when warranted.
The RT data are shown in Figure 2A. Cue–prime incongruent trials (772 ms) were slower than congruent trials (751 ms), F(1,35) = 20.70, MSE = 1,568.47, p <.001, ηp2 =.37. Prime–target incongruent trials (765 ms) were slower than congruent trials (758 ms), F(1,35) = 4.19, MSE = 745.47, p <.05, ηp2 =.11 (for the comparable-sized prime–response congruency effect, p =.098, ηp2 =.08). Response incongruent trials (786 ms) were slower than congruent trials (738 ms), F(1,35) = 83.08, MSE = 1,973.66, p <.001, ηp2 =.70. There was an interaction between cue–prime congruency and prime–target congruency, F(1,35) = 6.74, MSE = 1,059.93, p <.05, ηp2 =.16 (for the comparable interaction involving prime–response congruency, p <.05, ηp2 =.15), reflecting a prime–target congruency effect on cue–prime congruent trials (16 ms) but not on incongruent trials (−3 ms). No other interactions were significant (all ps >.18).
Figure 2.
Congruency data (bars) and predictions of the retrieval model (points) for response time and error rate (panels A and B, respectively). Error bars represent standard errors of the means. CP = cue–prime, PT = prime–target, PR = prime–response, Resp = response, Incong = incongruent, Cong = congruent.
The ER data are shown in Figure 2B. Cue–prime incongruent trials (4.5%) were more error-prone than congruent trials (3.9%), F(1,35) = 6.63, MSE = 3.73, p <.05, ηp2 =.16. Prime–target incongruent trials (4.5%) were more error-prone than congruent trials (3.9%), F(1,35) = 6.35, MSE = 3.91, p <.05, ηp2 =.15, though the same did not hold for prime–response congruency, where a 0.2% difference failed to reach significance, p =.27. Response incongruent trials (6.9%) were more error-prone than congruent trials (1.6%), F(1,35) = 74.22, MSE = 26.77, p <.001, ηp2 =.68. There was an interaction between cue–prime congruency and response congruency, F(1,35) = 8.47, MSE = 4.67, p <.01, ηp2 =.19, reflecting a larger response congruency effect on cue–prime incongruent trials (6.0%) than on congruent trials (4.5%). The only other interaction near significance was between cue–prime congruency and prime–response congruency, F(1,35) = 3.75, MSE = 4.44, p =.061, ηp2 =.10, reflecting a prime–response congruency effect on cue–prime congruent trials (0.7%) but not on incongruent trials (−0.3%). Note that the prime–target congruency effect was comparable on cue–prime congruent and incongruent trials (0.7% and 0.5%, respectively). No other interactions approached significance (all ps >.13). The ER data were generally consistent with the RT data (see Figure 2) and there was no evidence of a speed–accuracy tradeoff.
Discussion
The transition analyses showed that our cue–prime–target procedure yielded typical task-switching data, with large switch costs in RT and ER. The switch cost in RT decreased with both CPI and PTI, consistent with several studies involving one cue per task where reductions in switch cost across preparation intervals have been obtained (e.g., Koch, 2001, Experiment 4; Logan & Bundesen, 2003; Mayr, 2002; Meiran, 1996; Meiran et al., 2000; cf. Altmann, 2006).
The congruency analyses showed a somewhat complex pattern of effects. Response congruency yielded the largest effects in both RT and ER, but there were also smaller cue–prime and prime–target (or prime–response) congruency effects, with the latter being largely restricted to cue–prime congruent trials, more so for RT than for ER (where prime–target and prime–response congruency effects were rather weak). The question of interest is whether and how our model of compound cue retrieval can account for this pattern of congruency effects. If the data can be modeled by including the prime as a joint cue in the retrieval process (i.e., as an additional term in compound cue retrieval), then the present set of congruency effects would be explained in much the same way as the cue–target congruency effects in Schneider and Logan (2005).
Modeling
Basic Framework
The present modeling framework is an extension of the model for compound cue retrieval developed by Schneider and Logan (2005). Compound cue retrieval involves using multiple pieces of evidence in combination to select a response from long-term memory (Logan & Bundesen, 2003; Ratcliff & McKoon, 1988). The evidence drives a random-walk decision process (for an overview, see Ratcliff, 2001) that involves stochastic accumulation of evidence for alternative responses until a response boundary is reached, meaning that the evidence in favor of one response has exceeded the evidence in favor of the other response by some criterion. At this point, the response associated with that boundary (i.e., the response for which there is the most evidence) has been selected and can be executed. The specific random-walk process used for compound cue retrieval is Nosofsky and Palmeri’s (1997) exemplar-based random-walk model, which belongs to a broader family of models of attention and memory (Logan, 2002) and the general class of sequential sampling models (Ratcliff & Smith, 2004).
The compound cue retrieval process begins to accumulate evidence toward a specific response after all stimuli presented during a trial have been encoded, yielding semantic representations of their associated response categories (Arrington & Logan, 2004; Arrington et al., 2007). Stimuli are represented by η values indicating the strength of evidence they provide for each response category. The total evidence for response category i is the product of the evidence from cue x, prime y, and target z (cf. Hintzman, 1986; Raaijmakers & Shiffrin, 1981; see Logan, 2002, pp. 385–386, for discussion of why η values would multiply):
| (1) |
This multiplicative combination of evidence is the essence of compound cue retrieval. Note that in Schneider and Logan (2005), the cue and the prime were one and the same, resulting in only two multiplicands in Equation 1.
An assumption made by Schneider and Logan (2005) about compound cue retrieval is that if a stimulus has yet to be encoded, its η value equals zero. When this happens, the products calculated from Equation 1 will equal zero for all response categories, so no evidence will be accumulated toward selecting a response. An implication of this assumption is that response selection and the congruency effects attributed to it are not affected by manipulations of CPI and PTI because compound cue retrieval does not lead to evidence accumulation until both intervals have elapsed. The null interactions between the various types of congruency and CPI and PTI in the data (see the Results section) provide some support for this constraint on response selection. However, it is important to be clear that this assumption and its implications do not rule out and should not be confused with effects of CPI and PTI on alternative stages of processing (e.g., cue encoding) involved in producing other effects (e.g., transition effects). The part of Schneider and Logan’s (2005) model dealing with priming of cue encoding explicitly relates changes in CTI to differences in cue-encoding time that are manifest in transition effects. Understanding that compound cue retrieval is a different part of the model is crucial for understanding the effects that specific independent variables may or may not have on response selection.
The total evidence for each response category determines how quickly that category is retrieved from long-term memory. Assuming no differential biases toward specific response categories across conditions, η values correspond to rates of retrieval from long-term memory (see Schneider & Logan, 2005, pp. 348–349). As a result, the probability of retrieving response category i is the ratio of its evidence over the summed evidence for all response categories j in the response set R (Luce, 1959):
| (2) |
Given that two response categories were assigned to each response key in the experiment and subjects had to choose a response key to press, response key k is chosen with probability:
| (3) |
In other words, the probabilities of retrieving the two response categories mapped onto the same response key are summed to give the probability of choosing that key. The probabilities yielded by Equation 3 represent the rates at which evidence accumulates for selecting a response during the random-walk decision process (Nosofsky & Palmeri, 1997). Assuming that the correct and incorrect responses (kc and kic, respectively) have unequal probabilities, which they did in all our model fits, the time per step of the random walk (RTstep) and the number of steps (Nstep) it takes for the random walk to reach response boundary A for a correct response instead of response boundary B for an incorrect response are given by:
| (4) |
and
| (5) |
where
| (6a) |
and
| (6b) |
The total time for compound cue retrieval, RTCCR, is the product of the time per step and the number of steps of the random walk:
| (7) |
To generate a prediction for RT, compound cue retrieval time is added to a base RT value (RTbase) that represents the time required by all non-decisional processes (e.g., stimulus encoding and response execution):
| (8) |
To generate a prediction for accuracy, the probability of choosing the correct response is:
| (9) |
Equations 1–9 represent the basic framework for modeling compound cue retrieval, which only differs from that of Schneider and Logan (2005) by the inclusion of the prime as a term in the equations. Within this framework, we developed four models to investigate the role of primes in performance. One model involves no priming and the other models implement priming in different ways, with primes affecting the retrieval process, response boundaries, or response execution. These models correspond to the four alternatives outlined earlier.
Models
No priming
In this model, primes have no differential effects on performance across conditions. For cues and targets, we assume there are different evidence parameters (η values) for associated and unassociated response categories (ηct-a and ηct-u, respectively). Table 2 indicates which of these evidence parameters is used in Equation 1 for each response category for the example stimuli in Table 1. For primes, we assume a single evidence parameter, ηprime-u, that is set equal to ηct-u for all conditions, making it a constant in Equation 1. For example, for a trial involving the cue Magnitude, the prime Odd, and the target 3, the evidence from the cue, η(i|x), would be ηct-a for low and high and ηct-u for odd and even, the evidence from the prime, η(i|y), would be ηprime-u for all categories, and the evidence from the target, η(i|z), would be ηct-a for low and odd and ηct-u for high and even. We assume equal boundaries for the random walk (represented by C, where A = B = C) and a single RTbase value. The no-priming model has four free parameters: ηct-a, ηct-u, C, and RTbase.
Table 2.
Evidence parameters used to model different experimental conditions
| Example Stimuli |
Evidence |
|||||
|---|---|---|---|---|---|---|
| Cue x | Prime y | Target z | Category i | η(i|x) | η(i|y) | η(i|z) |
| Parity | Low | 8 | odd | ηct-a | ηprime-u | ηct-u |
| even | ηct-a | ηprime-u | ηct-a | |||
| low | ηct-u | ηprime-p | ηct-u | |||
| high | ηct-u | ηprime-a | ηct-a | |||
| Parity | Low | 7 | odd | ηct-a | ηprime-u | ηct-a |
| even | ηct-a | ηprime-u | ηct-u | |||
| low | ηct-u | ηprime-p | ηct-u | |||
| high | ηct-u | ηprime-a | ηct-a | |||
| Parity | Low | 4 | odd | ηct-a | ηprime-u | ηct-u |
| even | ηct-a | ηprime-u | ηct-a | |||
| low | ηct-u | ηprime-p | ηct-a | |||
| high | ηct-u | ηprime-a | ηct-u | |||
| Parity | Low | 3 | odd | ηct-a | ηprime-u | ηct-a |
| even | ηct-a | ηprime-u | ηct-u | |||
| low | ηct-u | ηprime-p | ηct-a | |||
| high | ηct-u | ηprime-a | ηct-u | |||
| Parity | Odd | 4 | odd | ηct-a | ηprime-p | ηct-u |
| even | ηct-a | ηprime-a | ηct-a | |||
| low | ηct-u | ηprime-u | ηct-a | |||
| high | ηct-u | ηprime-u | ηct-u | |||
| Parity | Odd | 8 | odd | ηct-a | ηprime-p | ηct-u |
| even | ηct-a | ηprime-a | ηct-a | |||
| low | ηct-u | ηprime-u | ηct-u | |||
| high | ηct-u | ηprime-u | ηct-a | |||
| Parity | Odd | 7 | odd | ηct-a | ηprime-p | ηct-a |
| even | ηct-a | ηprime-a | ηct-u | |||
| low | ηct-u | ηprime-u | ηct-u | |||
| high | ηct-u | ηprime-u | ηct-a | |||
| Parity | Odd | 3 | odd | ηct-a | ηprime-p | ηct-a |
| even | ηct-a | ηprime-a | ηct-u | |||
| low | ηct-u | ηprime-u | ηct-a | |||
| high | ηct-u | ηprime-u | ηct-u | |||
Note. The evidence parameters are used in Equation 1 to calculate the η product for each response category. For the no-priming, boundary, and execution models, ηprime-u = ηprime-a = ηprime-p. Table 1 indicates the congruency relations associated with each set of stimuli. Table 3 indicates the best-fitting parameter values of each model for the group fits.
Retrieval
In this model, primes affect the retrieval process (more specifically, the rate of evidence accumulation) by providing differential evidence in favor of specific response categories. Instead of assuming a single evidence parameter for primes, there are different evidence parameters for strongly associated, moderately associated, and unassociated response categories (ηprime-p, ηprime-a, and ηprime-u, respectively). Table 2 indicates which of these evidence parameters is used in Equation 1 for each response category for the example stimuli in Table 1. For example, for a trial involving the prime Odd, the evidence from the prime, η(i|y), would be ηprime-p for odd, ηprime-a for even (because odd and even are associated; see Nelson, McEvoy, & Schreiber, 1999), and ηprime-u for low and high. Consequently, the evidence from the prime is not a constant in Equation 1. As in the no-priming model, ηprime-u is set equal to ηct-u. In the model fits reported below, ηprime-p was estimated as a proportion of ηct-a and ηprime-a was estimated as a proportion of ηprime-p to reflect the idea that primes would exert a fraction of the effects of cues and targets because they are potentially useful (if valid) but not necessary for accurate task performance. However, note that this is equivalent to letting ηprime-p and ηprime-a be free parameters subject to ordinal constraints; therefore, for ease of exposition and cross-model comparisons, we will refer to η values rather than proportions. The retrieval model has six free parameters: ηct-a, ηct-u, ηprime-p, ηprime-a, C, and RTbase.
Boundary
In this model, primes affect the response boundaries rather than the rate of evidence accumulation toward those boundaries. This model is equivalent to the no-priming model except A ≠ B in Equations 5, 6a, 6b, and 9, allowing for different response boundaries for primed and unprimed responses (Cprimed and Cunprimed, respectively, where the correspondence with A and B depends on prime–response congruency). For example, for a trial involving the prime Odd, the boundary for the response key onto which odd is mapped would be primed (i.e., Cprimed) and the alternative boundary would not be primed (i.e., Cunprimed). If Cprimed ≠ Cunprimed, then this creates an asymmetry whereby the random walk does not have to go as far to reach one boundary as it does to reach the other. In terms of prime–response congruency, the prime creates an asymmetry such that on a prime–response congruent trial, the correct response boundary is primed (i.e., A = Cprimed, B = Cunprimed), whereas on a prime–response incongruent trial, the incorrect response boundary is primed (i.e., B = Cprimed, A = Cunprimed). The boundary model has five free parameters: ηct-a, ηct-u, Cprimed, Cunprimed, and RTbase.
Execution
In this model, primes do not affect response selection at all. Instead, they affect execution of the manual response. This model is equivalent to the no-priming model except there are different values of RTbase for primed and unprimed responses (RTbase-primed and RTbase-unprimed, respectively). For example, for a trial involving the prime Odd, execution of the response onto which odd is mapped would be primed (i.e., RTbase-primed) and the alternative response would not be primed (i.e., RTbase-unprimed). If RTbase-primed ≠ RTbase-unprimed, then one response can be executed faster than the other. In terms of prime–response congruency, on a prime–response congruent trial, execution of the correct response is primed, whereas on a prime–response incongruent trial, execution of the incorrect response is primed. The execution model has five free parameters: ηct-a, ηct-u, C, RTbase-primed, and RTbase-unprimed.
Summary
Although these models may not exhaust the space of possibilities by which priming could occur, they allow for a comparison of alternative models constructed within the same framework. In three of the models (no priming, boundary, and execution), primes do not affect the retrieval process itself (i.e., they do not change the probabilities in Equations 2 and 3) because a single evidence parameter, ηprime-u, is used for all conditions. It is only in the retrieval model that primes differentially affect the rate of evidence accumulation, making this model the closest conceptually to the way we modeled priming from category-label cues in Schneider and Logan (2005). Consequently, the extent to which the retrieval model accounts for the data better than the alternative models can be taken as validation of our previous modeling efforts and support for compound cue retrieval as a mechanism for response selection in task-switching situations.
Model Fitting
Each model was fit to both the RT and ER congruency data (a total of 16 data points) using the Solver routine in Microsoft Excel to minimize the root-mean-squared deviation (RMSD) between data and model predictions. To generate this composite measure and give relatively equal weight to both dependent variables, we converted ER to accuracy (percentage of correct responses) and multiplied it by 10 to place it on a similar scale to RT (as in Schneider & Logan, 2005). This approach seemed to work well, yielding similar SDs across conditions (29 for both RT and scaled accuracy) and ranges (80 for RT and 66 for scaled accuracy). For the model predictions reported below, we converted accuracy back to ER. From the composite fits, we calculated separate RMSDs for RT and accuracy as well as the proportion of variance explained by the model (r2) in each case.
We fit the models to the group data in Figure 2 and to the individual-subject data. However, the group data were much more stable than the individual-subject data for model fitting, especially with respect to the smaller congruency effects in the data, some of which were less than 10 ms in RT or less than 1.0% in ER. Although these small effects were reliable across subjects (see the Results section), they were not necessarily present in every subject’s data pattern. Distortions in the data pattern due to noise at the individual-subject level may outweigh possible distortions due to averaging at the group level, and under these circumstances, group fits may be better than individual-subject fits (Cohen, Sanborn, & Shiffrin, in press). For these reasons, we report the results of both kinds of fits (which produced similar results), but we focus on the fits to group data.
The model fits were constrained as follows: First, all parameter values > 0. For the η values, this constraint means that stimuli provide evidence for and not against response categories. Second, A and B ≤ 10 and A = B for all but the boundary model. Third, all η values ≤ 1 to provide an upper bound on the evidence from each stimulus. Fourth, ηct-u = ηprime-u ≤ ηprime-a ≤ ηprime-p ≤ ηct-a, which reduces to ηct-u = ηprime-u ≤ ηprime-a = ηprime-p ≤ ηct-a for all models except for the retrieval model. This constraint can be decomposed as follows: For all models, ηct-u ≤ ηct-a to capture the assumption that cues and targets associated with a response category are likely to provide more evidence for that category than unassociated cues and targets. We set ηct-u = ηprime-u because unassociated primes are likely to be unassociated with a response category to the same degree as unassociated cues and targets. All ηprime values fall within the range of the ηct values to capture the idea that primes with some degree of association would exert a fraction of the effects of associated cues and targets because they are potentially useful (if valid) but not necessary for accurate task performance. For all models except for the retrieval model, ηprime-u = ηprime-a = ηprime-p so that primes do not differentially affect the retrieval process in those models. For the retrieval model, ηprime-u ≤ ηprime-a ≤ ηprime-p to allow for differential priming effects on retrieval. The consequences of having certain ηprime values be equal to each other in the retrieval model are explored below. Relaxing most of these constraints had little effect on the group fits.
Results
Group fits
All models produced a response congruency effect in RT (48 ms for all models compared with an observed effect of 48 ms) and ER (5.2%, 5.0%, 5.2%, and 5.2% for the no-priming, retrieval, boundary, and execution models, respectively, compared with an observed effect of 5.3%). This occurred because the effect is largely driven by the evidence from the target and how probabilities of retrieving different response categories are mapped onto response keys (Equation 3). For example, for a trial involving the cue Parity and the target 3, the probability of selecting the response key for odd will be higher if odd and low are mapped onto the same key (response congruent) than if they are mapped onto different keys (response incongruent). Note that although Schneider and Logan (2005, p. 362) mentioned that compound cue retrieval could produce a response congruency effect, the present study represents the first time we have actually fit models to response congruency data and shown that compound cue retrieval can produce an effect of comparable magnitude to what is observed in data.
The models differ when it comes to the other congruency effects. The no-priming model failed to produce cue–prime, prime–target, and prime–response congruency effects. It predicted the same value for all response incongruent trials (the tall bars in Figure 2) and the same value for all response congruent trials (the short bars in Figure 2). The boundary and execution models also failed to produce a cue–prime congruency effect; however, they did produce a prime–target congruency effect on RT that was restricted to cue–prime congruent trials, though the effect was smaller (6 ms) than in the data (16 ms). Although the boundary and execution models also produced a prime–response congruency effect, they did not produce the observed interaction with cue–prime congruency. Neither model was able to produce the interaction between cue–prime congruency and response congruency in ER, and given that the execution model only differs from the no-priming model in its effects on RT, it also failed to produce a prime–target congruency effect in ER. In summary, none of these models—no priming, boundary, or execution—provided a satisfactory account of the data.
In contrast, the retrieval model captured the major effects in the data. Its predictions are plotted with the data in Figure 2. It was the only model to produce a cue–prime congruency effect, equaling the magnitudes of the effect in both RT and ER (21 ms and 0.6%, respectively). It produced prime–target and prime–response congruency effects on RT that were restricted to cue–prime congruent trials, but unlike the boundary and execution models, the magnitude of the effect (13 ms) was much closer to the data (16 ms). It also produced a prime–target congruency effect on ER, though the effect was somewhat smaller (0.2%) than in the data (0.6%). In contrast with the other models, the retrieval model also produced the interaction between cue–prime congruency and response congruency in ER, where the response congruency effects on cue–prime incongruent and congruent trials (5.6% and 4.5%, respectively) were close to those in the data (6.0% and 4.5%, respectively).
Overall, the retrieval model provided a superior account of the congruency effects in the RT and ER data, a conclusion that is also borne out by the measures of goodness of fit (summarized in Table 3, which also gives the best-fitting parameter values for each model). The composite RMSD was smaller for the retrieval model (4.0) relative to all other models (9.6, 9.4, and 9.4 for the no-priming, boundary, and execution models, respectively). None of the priming models are nested within one another (i.e., one priming model cannot be formed from another priming model just by holding certain parameter values constant), so it is not possible to compare their fits using nested model comparisons. However, the no-priming model is nested within all the priming models, so it can be used as a baseline to assess the degree to which each implementation of priming improves the goodness of fit to the data over no priming. Nested model comparisons involving the composite r2 values indicated that the retrieval model fit significantly better than the no-priming model, F(2,10) = 33.97, p <.001, whereas the boundary and execution models did not fit significantly better than the no-priming model, both Fs(1,11) < 1. However, these comparisons should be interpreted with some caution because the composite r2 values are inflated by global differences between RT and scaled accuracy that are captured by all models. For this reason, it is useful to examine the separate fit indices for both variables, which are also provided in Table 3. The retrieval model produced an excellent fit to RT (RMSD = 4.4 and r2 =.97) and scaled accuracy (RMSD = 3.6 and r2 =.98), whereas the other models achieved much poorer fits to RT (mean RMSD = 12.1 and mean r2 =.80) compared with scaled accuracy (mean RMSD = 5.7 and mean r2 =.95).
Table 3.
Best-fitting parameter values and measures of goodness of fit for the group fits
| Model |
||||
|---|---|---|---|---|
| Variable | No Priming | Retrieval | Boundary | Execution |
| Parameters | ||||
| ηct-u | .065 | .055 | .063 | .065 |
| ηct-a | .408 | .384 | .402 | .408 |
| ηprime-u | .065 | .055 | .063 | .065 |
| ηprime-a | .065 | .059 | .063 | .065 |
| ηprime-p | .065 | .062 | .063 | .065 |
| C | 2.25 | 2.07 | - | 2.25 |
| Cunprimed | - | - | 2.22 | - |
| Cprimed | - | - | 2.18 | - |
| RTbase | 533 | 498 | 524 | - |
| RTbase-unprimed | - | - | - | 536 |
| RTbase-primed | - | - | - | 529 |
| Measures of goodness of fit | ||||
| RMSD | 9.6 | 4.0 | 9.4 | 9.4 |
| r2 | .9995 | .9999 | .9995 | .9995 |
| RMSD (RT) | 12.4 | 4.4 | 12.0 | 12.0 |
| r2 (RT) | .7877 | .9728 | .8002 | .8016 |
| RMSD (Acc) | 5.7 | 3.6 | 5.8 | 5.7 |
| r2 (Acc) | .9553 | .9839 | .9528 | .9553 |
Note. RMSD = root-mean-squared deviation between data and model predictions; r2 = proportion of variance in the data explained by the model; RT = response time; Acc = scaled accuracy. See text for descriptions of model parameters. Bold-faced parameters were free parameters in the model fits.
Individual-subject fits
The fits to individual-subject data yielded similar results. The mean fit indices are summarized in Table 4. For the composite and separate fit indices, RMSD was smaller and r2 was larger for the retrieval model compared with the other models. Moreover, the means of the individual-subject predictions from the retrieval model were almost identical to the group predictions plotted in Figure 2 (RMSD = 2.0 and r2 =.99998). Nested model comparisons involving the composite r2 values indicated that the retrieval model fit significantly better than the no-priming model for 14 of the 36 subjects, whereas the boundary and execution models fit significantly better than the no-priming model for 9 and 10 of the 36 subjects, respectively. For readers who are curious as to why the retrieval model did not fit significantly better than the no-priming model for a greater number of subjects, we reiterate the earlier point that the composite r2 values are inflated by global differences between RT and scaled accuracy, and at both the group and individual-subject levels, this works against finding significant differences between model fits. In principle, this issue could be addressed by performing nested model comparisons separately for RT and scaled accuracy, but given that there are only eight data points per dependent variable, such comparisons would have extremely low statistical power. However, if one focuses on numerical differences between model fits, it is noteworthy that the mean r2 value calculated separately for RT was much higher for the retrieval model (r2 =.63) compared with all other models (r2 =.33,.44, and.48 for the no-priming, boundary, and execution models, respectively; see Table 4).
Table 4.
Mean best-fitting parameter values (with 95% confidence intervals) and measures of goodness of fit for the individual-subject fits
| Model |
||||
|---|---|---|---|---|
| Variable | No Priming | Retrieval | Boundary | Execution |
| Parameters | ||||
| ηct-u | .083 ±.022 | .084 ±.030 | .084 ±.026 | .083 ±.023 |
| ηct-a | .506 ±.070 | .493 ±.071 | .514 ±.074 | .507 ±.069 |
| ηprime-u | .083 ±.022 | .084 ±.030 | .084 ±.026 | .083 ±.023 |
| ηprime-a | .083 ±.022 | .093 ±.033 | .084 ±.026 | .083 ±.023 |
| ηprime-p | .083 ±.022 | .097 ±.034 | .084 ±.026 | .083 ±.023 |
| C | 2.62 ± 0.48 | 2.77 ± 0.68 | - | 2.63 ± 0.50 |
| Cunprimed | - | - | 2.62 ± 0.51 | - |
| Cprimed | - | - | 2.61 ± 0.53 | - |
| RTbase | 465 ± 66 | 460 ± 54 | 439 ± 71 | - |
| RTbase-unprimed | - | - | - | 471 ± 65 |
| RTbase-primed | - | - | - | 464 ± 66 |
| Measures of goodness of fit | ||||
| RMSD | 23.5 | 19.0 | 22.0 | 21.8 |
| r2 | .9972 | .9982 | .9975 | .9977 |
| RMSD (RT) | 28.0 | 21.5 | 25.8 | 25.1 |
| r2 (RT) | .3315 | .6347 | .4441 | .4823 |
| RMSD (Acc) | 15.5 | 14.4 | 15.3 | 15.5 |
| r2 (Acc) | .5698 | .5913 | .5600 | .5698 |
Note. RMSD = root-mean-squared deviation between data and model predictions; r2 = proportion of variance in the data explained by the model; RT = response time; Acc = scaled accuracy. See text for descriptions of model parameters. Bold-faced parameters were free parameters in the model fits.
The means of the best-fitting parameter values and their associated 95% confidence intervals are also summarized in Table 4. These values are generally in agreement with the values obtained from the group fits (see Table 3), although for each model there was either one (execution model) or two (no-priming, retrieval, and boundary models) group parameters that fell outside of the individual-subject confidence intervals. An important consideration when interpreting these results is that on occasion, a “best-fitting” parameter value from an individual-subject fit was equal to or near the minimum or maximum value allowed during model fitting, impairing reliable estimation of other parameter values.
Model Flexibility and Complexity
For both the group fits and the individual-subject fits, the retrieval model provided a better account of the data than the alternative models. We interpret these results as support for the idea that primes participate directly in the process of retrieving a response, consistent with the modeling by Schneider and Logan (2005). However, an alternative interpretation is that the retrieval model produced a superior fit only because it is more flexible or more complex than the other models. In this section, we investigate whether model flexibility and complexity mitigate the conclusions we have drawn from the model fits.
Model flexibility
Is the retrieval model more flexible than the alternative models in accounting for data? To address this question, we investigated how well each model could fit data that was generated by itself and by the other models (e.g., see Cohen et al., in press). Using the fits to individual-subject data, we calculated the means of the individual-subject predictions for each model and used them as the “data” to which all models were fit. For example, if the model generating the data was the no-priming model, then the means of the individual-subject predictions of the no-priming model were used as the data to which all models were fit. Every model was used to generate data; therefore, each model was fit to four data sets. If the retrieval model is more flexible than the alternative models, then it should fit each data set almost as well as the model that generated the data.
The RMSD values for all fits are provided in Table 5. When the no-priming model generated the data, all models fit equally well with negligible RMSD values. This result is not surprising because the no-priming model is nested within the other models, so all of the priming models can be reduced to the no-priming model and produce the same predictions. When one of the priming models generated the data, the results were more telling: In each case, the model generating the data provided the best fit to the data. For example, when the retrieval model generated the data, it provided a much better fit (RMSD = 0.89) than the alternative models (mean RMSD = 10.21). Critically, when either the boundary model or the execution model generated the data, the retrieval model produced only the third-best fit (see the third and fourth columns of Table 5). The execution model produced the second-best fit to the data generated by the boundary model, whereas the boundary model produced the second-best fit to the data generated by the execution model, possibly suggesting some degree of model mimicry. These results indicate that the retrieval model is not overly flexible in its ability to fit data because it did not provide the best (or even the second-best) fit to data generated by the other priming models. Thus, the superior fit of the retrieval model to the experimental data cannot be attributed to greater flexibility (see also Cohen et al., in press).
Table 5.
Root-mean-squared deviations between the data generated by each model (the means of the individual-subject predictions) and the predictions of each model fit to that data
| Model Generating Data |
||||
|---|---|---|---|---|
| Model Fit to Data | No Priming | Retrieval | Boundary | Execution |
| No Priming | 0.01 | 10.50 | 1.84 | 2.26 |
| Retrieval | 0.01 | 0.89 | 1.35 | 1.84 |
| Boundary | 0.01 | 10.02 | 0.45 | 1.31 |
| Execution | 0.01 | 10.12 | 0.67 | 0.01 |
Note. The no-priming model is nested within the other models.
A further conclusion that can be drawn from these results is that averaging over individual subjects who had different sets of best-fitting parameter values did not distort the group data patterns to which the models were fit. For each of the priming models, the model that generated the data at the individual-subject level was also the model that provided the best fit to the group data derived by averaging the individual-subject predictions (see Table 5). This correspondence suggests that the earlier model fits to the group data from the experiment were not compromised by averaging, although we note that this conclusion does not necessarily extend beyond the class of models investigated in the present study.
Model complexity
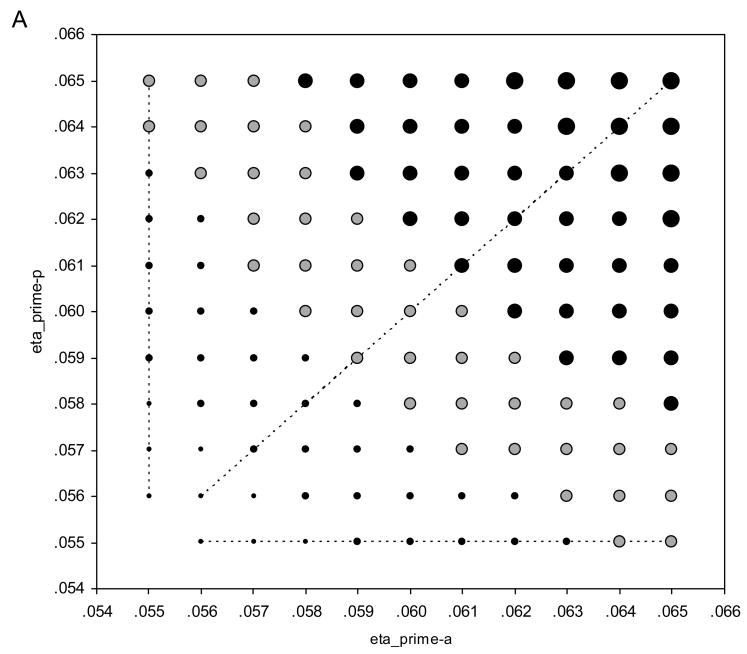
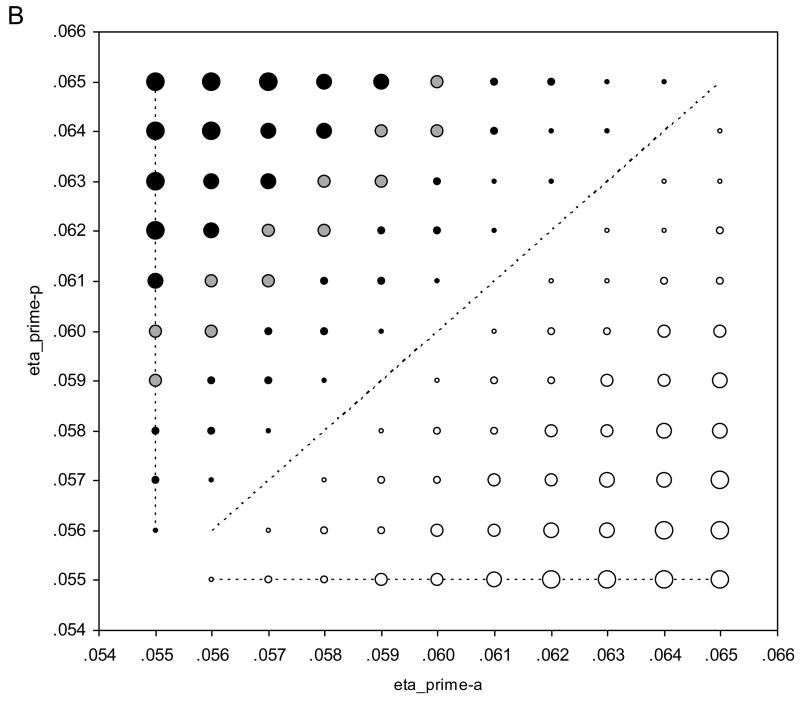
Although the retrieval model provided a better account of the data than the alternative models, it did so with at least one more free parameter than any other model (recall that the no-priming, boundary, execution, and retrieval models have four, five, five, and six free parameters, respectively). Is the superior fit of the retrieval model due solely to its greater complexity? To address this question, we conducted parameter sensitivity analyses (e.g., see Li, Lewandowsky, & DeBrunner, 1996) to determine how strongly the predictions of the retrieval model depend on the two free parameters (ηprime-p and ηprime-a) that make it more complex than the no-priming model. For these analyses, we focused on two effects in the RT data that were central to the success of the retrieval model: the cue–prime congruency effect and the cue–prime congruency × prime–target congruency interaction. For each analysis, we generated the predictions of the retrieval model as ηprime-p and ηprime-a were varied independently from.055 to.065 in steps of.001 while keeping all other parameter values fixed at their best-fitting values from the group fit (see Table 3; note that ηprime-u =.055). Instead of evaluating changes in RMSD or r2 across the parameter space (cf. Li et al., 1996), we focused on the magnitude and direction of the effect produced by each combination of parameter values.
The results are presented in Figure 3A for the cue–prime congruency effect and in Figure 3B for the cue–prime congruency × prime–target congruency interaction effect (represented by the contrast: cue–prime congruent/prime–target incongruent – cue–prime congruent/prime–target congruent – cue–prime incongruent/prime–target incongruent + cue–prime incongruent/prime–target congruent). The points in each plot, from smallest to largest, represent effects of 1–8 ms, 9–16 ms, 17–24 ms, 25–32 ms, and 33+ ms, respectively (the absence of a point represents an effect of 0 ms). Filled and unfilled points represent positive and negative effects, respectively. Gray-filled points represent the observed effects in the data. Dashed lines represent trajectories through the parameter space where two of the three ηprime values are equal, making the retrieval model equivalent to a five-parameter model (like the boundary and execution models). The bottom-left corner of each plot is where all three ηprime values are equal, making the retrieval model identical to the four-parameter no-priming model.
Figure 3.
Parameter sensitivity plots for the cue–prime congruency effect and the cue–prime congruency × prime–target congruency interaction effect (panels A and B, respectively) for response time produced by the retrieval model. See text for details. eta_prime-p = ηprime-p; eta_prime-a = ηprime-a.
Regarding the cue–prime congruency effect (see Figure 3A), it is evident that the retrieval model can produce the effect over a wide range of parameter values, with the only exception being when all three ηprime values are equal. There is a region of the parameter space spanning from the upper-left corner to the lower-right corner of the plot where the model produces an effect that approximates the magnitude of the observed effect in the data. Critically, there are several points (viz., the gray-filled points that fall on the dashed lines) where the retrieval model produces an effect of the appropriate magnitude even though it is equivalent to a five-parameter model, making it no more complex than the boundary or execution models. Thus, a simpler version of the retrieval model that has the same number of free parameters as the alternative priming models can produce the cue–prime congruency effect, implying that its ability to do so is not a consequence of model complexity but a reflection of the way in which priming is instantiated in the model.
Regarding the cue–prime congruency × prime–target congruency interaction (see Figure 3B), it is evident that a more constrained range of parameter values is required to produce the effect. As in the preceding analysis, no effect is produced when all three ηprime values are equal. There is also no effect when the retrieval model is reduced to a five-parameter model by making ηprime-p = ηprime-a (the diagonal dashed line in the plot). When ηprime-p < ηprime-a (the lower-right “triangle” of the plot), the model produces an effect in the wrong direction. It is only when ηprime-p > ηprime-a (the upper-right “triangle” of the plot) that the model produces an effect in the correct direction and, for a small region of the parameter space, an effect of the appropriate magnitude. Critically, there are points (viz., the gray-filled points that fall on the vertical dashed line) where the retrieval model produces an effect of the appropriate magnitude even though it is equivalent to a five-parameter model, illustrating once again that the model’s ability to produce the effect is not a consequence of model complexity.
The parameter sensitivity plots in Figure 3 indicate that a five-parameter version of the retrieval model, where ηprime-p > ηprime-a = ηprime-u, can produce effects of the appropriate magnitudes. From a mathematical modeling perspective, one might prefer the five-parameter model over the original six-parameter model (where ηprime-p > ηprime-a > ηprime-u) because of its parsimony (i.e., it can account for the same effects with one less free parameter). From a cognitive modeling perspective, we prefer the six-parameter model because of theoretical considerations related to how the model parameters map onto psychological constructs. To elaborate, each ηprime value represents the strength of association between a prime word and a response category in semantic memory. On the basis of free association norms (Nelson et al., 1999) and intuitive reasoning, we argue that each prime is differentially associated with each category. For example, we assume that the category odd has a strong association with the prime Odd (ηprime-p, because the word is an orthographic representation for the category), a moderate association with the prime Even (ηprime-a, because of semantic associations between odd and even in memory), and no associations with the primes Low and High (ηprime-u). Separate ηprime values are required to represent these differential associations, with ηprime-p > ηprime-a > ηprime-u (see also Schneider & Logan, 2005). Thus, we have a prime example (pardon the pun) of a situation in which the evaluation of model complexity should go beyond counting the number of free parameters and include consideration of psychological constraints related to the meaning of those parameters.
General Discussion
The goal of the present study was to test a model of compound cue retrieval, a mechanism by which responses can be selected in task-switching situations. Compound cue retrieval has been neglected in previous investigations of our modeling work, with the only test of it coming in the study in which the mechanism was formally developed (Schneider & Logan, 2005). However, the use of category-label cues in that study masked an important distinction between cues and primes (Kantowitz & Sanders, 1972; Sudevan & Taylor, 1987), making it unclear whether compound cue retrieval could accommodate the distinction and leaving an open question as to the locus of prime-based effects.
In the present study, we used a cue–prime–target procedure that allowed us to make a clear distinction between cues and primes and to examine a broad range of congruency effects in task-switching performance. We explored four models by which prime-based effects might or might not occur (no-priming, retrieval, boundary, and execution models) and found that only the retrieval model—wherein primes affect the rate of evidence accumulation during response selection—was able to account for the complex pattern of congruency effects in both the RT and ER data, regardless of whether model fitting was done at the group or individual-subject level. Additional analyses revealed that the superior fit of the retrieval model could not be explained by model flexibility or complexity.
The retrieval model is consistent with how category-label cues and the associated cue–target congruency effects were modeled in Schneider and Logan (2005), thereby validating that modeling effort. At the heart of the retrieval model is the idea that the cue, prime, and target combine multiplicatively in response selection (Equation 1), serving as joint cues for retrieving response categories from long-term memory. This is the essence of compound cue retrieval as a mechanism for response selection in task switching, enabling different responses to the same stimulus in different task contexts. In the remainder of this article, we draw connections between our model and current theorizing about response congruency effects and highlight relations between compound cue retrieval and other theoretical proposals for response selection in task switching.
Response Congruency
The largest congruency effect in both the RT and ER data was the response congruency effect, for which there has been a recent surge of interest in the task-switching literature (e.g., Brown et al., 2007; Kiesel et al., 2007; Meiran, 2005; Meiran & Kessler, 2008; Wendt & Kiesel, 2008). Drawing upon distinctions made by Pashler and Baylis (1991), Meiran and Kessler (2008) outlined two routes by which response congruency effects could occur. The mediated route involves translating a target representation into a response-category representation, which in turn is translated into a response representation that can eventually be used for response execution. The route is said to be mediated because of the intermediate formation of the response-category representation in what Meiran and Kessler referred to as active long-term memory. In contrast, the non-mediated route involves translating a target representation directly into a response representation, bypassing the formation of a response-category representation. Meiran and Kessler argued that response congruency effects reflect the mediated route and they provided some evidence in support of this argument.
Our modeling of response congruency effects using compound cue retrieval is very much consistent with Meiran and Kessler’s (2008) proposal (see also Meiran, 2000). In all four models (recall that they all produced response congruency effects), what matters in the evidence accumulation process is not the specific targets per se, but the strengths of evidence for response categories associated with those targets. A critical aspect of compound cue retrieval is the formation of these response-category representations, which then map onto response keys in such a way (see Equation 3) that the probability of choosing the correct response is greater on congruent trials than on incongruent trials, producing response congruency effects in RT and ER. Thus, the model instantiates and uses the mediated route to generate response congruency effects.
Although the response congruency effect arises from a mediated route in compound cue retrieval, the model is not incompatible with the effect also arising in part from a non-mediated route involving direct target–response translation, for which there is some evidence (Kiesel et al., 2007; Wendt & Kiesel, 2008). On some trials, particularly those involving congruent targets, it would likely be more efficient to bypass compound cue retrieval and directly select a response. One could even imagine a race occurring between the mediated and non-mediated routes on each trial (Logan, 1988), with a response congruency effect arising from whichever route wins the race. This sort of race was not instantiated in our model, but there is nothing in the model that precludes it.
Theoretical Relations
While many theories of task switching are more concerned with higher-level processing associated with switching tasks (e.g., task-set selection, attentional control setting, rule retrieval) than with lower-level processing associated with performing tasks (e.g., stimulus encoding, response selection, response execution), there are formal models that address the question of how response selection occurs in task-switching situations (e.g., Brown et al., 2007; Gilbert & Shallice, 2002; Meiran, 2000; Sohn & Anderson, 2001). Our model of compound cue retrieval is similar in certain respects to some of these models and it is worth highlighting these similarities to show that the present theoretical stance is not restricted to our specific modeling framework.
In Gilbert and Shallice’s (2002) parallel distributed processing (PDP) model of task switching, the evidence that is used to select a response comes from two main inputs. First, there is bottom-up input in the form of a target representation. Second, there is top-down input reflecting the current task demand, which would presumably be indicated by a cue representation in the context of a task-cuing procedure. Both inputs are summed (along with other inputs) to determine the evidence for various responses. A response has been selected when the evidence for one response exceeds that of the other responses by some criterion. The use of multiple inputs to drive an evidence accumulation process is similar to compound cue retrieval at a conceptual level. Furthermore, response selection in the PDP model is similar to our model at a formal level, with Gilbert and Shallice (2002, p. 310) noting that their model implements a random walk to select a response. Given these similarities, it might be possible for the PDP model to account for the congruency effects from our cue–prime–target procedure by including the prime as an additional source of bottom-up input in the evidence accumulation process, as in the retrieval model.
A somewhat different conception of response selection was proposed by Meiran (2000) in his model of task switching, wherein targets and responses are represented at a cognitive level in terms of response categories. A target representation is determined by perceptual input (e.g., the target) and by task-set input that biases the representation toward task-relevant response categories. Task-set input presumably arises from a cue representation indicating the relevant task to which the target representation should be biased. To select a response, the evidence for each response category in the target representation is multiplied by the corresponding evidence in the response representation (which reflects the response given on the previous trial); these products are then summed to yield what Meiran calls potency values for each response. The difference in potency values determines response strength, which determines how quickly (and conceivably also how likely) a response will be selected. The focus on response-category representations in response selection resonates with our model of compound cue retrieval, as does the multiplicative combination of different inputs to yield potency values (which might be loosely mapped onto the η products in Equation 1). The idea that the speed of response selection is determined by differences in potency is similar to the notion that the random walk in compound cue retrieval will finish sooner as the difference in η values in favor of selecting the correct response (or the retrieval probability in Equation 3) becomes more extreme. If Meiran’s model were applied to our cue–prime–target procedure, primes would likely be modeled by having them bias target representations in much the same way as cue-elicited task sets. This would affect the potency values used in response selection, similar to how primes affect the η products used in response selection in the retrieval model.
The models of Gilbert and Shallice (2002) and Meiran (2000) are two examples of how the ideas embodied in our model of compound cue retrieval can be interpreted in the context of other modeling frameworks. While these models differ from one another on the surface, there appear to be some deeper conceptual similarities in how they achieve response selection in task-switching performance. Identifying these similarities is important during a time when there seems to be an ever-increasing number of models in the literature and a tendency to focus on differences between models rather than the similarities that may spawn more integrative theory development. By taking ideas that are common to several models and using them to build newer and better models of task switching, researchers may be able to take bigger steps toward understanding the flexibility ascribed to cognitive control and how it is that people can give different responses to a stimulus such as 42. Once that is done, then perhaps the next steps will be toward understanding the answer to life, the universe, and everything.
Acknowledgments
This research was supported by National Institute of Mental Health Grant R01-MH073879-01 and National Science Foundation Grant BCS 0646588 to Gordon D. Logan. We thank Julie Delheimer for running the experiment.
Footnotes
The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at (http://www.apa.org/journals/xlm).
References
- Adams D. The hitchhiker’s guide to the galaxy. London: Pan Books; 1979. [Google Scholar]
- Altmann EM. Task switching is not cue switching. Psychonomic Bulletin & Review. 2006;13:1016–1022. doi: 10.3758/bf03213918. [DOI] [PubMed] [Google Scholar]
- Altmann EM. Cue-independent task-specific representations in task switching: Evidence from backward inhibition. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2007;33:892–899. doi: 10.1037/0278-7393.33.5.892. [DOI] [PubMed] [Google Scholar]
- Arrington CM, Logan GD. Episodic and semantic components of the compound-stimulus strategy in the explicit task-cuing procedure. Memory & Cognition. 2004;32:965–978. doi: 10.3758/bf03196874. [DOI] [PubMed] [Google Scholar]
- Arrington CM, Logan GD, Schneider DW. Separating cue encoding from target processing in the explicit task-cuing procedure: Are there “true” task switch effects? Journal of Experimental Psychology: Learning, Memory, and Cognition. 2007;33:484–502. doi: 10.1037/0278-7393.33.3.484. [DOI] [PubMed] [Google Scholar]
- Brown JW, Reynolds JR, Braver TS. A computational model of fractionated conflict-control mechanisms in task-switching. Cognitive Psychology. 2007;55:37–85. doi: 10.1016/j.cogpsych.2006.09.005. [DOI] [PubMed] [Google Scholar]
- Cohen AL, Sanborn AN, Shiffrin RM. Model evaluation using grouped or individual data. Psychonomic Bulletin & Review. doi: 10.3758/pbr.15.4.692. in press. [DOI] [PubMed] [Google Scholar]
- Coles MGH, Gratton G, Bashore TR, Eriksen CW, Donchin E. A psychophysiological investigation of the continuous flow model of human information processing. Journal of Experimental Psychology: Human Perception and Performance. 1985;11:529–553. doi: 10.1037//0096-1523.11.5.529. [DOI] [PubMed] [Google Scholar]
- Forstmann BU, Brass M, Koch I. Methodological and empirical issues when dissociating cue-related from task-related processes in the explicit task-cuing procedure. Psychological Research. 2007;71:393–400. doi: 10.1007/s00426-005-0040-4. [DOI] [PubMed] [Google Scholar]
- Gilbert SJ, Shallice T. Task switching: A PDP model. Cognitive Psychology. 2002;44:297–337. doi: 10.1006/cogp.2001.0770. [DOI] [PubMed] [Google Scholar]
- Gratton G, Coles MGH, Sirevaag EJ, Eriksen CW, Donchin E. Pre- and poststimulus activation of response channels: A psychophysiological analysis. Journal of Experimental Psychology: Human Perception and Performance. 1988;14:331–344. doi: 10.1037//0096-1523.14.3.331. [DOI] [PubMed] [Google Scholar]
- Hintzman DL. “Schema abstraction” in a multiple-trace memory model. Psychological Review. 1986;93:411–428. [Google Scholar]
- Jost K, Mayr U, Rösler F. Is task switching nothing but cue priming? Evidence from ERPs. Cognitive, Affective, & Behavioral Neuroscience. 2008;8:74–84. doi: 10.3758/cabn.8.1.74. [DOI] [PubMed] [Google Scholar]
- Kantowitz BH, Sanders MS. Partial advance information and stimulus dimensionality. Journal of Experimental Psychology. 1972;92:412–418. doi: 10.1037/h0032359. [DOI] [PubMed] [Google Scholar]
- Kiesel A, Wendt M, Peters A. Task switching: On the origin of response congruency effects. Psychological Research. 2007;71:117–125. doi: 10.1007/s00426-005-0004-8. [DOI] [PubMed] [Google Scholar]
- Koch I. Automatic and intentional activation of task sets. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2001;27:1474–1486. doi: 10.1037//0278-7393.27.6.1474. [DOI] [PubMed] [Google Scholar]
- Li SC, Lewandowsky S, DeBrunner VE. Using parameter sensitivity and interdependence to predict model scope and falsifiability. Journal of Experimental Psychology: General. 1996;125:360–369. [Google Scholar]
- Logan GD. Toward an instance theory of automatization. Psychological Review. 1988;95:492–527. [Google Scholar]
- Logan GD. An instance theory of attention and memory. Psychological Review. 2002;109:376–400. doi: 10.1037/0033-295x.109.2.376. [DOI] [PubMed] [Google Scholar]
- Logan GD, Bundesen C. Clever homunculus: Is there an endogenous act of control in the explicit task-cuing procedure? Journal of Experimental Psychology: Human Perception and Performance. 2003;29:575–599. doi: 10.1037/0096-1523.29.3.575. [DOI] [PubMed] [Google Scholar]
- Logan GD, Bundesen C. Very clever homunculus: Compound stimulus strategies for the explicit task-cuing procedure. Psychonomic Bulletin & Review. 2004;11:832–840. doi: 10.3758/bf03196709. [DOI] [PubMed] [Google Scholar]
- Logan GD, Schneider DW. Interpreting instructional cues in task switching procedures: The role of mediator retrieval. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2006a;32:347–363. doi: 10.1037/0278-7393.32.3.347. [DOI] [PubMed] [Google Scholar]
- Logan GD, Schneider DW. Priming or executive control? Associative priming of cue encoding increases “switch costs” in the explicit task-cuing procedure. Memory & Cognition. 2006b;34:1250–1259. doi: 10.3758/bf03193269. [DOI] [PubMed] [Google Scholar]
- Logan GD, Schneider DW, Bundesen C. Still clever after all these years: Searching for the homunculus in explicitly cued task switching. Journal of Experimental Psychology: Human Perception and Performance. 2007;33:978–994. doi: 10.1037/0096-1523.33.4.978. [DOI] [PubMed] [Google Scholar]
- Luce RD. Individual choice behavior. New York: Wiley; 1959. [Google Scholar]
- Mayr U. Inhibition of action rules. Psychonomic Bulletin & Review. 2002;9:93–99. doi: 10.3758/bf03196261. [DOI] [PubMed] [Google Scholar]
- Mayr U. What matters in the cued task-switching paradigm: Tasks or cues? Psychonomic Bulletin & Review. 2006;13:794–799. doi: 10.3758/bf03193999. [DOI] [PubMed] [Google Scholar]
- Meiran N. Reconfiguration of processing mode prior to task performance. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1996;22:1423–1442. [Google Scholar]
- Meiran N. Modeling cognitive control in task-switching. Psychological Research. 2000;63:234–249. doi: 10.1007/s004269900004. [DOI] [PubMed] [Google Scholar]
- Meiran N. Task rule-congruency and Simon-like effects in switching between spatial tasks. Quarterly Journal of Experimental Psychology. 2005;58A:1023–1041. doi: 10.1080/02724980443000421. [DOI] [PubMed] [Google Scholar]
- Meiran N, Chorev Z, Sapir A. Component processes in task switching. Cognitive Psychology. 2000;41:211–253. doi: 10.1006/cogp.2000.0736. [DOI] [PubMed] [Google Scholar]
- Meiran N, Kessler Y. The task rule congruency effect in task switching reflects activated long-term memory. Journal of Experimental Psychology: Human Perception and Performance. 2008;34:137–157. doi: 10.1037/0096-1523.34.1.137. [DOI] [PubMed] [Google Scholar]
- Monsell S. Control of mental processes. In: Bruce V, editor. Unsolved mysteries of the mind. Hove, England: Erlbaum; 1996. pp. 93–148. [Google Scholar]
- Monsell S, Mizon GA. Can the task-cuing paradigm measure an endogenous task-set reconfiguration process? Journal of Experimental Psychology: Human Perception and Performance. 2006;32:493–516. doi: 10.1037/0096-1523.32.3.493. [DOI] [PubMed] [Google Scholar]
- Monsell S, Sumner P, Waters H. Task-set reconfiguration with predictable and unpredictable task switches. Memory & Cognition. 2003;31:327–342. doi: 10.3758/bf03194391. [DOI] [PubMed] [Google Scholar]
- Nelson DL, McEvoy CL, Schreiber TA. The University of South Florida word association, rhyme, and fragment norms. 1999 doi: 10.3758/bf03195588. Retrieved February 5, 2004 from http://w3.usf.edu/FreeAssociation/ [DOI] [PubMed]
- Nosofsky RM, Palmeri TJ. An exemplar-based random walk model of speeded classification. Psychological Review. 1997;104:266–300. doi: 10.1037/0033-295x.104.2.266. [DOI] [PubMed] [Google Scholar]
- Pashler H, Baylis G. Procedural learning: 2. Intertrial repetition effects in speeded-choice tasks. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1991;17:33–48. [Google Scholar]
- Raaijmakers JGW, Shiffrin RM. Search of associative memory. Psychological Review. 1981;88:93–134. [Google Scholar]
- Ratcliff R. International encyclopedia of the social and behavioral sciences. Vol. 6. Oxford: Elsevier; 2001. Diffusion and random walk processes; pp. 3668–3673. [Google Scholar]
- Ratcliff R, McKoon G. A retrieval theory of priming in memory. Psychological Review. 1988;95:385–408. doi: 10.1037/0033-295x.95.3.385. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL. A comparison of sequential sampling models for two-choice reaction time. Psychological Review. 2004;111:333–367. doi: 10.1037/0033-295X.111.2.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider DW, Logan GD. Modeling task switching without switching tasks: A short-term priming account of explicitly cued performance. Journal of Experimental Psychology: General. 2005;134:343–367. doi: 10.1037/0096-3445.134.3.343. [DOI] [PubMed] [Google Scholar]
- Schneider DW, Logan GD. Priming cue encoding by manipulating transition frequency in explicitly cued task switching. Psychonomic Bulletin & Review. 2006;13:145–151. doi: 10.3758/bf03193826. [DOI] [PubMed] [Google Scholar]
- Schneider DW, Logan GD. Task switching versus cue switching: Using transition cuing to disentangle sequential effects in task-switching performance. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2007;33:370–378. doi: 10.1037/0278-7393.33.2.370. [DOI] [PubMed] [Google Scholar]
- Sohn MH, Anderson JR. Task preparation and task repetition: Two-component model of task switching. Journal of Experimental Psychology: General. 2001;130:764–778. [PubMed] [Google Scholar]
- Sudevan P, Taylor DA. The cuing and priming of cognitive operations. Journal of Experimental Psychology: Human Perception and Performance. 1987;13:89–103. doi: 10.1037//0096-1523.13.1.89. [DOI] [PubMed] [Google Scholar]
- Travers S, West R. Neural correlates of cue retrieval, task set reconfiguration, and rule mapping in the explicit cue task switching paradigm. Psychophysiology. 2008;45:588–601. doi: 10.1111/j.1469-8986.2008.00658.x. [DOI] [PubMed] [Google Scholar]
- Wendt M, Kiesel A. The impact of stimulus-specific practice and task instructions on response congruency effects between tasks. Psychological Research. 2008;72:425–432. doi: 10.1007/s00426-007-0117-3. [DOI] [PubMed] [Google Scholar]