Abstract
Cells containing pathogenic mutations in mitochondrial DNA (mtDNA) generally also contain the wild-type mtDNA, a condition called heteroplasmy. The amount of mutant mtDNA in a cell, called the heteroplasmy level, is an important factor in determining the amount of mitochondrial dysfunction and therefore the disease severity. mtDNA is inherited maternally, and there are large random shifts in heteroplasmy level between mother and offspring. Understanding the distribution in heteroplasmy levels across a group of offspring is an important step in understanding the inheritance of diseases caused by mtDNA mutations. Previously, our understanding of the heteroplasmy distribution has been limited to just the mean and variance of the distribution. Here we give equations, adapted from the work of Kimura on random genetic drift, for the full mtDNA heteroplasmy distribution. We describe how to use the Kimura distribution in mitochondrial genetics, and we test the Kimura distribution against human, mouse, and Drosophila data sets.
Introduction
Mitochondrial DNA (mtDNA) encodes several subunits of the electron transfer chain. Defects in human mtDNA cause a wide range of disease conditions, mainly resulting from the impairment of ATP production in the cell. Some examples of the inheritable pathogenic point mutations in mtDNA are the m.3243A > G (MIM #590050.0001) mutation causing mitochondrial encephalomyopathies lactic acidosis and stroke-like episodes (MELAS, MIM #540000),1 the m.8344A > G (MIM #590060.0001) mutation causing myoclonic epilepsy with ragged-red fiber (MERRF, MIM #545000),2 the m.8993T > G (MIM #516060.0001) mutation causing neuropathy, ataxia, and retinitis pigmentosa (NARP, MIM #551500)3,4 and a number of different point mutations causing Leber's hereditary optic neuropathy (LHON, MIM #535000).5–7
Any individual cell contains many copies of the mitochondrial genome. The mtDNA copy number per cell ranges from a few hundred to a few hundred thousand copies. Generally, cells containing a pathogenic mtDNA mutation also contain the wild-type genome, a condition called heteroplasmy. Important exceptions to this rule are the mitochondrial diseases such as LHON, which have a low penetrance of the disease phenotype within families carrying the mutation. Individuals may be homoplasmic for these particular pathogenic mutations, often while remaining asymptomatic, and this is generally attributed to the lack of some necessary pathogenesis cofactor, either genetic or environmental.
MtDNA is transmitted through the maternal lineage in humans.8 In pedigrees with an inheritable heteroplasmic mtDNA mutation, the measured heteroplasmy level often shifts by large and apparently random amounts between mother and offspring.9–11 These variations cause complications in estimating the recurrence risks of these genetic diseases and therefore in giving accurate genetic counseling to a female carrying a pathogenic mtDNA mutation.12–14
The inheritance of mtDNA heteroplasmy is described by the expected probability distribution of heteroplasmy values in a sibling group. Until now, our ability to predict heteroplasmy distributions has been limited to predicting the mean value and the variance, the two lowest-order statistics. On the basis of neutral genetic drift and standard haploid population genetics, we have been able to predict that the mean heteroplasmy in the offspring should be equal to the mother's heteroplasmy and that the variance of the offspring heteroplasmy should have the following form15:
| (1) |
The variance of heteroplasmy, V, in a group of individuals with a single common maternal ancestor after t generations can be calculated from the initial gene frequency, p0, and the effective population size, Neff. This variance equation is generally referred to in this field as the Sewell-Wright formula. We note again that these equations are based on the assumption of random genetic drift.
Although the mean and variance of the heteroplasmy distribution in a population is useful information, it is very limited information. It does not give us the heteroplasmy distribution itself. In particular, this is a problem if the heteroplasmy distribution is not symmetric, which must be the case at high and low heteroplasmy levels, two extremes of enormous practical importance. Ideally, we would want to be able to predict the entire heteroplasmy probability distribution. Fortunately, this problem was solved in 1955 by Motoo Kimura.16 His solution was for gene frequency probabilities in diploid populations, but the application of this theory to mitochondrial heteroplasmy is straightforward. The variance in Equation 1 can be derived from Kimura's theory, so the full Kimura theory does not displace the previous work that has been done in mitochondrial genetics on the basis of this variance equation. Instead, it greatly extends our capability to calculate the full heteroplasmy distribution.
Kimura derived a set of probability distribution functions to explain the gene frequency distribution of populations under pure random genetic drift. The underlying assumptions of this derivation are nonoverlapping generations, no selection, no migration, no de novo mutation, and a finite and steady population size.16 Kimura made the assumption of a constant population size to simplify the mathematics. Other work17 has shown that this assumption is not necessary. If the population size is allowed to vary, either through fluctuations18 or through events such as population bottlenecks,17 then the definition of the effective population size in terms of the actual population size becomes complicated. That complication does not concern us here because we will treat the effective population size, Neff, merely as a parameter of the model. The solution of this model consists of three equations: a probability f(0,t) for losing an allele, a probability f(1,t) for fixing on that allele, and a probability distribution function ϕ(x,t) that the allele is present at frequency x in the population.
| (2) |
| (3) |
| (4) |
The meaning of each variable in these equations is the same as for the Sewall-Wright variance formula (Equation 1). The interpretation in terms of mitochondrial heteroplasmy is straightforward; p0 is the mtDNA heteroplasmy level in the maternal lineage founder and is also the mean heteroplasmy in the offspring distribution, f(0,t) and f(1,t) are the probabilities of fixing on the wild-type or mutant, respectively, in generation t, and x is the offspring heteroplasmy level. The function F(1 − i, i + 2, 2, z) is the hypergeometric function. For simplicity, we will refer to Equations 2–4 as the Kimura distribution. Because this is a probability distribution, the integration of all three terms is equal to unity.
| (5) |
Although the mathematical form of the Kimura distribution is certainly complicated, and although care must be taken in the numerical calculation of these equations, the distribution values can be calculated. In this paper, we apply the Kimura distribution to measurements of the mtDNA heteroplasmy distributions in humans, mice, and Drosophila.
Material and Methods
Experimental Data
The observed heteroplasmy distributions used in this paper have been collected from several sources in the published literature.19–22 For experimental data that were available only in graphical form, we used the software Engauge Digitizer to determine approximate numerical values. The experimental data sets analyzed here covered three organisms; human,19 mouse,21 and Drosophila.20,22 The human study protocol was approved by the participating institutional review boards.
Setting the Parameter Values for Kimura's Probability Distribution
The variance formula as it is normally written is a function of three parameters; p0, t, and Neff. However, the form of the equations allows us to combine the t and Neff parameters into a single parameter that we call b, as follows.
| (6) |
The new parameter b is then defined as
| (7) |
Substituting these parameters into the Kimura probability density functions simplifies them to a two-parameter model, with parameters p0 and b, which both range from zero to one.
| (8) |
| (9) |
| (10) |
Given a data set of mtDNA heteroplasmy values for a set of individuals arising from a common founder, we can fit a Kimura probability distribution to the heteroplasmy values by determining the values for the two parameters p0 and b. These two parameters can be determined from the two lowest-order statistics of the data set; the mean and the variance. We take the parameter p0 to be equal to the mean heteroplasmy value of the data set. Then we can use Equation 6 to determine the parameter b from p0 and the variance of the data. The entire data set, including heteroplasmy values fixed at the two extremes of 0 and 1, is used in the calculation of the variance and p0 and then is used in the calculation of b.
Calculating the Numerical Value of the Hypergeometric Function
Accurately calculating the numerical value of the hypergeometric function F(a,b,c,z) is a difficult technical problem. Because this is a fundamental mathematical function, this issue has been faced in many different scientific fields. Recently, as a solution to this problem occurring in a spectroscopy application, Hoang-Binh23 developed an accurate and practical algorithm for the numerical calculation of hypergeometric functions, and we have followed this method. This method uses the following recurrence relation:
| (11) |
| (12) |
| (13) |
Numerical Calculation of the Kimura Probability Distributions
The infinite series in Equations 8–10 were truncated when the difference between the i + 1 and i terms became less than 10−4. Note that the infinite series in Equations 8–10 have oscillating sign terms, so numerical convergence of these series is slow. We tested the accuracy of the resulting probability distributions by calculating the integral in Equation 5; this integral which should be unity. The difference of the numerical calculation from unity in the results presented here was typically on the order of 10−5, and the maximum difference was less than 0.004. All calculations were carried out in C programs, which are available from the authors (details are given in Web Resources).
Statistical Test
We applied the Kolmogorov-Smirnov (KS) test to compare the experimental data for mtDNA heteroplasmy distributions to the Kimura probability distributions. Because the parameters for the theoretical Kimura probability distributions were determined from the statistics of the experimental data sets, the p values of this comparison had to be determined from Monte-Carlo simulations.24 For the Monte-Carlo simulations, 1000 simulated data sets with the same population size as the experimental data set were drawn from the theoretical distribution, and the p values were determined from the fraction of simulated data sets whose maximum deviation from the theoretical probability distribution was larger than the maximum deviation of the experimental data set.
Results
The Kimura distribution represents the distribution of heteroplasmy that develops through random genetic drift in a population of cells or individuals who all are descended by an equal number of generations from a single heteroplasmic progenitor cell or individual. To compare the Kimura distribution to experimental data, we need data sets that satisfy this condition and also contain a large number of individual heteroplasmy measurements so that the probability distribution of the heteroplasmy measurements can be determined. From a search of the literature, we identified four publications19–22 containing a total of 16 data sets to analyze. For each data set, we used the mean and variance of the heteroplasmy measurements to set the p0 and b parameters in the Kimura distribution as described in the Material and Methods. Then histograms of the measured heteroplasmy distributions were compared to histograms of the fit Kimura distributions. Finally, a KS test comparing the cumulative probability distributions of the experimental data with the theoretical Kimura probability distributions was carried out. The 16 data sets analyzed consisted of one human data set, eight mouse data sets, and seven Drosophila data sets.
Human Data
No human pedigree data set is large enough to make a good test of the Kimura distribution. However, there is one human data set that is large enough. Brown et al.19 published a study of the heteroplasmy distribution of 82 single primary oocytes derived from an ovary of a female with the pathogenic 3243A > G mtDNA point mutation. This tissue sample was available because this woman underwent a hysterectomy for reasons unrelated to any mitochondrial disease. This woman was asymptomatic and had a mutation level of 18.11% determined from a quadriceps biopsy and of 7.24% of the mutant type in her leukocytes.19 We note here that the mutation level of the 3243A > G mutation decreases with age in blood samples.25
Figure 1 presents the comparison of the measured heteroplasmy distribution in the human primary oocytes and the Kimura distribution fit to the data. The Kimura distribution is a very good fit to the measured heteroplasmy distribution, and this is confirmed by the KS test, which gives a p value of 0.827 for the null hypothesis that the experimental data are consistent with the Kimura distribution (Table 1). The limited amount of human heteroplasmy data currently available indicates that the theoretical Kimura probability distribution is a good tool for calculating the distribution of mtDNA heteroplasmy in a population derived from a single founder.
Figure 1.
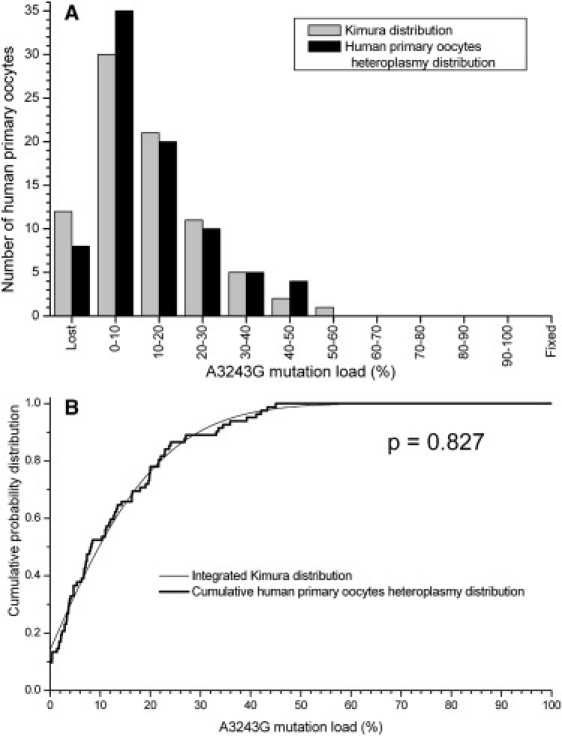
The Heteroplasmy Distribution of the A3243G mtDNA Mutation in a Sample of Human Primary Oocytes Is Compared to the Kimura Distribution
(A) Frequency histogram of the heteroplasmy in both the data and the Kimura distribution fit to the data. Parameter values for the Kimura distribution are given in Table 1 for all figures.
(B) Cumulative probability distribution functions for the data and the Kimura distribution fit to the data. A KS test indicates that there is no significant difference between the measured and the theoretical probability distributions.
Table 1.
The Parameters Estimated from Experimental Data: The Mean Heteroplasmy, p0, and the b Parameter Calculated from the Variance and the p Value Calculated from the KS Test
| Organism | Lineage | Sample | Generations | Mean Heteroplasmy, p0 | Variance | N | b | KS Test p Value |
|---|---|---|---|---|---|---|---|---|
| Humans | ||||||||
| N/A | primary oocytes | - | 0.1264 | 0.01432 | 82 | 0.8705 | 0.827 | |
| Mice | ||||||||
| 515 | tail biopsy | 1 | 0.051 | 0.00240 | 41a | 0.9505 | 0.646 | |
| 515 | mature oocytes | - | 0.047 | 0.00646 | 31 | 0.8558 | 0.049∗ | |
| 517 | tail biopsy | 1 | 0.076 | 0.00447 | 43 | 0.9363 | 0.75 | |
| 517 | mature oocytes | - | 0.094 | 0.0119 | 26 | 0.8604 | 0.834 | |
| 603A | mature oocytes | - | 0.009 | 0.000185 | 49 | 0.9793 | 0.681 | |
| 603A | primary oocytes | - | 0.011 | 0.00023 | 49a | 0.9789 | 0.037∗ | |
| 603B | mature oocytes | - | 0.031 | 0.00098 | 31 | 0.9674 | 0.435 | |
| 603B | primary oocytes | - | 0.025 | 0.000638 | 46a | 0.9738 | 0.223 | |
| Drosophila mauritiana | ||||||||
| H1 | unfertilized eggs | 30 | 0.4150 | 0.18670 | 60 | 0.2310 | 0.004∗∗ | |
| H1-31M | 3 | 0.1784 | 0.00952 | 59 | 0.9350 | 0.587 | ||
| H1-18D | 3 | 0.4763 | 0.01711 | 31 | 0.9314 | 0.993 | ||
| H1-12B | 5 | 0.8155 | 0.02791 | 52 | 0.8146 | 0.865 | ||
| G20-5 | 3 | 0.3250 | 0.01257 | 55 | 0.9430 | 0.922 | ||
| G71-12 | 3 | 0.5834 | 0.01804 | 50 | 0.9258 | 0.542 | ||
| Drosophila simulans | ||||||||
| 6YF16 | 3 | 0.1270 | 0.0096 | 44 | 0.9131 | 0.79 | ||
The “generations” column gives the number of organism generations, and thus this value is not given for samples of mature oocytes or primary oocytes. The p0 parameter is obtained from the average of the heteroplasmy measurements. N is the number of samples from the experiment. The p value is the level of significance for the null hypothesis that the experimental heteroplasmy distribution matches the Kimura distribution. The asterisks indicate significance levels: ∗ 0.01 < p < 0.05 and ∗∗ p < 0.01.
In these three cases, we found discrepancies between the number of samples listed in the cited paper21 and the number of samples actually given in the data set.
Mouse Data
Given the limited amount of human data available, it is important to extend this analysis to the existing animal models for the inheritance of mtDNA heteroplasmy. Jenuth et al.21 published a seminal paper on a mouse model of mtDNA heteroplasmy inheritance. In this study, they used mice that were heteroplasmic for two mtDNA haplogroups, NZB and BALB. These heteroplasmic mice were produced by an electrofusing cytoplast technique. The data in this study included heteroplasmy measurements on sets of primary oocytes (as in the human data analyzed above), mature oocytes, and tail samples from offspring; each data set was derived from a single founder female.
Figures 2–5 present the comparisons of the Kimura distributions to the heteroplasmy distributions in eight data sets from the mouse model. In six of the eight data sets, the null hypothesis is not rejected, indicating that the Kimura distribution is a good representation of the distribution of the heteroplasmy values in these data sets (Table 1). The null hypothesis was rejected in two of the data sets: the mature oocytes from line 515 (Figures 2C–2D, p = 0.049) and the primary oocytes from line 603A (Figures 4C and 4D, p = 0.037). For the data set consisting of line 515 mature oocytes, the difference between the observed heteroplasmy distribution and the fit Kimura distribution is largest for the number of cells with zero heteroplasmy for the BALB mtDNA haplotype, and fewer of these cells were observed in the experiment than were predicted by the Kimura distribution. For the data set of primary oocytes from the 603A mouse line (Figures 4C and 4D), the largest difference between the observed heteroplasmy distribution and the Kimura distribution is the lack of observation of any cells with NZB haplotype heteroplasmy in the range 0.1%–0.5%, despite the large number of cells with levels of 0% and 0.5%–1.0% in the neighboring bins. Jenuth et al. remarked on this odd result of the missing heteroplasmy values.21 For the other six mouse data sets, the Kimura distributions do provide a good representation of the observed mtDNA heteroplasmy distributions (Figures 2–5).
Figure 2.
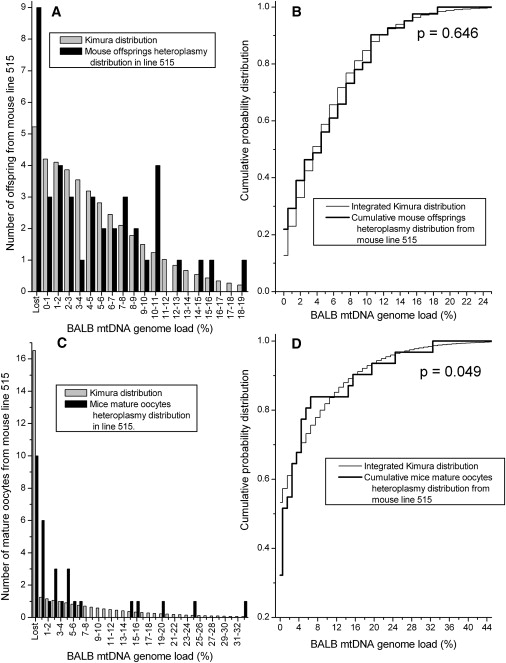
The Measured Heteroplasmy Distribution from Offspring and Mature Oocytes in the Heteroplasmic Mouse Line 515 Is Compared to the Kimura Distribution
(A) The heteroplasmy frequency histogram from the offspring.
(B) KS test comparing the offspring heteroplasmy data to the Kimura distribution fit to the data.
(C) The heteroplasmy frequency histogram of the mature oocytes in the 515 line.
(D) KS test for the line 515 mature oocyte data. There is a significant difference between the two distributions in the mature oocyte data.
Figure 3.
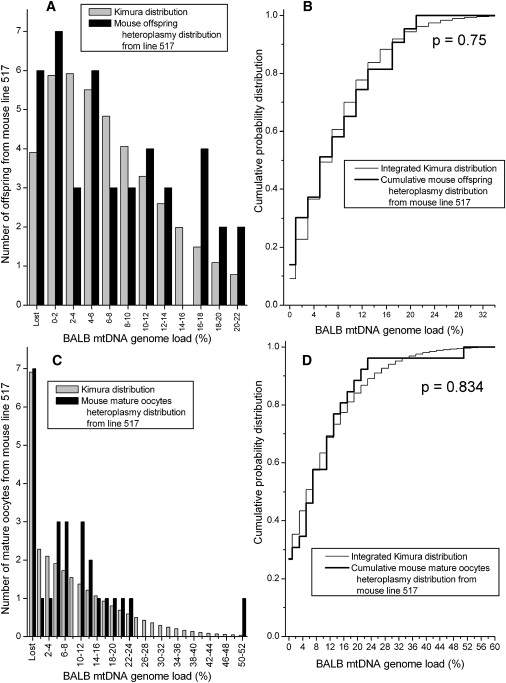
The Measured Heteroplasmy Distribution from Offspring and Mature Oocytes in the Heteroplasmic Mouse Line 517 Is Compared to the Kimura Distribution
(A) The heteroplasmy frequency histogram from the offspring.
(B) KS test comparing the offspring heteroplasmy data to the Kimura distribution fit to the data.
(C) The heteroplasmy frequency histogram of the mature oocytes in the 517 line.
(D) KS test for the data from line 517 mature oocytes.
Figure 4.
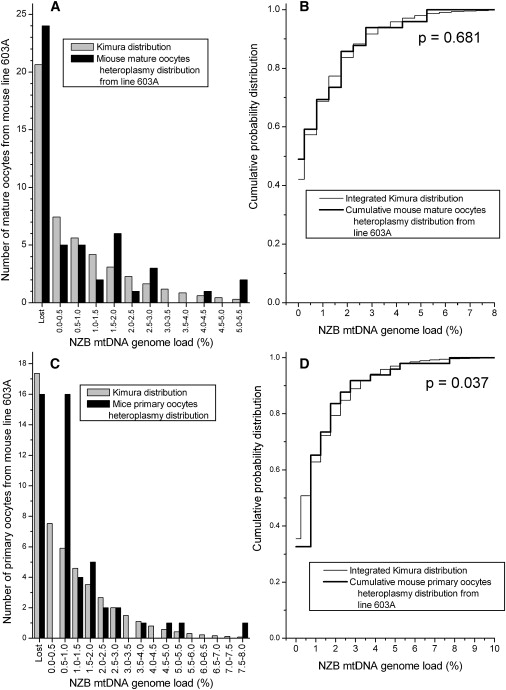
The Measured Heteroplasmy Distribution from Mature Oocytes and Primary Oocytes in the Heteroplasmic Mouse Line 603A Is Compared to the Kimura Distribution
(A) The heteroplasmy frequency histogram of the mature oocytes in the 603A line.
(B) KS test for the data from line 603A mature oocytes.
(C) The heteroplasmy frequency histogram of the primary oocytes in the 603A line.
(D) KS test for the data from line 603A primary oocytes. There is a significant difference between the two distributions for the primary oocyte data.
Figure 5.
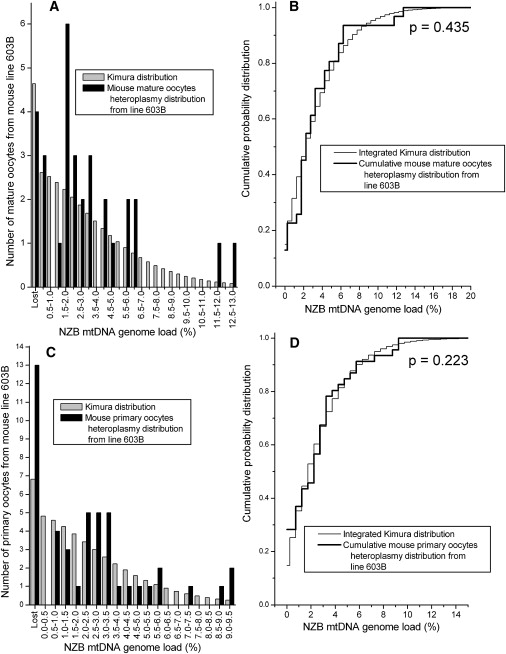
The Measured Heteroplasmy Distribution from Mature Oocytes and Primary Oocytes in the Heteroplasmic Mouse Line 603B Is Compared to the Kimura Distribution
(A) The heteroplasmy frequency histogram of the mature oocytes in the 603B line.
(B) KS test for the data from line 603B mature oocytes.
(C) The heteroplasmy frequency histogram of the primary oocytes in the 603B line.
(D) KS test for the data from line 603B primary oocytes.
Drosophila Data
The Drosophila data sets consist of data from two species, D. mauritiana and D. simulans. In both cases the heteroplasmy measurements were made in a sample of unfertilized eggs.
For D. mauritiana we had six data sets for which the mtDNA heteroplasmy was defined by the difference in the length of an A+T-rich region of the mitochondrial genome.22 Figures 6 and 7 present the comparisons of the fit Kimura distributions to the measured Drosophila heteroplasmy distributions. For five of the six data sets, the null hypothesis is not rejected (Table 1), and the fit Kimura heteroplasmy distributions show a very good correspondence to the observed heteroplasmy distributions. For one data set (Figures 6A and 6B, p = 0.004), the differences between the Kimura distribution and the measured heteroplasmy distribution are quite large. This is interesting because this data set is unique in another way: The number of generations from the founder in this data set is very large at 30 generations, about ten times larger than the number of generations in the other five data sets.
Figure 6.
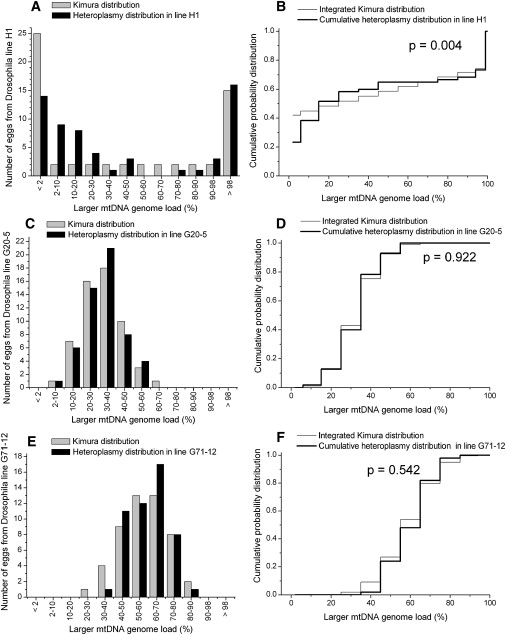
The Measured Heteroplasmy Distribution from Unfertilized Eggs in the Heteroplasmic Drosophila mauritiana Lines H1, G20-5, and G71-12 Is Compared to the Kimura Distribution
(A) The heteroplasmy frequency histogram of the Drosophila line H1 and the Kimura distribution fit to the mean and variance values from these data.
(B) The KS test comparing the data with the Kimura distribution. There is a significant difference between the two distributions for line H1.
(C) The heteroplasmy frequency histogram for the Drosophila line G20-5 is compared to the Kimura distribution.
(D) KS test comparing the data for Drosophila line G20-5 to the Kimura distribution.
(E) The heteroplasmy frequency histogram from the Drosophila line G71-12 is compared to the Kimura distribution.
(F) KS test comparing the data for Drosophila line G71-12 to the Kimura distribution.
Figure 7.
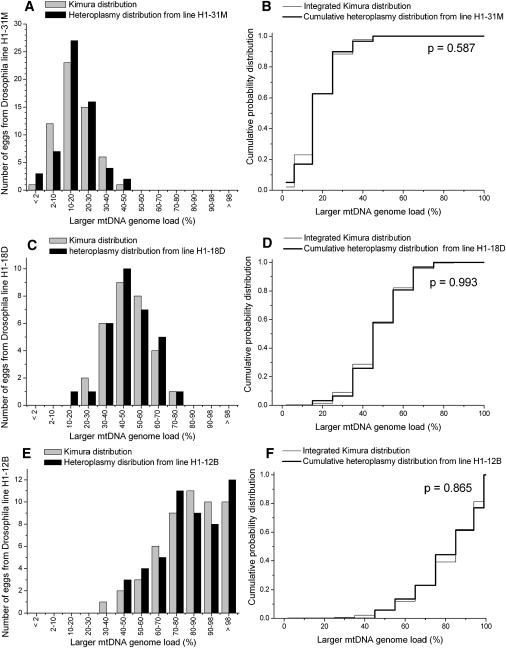
The Measured Heteroplasmy Distribution from Unfertilized Eggs in the Heteroplasmic Drosophila mauritiana Lines H1-31M, H1-18D, and H1-12B Is Compared to the Kimura Distribution
(A) The heteroplasmy frequency histogram from the Drosophila line H1-31M and the Kimura distribution.
(B) The KS test comparing the heteroplasmy data for Drosophila line H1-31M to the Kimura distribution.
(C) The heteroplasmy frequency histogram from the Drosophila line H1-18D is compared to the Kimura distribution.
(D) KS test comparing the Drosophila line H1-18D to the Kimura distribution.
(E) The heteroplasmy frequency histogram from Drosophila line H1-12B is compared to the Kimura distribution.
(F) KS test comparing data for Drosophila line H1-12B and the Kimura distribution.
The D. simulans data consist of a single data set where the mtDNA heteroplasmy was generated by cytoplasmic injection forming a mixture of the siIII and siII mtDNA genomes,20 two naturally occurring mtDNA sequences in this species. The comparison of the data to the Kimura distribution is given in Figure 8. Here the null hypothesis is not rejected, and the Kimura distribution is a good representation of the observed mtDNA heteroplasmy distribution.
Figure 8.
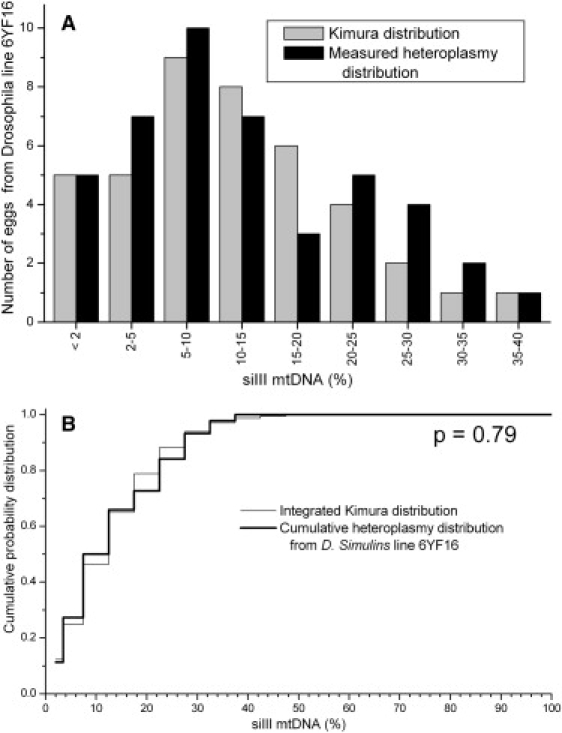
Comparison of Measured Heteroplasmy Distribution from Drosophila simulans Unfertilized Eggs with the Kimura Distribution
(A) Heteroplasmy frequency histogram and the Kimura distribution fit to these data.
(B) KS test comparing the data to the Kimura distribution.
Discussion
In the field of mitochondrial genetics, the Sewall-Wright variance formula has been generally used as the primary data analysis method for determining the effect of random genetic drift on mtDNA heteroplasmy values. Researchers have used this simple function both to examine the ability of random genetic drift to explain mtDNA segregation and to predict the rate of mtDNA segregation from assumptions about the size of the mtDNA segregating unit.19,21,22 The advantage of the Sewall-Wright variance formula is its simplicity and ability to estimate most parameters from experimental data (although estimating the effective population size Neff in Equation 1 has always been a problem).
However, the weakness of this simple approach is that it concentrates on just the two lowest-order statistics, the mean and the variance, and it ignores the rest of the information that is present in the total heteroplasmy distribution. This is of particular importance when the heteroplasmy distribution is not symmetric (not a normal distribution), as it must be at the extremes of low and high heteroplasmy. The shape of the heteroplasmy distribution at high-mutation heteroplasmy values is important for understanding the consequences of pathogenic effects, which generally only appear in individuals with a high level of the mtDNA mutation. The distribution at low heteroplasmy values is important because this range is directly affected by any de novo mutation rate. The heteroplasmy distribution near zero also is important for determining the clearance of a pathogenic mutation from a population. Because these extremes are arguably the most important parts of the heteroplasmy range, any approach that implicitly assumes a normal distribution has severe limitations. Using the Kimura distribution as a model for the heteroplasmy distribution across its entire range from 0%–100%, as well as the fixation rate on the extremes, frees us from those limitations and gives us a significant new tool in our analysis of mtDNA heteroplasmy inheritance.
The additional information that we can get from using the Kimura distribution comes at a cost: the increased mathematical complexity of Equations 2–5. These equations are difficult to use, and the numerical computation must be done carefully if accuracy problems are to be avoided.23 Two possible alternatives to the Kimura distribution are the normal distribution and the binomial distribution. Examples of the Kimura distribution, the normal distribution, and the binomial distribution with equal values for the mean and the variance in all three distributions are given in Figure 9. As discussed above, normal distributions (Figure 9B) do not correctly describe heteroplasmy distributions over the finite range of 0%–100% and do not address the important question of fixation. Although binomial distributions are nonsymmetric, cover only a finite heteroplasmy range, and can deal with fixation, they assume that heteroplasmy values come only in discrete steps (Figure 9C), which is not consistent with the available heteroplasmy distribution data. Despite its mathematical complexity, the Kimura distribution is the best available tool for describing mtDNA heteroplasmy distributions.
Figure 9.
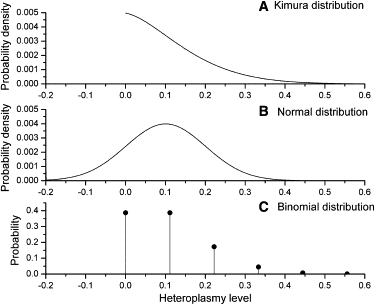
Comparison of a Kimura Distribution, Normal Distribution, and Binomial Distribution with Mean = 0.1 and Variance = 0.01
(A) Kimura distribution. The probability density ϕ(x) is plotted.
(B) Normal distribution.
(C) Binomial distribution. The mean and variance values require a range of discrete states from zero to nine, giving discrete probability values of 0, 1/9, 2/9, etc.
An alternative computational approach to determining heteroplasmy distributions is the use of direct simulation models. These include simulations of mtDNA replication in individual cells,26,27 simulations of mtDNA dynamics in embryogenesis,28 and relatively simple multiple sampling models.29 We note that Poulton29 presented one heteroplasmy distribution from a multiple-sampling simulation model that at least qualitatively resembles the Kimura distribution. Direct simulation models have the advantage of flexibility in that additional mechanisms such as selection effects and de-novo mutations can easily be added to the simulation, but they have the limitation of only presenting results for specific parameter values. The equations of the Kimura distribution have the advantage of explicit definition (something that is often not clear in a simulation) and the presentation of results for all possible parameter values. These two computational approaches are complimentary. Indeed, as discussed below, the Kimura distributions can be used as a tool in developing population-level simulation models of mitochondrial genetics.
Only one human data set19 was large enough to allow a useful comparison against the Kimura distribution. It would be extremely useful to have further human data sets of this type, covering a wide range of mean heteroplasmy values, in order to more thoroughly test the application of the Kimura distribution to human mtDNA heteroplasmy distributions. Further human data sets would also allow us to explore important questions such as how much the b parameter in this model varies across the population (essentially, this corresponds to how variable the inheritance bottleneck is in the human population30–32). With the limited human data currently available, and the data from the mouse and Drosophila models, the Kimura distributions are consistent with the experimental data in 13 of the 16 data sets analyzed.
Because the Kimura distribution only represents the effects of random genetic drift, deviations from that distribution may give us information about the other mechanisms that are occurring, most importantly selection effects and de novo mutation. Of the three data sets in which the null hypothesis was rejected, the data in Figures 6A and 6B are of particular interest. These data are from the 30th generation after the founder female, by far the longest generational separation in any of these data sets. It is reasonable to assume that this large number of generations would accentuate effects such as selection or de novo mutations, which might be negligible over shorter time spans. With the very large variance in this data set (Table 1), the theoretical distribution is relatively flat, and there are sharp peaks at the fixed points 0% and 100%, which act as absorbing states in the random-drift model (in other words, once a female individual fixes at either extreme, all descendents remain at that fixed state). In contrast, the observed heteroplasmy distribution has a “U” shape, such that the probability distribution rises toward each end of the heteroplasmy extreme. It is difficult to construct a mechanism whereby selection could form such a distribution, unless one were to argue for a selection mechanism that had maximum effect at around 50% heteroplasmy and low effects at either heteroplasmy extreme. A more plausible explanation would be that the two fixed states in this case were not absolutely fixed and that there was some production of heteroplasmic descendents from homoplasmic females in both fixed states. These de novo mutation mechanisms, acting over 30 generations, could form the U-shaped distribution seen in Figure 6A. One could also speculate that the shape of the observed heteroplasmy distribution in Figure 6A suggests that the de novo mutation rate of the formation of the longer genome from the shorter genome (i.e., away from the fixed state at heteroplasmy 0%) is the larger of the two mutation rates.
Finally, let us discuss the roles of the parameters p0 and b. We defined the parameter b (Equation 7) to replace a combination of the parameter t, the number of generations, and the parameter Neff, a statistical parameter related to the number of segregating units of mtDNA (though not necessarily directly equal to it). In this paper we have analyzed only a single generation at a time, and we have not applied this analysis to follow the heteroplasmy distribution over multiple generations. One could certainly use the Kimura distribution to follow the distribution over multiple generations, in which case the formulation of Equations 2–5, which are written in terms of t and Neff, should be used. The parameter p0 can be interpreted as either the mean heteroplasmy in the data set or the heteroplasmy in the founder. In the case of pure random drift, the two are the same, but other effects may cause a shift in mean heteroplasmy over the generations. This distinction in the definition of p0 may be important in some cases. One example of this is the D. Simulans data set (Figure 8), Even though the Kimura distribution fit to this data is a good model of the heteroplasmy distribution (p = 0.79), in that experiment the mean heteroplasmy was observed to shift from an initial value of 38.5% in the founder to a value of 12.7% in the third generation.20 This was reasonably interpreted as indicating a selection effect in this experiment. Despite the apparently strong selection effect, the heteroplasmy distribution in the third generation is still well described by a Kimura distribution with the value p0 = 0.127. The lesson here is that even if a Kimura distribution, derived from neutral-drift theory, fits the observed heteroplasmy distribution, this is not enough in itself to allow us to determine that neutral drift alone has shaped that heteroplasmy distribution. Instead, the old standard method of measuring the changes in the mean heteroplasmy over a number of generations must continue to be used. The use of the Kimura distribution adds valuable information to our previous analysis techniques, but it does not invalidate them.
What the Kimura-distribution theory presented here allows us to do that we could not do before is to predict the complete probability distribution, including the probability of fixing on the wild-type and on the mutant mtDNA, for mtDNA heteroplasmy values in a group of offspring. Although this predictive ability is under the assumption of random genetic drift, this is a necessary first step to which important complications such as selection effects and de-novo mutations may then be added in further development of this theoretical model. The comparisons of the Kimura distributions to the experimental data sets presented in this paper are one use of these equations, but these comparisons are primarily made here as a validation of the application of this theory to mitochondrial genetics. The Kimura distribution equations give us a theoretical framework for the field of mitochondrial heteroplasmy.
A recent study by Elliot et al.33 of the prevalence of a set of ten pathogenic mtDNA point mutations has shown that these pathogenic mutations are relatively common in the general population, where it has been measured that 1 in 200 individuals carries one of these ten mtDNA mutations. With this new appreciation of how widespread mtDNA heteroplasmy actually is, the ability to calculate the complete heteroplasmy distribution by using the Kimura distribution as a model of random genetic drift is an important tool for understanding the heteroplasmy distribution in the general population.
One potential application of this new theoretical tool is the calculation of simulated pedigrees. These simulated pedigrees may be used as tools for analyzing clinical pedigrees, for example in a Monte-Carlo test to define a p value for a particular clinical pedigree tested against the null hypothesis of random genetic drift. One could also use the theoretical heteroplasmy distribution to calculate disease occurrence probabilities, based on a heteroplasmy threshold for the disease phenotype, for use in genetic counseling. Further testing of the theory, and in particular more human data such as that in Figure 1, will be needed before that becomes a practical application. Finally, the calculation of simulated pedigrees based on this theoretical heteroplasmy distribution could be extended to model large-scale populations. That model could be tested against recent33 and future measurements of the occurrence of mtDNA heteroplasmy and will help us understand the development and spread of pathogenic mtDNA mutations in the human population.
Web Resources
The URL for data presented herein is as follows:
Kimura Distribution software, http://staff.vbi.vt.edu/dsamuels/2008_Kimura/software
Acknowledgments
P.W. is supported by Thailand's Commission on Higher Education, Royal Thai Government under the program “Strategic Scholarship for Frontier Research Network.” P.F.C. is a Welcome Trust Senior Clinical Research Fellow.
References
- 1.Goto Y., Nonaka I., Horai S. A mutation in the transfer RNALEU(UUR) gene associated with the MELAS subgroup of mitochondrial encephalomyopathies. Nature. 1990;348:651–653. doi: 10.1038/348651a0. [DOI] [PubMed] [Google Scholar]
- 2.Shoffner J.M., Lott M.T., Lezza A.M.S., Seibel P., Ballinger S.W., Wallace D.C. Myoclonous epilepsy and ragged-red fiber disease(MERRF) is associated with a mitochondrial DNA transfer RNALYS mutation. Cell. 1990;61:931–937. doi: 10.1016/0092-8674(90)90059-n. [DOI] [PubMed] [Google Scholar]
- 3.Holt I.J., Harding A.E., Petty R.K.H., Morganhughes J.A. A new mitochondrial disease associated with mitochondrial DNA heteroplasmy. Am. J. Hum. Genet. 1990;46:428–433. [PMC free article] [PubMed] [Google Scholar]
- 4.Uziel G., Moroni I., Lamantea E., Fratta G.M., Ciceri E., Carrara F., Zeviani M. Mitochondrial disease associated with the T8993G mutation of the mitochondrial ATPase 6 gene: A clinical, biochemical, and molecular study in six families. J. Neurol. Neurosurg. Psychiatry. 1997;63:16–22. doi: 10.1136/jnnp.63.1.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wallace D.C., Singh G., Lott M.T., Hodge J.A., Schurr T.G., Lezza A.M.S., Elsas L.J., Nikoskelainen E.K. Mitochondrial DNA mutation associated with lebers hereditary optic neuropathy. Science. 1988;242:1427–1430. doi: 10.1126/science.3201231. [DOI] [PubMed] [Google Scholar]
- 6.Howell N., Bindoff L.A., McCullough D.A., Kubacka I., Poulton J., Mackey D., Taylor L., Turnbull D.M. Leber hereditary optic neuropathy - Identification of the same mitochondrial NDI mutation in 6 pedigrees. Am. J. Hum. Genet. 1991;49:939–950. [PMC free article] [PubMed] [Google Scholar]
- 7.Johns D.R., Neufeld M.J., Park R.D. An ND6 mitochondrial DNA mutation associated with leber hereditary optic neuropathy. Biochem. Biophys. Res. Commun. 1992;187:1551–1557. doi: 10.1016/0006-291x(92)90479-5. [DOI] [PubMed] [Google Scholar]
- 8.Giles R.E., Blanc H., Cann H.M., Wallace D.C. Maternal inheritance of human mitochondrial DNA. Proc. Natl. Acad. Sci. U.S.A. 1980;77:6715–6719. doi: 10.1073/pnas.77.11.6715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Larsson N.G., Tulinius M.H., Holme E., Oldfors A., Andersen O., Wahlstrom J., Aasly J. Segregation and manifesations of the mtDNA trans RNALYSA>G(8344) mutation of myoclonous epilepsy and ragged-red fibers (MERRF) syndrome. Am. J. Hum. Genet. 1992;51:1201–1212. [PMC free article] [PubMed] [Google Scholar]
- 10.Chinnery P.F., Andrews R.M., Turnbull D.M., Howell N. Leber hereditary optic neuropathy: Does heteroplasmy influence the inheritance and expression of the G11778A mitochondrial DNA mutation? Am. J. Med. Genet. 2001;98:235–243. doi: 10.1002/1096-8628(20010122)98:3<235::aid-ajmg1086>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 11.Sekiguchi K., Kasai K., Levin B.C. Inter- and intragenerational transmission of a human mitochondrial DNA heteroplasmy among 13 maternally-related individuals and differences between and within tissues in two family members. Mitochondrion. 2003;2:401–414. doi: 10.1016/S1567-7249(03)00028-X. [DOI] [PubMed] [Google Scholar]
- 12.Chinnery P.F., Howell N., Lightowlers R.N., Turnbull D.M. Genetic counseling and prenatal diagnosis for mtDNA disease. Am. J. Hum. Genet. 1998;63:1908–1910. doi: 10.1086/302157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thorburn D.R., Dahl H.H.M. Mitochondrial disorders: Genetics, counseling, prenatal diagnosis and reproductive options. Am. J. Med. Genet. 2001;106:102–114. doi: 10.1002/ajmg.1380. [DOI] [PubMed] [Google Scholar]
- 14.Brown D.T., Herbert M., Lamb V.K., Chinnery P.F., Taylor R.W., Lightowlers R.N., Craven L., Cree L., Gardner J.L., Turnbull D.M. Transmission of mitochondrial DNA disorders: Possibilities for the future. Lancet. 2006;368:87–89. doi: 10.1016/S0140-6736(06)68972-1. [DOI] [PubMed] [Google Scholar]
- 15.Wright S. Statistical genetics and evolution. Bull. Am. Math. Soc. 1942;48:223–246. [Google Scholar]
- 16.Kimura M. Solution of a process of random genetic drift with a continuous model. Proc. Natl. Acad. Sci. USA. 1955;41:144–150. doi: 10.1073/pnas.41.3.144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Maruyama T., Kimura M. Genetic-variability and effective population-size when local extinction and recolonization of sub-populations are frequent. Proc. Natl. Acad. Sci. U.S.A. 1980;77:6710–6714. doi: 10.1073/pnas.77.11.6710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Iizuka M. The effective size of fluctuating populations. Theor. Popul. Biol. 2001;59:281–286. doi: 10.1006/tpbi.2001.1521. [DOI] [PubMed] [Google Scholar]
- 19.Brown D.T., Samuels D.C., Michael E.M., Turnbull D.M., Chinnery P.F. Random genetic drift determines the level of mutant mtDNA in human primary oocytes. Am. J. Hum. Genet. 2001;68:533–536. doi: 10.1086/318190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.de Stordeur E., Solignac M., Monnerot M., Mounolou J.C. The generation of transplasmic Drosophila simulans by cytoplasmic injection- Effects of segregation and selection in the perpetuation of mitochondrial DNA heteroplasmy. Mol. Gen. Genet. 1989;220:127–132. doi: 10.1007/BF00260866. [DOI] [PubMed] [Google Scholar]
- 21.Jenuth J.P., Peterson A.C., Fu K., Shoubridge E.A. Random genetic drift in the female germline explains the rapid segregation of mammalian mitochondrial DNA. Nat. Genet. 1996;14:146–151. doi: 10.1038/ng1096-146. [DOI] [PubMed] [Google Scholar]
- 22.Solignac M., Genermont J., Monnerot M., Mounolou J.C. Genetics of mitochondria in Drosophila mtDNA inheritance in heteroplasmic strains of Drosophila mauritiana. Mol. Gen. Genet. 1984;197:183–188. [Google Scholar]
- 23.Hoang-Binh D. A program to compute exact hydrogenic radial integrals oscillator strengths, and Einstein coefficients, for principal quantum numbers up to n approximate to 1000. Comput. Phys. Commun. 2005;166:191–196. [Google Scholar]
- 24.Press W.H. Cambridge University Press; Cambridge, UK: 1992. Numerical recipes in C: The art of scientific computing. [Google Scholar]
- 25.Rajasimha H.K., Chinnery P.F., Samuels D.C. Selection against pathogenic mtDNA mutations in a stem cell population leads to the loss of the 3243A -> G mutation in blood. Am. J. Hum. Genet. 2008;82:333–343. doi: 10.1016/j.ajhg.2007.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chinnery P.F., Samuels D.C. Relaxed replication of mtDNA: A model with implications for the expression of disease. Am. J. Hum. Genet. 1999;64:1158–1165. doi: 10.1086/302311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Coller H.A., Khrapko K., Herrero-Jimenez P., Vatland J.A., Li-Sucholeiki X.C., Thilly W.G. Clustering of mutant mitochondrial DNA copies suggests stem cells are common in human bronchial epithelium. Mut. Res. 2005;578:256–271. doi: 10.1016/j.mrfmmm.2005.05.014. [DOI] [PubMed] [Google Scholar]
- 28.Cree L.M., Samuels D.C., Lopes S., Rajasimha H.K., Wonnapinij P., Mann J.R., Dahl H.H.M., Chinnery P.F. A reduction of mitochondrial DNA molecules during embryogenesis explains the rapid segregation of genotypes. Nat. Genet. 2008;40:249–254. doi: 10.1038/ng.2007.63. [DOI] [PubMed] [Google Scholar]
- 29.Poulton J., Macaulay V., Marchington D.R. Is the bottleneck cracked? Am. J. Hum. Genet. 1998;62:752–757. doi: 10.1086/301811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Birky C.W. The inheritance of genes in mitochondria and chloroplasts: Laws, mechanisms, and models. Annu. Rev. Genet. 2001;35:125–148. doi: 10.1146/annurev.genet.35.102401.090231. [DOI] [PubMed] [Google Scholar]
- 31.Chinnery P.F., Thorburn D.R., Samuels D.C., White S.L., Dahl H.H.M., Turnbull D.M., Lightowlers R.N., Howell N. The inheritance of mitochondrial DNA heteroplasmy: Random drift, selection or both? Trends Genet. 2000;16:500–505. doi: 10.1016/s0168-9525(00)02120-x. [DOI] [PubMed] [Google Scholar]
- 32.Poulton J., Marchington D.R. Segregation of mitochondrial DNA (mtDNA) in human oocytes and in animal models of mtDNA disease: clinical implications. Reproduction. 2002;123:751–755. doi: 10.1530/rep.0.1230751. [DOI] [PubMed] [Google Scholar]
- 33.Elliott H.R., Samuels D.C., Eden J.A., Relton C.L., Chinnery P.F. Pathogenic mitochondrial DNA mutations are common in the general population. Am. J. Hum. Genet. 2008;83:254–260. doi: 10.1016/j.ajhg.2008.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]


