Modelling evolutionary cell behaviour using neural networks: Application to tumour growth

Abstract

In this paper we present a modelling framework for cellular evolution that is based on the notion that a cell’s behaviour is driven by interactions with other cells and its immediate environment. We equip each cell with a phenotype that determines its behaviour and implement a decision mechanism to allow evolution of this phenotype. This decision mechanism is modelled using feed-forward neural networks, which have been suggested as suitable models of cell signalling pathways. The environmental variables are presented as inputs to the network and result in a response that corresponds to the phenotype of the cell. The response of the network is determined by the network parameters, which are subject to mutations when the cells divide. This approach is versatile as there are no restrictions on what the input or output nodes represent, they can be chosen to represent any environmental variables and behaviours that are of importance to the cell population under consideration. This framework was implemented in an individual-based model of solid tumour growth in order to investigate the impact of the tissue oxygen concentration on the growth and evolutionary dynamics of the tumour. Our results show that the oxygen concentration affects the tumour at the morphological level, but more importantly has a direct impact on the evolutionary dynamics. When the supply of oxygen is limited we observe a faster divergence away from the initial genotype, a higher population diversity and faster evolution towards aggressive phenotypes. The implementation of this framework suggests that this approach is well suited for modelling systems where evolution plays an important role and where a changing environment exerts selection pressure on the evolving population.

1 Introduction

The genetic regulatory machinery of prokaryotic and eukaryotic cells is very complex and only isolated proportions have been fully documented. It contains a large number of pathways that regulate cell behaviour, and these pathways do not only function separately, but there exists a degree of non-linear cross-talk between them. This is in stark contrast with the genetic code, which is “linear” in its form and has now been completely mapped out for a number of organisms (The C. Elegans Sequencing Consortium, 1998; Goffeau et al., 1996; Venter, 2001). Our understanding of how cells respond to external stimuli is thus very difficult to infer from the knowledge about the regulatory pathways. If one would further like to model how the behaviour of cells changes due to mutation and evolution the task becomes even more difficult. In order to make this type of modelling possible one has to simplify the system to a level which is both conceptually and computationally feasible. In this paper we introduce a modelling framework for cell behaviour, which while remaining conceptually simple still has the capability of capturing the dynamics of regulatory pathways and can easily be implemented in an agent-based model of cellular evolution.

A cell can be thought of as a computing unit that given a certain input “calculates” an output or response. A classical example of this is when normal epithelial cells perform tosis (programmed cell death) when they lose adhesion to other cells (Giancotti and Rouslahti, 1999) or when they go into apoptosis due to hypoxic (low oxygen) conditions (Ganong, 1999). Another example is when growth factors stimulate cells to go into cell division (Alberts et al., 1994). In these examples information from the receptors, at the cell surface, is transmitted through molecular pathways and a response is produced. Ultimately, the genotype of a cell determines how it responds to certain stimuli (i.e. the genotype “processes” the input and produces an output), and this response can be thought of as the phenotype. The behaviour of the cell might then change the environment of the cell, effectively creating a feedback loop in the system (see fig. 1). In the spirit of this, we model the behaviour of the cell using a decision mechanism, that determines the actions of the cell based on the cell genotype, the micro-environment in which it resides and interactions between these. The decision mechanism is subject to mutations during cell division, which allows for evolutionary changes of cell behaviour. It has been argued that the regulatory pathways in cells resemble artificial neural networks (Bray, 1990, 1995) and the decision mechanism is therefore modeled using an artificial feed-forward neural network (Haykin, 1999). Although the decision mechanism of living cells is far more complex than a single neural network, consisting of numerous interconnected signaling pathways, we believe that using an approach that reflects the underlying dynamics of the process yields a model that is easier to integrate with experimental data in contrast to other more abstract modelling approaches like for example bit-string representations of the cell genotype (Kauffman, 1993). It should be noted though, that this modelling technique does not attempt to capture the precise dynamics of signaling pathways, but rather to serve as an abstract model of cell behaviour.

Figure 1.

A schematic representation of how a cell takes the micro-environment as an input which is then ultimately processed by the cell genotype which in turn decides on an output response which is the phenotype. The resulting cell phenotype then has the potential to modify the micro-environment thus setting up a possible feedback loop.

2 Previous Work

Artificial neural networks have traditionally been used for classification and prediction tasks, some examples are: detection of heart abnormalities (Leung et al., 1990), finger-print recognition (Baxt, 1991) and breast cancer prediction (Floyd et al., 1994). In these tasks the network is trained with a data set that consists of a number of variables from each sample together with the outcome of each sample (e.g. in the case of breast cancer the variables are uniformity of cell size, uniformity of cell shape, marginal adhesion etc. and the outcome is wether the breast contains a tumour or not). The goal of this procedure is to construct a network that will be able to predict the outcome of an unknown sample which was not in the training set. There are two approaches to solve this problem, either by using a single network that is optimised with respect to the training set using an error minimising algorithm like back-propagation (Haykin, 1999) or by an evolutionary algorithm where an evolving population of networks adapts by mutation and selection (Yao, 1993), where the fitness of a network is determined by how well it can classify the training set.

Another application, more in line with our use of neural networks, is the implementation of neural networks in evolving robot controllers (Meyer, 1998). Here the input to the network are sensors of the robot (e.g. proximity sensors) and the output of the network controls the motors. The networks are then trained to perform a given task (i.e. maneuver the robot in a certain way) and a fitness is assigned to each network depending on how well it manages the task. The fitness then determines if the network will reproduce (under mutations) or if it will be replaced by a more successful network, thus allowing the population of networks to evolve.

A more recent application of neural networks is to model cell signalling pathways, which was first suggested by Bray (1990). He argues that the performance of cell signalling networks is similar to that of artificial neural networks and that neural networks therefore can be used to model and simulate real signalling pathways. Further he argues that evolution and adaptation of signalling pathways occur by small changes in the network parameters that alter the network connections, and change the behaviour of the cell. He also makes a comparison to the traditional use of neural networks, stating that:“…systems of interacting proteins act as neural networks trained by evolution to respond appropriately to patterns of extracellular stimuli” (Bray, 1995).

Vohradsky (2001) used a neural network approach to model the λ bacteriophage lysis/lysogeny decision circuit. This model, which incorporates multigenic regulation, is in good agreement with experimental results, gives further insight into the experimental observations and shows that neural networks can successfully be used to model regulatory pathways. A further development of this approach has been to use recurrent neural networks to reverse engineer the regulatory pathways of human cells using micro-array data (Narayanan et al., 2004; Blasi et al., 2005). In this approach the nodes represent expression levels of genes that regulate each other. Updating the network corresponds to tracking the time evolution of the expression levels and comparing these with real expression levels from micro-array data experiments allows connections between the nodes to be inferred. Weaver et al. (1999) used an extended version of this approach where they introduced nodes into the network that represented environmental variables that could affect the expression of the genes. Although this usage of neural networks still is under development it again shows that neural networks have the potential to serve as models for regulatory pathways.

3 Model

3.1 Background

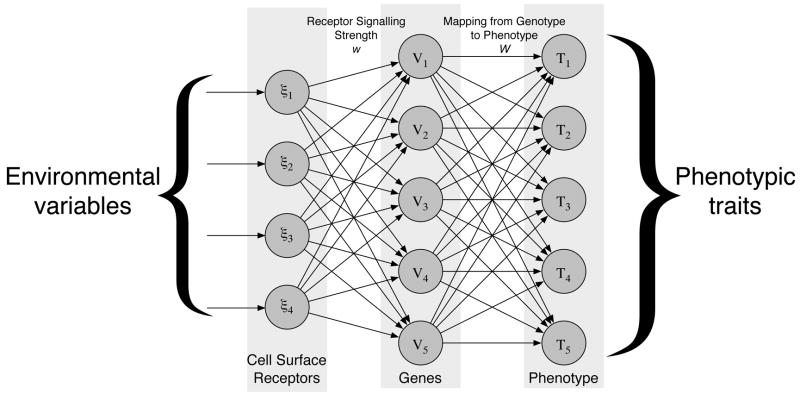
In contrast to the above neural network models of gene regulation our model will not focus on the detailed regulation of genes, but on how the behaviour of the cell is affected by the environment. The decision mechanism, which we will term the response network (fig. 2), consists of a number of nodes that can take real number values. The nodes are organised into three layers: one input layer, that takes information from the environment, one hidden layer, and finally an output layer that determines the action of the cell. The nodes in the different layers are connected with varying weights, determined by two matrices w and W, and the nodes in the hidden and output layer are equipped with internal thresholds θ and φ. The value of the input layer is determined by the micro-environment of the cell, these values are then fed through the network and produce a response in the output layer that determines the behaviour of the cell.

Figure 2.

The structure of the response network. Environmental variables are presented to the input-layer and then fed through the network where a phenotype is calculated.

The regulatory networks in real cells are of course much more complicated consisting of a large number of reactions, but as a feed-forward neural network with one hidden layer can approximate any continuous function (Castro et al., 2000), nothing is gained by adding more layers to the network. If a trait of the cell changes according to a certain function of the environmental input, this behaviour can always be captured by a network with only one hidden layer, although the underlying dynamics may involve a large number biochemical reactions. The nodes in the network therefore do not represent expression levels of single genes, but rather genes that are co-regulated or affected by the same external stimuli.

In the view of the recurrent neural networks employed in (Narayanan et al., 2004; Blasi et al., 2005; Weaver et al., 1999) and also of the Boolean network model of the genetic regulatory network (Kauffman, 1969), the output from the response network can be viewed as the steady-state of the gene regulatory network, which then corresponds to a certain phenotype or behaviour (Huang et al., 2005), i.e. the state of the output layer corresponds to a fixed-point (or limit-cycle) in the recurrent (or Boolean) network model of gene regulation. This of course assumes that the intra-cellular dynamics occur on a much faster time-scale than changes in the extra-cellular environment.

In contrast to the above networks feed-forward neural networks are not capable of memory storage, i.e. the state of the network at time t + 1 is not a function of the previous state at time t. This is naturally a drawback, as many cellular processes, such as the cell-cycle and chemotaxis, are memory-dependent, but this can easily be incorporated into the model by allowing connections within the hidden layer. This would effectively change the network into a recurrent neural network, with the special property that certain nodes (the input layer) only have outgoing links, and another subset of nodes (the output layer) only have incoming links.

This neural network approach only serves as an abstract model of cellular behaviour, but still shares some features of the real signaling and regulatory network of the cell. The input layer of the network can be thought of as receptors on the cell surface that interact with extra-cellular molecules. The weight matrix between the input and hidden layer represent the signaling strength of these receptors. The hidden layer functions as regulatory genes that control the behaviour of the cell through the weights of the connection matrix between the hidden and output layer. Finally the output layer can be thought of as the phenotype, as it determines the behaviour of the cell (see fig. 2). With this analogy in mind we can think of changing a connection between the input and hidden layer as changing the expression level of a certain type of receptor and changing a connection between the hidden and output layer as altering the expression level of a regulatory gene.

3.2 Definition

We will now discuss in detail the structure of the response network and how is processes information from the environment. The node values of the input layer are defined by the micro-environment, which in turn determine the values of the hidden layer nodes through a weighted sum and a transfer function (eq. 1). A similar procedure is then applied from the hidden to the output layer, from which the behaviour of the cell is determined. The use of this transfer function ensures that the values of the output nodes are always in the interval [0, 1].

$$g(x)=\frac{1}{1+e^{-\beta x}}$$ (1)

More formally, if we let ξ be the input vector, then the state of node j in the hidden layer is given by,

$$V_j=g(\sum _k{w}_{jk}{\xi }_k-{\theta }_j)$$ (2)

where θ_j is the threshold for node j in the hidden layer. Now the state of node i in the output layer is given by,

$$T_i=g(\sum _j{W}_{ij}{V}_j-{\phi }_i)=g(\sum _j{W}_{ij}g(\sum _k{w}_{jk}{\xi }_k-{\theta }_j)-{\phi }_i).$$ (3)

The output from the network is deterministic and depends only on the weight matrices w, W, the threshold vectors θ, φ and the environmental input vector ξ. The phenotype of the cell is then determined by the values of the nodes in the output layer. The assignment of phenotypic traits determined by the output nodes is model-dependent and can be chosen to be any traits whose evolution one is interested in studying. The output of the network is continuous and in the range [0, 1], which means that it can either represent a continuous behaviour like motility (by mapping [0, 1] to the range of possible cell velocities), or a boolean type behaviour like cell division (by introducing an appropriate threshold value). The same versatility applies to the input nodes, they can represent any environmental factor that is relevant for the cell.

3.3 Cell division and mutations

The crucial part of this modelling approach is that the cell behaviour can vary by introducing changes to the network parameters (i.e. the weight matrices and threshold vectors). These changes are meant to represent mutations that occur in the daughter cells genome during cell division. The network wiring of the parent cell, which is represented by the two matrices w, W and the thresholds θ and φ, are copied to the daughter cells under mutations. The number of mutations that occur in the daughter cells wiring is chosen from a Poisson distribution with parameter p. We do not assume any directionality in the mutations and these are therefore distributed equally over the matrices and threshold vectors, i.e. they are equally likely to affect any phenotypic trait. The parameter p is thus the average number of mutations per cell division, as the mean value of a Poisson distribution equals the parameter in the distribution, which in this case is p. It should be noted that the mutation rate in this model does not correspond to the mutation rate in real cells, as the amount of information copied by a real cell is approximately 10⁸ orders higher in magnitude. The incorrect copying is modeled by adding a normal distributed number s ∈ N(0, σ) to the daughter cell matrix or threshold entry, which means that x → x +s, for those entries x that are chosen for mutation.

The mutations alter the connection strength between the nodes, which in turn changes how the cell responds to the micro-environment. If for example a mutation occurs in a connection that links the oxygen concentration with the apoptosis node this changes how the cell responds to the local oxygen concentration. This might give the daughter cell an advantage over other cells and if so the cell would be more likely to reproduce. The environment in which the cells live would then select for cells with a certain environment/phenotype mapping, effectively creating a selection pressure on the cell population. It should be noted that the fitness of the cell depends on both the phenotype of the cell and the environment in which lives, which implies that the fitness of the cell will always be implicit and not a pre-defined function of the genotype.

3.4 Network construction

In order for this model to be useful one has to define the weight matrices and node thresholds in the network, which corresponds to defining the initial mapping from environment to phenotype for the cells. As the response network essentially classifies different environmental conditions into different phenotypic categories the most straight-forward way to construct the network is to train it with appropriate environment/phenotype data using a standard training algorithm such as back-propagation (Haykin, 1999). This data would have the exact environmental conditions as input (ξ) and measurable phenotypic traits as output (T). An example of this could be to train the network with data that consists of the concentration of a certain chemical as input and the motility (in μm/s) of the cells as output from the network. This simple example only illustrates the technique, while the real training data would have to be multi-dimensional on both the input and output side in order to render the training successful.

Another possibility is to simultaneously measure the expression levels of genes using microarrays, and use this additional data to guide the parametrisation of the network. In this case the nodes in the hidden layer would correspond to groups of co-regulated genes, and the links between the expression levels of these genes and phenotypic responses could be inferred from the experiments. This procedure could potentially be very useful, as it would make it possible to assign meaning to the links in the network, and hence make more detailed predictions about the evolution on an intra-cellular level.

Gathering this type of data requires experiments that are both expensive, time-consuming and sometimes incredibly difficult. An alternative to this experimental-driven training of the network would be to train the network in a more qualitative fashion. If one for example has qualitative knowledge about the cell behaviour under certain conditions one could construct a data set from these and in turn use it to train the network. This would naturally not be as accurate as data from experiments, but could serve as a starting point for the network construction which subsequently could be improved with experimental data. A further way of constructing the network is to prescribe network parameters that give the desired behaviour without going through the process of training the network. This technique is the most straight forward, but can be difficult if the network under consideration is large.

4 Agent-based model of tumour growth

In this section we will give a concrete example of how this framework can be used in an agent-based model. The example we will discuss is a model of solid tumour growth (Gerlee and Anderson, 2007a, 2008), which was used to investigate the effect of tissue oxygenation on the growth and evolutionary dynamics of the tumour. It is a well known fact that evolution plays an extensive role in the development of cancer and that tumours consist of a large number of different subclones that compete for space and resources (Alexandrova, 2001; Nowell, 1976). Tumour cells behave as renegade cells that have lost their cooperative behaviour and this behaviour can be viewed as a disruption in how they process information from their micro-environment. This disruption is mainly due to genetic mutations that alter their ability to respond to the micro-environmental signals.

The specific model we consider here is a hybrid cellular automaton model, where the cells are represented as individual entities (“agents”), whose behaviour is determined by a response network, while chemical concentrations (oxygen, glucose etc.) are treated on a continuous level. The response network incorporates three layers covering the micro-environment, genes and phenotype.

Preliminary results from this model have shown that the tissue oxygen concentration affects both the growth and evolutionary dynamics of the tumour. For low oxygen concentrations there is a selection pressure for cells that can avoid apoptosis and proliferate even at very low oxygen concentrations. In the network wiring this manifests itself as a down-regulation of the apoptosis node and a up-regulation of proliferation node. On the other hand under normal oxygen concentrations this effect is heavily diminished. This shows that the environment of the cells creates a selection pressure for a certain cell phenotype and that this in turn affects the evolution of the response network. This behaviour has also been observed in in vitro experiments (Graeber et al., 1996; Kim et al., 1997), which suggests that the model captures the dynamics of the system in a correct way. Here we will present further analysis of the evolutionary dynamics that highlights the importance of competition for nutrients in tumour growth. In the next section we will give a brief description of the model, but for further details on the model and the previous results please refer to the original publication (Gerlee and Anderson, 2007a, 2008).

4.1 Model Description

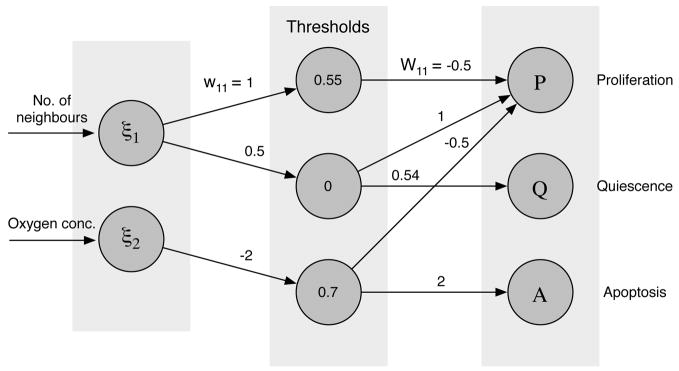
In the most basic setting of our model the only input to the network is the number of neighbours of the cell and the local oxygen concentration. The reason for this choice is that cancer cells often show weaker response to hypoxia-induced apoptosis (Lowe and Lin, 2000) and that they tend to adhere less to their neighbours (Cavallaro and Christofori, 2004). This implies that the input vector ξ will have two components, ξ = (n(x⃗, t), c(x⃗, t)), where n(x⃗, t) is the number of neighbours and c(x⃗, t) the oxygen concentration. The number of neighbours determines if the cell will proliferate (if n(x⃗, t) > 3) or become quiescent (if n(x⃗, t) ≤3), while the oxygen concentration influences the apoptotic response. If the oxygen concentration falls below a certain threshold c_ap the apoptosis node is activated and the cell dies. An initial network that fulfilled the above specifications was created and used as a “seed” in every simulation (see fig. 3) and the mutation rate was set to p = 0.01, just as in Anderson (2005).

Figure 3.

The layout of the initial network used in the agent-based model of tumour growth. The input to the network is the number of neighbours of the cell and the local oxygen concentration. The output of the network corresponds to proliferation (P), quiescence (Q) and apotosis (A), out of which the strongest is chosen.

In the model the output nodes represent the response for proliferation (P), quiescence (Q) and apoptosis (A). As these form a group of mutually exclusive behaviours (a cell can not perform these responses simultaneously) the behaviour with the strongest response is chosen from these three, we call this the life-cycle response. If the proliferation node has the strongest response the cell divides and produces a daughter cell, if the quiescence node has the strongest response the cell remains dormant and if the apoptosis node is strongest then the cell dies via apoptosis. The behaviour of the cell is affected by the local oxygen concentration, but also changes it, as the response of the cell affects the oxygen consumption. A proliferating cell consumes nutrient at a rate k, while a quiescent cell has a reduced consumption of k_q < k and apoptotic cells do not consume any nutrients. This gives rise to a complex feedback between the cells and the oxygen concentration that will dictate the growth dynamics of the tumour. The output of the network is also coupled to the proliferation age by letting cells with a stronger response divide faster and consequently consume more oxygen.

The dynamics of the cells is coupled with a continuous field of oxygen c(x⃗, t). The metabolism of cancer cells includes a large number of different chemicals that are all needed for maintenance and cell division, but it is known that oxygen limits the growth of the tumour (Sutherland, 1988). The time evolution of the oxygen field is governed by the following partial differential equation,

$$\frac{\partial c(\overrightarrow{x},t)}{\partial t}=D_c{\nabla }^{2}c(\overrightarrow{x},t)-f_c(\overrightarrow{x},t),$$ (4)

where D_c is the diffusion constant of oxygen and f_c(x⃗, t) gives the individual cell oxygen consumption rate for the cell at position x⃗ at time t. The oxygen field is solved on a grid with the same spatial step size as the cells using an ADI-scheme (Press et al., 1996). This choice of space step implies that the consumption term in (eq. 4) is determined by each individual cell, and f_c(x⃗, t) is thus defined in the following way,

$$f_c(\overrightarrow{x},t)=\{\begin{array}{ll}0\hfill & \begin{array}{l}\text{if}\text{the}\text{automaton}\text{element}\text{at}\overrightarrow{x}\text{is}\text{empty}\text{i}.\text{e}.\text{no}\text{tumour}\\ \text{cell}\text{at}\text{that}\text{lattice}\text{point}\end{array}\hfill \\ kF(\overrightarrow{x})\hfill & \begin{array}{l}\text{if}\text{the}\text{automaton}\text{element}\text{is}\text{occupied},\text{i}.\text{e}\text{tumour}\\ \text{cell}\text{exists}\text{at}\text{that}\text{lattice}\text{point}\end{array}\hfill \end{array}$$ (5)

where k is the base consumption rate and F(x⃗) is the modulated energy consumption of the individual cell occupying the automaton element at x⃗. The function F(x⃗) is an increasing function of the network response, and also influences the proliferation age by letting a cell with a higher response divide faster.

The two-dimensional tissue under consideration is represented by a N × N grid. Each grid point can either be occupied by a cancer cell or be empty and also holds the local concentration of oxygen. The grid is characterised by a grid constant d, which determines the size of the cells. The grid points are identified by a coordinate x⃗ = d(i, j) i, j = 0, 1, …., N − 1. The chemical concentrations interact with the cells according to cellular consumption rates and are given appropriate initial and boundary conditions. Each time step the chemical concentrations are solved using the discretised equations and every one of the tumour cells is updated in a random order. Every time step each cell is updated as follows:

1. The input vector ξ is sampled from the local environment (i.e the grid point where the cell resides).

2. A response R = R(ξ, G) is calculated from the network, where G represents the genotype of the cell, i.e. the network parameters, and ξ is the environmental input vector

3. The cell consumes oxygen according to its behaviour. If there is not sufficient oxygen present the cell dies from necrosis.

4. The life-cycle action determined by the network is carried out:

   • If proliferation (P) is chosen, check if the cell has reached proliferation age and if there is space for a daughter cell. If both are true the cell divides and the daughter cell is placed in a neighbouring grid point, if not the cell does nothing.

   • If quiescence (Q) is chosen the cell becomes quiescent.

   • If apoptosis (A) is chosen the cell dies.

If a cell dies from either apoptosis or necrosis it is no longer updated. Although the two death processes occur in different ways we will for simplicity treat them equally and consider the grid point where the cell resided as empty in the next time step.

4.2 Results

The oxygen concentration is known to be a key player in the growth of tumours. Before tumours have acquired their own blood supply through angiogenesis (Folkman, 2006), they have to rely on diffusion of oxygen from nearby blood-vessels. When the tumours reach a critical size this supply is not sufficient and cell death occurs in the centre of the tumour. This gives rise to the typical structure of a vascular tumours with a core of dead cells, followed by a rim of quiescent cells and finally an outer layer of proliferating cells (Sutherland, 1988). We have investigated the selection pressure that this type of growth exerts by analysing the evolutionary dynamics of the model under different oxygen concentrations. In order to determine the effects of the limited oxygen supply we have studied the extremes of the situation for an extended period of time. In one case the tumour is allowed to grow in an unlimited supply of oxygen, while in the other case the oxygen concentration is lower than in normal tissue. In the following we will refer to the unlimited supply as the high oxygen case and the other as the low oxygen case. This is of course not a realistic situation, but rather a way to highlight the impact of the limited oxygen supply on the growth of the tumour. For a more in depth investigation of the impact of the oxygen concentration, where an intermediate case also is investigated please consider Gerlee and Anderson (2007a).

Each simulation was started with 4 ancestral cells at the centre of the grid. In the low oxygen case the concentration was initialised to a homogeneous concentration of c₀ in the entire domain and the boundary condition was set to c(x⃗, t) = c₀, this imitates the situation where the tissue under consideration is surrounded by blood vessels that supply the tumour with oxygen via perfusion. The grid size was set to N = 300, which if we assume radial symmetry in a 3-dimensional setting would correspond to a tumour consisting of approximately 150³ or 3 million cells. Each simulation lasted 100 time steps (each time step corresponds to 1 cell generation ≈ 16 h) and to quantify the growth dynamics of the model we looked at the spatial distribution of cells and oxygen concentration in the tissue. The evolutionary dynamics were analysed by looking at average phylogenetic depth from the ancestral cell, the population diversity and the time evolution of the phenotypes in the population.

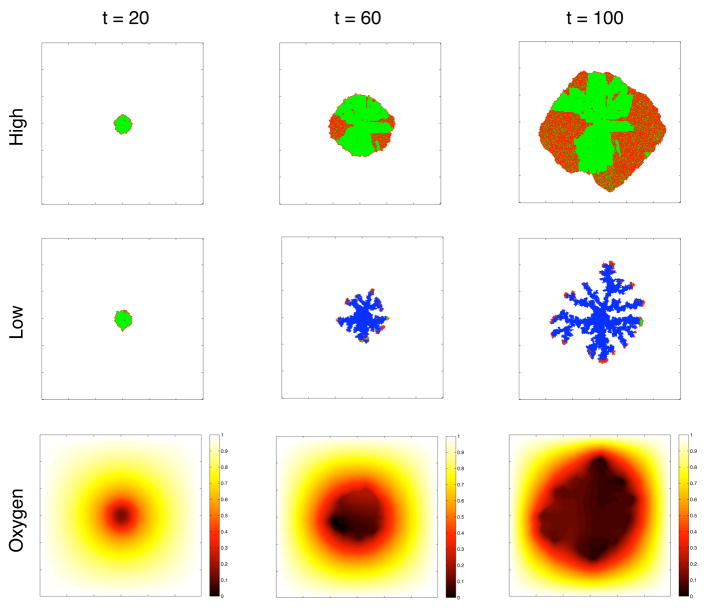
Figure 4 shows the spatial distribution of different cell types at t = 20, 60 and 100 for the two different simulations and also the oxygen distribution in the low oxygen case. This clearly shows that the limited oxygen supply influences the growth dynamics of the tumour. In the high oxygen case the tumour only consists of proliferating (red) and quiescent (green) cells growing with a more compact and rounded morphology, while in the low oxygen case the tumour consists mostly of dead cells (blue) with proliferating cells at the tip of the more skeletal fingered structure. This structure is induced by the fact that the oxygen is limited and as can be seen in the lower panel a gradient of oxygen appears early in the simulation (t=20). The limited supply of oxygen means that the oxygen level drops below the apoptotic threshold c_ap in the centre of the tumour, which leads to the development of a necrotic core. Evidence of evolutionary dynamics can also be observed in this figure. In the high oxygen case we can see cells that try to proliferate although they are surrounded by other cells. These cells have lost contact inhibition and ignore the fact there is no space to divide. The oxygen distribution also reveals a change in the cell phenotypes. The lowest observed oxygen concentrations in the three time points are different. At t = 20 the lowest concentration is 0.2, which agrees with the apoptotic threshold of the initial genotype, but for t = 60 and t = 100 the lowest observed oxygen level is down to zero. This corresponds to a complete loss of apoptotic response and the cells die because there is simply no oxygen available to consume.

Figure 4.

The two upper panels show the spatial distribution of cells at t =20, 60 and 100. Proliferating cells are coloured red, quiescent green and dead cells are blue. We can see a clear difference in the morphology of the tumours in the low and high oxygen case. The lower panel shows the oxygen concentration in the low oxygen case.

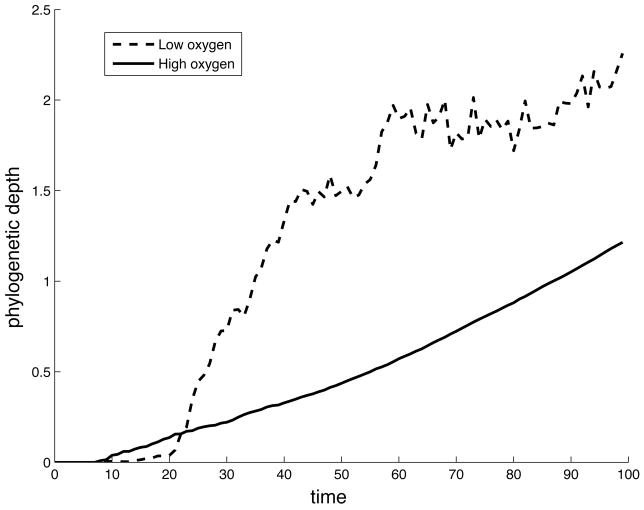
The phylogenetic depth is defined as the cumulative number of generations in which a cell’s genotype differs from its parent, or equivalently the number of mutations a cell has acquired compared to the ancestral genotype (Lenski et al., 2003). The phylogenetic depth was averaged over all cells present on the grid each time step of the simulation. The time evolution of this measure for both the low and high oxygen case can be seen in fig. 5. This reveals a difference between the two growth conditions, where we observe a faster increase of phylogenetic depth in the low oxygen concentration.

Figure 5.

The time evolution of the average phylogenetic depth for the low and high oxygen case.

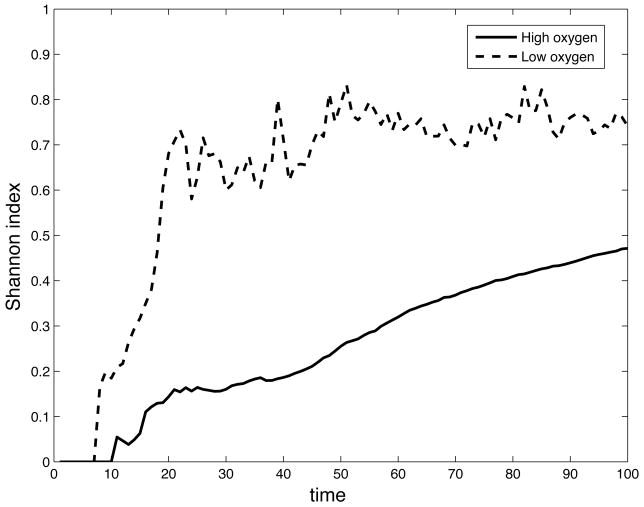
The network dynamics were also measured on the genotype level by looking at the Shannon index, a measure of the genotypic diversity in the population. It is given by,

$$H=-\frac{1}{ln(N_g)}\sum _{i=0}^{N_g}(p_{i}ln{p}_i)$$ (6)

where p_i is the probability of finding genotype i in the population and N_g is the number of distinct genotypes present in the population. The Shannon index reaches its maximum of 1 when all existing genotypes are equally probable (i.e p_i = 1/N_g for all i), and its minimum 0 when the population consists of only one genotype. Figure 6 shows the time evolution of the Shannon index, and again we can observe a difference between the two cases. In both cases the Shannon index attains its minimum H(0) = 0 at the beginning of the simulation because at this point only the initial genotype is present in the population, but early in the simulation (t ≈ 10) the diversity in the low oxygen case increases sharply and settles around a value of H ≈0.7, while the in the high oxygen case increases slower and reaches a value of H ≈ 0.5 at the end of the simulation.

Figure 6.

The time evolution of the Shannon index (eq. 6) for the low and high oxygen case.

The phenotype of a cell is a function of its immediate micro-environment, and therefore in order to quantify the behaviour of the cell we need to devise a measure that takes this into account. We do this by identifying each point in the two dimensional input space ξ = (n, c) with the response it produces R = (P, Q, A). In this way each response corresponds to a subset of the input space and we now measure the fraction of the input space that each of the corresponding responses occupies. This gives us a 3-dimensional vector S, that we term the average phenotype or response vector, and which reflects the behaviour of the cell. Formally we define three sets x_i = {ξ ∈ I; R(ξ) = i}, where R(ξ) is the network response to input vector ξ, i = P, Q, A and I = [0, 1] × [0, 4] is the set of all possible inputs to the network. The sizes of these subsets are now given by,

$$\mid x_i\mid =\frac{1}{B}\underset{I}{\int }{\delta }_{i,R(x)}dx$$ (7)

where δ_ij is the Kronecker delta (δ_ij = 1 if i = j, 0 otherwise) and B = 4 is the area of the entire input space. The average phenotype can now be defined as S = (|x_P|, |x_Q|, |x_A|). The initial genotype has a measure of S = (0.67, 0.18, 0.15), which means that 67 % of the input space corresponds to proliferation, 18 % to quiescence and 15 % to apoptosis. Note that this measure does not give any detailed information about the specific cell behaviour, but rather serves as a measure of the “average” behaviour of the cell or the potential the cell has for each response. The measure can also be interpreted as the probability of a certain response if a random point in the input space is used.

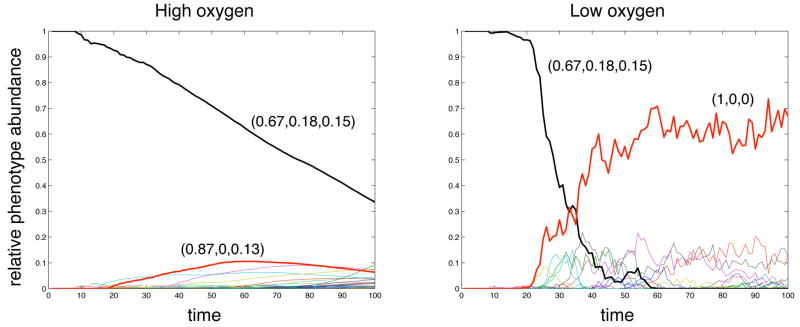
This measure was used to analyse the evolution of phenotypes in the population by measuring the abundance of different average phenotypes in the population. Note that this is different from measuring the abundance of different genotypes in the population as two distinct genotypes may give rise to the same average phenotype. The time evolution of the phenotypes was tracked for both oxygen cases and is shown in fig. 7, where each line corresponds to a unique average phenotype and the most significant phenotypes have been highlighted. In the high oxygen we observe a steady decline of the initial phenotype and the emergence of several new phenotypes all with low abundances. This is in contrast with the dynamics in the low oxygen case where the initial phenotype decreases more rapidly and the population becomes dominated by a single phenotype.

Figure 7.

The time evolution of the average phenotypes in the population for the high and low oxygen case. The most abundant phenotypes have been highlighted and their response vectors are displayed.

4.3 Discussion

From the above results it is clear that the limited oxygen supply influences the dynamics of the system. We can see a difference on the morphological level of the tumour, where a low oxygen concentration gives rise to an irregular branched tumour morphology, in contrast to the high case which results in a tumour with a smooth boundary. This behaviour has been observed both in real tumours (Höckel et al., 1996) and in other models of tumour growth (Ferreira et al., 2002; Anderson, 2005; Anderson et al., 2006). In fact for a simplified version of this model (without the evolutionary component) it has been shown that branch width depends directly on the supply of oxygen, and that a lower oxygen concentration gives rise to thinner branches (Gerlee and Anderson, 2007b). The composition of cell types in the two cases is also different. In the high oxygen case the population consists of proliferating and quiescent cells, while in the low oxygen case the population is dominated by dead cells with only a few proliferating cells on the tips of the branches. This is due to the oxygen gradient that develops when the supply of oxygen is limited.

Apart from the morphological changes we also observe changes in the evolutionary dynamics of the system. The limited supply of oxygen exerts a selection pressure on the population, which drives the evolutionary dynamics. When the oxygen is unlimited the cells only have to compete for space, but in the low oxygen case the behaviour of the cells with respect to the oxygen concentration becomes important. The selection pressure on the population is therefore different in the two cases and this is reflected in all aspects of the evolutionary dynamics that we have analysed. In the low oxygen case the selection pressure can be said to be stronger, as in this case cells that get trapped within the tumour are likely to go into apoptosis and die due to the low oxygen concentration inside the tumour. This is reflected in the time evolution of the phylogenetic depth. In the low oxygen case we see a more rapid accumulation of mutations in the population, which suggests that evolution proceeds at a high rate due to the harsh growth conditions. It should also be noted that the total number of cell divisions is lower in the low oxygen case (approx. 20 000) compared to the high (approx. 35 000), which means that even though the number of possible mutations is considerably smaller in the low case we still observe a larger phylogenetic depth.

The Shannon index also reveals a difference in the evolutionary dynamics. What we observe is a higher genotypic diversity when the supply of oxygen is lower. This means that the population is not dominated by a few genotypes, as in the high oxygen case, but that we have a more even distribution in the genotype size distribution. This is a result of the turn-over of cells in the low oxygen case and of the tumour morphology that the limited supply of oxygen induces. In the low oxygen case the living cells reside on the tips of the fingered tumour. As there is no contact between these tips they are essentially isolated colonies of cells that evolve independently. This structure facilitates a higher diversity in the population and as a result we see a faster increase in the population diversity compared to the high oxygen case. These observations are also in agreement with experimental studies of diversity in bacterial colonies that grow in structured and unstructured environments (Korona et al., 1994).

If we now turn to fig. 7 we can also see a difference in the evolution of the average phenotypes in the tumour. In the high oxygen case we observe a steady decline of the initial phenotype (shown in black). As the tumour grows new phenotypes are constantly created due to mutations, but the weak selection pressure in this environment implies that no phenotype comes to dominate the population, and as a consequence we observe a large number of phenotypes with low abundances. The only selection that occurs here is due to the fact that cells with a stronger network response divide faster. This is why we observe a temporary increase in one phenotype which has increased its proliferative response (shown in red), but this effect is weak and does not lead to a selective advantage strong enough to make it dominant in the population. The situation in the low oxygen case on the other hand is quite different. Although the decrease in the initial phenotype (shown in black) starts slightly later, it occurs much faster and by t ≈ 60 it has gone extinct. We also observe the emergence of a single dominant phenotype (shown in red), which at the end of the simulation compromises approximately 70 % of the population. This phenotype, characterised by the response vector S = (1, 0, 0), has lost all growth inhibition and can be said to be the most aggressive phenotype, as it will try to proliferate in all possible growth conditions. The fact that we observe a single dominant phenotype in the low oxygen case might seem contradictory to the measurements of the genotypic diversity, which showed that the population is more diverse in the low oxygen case. The explanation to this is that although the population is more diverse on the genotype level the phenotypes expressed by these genotypes are less diverse, and in fact most cells in the population express the most aggressive (1,0,0)-phenotype. This implies that the selection occurring at the phenotype scale is not carried down to the genotype level. This is in part due to the fact that multiple genotypes can generate similar phenotypes, but also appears to be due to the morphological isolation of subclones of cells in the more fingered tumours.

5 Conclusion

The modelling framework presented in this paper is versatile as there are no restrictions to what the input (external stimuli) or output (phenotypic traits) represent. This means that it can be used to model any situation where a population of cells evolve due to a selection pressure from the environment. In the example discussed it was applied to human cancer cells, but it applies equally to bacteria, fungi and other unicellular organisms.

An advantage of this model is that the evolution is modelled in a open-ended fashion. The phenotypes that might occur in a simulation are not a priori defined in the model, but emerge as a consequence of mutations and the selective pressure. The number of possible phenotypes is essentially unlimited as they evolve from an initial network, which is changed by adding random numbers to the network parameters. This is of course not fully realistic as the number of possible genotypes for a real cell is limited, but still very large. A model that overestimates the number of possible genotypes is quite likely better than one that restricts itself to a few predefined ones, as long as the resulting phenotypes are realistic. The model also makes a distinction between the genotype and phenotype of the cells. This allows for a higher degree of genotypic diversity in the population, which might have important implications for the adaptability of the population especially during rapid changes in the environment.

Another interesting feature of the model is that connections that were not in the initial network may emerge in evolution. The existence of pathways that correspond to these connections could then be tested experimentally. The model can therefore not only be used to predict the outcome of cellular evolution, but could also suggest new hypotheses regarding regulatory pathways. The model can also be used to perform in silico experiments by manually removing or down-regulating input nodes, which would correspond to mutations that would knock-out or down-regulate the expression of receptors that correspond to the node in question. This knock-out genotype could then be inserted into a population of wild-type cells to see if the mutant has a selective advantage. A limitation of the model is that it does not capture the true dynamics of the regulatory mechanisms of the cell, but instead integrates all the separate pathways into one neural network. Although this limits the accuracy of the model, it makes it possible to model behaviours that are still not fully understood on the molecular level.

An example of how this framework can be used was presented in the context of a model of solid tumour growth. The results show that the limited oxygen supply observed in a vascular tumours has an impact on both the growth and evolutionary dynamics of the tumour. Our simulations show that a tumour grown in a limited supply of oxygen exhibits a faster divergence from the initial genotype and a larger genotypic diversity that counter-intuitively leads to a convergence of the selection of more aggressive phenotypes. This suggests that tumours that grow in a low oxygen concentration have the potential to be more aggressive, something that has been confirmed experimentally (Graeber et al., 1996; Kim et al., 1997; Koshikawa et al., 2006). In conclusion this highlights the importance of the tumour micro-environment and that external factors can play an important role in the evolutionary dynamics of tumour growth. This implementation highlights the potential of this framework to capture the complex dynamics of clonal evolution in an accurate way and that it can give important insights into solid tumour growth. This further emphasises that the modelling framework considered here is well-suited for systems where the environmental response of cells changes due to mutation and selection and where evolution plays an important role in the dynamics of the system.