A new method to evaluate the completeness of case ascertainment by a cancer registry

Abstract

Background

Epidemiologic research into cancer and subsequent decision making to reduce the cancer burden in the population are dependent on the quality of available data. The more reliable the data, the more confident we can be that the decisions made would have the desired effect in the population. The North American Association of Central Cancer Registries (NAACCR) certifies population-based cancer registries, ensuring uniformity of data quality. An important assessment of registry quality is provided by the index of completeness of cancer case ascertainment. NAACCR currently computes this index assuming that the ratio of cancer incidence rates to cancer mortality rates is constant across geographic areas within cancer site, gender, and race groups. NAACCR does not incorporate the variability of this index into the certification process.

Methods

We propose an improved method for calculating this index based on a statistical model developed at the National Cancer Institute to predict expected incidence using demographic and lifestyle data. We calculate the variance of our index using statistical approximation.

Results

We use the incidence model to predict the number of new incident cases in each registry area, based on all available registry data. Then we adjust the registry-specific expected numbers for reporting delay and data corrections. The proposed completeness index is the ratio of the observed number to the adjusted prediction for each registry. We calculate the variance of the new index and propose a simple method of incorporating this variability into the certification process.

Conclusions

Better modeling reduces the number of registries with unrealistically high completeness indices. We provide a fuller picture of registry performance by incorporating variability into the certification process.

Introduction and motivation

Cancer surveillance requires a reliable and comprehensive system for gathering information about newly diagnosed cancer patients. Epidemiologic research and subsequent decisions made to improve public health and reduce the cancer burden in the population are dependent on the quality of available data. The more reliable the data, the more confident we can be that the decisions made would have the desired effect in the population. The data from population-based cancer registries are a key component in any such research. Thus, it is very important to ensure that these data meets the highest standards of quality and reliability so that researchers may use these data with confidence and have faith in their analyses.

There is a network of population-based cancer registries across North America [1] which collect information about newly diagnosed cancer patients. The North American Association of Central Cancer Registries (NAACCR) certifies the data collected by these registries and develops uniform data standards for cancer registration [2]. This is particularly important as the different registries across USA and Canada are funded through different mechanisms and by different agencies, which leads to different collection methods and processing systems for data [3–5]. NAACCR’s certification process ensures that the data meet essential standards of quality and reliability.

NAACCR assesses the quality of the data collected and certifies central cancer registries using a variety of criteria. The index of completeness of incident case ascertainment by a registry is one vital criterion. A cancer registry may not be able to collect accurate information on all the incident cancer cases in its area within the time frame set for data submission. Some of these cases may be missed initially but collected later, while some may never be collected at all. The index of completeness of case ascertainment quantifies the percentage of actual incident cancer cases that are reported by a registry within the data submission time frame. The aim is to provide a ranking of registries with respect to their ability to collect data timely and accurately. Registries may be certified by NAACCR as meeting the gold or silver standard, or as being uncertified. In terms of completeness, gold certification requires 94% completeness or higher, while silver requires between 89% and 94% completeness. Registries having less than 89% completeness are uncertified.

The actual number of incident cancer cases in a registry is an unobserved quantity which must be estimated from available data. The current NAACCR estimation methodology depends on the assumption that the ratio of incidence to mortality rates is constant across geographic areas for a given cancer site, race, and gender group.

In this article we propose a new method by which the assessment of completeness of case ascertainment can be made more accurate and the certification process made more reliable. In our method, we relax the overly simplistic assumption of constancy of the incidence-to-mortality rate ratio. Instead we predict the true incidence in a registry by a statistical model, incorporating information on geographic, socio-demographic, health, and lifestyle factors. We compare this new method with the current NAACCR method. We also provide an estimate of the variance of the proposed index and utilize it to suggest a fairer decision-making process for certification. NAACCR does not calculate variance estimates for its current index.

In the next section, we outline the methodology currently in use at NAACCR to assess the completeness of case ascertainment and discuss its advantages and disadvantages. In subsequent sections we outline our new methodology for assessment and certification and discuss its impact.

A discussion of the current methodology used by NAACCR to compute the index of completeness of case ascertainment

The current NAACCR methodology to estimate the index of completeness of case ascertainment depends on the assumption that the ratio of incidence to mortality rates is approximately constant across geographic areas for a given cancer site, race, and gender group [6, 7]. For a given registry, for any one cancer site, gender, and race we can then calculate

where incidence and mortality are age-adjusted rates for the same year and SEER is the Surveillance, Epidemiology and End Results program of the National Cancer Institute (NCI). The expected registry incidence is then compared to the observed registry incidence to obtain a cancer site, gender, and race-specific completeness index for the registry. These completeness indices are then weighted by race and gender, combined, and adjusted for duplicate records to obtain an overall measure of the completeness of case ascertainment [8, 9]. NAACCR currently uses race groups White (W) and Black (B) and 19 cancer sites to calculate the completeness index. Details of NAACCR’s methodology can be found in Appendix 1.

Thus, the current NAACCR methodology essentially predicts the expected incidence of cancer in a registry based only on mortality data. However, a variety of other data are available and known to influence cancer incidence rates, such as the proportion of the population that adheres to recommended cancer screening schedules. NAACCR makes no attempt to incorporate these data to obtain better estimates of incidence.

NAACCR does not publish any estimates of the variance of its estimated completeness index by registry, although it is known anecdotally that some registries are more reliable than others. No use is made of the variability of the completeness index while certifying a registry. Due to the natural variability of cancer rates and small numbers of cases in a small population, a small registry may have widely variable completeness indices from one year to another. If the certification process does not account for this variability, their data may be differently certified from year to year, giving a possibly false picture of the reliability and usability of their data, even though the registry is not statistically significantly better or worse. While certification is not solely based on the index of completeness, it remains a very important measure of registry quality, and it is unsatisfactory that there is no attempt to quantify its reliability for each registry.

There are known to be delays in cancer incidence data collection that vary by cancer site. Ideally, a registry would record and report every primary cancer in its area in a timely and accurate manner. The SEER registries, for example, are given 19 months to report all cases for a given year. However, there is sometimes a delay in reporting, and new cases will be discovered after the stipulated submission date. Cancers which tend to be detected and treated in outpatient settings such as melanoma are subject to significant delays in reporting because of the difficulty of collecting data in these settings. Occasionally, reported data need to be corrected as new information is obtained. Obviously, reporting delays and data corrections affect the reported incidence rates. NAACCR has made no attempt to adjust the expected incidence figures used in its method for reporting delays or corrections. Because of this omission, the NAACCR method does not have the power to distinguish between registries that take greater and lesser pains with timeliness and the correctness of initially reported data.

The current NAACCR method to calculate completeness makes use of data only on the race groups White and Black. There are clearly drawbacks to excluding other race groups in the calculation, particularly for registries that have diverse populations.

Methods

New methodology for predicting cancer incidence and calculating completeness

Recently, a new methodology has been developed at NCI [10, 11], which predicts expected incidence based on a statistical model including geographic, socio-demographic, health-related, and lifestyle-related data as explanatory variables. It includes mortality rates as one of many explanatory variables used and thus can be viewed as an extension of the NAACCR model. The new model also includes spatial random effects to account for the similarity of incidence patterns in neighboring counties, enabling the sharing of information across regions to obtain better predictions in sparse data areas. This model has been shown to provide improved estimates of the number of new cancer cases than the NAACCR model [12]. Further details of the model are provided in Appendix 2.

The incidence rates predicted by this model are used as the expected incidence rates in calculating completeness. These are used to calculate the race, gender, and cancer-site-specific completeness figures, which are weighted for race and gender and summed over cancer sites (as in the NAACCR method) to produce a completeness index for a registry.

Adjustment for reporting delays and data corrections

NCI has investigated the impact of imperfect reporting on incidence rates [13, 14] and developed adjustment factors to be used to obtain reporting adjusted incidence rates. These delay factors can be obtained from NCI’s Cancer Query System (available online at http://srab.cancer.gov/delay/canques.html)

We apply these adjustment factors to predictions from the NCI incidence model to obtain delay adjusted expected incidence rates. These adjusted expected incidence rates were used to calculate the completeness index as outlined above. By doing this, we have the power to identify registries which make greater efforts to report correct data in a timely fashion. Registries that are less timely and accurate will have observed rates that are smaller percentages of the adjusted expected incidence rates and thus have lower completeness indices.

To use the delay factors for all registries, we first adjusted for registry-specific differences. The registries in the US are funded by two sources—some are funded wholly or partially by the SEER program of the NCI, and some are funded exclusively by the National Program of Cancer Registries (NPCR) of the Centers for Disease Control (CDC). This leads to different data collection procedures and protocols for the two kinds of registries. Data are currently not available from the NPCR registries to calculate NPCR-specific delay factors. Thus, as the delay factors are derived from SEER data only, they may not apply directly to NPCR data. However, once an adjustment is made for funding source, the use of the SEER delay factors is justifiable as all registries can be assumed equivalent after adjustment. This adjustment was accomplished by adding a factor for funding source to the prediction model. As more data become available from the NPCR registries to calculate their delay factors directly, this adjustment will become unnecessary.

Calculating variance

We calculate the variance of the new index. The variability in the new index can be partitioned into three parts: a component due to the variability of the observed incidence rates, a component due to the variability of the model-predicted incidence rates and a component accounting for the variability due to the covariance between the observed and model predicted rates. Of these three, the largest is that due to the observed rates as this is the variability of a single realization of a random quantity. The variability of the model predicted rates, which are based on larger amounts of data and are essentially the mean of a number of realizations of a random quantity, is relatively small. Both these terms may be calculated approximately by the delta method under the assumption of asymptotic normality of the log rates [15]. The third component is difficult to compute, but its contribution to the variance is likely to be small unless the registry is extremely large and contributes a large proportion of the data used in prediction. Moreover, the structure of the completeness index, where the observed rates appear in the numerator and the predicted rates in the denominator, assures that this covariance term is negative. Thus omitting this term makes for a more conservative estimate of the variance. Technical details of the variance calculation can be found in Appendix 3.

Decision making for certification

NAACCR uses its calculated completeness index and some other criteria to certify the quality of data obtained by each registry each year. When using the new completeness index, registries would have to meet these criteria for certification. Note that in NAACCR’s method of assigning certification status no use is made of the variability of the completeness index. By using only the point estimates, i.e., ignoring variance, in a small registry there can be the appearance of improvement or deterioration in completeness when in fact the registry is not statistically significantly better or worse. This is due to the natural variability of cancer rates due to small numbers of cases in a small population. Conversely, larger population registries tend to have very stable completeness indices because of large case counts. Thus it may appear that they are not making much progress in moving to a higher certification category. If funding decisions are made on the basis of degree of improvement, for example, larger registries may lose out unfairly.

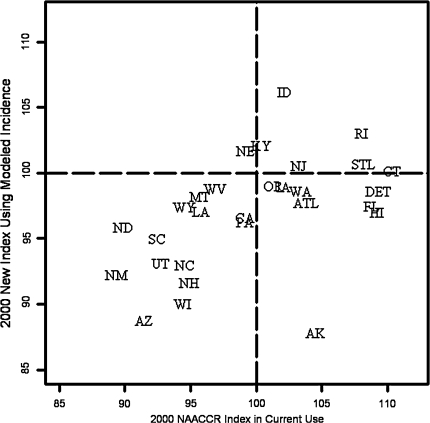
We developed a simple method to incorporate the uncertainty in the completeness index into the certification process. Using the estimate of variance and under the assumption of asymptotic normality of the new completeness index, confidence intervals may be calculated for the completeness index for each registry. This leads to confusion as to the certification status of the registry as confidence intervals may overlap more than one certification interval (Fig. 2). The question then arises as to how to certify a registry in the presence of information on the variability of its completeness index. We propose presenting the information on variability by estimating the probabilities of the registry falling into each certification interval. For each registry we obtain three estimated probabilities—the chance of being certified as gold, of being certified as silver, and of being uncertified. Our certification rule is to assign certification status to the registry that has the highest estimated probability. Presenting all the three estimated probabilities gives an idea of the variability, and registries within each certification status may be ranked by their probabilities of certification.

Fig. 2.

Ninety-five percent confidence intervals about the new completeness index for each registry

Data

Data on the observed incidence rates were obtained from the 1995–2000 CINA Deluxe data set. CINA Deluxe is a research data file derived from central cancer registries that meet NAACCR high data quality criteria (at a minimum of the silver standard for certification) for each diagnosis year at the time of data submission. Permission to use this data set was obtained from NAACCR. We only used data from year 2000. Special permission was obtained from individual registries to use county-level data in the modeling—not all registries gave this permission and thus had to be dropped from our analyses, leaving 29 registries for analysis (listed in Table 2).

Table 2.

Results of certifying by new algorithm

Registry	P(Gold)	P(Silver)	P(Uncertified)	New result	Current result
AKa	6.94	32.48	60.58	Uncertified	Gold
AZa	0.00	43.58	56.42	Uncertified	Silver
CA	100.00	0.00	0.00	Gold	Gold
CT	100.00	0.00	0.00	Gold	Gold
FL	100.00	0.00	0.00	Gold	Gold
ATL(Atlanta)	98.59	1.41	0.00	Gold	Gold
HI	98.29	1.71	0.00	Gold	Gold
ID	99.99	0.01	0.00	Gold	Gold
IA	99.95	0.05	0.00	Gold	Gold
KY	100.00	0.00	0.00	Gold	Gold
LA	99.76	0.24	0.00	Gold	Gold
DET(Detroit)	100.00	0.00	0.00	Gold	Gold
MT	78.95	16.95	4.10	Gold	Gold
NE	99.99	0.01	0.00	Gold	Gold
NHa	18.33	67.25	14.42	Silver	Gold
NJ	100.00	0.00	0.00	Gold	Gold
NM	20.68	74.39	4.93	Silver	Silver
NCa	12.51	87.49	0.00	Silver	Gold
NDa	66.64	27.11	6.25	Gold	Silver
OR	99.93	0.07	0.00	Gold	Gold
PA	99.99	0.01	0.00	Gold	Gold
RI	99.99	0.01	0.00	Gold	Gold
SCa	82.32	17.68	0.00	Gold	Silver
UT	35.89	61.83	2.28	Silver	Silver
WA	100.00	0.00	0.00	Gold	Gold
STL(Seattle)	100.00	0.00	0.00	Gold	Gold
WV	99.88	0.12	0.00	Gold	Gold
WIa	0.02	85.04	14.94	Silver	Gold
WY	80.17	17.91	1.92	Gold	Gold

^aDenotes those registries which are certified differently using the current index and the current algorithm. The results for AK and AZ are discussed further in the text and may not be reliable

The data on the predictors in the incidence model were obtained from several sources. Socio-demographic variables were constructed from census data [16] for urban/rural status, per capita income, poverty, education, crowded housing, female-headed households, home value, unemployment, and percent population of minority race/ethnicity (Asian/Pacific Islander, American Indian/Alaskan Native, Black, Hispanic origin). The density of the number of physicians and screening mammogram facilities were included as measures of availability of relevant medical services [16]. Lifestyle factors (ever smoked, obesity, no health insurance, cancer screening) were obtained from Behavioral Risk Factors Surveillance System (BRFSS), a nationwide telephone health survey, conducted by the states and coordinated by the CDC that collects health risk data. Mortality data were obtained from the National Center for Health Statistics (NCHS). All variables were selected from those available at regular intervals for every US county.

Results

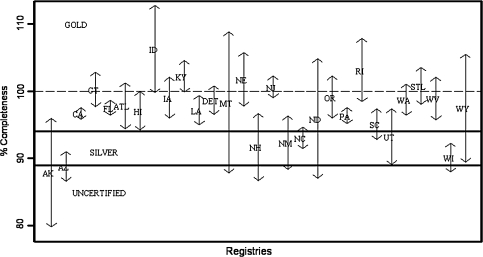
Both the new index and the index NAACCR uses currently were calculated for 29 registries on the CINA Deluxe data set that permitted the use of 2,000 data. Figure 1 shows the results obtained. For both indices, there are several registries that exceed 100% completeness. This is undesirable as it generally shows that the expected incidence rates were ill predicted for that registry. While it is impossible for any model to always predict expected rates higher than observed rates, as no statistical model can be 100% accurate, a good model should do this infrequently. The new index is an improvement on the NAACCR index, exceeding 100% completeness for 7 of 29 registries as compared to 14 of 29 for the NAACCR method. Thus the new method leads to fewer unrealistic indices of above 100%.

Fig. 1.

Comparison of current and proposed completeness indices with current index adjusted for registry funding source and for reporting delay and data corrections

We compared the two indices with respect to certification (Table 1). Normally, certification is based on several criteria in addition to completeness. However, we do not have information on all these criteria. Hence, in this exercise, we have compared “certification” status under the hypothesis that certification is based solely on completeness. This gives us some idea of how the new index may affect certification if used in place of the current index. Since we have access only to certified data (silver standard or higher), it is hard to draw any concrete conclusions. There is a slight indication that the new index may be stricter than the current index as it downgrades some registries to uncertified, but it is difficult to be sure as the two registries that move down to uncertified status are both small-population registries with a large proportion of race groups other than black and white. This is discussed in greater detail in the next section.

Table 1.

Comparing certification by current and new indices

	Certification by NAACCR index
		Gold	Silver	None	Total
Certification by new index	Gold	20	2	?	22
	Silver	3	2	?	5
	None	1	1	?	2
	Total	24	5	?	29

? denotes unknown status due to lack of data

Figure 2 shows the 95% confidence intervals about the index for each registry. Some intervals are very wide and cover several certification categories as expected, making assigning a certification status difficult. We calculated certification using the new decision-making algorithm outlined in the methods section (Table 2).

Discussion

The new methodology improves on the current methodology in several ways. To find the completeness of case ascertainment by a registry, we need to know the unobserved true total number of cases for the registry. This must be estimated from a model under a set of assumptions. The current NAACCR method uses one such model, where it is assumed that the ratio of incidence to mortality is a constant across registries for each cancer site. Thus, incidence is being predicted based on the single covariate mortality. Furthermore, the model is effectively a constrained one, due to the assumption of the constancy of the ratio of incidence to mortality. The new methodology improves on this model by predicting expected incidence based on many covariates, including mortality. The prediction is unconstrained in the sense that no assumptions are made about the constancy of model coefficients which are estimated from available data. The model may be extended and improved by adding covariates as needed. For example, we adjusted for registry-specific funding source differences by adding as covariate the funding source for each registry, thus improving the final completeness estimates.

The assumption that the ratio of incidence to mortality is constant across all registries is extremely restrictive as there is no allowance for spatial variation across the registries. By adding appropriate error terms to the new method model we can adjust for any spatial variability that remains unaccounted for after incorporating all the available covariates. Such error terms were used at the initial stages of modeling but were found to be insignificant and were dropped from the model. Thus we may be fairly sure that the covariates in our model account for the variability over different regions.

We also calculated the variance of the new index. The variance of the index should be incorporated in the certification process to be fair to all registries. When using only the point estimates of completeness, the certification status of a registry may be very misleading in case of small registries where the natural variability of cancer rates due to small numbers of cases in a small population may lead to falsely inflated certification status. Conversely, larger population registries, which tend to have very stable completeness indices because of large case counts, may be penalized for an apparent lack of progress. In either case, researchers cannot be fully confident that the certification process has captured all the elements of the quality of the data and cannot be entirely sure of their analyses based on that data. Because standard confidence intervals are somewhat confusing to interpret in this context, we have proposed a simple way of incorporating variability in the certification process.

The new method also accounts for the timeliness and accuracy of incident case reporting by a registry when calculating completeness. Registries that take care to report data timely and accurately should be credited for their efforts. Because the underlying incidence prediction model is flexible and allows for adjustment, we were able to couple it with the delay and correction factors derived from SEER registry data to approximately identify timely registries. This results in an index that is more realistic and philosophically more satisfying. It would be better if we were able to derive delay and correction factors based on NPCR data as well, but currently not enough data are available to do this as the records for NPCR registries are not long enough. We do expect to have such data in the future and should be able to improve the corrections done to the expected incidence to account for delay.

We note here that NAACCR only looks at the accuracy and timeliness of data at a single time point for certification. Ideally, registries should find all cases in their catchment area within the specified time. This goal is however somewhat impractical in cases of cancers which are mostly treated in the outpatient setting. Thus, registries should be encouraged to collect data on cases that they missed within the initial deadline for data submission. Registries which put effort into this, will, over several years, have more accurate and complete data for researchers, even if some cases were missed initially. Currently NAACCR does not have any mechanism in place to identify and reward such registries. In the interests of high-quality data, some sort of re-certification procedure seems to be called for.

The current and the new indices are based only on White and Black data. It may be more desirable to calculate the index based on all races combined for small population registries with a large proportion of their population in races other than Black and White. For such small registries, the case counts are likely to be small, particularly for rarer cancers. In this situation, if a proportion of the cases are further eliminated because they occur in race groups other than Black and White, the case counts may become very small, making the overall index unnecessarily much more variable and uncertain and may lead to unreliable certification results. For example, in Table 2, AK drops to uncertified from gold, which is probably a reflection of the fact that it has a small population with a large proportion of race groups that are non-Black and non-White rather than the quality of the case collecting efforts of the registry. The same may also be true of AZ.

A limitation of the new index is that it requires more computation to estimate the expected incidence. However, the extra work to compute the expected incidences can be performed once centrally and need not be a burden on individual registries. Thus individual registries would be able to calculate their completeness index exactly as they do now by obtaining their pre-calculated expected values from a central data set.

In conclusion, statistical modeling predicts expected incidence using a more objective model, based on more information than the current incidence to mortality ratio based method. The new method is more flexible than the current method and can be easily modified to include further predictors or adjust for new information if needed. In particular, adjusting for differences between SEER-NPCR and NPCR-only funded registries and for reporting delay and data corrections helps to reduce unrealistic over 100% completeness index values.

We have calculated the variance of our index and demonstrated a method of integrating the uncertainty of the index in the certification process. We feel this is important to get a fuller picture of registry quality.

The new index may certify a registry differently from the current method. It is hard to draw firmer conclusions working with only certified data. In future, if we can obtain permission to use such data, we would be interested in looking at the full impact of the method change on certification decisions for registries both certified and uncertified.

Appendix 1: An outline of the methodology currently used by NAACCR to compute the index of completeness-of-case ascertainment

In this appendix we describe the method currently adopted by NAACCR to quantify the completeness-of-case ascertainment. The decisions inherent in this method, such as choice of data sets, assumptions made, race groups used, assumed values of constants, and so on, were decided solely by NAACCR. For more details on this method, see [8].

Basic principles

The current NAACCR methodology to estimate the index of completeness of case ascertainment depends on the assumption that the ratio of incidence to mortality rates is approximately constant across geographic areas for a given cancer site, race, and gender group [6, 7]. The stability of this ratio is exploited to estimate the expected incidence in a geographic area (e.g., a registry). The basic relationship for a registry, for any one cancer site, gender, and race can be written as

where incidence and mortality are age-adjusted rates for the same year and SEER is the Surveillance, Epidemiology and End Results program of the National Cancer Institute (NCI). To ensure stability, registry-level mortality is adjusted as we shall detail later. The expected registry incidence is then compared to the observed registry incidence to obtain a site, gender, and race-specific completeness index for the registry. These completeness indices are then weighted, combined, and adjusted for duplicate records to obtain an overall measure of the completeness of case ascertainment [8, 9]. NAACCR currently uses race groups White (W) and Black (B), and 19 cancer sites to calculate the completeness index.

Registry-level mortality is adjusted for stability before using calculating the registry-level expected incidence. To perform the adjustments, each registry collects the following data in its catchment region:

1. The age-adjusted incidence rate for the reporting year for each site, gender, and race. This is the Observed Incidence Rate (OIR).

2. The age-adjusted two-year annual average mortality rate for each site, gender, and race. This is the Current Mortality Rate (CMR). If the registry population is below 500,000, the three year average mortality rate is used.

3. The age-adjusted five-year annual average mortality rate for each site, gender, and race. This is the Reference Mortality Rate (RMR).

4. The observed number of incident cases (OI) for the reporting year.

5. The percentage of duplicate data records (DUP).

Adjusting CMR for case fatality

The CMR is first adjusted for the local case-fatality ratio. The case-fatality ratio for a given cancer site is the ratio of the number of people who die of the cancer to the number of incident cases of the cancer. Differences between the registry and national-level case-fatality ratios may artificially influence the estimated expected incidence, unless adjusted for. For example, if more people die in a particular area without a rise in the number of incident cases as compared to the nation, i.e., the area has a higher case-fatality ratio than the nation, the estimated expected incidence obtained by the basic relationship outlined above would be falsely inflated. Thus, in this case, the CMR must be deflated to ensure the local incidence-to-mortality rate ratio can be considered approximately equal to the national incidence to mortality rate ratio.

To do this, the age-adjusted five-year average U.S Mortality Rate (USMR) for the given cancer site, race, and gender is compared to the RMR. The difference between the RMR and USMR is attributable to several causes, including deterministic factors and random variation. NAACCR assumes that a proportion α of the standardized difference between the two mortality rates is due to differential case fatality, and the CMR is adjusted accordingly to get the Adjusted Current Mortality Rate (ACMR) in the given site, gender, and race group. Thus, if

the Adjusted Current Mortality Rate (ACMR) is

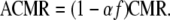If α is 0, i.e., we attribute none of the differences between the RMR and USMR to differential case fatality, ACMR equals CMR. If α is 1, i.e., we attribute the entire difference between the RMR and USMR to differential case fatality,

The adjustment to the mortality rate is by cancer site, allowing for different case fatalities for different cancers.

It is also possible to choose different α values for different cancer sites according to whether the case-fatality ratio is higher or lower than the national average. Currently α is fixed by NAACCR at 0.2 for all sites, genders, races, and registries, i.e., 20% of the difference between RMR and USMR is attributed to differential case fatality.

The Expected Registry-Specific Age-Adjusted Incidence Rate (EIR) for the given cancer site, gender, and race is then obtained (by using the basic relationship) as

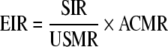where SIR = age-adjusted five-year average SEER incidence rate.

Obtaining the registry specific index of completeness of case ascertainment

Once EIRs have been calculated for each cancer site, sex, and race, interim percentage completeness (IC_gr, where g is a gender—male (M) or female (F)—and r a race group—white (W) or black (B)) is calculated for each race-gender combination as

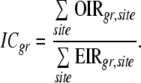Next, the IC_grs are weighted and combined over gender to give race-specific indices. The combination weights are based on the population proportions of the two genders in each race group. Currently NAACCR uses data on races White and Black only to calculate the index and ignores data collected on other race groups by a registry. The consequences of ignoring data on races other than Black and White are examined in the discussion section. A similar adjustment is then done to combine the race-specific completeness indices C_W and C_B, using population weights, to obtain the Race Proportional Completeness Index (RPC) for the registry.

To obtain the final completeness index (C) for registry, duplicate records are taken into account. We obtain the adjusted observed and expected number of incident cases (AOI and AEI, respectively) for a registry as

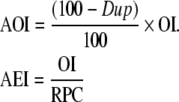Then

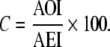In the absence of duplicate records, C = RPC.

This process is repeated to obtain registry-specific completeness indices for all registries in North America.

Appendix 2 : The spatial prediction model for cancer incidence

The number of new cancer cases in county i (i = 1,...,I), age group j (j = 1,...,J), registry k (k = 1,...,17), region r (r = 1,2,3,4 defining Census Regions Northeast (NE), Midwest (MW), South (S), and West (W), respectively), denoted d_ij[kr], is assumed to be Poisson distributed, with mean n_ij[kr]λ_ij[kr] and variance ϕn_ij[kr]λ_ij[kr], where n_ij[kr] is the corresponding population at risk and ϕ measures overdispersion beyond the standard Poisson variance. (Subscripts k and r are bracketed because they are superfluous, i.e., they are uniquely determined by county i.) We further assume a log-linear rate structure, i.e.,

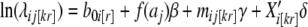1

where a_j is the centered midpoint of age group j, m_ij[kr] is the logarithm of the mortality rate for county i, age group j, X_i[kr] is a p-dimensional vector of covariates for county i and β, γ and δ are parameters to be estimated. A cubic function of centered ages (f(a_j)) was necessary to accommodate downturns in some cancer rates at the oldest ages. The county intercepts, b_0i[r], are considered to be normally distributed random effects of available counties within each region with mean vector β₀ (r × 1) and variance matrix ∑, where ∑ incorporates a spatial covariance structure as necessary.

The following variables were included as predictors in the model:

• Age: age (0–4, 5–14, 15–24,…,75–84, 85+), age², age³ (centered);

• Year: year, year², year³ (centered)—included for full time span, although only the results for year 2000 are used for the completeness analysis;

• Race: Black, Other (White = referent);

• Log mortality rate;

• Ethnicity/origin: % Hispanic, Black, Asian/Pacific Islander, American Indian/Alaskan Native;

• Medical facilities: number of physicians and mammogram screening facilities per 1,000 population;

• Household characteristics: % female head of household, % households with an average of more than 1 person per room;

• Socioeconomic status:

• Income: median per capita income, % persons living below the federal poverty level;

• Education: % persons ages 25 and over with less than nine years of education and % with 4+ years of college;

• Other: % unemployment;

• Urban/rural indicators: urban/rural continuum code [17] grouped into 5 categories, population density;

• Geography: Census Region (Northeast, Midwest, South, West), latitude, longitude;

• Lifestyle: % adults who ever smoked at least 100 cigarettes, % adults at risk of obesity (body mass index > 120% of sample median), % women ages 50–64 who had had mammogram during the last two years, % adults with no health insurance (note that because of collinearity, mammography use and obesity could not be included in the same model);

• Cancer registry system: NCI/SEER or CDC/NPCR.

The model parameters were estimated using the SAS GLIMMIX macro for PROC MIXED. All two-factor interactions were included in an initial model; nonsignificant interactions and main effects were removed by a backwards stepwise regression process prior to application of the spatial model.

The model was validated in a separate study using a more restricted input dataset consisting of 1999–2001 data from the 17 SEER registries (see http://seer.cancer.gov/ for definitions). Results from the spatial model described above (excluding the time covariate) and corresponding results derived from the same method used by NAACCR for the four major cancer sites were compared to the numbers of cases reported by each registry in the U.S. Cancer Statistics Report for each of the three years 1999–2001 [18–20]. The measure of closeness of each estimate to the reported figure was the sum of squared deviations at the state level (i.e., (estimated #−reported #)², summed over all available states). Results (Table 3) showed either that the methods gave similar results (lung and colon cancer) or that the new spatial model was much better (lower sum) than the previous method (breast and prostate cancer) [see 11, 12].

Table 3.

Comparison of the model used by NAACCR to the new spatial model

Gender	Cancer site	Sum of squared deviations for previous NAACCR method	Sum of squared deviations for new spatial model
Female	Breast	36,774,000	1,817,554
	Lung and bronchus	5,371,894	8,333,344
	Colon and rectum	3,306,224	3,573,888
Male	Prostate	49,125,857	21,639,454
	Lung and bronchus	12,702,367	11,499,802
	Colon and rectum	3,306,695	3,443,079

Appendix 3: Calculating the variance of the new completeness index

The delta method [see 15] may be used to calculate the variance of the new index under the assumption that the logarithm of the age-specific rates for each race, gender, and cancer site is normally distributed. This assumption we have already made in order to perform the incidence modeling and thus, no new assumption is specifically needed for calculating the variance. Thus assume

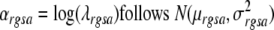1

where r denotes race, g denotes gender, s denotes cancer site and a denotes age group and λ denotes incidence rate. The age adjusted rate can then be written as

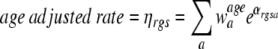where 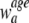is the standard population weight associated with the age group a.

Then, the completeness index C_ρ for a registry ρ can be written as

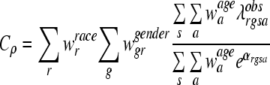where λ^obs is the observed age specific incidence rate in the appropriate age, race, gender, and cancer site group, 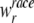is the population-based weight for the rth race category; and 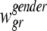is the population-based weight for the gender g within race group r. Note that, parallel to (1) we can assume

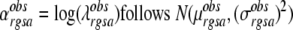2

We note here that C_ρ is a function of observed (numerator term) and expected (denominator term) incidence rates so if O denotes the set of observed incidence rates and E denotes the set of expected incidence rates we can write the completeness index as

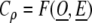In that case, by the delta method, the variance of C_ρ can be written symbolically as

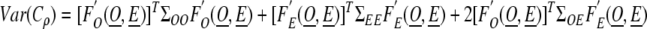where 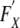denotes the derivative of F with respect to the set of variables X and Σ_XY is the covariance matrix of the set of variables X and Y. The third term in the above equation involves the covariances between the model predicted rates and the observed rates. This is likely to be small unless the registry ρ is very large and contributes a large amount of the observed data in the model, dominating other registries. Thus, for a small registry, the covariances would be small and the third term could be neglected. Note that due to the form of the completeness index with the observed rates in the numerator and the expected rates in the denominator, and the fact that observed and predicted rates are positively correlated implies the third term is negative. Thus, omitting the third term even in the case of a large registry would make the estimate of the variance of the completeness index to be larger (more conservative). Using assumptions (1) and (2) and repeated applications of the delta method, we can then calculate a conservative estimate of the variance of the completeness index.