ACTIN BUNDLING: INITIATION MECHANISMS AND KINETICS

Abstract

Bundling of rapidly polymerizing actin filaments underlies dynamics of filopodial protrusions that play an important role in cell migration and cell-cell interaction. Recently, formation of actin bundles has been reconstituted in vitro and two scenarios of bundle initiation, involving binding of two filament tips and, alternatively, linking of the tip of one filament to the side of the other, -have been discussed. A first theoretical analysis is presented indicating that the two mechanisms can be distinguished experimentally. While both of them result counter-intuitively in comparable numbers of bundles, these numbers scale differently with the average bundle length. We propose an experiment for determining which of the two mechanisms is involved in the in vitro bundle formation.

Filamentous actin constitutes an important component of cell cytoskeleton [1]. Structure and patterns of actin meshwork change dynamically as filaments polymerize, branch, and bundle, which enables living cells to vary their shape and migrate. One such dynamic pattern, used by cells to explore their environment and build adhesive outposts, are filopodia - long, finger-like protrusions that result from formation and growth of bundles of actin filaments [2–4]. The filaments are thought to be held in a bundle by linker proteins such as fascin [5]. Recently, actin bundles have been reconstituted in vitro in the presence, or after addition, of fascin [6, 7]. In these experiments, the bundles emerge from a dense quasi-two-dimensional meshwork of actively polymerizing filaments and form star-like structures (Fig 1 a). Importantly, the conditions of the in vitro polymerization and bundling are strongly non-equilibrium. This is due to the excess of fascin and Arp2/3, the protein promoting nucleation of new filaments through branching [8]. In addition, the assays do not include any capping proteins or depolymerization factors.

FIG. 1.

(a) Star-like structure of actin bundles reconstituted in vitro (adapted from [7]). (b) Snapshot of the aster after depletion of monomers in a typical Monte Carlo realization based on Eq (1). Parameters mimic experimental conditions in [7]: Y ₀= 4.5 · 10⁶, (τ_p)⁻¹ = 75 s⁻¹, (τ_n)⁻¹ = 5 · 10⁻⁶ s⁻¹, α_cδ/h = 10⁻² (the aster thickness h is on the order of several δ). Heavy lines are actin bundles, light lines depict free filaments. (c) Diagram of processes affecting dynamics of filaments and bundles: A-nucleation of a linear filament, B-initiation of a bundle (shown for the ”tip-side” mechanism), C-incorporation of an unbundled filament into an existing bundle.

It is generally accepted that the bundle arises from two filaments zipped up by a linker protein [6, 7] but initiation mechanisms are a subject of active research. Two scenarios have been recently proposed [6, 9, 10]. One involves binding of two filament tips into a tip complex, which triggers the zipping if the filaments are at a sufficiently small angle [6, 11–14]. In an alternate scenario, binding of the tip of one filament to the side of the other is thought to be sufficient for the initiation of linking [10], again on a condition of a small angle between the filaments. In this Letter, we analyze how the two mechanisms would affect dynamics of bundling in order to determine if they are experimentally distinguishable. Our results indicate that while, surprisingly, both of them may result in comparable numbers of bundles, these numbers scale differently with the average linear size of the aster. Therefore, the mechanisms can be distinguished by measuring the size dependence of the final number of bundles.

Development of the system of actin filaments and bundles in non-equilibrium assays is analyzed with the aid of a model, which accounts for four essential processes: Arp2/3-mediated nucleation of filaments, polymerization of filaments (both individual and in the bundle), initiation of a bundle from two unbundled filaments, and thickening of a bundle as it absorbs individual filaments [15] (Fig 1 c). Effects of slower processes, such as depolymerization in the absence of depolymerization factors [7, 16] and thermal fluctuations of the filaments [17], can be ignored because a pool of actin monomers in the in vitro assays is exhausted quickly due to the facilitated nucleation and rapid polymerization of filaments [7]. Aside from a small number of seed filaments, all new linear filaments nucleate from Arp2/3 complexes at the sides of the existing filaments (Fig 1 c-A) (new filaments do not nucleate from the bundles, possibly because of a dense decoration of those by the linker [5, 6]). Because each nucleated filament has one point of origin and one growing tip, the whole branched system, despite its complexity, can be unambiguously described as a set of linear filaments. To initiate a bundle (Fig 1 c-B) or to link an unbundled linear filament to an existing bundle (Fig 1c-C), the linker must bend the filaments. This is modeled as an ”all-or-none” transition [11, 13, 14] depending on whether the angle between the filaments (or between a filament and a bundle) is below or above a critical value, α_c, determined by cross-linking strength and elastic properties of the filaments and estimated to be in the range 0.005–0.5 [13, 14].

Because of the abundance of the linker protein [7, 18], the initiation of a bundle and the absorption of filaments by existing bundles are approximated as collision-controlled, so that the problem involves only two time scales determined by the initial frequency of polymerization events and the frequency of nucleation. The initial polymerization frequency is ${\tau }_p^{-1}=k_p{C}_0$ where k_p is the rate constant for binding of a monomer to a filament plus end and C₀ is the initial monomer concentration. For typical values of C₀(~ 7.5 μM) and k_p(~ 10 μM⁻¹s⁻²), ${\tau }_p^{-1}\approx 75{\text{s}}^{-1}$ [7, 19]. The Arp2/3-mediated nucleation involves two main steps: formation of a complex of Arp2/3 with one or two actin monomers and its subsequent attachment to an existing filament [20]. Consistently with the fact that the overall polymerization rate does not depend significantly on the mass of the seed filaments [21], we treat the complex formation as a time-limiting step, though the results are not affected by this assumption. The nucleation frequency depends on the Arp2/3 concentration. For saturating concentrations ~ 0.1 μM used in the experiments, τ_n/τ_p is estimated to be on the order of 10⁶–10⁷ [19, 22].

Formally, a state S of the system is defined by the number of monomers Y [23], the set of unbundled linear filaments, {f_i: i = 1, …, X}, and the set of bundles, {b_j: j= 1, …, B}: S ≡ (Y, {f}, {b}) (X and B are the numbers of free filaments and bundles, respectively) [25]. The linear filament is modeled as a two-dimensional vector with a fixed origin. The bundle b_j is defined by a backbone vector with a fixed origin and by a set of filaments f_kj, k = 1, …, N b_j all of which have the direction of the backbone and are separated from it by the distance on the order of the monomer size δ; the backbone length is defined as the maximum length of filaments in the bundle. The direction of a newly formed bundle is defined as a normalized sum of unit vectors of the filaments initiating the bundle to reflect their bending caused by the linker. The initial state of the system is S₀ = (Y₀, {f}₀, ∅), where {f}₀ is a set of X₀ short, randomly oriented seed filaments of length L₀ with the ”minus-ends” placed randomly in Ω₀ ⊂ R², $\sqrt{\mid {\mathrm{\Omega }}_0\mid }\sim L_0$.

In our analysis, we utilize both detailed spatial simulations and mean-field approaches. The detailed dynamics are described by the probability P (S, t|S₀, 0) for the system to be in a state S at time t, given an initial state S₀ at t = 0. The governing equation [26],

$${\partial }_{t}P=\sum _{s^{\prime }(\ne s)}{W}_{s^{\prime }\to s}P(S^{\prime },t\mid S_0,0)-W_{s\to s^{\prime }}P(S,t\mid S_0,0),$$ (1)

is solved numerically using Kinetic Monte-Carlo techniques (a snapshot of a typical realization is shown in Fig 1 b). The transition rates W_{S′ → S} in Eq (1) are nonzero only for the intermediate states S′ that are ”separated” from S by a single transition corresponding to either of four processes included in the model [25]. Importantly, the transition rate for the bundle initiation involves a collision factor that depends on a particular mechanism: for the mechanism relying on the tip-tip binding, the factor is nonzero only when the distance between the two tips becomes sufficiently small (tip-tip collisions), whereas for the ”tip-side” mechanism, this factor reflects a collision of the tip of one filament with the side of the other.

Insight into behavior of the system can also be gained from a non-spatial mean-field approximation formulated in terms of averages, such as 〈B〉 = Σ_S B (S)P (S, t|S₀, 0), etc., as it allows one to obtain important estimates based on analytical solutions [25]. In this approximation, the number of monomers Y, the total number of filaments E (both individual and in bundles), and the average linear size (radius) of the aster L form a closed system [25] yielding estimates for the characteristic time of aster formation, the final size of the aster (the aster size at t → ∞), and the final number of all filaments:

$$\tau =\sqrt{2{\tau }_p{\tau }_n},L_{\infty }=\delta \sqrt{\frac{2{\tau }_n}{{\tau }_p}},E_{\infty }=Y_0\sqrt{\frac{2{\tau }_p}{{\tau }_n}}.$$ (2)

(here and below, the angular brackets denoting ensemble averaging are omitted for brevity). The results (2), obtained in the limit X₀/E_∞ ≪1, agree with the solutions of Eq (1) [25]. Also, with the estimates of τ_p and τ_n as above, the characteristic time τ is in the 20 to 100-second range which agrees with the experiments [7].

An upper bound for the number of bundles B can be obtained by ignoring incorporation of individual filaments into existing bundles. For the ”tip-tip” mechanism, the upper mean-field estimate of the final number of bundles is [25]:

$$B_{\infty }^{\text{tip}-\text{tip}}=\frac{8}{{\pi }^3}\frac{{\alpha }_c\delta }{h}{Y}_0^2{\left(\frac{{\tau }_p}{{\tau }_n}\right)}^{3/2}.$$ (3)

where the aster thickness h is on the order of several δ. Indeed, $B_{\infty }^{\text{tip}-\text{tip}}$ can be viewed as the total number of ”favorable” tip-tip collisions over the time τ: $B_{\infty }^{\text{tip}-\text{tip}}\approx \tau R_{\text{coll}}$ where the collision frequency R_coll is expressed in terms of the average relative velocity of the tips υ_rel and the average tip density ρ̄_X as R_coll = (α_c/π)δ²υ_relXρ̄_X. Using υ_relτ ~ L_∞, ${\overline{\rho }}_X\sim X/(L_{\infty }^{2}h)$, and X ~ E_∞, the final number of bundles is estimated as $B_{\infty }^{\text{tip}-\text{tip}}\sim ({\alpha }_c{\delta }^2/h)E_{\infty }^2/L_{\infty }$, which, with the account of Eqs (2), is essentially equivalent to (3). Fig 2a illustrates agreement of the mean-field approximation (3) and the solution of Eq (1) obtained for the ”tip-tip” mechanism in the absence of filament absorption. Interestingly, the upper bound (3) provides a reasonably accurate approximation for the final number of bundles even when the filament absorption is taken into account, as illustrated by Fig 2b. In this case, the bundles become thicker, and the average number of filaments per bundle, shown in the inset of Fig 2b, is comparable with experimental observations in [27].

FIG. 2.

The ”tip-tip” mechanism: number of bundles for varying τ_p and τ_n. (a) Mean-field estimates (3) vs. numerical solution of Eq (1) based on 10² to 10³ realizations, for varying τ_n/τ_p. (b) Mean-field solution in the absence of filament absorption (solid line) and results of spatial simulations with absorption taken into account (dots with error bars); α_cδ/h = 0.03, p = 5; error bars correspond to standard deviation based on 50 to 120 realizations. The inset: average number of filaments per bundle, N b, vs. τ_n/τ_p.

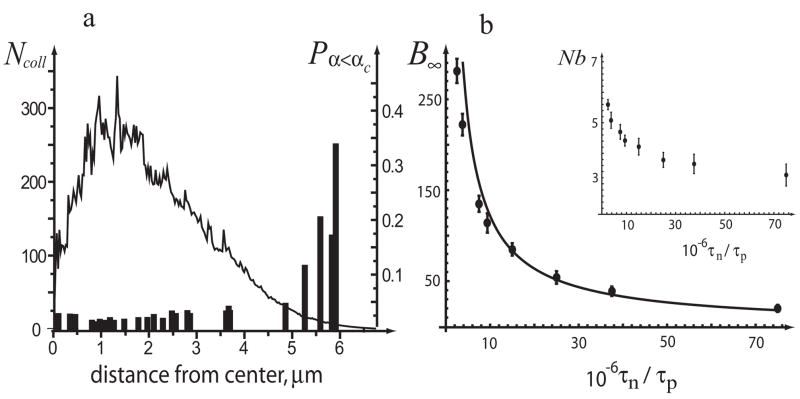
Intuitively, the ”tip-side” mechanism should result in a much larger number of bundles because of higher frequency of collisions. Indeed, the mean-field collision rate for this mechanism is R_coll ∝ Xρ̄_M, where ρ̄_M is the average density of the filamentous actin. However, spatial correlations in the system of filaments, not included in the mean-field approach, effectively reduce the number of favorable tip-side collisions. While the Monte Carlo simulations confirm that the frequency of all collisions is proportional to Xρ̄_M, the local density of filamentous actin ρ_M, unlike ρ_X, is non-uniform in space and ”out of phase” with the fraction of collisions occurring at a sufficiently small angle (Fig 3a). The latter is skewed towards the periphery of the system, indicating that elongated filaments have better chances to collide at a small angle. The resulting decrease in the number of favorable tip-side collisions leads to a counterintuitive conclusion: for realistic τ_p, τ_n, h and α_c, both $B_{\infty }^{\text{tip}-\text{side}}$ and $B_{\infty }^{\text{tip}-\text{tip}}$ may fall into the experimentally observed range of tens to hundreds. Interestingly, the effect can be captured by simply reducing the mean-field estimate for the ”tip-side” mechanism by a certain factor. As shown in Fig 3 b, the corrected mean-field result [25],

FIG. 3.

The ”tip-side” mechanism: numerical solution of Eq (1) and mean-field estimates: (a) Number of all tip-side collisions, N_coll (solid line), and fraction of collisions, P_{α< αc},, occurred at a sufficiently small angle, α < α_c = 0.2 (histogram), integrated over first 30 s in one Monte Carlo realization and shown as functions of distance from the aster center. (b) Mean-field solution (4) in the absence of filament absorption (solid line) and results of spatial simulations with absorption taken into account (dots with error bars); α_cδ/h = 0.03, p = 5; error bars correspond standard deviation based on 50 to 120 realizations. The inset: average number of filaments per bundle, N b, vs. τ_n/τ_p.

$$B_{\infty }^{\text{tip}-\text{side}}=\frac{{\alpha }_c^{\ast }\delta }{{\pi }^{2}h}{Y}_0^2\frac{{\tau }_p}{{\tau }_n}.$$ (4)

with ${\alpha }_c^{\ast }=0.07{\alpha }_c$, accurately approximates the solution of Eq (1) for the case of the tip-side binding.

Comparing Eqs (3) and (4) with the account of (2) leads to an important observation: the final numbers of bundles in the two mechanisms scale differently with the final linear size of the aster: $B_{\infty }^{\text{tip}-\text{tip}}\propto {(L_{\infty })}^{-3}$ and $B_{\infty }^{\text{tip}-\text{side}}\propto {(L_{\infty })}^{-2}$. We therefore conclude that, while $B_{\infty }^{\text{tip}-\text{tip}}$ and $B_{\infty }^{\text{tip}-\text{side}}$ may fall in the same range due to possible variations in parameter values, their dependence on the final linear size of the aster is described by a power law with different exponents (Fig 4), so the two mechanisms can be distinguished experimentally. For this, we propose to perform a series of the in vitro experiments, as described in [6, 7], with a same initial concentration of actin monomers, and after the polymerization is over, measure the number of bundles as a function of the linear size of the aster. The data are expected to be less noisy if the experiments are conducted with a fixed saturating concentration of fascin and with varying saturating amounts of Arp2/3. Our theory predicts that in these conditions, the measured dependence will be described by the power law, B_∞ ∝ (L_∞)^−β. The data yielding β ≈ 3 would indicate that the bundles initiate from the binding of the tips whereas values of β between 1 and 2 would point to the ”tip-side” mechanism. Our results also indicate (Fig. 2 in the supplementary material [25]) that if both mechanisms function simultaneously, the ”tip-side” mechanism dominates, i.e. virtually all bundles originate from the tip-side collisions, unless the tip-tip interaction is much stronger. In the latter case, the (B_∞, L_∞) data are fitted by the power law with β between 2 and 3.

FIG. 4.

B _∞ − L _∞ diagram for the ”tip-tip” and ”tip-side” mechanisms in the log-log representation. Experimental data are expected to result in a band of points. While the width of the band depends on variations in α_cδ/h, reflecting varying abundance and activity of fascin, elasticity of filaments, thickness of the aster etc., the slope of the band β, predicted to have different values for the two mechanisms of bundle initiation, can be used for distinguishing between them. Results of spatial stochastic simulations from Figs. 2b and 3b (open circles) are fitted by straight lines with the slopes β ≈ 1.6, for the ”tip-side” mechanism, and β ≈ 2.8, for the ”tip-tip” mechanism. (The corresponding bands are shown for realistically possible ranges of α_c δ/h: (0.0005, 0.007) and (0.003, 0.05), for the ”tip-side” and ”tip-tip” initiation, respectively.)

In summary, we have analyzed the dynamics of bundling of actin filaments for two different mechanisms of bundle initiation. In one, binding of the tips of neighboring filaments initiates linking of the filaments into a bundle. In an alternative scenario, the initiation of a bundle is brought about by linking the tip of one filament to the side of the other. Our analysis indicates that while both mechanisms may result in comparable numbers of bundles, the dependence of the final number of bundles on the final linear size of the aster is described by a power law with different exponents: B_∞ ∝ (L_∞)^−β with β ≈ 3, for ”tip-tip” mechanism, and β between 1 and 2, for the ”tip-side” mechanism; intermediate values of β would indicate presence of both mechanisms, with the tip-tip interaction being much ”stickier” than that between the tip and the side. Based on this finding, we propose an experiment that would distinguish the two mechanisms in the in vitro conditions. The mathematical formalism developed here can be applied to modeling non-equilibrium dynamics of filopodia in vivo.