Explaining the moon illusion

Abstract

An old explanation of the moon illusion holds that various cues place the horizon moon at an effectively greater distance than the elevated moon. Although both moons have the same angular size, the horizon moon must be perceived as larger. More recent explanations hold that differences in accommodation or other factors cause the elevated moon to appear smaller. As a result of this illusory difference in size, the elevated moon appears to be more distant than the horizon moon. These two explanations, both based on the geometry of stereopsis, lead to two diametrically opposed hypotheses. That is, a depth interval at a long distance is associated with a smaller binocular disparity, whereas an equal depth interval at a smaller distance is associated with a larger disparity. We conducted experiments involving artificial moons and confirmed the hypothesis that the horizon moon is at a greater perceptual distance. Moreover, when a moon of constant angular size was moved closer it was also perceived as growing smaller, which is consistent with the older explanation. Although Emmert's law does not predict the size–distance relationship over long distances, we conclude that the horizon moon is perceived as larger because the perceptual system treats it as though it is much farther away. Finally, we observe that recent explanations substitute perceived size for angular size as a cue to distance. Thus, they imply that perceptions cause perceptions.

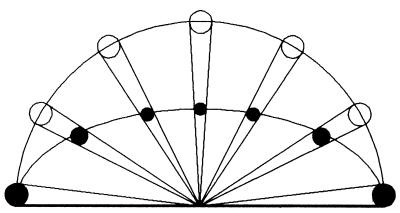
Regardless of its elevation in the sky, the moon's angular size at the eye remains the same. Yet the horizon moon may appear to be nearly twice the diameter of the elevated moon (1, 2). Over the centuries many different explanations were offered for this immensely powerful real-world illusion (3). Today most attention is paid to two diametrically opposed general explanations. Each explanation is exemplified by several different versions, but all reflect two basically different views of how the perceptual system computes size and distance. The older explanation is typified by the so-called apparent distance theory (3, 4). Basically, it holds that the perceived distance to the moon at the horizon is greater than that to the zenith moon. Fig. 1 shows how the horizon moon's greater perceived distance could cause it to be perceived as larger. This figure illustrates a version of the theory in which the perceived size of the moon is proportional to its perceived distance, a relationship known as Emmert's law.

Figure 1.

Regardless of its elevation, the distance between an observer (at the center of the horizontal line) and the moon remains constant (unfilled circles). However, a moon perceived as growing closer as its elevation increases (filled circles), must appear as growing smaller.

Another version of the apparent distance theory presumes an inherent anisotropy of visual space in which vertical distances are underestimated as compared with distances in the horizontal direction (5, 6). This apparent distance theory emphasizes the angle of regard, giving much less weight to the distance cues provided by the terrain. Although Kaufman and Rock (1) found only a weak effect of angle of regard, they did discover that terrain in one direction and its absence in the other plays a vital role. All versions of the theory are based on the notion that the horizon moon is effectively at a greater perceptual distance than the elevated moon. Apparent distance theories presume that perceiving the size of the moon involves the same mechanisms as those involved in perceiving the sizes of ordinary objects. Accurate perception of an object's size regardless of its distance is referred to as size constancy. Because the angular size of an object is inversely proportional to its distance (Euclid's law), size constancy is possible only if distance is taken into account (7, 8). Information regarding distance is derived from various cues such as the convergence of the eyes and perspective (9). As such cues are made less salient, the size of a distant object is matched more closely to the angular size of a nearby object than its linear size (7).

Observers asked to judge relative distances to the horizon and elevated moons usually respond by asserting that the horizon moon is closer. This is directly at odds with apparent distance theories, thus creating a serious problem for them. This size-distance paradox is not limited to the moon illusion. When any object of constant angular size is viewed in darkness with exaggerated convergence, it is described as both smaller and farther (10). Such observations lead to the idea that perceived size may not be based on perceived distance.

Recent theories postulate that the elevated moon's small apparent size is not related to its perceived distance. Rather, the perceived size of the moon is the dominant cue to its distance. This is just the opposite of the apparent distance theory. Accommodation of the eyes is one factor purported to directly affect the perceived size of the moon. That is, the accommodation of the eyes increases while viewing the elevated moon. It is proposed that this leads to a reduction in the perceived size of the moon (11).

Although accommodation is traditionally considered a cue to distance, in this theory it has a direct effect on perceived size. Viewing the elevated moon in empty space presumably causes the eye to tend toward its resting focus (12). The reduced size then acts as a cue to distance, and the moon appears to be farther. Reduction in size caused by increased accommodation is called accommodative micropsia. A similar reduction in size occurs with an increase in convergence, hence the appellation convergence micropsia. This paper raises fundamental questions about the overall applicability of these micropsia-based theories, which are widely cited in today's debate about the moon illusion.

To appreciate the differences among various theories we must consider the different meanings of size. Briefly, if a subject matches the length in meters of a distant rod to that of a nearby rod, as in a size constancy experiment, we refer to perceived linear size. Alternatively, if a subject adjusts the length of a nearby rod so that it subtends the same angle at the eye as a distant rod, we refer to perceived angular size. McCready (13) considers perceiving angular size to be equivalent to the perception of the difference in visual directions to the two ends of the rod. It is noteworthy that an infinite number of distal rods of different lengths and orientations may subtend the same visual angle, and therefore visual angle per se cannot represent any specific object.

Roscoe (11) proposes that retinal size is perceptible. Perceiving a retinal image is tantamount to perceiving the distribution of activity across the mosaic of retinal receptors. However, perception is of objects and not of neural activity, so strictly speaking, image size per se may not be perceptible. Of course, retinal size is equivalent to angular size and just as ambiguous. Alternatively, one and only one physical object corresponds to the perception of an object of a particular linear size, even if the perception is invalid. Obviously, perceiving linear size is possible if, and only if, information regarding distance to the object is available. If this information is incorrect (e.g., when convergence is increased by means of a prism), linear size is misperceived, but it still corresponds to a physical object at a particular distance. Hypothetically, if two objects were presented in the absence of all cues to distance, perceivers may determine whether they have the same or different retinal sizes. However, this determination may equally well be based on the assumption that both distal objects are at the same distances.

Despite controversy concerning the perceptibility of angular size per se (14, 15), several theories attribute the moon illusion to a difference in the perceived angular size of the moon (11, 16–18). As stated, some hold that a diminution of the image of the elevated moon is a direct effect of the increase in accommodation when the moon is viewed through empty space (11, 17). Similarly, convergence purportedly increases when the eyes roll upwards to view the elevated moon, and the terrain induces a lessening of convergence when viewing the horizon moon (17). Generally, theories based on oculomotor micropsia hold that the elevated moon appears as smaller and farther than the horizon moon.

Although Baird et al. (18) do not relate the illusion to oculomotor micropsia, they do consider the illusion to be one of perceived visual angle. Thus, the perceived angular size of the moon is determined by the ratio of its angular extent to that of its surrounding context. This causes the elevated moon to appear as smaller and therefore as farther. Thus, perceived angular size governs perceived distance.

Taking yet a different approach, Gregory suggests that the size of the horizon moon is scaled by cues to distance (as in apparent distance theories), but there are no distance cues for the elevated moon. In that case the moon takes on a default size, which happens to be smaller than that of the horizon moon (19). In this context Gregory does not distinguish between apparent angular size and apparent linear size. However, once established, the larger size of the horizon moon operates in a “top-down” fashion, and modifies its perceived distance so that it seems closer than the smaller and more distant elevated moon. Again, perceived size acts as the predominant cue to relative perceived distance. This is to be contrasted with Gogel's proposal that the elevated moon takes on a default distance, which scales the moon's apparent linear size (20). Because the default perceived distance is smaller than the distance to the horizon moon, the elevated moon is perceived as both smaller and nearer, placing Gogel squarely in the camp of the apparent distance theorists.

The notion that perceived angular size of the moon determines its perceived distance is diametrically opposed to the apparent distance theory. This opposition provides an opportunity to test two mutually exclusive hypotheses regarding the moon illusion. These are:

(i) The binocular disparity of a point perceived as being halfway along the line of sight to the horizon moon is substantially smaller than the disparity of a point similarly perceived as being half the distance to the elevated moon seen against an empty sky.

(ii) The binocular disparity of a point perceived as being halfway along the line of sight to the elevated moon is substantially smaller than the disparity of a point similarly perceived as being half the distance to the moon seen above the terrain at the horizon. This is precisely the opposite of Hypothesis i.

We now provide the rationale for these hypotheses.

Binocular disparity alone can signify neither distance to objects nor the amount of depth between them. Disparity must be calibrated by information regarding distance. This follows from the geometry. In general, the relative disparity

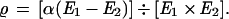Where α = distance between the eyes,

E₁ = distance in meters to one object,

E₂ = distance in meters to a more distant object.

If we let (E₁ − E₂) = δ, then the depth

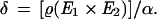In words, the depth associated with a particular binocular disparity ϱ is proportional to the product of the distances to the two objects. Where the depth δ is small relative to the viewing distance, the magnitude of the depth increases approximately as the square of the distance. This suggests that the perceived depth associated with a given disparity is powerfully affected by viewing distance. For example, Wallach and Zuckerman's (21) data show that the perceived depth associated with a relatively small fixed disparity increases approximately with the square of distance up to about 2 m. By contrast, the linear size of an object of fixed angular size geometrically increases only as the first power of its distance. The effect of distance on depth represented by disparity diminishes as distance cues are made less effective. Unfortunately, most systematic studies of the effect of distance on disparity have been limited to distances of about 2 m. However, Cormack (22) demonstrated that depth perceived in the afterimage of a stereogram increases in accord with the geometry of stereopsis up to a distance as great as 20 m. He further showed that depth continues to increase at greater distances, but at a slower rate. For a constant binocular disparity over long distances, therefore, perceived depth is a monotonic function of perceived distance.

In addition to pictorial cues, oculomotor cues (e.g., perspective) serve to calibrate disparity (21). The weights given to these cues by the perceptual system may differ with distance. Thus, oculomotor cues become less effective at long distances, where the perceptual system is more dependent on pictorial cues. Because the threshold for detecting depth due to disparity is as small as 1 arc-sec (23), disparity results in detection of depth beyond the effective range of convergence. In fact, the disparity between the moon and objects at 1 km is approximately 12 arc-sec. Depth is surely visible between objects several hundred meters away from a subject and the moon. Beyond the range of convergence, pictorial cues to distance must play a dominant role in determining the perceived depth represented by relative disparity.

Half-Distance Experiment

Method.

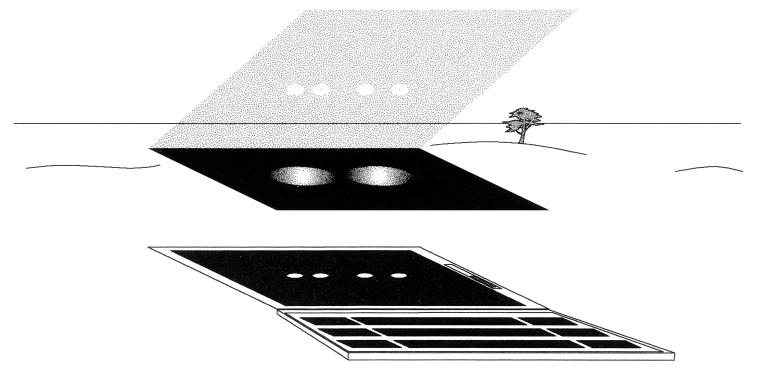
These considerations motivated an experiment in which subjects viewed two virtual moons adjacent to each other on the sky. “Moons” were luminous disks produced on an IBM ThinkPad flat panel display mounted in a stereoscopic optical apparatus as depicted in Fig. 2. One of them (the variable moon) was initially perceived as closer, or at the same distance as, the other (the reference moon). When near the horizon, the reference moon had zero disparity, relative to objects at the horizon.

Figure 2.

Schematic of apparatus. The active matrix screen of the computer was mounted horizontally in a frame 38.3 cm beneath a black screen containing two apertures, 6.4 cm apart. Each aperture contained a 38.3-cm focal-length lens. A partially silvered front-surface 40 × 40 cm mirror was mounted at a controllable angle above the lenses, so that subjects looking through the mirror viewed virtual images of 0.62° diameter “moons.” Two moons were located under each lens to produce four virtual images at optical infinity. Subjects looking through the mirror fused the two sets of moons and saw one pair of moons in the sky.

Fig. 3 is a stereogram that simulates our situation. It depicts a landscape containing two moons, with the left-hand moon appearing both closer and smaller than the identical right-hand moon. The initial depth between the moons in the experiment was produced by a small, randomly selected, binocular disparity ranging from 0° (no depth) to 0.56° (a distance of about 6.5 m between the subject and the variable moon). Pressing a key increased or decreased the initial disparity in 2-arc-min steps, thus altering only the stereoscopic depth in the display. Subjects were asked to change the distance of the variable moon so that it bisected the space between themselves and the distant reference moon. Another key press recorded this setting, and a new trial was begun.

Figure 3.

Stereogram of a Tuscan landscape (photograph © 1999 by Ansen Seale), modified, with permission, to include identical moons in each half-field. Fusing the two half-fields creates the impression that the left-hand moon is closer and also substantially smaller than the right-hand moon, as reported by subjects of Experiment (i) described in text. One should view the scene by staring at a point some distance behind the page. An animation simulating the experiment is available in the supplementary material on the PNAS web site, www.pnas.org.

One hundred trials, each beginning with a randomly selected disparity, were conducted per subject for each condition. The elevation of the fused images was determined by the angle of the mirror that placed the reference moon either about 1.5° above the horizon, or at 45° to produce an elevated moon viewed through empty space against the sky. In both conditions, the center of the half-image of the left-hand variable moon was always 1.35° from the reference moon. The corresponding distance in the right half-field was adjusted by pressing a key.

The theories discussed above imply mutually exclusive outcomes. As stated earlier, the apparent distance theory predicts that a smaller disparity would be needed to bisect the distance between the subject and the horizon reference moon than that between the subject and the elevated reference moon. Theories based on the proposition that the perceived distance to the moon is determined by its relative size predict the opposite result, because the reference moon above the horizon is perceived as larger than the elevated reference moon.§

Subjects L.K. and W.H. were 70 years old and B.B. was 62 years old. W.H. had lens implants subsequent to cataract surgery. L.K. was presbyopic, but had normal distance vision. B.B., also presbyopic, wore contacts to correct distance vision. W.Y. was 30 years old, and F.D. was 22 years old. The experiment was conducted on a hilltop on the C.W. Post campus of Long Island University in Brookville, NY. Subjects looking through the combining glass and fusing the virtual moons saw them side-by-side and slightly above a very distant horizon or in an empty sky. All of the experiments were performed in midmorning on nearly cloudless days. The horizon was composed of hazy hills many kilometers away, across Long Island Sound (which was itself hidden by several kilometers of intervening terrain and treetops). When the moons were elevated there were no nearby features or clouds. Although all of the moons were identical in angular size (0.6°), it was evident that the horizon moon was much larger than the elevated moon.

Results.

The mean relative disparities at which the variable moon bisected the distance between the subject and the reference moon are shown for each subject in Table 1A. Corresponding estimates of the standard errors (SE) are included. The basic data show that, on average, the angular disparity of the variable moon relative to the reference moon is about 3.4 times greater when the moons are elevated than when the moons are viewed above the ground plane. This larger relative disparity corresponds to a much greater depth between the elevated reference and the variable moons, as compared with the perceived depth between the horizon moons.

Table 1.

Mean disparities in size of moon when perceived at half distance, relative to reference moon (A) and when perceived as half-size relative to original (B)

Subject	MH	ME	SEH	SEE
	(A) Half-distance data
W.H.	6.293	21.976	0.259	1.189
B.B.	16.877	26.649	1.564	1.242
F.D.	5.409	23.158	0.334	1.027
W.Y.	10.071	48.817	0.534	1.948
L.K.	3.132	20.292	0.203	0.242
	(B) Half-size data
W.H.	52.382	215.308	1.385	8.703
B.B.	69.599	73.209	1.611	2.012
F.D.	51.983	92.365	1.230	4.463
M.S.	33.931	39.964	2.953	1.501
L.K.	23.777	34.618	0.482	0.797

(A) Mean disparities of elevated and horizon variables and moons relative to reference moons in arc-min, at half-distance for each of five subjects, and SE. (B) Mean disparities and distances of moon when adjudged to be one-half its original size. M_H, horizon moon; M_E, elevated moon; SE_H and SE_E, estimates of standard errors in perception of horizon and elevated moons, respectively. 

To estimate the perceived distances to the variable moons when subjects had bisected the space between themselves and the reference moon, we divided the average interocular distance of 0.064 m by the mean disparities in radians, and computed averages across subjects. On average, subjects placed the variable horizon moon at the same distance as an object 36.17 m away from them. In the case of the variable elevated moon, the corresponding distance was 8.62 m. Thus, the horizon moon was placed approximately 4.2 times farther away than the elevated variable moon. Despite a wide range of mean half-distance settings, all five subjects placed the horizon variable farther away than they did the elevated variable, with ratios ranging from 1.58 to 6.48. These results confirm Hypothesis i, which is based on classic apparent-distance theory, and are inconsistent with Hypothesis ii, which is associated with theories holding that the perceived size of the moon determines its perceived distance.

Discussion.

How do we reconcile these results with the fact that subjects tend to describe the larger-appearing horizon moon as closer and not as farther? Rock and Kaufman (2) suggested that distance cues act to scale size. Once scaled, observers use the perceived size of the moon to make a logical choice when asked about distances. They supported this choice by presenting large and small moons. Nine of 10 subjects described the larger moon as closer, regardless of whether it was elevated or at the horizon. However, we now know that this result is also consistent with the opposing theories. But if the moon's perceived size determines its perceived (as opposed to judged) distance, then the half-distance measures should be opposite to those we obtained.

Gregory (24) noted that converging lines drawn on paper could be seen as flat or as representing parallel lines receding into the distance. Although subjects perceive the drawings as flat, objects are distorted in shape or size because of the presence of such lines. The lines act as distance cues when they promote size constancy. Gregory suggested that these cues, presented on flat paper, are sufficient to trigger constancy scaling, in much same way as do the distance cues in normal scenes. However, when confronted with conflicting information regarding the flatness of the drawing, subjects need not be aware that different distances result in the distortions of shape and size. This notion, that distance cues can promote constancy without viewers being aware that they are doing so, is similar to Rock and Kaufman's proposal (2).

We know that distance information scales disparity among objects along the line of sight. Based on our data, it is evident that differences in apparent size do not scale differences in depth between the variable and reference moons. Hence, illusory differences in size do not act as distance cues. They scale neither distance nor depth. It is possible that subjects are simultaneously processing seemingly conflicting information, i.e., illusory differences in size and actual cues to distance, in different ways.

The Moon's Size and Its Perceived Distance

Method.

Our own observations revealed that increasing the absolute disparity of a moon results in two concomitant changes. First, the moon appears to grow smaller. Second, it also appears to come closer. This is easily understood in the case of the horizon moon, because as the disparity increased, subjects were able to see the moon at the same distances as objects that were closer to them. However, without the benefit of objects in the intervening space, the elevated moon exhibited the same behavior. As it grew smaller, it seemed to come closer. These observations were made in connection with our second experiment (see Table 1B), in which we sought to test the applicability of Emmert's law to the perceived size of the moon.

Historically, the apparent-distance theory is related to Emmert's law, which holds that the perceived size of an afterimage (or any object of constant angular size) is proportional to its perceived distance (25). However, a simple proportional relationship is unlikely at very large distances (26). In this experiment, we test for departures from Emmert's law, by testing the hypothesis that a moon at the half-distance should be perceived as one-half the size of a reference moon of the same angular size.

One moon was presented to each eye. These were fused to form a single moon that initially was at the distance of the reference moon (zero disparity). Five subjects decreased the distance to the moon (by increasing the absolute disparity), until it appeared to be one-half its original size. This was done for the moon seen just over the horizon and for the elevated moon viewed in an empty sky.

Results.

All subjects described the moon as drawing closer as its size diminished (see results shown in Table 1B). Note that M.S., a 22-year-old male with normal vision, replaced W.Y., who had served as a subject in the first experiment (Table 1A). Table 1B contains the mean absolute disparities at which each subject judged the moon to be one-half its original size. This disparity was far greater than the disparity of the variable moon at the half-distance of the first experiment. Overall, the average distance to the horizon moon, when it was judged to be one-half its original size, was 5.47 m. The corresponding distance of the elevated moon was 3.65 m. Therefore, under the conditions of this experiment, Emmert's law does not determine the magnitude of the moon illusion.

Discussion.

These results are consistent with those reported by Enright (27), who found only an 8% reduction in the size of a moon that was moved from a distance of about 3 km to 60 m. Our results demonstrate that this effect becomes progressively larger, so that the moon's size is reduced by half at distances within about 10 m. Consequently, the size of the moon varied as some positive function of distance. By contrast, if the moon's size is the predominant cue to its distance, and if then it had been seen as growing smaller, it should have appeared to move away, or if it had been perceived as moving closer, its perceived size should have increased.

Although this experiment showed that perceived size is not proportional to perceived distance, the horizon moon was still 1.5 times farther away than the elevated moon when it was judged to be one-half its original size. If the elevated moon had initially been perceived as more distant than the horizon moon, then it is plausible to consider that it should have reached its half-size when it was farther away than the horizon moon. The opposite is the case, which is consistent with the proposition that the perceptual system responds to the horizon moon as though it were more distant than the elevated moon.

The perceived half-distance to the elevated variable moon was approximately 8.6 m, more than twice the distance at which the same moon is judged to be half its original size. Similarly, the half-distance in the horizontal direction is about 36 m. This is about 6 times the distance at which the horizon moon is judged to be one-half its original size. In the second experiment, the size reduction actually became visible almost as soon as the moon was moved. However, subjects had to move the moon close enough for convergence to begin to function, and this process accelerated its reduction in perceived size. Emmert's law may hold where oculomotor cues are given more weight (i.e., at close distances), but the cues that operate at longer distances fail to support it fully. Even so, the presence of terrain well beyond the effective distance of convergence led to a more rapid reduction in the perceived size of the horizon moon, as compared with the elevated moon.

The Natural Moon

Finally, we briefly report observations involving the natural moon. The authors, one naive subject, and two of the original subjects viewed the moon at different locations, but when its angle of elevation was about 30°. The moon was adjacent to the top of a clearly visible nearby object at a horizontal distance of about 15 m. The observers closed one eye after viewing the moon binocularly. Four estimated that the moon became 20–25% smaller, and one estimated a reduction of 10%. Two observers viewed the moon through apertures to occlude all other objects; monocular viewing failed to produce the reduction in moon size. Although the natural moon was elevated, its binocular disparity relative to a nearby object caused it to be seen as farther away than that object. Monocular viewing eliminated this disparity, and lacking other depth cues, observers responded as though the moon were equidistant with the relatively close foreground objects (20, 28).

Conclusions

We found that the perceptual system responds as though the horizon moon were at a greater distance than the elevated moon. This is consistent with theories that attribute the illusion to the effects of cues signifying that the horizon moon is much more distant than the elevated moon. Cues to distance are physical properties of stimuli, or physiological states (e.g., convergence) affected by those properties. Different cues lead to different perceptual states. Thus, the term apparent in so-called apparent-distance theories is inappropriate. Rather, we suggest that the physical cues to distance affect both perceived distance and perceived size. The opposing apparent-visual-size theories substitute perceived size for angular size as a cue to distance. Thus, they imply that perceptions cause perceptions.

In reporting on their impressions of size and distance, subjects attend differently to different aspects of their perceptions. As in the case of geometrical illusions printed on paper, sometimes these reports are at odds with some aspects of their perceptions, although consistent with other aspects. This accounts for the size–distance paradox. Our results contradict predictions that are based on the assumption that the apparent angular size of the moon determines its relative perceived distance. Mechanisms proposed in the literature to account for differences in perceived angular size are entirely speculative and largely unsupported by direct evidence (see Appendix). At our latitude in New York, the natural moon is never at a higher elevation than about 60°, and it is most often much lower. On most occasions of viewing the elevated moon, the terrain may therefore be barely visible in peripheral vision. Thus, some information regarding distance to the sky may be gleaned from peripheral vision, and is certainly picked up through ordinary eye and head movements. Furthermore, in natural circumstances, the elevated moon may be only a few degrees above trees, tall buildings, and hills. In addition, the elevated moon could certainly be placed at, or somewhat beyond, the effective distance of convergence. This distance is approximately the same as the half-distance of our first experiment, where the elevated moon was viewed in an empty sky. Strictly speaking, it is not true that there are no cues to the distance of the elevated moon, although these cues are less salient than those associated with the terrain. Consequently, we propose that in normal circumstances, the perceived distance to the elevated moon is a compromise between the distance of convergence and other information picked up peripherally, or remembered shortly after scanning the scene.

The cues most relevant to the moon illusion are those related to the distance between the observer and other external objects. We suggest this to be the reason that the illusion was found to seem much weaker in some simulations. For example, when viewed above the horizon of a projected stereogram of a terrain, the moon is only slightly larger than when it is viewed on the same, but dark nearby screen (2). Similarly, although depth cues in ordinary pictures signify that the moon is more distant than objects in the foreground, the illusion is quite weak (29). However, these depth cues are scaled by the distance between the observer and the page. In the natural world, the observer is part of the scene, and the distances to points on the terrain scale depth cues differently.

Although we attribute the illusion to a greater effective distance to the horizon moon, we found that Emmert's law is not an accurate predictor of the size–distance relationship. Additional work is required to determine how different visual cues influence the exact functional relationship between size and distance in different perceptual regimes.

Finally, the results of these experiments are inconsistent with theories that attribute the illusion to micropsia; they are also inconsistent with theories that postulate a default size for the elevated moon, which then determines its perceived distance. As pointed out in the Appendix, there is a paucity of real evidence to support these theories, and there is an important logical flaw.

Appendix

It is indisputable that viewing an object while accommodating for a closer distance reduces its perceived size. But there is no evidence that this classic effect produces a sufficiently large difference in size to account for the moon illusion. Also, the eye does tend toward a resting focus of about 2 m in a totally empty visual field (12).

Roscoe, however, describes an increase in accommodation when subjects are viewing a luminous and apparently sharp elevated moon. Nevertheless, Roscoe considers this to be an example of the same empty field myopia (11). Further, he reports no data indicating that the magnitude of the moon illusion actually varies with the magnitude of the increase in accommodation. His effect could be related to the fact that one eye was occluded (effectively in an empty visual field), and may not have any bearing on the moon illusion.

Although Enright also suggests a role for accommodation, his own studies showed that the increase in accommodation vanishes during repeated measurements (17). Holway and Boring (30) concluded that elevation of the eyes in the head accounts for most of the variance in the moon illusion as they measured it, but they could not present a plausible explanation. Kaufman and Rock (1, 4) disputed this result. Enright (17) accepted the conclusion that elevated eyes per se will not produce the illusion, but suggested instead that a transitory change in vergence occurring while the eyes roll upwards results in convergence micropsia for the elevated moon. However, there is no reported evidence to support this conjecture.

McCready suggested that oculomotor micropsia occurs because the angle subtended by an object at a hypothetical egocenter, which lies between the eyes and about 10 cm behind them, is smaller than the angle subtended by the same object at the eye (13, 16). However, this is true only for nearby objects, and fails when the object of regard is at optical infinity. It must fail for the same reason that the moon follows you when you move your head laterally and does not change in size when your head moves fore and aft.

A square increasing in linear and in angular size on a video screen appears to move toward the subject (31). Subjects could null this apparent motion in depth by adjusting disparity. Thus, changing physical angular size is a cue to motion in depth. Wallach and Frey (32) caused a luminous diamond to enlarge as it moved along a 55-cm long track toward the observer, thus simulating passage along a path of 367 cm. Subjects altered convergence and accommodation in following this moving diamond. Subsequent to watching this changing size, the perceived distance of a stationary three-dimensional object was altered, which signified that static accommodation and convergence were recalibrated by changing size. Significantly, the index of this altered perceived distance was a large increase in the amount of depth related to the disparity between the nearer and farther parts of the stationary object. Our first experiment also relied on perceived depth represented by disparity as an index of relative perceived distance.

In these experiments, changes in size affected perceived distance, but the changes were in actual angular size. Theories that attribute the moon illusion to differences in perceived size (angular or otherwise) assume that perceived size per se is a major cue to distance. Actual angular size differences do play an important role in depth perception. For example, perspective can be described as a gradient of angular sizes of similar elements along the ground plane. Because gradients in angular size give rise to perceptions of distance, perspective is described as a Euclidean cue (9). By contrast, treating illusory differences in size as cues to perceived distance implies that perceptions cause perceptions. This is a perilous concept as explanations based on it are essentially tautological.