Structural rearrangement of CaMKIIα catalytic domains encodes activation

Abstract

At its fundamental level, human memory is thought to occur at individual synaptic contact sites and manifest as persistent changes in synaptic efficacy. In digital electronics, the fundamental structure for implementing memory is the flip-flop switch, a circuit that can be triggered to flip between two stable states. Recently, crystals of Ca²⁺/calmodulin-dependent protein kinase IIα (CaMKIIα) catalytic domains, the enzymatic portion of a dodecameric holoenzyme involved in memory, were found to form dimers [Rosenberg OS, Deindl S, Sung RJ, Nairn AC, Kuriyan J (2005) Structure of the autoinhibited kinase domain of CaMKII and SAXS analysis of the holoenzyme. Cell 123:849–860]. Although the formation of dimers in the intact holoenzyme has not been established, several features of the crystal structure suggest that dimers could act as a synaptic switch. ATP-binding sites were occluded, and the T286 autophosphorylation site responsible for persistent kinase activation was buried. These features would act to stabilize an autoinhibited “paired”-enzyme state. Ca²⁺-calmodulin binding was postulated to trigger the formation of an active state with unpaired catalytic domains. This conformation would allow ATP access and expose T286, autophosphorylation of which would act to maintain the “unpaired” conformation. We used fluorescence anisotropy and FRET imaging of Venus-tagged CaMKIIα to test the hypothesis that neuronal CaMKIIα can flip between two stable conformations in living cells. Our data support the existence of catalytic domain pairs, and glutamate receptor activation in neurons triggered an increase in anisotropy consistent with a structural transition from a paired to unpaired conformation.

Ca²⁺/calmodulin-dependent protein kinase IIα (CaMKIIα) is a multimeric serine/threonine kinase involved in the regulation of synaptic strength and the retention of spatial memory (1). It is one of the most abundant proteins found in the brain and is greatly enriched at postsynaptic densities (2). In response to synaptic activity, extracellular calcium enters the postsynaptic compartments and binds to calmodulin. In turn, CaMKIIα binds the Ca²⁺/calmodulin complex, is “activated,” and translocates to postsynaptic spines (3–6). Ultimately, CaMKII activation is thought to modulate synaptic efficacy (7). CaMKIIα also possesses the ability to become calcium-independent by autophosphorylation (8) and can remain functional for at least several hours after activation (9).

Each CaMKII subunit is composed of an N-terminal catalytic domain, a regulatory domain, and a C-terminal association domain, that assemble to form a holoenzyme whose structure has been extensively studied in vitro (10–15). Electron microscopy (EM) imaging of single particles of CaMKII isolated from rat brain revealed “flower-like” structures with association domains in a central core and catalytic domains radiating out like petals (15). Morris and Torok (10), also using EM, proposed a model for CaMKIIα in which 12 catalytic domains are coplanar and distributed evenly around the association domain core. In their model, the distance between neighboring catalytic domains was much <10 nm. In contrast, a study by Kolodziej and colleagues (16), using 3D EM imaging, proposed a model whose kinase domains projected above and below the midplane of the association domain core. In this model, the distance between each catalytic domain was >10 nm. Both of these EM studies reached similar conclusions with regard to the stoichiometry of the holoenzyme (12 subunits) and the symmetry of the association domain core (6-fold), but it is unclear why there was disagreement regarding the spatial distribution of catalytic domains about the association domain core.

By using X-ray crystallography, Kuriyan's group (13) analyzed crystals formed from isolated association domains of CaMKII and found that they assembled into tetradecameric structures with 7-fold symmetry. Subsequently, the Kuriyan group (11) reported that the observed 7-fold symmetry may have arisen from the absence of the regulatory and catalytic domains. They came to this conclusion as a result of a comparative EM analysis of the intact CaMKII holoenzyme and the truncated CaMKII subunits comprising only association domains. This discrepancy regarding the stoichiometry and symmetry of the association domain core may reflect some inherent property of the holoenzyme (11). Alternatively, it may serve to reveal the difficulty of extrapolating the structure of intact proteins from the structure of isolated protein fragments. Regardless, it demonstrates the importance of verifying structural details with multiple approaches and under physiological conditions.

By using X-ray crystallography, the Kuriyan group also demonstrated that autoinhibited catalytic domains isolated from Escherichia coli expressing a truncated Caenorhabditis elegans CaMKII (residues 1–340 of Unc-43) form dimers (12). A surprising feature of this dimer structure was that ATP access to the kinase ATP-binding site was occluded. Similarly, the T286 autophosphorylation site, a residue that renders the enzyme calcium-independent when phosphorylated (17), was buried in the dimer interface and was therefore inaccessible. Thus, if catalytic domains do form dimers in vivo, presumably they must separate to allow ATP access for kinase activity and to allow autophosphorylation for persistent activation. This hypothesis is consistent with recent FRET (Förster resonance energy transfer) imaging that indicates that CaMKIIα undergoes a conformational change upon activation (18). Furthermore, this crystal structure also suggests that autophosphorylation at T286 is not required for kinase activation, but if phosphorylated would subsequently prevent the reformation of catalytic domain dimers. Another distinguishing aspect of the Kuriyan model is that autoinhibition is thought to arise from interactions of regulatory and catalytic regions from separate (paired) subunits.

In the Kuriyan study (12) the structure of the autoinhibited holoenzyme was modeled by combining the crystal structure of catalytic domain dimers with a dodecameric association domain model (based on the tetradecameric crystal structure of isolated association domains), as constrained by small angle X-ray scattering of the intact holoenzyme. This holoenzyme model is best described as six pairs of catalytic domains distributed evenly around a central hub of association domains and was similar to a model proposed by Morris and Torok (10). Kuriyan and colleagues (12) also proposed that upon activation, catalytic domain pairs should separate. If applicable to the CaMKIIα structure in living cells, the structural model proposed by Kuriyan and colleagues could potentially behave as a circular array of flip-flop switches in which each of the six catalytic domain pairs acts as a separate “switch.” Given (i) the potential difficulties already encountered by inferring structure from protein fragments as outlined above, (ii) the fact that the Kuriyan model is based on the in vitro structure of an invertebrate CaMKII, (iii) the apparent limitations of interpreting single-particle EM images as demonstrated by the different catalytic domain distributions proposed by different groups, and (iv) the absence of corroborating evidence that CaMKIIα catalytic domains do actually form dimers in vivo, we sought to test the CaMKIIα model proposed by Kuriyan and colleagues in living cells.

Here, using time-resolved and steady-state fluorescence anisotropy and its ability to detect energy migration FRET (emFRET) and molecular rotation, we found that (i) in living cells Mus musculus CaMKIIα catalytic domains are arranged as pairs in the intact holoenzyme, (ii) glutamate receptor activation in neurons triggered an increase in anisotropy consistent with a structural transition from a paired to unpaired conformation, and (iii) this transition did not require autophosphorylation at T286. Our data are consistent with the idea that in CaMKIIα holoenzymes the transition of catalytic domains between paired and unpaired states may be the basis through which the enzyme encodes memory of past synaptic activity.

Results

Catalytic Domains Are Arranged as Pairs in the Intact Autoinhibited Holoenzyme.

The defining features of the CaMKIIα structural model proposed by Kuriyan and colleagues (12) is that six pairs of catalytic domains are distributed evenly around a central hub of association domains in the autoinhibited holoenzyme and that upon activation, these pairs separate (Fig. 1A). To test this hypothesis, our strategy was to use FRET microscopy to determine whether fluorescent protein (FP)-tagged CaMKIIα holoenzymes in vivo are arranged as pairs. FRET can potentially detect catalytic domain pairing because energy transfer only occurs if fluorophores reside within 10 nm of each other (19–21). A FRET approach seemed reasonable because it has already been shown that tagging the N and C termini of CaMKIIα with FPs did not alter catalytic activity or the ability of the kinase to form holoenzymes (18), thus FPs attached to either the catalytic or association domains of CaMKIIα could be used to decipher the structure of the holoenzyme. We specifically chose time-resolved fluorescence anisotropy as the method to measure emFRET because in addition to measuring the proximity between fluorophores, this method can also estimate the number of FPs participating in energy migration and measure the molecular rotation of an FP when attached to CaMKIIα (22, 23).

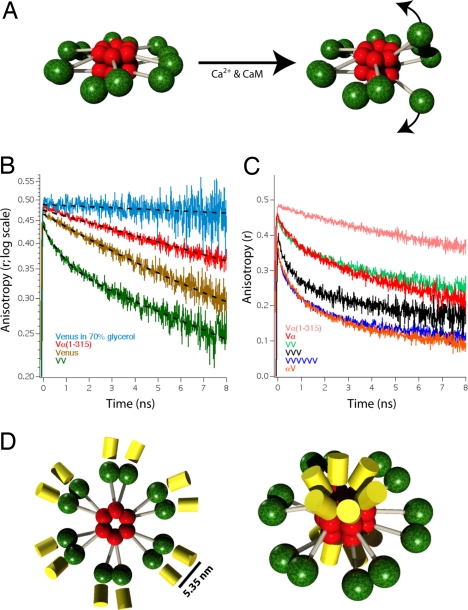
Fig. 1.

Time-resolved fluorescence anisotropy of Venus-tagged CaMKIIα. (A) Model for the holoenzyme structure before and after activation of one of its six pairs of catalytic domains is depicted. Red spheres indicate association domains, green spheres indicate catalytic domains with regulatory and variable domains depicted as gray cylinders. (B) Fluorescence anisotropy decay curves of HeLa cells expressing Vα(1–315), Venus, and VV (a concatamer of 2 Venus molecules). Each curve is an average of five traces from five cells. A decay curve of Venus in 70% glycerol is also depicted (n = 2). Dashed lines are single-exponential curve fits except for the VV construct where a double-exponential model was used. (C) Fluorescence anisotropy decay curves of Vα and αV are plotted with decay curves of VV (from B), VVVVVV (a concatamer of six Venus molecules), and Vα(1–315) (from B). Each curve is an average of five traces. (D) Diagram depicting the autoinhibited CaMKIIα holoenzyme model with Venus attached either to the N terminus (Left) or C terminus (Right) that are consistent with the Vα and αV anisotropy decay curves.

Venus (24), a yellow GFP spectral variant, was selected to tag CaMKIIα in our experiments because Venus can efficiently transfer energy by emFRET (25). This arises because Venus has a small Stokes shift (high spectral overlap of excitation and emission), and accordingly the Venus to Venus Förster distance for energy transfer is 4.95 nm (26). To avoid nonspecific interactions between fluorescent protein tags, a monomeric variant of Venus was used in all experiments (27). In our first experiment we compare the fluorescence anisotropy decay of a Venus-tagged (N terminus) CaMKIIα mutant that lacks the association domain, Vα(1–315), with the anisotropy decays of free monomeric Venus, and a dimeric Venus concatamer (VV) to determine whether catalytic domains [Vα(1–315)] form dimers when expressed in HeLa cells (Fig. 1B). We also measured the anisotropy decay of purified Venus in 70% (wt/wt) glycerol as a control for our ability to resolve slow rotational motion. Vα(1–315) is similar but slightly shorter than the truncated UNC-43(1–340), used to form catalytic domain crystals (12).

The anisotropy decay of free Venus (Fig. 1B, yellow trace) was well fit to a single exponential decay model with a rotational correlation time of 17.4 ± 0.2 ns (mean ± SD). The rotational correlation time (θ) is the time constant of this slow anisotropy decay component and serves as a measure of molecular rotation (25). This value was similar to rotational correlation times measured for GFP (23, 28). The two-photon limiting anisotropy of Vα(1–315) (the anisotropy at t = 0) was found to be 0.48. The anisotropy decay of VV (green trace) was well fit to a double-exponential decay model. Cells expressing Vα(1–315) (red trace) had an anisotropy decay that was well fit to a single exponential decay model with a rotational correlation time (θ = 28.4 ± 0.3 ns) that was slightly slower than that of free Venus. For comparison, the anisotropy decay of free Venus in a 70% solution of glycerol was measured and decayed as a single exponential with a rotational correlation time of 134 ± 16 ns. The absence of a fast anisotropy decay component in the Vα(1–315) trace indicates that there was no appreciable emFRET and suggests that free catalytic domains do not form dimers when expressed in cells. Although unlikely, we cannot rule out the possibility that Vα(1–315) dimers did form when expressed in HeLa cells, but emFRET did not occur because the Venus to Venus dipole orientation factor (κ²) had a value of 0. An alternative explanation for the absence of FRET between Venus-tagged catalytic domains is that catalytic domains have an affinity for each other that is too low to form pairs without association domains, consistent with the requirements of a flip-flop switch. We next turned to the intact holoenzyme.

The N-terminal catalytic domains of CaMKIIα were tagged with Venus (Vα). An anisotropy decay curve generated from HeLa cells expressing Vα is shown in Fig. 1C (red trace). For comparison, we have replotted the anisotropy decay curves of Vα(1–315) (Fig. 1C, pink trace) and VV (green trace) on this graph. The Vα anisotropy curve had a fast decay component indicating the presence of emFRET and a slow rotational component similar to that of Vα(1–315). The fast component in Vα was almost identical to the fast component of VV, a Venus dimer. Oligomers composed of three (black trace) and six (blue trace) concatenated Venus molecules (VVV and VVVVVV, respectively) are plotted to illustrate how the number of Venus molecules participating in energy migration influences anisotropy decay. Note that as the number of Venus molecules in our control constructs increases, the anisotropy values decrease, and the amplitude of the fast component of the anisotropy decay curves increases. The failure of the anisotropy decay curve of Vα to drop by more than half that of the limiting anisotropy (22, 25) and its similarity to the VV dimer decay curve led us to the conclusion that catalytic domains of autoinhibited CaMKIIα are organized as discrete pairs.

The holoenzyme models proposed by Kuriyan (12), Morris and Torok (10), and by Kolodziej et al. (16) all envision a central core of 12 association domains with 6 above and 6 below the midplane. Thus, our expectation when tagging the C terminus of CaMKIIα with Venus (αV) was that the FPs would project out of the core of each holoenzyme in a similar fashion with 6 above and 6 below the midplane (Fig. 1D Right). A holoenzyme tagged in this way should generate an anisotropy decay curve that would resemble that of a Venus hexamer, like our VVVVVV control construct. Indeed, the anisotropy decay observed in cells transfected with CaMKIIα tagged at the association domain (αV; Fig. 1C, orange trace) had fast and slow decay component that appeared similar to that of VVVVVV (blue trace). Thus, a structural motif shared by all three models, a central association domain core composed of two stacked rings of hexamers, is consistent with the anisotropy decay observed for αV.

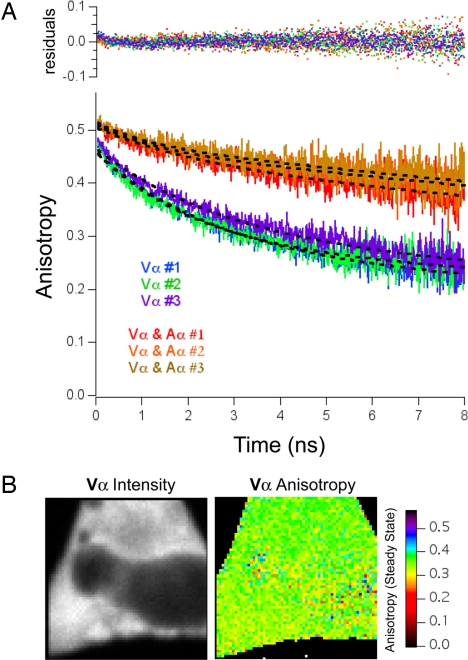
We next sought to determine the distance between members of catalytic dimer pairs to understand better the structure of the CaMKIIα holoenzyme. We also wanted to compare the rotational correlation time of Vα to Vα(1–315) to ascertain how rigidly attached Venus is to these constructs. To accomplish this we needed to measure accurately both the fast and slow correlation time of Vα. Although direct curve fitting of the Vα decay could provide estimates of these values, considering the difficulty of measuring slow rotation with a short-lived fluorophore (25), a global fitting strategy was adopted to constrain the four fitting parameters of a double-exponential decay model (29). Vα was expressed alone or with excess Amber-tagged CaMKIIα (Aα) in HeLa cells, and anisotropy curves were acquired. Amber is a single-point mutation in Venus that prevents it from forming a fluorophore (30). If the relative expression of Aα and Vα varied from cell to cell, the magnitude of the fast correlation time should vary as well because the fast correlation time arises from Vα–Vα pairs only, not from Aα–Aα or Aα–Vα catalytic pairs. In contrast, the rotational correlation time of Vα should not vary with coexpression of Aα, and therefore this variable could be linked in our dataset. Global fitting yielded a rotational correlation time (θ) of 49.8 ± 3.8 ns for Vα with a χ² value of 1.08 (Fig. 2A). Global fitting also yielded a value of 2.6 ± 0.4 ns (mean ± SD, n = 3 curves, five cells each) for the unlinked fast decay time (ϕ) from cells transfected with only Vα and a limiting anisotropy of 0.461 ± 0.019. It is also important to point out that although the fluorescence intensity of Vα varied from region to region across the cell (Fig. 2B Left), the Vα anisotropy value did not (Right), indicating that this signal arose primarily from intraholoenzyme energy migration.

Fig. 2.

Global fitting of Venus–CaMKIIα anisotropy decay curves. (A) Anisotropy decay curve of cells expressing Vα alone (blue, green, and purple traces) or Vα coexpressed with an excess of Amber–CaMKIIα (Vα and Aα; red, orange, and yellow traces). The transfection ratio used was 1:6, and each trace is an average of anisotropy measurements from five cells. Dashed lines are the results of a global fit to a double-exponential model. Global fitting was performed by using the following equation: r(t) = r₁·e^(−t/ϕ) + r₂·e^(−t/θ), where the rotational correlation time (θ) was linked between all six curves, and the limiting anisotropy (r₀) is equal to r₁+ r₂. Residuals are plotted on the Top. (B) Intensity and steady-state anisotropy images of Vα expressed in HeLa cells.

With knowledge of the Vα fast correlation time, the emFRET transfer rate was found to be 0.19 ± 0.03 ns⁻¹ (n = 3), and the Venus to Venus separation distance in Vα was 5.35 nm. Based on the diameter of 23.5 nm for the autoinhibited holoenzyme (12), the 12 Venus molecules would have a separation distance of ≥6.1 nm if they were distributed evenly around the association domain core. Our calculation of a 5.35 nm separation distance suggests an uneven pairing of catalytic domains as depicted in Fig. 1D.

Further, the fast decay component of Vα had an amplitude of 0.187 ± 0.012 (n = 3). Because this decay amplitude was less than half that of the limiting anisotropy (22, 25) and because the time constant of this component was faster than the fluorescent lifetime of Venus (3.3 ± 0.03 ns; mean ± SD, n = 20), these data strongly suggest that in Vα, emFRET arises principally between two Venus molecules. Taken together, our data provide direct evidence that catalytic domains are organized as dimers in CaMKIIα holoenzymes in living cells.

Steady-State Anisotropy Measurements of the Activation of CaMKIIα in Hippocampal Neurons.

To test directly the hypothesis that catalytic domain pairs separate upon activation, we turned to the more physiologically relevant environment of cultured hippocampal neurons. Our first concern upon switching cell types was that high levels of endogenous CaMKIIα subunits found in neurons might coassemble with transiently expressed Venus-tagged CaMKIIα subunits and reduce measured anisotropy values. To address this issue, we compared the steady-state anisotropy values generated from both HeLa cells and neurons expressing either Vα or αV. Values were found to be 0.34 ± 0.01 and 0.36 ± 0.01 for Vα expressed in HeLa cells and neurons, respectively (mean ± SD, n = 10). For αV, the anisotropy values were 0.25 ± 0.02 and 0.26 ± 0.02 when expressed in HeLa cells and neurons, respectively (n = 10). ANOVA revealed that there was no significant difference between anisotropy values acquired from HeLa cells or neurons, expressing either Vα or αV (P > 0.05 for each), but did detect a difference between constructs regardless of cell type (P < 0.001 for each). These results suggest that expression of endogenous CaMKII did not significantly alter our measured anisotropy values.

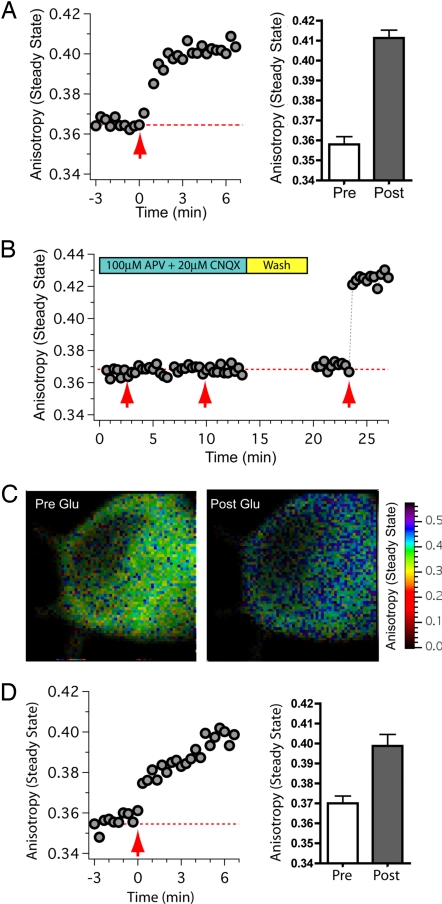
Accordingly, neuronal cultures were transfected with Vα, and steady-state anisotropy values were measured before, during, and after perfusion with glutamate/glycine (Fig. 3A). An increase in anisotropy consistent with the separation of catalytic domain pairs was observed in 8 of 10 neurons tested, whereas 2 neurons failed to respond. When receptor activation was blocked with glutamate receptor blockers [100 μM 2-amino-5-phosphonovaleric acid (APV) and 20 μM 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX)] glutamate/glycine application failed to elicit a change in anisotropy in 10 of 10 neurons (Fig. 3B). Subsequent removal of APV and CNQX and reapplication of glutamate/glycine resulted in an increase in anisotropy in 7 of the 10 neurons. Intensity-weighted steady-state anisotropy images of the neuronal soma from which the trace in Fig. 3B was obtained are shown in Fig. 3C. The images were acquired immediately before (Pre Glu) and after (Post Glu) the third application of glutamate/glycine (Fig. 3C). Together, these experiments indicate that the rise in anisotropy was not caused by perfusion artifacts. Furthermore, all anisotropy experiments were performed by using two-photon excitation with low laser power, and the absence of photobleaching was verified in every experiment. It is likely that the rise in anisotropy resulted from a decrease in emFRET (rather than decreased rotation) as the anisotropy decay of a Venus-tagged constitutively active mutant of CaMKIIα (T286D) acquired from regions where the kinase did not aggregate decayed as a single exponential with a rotational correlation time of 44.9 ± 1.0 ns and lacked a fast emFRET decay component. Thus, the increase in the steady-state anisotropy value of Vα, when expressed in hippocampal neurons and initiated by exposure to glutamate/glycine, most likely indicates that catalytic domain pairs separate upon activation.

Fig. 3.

Activation of CaMKIIα initiates catalytic dimer separation. (A) Time course of anisotropy values acquired from somas of hippocampal neurons expressing Vα. Glutamate and glycine were applied at time = 0 (red arrow). Bar graph shows the ensemble steady-state anisotropy values before (Pre; mean ± SD, n = 10 cells) and after stimulation (Post; n = 8 cells). (B) Time course of anisotropy values acquired from neurons expressing Vα in the presence of APV and CNQX as indicated. The first and second red arrows indicate the times at which glutamate/glycine (with APV and CNQX) was applied. Subsequently, the chamber was washed with PBS and challenged with agonist again in the absence of APV and CNQX (indicated by the third red arrow). (C) Intensity-weighted steady-state anisotropy images of the neuronal soma in B before and just after the third application of glutamate/glycine. (D) Time course of anisotropy values acquired from neurons expressing Vα(T286A). Glutamate and glycine were applied at time = 0 (red arrow). Bar graph shows the ensemble steady-state anisotropy values before (Pre; mean ± SD, n = 9 cells) and after stimulation (Post; n = 8 cells).

As observed for Vα, a glutamate/glycine-evoked increase in anisotropy was also observed in 8 of 9 neurons expressing Vα(T286A) (Fig. 3D). Because Vα(T286A) cannot be phosphorylated at T286 it appears that the destabilization of catalytic domain pairing does not require autophosphorylation at this site.

Discussion

By using live-cell fluorescence anisotropy imaging we tested three key predictions based on the CaMKIIα structural model of Kuriyan and colleagues (12): (i) that catalytic domains of mammalian CaMKIIα are organized as dimers in the autoinhibited holoenzyme, (ii) that catalytic domain dimers separate upon activation, and (iii) that autophosphorylation at T286 is not required for catalytic domain separation. Our experimental results support all three of these predictions.

We found that the Vα anisotropy decayed as a double exponential, indicating that FRET was occurring between Venus fluorophores in this complex. Global fitting revealed a fast emFRET decay component whose amplitude was <50% of the limiting anisotropy, suggesting energy migration between only 2 fluorophores. Furthermore, the Vα anisotropy decay was similar to the decay of VV but was clearly distinct from monomeric Venus or VVV. Thus, we conclude that in living cells the catalytic domains of the autoinhibited holoenzyme are organized as dimers.

It is worth considering what anisotropy decay curves would be expected for Vα if catalytic domains were organized as proposed by Morris and Torok (10), or by Kolodziej and colleagues (16). In the first model, catalytic domains are coplanar and spaced evenly around the association domain core. Assuming a diameter of 23.5 nm for the autoinhibited holoenzyme, we would expect a separation distance between catalytic domains of 6.1 nm. Energy migration would occur between all 12 Venus-tagged subunits, resulting in a drop in the fast anisotropy decay component well below half that of the limiting anisotropy in this model (22). This, however, was not observed. In contrast, the Kolodziej model distributes catalytic domains evenly above and below the midplane such that each catalytic domain is ≥ to 10 nm from its neighbors. Thus, dimer formation is not possible with this structure, and we would expect the anisotropy of Vα to decay as a single exponential. This too was not observed. Accordingly, we conclude that the holoenzyme model proposed by Kuriyan and colleagues (12) best describes the distribution of catalytic domains in the autoinhibited mammalian CaMKIIα and is depicted with attached Venus molecules in Fig. 1D.

Changes in the conformation of CaMKIIα coincident with activation have been demonstrated by using FRET in which the C and N termini of the CaMKIIα subunit were tagged with fluorescent proteins (18). A decrease in FRET was observed, consistent with an increase in the separation distance between the catalytic and association domains. Here, we observed a strong emFRET signal between fluorophores attached to the catalytic domains of the autoinhibited enzyme. Further, when Vα was expressed in neurons, we observed an increase in anisotropy upon application of glutamate/glycine, reflecting a decrease in emFRET (Fig. 3). Autophosphorylation at T286 was not required for this structural rearrangement of catalytic domains because an increase in anisotropy was also observed using the Vα(T286A) mutant that cannot be phosphorylated at this site (Fig. 3D).

Taken together with the prior FRET studies, our results demonstrate that activation induces a physical extension of the holoenzyme in which the catalytic domains of CaMKIIα move away from both its dimer partner and the core of the holoenzyme. Although it is possible that catalytic domains that have undergone separation may remain within the midplane of the holoenzyme, this seems unlikely when considering the measured diameter of the activated holoenzyme (26.0 nm) (12). If Venus molecules remain in the midplane upon activation, steady-state anisotropy values would be expected to decrease with a transition from a dimer to that of a dodecamer (12 Venus molecules distributed evenly around the association core with a ≈6.7-nm separation distance between catalytic domains). Instead, activation of CaMKIIα resulted in an increase in anisotropy values, consistent with a change from a dimer to a monomer. Thus, catalytic domains most likely swing up and out of the midplane of the holoenzyme and away from the association domain core. Further support for this structure of CaMKIIα is that the diameter of the activated holoenzyme was found to be larger than that of the autoinhibited holoenzyme (12), which could be viewed as a natural consequence of enzyme extension upon activation.

Fluorophore tagging of a protein can alter its function and may not reveal the exact position of the protein. This is particularly problematic for fluorescent proteins because of their relatively large size. FP attachment to CaMKIIα did not alter catalytic activity nor its ability to form holoenzymes (18). Still, it is important to note that FRET measurements report on the proximity between fluorophores and only indirectly on the arrangement of the protein domains to which they are attached. Thus, although we cannot rule out the possibility that upon activation catalytic domains become closer while the attached Venus molecules increase in separation distance, the simplest interpretation is that catalytic domains and their attached Venus molecules move in concert to increase the separation distance between catalytic domains.

Changes in FRET can arise from changes in separation distance or from changes in dipole–dipole orientation. Our data indicate that the dipole–dipole orientations between Venus molecules, tagged to the N terminus of CaMKIIα, are not rigidly constrained in terms of rotational mobility. This conclusion is based on the similarity between the rotational correlation times of Vα(1–315) and Vα. The mass of Vα should be ≈12 times greater than that of Vα(1–315). If Venus was rigidly attached to monomeric Vα(1–315) or to the Vα holenzyme, this difference in mass should, in theory, manifest as a 12-fold difference in the rotational correlation time. This was not observed. Rather, the similarity of their rotational correlation times (28.4 and 49.8 ns, respectively) indicates that the dipole orientation of Venus when tagged to CaMKIIα using a 15-amino acid linker is not strongly constrained, and therefore observed changes in emFRET with Vα most likely reflect changes in separation distance.

FRET measurements of a population of Vα enzymes will be proportional to the average separation distance and dipole–dipole orientation between fluorophores. These measurements are time averages. Therefore, our conclusion that catalytic domains of the autoinhibited holoenzyme are arranged in pairs should in no way imply the existence of a rigid structure. An alternative interpretation is that a dynamic interaction between neighboring catalytic domains exists with a propensity of dwelling in close proximity to each other while in the autoinhibited state. Regardless of whether the structure of the autoinhibited kinase is fixed or dynamic, either interpretation is consistent with our conclusion that catalytic domains are arranged as pairs. Because CaMKII holoenzymes are thought to be composed of a mixture of α- and β-subunits (15, 31), the existence of catalytic domain pairing raises interesting possibilities regarding their function. As an example, the subunit composition of pairs might explain the variability of the Ca/CaM threshold required for activation (31).

In conclusion, live-cell anisotropy experiments indicate that (i) catalytic domains of mammalian CaMKIIα are organized as dimers in the autoinhibited holoenzyme, (ii) catalytic domain dimers separate upon activation, and (iii) autophosphorylation at T286 is not required for catalytic domain separation. It is possible then, that structural rearrangements of CaMKIIα catalytic domain dimers behave as switches. Further, if a single holoenzyme has six independent catalytic domain pair switches, the number of activated pairs in each holoenzyme could potentially encode graded information. In addition, the arrangement of paired and unpaired catalytic dimers within a holoenzyme may also have meaning. CaMKII is known to interact with many other proteins (32), and we therefore speculate that certain patterns of paired and unpaired domains might favor one interaction over another. The presence of catalytic domain pairing, demonstrated here to exist in living neurons, reveals mechanisms through which the structure of CaMKII holoenzymes might encode and retain information of past synaptic activity.

Methods

Molecular Biology and Cell Culture.

Venus- and Amber-tagged CaMKIIα subunits and Venus concatamers were constructed by using standard molecular biological techniques. Similarly, HeLa cell culture, hippocampal neuronal cultures, and transfections were conducted by using standard cell biological techniques. For a detailed description, see supporting information (SI) Methods.

Two-Photon Fluorescence Anisotropy Measurements.

Anisotropy curves were acquired by using a 90-MHz, 200-fs Ti:sapphire laser (Coherent Chameleon) tuned to 940 nm for excitation delivered through a 20- × 0.5-N.A. water-immersion objective on a Zeiss LSM510 META microscope. Power at the objective was kept low (between 2 and 3.5 mW) to avoid bleaching the sample. Emitted photons were collected by using a 0.9-N.A. condenser to avoid depolarization caused by high-N.A. optics and filtered with a BG39 before entering a polarizing beam splitter (Becker and Hickl). Linear polarizers (Meadowlark), oriented parallel and perpendicular, were placed just before entering 2-microchannel plate photomultipliers (R3809U-52; Hamamatsu) in which parallel and perpendicular photons were detected. A Becker and Hickl SPC-830 card and a HRT-41 router were used as an interface between the photodetectors and a PC running SPCM software (Becker and Hickl), each of which coordinated the detection of excitation pulses with photons emitted from the sample. Photon count rates were kept <20,000 cps to avoid pulse pile-up errors. Excitation pulses were detected by an external photodiode. “Parallel” and “perpendicular” traces were collected (1,024 time bins) with peak counts for parallel traces of ≈8,000. Dark-count subtraction (≈5 counts per time bin) was performed, and anisotropy values were calculated by using Eq. 1 for each point, yielding an anisotropy curve. Data were processed by using IGOR Pro (Wavemetrics). Photons were collected for 4 min in all experiments except those found in Fig. 2, in which a 2-min collection time was used. Epifluorescence detected by using internal Zeiss photomultipliers on the back-scattered light pathway was used to monitor bleaching. Only cells with a stable fluorescence baseline were used. All recordings took place at room temperature.

Time-resolved anisotropy decay curves were calculated from fluorescence lifetime decay curves by using Eq. 1,

where ‖(t) is the number of parallel photons detected as a function of time after excitation, ⊥(t) is the number of perpendicular photons detected as a function of time, and G is the instrumentation correction factor. The G factor was measured as described in ref. 33 and had a value of 1.25 ± 0.05.

Curve Fitting.

Single-exponential curve fitting and global fitting (29) with a double-exponential decay model were performed by using IGOR Pro software.

Estimating Separation Distance from Anisotropy Decay.

For a dimer, the fast-anisotropy decay correlation time related to emFRET, ϕ, is (23):

where ω is the emFRET transfer rate. Thus, for Vα where ϕ is 2.6 ns, ω is 0.19 ns⁻¹.

The separation distance, R, can be calculated from the emFRET transfer rate by using the Förster equation (19):

where τ is the Venus fluorescence lifetime (3.3 ns) and R₀ is the Venus–Venus Förster distance (4.95 nm) (26), assuming a κ² value of 2/3.

Steady-State Anisotropy Images.

Steady-state anisotropy images were acquired in the same manner as time-resolved anisotropy measurements, except parallel and perpendicular photons were counted without correlation to the laser pulse for each pixel. Also, the “imaging mode” of the SPC-830 was used. Anisotropy values were then calculated by using Eq. 1.

Agonist Application to Hippocampal Neurons.

Regions of interest were continuously scanned (200 ms/scan) while parallel and perpendicular photons were counted. Steady-state anisotropy values were calculated by using Eq. 1 at 20-s intervals that were then plotted against time. The intensity image was calculated for each pixel by using Eq. 4

in which I is the total fluorescence intensity value, ‖ is the number of parallel photons detected, ⊥ is the number of perpendicular photons detected, and G is the instrumentation correction factor. Before each experiment, neuronal growth medium was exchanged for PBS, and constant perfusion of PBS was initiated. Where indicated in Fig. 3, 3 mL of PBS with 100 μM glutamate and 10 μM glycine was bath applied. A 35-mm dish with a water-immersion objective in place can hold ≈3.0 mL of solution. Overflow was removed with tubing under negative pressure attached to an in-house vacuum source.

For experiments involving the NMDA and AMPA/kainate receptor antagonists, 100 μM APV (Sigma) and 20 μM CNQX (Tocris) were placed in the bath, in the perfusion buffer, and in the buffer containing glutamate and glycine. After agonist challenge in the presence of antagonists, the blockers were washed out within a period of 3 min (≈10 bath exchanges), and the experiment was resumed with blocker-free buffer and agonists.