Flow-induced clustering and alignment of vesicles and red blood cells in microcapillaries

Abstract

The recent development of microfluidic devices allows the investigation and manipulation of individual liquid microdroplets, capsules, and cells. The collective behavior of several red blood cells (RBCs) or microcapsules in narrow capillaries determines their flow-induced morphology, arrangement, and effective viscosity. Of fundamental interest here is the relation between the flow behavior and the elasticity and deformability of these objects, their long-range hydrodynamic interactions in microchannels, and thermal membrane undulations. We study these mechanisms in an in silico model, which combines a particle-based mesoscale simulation technique for the fluid hydrodynamics with a triangulated-membrane model. The 2 essential control parameters are the volume fraction of RBCs (the tube hematocrit, H_T), and the flow velocity. Our simulations show that already at very low H_T, the deformability of RBCs implies a flow-induced cluster formation above a threshold flow velocity. At higher H_T values, we predict 3 distinct phases: one consisting of disordered biconcave-disk-shaped RBCs, another with parachute-shaped RBCs aligned in a single file, and a third with slipper-shaped RBCs arranged as 2 parallel interdigitated rows. The deformation-mediated clustering and the arrangements of RBCs and microcapsules are relevant for many potential applications in physics, biology, and medicine, such as blood diagnosis and cell sorting in microfluidic devices.

In thermal equilibrium, lipid vesicles and red blood cells (RBCs) show a rich variety of shapes, depending on the environmental conditions. These shapes can be understood quantitatively on the basis of a mechanical and thermodynamical model of 2D elastic membranes (1–5). The membrane of RBCs consists of a lipid bilayer (in the fluid state) to which a spectrin network is attached. This network is responsible for the shear elasticity of the composite membrane. Under physiological conditions, RBCs adopt a biconcave-disk shape with constant area S and volume V, a mean radius R₀ = $\sqrt{S/4\pi }$ = 3.4 μm, and a reduced volume V/(4πR₀³/3) ≃ 0.6.

The spectrin network enables RBCs to remain intact while deforming in blood flow through narrow capillaries. Physiologically, the main effect of RBC deformation is a reduction of the flow resistance. Recently, it has been found that RBC deformation also induces ATP release from RBCs, which induces nitric oxide synthesis and enhances the vascular caliber (6, 7). Thus, the shape deformation of RBCs in microvessels plays a key role in the regulation of oxygen delivery. The deformability of RBCs can be reduced, for example, in diseases such as diabetes mellitus (8) and sickle cell anemia (9).

The flow behavior of related systems containing deformable particles with elastic membranes is also interesting, such as suspensions of elastic microcapsules, which have been suggested as potential drug carriers (10, 11). Therefore, it is very important to understand the general problem of “elastic vesicles” in microcapillary flow. Such a system is characterized by the bending and shear elasticity of the membrane, the reduced volume of the vesicle, the volume fraction of vesicles in the solution, the capillary radius, and the flow velocity.

Under flow, individual lipid vesicles and RBCs show a complex behavior already at high dilution. For example, in simple shear flow, various dynamic states have been found for lipid vesicles, such as steady tank-treading, unsteady tumbling, oscillatory motion (12–16), and flow-induced shape transitions (17–19). In narrow capillaries, individual RBCs adopt a parachute shape at higher flow velocities (8, 20–26).

However, much less is known about the collective flow behavior at higher volume fractions of lipid vesicles and RBCs in confined geometries. The volume fraction of RBCs in human blood is large, with a hematocrit H ≃ 45%. In microvessels, the tube hematocrit H_T is lower, because of entrance effects from a larger vessel and the Fahraeus–Lindqvist effect (depletion layer near the walls), and can be reduced to H_T ≃ 10–20% with large fluctuations (27). At these concentrations, the interaction between RBCs strongly affects the flow behavior. The flow behavior of RBCs at physiological conditions in wider capillaries (with a tube diameter of several RBC diameters) has been studied recently by computer simulations (28–30). In contrast, we focus here on flows in narrow capillaries, where the tube diameter just exceeds the cell size. Our study is motivated by recent developments of microfluidic devices (31) that allows the investigation and manipulation of individual liquid droplets (32) and cells (8, 9, 33, 34). We used computer simulations to study RBC-like vesicles, which have the same reduced volume as real RBCs, but a lower bending rigidity and shear modulus. We investigated both the clustering of RBC-like vesicles at low volume fractions and their shapes, arrangements, and flow resistance at high volume fractions.

Results

We studied the hydrodynamic behavior of RBC-like vesicles in a narrow cylindrical capillary with a radius R_cap = 1.4 R₀. We considered only the hydrodynamic interaction and excluded-volume repulsion between RBCs, but excluded attractive interactions and depletion effects; this condition corresponds to RBC suspensions without fibrinogen and other plasma proteins that induce RBC aggregation (35). To model RBCs in capillary flow, we used multiparticle collision dynamics (MPC) (36), a particle-based mesoscale simulation technique, to describe the fluid hydrodynamics and a triangulated-network model for the composite membrane (18, 26). The membrane is impenetrable to the fluid and is characterized by a bending rigidity κ and a shear modulus μ. The model RBCs have a reduced volume V* = V/(4πR₀³/3) = 0.59, where the thermal-equilibrium shape of a lipid vesicle is a biconcave disk (discocyte) (2, 17).

We considered pressure-driven flow that is characterized by the mean flow velocity v₀ in the absence of RBCs. Our results are presented in dimensionless quantities (denoted by *), i.e., length and time are given in units of the capillary radius R_cap and the characteristic shape relaxation time τ = η₀ R_cap³/κ, respectively, where η₀ is the viscosity of the embedding fluid. Details about the model and simulation technique can be found in Methods. To investigate many-body effects in the capillary flow of RBCs, we considered a number n_ves of vesicles in tube segments of length L_z with periodic boundary conditions in the flow direction. We compared the flow behavior of a single elastic vesicle (n_ves = 1) in a short tube segment (corresponding to an infinitely long tube with a regular array of identically-shaped RBCs) with that of n_ves = 6 elastic vesicles in a longer tube segment with the same or similar volume fraction.

Regular Arrays of RBCs.

For n_ves = 1, the RBC-like vesicles are located near the center of the capillary because of the hydrodynamic lift force (37, 38) near the capillary wall. For low volume fractions (i.e., large L_z/R_cap), it was shown in ref. 26 that RBCs retain their discocyte shape for small v*₀ ≡ v₀τ/R_cap, but adopt a parachute-like shape for large v*₀ (see Fig. 1A). For larger vesicle volume fractions, this transition is strongly affected by the hydrodynamic interaction between vesicles, because the flow field near a vesicle is modified by the presence of its periodic images. For RBC distances L*_ves ≡ L_z/n_vesR_cap ≳ 1.5, the transition is abrupt at constant v*₀ = v*_c ≃ 5, and the vesicle shape is independent of L*_ves. However, the transition becomes gradual for small vesicle distances L*_ves ≲ 1.5, and a shallow bowl shape is observed, because neighboring vesicles partially shield the flow forces at high volume fractions. The critical distance L*_ves ≃ 1.5 is consistent with the theoretical predictions obtained by solving the Stokes equation for the flow of a periodic array of rigid spheres (39); here the spheres are hydrodynamically isolated for L*_ves ≥ 2.

Fig. 1.

Conformations of elastic vesicles for various densities and mean flow velocities v*₀, for a single vesicle in the simulation cylinder (n_ves = 1) with various lengths L*_ves. The hematocrit is given by H_T = n_vesV_ves/πL_zR_cap² = 0.28/L*_ves, where V_ves is the volume of single vesicle. (A) Average asphericity 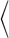α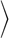, which measures the deviation from a spherical shape, as a function of the mean flow velocity v*₀. Here, the asphericity is given by α = [ (λ₁ − λ₂)² + (λ₂ − λ₃)² + (λ₃ − λ₁)²]/2R_g⁴, with the eigenvalues λ₁ ≤ λ₂ ≤ λ₃ of the gyration tensor and the squared radius of gyration R_g² = λ₁ + λ₂ + λ₃. RBCs transits from the discocyte (with 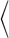α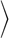 ≃ 0.15) to the parachute shape (with 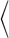α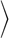 ≲ 0.05). Simulation snapshots show the parachute (Lower Left) and bowl (Upper Right) shapes for v*₀ = 7.7 with L*_ves = 2.25 and L*_ves = 1, respectively. (B) Average inclination angle 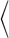θ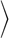 for a discocyte vesicle for low flow velocities v*₀ < v*_c, as a function of the vesicle distance L_ves. The inclination angle θ measures the deviation of the vesicle symmetry axis (determined by the eigenvector associated with the minimum eigenvalue of the gyration tensor) with the flow direction (z axis).

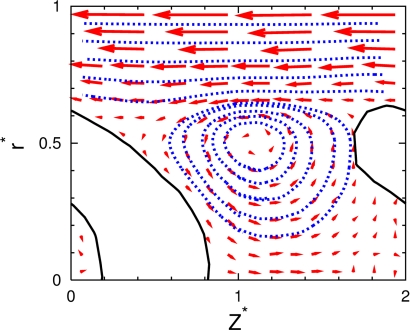
Because of the interplay between the rigid motion of the (deformed) RBCs and the ideally parabolic flow profile of the fluid, an interesting flow pattern emerges between neighboring RBCs. In a comoving frame, a vortex appears, which is called a “bolus” (39). This fluid motion is very nicely revealed in our simulations (see Fig. 2). A similar bolus has been observed experimentally for RBC flow in glass capillaries by tracking the motion of small colloidal particles in the fluid (21).

Fig. 2.

Streamlines (blue) and velocity field (red arrows) of the flow between 2 vesicles, in the comoving frame with the vesicle velocity at L*_ves = 2 (H_T = 0.14) and v*₀ = 10. A sliced snapshot (black line) of the vesicle is also shown. A flow vortex (bolus) is seen between vesicles.

Although RBCs retain a discocyte shape for small flow velocities (with v*₀ < v*_c), hydrodynamic interactions are strong enough to determine the orientation of the disks for L*_ves ≲ 2.5. With decreasing L*_ves, the rotational symmetry axis turns continuously from a perpendicular to a more parallel orientation [with respect to the flow (z) direction] (see Fig. 1B). The inclination angle 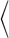θ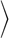 is essentially independent of v*₀, because the shape deformation caused by flow forces is weak.

RBC Arrangements at High Hematocrit.

The main aim of our simulations, the investigation of clustering and spatial arrangements of RBC-like vesicles in capillary flow, requires more systems with several particles. We focus on n_ves = 6 vesicles in a longer tube segment, again with periodic boundary conditions. Compared with the results for regular arrays in the previous section, the flow behavior changes drastically.

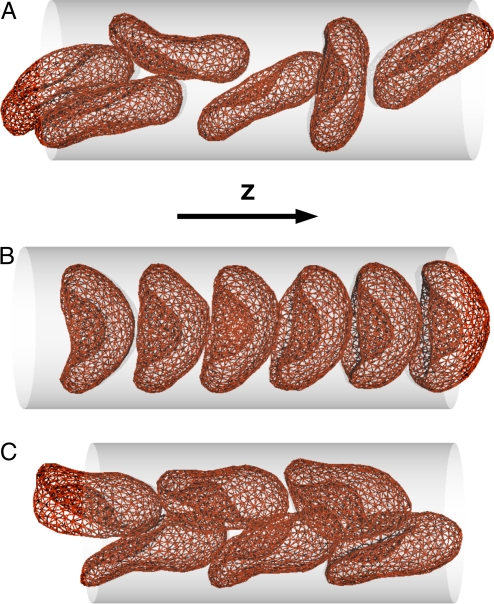
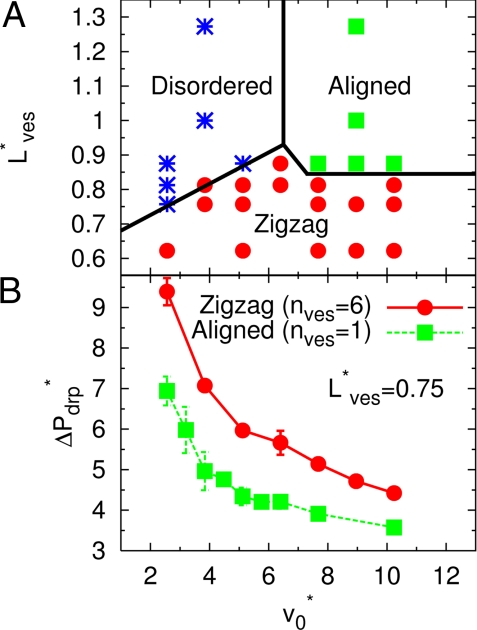
We consider first the case of high volume fractions (see Figs. 3 and 4). After switching on a slow flow, the uniformly-tilted discocytes of Fig. 1B now exist only for a short time, and then relax into a “disordered-discocyte” phase with random orientations (see Fig. 3A). In this phase, no significant long-range spatial correlations are present, whereas transient clusters of 2 or 3 stacked discocytes are observed frequently. The “aligned-parachute” phase, which is expected from the single-vesicle simulations (26), remains stable only for large L*_ves ≳ 0.85 (corresponding to H_T = 0.28/ L*_ves ≲ 0.33) (see Fig. 3 B and C). For high flow velocities and smaller L*_ves, a new “zigzag” phase appears. In this phase, slipper-shaped RBCs form 2 regular, interdigitated parallel rows. For an isolated RBC, the slipper shape appears only as a transient metastable state at velocity near the discocyte-to-parachute transition (26); in contrast, in the zigzag phase, the hydrodynamic interactions between interdigitated vesicles stabilize the slipper shape. A similar zigzag conformation of slipper RBCs was observed experimentally in glass capillary (21) and microvessels (20). Of the 3 phases shown in Fig. 4A, only the aligned-parachute phase is axisymmetric; therefore, the assumption of axial symmetry in previous calculations (22–25) is often not justified.

Fig. 3.

Snapshots of n_ves = 6 elastic vesicles in the simulation channel. (A) Disordered-discocyte phase for L*_ves = 0.875 (H_T = 0.32) and v*₀ = 2.5, where vesicles appear usually as discocytes; the degree of shape deformation increases with increasing v*₀. (B) Aligned-parachute phase for L*_ves = 0.875 (H_T = 0.32) and v*₀ = 10. (C) Zigzag-slipper phase for L*_ves = 0.75 (H_T = 0.37) and v*₀ = 10.

Fig. 4.

Phase diagram and pressure drop of dense RBC suspensions in flow. (A) Phase behavior as a function of average vesicle distance L*_ves and mean flow velocity v*₀ for n_ves = 6. The hematocrit varies between H_T = 0.22 and H_T = 0.45, because H_T = 0.28/ L*_ves. Symbols represent the disordered-discocyte (*), aligned-parachute (■), and zigzag-slipper (●) phases, respectively. The phase boundaries are drawn to guide the eye. (B) Pressure drop ΔP*_drp per vesicle for the aligned-parachute phase (simulations with n_ves = 1) and the zigzag-slipper phase (simulations with n_ves = 6) at the same volume fraction (L*_ves = 0.75, corresponding to H_T = 0.37). The pressure drop is given by ΔP*_drp = ΔP_drpR_cap/η₀n_vesv_m = 8 (v₀ − v_m)L_z/n_vev_mR_cap, where v_m is mean fluid velocity in the presence of vesicles.

Interestingly, the zigzag phase for n_ves = 6 produces a larger pressure drop ΔP*_drp than the periodic parachute phase for n_ves = 1 under equivalent conditions, as shown in Fig. 4B. Thus, the zigzag phase is stable despite its higher viscous dissipation, which implies that flow effects are so strong that they drive the system outside the “linear-response” regime [which is characterized by minimal entropy production (40)]. The mechanism may be the destabilization of the aligned-parachute phase caused by thermal fluctuations, which can be explained as follows. As one vesicle moves away from the center by the thermal fluctuations, it slows down, whereas the fluid flow on the other side increases; this flow pushes the subsequent vesicle in the opposite direction (see Movie S1). When this force exceeds the lift force from the wall, axisymmetric conformations become unstable. Although we did not observe a 2-phase coexistence at the present condition (R_cap = 1.4 R₀), the parachutes stayed aligned for a short time, which indicates that this phase would be metastable in the absence of the thermal fluctuations. Simulations for a smaller capillary radius R_cap = 1.2 R₀ show that the zigzag and parachute phases can coexist. Therefore, the transition between these 2 (meta) stable configurations is discontinuous at smaller R_cap, but becomes continuous because of thermal fluctuations at larger capillary radii.

To investigate the sensitivity of our results to the number of vesicles in the simulation channel, we have also performed some simulations with n_ves = 3, 4, and 5. The results show that for n_ves = 6 the results for the pressure drop are well converged. The zigzag phase is clearly favored by an even number of vesicles. It is therefore interesting to note that we also found a zigzag phase for n_ves = 5; however, in this case one of the vesicles forms a “defect” in the regular arrangement.

Finally, we want to briefly discuss the effect of the elastic parameters on the phase behavior. We have to distinguish 2 contributions, the magnitude of the elastic moduli and their ratio, which is characterized by the Föppl–van Karman number μR₀²/κ. The magnitude of κ and μ mainly affect the location of the discocyte-to-parachute transition, which increases linearly with increasing stiffness, as shown for isolated vesicles in ref. 26 (see Methods for more information). This result can be used to predict the dependence of the disordered-to-aligned transition in Fig. 4A on κ and μ. More subtle is the dependence of the phase diagram on the Föppl–van Karman number. Vesicle shapes become more pointed at the rear edge for larger μR₀²/κ; however, this should only weakly affect the flow behavior. Indeed, a comparison of the phase diagrams at high H_T for κ/k_BT = 20, μR₀²/κ = 5.5 and κ/k_BT = 10, μR₀²/κ = 44 yields a quantitatively similar behavior.

RBC Clustering in Dilute Suspensions.

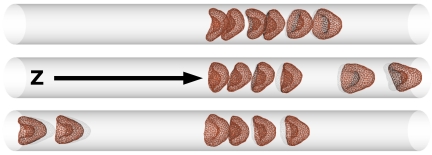
Next, we investigated the hydrodynamic interactions between vesicles in a dilute suspension by simulating n_ves = 6 vesicles in a capillary of length L*_z = 20 (corresponding to H_T = 0.084), at flow velocities above the discocyte-to-parachute transition point, v*₀ > v*_c ≃ 5. Vesicles approach each other and form clusters (see Fig. 5). As shown in more detail below, the physical origin of cluster formation is 2-fold. First, a single, free vesicle flows faster than a cluster of several vesicles, because it becomes more deformed by the flow and can stay closer to the center of the capillary. Second, cluster life time is increased because of hydrodynamic attractions. Clusters can break up and form new clusters. In most of these cases, a n-vesicle cluster breaks up into a (n − 1)-vesicle cluster and a free vesicle, which then rejoins the neighboring cluster (see Movie S2).

Fig. 5.

Sequential snapshots of 6 elastic vesicles in dilute suspension (H_T = 0.084) at v*₀ = 7.7.

The spatial pair-correlation function G(z*_nb) between the center-of-mass positions of the vesicles along the z direction (see Fig. 6A) shows several clear peaks of neighboring vesicles in the clusters. In contrast, hard-sphere particles in thermal equilibrium in a 1D channel show hardly any spatial correlations at such a low volume fraction (41). The nearest-neighbor distance z*_nb ≃ 1.1 is slightly below the critical length L*_ves ≃ 1.5, where hydrodynamic interactions start to affect the vesicle deformation for n_ves = 1 (see Fig. 1A). Thus, the vesicles in clusters hydrodynamically interact with each other, but separated clusters are hydrodynamically isolated.

Fig. 6.

Pair distribution function G(z*_nb) (A) and cluster-size probabilities P(n_cl) (B) in dilute suspension with H_T = 0.084. The black and red solid lines represent data v*₀ = 7.7 and 10, respectively. Results are obtained from simulations with n_ves = 6 vesicles. The dotted line in A represents the pair distribution function of only the nearest-neighbor vesicles at v*₀ = 10. In B, vesicles closer than 2.5 R_cap are defined to belong to the same cluster.

Fig. 6B displays the probability P(n_cl) = n_cl f(n_cl)/Σ′_ncl n′_clf(n′_cl),of finding a cluster containing n_cl vesicles, where f(n′_cl) is the total number of clusters of size n′_cl that appear during a simulation run. The probability exhibits a minimum for a 5-vesicle cluster, because such a cluster can only pair with a single free vesicle, which has a very short lifetime. Two 3-vesicle clusters, or a 2- and a 4-vesicle cluster, can exist as pairs, because their mean velocities are identical or differ only slightly, respectively, so that they have longer lifetimes than single vesicles. As v*₀ decreases approaching the critical velocity v*_c of the discocyte-to-parachute transition, the shape fluctuations of the vesicles increase. Therefore, break-up events occur more often and the peaks of G(z*_nb) become smaller (see Fig. 6). Because 6-vesicle clusters disturb the Poiseuille flow less than 6 separated vesicles, the pressure drop ΔP*_drp per vesicle in clusters is smaller than for single vesicles. This is similar to the “peloton effect” for liquid drops discussed in ref. 32.

For larger flow velocity, v*₀ = 10, the peak of the cluster containing all vesicles in our simulation system becomes very pronounced. Based on this result, we predict that RBCs in microvessels will form very large clusters, with large RBC-free regions in between. This idea is consistent with the experimental observation that in capillary blood flow in vivo, large temporal fluctuations of H_T are observed (27); long chains of rushing RBCs are seen in one period, but no RBCs at all are seen in another period. Also, clusters of a few RBCs have been observed in RBC flow through glass capillaries (21).

The behavior of vesicles is quite different from that of spherical colloids in capillary flow for R₀ > R_cap/2. Because of the absence of a lift force (as a consequence of the reversibility of the Stokes equation), we expect these colloids to move with different velocities depending on their distance from the wall, and thus to see jamming when fast particles try to overtake slow ones. Thus, it is the driving of the system by the external flow in combination with hydrodynamic interactions and vesicle deformation, which give rise to the novel flow behavior described above. The intricate interplay between these effects leads to the cluster-size dependence of vesicle deformation, the focusing of vesicles in the center of the flow, and the effective hydrodynamic attractions caused by vortex formation between subsequent vesicles (see Fig. 2).

Summary

We have shown that mesoscale hydrodynamics simulations reveal a complex flow behavior of RBC-like vesicles in microchannels. This type of cell flow study in silico can be used in the future to address many questions in microfluidic flows, such as the dependence of flow properties on the channel geometry or changes in flow behavior caused by disease-related variations of the membrane elasticity.

Methods

Mesoscale Hydrodynamics.

MPC (36) is a particle-based hydrodynamics method, where fluid is described by point-like particles with mass m and number density n_s. The MPC algorithm consists of 2 alternating steps: a free streaming of particles and a collision step where the particles are first sorted into the cells of a cubic lattice with lattice constant a, then the particle velocities, relative to the center-of-mass velocity of the cell, are rotated by an angle of π/2 about a randomly chosen axis. The momentum and energy are conserved. We use a fluid density n_s = 10/a³ and a capillary radius R_cap = 8 a, which implies that the number of fluid particles is ≈200,000 for the largest systems studied.

Membrane Model.

Each elastic vesicle is modeled as a collection of 500 vertices interconnected by 2 triangular networks of bonds (3, 5, 26), a fixed network whose bonds are harmonic springs, and a dynamically triangulated network (1) whose bonds undergo “flips.” The elastic, fixed network models the spectrin cytoskeleton of a RBC, whereas the fluid, dynamic network models the viscous lipid bilayer (18). The membrane vertices have an excluded-volume interaction through a repulsive potential. The minimum distance between vertices on 2 different vesicles is l_min = 0.77 a, which is larger than that between 2 vertices on the same membrane (l_min = 0.67 a) to prevent interpenetration of 2 neighboring vesicles. The bending and shear modulus of RBCs have been measured to be κ/k_BT ≃ 50 and μR₀²/k_BT ≃ 10⁴, respectively, where k_BT is the thermal energy (42). These elastic parameters of RBCs are affected for various diseases (8, 9). We consider the more general case of elastic vesicles in microcapillary flow. In this study, we mainly used κ/k_BT = 20 and μR₀²/k_BT = 110, corresponding to a Föppl–van Karman number μR₀²/κ = 5.5, which is sufficient to produce parachute shapes in flow at higher flow velocities (26). We have also studied the flow behavior of vesicles with elastic moduli κ/k_BT = 10 and μR₀²/k_BT = 440, corresponding to a Föppl–van Karman number μR₀²/κ = 44.

RBCs in Flow.

The MPC fluid particles are scattered off the capillary walls or the membrane triangles via a bounce-back rule that produces no-slip boundary conditions (18). The volume and surface area of the vesicle are fixed by a global volume-constraint potential and a local area-constraint potential. The error bars are calculated from several independent simulation runs that started from different initial conditions. The results are independent of the initial conditions. With a RBC radius of R₀ = 3.4 μm and the viscosity η₀ = 10⁻³ Pas of water, we obtain R_cap = 4.6 μm and a characteristic velocity R_cap/τ = 4 μm/s. The other parameters were the same as described in ref. 26.

A gravitation force mg is used to generate flow along capillary (z) axis, which corresponds to a uniform pressure gradient ∇_z P = −mn_sg. In the absence of elastic vesicles, this field yields a mean flow velocity v₀ = mn_sgR_cap²/8η₀.

For an isolated elastic vesicle, the transition velocity from discocyte to parachute depends linearly on the elastic bending and stretching forces (26), v_m^cτ/R_cap = 0.1 μR₀²/κ + 4, where v_m is mean fluid velocity. Fluids inside and outside of the vesicle have the same viscosity η₀ and do not penetrate the membrane. We chose parameters to keep the Reynolds number low, Re < 1, in all simulations (26).