Economic decision-making compared with an equivalent motor task

Abstract

There is considerable evidence that human economic decision-making deviates from the predictions of expected utility theory (EUT) and that human performance conforms to EUT in many perceptual and motor decision tasks. It is possible that these results reflect a real difference in decision-making in the 2 domains but it is also possible that the observed discrepancy simply reflects typical differences in experimental design. We developed a motor task that is mathematically equivalent to choosing between lotteries and used it to compare how the same subject chose between classical economic lotteries and the same lotteries presented in equivalent motor form. In experiment 1, we found that subjects are more risk seeking in deciding between motor lotteries. In experiment 2, we used cumulative prospect theory to model choice and separately estimated the probability weighting functions and the value functions for each subject carrying out each task. We found no patterned differences in how subjects represented outcome value in the motor and the classical tasks. However, the probability weighting functions for motor and classical tasks were markedly and significantly different. Those for the classical task showed a typical tendency to overweight small probabilities and underweight large probabilities, and those for the motor task showed the opposite pattern of probability distortion. This outcome also accounts for the increased risk-seeking observed in the motor tasks of experiment 1. We conclude that the same subject distorts probability, but not value, differently in making identical decisions in motor and classical form.

In everyday life, we face many decision problems with the same formal structure. Rushing to class, for example, we may consider crossing a busy street against the light. The decision to cross or not to cross against the light can be represented by first listing all of the possible outcomes O₁, …,O_n (late for class, run over by a taxi, ticketed for jaywalking, etc). A decision to cross the street effectively assigns probabilities p₁,…,p_n to the outcomes, a decision not to cross assigns different probabilities p′₁, …,p′_n. An economist would immediately recognize that we are choosing between lotteries (p₁,O₁; … ;p_n,O_n) and (p′₁,O₁; … ;p′_n,O_n).

Decision-making is typically modeled as a choice among lotteries. A lottery consists of mutually exclusive outcomes (O₁, …,O_n) that have corresponding probabilities of occurrence(p₁, …,p_n), Σ_i=1ⁿp_i = 1. It is denoted by listing probability–outcome pairs (p₁,O₁; … ; p_n,O_n). An example would be a choice between (0.5,$10000; 0.5,$0) and (1,$4000); a 50:50 chance at $10000 or nothing versus a certain gain of $4000. If the subject knows the probabilities as well as the outcomes, then he is engaged in decision-making under risk (1). We will sometimes omit the 0 outcome and its associated probability; the first lottery in the example then becomes (0.5,$10000).

Recent research in perception and action indicate that performance in many perceptual and motor decision tasks that are formally equivalent to decisions under risk is remarkably close to the performance expected of an “ideal” observer or mover that maximizes expected utility (2–8). Observed performance in making perceptual and motor decisions is in sharp contrast to that found in decision-making under risk, where patterned deviations from utility maximization have been repeatedly demonstrated (9).

However, there are several important differences in experimental design that could account for the discrepancy. Subjects in previous perception and motor experiments made long series of choices and accumulated winnings over the course of the experiment. Economic decision-makers faced with series of decisions spontaneously move closer to maximizing expected utility in decision-making under risk (10–12). Furthermore, the gain or loss associated with each trial in the motor tasks was small and feedback was immediate. Studies of risky choice found that subjects are closer to maximizing expected value for small stakes (13, 14) and when subjects receive considerable feedback over the course of the experiment (15). Consequently, we cannot conclude from previous experiments that performance in decision-making under risk is different from performance in an equivalent visual or motor task.

In this study, we conducted 2 experiments in which we eliminated these differences in experimental design and directly compared decision under risk with a precisely equivalent motor task. In experiment 1, we paired a classical lottery task (16, 17) intended to test for failures of the independence axiom of expected utility theory (EUT) (18) with an equivalent motor task. Each subject completed both the classical experiment and its motor analogue, allowing us to directly compare performance across task modalities within subject. In experiment 2, we extended the first experiment to parametrically estimate and compare the subjective transformation of both outcome value and probability between economic and motor decision tasks in the framework of cumulative prospect theory (CPT) (19). We could then compare how each subject made use of probability and value information in motor and classical tasks.

Experiment 1

The goal of experiment 1 is to compare economic decision-making with an equivalent motor task and test the independence axiom of EUT in both modalities. We will first describe how we translate a lottery to an equivalent motor task and then introduce the independence axiom of EUT and explain why we are testing it.

Construction of a Motor Lottery.

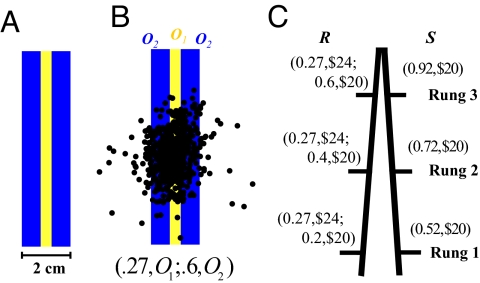
On each trial in a rapid-pointing task, the subject had only 700 ms to attempt to touch a target configuration on a touch screen with his/her index finger. Fig. 1A illustrates a typical target configuration. Subjects received the highest payoff O₁ if they hit the yellow stripe, second highest payoff O₂ for hitting either of the same-sized blue regions symmetrically placed around the yellow stripe, and 0 for hitting anywhere else on the screen. Because the subjects had to complete movements in a short period (700 ms), they were not fully in control of the outcome of their planned movements. This uncertainty in movement, referred to as motor uncertainty here, has been proposed to arise from the accumulation of online neuromuscular noise (20) or more recently, firing rate variability during movement preparation (21). In Fig. 1B we superimposed the movement endpoints from one of our subjects on the target configuration. In past work we found that the endpoint distribution was very close to an isotropic Gaussian (6–8), and in the current experiment we verified that each subject's end point distribution was also close to an isotropic Gaussian and estimated the single parameter σ that characterized the Gaussian separately for each subject (see Materials and Methods). The end point distribution induces a probability distribution over the possible outcomes (O₁,O₂,O) conditional on the subject's motor uncertainty. For this subject, the configuration shown was equivalent to a lottery (0.27,O₁; 0.6,O₂; 0.13,0). To distinguish such a lottery from the “classical” lottery, where probability information is explicitly given, we refer to a lottery of this type as a “motor lottery.” Subjects were first trained to hit target configurations similar to the one we just described until their performance had stabilized and we could reliably estimate σ. We emphasize that, during training, the subjects simply tried to hit target configurations, a simple motor task; they did not choose between motor lotteries as they would in the main experiment (see Materials and Methods).

Fig. 1.

Construction of a motor lottery and task design. (A) A stimulus configuration containing 2 non-zero monetary outcomes, O₁ and O₂, where O₁ > O₂ > O. The subject earned O₁ by hitting the yellow bar, O₂ by hitting either of the blue bars, and O if his/her movement endpoint fell elsewhere on the touch screen. The subject had to complete the pointing movement in <700 ms to avoid a large penalty. (B) From one subject with motor uncertainty σ = 6.57 mm, 623 movement endpoints were superimposed on the configuration. For this subject, this configuration was equivalent to a lottery (0.27,O₁; 0.6,O₂; 0.13,O). (C) Common consequence task. The bottom rung was the pair R (0.27,$24; 0.2,$20,0.53,0) and S (0.52,$20; 0.48,0). Each higher rung was constructed by adding a “common consequence” (0.2,$20) to both lotteries in the rung below it. The lottery in each pair with the higher probability of winning the highest amount ($24 in this example) and the zero outcome was designated as “riskier” (R), whereas the other lottery was designated as safer (S). If the subject's frequency of choosing the R lotteries is the same across rungs, his performance is consistent with the independence axiom.

The Independence Axiom.

The independence axiom specifies constraints on choice that any EUT decision-maker would exhibit. Suppose that a subject consistently prefers the lottery (0.33,$2500; 0.67,$0) to the lottery (0.34,$2400; 0.66,$0). This choice would be explained in terms of EUT by postulating that

where U (·) denotes the subjective utility of each outcome (22). Now, suppose we add a “common consequence” 0.66U($2400) to both side of Eq. 1. Then we have the inequality

consistent with a preference for the lottery (0.33,$2500; 0.66,$2400,0.01,$0) over receiving $2400 for sure. The independence axiom is simply the claim that adding such a common consequence should not alter preference. In experiments, however, subjects often violate this prediction (23–26). For the example above, Kahneman and Tversky (24) reported that 83% of the subjects chose (0.33,$2500; 0.67,$0) over (0.34,$2400; 0.66,$0). However, 82% of the subjects chose to receive $2400 “for sure” over (0.33,$2500; 0.66,$2400,0.01,$0).

One prominent interpretation of the violation of the independence axiom is that choosers distort probability information when making decisions (24). For example, in prospect theory (24), the probability weighting function was proposed to characterize the transformation of objective probability information to probability weight and used to explain such violations.

In experiment 1, we modified the common consequence design of Wu and Gonzalez (16, 17) to examine violations of the independence axiom of EUT in both classical and motor tasks. Subjects in the common consequence task faced a series of lottery pairs, in motor or classical form, and had to choose the one they preferred in every trial (see Materials and Methods). A schematic of the design is illustrated in Fig. 1C. The common consequence task is appropriate for a first comparison between decision-making in classical form and in motor form because one critical difference between them is how probability information is revealed. In the classical tasks, probability is explicitly given to the chooser. In the motor task, probability is not explicitly given: It is implicit in the subject's own motor uncertainty.

Results.

We first compared choice patterns between the classical and the motor lottery tasks at the group level. We adopted the terminology in Wu and Gonzalez (16, 17) in defining one lottery in each pair as the “riskier” lottery and the other lottery as the “safer” lottery: The riskier lottery always had both the higher probability of winning the highest monetary amount and also the higher probability of winning nothing (See Materials and Methods for detail). We wish to emphasize that there are alternative definitions of risk in the literature. For example, the variance of the probability distribution over outcomes is often used to define the level of risk for a lottery (26). In our design, the riskier lottery in each rung always had greater variance than the safer lottery.

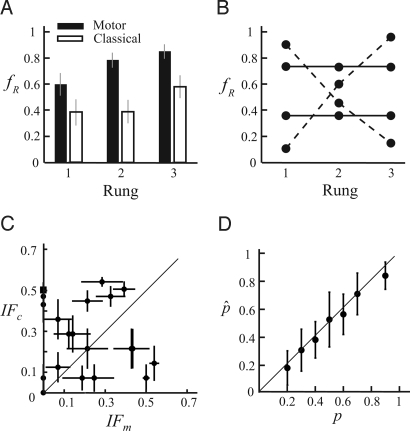
In Fig. 2A we plotted the mean frequency of choosing the riskier lottery, f_R (averaged across subjects) in the common consequence tasks. We found that the subjects on average chose the riskier lottery in the motor task more often than in the classical task across all rungs (P < 0.05 for each rung). In general, we found increased preference for the riskier lottery in the motor condition as the overall chance of winning increased. Compared with the motor tasks, subjects in the classical tasks tended to be more averse to risk. They tended to choose the safer lottery at rungs 1 and 2 and seemed to be indifferent between the riskier and the safer lottery at rung 3 (P > 0.05), when the overall probability of winning reached close to or above 90% for both lotteries.

Fig. 2.

Choice data in experiment 1. (A) Mean frequency (collapsed across subjects) of choosing the risky lottery f_R was plotted as a function of rung. (B) Hypothetical choice patterns. The solid horizontal lines represent hypothetical patterns of frequencies that do not vary across rungs, consistent with the independence axiom. The dashed lines correspond to patterns of choice that violate the independence axiom. (C) Index of failure. For each subject, we plotted IF of the classical tasks (IF_c) against IF of the motor tasks (IF_m). IF was computed by taking the standard deviation of f_R. The error bars correspond to ±1 SD computed by an application of Efron's bootstrap (27). (D) Averaged verbal estimates on the probability of hit (p̂) were plotted against estimates of probabilities (p) based on subjects' performance during training. The error bars represent ±1 SD of the subjects' verbal estimates.

Our second analysis focused on violations of the independence axiom in the two tasks. In Fig. 2B, we illustrate some possible choice patterns of the experiment. On the horizontal axis we plotted the rung of the ladder in the common consequence design and on the vertical the frequency of choosing the riskier lottery f_R in each pair. If a subject's performance is consistent with the independence axiom, then his probability of choosing the riskier lottery will be independent of the rung of the ladder. The 2 solid horizontal lines illustrate the possible performance of 2 hypothetical subjects in the task—one tends to prefer the riskier option, whereas the other tends to prefer the safer choice, but both conform perfectly to the independence axiom. In contrast, the dashed lines correspond to patterns of performance violating the independence axiom: Subjects change from risky to safe or vice versa as a function of rung.

To quantitatively examine violation of the independence axiom, we computed the standard deviation of f_R as an index of failure (IF) of the independence axiom. For example, IF = 0 indicates that f_R was constant across the rungs. The higher the IF, the less consistent in preference a subject is across the rungs.

In Fig. 2C, for each subject we plotted the IF of the classical tasks against the motor tasks. The error bars represent ±1 SD computed by an application of Efron's bootstrap (27). If subjects had lower IF in motor tasks, we would expect points to fall above the identity line. Among 20 subjects, we found that half of the subjects' IFs were smaller in the motor task than in the classical task, indicating that the independence axiom was violated to a lesser extent in the motor task in those subjects. For the remaining half, we found that 6 subjects showed greater violation of the axiom in the motor condition, whereas 4 did not differ between motor and classical. Although slightly more subjects violated the axiom to a lesser extent in the motor tasks, it was not conclusive that the subjects violated the axiom less in one task over the other.

Taken together, our results are consistent with the claim that subjects violated the independence axiom in both tasks to the same extent.

It is possible that the choice pattern observed in motor tasks reflected inaccurate estimates of the probabilities of hitting target bars. For example, the risk-seeking choice observed in the averaged subject's data (Fig. 2A) when the chance of winning was high could be due to an overestimation of the probability of hit. Therefore, we asked the subjects to estimate their probability of hitting selected targets at the end of the decision-making session. The averaged verbal estimates plotted as a function of probability (Fig. 2D) fell near the identity line when the probability was between 0.2 and 0.9. We will return to this point in Discussion.

To summarize, we found that the subjects exhibited different choice patterns between motor lottery and economic lottery tasks. When the probability was implicit in the subjects' own motor uncertainty, they tended to be more risk-seeking compared with their choices in the economic task, for which probability information was explicitly provided. We found no evidence that subjects were more prone to violate the independence axiom in one task more than the other.

Experiment 2

Violations of the independence axiom are often attributed to distortions of probability information (24). However, without explicitly estimating probability distortion, we cannot attribute differences in the choice patterns we observed in experiment 1 solely to different patterns of probability distortion. It is possible that both the subjective desirability of outcomes and the distortion of probability information contribute to the different patterns we observed between classical economic lottery tasks and motor lottery tasks.

In this experiment, we explicitly modeled and estimated the subjective transformation of both outcomes and probability. We asked the following question: Could the difference in subjects' choice between motor and classical be attributed to different patterns of use of probability information?

Estimating Model Parameters.

We extended the lottery task design in experiment 1 and parametrically estimated the distortion of information about value and probability in the framework of CPT (19). To keep our lottery task as simple as possible, all of the lotteries had only 1 non-zero outcome. CPT, proposed by Tversky and Kahneman (19) as a major upgrade of its predecessor, prospect theory (24), is a popular descriptive model of choice in psychology and behavioral economics. In CPT, both the subjective desirability of outcomes and the distortion of probability are modeled as transformations of objective quantities. The subjective desirability of outcomes O₁,…,O_n in lottery (p₁,O₁;…;p_n,O_n) is modeled by a value function with the following form:

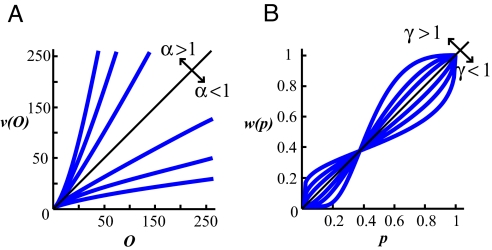
In the present context, we only consider O ≥ 0. In Fig. 3A, we plotted v(O) against O with several different values of α. It should be clear that v(O) is concave when α < 1, and convex when α > 1.

Fig. 3.

CPT. (A) The value function in CPT is used to model the utility of outcome (O) in a lottery. It has the form v(O) = O^α. Different curves showed different values of α. (B) The probability weighting function (w) characterizes the distortion of probability information. Here we illustrate several possible shapes of the probability weighting function with the form w(p) = exp[−(−ln(p))^γ], 0 < p < 1.

To model distortions of probability information, we used the following 1-parameter probability weighting function taken from Prelec (28):

A typical probability weighting function has an inverse S-shape, which captures overweighting of small probabilities (typically when p < 0.35) and underweighting of moderate-to-large probabilities. This shape has been consistently inferred from subjects' choice data (16, 17, 19, 28). In Fig. 3B, we plotted possible values of γ in Eq. 4: When γ < 1, w(p) exhibited the typical shape. However, when γ > 1, the distortion goes in the opposite direction with underweighting of small probabilities and overweighting of moderate to large probabilities.

It should be noted that CPT is a rank-dependent model: The outcome–probability pairs in the lottery are ranked according to the outcome values. The cumulative prospect of a lottery is the sum of the rank ordered value of each outcome v(O) weighted by its decision weight. By definition, decision weight is not always equivalent to the probability weight in this model except for the most extreme outcome(s) (positive or negative). In this experiment, however, all of the lotteries had only 1 non-zero outcome. Hence, the decision weight of the non-zero outcome is indeed the probability weight. This simpler lottery design avoided possible complexities resulting from the rank-dependent assumption.

The design and methods in experiment 2 were identical to experiment 1 except that we expanded the range of both outcome and probability in the lottery task so that we could reliably extract the value function and the probability weighting function for each subject and we changed the timing within trials (see Materials and Methods for details). For the details of our parameter estimation procedure, please see SI Materials and Methods.

Results

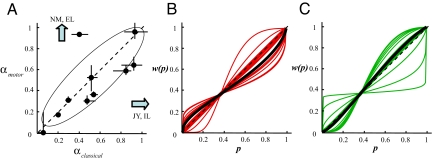
In Fig. 4A, for each subject we plotted the estimate of the value function parameter α in the motor task (α_motor) against α in the classical task (α_classical). Each data point represents a single subject. The error bars represent the interquartile range computed through an application of Efron's bootstrap method (27). If the subjects did not differ in the value function between the 2 tasks, then the points should fall on or near the diagonal line. We found that, in 10 of 14 subjects, α_motor was not significantly different from α_classical (z test, p > 0.05). For the remaining 4 subjects, whose data points were not shown in the graph, 2 exhibited greater α_motor (subjects N.M. and E.L.), whereas the other 2 showed greater α_classical (subjects J.Y. and I.L.). The median (n = 14) of α_motor = 0.5603 was identical to the median of α_classical = 0.5604. In brief, there is no significant difference across subjects in the use of value information between the 2 tasks.

Fig. 4.

Parameter estimation results in experiment 2. (A) The estimate of the value function parameter, α, in the motor task (α_motor) is plotted against the parameter estimate in the classical economic task (α_classical). Each point represents a single subject. The error bars represent the bootstrap interquartile range. Ten of the 14 subjects' results are shown in the graph. The results for the other 4 subjects fall outside the area of the plot as indicated in the graph. (B) The estimated probability weighting function w(p) in the economic task is plotted for each subject (red). The dashed line indicates the identity line, whereas the black thick curve indicates the median w(p). (C) The estimated w(p) in the motor task is plotted for each subject (green). The black thick curve indicates the median w(p).

In Fig. 4 B and C, we plotted the estimated probability weighting function w(p) for each subject in the classical task (Fig. 4B) and in the motor (Fig. 4C). Each curve represents 1 subject. The dark, thick curve in each graph indicates the median w(p). We found that most subjects in the classical task (11 of 14) tended to exhibit the typical shape of the weighting function (γ < 1); most subjects overweighted small probabilities and underweighted moderate-to-large probabilities. The results in the motor task were markedly different: only 3 subjects of 14 had a value of γ < 1; the remaining 11 of 14 showed the opposite pattern (γ > 1), underweighting small probabilities and overweighting large. We tested whether the distribution of subjects with γ < 1 differed in the 2 tasks and found that they did (Fisher's exact test, p = 0.0070).

In the paper that attempted to formally address the relation between subjects' choice pattern and the curvature of the probability weighting function, Wu and Gonzalez (16) proposed that, assuming a concave value function, the concavity in w(p) is associated with increased risk seeking, whereas convexity is associated with increased risk aversion. Because most subjects' value functions were concave (α < 1), the result that most subjects' w(p) were concave when probability was moderate to large would predict increased risk-seeking in the motor task. In fact, this prediction is consistent with the result in experiment 1 in the motor task given that the subjects showed increased frequency of choosing the riskier option when the overall probability of winning was from 0.5 to 0.9.

To summarize, in this experiment we found that, although most subjects did not show significant differences in their estimated value functions between the 2 tasks and there was no obvious pattern of difference across subjects, the probability weighting functions observed in the 2 tasks were markedly different. Although most subjects showed the typical shape of the weighting function in the classical tasks, all but 3 of 14 subjects showed the opposite pattern of distortion in the motor task. That is, when the probability was implicit in the subjects' own motor uncertainty, subjects tended to underweight small probabilities and overweight moderate-to-large probabilities. The results serve as evidence to parametrically reveal, on a subject-by-subject basis, differences in the probability weighting function that are task-dependent and that are subject to how probability information is revealed to the chooser.

In both of the experiments reported here, EUT failed to predict performance in both motor and classical decision-making tasks, though for different reasons. Although expected utility maximization is often treated as a benchmark against which performance is measured in experimental investigations of perceptual and motor performance, there are alternative systems of preferences over lotteries that are complete and transitive but do not lead to maximization of expected utility (29). In evaluating human performance, researchers should consider the possibility that in focusing on EUT as a benchmark for human performance we have mistaken the actual goals implicit in human decision-making.

Discussion

In modern decision research, it has been systematically and repeatedly demonstrated that human choice in economic decision tasks deviates from the predictions of EUT (9, 23–26). Recently, results from various perceptual and motor decision tasks suggested that humans come close to maximizing expected utility in their performance (see ref. 30 for review). What is intriguing is that many of these tasks possessed lottery structures and hence are a form of decision under risk. One critical difference between the perceptual or motor tasks and the classical lottery tasks used in decision under risk was how probability information was revealed to the chooser. In the classical economic tasks, information about probability was stated explicitly to the subjects. In the perceptual or motor tasks, the probability information was implicit in the subjects' perceptual or motor uncertainty. However, because of differences in experimental design, none of the studies to date can be considered as a valid comparison between economic decision under risk and motor or perceptual decision under risk.

In this study we investigated how economic decision-making differed from motor decision making by developing a method to translate the classical economic tasks to an equivalent motor task. In experiment 1, we examined the violation of the independence axiom of EUT, a well-established finding in human economic decision-making, in economic tasks and in motor tasks with equivalent design and on a subject-by-subject basis. Our results revealed that subjects' choice pattern differed between the motor and the economic tasks: Subjects in the motor task tended to choose the riskier option more often and, as the overall probability of winning increased, showed more preference toward the riskier option (Fig. 2A). Additionally, the independence axiom was violated to roughly the same extent in both tasks by most subjects.

Based on the results in experiment 1, it is not clear whether we could attribute different choice patterns between classical and motor tasks solely to possible differences in the way probability information is distorted. To explicitly test this hypothesis, in experiment 2 we extended the concept of experiment 1 but expanded the range of outcome values and probabilities so that we could parametrically estimate the subjective transformation of both outcome and probability within the framework of CPT.

We found no evidence of a patterned difference in subjects' value functions across the 2 tasks. However, the shape of the probability weighting function was markedly different. Subjects in the classical economic task exhibited the typical shape of the weighting function: They tended to overweight small probabilities and underweight moderate-to-large probabilities. On the other hand, the same subjects showed the exact opposite pattern of distortion in the motor task: They tended to underweight small probabilities and overweight moderate to large probabilities. As reported in the discussion of Fig. 2D, subjects had accurate estimates of their probability of success in the motor task and consequently the differences in probability weighting functions found in experiment 2 correspond to an actual difference in the use of probability information.

Our results are closely connected to an area of research that investigates how experience in decision making could affect choice and the use of information. It has been pointed out that experience with payoff distribution of different options could alter choice (12, 15, 25, 26), which can be attributed to changes in the shape of the probability weighting function (25). It is now widely recognized that subjects perceive outcomes and probability differently when engaged in an experience-based decision compared with tasks for which information about outcome and probability are given explicitly to the subjects (25, 26). In field experiments, List and colleagues (31–33) showed how experiences in the marketplace could eliminate choice anomalies (e.g., the endowment effect) typically observed in inexperienced subjects. Our results tie closely to both lines of research to the extent that motor decision-making is a kind of experience-based decision-making. The subjects acquired the knowledge about probability through repeatedly performing a rapid-pointing task during the initial motor-training session (see Materials and Methods). In essence, probability is implicit in the subjects' experience in the pointing task during training. What we found in experiment 2 is that when probability information is implicit in the subjects' motor experience, the typical probability weighting function is the mirror reflection of the typical shape that has been shown in many previous studies for which probability was explicitly provided to the subjects.

Given that probability weighting functions change with task, it is natural to ask what determines the probability weighting function in any particular task. Certainly novelty is a possible factor but so is, for example, possible beliefs about locus of control: If subjects believe they can control their motor uncertainty, for example, they may be willing to accept what is objectively greater risk even though we know that they cannot, based on measured performance in a large number of studies. A complete theory of decision-making requires a characterization of the effects of experience and task modality on choice and how information about outcome value and probability are used when making decisions.

Materials and Methods

Subjects and Instructions.

Twenty subjects (9 male, 11 female) in experiment 1 and 14 subjects (7 male, 7 female) in experiment 2, all from the Department of Psychology and Center for Neural Science at New York University, participated in the experiments. All subjects gave informed consent and were paid $12/h for participation plus a possible bonus (see “Lottery execution” in Procedure for details). All were unaware of the purpose of the experiment.

Procedure.

The procedure in both experiments was identical. There were 2 sessions in the experiment, the motor-training session and the decision-making session. We wish to emphasize that during motor-training, the subjects did not know about the later decision making session.

Motor-training session.

Subjects learned to hit single target configurations similar to that shown in Fig. 1A. The training session consisted of 320 training trials that took ≈35–45 min to finish. There were 2 types of target configurations: a single yellow rectangular region (single-region configuration) or a more complicated region with 2 equally sized blue bars displayed symmetrically on the side of a yellow bar (multiregion configuration). In experiment 1, the subjects faced both kinds of configurations. In experiment 2, they faced only the single rectangular configuration.

In every trial, a target configuration was presented on a touch screen and subjects had only 700 ms to hit it. If she/he did not hit the screen within 700 ms after target presentation, she/he would lose 700 points. Hitting the central yellow stripe would earn a reward of 100 points ($0.05), whereas 50 points was the reward for hitting the blue region.

The goal of this session was, for the experimenter, to check whether the subjects' performance reached an asymptotic level so that we could reliably estimate his/her unique motor uncertainty. Typically, subjects' endpoint distributions in this task were very close to isotropic bivariate Gaussian as found previously (6–8), and we characterized motor uncertainty by estimating the SD (σ) of the distribution separately for each subject.

Decision-making session.

Subjects returned the following day after training to participate in the decision-making session. There were 2 types of tasks, an economic lottery task and a motor lottery task. In the economic task, the subjects chose between pairs of lotteries for which information about outcome and probability were explicitly given. The motor lottery task was created uniquely for each subject based on his/her motor uncertainty (σ) such that it is mathematically equivalent to the economic lottery task. Fig. 1A illustrates a possible motor lottery. Notice that in a motor lottery, information about probability was implicit in the subjects' own σ. As in the economic lottery task, in the motor lottery task the subjects were also instructed to choose the motor lottery they preferred. There was no constraint on choice time. The subjects were told that at the end of the experiment, two of the chosen lotteries (one from the motor lottery task, the other from the economic lottery task) would be selected at random and executed. As described below, the economic lottery was executed by a lottery machine, whereas the motor lottery was executed by the subjects' own movement in the rapid-pointing task.

In experiment 1, we modified the common consequence task in Wu and Gonzalez (16, 17). As shown in Fig. 2, the common consequence task contained 3 rungs. The bottom rung consisted of 2 lotteries, R (0.27,$24;0.2,$20) and S (0.52,$20). We adopted the terminology from Wu and Gonzalez and called the first lottery the riskier lottery (R) and the second lottery the safer lottery in the sense that R has a higher probability of winning the highest outcome ($24) among the two lotteries but also has a higher probability of winning nothing compared with the safer lottery (S). We note that this definition for the degree of risk is not unique; there are other definitions of risk used in the literature. For example, risk is sometimes defined as the variance of the probability distribution over outcomes in a lottery [see Weber et al. (26) and Preuschoff et al. (34)], We note that, in experiment 1, the riskier lottery in each rung according to Wu and Gonzalez' definition was also the lottery with greater variance. Each upper rung was constructed by adding a common consequence (0.2,$20) to the lower rung. For each rung, we slightly jittered the outcomes and the probabilities to create 8 repetitions. The payoff of O₁ ranged from $18 to $25 and (O₁ − O₂) was fixed at $4. The amount of jittering in both outcome and probability were always identical between the motor and the classical lottery tasks. The 2 tasks (classical lottery task and motor lottery task) were run in blocks, and the order in which subjects completed the economic and the motor block was counterbalanced across subjects. The subjects were unaware of the second block when performing in the first block.

In experiment 2, we modified the common ratio task in Kahneman and Tversky (24). All of the lotteries we created had only 1 non-zero outcome. The outcome ranged from gaining $30 to gaining $150 and was randomly chosen from a uniform distribution within this interval. The probabilities ranged from 0.2 to 0.96. Each task modality had 120 trials, making a total of 240 trials, which took ≈70 min to complete. There were 2 minor differences in design from experiment 1. First, in every trial, the lotteries were presented for 4 s and were followed by a short fixation period. After the fixation period, the lotteries reappeared and the subject had 1 s to indicate his/her choice by pressing a button. Second, in experiment 2, we did not run each task in separate blocks of trials. In 8 blocks of trials (32 trials per block), each block contained the same number of classical lottery tasks and motor lottery tasks presented at random order. For more details on the lottery design, see SI Materials and Methods and Fig. S1.

Lottery execution.

After the subjects completed the decision-making session, 2 of their chosen lotteries (one from the classical lotteries, the other from the motor lotteries) were selected at random. The 2 lotteries were then executed to determine the subjects' final payoffs of the experiment, which was the sum of the participation fee and the amount she/he won for playing the 2 lotteries. The classical lottery was executed by a computer-programmed lottery machine (experiment 1) or a lottery box that contained numbered ping-pong balls from which subjects picked 1 ping-pong ball out of 100 to determine whether she/he won or not (experiment 2). For the motor lottery, it was executed by the subjects performing a 1-shot pointing task to the selected motor lottery. We allowed the subjects to warm up as many trials as they wanted (the mean warm-up trials was 30) before doing the 1-shot task. The subjects were paid $12/h for participation in both experiment 1 and experiment 2. The maximum payoff of a lottery in experiment 1 was $25. Hence, the subjects could receive a bonus of up to $50 that depended on the outcome of lottery executions. The maximum payoff of a lottery in experiment 2 was $150; hence, the subjects could earn up to a $300 bonus. The subjects, on average, earned $67 in experiment 1 and $75 in experiment 2.