Abstract
Objective
To determine how alternative statistical risk-adjustment methods may affect the quality measures (QMs) in nursing home (NH) report cards.
Data Sources/Study Settings
Secondary data from the national Minimum Data Set files of 2004 and 2005 that include 605,433 long-term residents in 9,336 facilities.
Study Design
We estimated risk-adjusted QMs of decline in activities of daily living (ADL) functioning using classical, fixed-effects, and random-effects logistic models. Risk-adjusted QMs were compared with each other, and with the published QM (unadjusted) in identifying high-and low-quality facilities by either the rankings or 95 percent confidence intervals of QMs.
Principal Findings
Risk-adjusted QMs showed better overall agreement (or convergent validity) with each other than did the unadjusted versus each adjusted QM; the disagreement rate between unadjusted and adjusted QM can be as high as 48 percent. The risk-adjusted QM derived from the random-effects shrinkage estimator deviated nonrandomly from other risk-adjusted estimates in identifying the best 10 percent facilities using rankings.
Conclusions
The extensively risk-adjusted QMs of ADL decline, even when estimated by alternative statistical methods, show higher convergent validity and provide more robust NH comparisons than the unadjusted QM. Outcome rankings based on ADL decline tend to show lower convergent validity when estimated by the shrinkage estimator rather than other statistical methods.
Keywords: Nursing home, quality report cards, activities of daily living, risk adjustment, MDS
The quality of long-term care received by nursing home (NH) residents remains a persistent concern for consumers, their families and policy makers (Vladeck 1980; Institute of Medicine 1986; Capitman and Bishop 2004). Since the 1987 Nursing Home Reform Act, continued efforts have been made to establish a national system for assessing, monitoring, and publicly reporting NH quality (Morris et al. 1990; Zimmerman et al. 1995; General Accounting Office 2002; Mor 2004). In November 2002, as part of its Nursing Home Quality Initiative, the Centers for Medicare and Medicaid Services (CMS) launched a national report card with NH quality measures (QMs), the “Nursing Home Compare” website, that publishes and regularly updates a set of key outcome-based measures derived from the Minimum Data Set (MDS) (General Accounting Office 2002; Arling et al. 2007; Mukamel et al. 2008).
Making the facility performance data available to the public is expected to empower consumers to compare and choose NH services based on quality, and to stimulate quality improvement through market competition. Given its potential impact (Chernew and Scanlon 1998; Mukamel et al. 2004, 2007), it is critical that the QMs accurately differentiate homes with good quality from those with poor quality.
Because health outcomes are determined by both care quality and resident frailties and comorbid conditions, it is imperative to adjust for case mix variations among facilities before their outcomes are compared (Iezzoni 2003). Failure to do so may introduce a bias where facilities treating the sickest residents may have worse outcomes even when they provide the best of care. Many quality report cards for hospitals and physicians recognize this issue and provide risk-adjusted outcome rates. However, several studies have noted that the online NH QMs take only minimal steps to adjust for resident characteristics (General Accounting Office 2002; Arling et al. 2007; Mukamel et al. 2008), and may not sufficiently “level the playing field” for NH comparisons. These studies have advocated using more extensive, statistical risk adjustment in these QMs.
Despite the essential role of risk adjustment in making fairer outcome comparisons, however, risk adjustment may introduce an uncertainty (Iezzoni 1997) when alternative statistical methodologies do not agree on the identity of high-and low-quality providers (DeLong et al. 1997; Hannan et al. 1997; Iezzoni 1997; Shahian et al. 2001; Glance et al. 2006a; Li et al. 2007). A growing literature on this issue has focused on the use of appropriate severity measures for risk adjustment (Hannan et al. 1997; Iezzoni 1997; Shahian et al. 2001). More recently, analysts also examined the choice among statistical models, such as logistic or multilevel (random-effects) regression models, in computing and comparing risk-adjusted rates. Their findings suggest that alternative statistical methods may estimate outcomes differently (DeLong et al. 1997; Shahian et al. 2001; Glance et al. 2006a; Li et al. 2007).
This study was designed to explore the implications of alternative statistical methods—the classical, fixed-effects, and random-effects logistic models—in constructing and interpreting the national NH QMs. Focusing on 1 of the 19 outcomes currently published (Mukamel et al. 2008), we first developed extensively risk-adjusted measures using a common set of MDS risk factors but different modeling approaches. We then compared the current CMS QM (unadjusted) and these risk-adjusted measures in identifying outstanding or poor-performing facilities. The outcome examined was decline in activities of daily living (ADLs) for long-term care residents. We chose this outcome because physical function (as measured by ADLs) is central to the well-being of NH residents (Institute of Medicine 1986). Furthermore, it has been shown to be amenable to appropriate interventions (Granger et al. 1990; Spector and Takada 1991; Kane et al. 1996) and been used in various studies of NH quality (Mukamel 1997; Mukamel and Brower 1998; Rosen et al. 2000, 2001).
BACKGROUND
The MDS and NH QMs
In 1986, the Institute of Medicine's Committee on Nursing Home Regulation reported widespread quality deficiencies across the nation (Institute of Medicine 1986), and recommended strengthened NH regulations, revisions of oversight and enforcement mechanisms, and changes in quality assessment toward a more resident-centered and health outcome-oriented approach. Based on these recommendations, the Omnibus Budget Reconciliation Act of 1987 and subsequent legislations established new standards of NH care “to attain or maintain the highest practicable physical, mental, and psychosocial well-being” (Capitman and Bishop 2004). As a part of these efforts, the Health Care Financing Administration (now CMS) mandated the implementation of standardized, comprehensive Resident Assessment Instrument (RAI) for health assessment and care planning (Fries et al. 1997). A key component of the RAI is the MDS, a structured assessment tool for periodic collection of multiple domains of resident information, including physical function, cognition, emotion, behavior, nutrition, diagnoses, procedures, and treatments received (Morris et al. 1990; CMS 2002).
By virtue of their longitudinal nature, the MDS records can be used to document changes in resident conditions, such as functional decline or development of pressure ulcers, which can then be translated into meaningful quality-of-care indices (Zimmerman et al. 1995; Mukamel 1997; Rosen et al. 2001; Mor 2004). In a multistate demonstration sponsored by CMS, Zimmerman et al. (1995) developed a set of MDS-based clinical quality indicators (QIs). In April 2002, CMS began its pilot publication of a set of NH QMs in six states, and soon expanded it to national public reporting in November 2002. These QMs were partly selected from the QIs developed by Zimmerman et al. (1995) and partly from new development (Manard 2002). Currently, there are 19 QMs (14 for long-stay residents, and five for postacute care patients) that are published, with periodic updates, on the CMS-maintained “Nursing Home Compare” website (http://www.medicare.gov/NHCompare).
Issues of Inadequate Risk Adjustment
The CMS QMs incorporate several mechanisms to account for resident characteristics. First, exclusions are used to create a relatively homogenous resident cohort on whom to calculate each QM. For example, the sample used for calculating the measure of ADL decline excludes those who were at highest level of physical dependence at “baseline” and thus would not deteriorate further (see Appendix SA2). Second, stratification between high-and low-risk residents is used for the measure of pressure sore, i.e., facility rates are reported for predefined high-and low-risk residents separately. Finally, classical logistic regression is used for five QMs, each adjusting for a limited number (1–3) of risk variables. A detailed description of the CMS approach can be found elsewhere (Mukamel et al. 2008).
Despite these efforts to make NH comparisons fairer, it is possible that QMs with limited risk adjustment may not accurately identify poorly performing facilities. Because a broad array of resident characteristics can affect outcomes and these characteristics may not be randomly distributed over facilities, ignoring the effect of these risk factors (i.e., those not adjusted for in the CMS QMs) may bias quality estimation (Localio et al. 1997). For example, Mukamel et al. (2008) examined several CMS QMs, and found that QMs with additional adjustment for MDS risk factors resulted in different facility rankings than the rakings based on the corresponding CMS QMs. Two other studies expressed similar concerns about the potentially insufficient risk adjustment in CMS QMs (General Accounting Office 2002; Arling et al. 2007).
CMS and its contracting researchers have recognized this issue and suggested that adjusting for the type of residents in facilities requires further research that should include (1) research regarding the selection of appropriate risk factors; (2) comparisons of different risk-adjustment methodologies, as applied to each QM; and (3) validation of different risk-adjustment methods (General Accounting Office 2002). This study extends previous research (Arling et al. 2007; Mukamel et al. 2008) (those have demonstrated more appropriate choice of risk factors) along this line by comparing and validating alternative statistical methods for risk adjustment.
Regression-Based Risk Adjustment
As can be seen in many acute care report cards, multivariate statistical regression is commonly used for risk adjustment (Iezzoni 2003). Compared with the CMS method such as risk stratification or exclusion, the regression-based approach is more flexible in that it can account for a large number of patient characteristics affecting outcomes (Mukamel et al. 2008). Although the regression-based method may be technically less straightforward, its basic analytical procedure is easy to follow: first, the regression model is estimated to predict the expected outcome (e.g., probability of functional decline) of each patient based solely on risk factors; second, the expected outcome of each facility can be computed as the summed risk of all patients in the facility divided by the total number of patients in it; finally, the risk-adjusted QM can be constructed based on the comparison of the facility's average observed outcome with expected outcome. Details of this observed-to-expected outcome comparison are presented in a recent study of hospital report card (Li et al. 2007).
Despite the flexibility of this approach in modeling risks, a precaution of performing such risk-adjusted analysis is to avoid “over-adjustment” (Mukamel et al. 2008). For example, weight loss may be a risk factor of functional decline (the “outcome”) for NH residents, whereas it itself is an outcome of NH care. Including weight loss in the regression of functional decline may be necessary to avoid biased outcome comparison, but could overstate a facility's performance, when solely judged by the QM of ADL decline, if the facility provides poor care for weight loss. However, CMS's publication of multidimensional QMs tempers this issue largely (Mukamel et al. 2008) because both outcomes are published and can be used to rank facilities explicitly. We will return to this issue later in “Discussion.”
Potential Impact of Alternative Statistical Models
Regression-based risk adjustment is expected to balance the effect of patients’ preexisting risks (e.g., baseline physical function) on health outcomes (e.g., future decline in ADLs), leaving residual outcome differences across facilities to reflect quality (Iezzoni 1997). The choice of statistical methodology, however, may have impacts on quality rankings. Although this issue has been examined in acute care outcomes (DeLong et al. 1997; Shahian et al. 2001; Glance et al. 2006a; Li et al. 2007), no study has explored the impact of alternative statistical methods on constructing the NH QMs. Current acute care report cards are frequently developed using classical regression models (Li et al. 2007). Although widely used, the classical regression may not be appropriate for data in which patients are “clustered” within facilities (DeLong et al. 1997). A basic assumption of classical regression is that all patients are independent observations in the dataset (Hosmer and Lemeshow 2000). However, outcomes data almost always violate this assumption because patients in the same facility tend to show similar (or correlated) health outcomes when receiving similar patterns of care in the facility. The assumption of independent outcomes in classical regression contradicts with the spirit of outcomes comparisons and reports, which are grounded on the belief that a common factor, “quality,” determines the health outcomes of patients in the same facility, and varies across facilities. Ignoring the “clustering” of patients due to “quality” or other factors may invalidate the empirical risk-adjustment model and lead to incorrect quality estimates (DeLong et al. 1997).
Two alternative approaches—fixed-effects and random-effects models—estimate quality explicitly in the regression models and assume independent outcomes among facilities but correlated outcomes within a facility (Greene 2001). Thus, although with their own limitations, the two approaches may be better suited for outcome comparisons.
In addition, the fixed-effects modeling is effective in dealing with the situation where facility quality correlates with patient characteristics (Greene 2001). The correlation may be caused by selective referrals where physicians refer sicker patients to better-performing hospitals or discharge patients with functional disabilities to NHs with better rehabilitative services. In such cases, the fixed-effects modeling can produce unbiased and consistent parameter estimation (Hsiao 2003). However, one disadvantage of this approach is that for facilities with small numbers of patients, the point estimate may be accompanied by a large variance and be unreliable. The fixed-effects approach has been implemented by the Agency for Healthcare Research and Quality's evidence-based hospital QIs (Agency for Healthcare Research and Quality 2002), and by a national report of Consumer Survey of Health Plans (CAHPS®) (Elliott et al. 2001).
The random-effects model assumes that facility quality arises from a distribution of population quality such as normal distribution (Brown and Prescott 1999). In such a model, the estimated quality is shrunken towards the overall performance estimate, or less widely spread, compared with its fixed-effects counterpart. The shrinkage is inversely proportional to the precision of facility estimate, which helps avoid extreme estimates for facilities with small numbers of patients (Goldstein and Spiegelhalter 1996). Consequently, the shrinkage estimates for small facilities are generally more conservative, but can cause bias in the point estimates of quality and thus erroneous quality rankings. Another drawback of the random-effects model, particularly in constructing risk-adjusted outcomes, is that the random estimates are assumed uncorrelated with patient characteristics (DeLong et al. 1997). This assumption may be violated when selective referrals based on performance exist. In such instances, the random-effects model will result in biased estimates (Brown and Prescott 1999).
Studies comparing these alternative models have resulted in inconclusive findings, with some reporting substantially changed facility profiling when different approaches are used (Greenfield et al. 2002; Huang et al. 2005), but others reporting relatively minor impacts on outcomes inferences (DeLong et al. 1997; Hannan et al. 2005; Glance et al. 2006a). Therefore, the choice of statistical methodology is likely an empirical question that depends on individual outcomes and populations.
METHODS
Data and Measures
We used the 2004 and 2005 national MDS datasets for all long-term care residents in facilities certified by the Medicare or Medicaid program. The MDS assessments are performed for each resident upon admission, quarterly thereafter, and whenever a significant change of health status occurs. Evidence suggests that MDS records meet acceptable standards of accuracy and reliability for research purposes (Hawes et al. 1995; Lawton et al. 1998; Mor et al. 2003). The MDS ADL score quantifies a resident's functioning in the last 7 days of assessment in bed mobility, transferring, eating, and toilet use. Each of the four components is scored on a five-point scale, with 0 standing for highest level of independence and 4 indicating total dependence (CMS 2002).
Defining the CMS QM
According to CMS's definition (Abt Associates Inc. 2004), a resident suffers functional decline between two adjacent quarters if he/she has at least two ADL components increased by one point or at least one ADL component increased by two points. We defined a binary variable yij for resident i in facility j that equaled 1 if the resident had functional decline in the first quarter of 2005 compared with the fourth quarter of 2004 (based on the quarterly assessment or nearest full assessment), and 0 otherwise. CMS exclusion criteria were then applied according to both resident and facility characteristics (Appendix SA2). CMS did not use stratification or regression adjustment in this QM.
We calculated the CMS QM rate as the percent of residents who had functional decline for each eligible facility, that is, long-term care facility with >30 residents at risk of functional decline (denominator). We further calculated the 95 percent confidence interval (CI) of this QM using normal approximation:
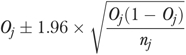 |
(1) |
where Oj is the CMS-unadjusted rate and nj is the number of at-risk residents in facility j.
Identifying and Estimating the Effect of Risk Factors
We identified risk factors of functional decline in the prior assessment (the fourth quarter of 2004 or nearest full assessment) according to previous literature and recommendations by an experienced geriatrician familiar with long-term care. We then estimated their effect using classical logistic regression models in both bivariate and multivariate analyses, and retained only variables that were significant at. 001 level in the final model. In addition, we used multivariate fractional polynomials (Royston and Sauerbrei 2003) to determine the optimal transformations of continuous covariates (i.e., length between prior and target assessments, and age). The final classical logistic model was estimated on exactly the same data as used for calculating the CMS QM:
| (2) |
where pij is the probability of functional decline for each resident, x-variables are the best set of risk factors, and βk are model parameters.
Calculating Risk-Adjusted QMs Alternatively
We estimated risk-adjusted QMs using different modeling approaches that are described below and summarized in Table 1.
Table 1.
Description of the Nursing Home Quality Measure of Decline in ADL Functioning, by Risk-Adjustment Methods
| Type of Risk-Adjustment Method | No. of Nursing Homes | Mean (%) | Median (%) | IQR (%) | Range (%) (Min–Max) |
|---|---|---|---|---|---|
| 0. CMS unadjusted | 9,336 | 17.96 | 16.44 | 11.11–23.40 | 0–78.85 |
| 1. Classical logistic regression based | 9,336 | 18.36 | 16.86 | 11.50–24.13 | 0–72.91 |
| 2. Fixed-effects logistic regression based | 9,336 | 16.35 | 14.82 | 9.87–21.67 | 0–71.04 |
| 3. Random-effects logistic regression based | 9,336 | 19.04 | 17.49 | 11.83–25.13 | 0–74.59 |
| 4. Random-effects logistic regression and shrinkage estimator based | 9,336 | 19.15 | 17.59 | 13.25–23.81 | 2.94–67.52 |
ADL, activities of daily living; IQR, interquartile range; CMS, Centers for Medicare and Medicaid Services.
Method 1
First, each resident's probability of experiencing functional decline (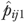 ) was predicted by the classical logistic model (equation (2)). Expected outcome rate for each facility
) was predicted by the classical logistic model (equation (2)). Expected outcome rate for each facility 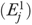 was then calculated as the sum of
was then calculated as the sum of 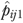 for residents in facility j divided by nj. To calculate the risk-adjusted QM
for residents in facility j divided by nj. To calculate the risk-adjusted QM  , we first calculated
, we first calculated
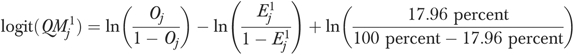 |
(3) |
where 17.96 percent is the overall rate of functional decline for all residents in the sample, and then back-transformed 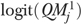 to the probability scale:
to the probability scale:
| (4) |
We used equations (3) and (4) to calculate 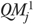 because a prior study (Li et al. 2007) has shown that it is consistent with the specification of the logistic model and better identifies outlier facilities than other measures such as those based on the difference or ratio between observed (Oj) and expected
because a prior study (Li et al. 2007) has shown that it is consistent with the specification of the logistic model and better identifies outlier facilities than other measures such as those based on the difference or ratio between observed (Oj) and expected 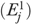 outcomes.
outcomes.
Finally, to calculate the 95 percent CI of 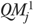 , we first calculated the 95 percent CI of Oj as
, we first calculated the 95 percent CI of Oj as
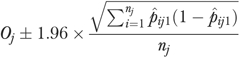 |
(5) |
which was developed by Hosmer and Lemeshow (1995) based on normal approximation of the binomial distribution. We then used the upper and lower bounds of the CI obtained above to calculate the 95 percent CI of 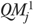 by repeating the calculations in equations (3) and (4) (Li et al. 2007).
by repeating the calculations in equations (3) and (4) (Li et al. 2007).
Method 2
We first estimated a fixed-effects logistic model
| (6) |
that incorporated the same set of x-variables as equation (2). This model was estimated using conditional maximum likelihood method (Pan 2002), where the NH fixed-effects  captures the effect of unmeasured facility characteristics after controlling for resident risks (Greene 2001). We then used this model to predict each resident's probability of functional decline
captures the effect of unmeasured facility characteristics after controlling for resident risks (Greene 2001). We then used this model to predict each resident's probability of functional decline 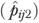 assuming null effect of
assuming null effect of 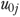 (i.e.,
(i.e., 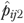 only incorporates resident risks but no facility effects), and calculated the expected rate for each facility
only incorporates resident risks but no facility effects), and calculated the expected rate for each facility 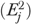 as the sum of
as the sum of 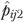 for residents in facility j divided by nj. Finally,
for residents in facility j divided by nj. Finally, 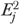 and
and 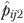 were used to calculate the risk-adjusted QM
were used to calculate the risk-adjusted QM 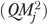 , and its 95 percent CI by repeating the calculations in equations (3)–(5) (replacing
, and its 95 percent CI by repeating the calculations in equations (3)–(5) (replacing 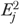 and
and 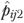 for
for 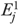 and
and 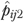 , respectively).
, respectively).
Method 3
We similarly estimated equation (6) but at this time 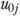 was assumed normally distributed with mean zero and variance
was assumed normally distributed with mean zero and variance 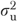 , and estimated as random-effects using SAS (SAS Corp., Cary, NC) Proc Glimmix (Littell et al. 2006). In a similar process, we predicted the resident's probability of functional decline (
, and estimated as random-effects using SAS (SAS Corp., Cary, NC) Proc Glimmix (Littell et al. 2006). In a similar process, we predicted the resident's probability of functional decline ( ) assuming null effect of
) assuming null effect of 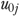 , and calculated the expected rate for each facility (
, and calculated the expected rate for each facility (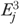 ) as the sum of
) as the sum of 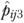 for residents in facility j divided by nj. Finally,
for residents in facility j divided by nj. Finally, 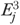 and
and 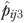 were used to calculate the risk-adjusted QM
were used to calculate the risk-adjusted QM 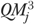 , and its 95 percent CI according to equations (3)–(5).
, and its 95 percent CI according to equations (3)–(5).
Method 4
Because the random-effects shrinkage estimator 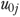 represents facility variations in outcome after adjusting for resident characteristics, we used this estimator to derive the risk-adjusted QM (
represents facility variations in outcome after adjusting for resident characteristics, we used this estimator to derive the risk-adjusted QM ( ) directly. We first calculated
) directly. We first calculated 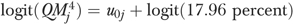 (note that
(note that 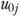 is on the logit scale) and then back-transformed
is on the logit scale) and then back-transformed  to the probability scale. The 95 percent CI of
to the probability scale. The 95 percent CI of 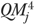 was similarly calculated using the estimated 95 percent CI of
was similarly calculated using the estimated 95 percent CI of 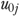 .
.
Comparing Statistical Models and QMs
Below we present a framework of validity criteria that can be used to guide our comparison of alternative methods at the regression model (or resident) level and at the QM (or facility) level. These different perspectives of validity have been described previously (Mukamel 1997; Iezzoni 2003) and their operational definitions are:
Validity criteria at the regression model level:
Face validity—The model accommodates variables that on face value are important clinical risk factors.
Content validity—The risk-adjustment model incorporates all concepts affecting outcome, i.e., complete risks, facility effects, and chance component.
Construct validity—The effects of risk factors on outcome are estimated in the expected direction.
Convergent validity—The effects of risk factors on outcome show close agreement when estimated by alternative models.
Predictive validity—The model predicts actual outcome well.
Validity criteria at the QM level:
Criterion validity—The QM reflects true quality of care.
Convergent validity—Facility rankings or identity of outliers based on QMs derived from alternative methods show close agreement.
The predictive validity of the classical, fixed-effects, and random-effects models was evaluated by the c-statistic, which equals the area under the receiver operating characteristic curve (Hanley and McNeil 1982). The c-statistic exams how well the model discriminates residents with and without functional decline by assigning a higher predicted probability to those with functional decline. The c-statistic ranges from 0.5 (random discrimination, no better than a flip of coin) to 1.0 (perfect discrimination).
At the QM level, we defined high-and low-quality facilities by either the ranking or the 95 percent CI of the QM derived from each method. First, facilities in the lowest 10 percent and highest 10 percent rankings were identified as “best 10 percent” and “worst 10 percent” facilities, respectively (because the QM represents an adverse outcome, lower QM rate indicates better quality). We also performed sensitivity analyses where we used alternative cutoffs (5 and 25 percent) to define best and worst facilities. Second, facilities were identified as high-quality outliers if the 95 percent CIs of their QM rates were below the overall rate 17.96 percent, and low-quality outliers if the 95 percent CIs were above 17.96 percent.
To quantify the convergent validity of alternatively calculated QMs, we calculated the κ statistic (Landis and Koch 1977) (1) between the CMS-unadjusted QM and each risk-adjusted QM, and (2) between each pair of risk-adjusted QMs, in identifying best and worst facilities or outliers. The κ measures the level of agreement between two raters evaluating an event on a categorical scale (Landis and Koch 1977). In this study, we defined the event scale as 1=best facilities (or high-quality outlier), 0=medium facilities (or nonquality outlier), and −1=worst facilities (or low-quality outlier). The κ ranges between 0 and 1, with 0 indicating no agreement beyond chance, and 1 indicating total agreement.
In comparing the CMS-unadjusted QM and each risk-adjusted QM, we further calculated (1) the false-positive rate for medium-quality facilities (i.e., those not identified as high-or low-quality facilities by each risk-adjusted QM were identified so by the unadjusted QM), and (2) the false-negative rate for high-and low-quality facilities separately (i.e., those identified as high-or low-quality facilities by each risk-adjusted QM were not identified so by the CMS-unadjusted QM) (Glance et al. 2006b).1
RESULTS
Descriptive Results
This study included 605,433 long-term care residents in 9,336 facilities (Table 1). The overall unadjusted QM rate was 17.96 percent, and it varied widely across facilities (interquartile range 11.11–23.40 percent, range 0–78.85 percent). The residents were on average 81 years old, and had different levels of ADL impairment at prior assessment (Table 2).
Table 2.
Resident Characteristics (n=605,433) and Estimates in Risk-Adjustment Models
|
Odds Ratio Estimated by |
||||
|---|---|---|---|---|
| Baseline Characteristic | Prevalence (%) or Mean±SD | Classical Logistic Model | Fixed-Effects Model | Random-Effects Model |
| Length (in weeks) between prior (or baseline) and target assessments | ||||
| length | 12.37±1.65 | 0.075 | 0.108 | 0.099 |
| ln(length) | 7.390 | 3.851 | 4.506 | |
| length× ln(length) | 2.287 | 2.092 | 2.139 | |
| Age in years† | 80.89±12.94 | 1.219 | 1.170 | 1.187 |
| ADL performance—bed mobility | ||||
| Independent | 36.47 | Reference | Reference | Reference |
| Supervision | 6.89 | 0.873 | 0.877 | 0.879 |
| Limited assistance | 18.06 | 0.777 | 0.675 | 0.702 |
| Extensive assistance | 31.46 | 0.518 | 0.372 | 0.406 |
| Total Dependence Or No Activity | 7.12 | 0.442 | 0.271 | 0.307 |
| ADL performance—transfer | ||||
| Independent | 25.61 | Reference | Reference | Reference |
| Supervision | 7.92 | 1.257 | 1.323 | 1.311 |
| Limited assistance | 19.39 | 1.362 | 1.439 | 1.420 |
| Extensive assistance | 31.72 | 1.101 | 1.202 | 1.175 |
| Total dependence or no activity | 15.36 | 0.819 | 0.894 | 0.875 |
| ADL performance—eating | ||||
| Independent | 48.32 | Reference | Reference | Reference |
| Supervision | 26.50 | 0.856 | 0.922 | 0.902 |
| Limited assistance | 9.96 | 0.836 | 0.883 | 0.870 |
| Extensive assistance | 9.38 | 0.636 | 0.641 | 0.639 |
| Total dependence or no activity | 5.85 | 0.489 | 0.525 | 0.518 |
| ADL performance—toilet use | ||||
| Independent | 19.23 | Reference | Reference | Reference |
| Supervision | 6.54 | 1.221 | 1.293 | 1.276 |
| Limited assistance | 16.41 | 1.296 | 1.329 | 1.323 |
| Extensive assistance | 33.76 | 1.112 | 1.140 | 1.139 |
| Total dependence or no activity | 24.07 | 0.903 | 0.975* | 0.960* |
| Short-term memory problem | 71.94 | 1.127 | 1.147 | 1.144 |
| Cognitive skills for daily decision making | ||||
| Independent or modified independent | 43.04 | Reference | Reference | Reference |
| Moderately impaired | 45.50 | 1.157 | 1.203 | 1.188 |
| Severely impaired | 11.46 | 1.454 | 1.587 | 1.545 |
| Rarely understand others or make self understood | 5.00 | 1.157 | 1.149 | 1.152 |
| Depression | 18.92 | 1.094 | 1.106 | 1.099 |
| Behavior problems in wandering | 9.52 | 1.094 | 1.038 | 1.052 |
| Bowel incontinence | 35.29 | 1.332 | 1.347 | 1.340 |
| Urinary incontinence | 47.38 | 1.262 | 1.289 | 1.281 |
| Urinary tract infection | 8.64 | 1.176 | 1.157 | 1.161 |
| Weight loss | 7.20 | 1.212 | 1.232 | 1.227 |
| Pressure ulcer | 7.31 | 1.282 | 1.314 | 1.308 |
| c-Statistic | 0.683 | 0.755 | 0.752 | |
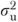 (standard error) (standard error) |
0.362 (0.007) | |||
p value>.01, all other p values <.001.
In the risk-adjustment models, age was transformed to 0 if age<65, and ln(age − 64) if age ≥65.
Statistical Models
In general, the classical, fixed-effects, and random-effects models had slightly different estimates (odds ratios) for individual risk factors (Table 2). The c-statistic was 0.68 for the classical model, which is comparable with results in previous studies (Mukamel 1997; Rosen et al. 2001), 0.76 for the fixed-effects model, and 0.75 for the random-effects model.
Agreement in NH Classifications
The average risk-adjusted rates ranged between 16.35 percent (fixed-effects estimate) and 19.15 percent (shrinkage estimator, Table 1). The rate based on shrinkage estimator exhibited the least variation across facilities, ranging from 2.94 to 67.52 percent.
Table 3 shows that the κ between CMS-unadjusted QM and each risk-adjusted QM ranged between 0.70 and 0.80 in ranking and classifying facilities. Compared with each adjusted QM, the unadjusted QM had a false-negative rate of over 0.20 in identifying the worst 10 percent facilities, and a false-negative rate between 0.14 and 0.26 in identifying the best 10 percent facilities (the false-positive rate of the unadjusted QM was <0.10). Table 4 shows that the pair-wise agreement between each risk-adjusted QM was very high (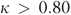 ) in rankings. However, the shrinkage estimator (method 4) tended to deviate nonrandomly from other estimates in identifying the best 10 percent facilities, the percent of differentially identified facilities being 18 percent [172/(172+761)], 17 percent [154/(154+779)], and 17 percent [155/(155+778)], respectively (see highlighted cells in Table 4). We varied the cutoff percentiles in classifying facilities and found similar results to those in Tables 3 and 4.
) in rankings. However, the shrinkage estimator (method 4) tended to deviate nonrandomly from other estimates in identifying the best 10 percent facilities, the percent of differentially identified facilities being 18 percent [172/(172+761)], 17 percent [154/(154+779)], and 17 percent [155/(155+778)], respectively (see highlighted cells in Table 4). We varied the cutoff percentiles in classifying facilities and found similar results to those in Tables 3 and 4.
Table 3.
Agreement in Nursing Home Quality Rankings—CMS-Unadjusted Measure Compared with Risk-Adjusted Measures
|
Rankings Based on Risk Adjustment |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Method 1* |
Method 2† |
Method 3‡ |
Method 4§ |
|||||||||
| Rankings Based on CMS-Unadjusted Method | Worst 10% | Medium 80% | Best 10% | Worst 10% | Medium 80% | Best 10% | Worst 10% | Medium 80% | Best 10% | Worst 10% | Medium 80% | Best 10% |
| Worst 10% | 731 | 193 | 0 | 712 | 212 | 0 | 714 | 210 | 0 | 716 | 208 | 0 |
| Medium 80% | 202 | 7,148 | 129 | 221 | 7,125 | 133 | 219 | 7,123 | 137 | 217 | 7,021 | 241 |
| Best 10% | 0 | 129 | 804 | 0 | 133 | 800 | 0 | 137 | 796 | 0 | 241 | 692 |
| False-positive rate** | 0.04 | 0.05 | 0.05 | 0.06 | ||||||||
| False-negative rate** | 0.22 | 0.14 | 0.24 | 0.14 | 0.23 | 0.15 | 0.23 | 0.26 | ||||
| Overall κ | 0.79 | 0.78 | 0.78 | 0.71 | ||||||||
Nursing homes in the worst 10% group are those whose point estimates of the quality measures of decline in ADL functioning are among the 10%highest of the rates of all nursing homes (n=9,336). Nursing homes in the medium 80% group are those whose point estimates of the quality measures of decline in ADL functioning are between the 10% highest and 10% lowest of the rates of all nursing homes (n=9,336). Nursing homes in the best 10% group are those whose point estimates of the quality measures of decline in ADL functioning are among the 10%lowest of the rates of all nursing homes (n=9,336).
Based on classical logistic regression model.
Based on fixed-effects model.
Based on random-effects model.
Based on the shrinkage estimators of the random-effects model.
Each risk-adjusted measure was treated as “gold standard” when calculating the false-positive (for the medium 80% group) and false-negative (for the worst or best 10% group) rates.
Table 4.
Agreement in Nursing Home Quality Rankings According to Different Risk-Adjustment Methods
|
Method 1* |
Method 2† |
Method 3‡ |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Worst 10% | Medium 80% | Best 10% | Worst 10% | Medium 80% | Best 10% | Worst 10% | Medium 80% | Best 10% | ||
| Method 2† | Worst 10% | 872 | 61 | 0 | ||||||
| Medium 80% | 61 | 7,358 | 51 | |||||||
| Best 10% | 0 | 51 | 882 | |||||||
| κ | 0.93 | |||||||||
| Method 3‡ | Worst 10% | 888 | 45 | 0 | 915 | 18 | 0 | |||
| Medium 80% | 45 | 7,387 | 38 | 18 | 7,438 | 14 | ||||
| Best 10% | 0 | 38 | 895 | 0 | 14 | 919 | ||||
| κ | 0.95 | 0.98 | ||||||||
| Method 4§ | Worst 10% | 850 | 83 | 0 | 853 | 80 | 0 | 856 | 77 | 0 |
| Medium 80% | 83 | 7,215 | 172 | 80 | 7,236 | 154 | 77 | 7,238 | 155 | |
| Best 10% | 0 | 172 | 761 | 0 | 154 | 779 | 0 | 155 | 778 | |
| κ | 0.84 | 0.85 | 0.85 | |||||||
Nursing homes in the worst 10% group are those whose point estimates of the quality measures of decline in ADL functioning are among the 10%highest of the rates of all nursing homes (n=9,336). Nursing homes in the medium 80% group are those whose point estimates of the quality measures of decline in ADL functioning are between the 10% highest and 10% lowest of the rates of all nursing homes (n=9,336). Nursing homes in the best 10% group are those whose point estimates of the quality measures of decline in ADL functioning are among the 10%lowest of the rates of all nursing homes (n=9,336).
Based on classical logistic regression model.
Based on fixed-effects model.
Based on random-effects model.
Based on the shrinkage estimators of the random-effects model.
In identifying “outliers” using the 95 percent CI of each QM, the overall κ ranged between 0.59 and 0.76 between CMS-unadjusted QM and each risk-adjusted QM (Table 5). Compared with each adjusted QM, the false-positive rate of the unadjusted QM was between 0.10 and 0.17, the false-negative rate was between 0.25 and 0.48 for identifying low-quality outliers, and was minimal (<0.01) for identifying high-quality outliers.
Table 5.
Agreement in Identifying Nursing Home Quality Outliers—CMS-Unadjusted Measure Compared with Risk-Adjusted Measures
|
Outlier Status Based on Risk Adjustment |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Outlier Status Based on CMS-Unadjusted Method |
Method 1* |
Method 2† |
Method 3‡ |
Method 4§ |
||||||||
| Low | Medium | High | Low | Medium | High | Low | Medium | High | Low | Medium | High | |
| Low | 928 | 85 | 0 | 773 | 240 | 0 | 946 | 67 | 0 | 945 | 68 | 0 |
| Medium | 598 | 5,728 | 17 | 258 | 5,978 | 107 | 867 | 5,458 | 18 | 445 | 5,861 | 37 |
| High | 0 | 704 | 1,276 | 0 | 453 | 1,527 | 0 | 729 | 1,251 | 0 | 1,171 | 809 |
| False-positive rate** | 0.12 | 0.10 | 0.13 | 0.17 | ||||||||
| False-negative rate** | 0.39 | 0.01 | 0.25 | 0.07 | 0.48 | 0.01 | 0.32 | 0.04 | ||||
| Overall κ | 0.69 | 0.76 | 0.64 | 0.59 | ||||||||
Low-quality outliers are nursing homes whose quality measures of decline in ADL functioning are significantly higher than the national average rate 17.96% according to the 95% confidence intervals of the measures. Nursing homes of medium quality are those whose quality measures of decline in ADL functioning do not significantly differ from the national average rate 17.96% according to the 95% confidence intervals of the measures. High-quality outliers are nursing homes whose quality measures of decline in ADL functioning are significantly lower than the national average rate 17.96% according to the 95% confidence intervals of the measures.
Based on classical logistic regression model.
Based on fixed-effects model.
Based on random-effects model.
Based on the shrinkage estimators of the random-effects model.
Each risk-adjusted measure was treated as “gold standard” when calculating the false-positive (for nursing homes of medium quality) and false-negative (for low-or high-quality outliers) rates.
Table 6 shows that the overall pair-wise agreement between risk-adjusted QMs was high (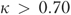 ) in identifying outliers. However, the shrinkage estimator deviated nonrandomly with other estimates in identifying high-quality outliers, the percent of differentially classified facilities being 37 percent [476/(476+817)], 49 percent [793/(793+841)], and 35 percent [448/(448+821)], respectively. In addition, there are cases that a pair of other risk-adjusted QMs tended to deviate nonrandomly in identifying either type of outliers (highlighted cells in Table 6).
) in identifying outliers. However, the shrinkage estimator deviated nonrandomly with other estimates in identifying high-quality outliers, the percent of differentially classified facilities being 37 percent [476/(476+817)], 49 percent [793/(793+841)], and 35 percent [448/(448+821)], respectively. In addition, there are cases that a pair of other risk-adjusted QMs tended to deviate nonrandomly in identifying either type of outliers (highlighted cells in Table 6).
Table 6.
Agreement in Identifying Nursing Home Quality Outliers According to Different Risk-Adjustment Methods
|
Method 1* |
Method 2† |
Method 3‡ |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Low | Medium | High | Low | Medium | High | Low | Medium | High | ||
| Method 2† | Low | 1,031 | 0 | 0 | ||||||
| Medium | 495 | 6,176 | 0 | |||||||
| High | 0 | 341 | 1,293 | |||||||
| κ | 0.80 | |||||||||
| Method 3‡ | Low | 1,519 | 294 | 0 | 1,031 | 782 | 0 | |||
| Medium | 7 | 6,205 | 42 | 0 | 5,889 | 365 | ||||
| High | 0 | 18 | 1,251 | 0 | 0 | 1,269 | ||||
| κ | 0.92 | 0.74 | ||||||||
| Method 4§ | Low | 1,349 | 41 | 0 | 1,020 | 370 | 0 | 1,384 | 6 | 0 |
| Medium | 177 | 6,447 | 476 | 11 | 6,296 | 793 | 429 | 6,223 | 448 | |
| High | 0 | 29 | 817 | 0 | 5 | 841 | 0 | 25 | 821 | |
| κ | 0.82 | 0.70 | 0.78 | |||||||
Low-quality outliers are nursing homes whose quality measures of decline in ADL functioning are significantly higher than the national average rate 17.96% according to the 95% confidence intervals of the measures. Nursing homes of medium quality are those whose quality measures of decline in ADL functioning do not significantly differ from the national average rate 17.96% according to the 95% confidence intervals of the measures. High-quality outliers are nursing homes whose quality measures of decline in ADL functioning are significantly lower than the national average rate 17.96% according to the 95% confidence intervals of the measures.
Based on classical logistic regression model.
Based on fixed-effects model.
Based on random-effects model.
Based on the shrinkage estimators of the random-effects model.
DISCUSSION
Although current NH QMs are not perfect (Mor et al. 2003), they will likely play an increasingly important role in market-driven quality improvement (Mukamel et al. 2007), and in emerging pay-for-performance (P4P) programs (Abt Associates 2006). It is thus important that their validity and accuracy be ensured and that the outcome information conveyed to the public be as robust as possible.
This study focused on one source of uncertainty in constructing risk-adjusted QMs—the use of classical, fixed-effects, and random-effects models for risk adjustment. Our discussion below is organized around the validity criteria defined previously. First, we believe that the fundamental requirement for a risk-adjustment model is that it adequately estimates the underlying relationship between resident outcome, risks, and facility quality of care. In this light, our regression-based risk adjustment shows higher face value than the CMS exclusion method because our methods incorporate a broad set of clinical variables affecting outcomes. In the comparison of alternative regression models, both the fixed-and random-effects approaches explicitly account for facility variations when modeling outcome (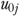 in equation (6)), and therefore have higher content validity than the classical logistic model. When ignoring the facility effect on outcomes, the classical logistic model showed lower predictive validity (c=0.68) than the other two models (c=0.75).
in equation (6)), and therefore have higher content validity than the classical logistic model. When ignoring the facility effect on outcomes, the classical logistic model showed lower predictive validity (c=0.68) than the other two models (c=0.75).
Nonetheless, the coefficients (or odds ratios) of resident risk factors estimated by these models were all in the expected direction (i.e., showed construct validity) and in general similar across models (i.e., showed high convergent validity). Because the estimated coefficients were used for calculating the risk-adjusted QMs in three of four methods, facility rankings and classifications (Table 4) by the first three methods were in very close agreement (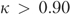 ), suggesting a high convergent validity at the QM level. However, method 4, which directly estimated quality from the random-effects shrinkage estimator
), suggesting a high convergent validity at the QM level. However, method 4, which directly estimated quality from the random-effects shrinkage estimator  , tended to deviated systematically from other methods in identifying the best 10 percent facilities, suggesting a relatively lower convergent validity. This is likely due to the differential “shrinkages” of
, tended to deviated systematically from other methods in identifying the best 10 percent facilities, suggesting a relatively lower convergent validity. This is likely due to the differential “shrinkages” of 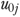 for facilities with extremely low rates or small number of residents, which led to biased rankings of facilities.
for facilities with extremely low rates or small number of residents, which led to biased rankings of facilities.
Also at the QM level, we found that the risk-adjusted QMs of ADL decline showed better overall agreement with each other (Table 4: 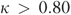 ) than did the CMS-unadjusted versus each adjusted QM (Table 3:
) than did the CMS-unadjusted versus each adjusted QM (Table 3: 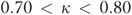 ) in identifying the worst and best 10 percent facilities. Similar conclusion for identifying statistical outliers (using the 95 percent CI of the QM) can be drawn by comparing the κ statistics in Tables 5 and 6. These results suggest that despite the variation of statistical methodology (that raises the issue of convergent validity), the extensively risk-adjusted QMs provide more robust (and thus more useful) outcome information than the corresponding unadjusted QM. Using each risk-adjusted QM as a benchmark, we found that the CMS-unadjusted QM misclassified a number of facilities (Tables 3 and 5). These findings reinforced previous studies documenting insufficient risk adjustment in current NH report cards (General Accounting Office 2002; Arling et al. 2007; Mukamel et al. 2008).
) in identifying the worst and best 10 percent facilities. Similar conclusion for identifying statistical outliers (using the 95 percent CI of the QM) can be drawn by comparing the κ statistics in Tables 5 and 6. These results suggest that despite the variation of statistical methodology (that raises the issue of convergent validity), the extensively risk-adjusted QMs provide more robust (and thus more useful) outcome information than the corresponding unadjusted QM. Using each risk-adjusted QM as a benchmark, we found that the CMS-unadjusted QM misclassified a number of facilities (Tables 3 and 5). These findings reinforced previous studies documenting insufficient risk adjustment in current NH report cards (General Accounting Office 2002; Arling et al. 2007; Mukamel et al. 2008).
An important limitation of our study is that we are unable to assess the criterion validity of each measure because we did not know the true “quality” rankings, if exist, against which to evaluate the estimates by each method. However, our study demonstrated a framework to explore the philosophical issues of alternative statistical models and their implications in NH QMs. Even in the absence of criterion validity, other aspects of validity can provide important and practical guide to the choice of appropriate method (Iezzoni 2003). In the case of NH report cards, we note that CMS currently releases the point estimate of QM that allows for straightforward comparisons using facility rankings. In addition, the NH P4P program in a CMS demonstration (Abt Associates 2006) also uses the QM rankings (and other indicators) to reward the best 10 or 20 percent facilities. In both cases we believe that (1) using extensively risk-adjusted QM of ADL decline would provide more robust quality information than the unadjusted QM, and (2) the risk adjustment should not be based on the random-effects shrinkage estimator because it tends to be biased due to differential shrinkages, and facility rankings derived from it show lower convergent validity than otherwise derived rankings based on the ADL outcome.
Another limitation of the study is that although our risk-adjustment models captured multiple resident characteristics, they did not account for time-variant factors and thus could be mis-specified; if the time-variant factors show confounding effect on the ADL outcome, estimates in these models will be biased. Finally, there are other methodological issues important to the NH report cards. For example, analysts may think that some of the risk factors in our models are themselves outcomes that reflect quality of care, and that adjusting for their effects would ignore facility variations in these dimensions of outcome. However, these risk factors are baseline outcomes that are not determined by current NH performance (note that CMS continuously updates its published QMs). In addition, as a prior study (Mukamel et al. 2008) pointed out, CMS publishes multidimensional QMs that include these outcomes (i.e., used as risk factors in our models); because facilities can be explicitly ranked along these other outcomes, there is no need to factor into their effects again when we focus on the QM of ADL decline. A fuller discussion of this and other issues (such as the longitudinal stability of QMs, measurement and reporting errors, and sample size issues) is beyond this study and can be found elsewhere (Mor et al. 2003; Arling et al. 2007; Mukamel et al. 2008).
In conclusion, this study suggests that the risk-adjusted QMs of ADL decline, even when estimated by alternative statistical methods, show higher face validity and convergent validity, and provide more robust NH comparisons than the unadjusted QM. The risk-adjusted QM rankings tend to show lower convergent validity when estimated by the random-effects shrinkage estimator rather than other statistical methods. The choice of statistical methodology may affect outcome inferences and should be made cautiously before embarking on risk-adjusted analyses.
Acknowledgments
This study was funded by the National Institute on Aging under grants AG029608 (to Y.L.) and AG020644 (to D.B.M.). The views presented in this manuscript are those of the authors and may not reflect those of the National Institute on Aging.
Disclosures: No conflicts of interest for any authors.
Prior Dissemination: None.
Footnotes
We assumed that the risk-adjusted QMs are an improvement to the unadjusted QM (Arling et al. 2007; Mukamel et al. 2008) despite variations of statistical methodology, and thus used each risk-adjusted measure as “gold standard.”
Supporting Information
Additional supporting information may be found in the online version of this article:
Appendix SA1: Author Matrix.
Appendix S12. Exclusion Criteria in the Definition of the CMS Quality Measure of ADL Functioning
Please note: Wiley-Blackwell is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
REFERENCES
- Abt Associates Inc. Cambridge, MA: Abt Associates Inc; 2006. Quality Monitoring for Medicare Global Payment Demonstrations: Nursing Home Quality-Based Purchasing Demonstration. [Google Scholar]
- Abt Associates Inc. Cambridge, MA: Abt Associates Inc; 2004. Quality Measures for National Public Reporting: User's Manual, v1.2. [Google Scholar]
- Agency for Healthcare Research and Quality. 2002. “AHRQ Quality Indicators—Guide to Inpatient Quality Indicators: Quality of Care in Hospitals—Volume, Mortality, and Utilization.” AHRQ Pub. No. 02-RO204. Rockville, MD. [DOI] [PubMed]
- Arling G, Lewis T, Kane R L, Mueller C, Flood S. Improving Quality Assessment through Multilevel Modeling: The Case of Nursing Home Compare. Health Services Research. 2007;42:1177–99. doi: 10.1111/j.1475-6773.2006.00647.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown H, Prescott R. Applied Mixed Models in Medicine. Chichester, UK: John Wiley & Sons Ltd; 1999. [Google Scholar]
- Capitman J, Bishop C. Long-Term Care Quality: Historical Overview and Current Initiatives. Washington, DC: National Commission for Quality Long-Term Care; 2004. [Google Scholar]
- Centers for Medicare and Medicaid Services (CMS). 2002. “Revised Long-Term Care Facility Resident Assessment Instrument, User's Manual, Version 2.0.” Revised June 2005.
- Chernew M, Scanlon D P. Health Plan Report Cards and Insurance Choice. Inquiry. 1998;35:9–22. [PubMed] [Google Scholar]
- DeLong E R, Peterson E D, DeLong D M, Muhlbaier L H, Hackett S, Mark D B. Comparing Risk-Adjustment Methods for Provider Profiling. Statistics in Medicine. 1997;16:2645–64. doi: 10.1002/(sici)1097-0258(19971215)16:23<2645::aid-sim696>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- Elliott M N, Swartz R, Adams J, Spritzer K L, Hays R D. Case-Mix Adjustment of the National CAHPS Benchmarking Data 1.0: A Violation of Model Assumptions? Health Services Research. 2001;36:555–73. [PMC free article] [PubMed] [Google Scholar]
- Fries B E, Hawes C, Morris J N, Phillips C D, Mor V, Park P S. Effect of the National Resident Assessment Instrument on Selected Health Conditions and Problems. Journal of the American Geriatrics Society. 1997;45:994–1001. doi: 10.1111/j.1532-5415.1997.tb02972.x. [DOI] [PubMed] [Google Scholar]
- General Accounting Office. 2002. “Public Reporting of Quality Indicators Has Merit, but National Implementation Is Premature.” Publication No. GAO-03-187. Washington, DC.
- Glance L G, Dick A W, Osler T M, Li Y, Mukamel D B. Impact of Changing the Statistical Methodology on Hospital and Surgeon Ranking: The Case of the New York State Cardiac Surgery Report Card. Medical Care. 2006a;44:311–9. doi: 10.1097/01.mlr.0000204106.64619.2a. [DOI] [PubMed] [Google Scholar]
- Glance L G, Dick A W, Osler T M, Mukamel D B. Accuracy of Hospital Report Cards Based on Administrative Data. Health Services Research. 2006b;41:1413–37. doi: 10.1111/j.1475-6773.2006.00554.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein H, Spiegelhalter D J. League Tables and Their Limitations: Statistical Issues in Comparisons of Institutional Performance. Journal of Royal Statistical Society A. 1996;159:385–443. [Google Scholar]
- Granger C V, Cotter A C, Hamilton B B, Fiedler R C, Hens M M. Functional Assessment Scales: A Study of Persons with Multiple Sclerosis. Archives of Physical Medicine and Rehabilitation. 1990;71:870–5. [PubMed] [Google Scholar]
- Greene W H. Econometric Analysis. Upper Saddle River, NJ: Prentice-Hall; 2001. [Google Scholar]
- Greenfield S, Kaplan S H, Kahn R, Ninomiya J, Griffith J L. Profiling Care Provided by Different Groups of Physicians: Effects of Patient Case-Mix (Bias) and Physician-Level Clustering on Quality Assessment Results. Annals of Internal Medicine. 2002;136:111–21. doi: 10.7326/0003-4819-136-2-200201150-00008. [DOI] [PubMed] [Google Scholar]
- Hanley J A, McNeil B J. The Meaning and Use of the Area under a Receiver Operating Characteristic (ROC) Curve. Radiology. 1982;143:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
- Hannan E L, Racz M J, Jollis J G, Peterson E D. Using Medicare Claims Data to Assess Provider Quality for CABG Surgery: Does It Work Well Enough? Health Services Research. 1997;31:659–78. [PMC free article] [PubMed] [Google Scholar]
- Hannan E L, Wu C, DeLong E R, Raudenbush S W. Predicting Risk-Adjusted Mortality for CABG Surgery: Logistic Versus Hierarchical Logistic Models. Medical Care. 2005;43:726–35. doi: 10.1097/01.mlr.0000167802.27044.44. [DOI] [PubMed] [Google Scholar]
- Hawes C, Morris J N, Phillips C D, Mor V, Fries B E, Nonemaker S. Reliability Estimates for the Minimum Data Set for Nursing Home Resident Assessment and Care Screening (MDS) Gerontologist. 1995;35:172–8. doi: 10.1093/geront/35.2.172. [DOI] [PubMed] [Google Scholar]
- Hosmer D W, Lemeshow S. Confidence Interval Estimates of an Index of Quality Performance Based on Logistic Regression Models. Statistics in Medicine. 1995;14:2161–72. doi: 10.1002/sim.4780141909. [DOI] [PubMed] [Google Scholar]
- Hosmer D W, Lemeshow S. Applied Logistic Regression. 2d Edition. New York: Wiley-Interscience Publication; 2000. [Google Scholar]
- Hsiao C. Analysis of Panel Data. 2d Version. Cambridge: Cambridge University Press; 2003. [Google Scholar]
- Huang I C, Dominici F, Frangakis C, Diette G B, Damberg C L, Wu A W. Is Risk-Adjustor Selection More Important Than Statistical Approach for Provider Profiling? Asthma as an Example. Medical Decision Making. 2005;25:20–34. doi: 10.1177/0272989X04273138. [DOI] [PubMed] [Google Scholar]
- Iezzoni L I. The Risks of Risk Adjustment. Journal of the American Medical Association. 1997;278:1600–7. doi: 10.1001/jama.278.19.1600. [DOI] [PubMed] [Google Scholar]
- Risk Adjustment for Measuring Health Care Outcomes. Chicago: Health Administration Press; 2003. [Google Scholar]
- Institute of Medicine. Improving the Quality of Care in Nursing Homes. Washington, DC: National Academies Press; 1986. [PubMed] [Google Scholar]
- Kane R L, Chen Q, Blewett L A, Sangl J. Do Rehabilitative Nursing Homes Improve the Outcomes of Care? Journal of the American Geriatrics Society. 1996;44:545–54. doi: 10.1111/j.1532-5415.1996.tb01440.x. [DOI] [PubMed] [Google Scholar]
- Landis J R, Koch G G. The Measurement of Observer Agreement for Categorical Data. Biometrics. 1977;33:159–74. [PubMed] [Google Scholar]
- Lawton M P, Casten R, Parmelee P A, Van Haitsma K, Corn J, Kleban M H. Psychometric Characteristics of the Minimum Data Set II: Validity. Journal of the American Geriatrics Society. 1998;46:736–44. doi: 10.1111/j.1532-5415.1998.tb03809.x. [DOI] [PubMed] [Google Scholar]
- Li Y, Dick A W, Glance L G, Cai X, Mukamel D B. Misspecification Issues in Risk Adjustment and Construction of Outcome-Based Quality Indicators. Health Services and Outcomes Research Methodology. 2007;7:39–56. [Google Scholar]
- Littell R C, Milliken G A, Stroup W W, Wolfinger R D, Schabenberger O. SAS for Mixed Models. 2d Edition. Cary, NC: SAS Institute Inc; 2006. [Google Scholar]
- Localio A R, Hamory B H, Fisher A C, TenHave T R. The Public Release of Hospital and Physician Mortality Data in Pennsylvania. A Case Study. Medical Care. 1997;35:272–86. doi: 10.1097/00005650-199703000-00007. [DOI] [PubMed] [Google Scholar]
- Manard B. Nursing Home Quality Indicators: Their Uses and Limitations. Washington, DC: AARP Public Policy Institute; 2002. [Google Scholar]
- Mor V. A Comprehensive Clinical Assessment Tool to Inform Policy and Practice: Applications of the Minimum Data Set. Medical Care. 2004;42:50–9. doi: 10.1097/01.mlr.0000120104.01232.5e. [DOI] [PubMed] [Google Scholar]
- Mor V, Angelelli J, Jones R, Roy J, Moore T, Morris J. Inter-Rater Reliability of Nursing Home Quality Indicators in the U.S. BMC Health Services Research. 2003;3:20. doi: 10.1186/1472-6963-3-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mor V, Berg K, Angelelli J, Gifford D, Morris J, Moore T. The Quality of Quality Measurement in U.S. Nursing Homes. Gerontologist. 2003;43(spec. no. 2):37–46. doi: 10.1093/geront/43.suppl_2.37. [DOI] [PubMed] [Google Scholar]
- Morris J N, Hawes C, Fries B E, Phillips C D, Mor V, Katz S, Murphy K, Drugovich M L, Friedlob A S. Designing the National Resident Assessment Instrument for Nursing Homes. Gerontologist. 1990;30:293–307. doi: 10.1093/geront/30.3.293. [DOI] [PubMed] [Google Scholar]
- Mukamel D B. Risk-Adjusted Outcome Measures and Quality of Care in Nursing Homes. Medical Care. 1997;35:367–85. doi: 10.1097/00005650-199704000-00007. [DOI] [PubMed] [Google Scholar]
- Mukamel D B, Brower C A. The Influence of Risk Adjustment Methods on Conclusions about Quality of Care in Nursing Homes Based on Outcome Measures. Gerontologist. 1998;38:695–703. doi: 10.1093/geront/38.6.695. [DOI] [PubMed] [Google Scholar]
- Mukamel D B, Glance L G, Li Y, Weimer D L, Spector W D, Zinn J S, Mosqveda L. Does Risk Adjustment of the CMS Quality Measures for Nursing Homes Matter? Medical Care. 2008;46:532–41. doi: 10.1097/MLR.0b013e31816099c5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukamel D B, Spector W D, Zinn J S, Huang L, Weimer D L, Dozier A. Nursing Homes’ Response to the Nursing Home Compare Report Card. Journals of Gerontology. Series B, Psychological Sciences and Social Sciences. 2007;62:S218–25. doi: 10.1093/geronb/62.4.s218. [DOI] [PubMed] [Google Scholar]
- Mukamel D B, Weimer D L, Zwanziger J, Gorthy S F, Mushlin A I. Quality Report Cards, Selection of Cardiac Surgeons, and Racial Disparities: A Study of the Publication of the New York State Cardiac Surgery Reports. Inquiry. 2004;41:435–46. doi: 10.5034/inquiryjrnl_41.4.435. [DOI] [PubMed] [Google Scholar]
- Pan W. A Note on the Use of Marginal Likelihood and Conditional Likelihood in Analyzing Clustered Data. American Statistician. 2002;56:171–4. [Google Scholar]
- Rosen A, Wu J, Chang B H, Berlowitz D, Ash A, Moskowitz M. Does Diagnostic Information Contribute to Predicting Functional Decline in Long-Term Care? Medical Care. 2000;38:647–59. doi: 10.1097/00005650-200006000-00006. [DOI] [PubMed] [Google Scholar]
- Rosen A, Wu J, Chang B H, Berlowitz D, Rakovski C, Ash A, Moskowitz M. Risk Adjustment for Measuring Health Outcomes: An Application in VA Long-Term Care. American Journal of Medical Quality. 2001;16:118–27. doi: 10.1177/106286060101600403. [DOI] [PubMed] [Google Scholar]
- Royston P, Sauerbrei W. Stability of Multivariable Fractional Polynomial Models with Selection of Variables and Transformations: A Bootstrap Investigation. Statistics in Medicine. 2003;22:639–59. doi: 10.1002/sim.1310. [DOI] [PubMed] [Google Scholar]
- Shahian D M, Normand S L, Torchiana D F, Lewis S M, Pastore J O, Kuntz R E, Dreyer PI. Cardiac Surgery Report Cards: Comprehensive Review and Statistical Critique. Annals of Thoracic Surgery. 2001;72:2155–68. doi: 10.1016/s0003-4975(01)03222-2. [DOI] [PubMed] [Google Scholar]
- Spector W D, Takada H A. Characteristics of Nursing Homes That Affect Resident Outcomes. Journal of Aging and Health. 1991;3:427–54. doi: 10.1177/089826439100300401. [DOI] [PubMed] [Google Scholar]
- Vladeck B. Unloving Care: The Nursing Home Tragedy. New York: Basic Books; 1980. [Google Scholar]
- Zimmerman D R, Karon S L, Arling G, Collins T, Ross R, Clark B R, Sainfort F. Development and Testing of Nursing Home Quality Indicators. Health Care Financing Review. 1995;16:107–27. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


