What's the Risk? A Simple Approach for Estimating Adjusted Risk Measures from Nonlinear Models Including Logistic Regression

Abstract

Objective

To develop and validate a general method (called regression risk analysis) to estimate adjusted risk measures from logistic and other nonlinear multiple regression models. We show how to estimate standard errors for these estimates. These measures could supplant various approximations (e.g., adjusted odds ratio [AOR]) that may diverge, especially when outcomes are common.

Study Design

Regression risk analysis estimates were compared with internal standards as well as with Mantel–Haenszel estimates, Poisson and log-binomial regressions, and a widely used (but flawed) equation to calculate adjusted risk ratios (ARR) from AOR.

Data Collection

Data sets produced using Monte Carlo simulations.

Principal Findings

Regression risk analysis accurately estimates ARR and differences directly from multiple regression models, even when confounders are continuous, distributions are skewed, outcomes are common, and effect size is large. It is statistically sound and intuitive, and has properties favoring it over other methods in many cases.

Conclusions

Regression risk analysis should be the new standard for presenting findings from multiple regression analysis of dichotomous outcomes for cross-sectional, cohort, and population-based case–control studies, particularly when outcomes are common or effect size is large.

The health services research literature fails to provide a satisfactory answer to the question: when outcomes are common (i.e., risk >0.05 in the highest risk category), how does one best quantify the result of a logistic regression (Lee 1981; Greenland and Holland 1991; Savitz 1992; Greenland 2004)? The simple-to-measure odds ratio can deviate greatly from the more intuitive risk ratio (Hosmer and Lemeshow 1989; Klaidman 1990; Teuber 1990; Altman, Deeks, and Sackett 1998; Beaudeau and Fourichon 1998; Rothman and Greenland 1998; Schwartz, Woloshin, and Welch 1999; Bier 2001). A widely cited formula (see Table 2, footnote, for the equation) for converting the odds ratio to the risk ratio oversimplifies the problem and produces confounded estimates (Zhang and Yu 1998; McNutt et al. 2003). Other nonlinear models such as Poisson and log-binomial regressions have their strengths and weaknesses (Wacholder 1986; Greene 2000; Robbins, Chao, and Fonseca 2002; McNutt et al. 2003; Cummings 2004; Deddens and Petersen 2004; Zou 2004; Spiegelman and Hertzmark 2005).

Table 2.

Simulation Results

Study*				Adjusted Risk Ratios†					Adjusted Risk Differences
Design	Baseline Risk	Effective RR	Effective RD	RRA	M–H	Log– Binomial	Poisson	Zhang and Yu	M–H	RRA	AOR‡
(A) Simulation 2: 3 trichotomous confounders
	0.05	1.51	0.025	1.51	1.51	1.51	1.51	1.52	0.024	0.025	1.55
	0.10	1.50	0.049	1.50	1.50	1.50	1.50	1.54	0.048	0.049	1.59
	0.20	1.50	0.101	1.50	1.50	1.50	1.50	1.57	0.099	0.102	1.74
	0.40	1.50	0.202	1.49	1.50	1.50	1.50	1.96	0.198	0.198	3.00
	0.05	4.01	0.168	4.03	4.03	4.03	4.03	4.27	0.164	0.168	4.92
	0.10	4.00	0.293	4.01	4.01	4.01	4.01	4.57	0.286	0.293	6.15
	0.20	4.00	0.617	3.98	4.01	4.01	4.02	5.34	0.626	0.621	50.19
(B) Simulation 3: 2 continuous confounders
	0.10	1.48	0.05	1.54	NA	1.49	1.50	1.48	NA	0.05	1.65
	0.20	1.50	0.10	1.55	NA	1.55	1.56	1.51	NA	0.11	1.76
	0.39	1.51	0.20	1.51	NA	1.52	1.53	1.43	NA	0.20	2.29
	0.59	1.46	0.27	1.45	NA	1.21	1.51	1.32	NA	0.26	4.73
	0.05	2.99	0.10	3.07	NA	3.07	3.06	2.96	NA	0.10	3.42
	0.10	2.97	0.20	3.14	NA	3.26	3.24	3.01	NA	0.21	4.06
	0.20	3.05	0.40	2.98	NA	3.23	3.18	2.77	NA	0.39	5.76
	0.29	2.87	0.56	2.86	NA	3.16	3.15	2.51	NA	0.54	14.54
	0.19	3.95	0.58	3.83	NA	4.17	4.16	3.45	NA	0.56	13.39

Table shows results of Simulations 2 and 3 using logistic regression. Each simulation incorporated substantial confounding (in each case the crude risk ratio varies from the adjusted risk ratio by more than 25%). N=100,000 per data set for Simulation 2 and 30,000 per data set for Simulation 3.

^*Study design determines baseline risk, effective risk ratio, and effective risk difference. Effective risk ratio (RR) and effective risk difference (RD) are defined as the crude risk ratio and risk difference, respectively, when the simulation is repeated without confounding. Baseline risk is the risk of a positive outcome for a typical observation in the absence of exposure. It differs from the crude risk in the absence of exposure.

^†RRA is regression risk analysis, the method described in this paper. M–H is the Mantel–Haenszel estimate of the adjusted risk ratio or the adjusted risk difference. NA indicates that the M–H estimate is not calculable because of the use of a continuous variable. Log–binomial and Poisson regressions are performed with SAS software in accordance with recommendations in the literature (Spiegelman and Hertzmark 2005). Zhang and Yu is the adjusted risk ratio using their equation: 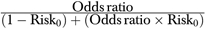, where Risk₀ is the crude risk of having a positive outcome among the unexposed (Zhang and Yu 1998).

^‡Adjusted odds ratio (AOR) from the logistic regression including modeled interactions.

Answering this simple question provides an opportunity to address a larger practical issue for health service researchers: how to interpret results from sophisticated nonlinear models so that the reader understands intuitively the meaning and magnitude of the finding. This paper proposes a general method for estimating risk ratios and risk differences from nonlinear multiple regression analysis, using the example of logistic regression. Beyond that it also can serve as a reminder of best practices for framing data analysis, as well as interpreting and reporting the results when using nonlinear models.

The fundamental problem driving these issues is how to estimate the effect of an explanatory variable upon an outcome variable after controlling for confounding effects. Extensions of this problem include estimating the effect of the predictor on outcomes within a definable subpopulation, or alternatively, making predictions at the population level. For these purposes health service researchers are rarely interested in coefficients from nonlinear models per se. Logistic regression is popular (Table 1) in part because its coefficients can be exponentiated into an estimate of the adjusted odds ratio (AOR) (Hosmer and Lemeshow 1989). Using the example of logistic regression, this paper demonstrates how to move from a nonlinear model to estimates of marginal effects that are quantified as the adjusted risk ratio (ARR) or adjusted risk difference (ARD). These are intuitive and easily understood terms. The method equips the analyst to report results in the terms in which the research question is likely to be framed.

Table 1.

Literature Citations Demonstrating the Frequency of Logistic Regression and Odds Ratio in Preference to Risk Ratio in the Medical Literature^*

Search Terms	References Since 1966	References Since 2004	Database
Logistic regression	82,811	32,857	PubMed
Poisson regression	3,326	1,568	PubMed
Binomial regression	716	436	PubMed
Odds ratio	72,943	32,189	PubMed
Adjusted odds ratio	13,346	6625	PubMed
Risk ratio	3,333	1,286	PubMed
Adjusted risk ratio	486	201	PubMed
Logistic regression and odds ratio	23,285	10,042	PubMed
Logistic regression and risk ratio	257	91	PubMed
Multivariate analysis and odds ratio	10,005	4,646	PubMed
Multivariate analysis and risk ratio	512	127	PubMed
Risk ratio and (Poisson regression or binomial regression)	87	53	PubMed
Zhang and Yu, JAMA (1998)	728	431	ISI Web of Knowledge

All searches include citations available on April 8, 2008.

† Excluding reviews. All searches were edited if necessary to distinguish between odds ratio and risk ratio. Multivariate regression included terms for multivariable regression.

This approach, we describe, is justifiable by maximum likelihood theory and thus applicable for all maximum likelihood models. Beyond maximum likelihood estimates (MLEs), this approach will work with alternative methods as long as the method is nonlinear and that E (y|x) is well approximated by the functional form used. It can be used to estimate the intuitive risk measures—ARDs and ARRs—not only for the common logistic model, but also for any other nonlinear model, such as Probit, Poisson, and log-binomial regressions. This method bridges the sophisticated mathematics underlying nonlinear models with an intuitive interpretation of the findings. Intuitive measures can make it easier for the typical analyst to add nuance to their research questions to take full advantage of these methods’ capacity.

We hope to improve typical practice by clarifying the important steps for this method, illustrating the range of issues that may be addressed, illuminating common pitfalls, and advocating a simple way to compute standard errors. As noted, although our points are more general our examples focus on logistic regression.

MATERIALS AND METHODS

Description of Regression Risk Analysis

We describe this method using the example of logistic regression: it can generate MLEs of the ARR (equation [1]) and the ARD (equation [2]). Conceptually, we define the ARR as the multiplicative increase in risk resulting from exposure, conditional on covariates. When no effect modification of the ARR is present, the estimator will be independent of covariates. The ARR is the ratio of the average predicted risk conditional on all observations being exposed, to the average predicted risk conditional on all observations being unexposed. Predicted risk for observation i is the predicted probability given covariates X_i and parameters β, as estimated by the logistic regression:

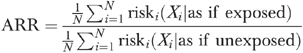(1)

The sample size is N and the risk for individual i is the probability that the outcome variable equals one, conditional on the covariates X. The ARD (equation [2]) is simply the difference between the numerator and the denominator in equation (1):

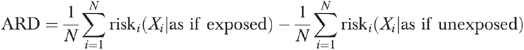(2)

Sample SAS and STATA programs to calculate these measures with standard errors are available from the authors upon request.

Theory

It is well understood that the logistic model can calculate an MLE of the natural logarithm of the odds that the outcome equals one, given values of the covariates (Hosmer and Lemeshow 1989). The invariance principle of maximum likelihood theory states that the algebraic manipulation of an MLE produces another MLE (Moody, Graybill, and Boes 1963). Because odds and risk are algebraically related (risk=odds/(1+odds)), the logistic model allows the calculation of the MLE of the risk for any specified combination of values (SAS Institute 1995). The denominator of equation (1) is the mean of this calculated risk for each observation when the exposure variable is assumed to be unexposed and represents an MLE of the unexposed (baseline) risk for a population whose covariates are distributed as for the observed covariates for the entire study population. The numerator in equation (1) represents an MLE of the adjusted risk among the exposed. This approach is a specific example of using what are called “recycled predictions.”

At least one of the AOR or the ARR must vary with covariates. Although an idealized logistic model is associated with a constant odds ratio, by including interaction terms logistic models can be fit even when the odds ratio is not constant (Hosmer and Lemeshow 1989). Although including appropriate interaction terms enhances the model fit, we found that the effect on the ARR is small unless outcomes are very common in the unexposed population. A further benefit of the ARR is that when the model includes interaction terms, the ARR is easier to compute and to interpret than the AOR.

Extensions

This method can be extended in important ways. First, it can be applied to various subpopulations of the data, for example to women, children aged 2–5 years, or for people in the first year of a study. Subgroup analyses may help answer specific research hypotheses that are not answerable with the entire sample: the method intrinsically takes into account that covariates may be distributed differently in different subgroups. For example, what would happen to traffic accidents if nondrinkers became heavy drinkers, or conversely if heavy drinkers stopped drinking (the answers may not be symmetric). Second, the method can be applied to continuous explanatory variables of interest, not just dichotomous ones. For example, consider age: one could compare people at their current age with someone 10 years their junior, or compare the risk of heart attack for persons of two specific ages (e.g., 85 compared with 65). Third, the method can be extended to interpret the combined effects of changes in two or more variables that are interacted (Ai and Norton, 2003; Norton, Wang, and Ai, 2004). Fourth, the method can be applied to any nonlinear model; regression risk analysis is not particular to logistic regression: it can be applied more broadly to any nonlinear estimator that provides a good approximation to how the outcome variable responds to the covariates. One theoretical justification for this approach is maximum likelihood theory. The function risk can be any probability function. Therefore, this approach is appropriate for any model with a dichotomous outcome, including probit, generalized linear models with binomial links, and nonlinear models that can be estimated with a dichotomous outcome (e.g., log-binomial, Poisson, negative binomial, and complementary log–log). Although we recognize that health services research emphasizes logistic (and to a lesser extent probit) models, exemplary analysis will include the careful selection—as well as careful analysis—of the link function.

Standard Errors

Estimates of the ARR or ARD should be reported with standard errors, like all estimated values. Standard errors can be calculated using numerical methods such as bootstrapping, or using the Delta method (Greene 2000). There are several reasons why bootstrapping is generally preferred. Bootstrapping allows for asymmetric confidence intervals appropriate to predictions from nonlinear models. Bootstrapping takes far less programming time (although often more computer time), and typically the cost of programming greatly exceeds the cost of computing. Finally, bootstrapping may be preferred when the data are adjusted for sampling weights or clustered, two common circumstances for which the Delta method is more complex. STATA allows easy adjustments for weights and clusters in its bootstrapping procedures.

Validation

We validated regression risk analysis using four series of Monte Carlo simulations all of which incorporated a Bernoulli distribution for the outcome variable. Each series consisted of multiple data sets of similar form but with different combinations of adjusted baseline risk and a constant ARR. All logistic models included interaction terms to produce the most parsimonious model. Log-binomial and Poisson regressions followed the recommendations of Spiegelman and Hertzmark (2005). The first two series of simulations extend the validation technique suggested by Zhang and Yu (1998), using data sets with three trichotomous confounders and one dichotomous predictor and one dichotomous outcome variable.

Simulation 1 contrasted regression risk analysis estimates of the ARR and ARD with Mantel–Haenszel (M–H) estimates in 15 data sets (N=18,988) with mild confounding. For each simulation extent of confounding was the ratio between the crude risk ratio and the ARR (or M–H estimate when available). Confounding of <10 percent is mild. Baseline risks (R₀) ranged from 0.01 to 0.6 and risk ratios from 1.5 to 4.0, with the product of the risk and risk ratio always ≤0.9. The second simulation (Table 2A) uses data sets (N=100,000) with three trichotomous confounders and confounding >25 percent to compare regression risk analysis ARR with AOR, log-binomial regression, Poisson regression, Zhang and Yu equation, and M–H (Wacholder 1986; SAS Institute 1995; Rothman and Greenland 1998; Zhang and Yu 1998; Spiegelman and Hertzmark 2005). Regression risk analysis and M–H ARD are also compared. The standard for this analysis and for the next simulation are the effective risk measures, defined as the crude risk ratio or difference obtained from otherwise identical data sets constructed without confounding. The third simulation (Table 2B) includes data sets with two continuous variables as confounders.

The data set for the fourth simulation was designed to assess regression risk analysis in the context of ceiling effects, when there is limited variation in the predictor variable at the upper extreme of a single confounding variable. This could occur when the correlation between a confounder and exposure are magnified at extreme values of the confounder's distribution, such as if age were the confounding variable and daily medication use the exposure. The proportion exposed will approach 100 percent for the older elderly.

We compared the precision of regression risk analysis ARR, Poisson regression, and the M–H ARR for random samples of various sizes from a data set with three categorical confounders (Table 3). Finally, we demonstrated the effect of omitting interaction terms from the logistic model in two data sets with one continuous confounder.

Table 3.

Simulation Results: Effect of Sample Size on ARR Precision^*: Regression Risk Analysis (RRA), Poisson, and Mantel–Haenszel (M–H) Estimates

Sample Size	LRA ARR	CI	Poisson	CI	M–H	CI
100,000	3.97	[3.87,4.07]	3.88	[3.79,3.98]	4.01	[3.77,4.26]
50,000	4.04	[3.89,4.18]	3.96	[3.83,4.08]	4.31	[3.94,4.71]
5,000	4.11	[3.62,4.60]	4.06	[3.62,4.50]	4.31	[3.22,5.77]
2,500	4.02	[3.36,4.67]	3.87	[3.28,4.46]	3.56	[2.51,5.05]
500	4.09	[2.35,5.83]	3.89	[2.33,5.44]	4.01	[1.67,9.63]
250	3.68	[1.13,6.22]	3.49	[1.46,5.52]	3.00	[0.86,10.41]

^*Precision is manifest as the 95% confidence interval (95% CI): All were calculated using STATA. RRA confidence interval was calculated using bias corrected bootstrapping in STATA.

ARR, adjusted risk ratio; LRA, logistic risk analysis.

RESULTS

In Simulation 1, the absolute value of the difference between the regression risk analysis and the M–H ARR across the 15 data sets averaged 0.00015 (range 0.000032–0.00036). The largest absolute difference in risk ratio was <0.025 percent of the M–H risk ratio. ARDs had a mean absolute difference of 9.76 × 10⁻⁶. We conclude that for simple models with limited confounding, regression risk analysis gives the same answer (within numerical precision) as M–H, a practical standard for comparison.

In data sets with categorical covariates and substantial confounding (Table 2A), regression risk analysis, Poisson regression, and log-binomial regression all produced ratio estimates virtually identical to the M–H estimate. AOR (Hosmer and Lemeshow 1989) and the Zhang and Yu equation (Zhang and Yu 1998) were biased, as is well known (McNutt et al. 2003). Regression risk analysis estimates of ARD closely approximated the standard.

When confounders were continuous and confounding exceeded 25 percent (Table 2B), a common situation where M–H cannot be estimated, regression risk analysis retained a high degree of accuracy. Omitted from the table are a similar number of simulations for which the log-binomial regression failed to converge. Only the regression risk analysis ARR retained its accuracy with increasing baseline risk and effect size, and never had convergence problems. Regression risk analysis estimates of the ARD were also highly accurate. Simulation 4 has no established standard for the ARR because the nominal risk ratio is limited by ceiling effects at the upper end of the distribution. Probability theory bounds the product of the baseline risk and the risk ratio (which equals the exposed risk) at unity, establishing an upper limit for the ARR estimates. Although the table is not shown, of the methods discussed, only the regression risk analysis ARR was always plausible. For example when the baseline risk was 0.33, the maximum plausible ARR is 3.03: the logistic risk analysis estimate was 1.89, while log-binomial regression=3.57, Poisson=3.55, and Zhang and Yu=3.72

Table 3 demonstrates the precision of regression risk analysis. The widths of the confidence intervals (based on 1,000 bootstrapped replications) are similar to those from Poisson regression. Regression risk analysis appears to be sufficiently precise to produce meaningful estimates when the sample size is adequate to use logistic regression (Concato et al. 1995).

We demonstrate the effect of including an interaction term in the logistic model by analyzing two data sets that were identical except for the adjusted risk in the unexposed (0.07 and 0.26, respectively). Regression risk analysis ARRs were estimated in each set (N≈45,000) from two logistic models, one including interactions and one not. Then each data set was divided into 13 smaller data sets on the basis of the covariate values in order to conduct separate logistic regressions on each subset to observe the distribution of AORs for each section of the data. As expected, there was less variation in the AOR when risk was 0.07 (range 2.9–4.0, coefficient of variation [CV]=8.4) than when it was 0.26 (range 5.1–16.4, CV=39.9). In the first data set the ARR with and without interactions were almost identical (2.972 versus 2.971, respectively), suggesting that noninteracted models may be parsimonious when outcomes are not common. Even with the greater variation of the second set the difference between the ARR in the interacted and noninteracted models was modest (3.01 versus 2.84).

DISCUSSION

Regression risk analysis is practical and accurate. It can be applied generally to maximum likelihood models to estimate the intuitive ARR and ARD.

Despite documented confusion in the interpretation of results (Klaidman 1990; Teuber 1990; Altman, Deeks, and Sackett 1998; Bier 2001) logistic regression and its AOR continue to represent the preferred compromise for health service researchers when analyzing complex multivariate data. Although plausible alternatives to logistic regression have been used to good effect by some analysts, log-binomial regression and Poisson regression have important limitations and have not been widely adopted by health care researchers, who continue to prefer logistic regression (Table 1) and our data confirm flaws with the equation of Zhang and Yu (Zhang and Yu 1998; McNutt et al. 2003).

A detailed review of the literature finds mathematically similar approaches in the statistics (“predictive margins”) and economics (“recycled predictions”) literature, but without original citation, validation, or mathematical justification (Oaxaca 1973; Breslow 1974; Lee 1981; Lane and Nelder 1982; Manning et al. 1987; Lee 1994; Ruser 1998; Graubard and Korn 1999; DeLeon, Lindgren, and Rogers 2001; Basu and Rathouz 2005; Sommers 2006; Allen et al. 2007). To our knowledge, this paper provides the first empirical validation of the mathematics and does so in terms that are relevant to applied researchers. The methods are not commonly employed in the health services research literature and their capacity to adjust risk ratios and risk differences has not been clearly articulated.

Our proposed approach makes these very sophisticated tools more readily available to the typical health service researcher. This method offers a final common pathway to link the analytic approach to various research questions. Because the research question dictates how the results are interpreted, this characteristic can improve the range, nuance, and accuracy of research findings. This approach simplifies the researcher's task regardless of whether they define one or more populations of interest, for example, to predict the effect of smoking cessation on women, current smokers, and/or a hypothetical population in which everyone smoked.

We hope that this paper improves typical practice by defining a clear approach, illustrating the range of issues that may be addressed, illuminating common pitfalls, and advocating a simple way to compute standard errors. Although our examples focus on logistic regression our points are more general.

Limitations

Regression risk analysis can be used when there is sufficient information to estimate a population risk, i.e., in cohort, cross-sectional and population-based case–control studies with dichotomous outcomes, but not in simple case–control designs. Computing the ARR or ARD for different subsamples may reveal policy relevant differences in the effect of the predictor variable for specific subpopulations.

These methods are theoretically derived and empirically validated using Monte Carlo simulations. Monte Carlo simulations are excellent for demonstrating the accuracy of these methods, but lack the narrative power of real world data. The authors reanalyzed Behavioral Risk Factor Surveillance Survey data originally reported by Mehrotra et al. (2004): the two odds ratios reported in the abstract, 3.6 for the odds of reporting arthritis if the respondent had class III obesity and 2.8 as the odds for making an attempt to lose weight when the respondent reported that their doctor advised them to do so, corresponded to ARRs of 1.81 and 1.38, respectively, illustrating the practical value of regression risk analysis.

Conclusion

Building upon epidemiological (Lee 1981, 1994; Wilcosky and Chambless 1985; Flanders and Rhodes 1987; Greenland 2004) and statistical (Moody, Graybill, and Boes 1963; Hosmer and Lemeshow 1989; Concato et al. 1995) foundations, we introduce regression risk analysis, a theoretically derived approach to estimating ARDs, ARRs, and their standard error. From the familiar logistic regression or other multiple regression models, regression risk analysis accurately adjusts risk ratios and risk differences for confounding whether confounders are categorical or continuous. The ability to calculate standard errors and confidence intervals makes statistical testing possible. Regression risk analysis is sufficiently precise to analyze data sets of modest size: it is practical.

Regression risk analysis offers an intuitive approach for obtaining risk measures directly from multiple regression analysis. It should change the norms for reporting health care research. We advocate its use whenever researchers might otherwise present odds ratios or other approximations to estimate effect size. Regression risk analysis can be used for all types of studies for which the population risk can be measured, including population-based case–control studies. In cases where outcomes are common for at least some combinations of covariates, regression risk analysis should replace the use of AORs completely.

Derived from maximum likelihood theory, regression risk analysis is an elegant solution to a longstanding problem in health care research. Although the most sophisticated analysts have generally found solutions for estimating these values, regression risk analysis makes available to the general research population a general and accessible method. Because these measures can be calculated from the familiar logistic regression model, we expect that health care researchers will accept it enthusiastically. For the first time, the general research community and consumers of research alike will be able to have an intuitive and accurate discussion of the findings of complex multivariate data analyses for dichotomous outcomes. The adoption of regression risk analysis will substantially increase the odds that the magnitude of an exposure's effect will be communicated clearly.

Supporting Information

Additional supporting information may be found in the online version of this article:

Appendix SA1: Author Matrix.

Please note: Wiley-Blackwell is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.