Abstract
Objective
To assess whether outpatient prescription drug utilization produces offsets in the cost of hospitalization for Medicare beneficiaries.
Data Sources/Study Setting
The study analyzed a sample (N=3,101) of community-dwelling fee-for-service U.S. Medicare beneficiaries drawn from the 1999 and 2000 Medicare Current Beneficiary Surveys.
Study Design
Using a two-part model specification, we regressed any hospital admission (part 1: probit) and hospital spending by those with one or more admissions (part 2: nonlinear least squares regression) on drug use in a standard model with strong covariate controls and a residual inclusion instrumental variable (IV) model using an exogenous measure of drug coverage as the instrument.
Principal Findings
The covariate control model predicted that each additional prescription drug used (mean=30) raised hospital spending by $16 (p<.001). The residual inclusion IV model prediction was that each additional prescription fill reduced hospital spending by $104 (p<.001).
Conclusions
The findings indicate that drug use is associated with cost offsets in hospitalization among Medicare beneficiaries, once omitted variable bias is corrected using an IV technique appropriate for nonlinear applications.
Keywords: Hospital spending, drug cost offsets, Medicare, indication bias, instrumental variables
Since the mid-1990s, prescription drugs have been the fastest rising component of national health expenditures and are projected to significantly outpace other service sectors for at least another decade to come (Heffler et al. 2005). This trend has resulted in demands by payors and policy makers that pharmaceutical companies demonstrate value for their products. One response by industry has been to incorporate economic evaluations in clinical trials (Ramsey et al. 2005). A Medline search of studies published in 2003 found 42 clinical trial-based economic evaluations of drugs (Doshi, Glick, and Polsky 2006). Many, but not all of these studies report that new drug therapies demonstrate cost savings or cost-effectiveness by reducing use of other medical resources such as hospitalizations, physician visits, and rehabilitative care. Because treatment is randomly assigned, clinical trial-based evaluations have high internal validity. However, they have limited external validity or generalizability, given their restrictive sample inclusion and exclusion criteria, artificially enhanced medication compliance, study protocol-driven medical resource use, and unrepresentative study sites (Ramsey et al. 2005). Hence, clinical trials provide limited information on the economic benefits of drug therapies when they are used in most real-world settings.
Observational studies using readily available administrative data and public use surveys can overcome the problems of external validity that plague economic evaluations in clinical trials. The challenge comes in assuring that the results from observational studies are internally valid. Various approaches are evident in the literature. A series of studies by Frank Lichtenberg (1996, 2001, 2002) used drug age (date from FDA approval) to assess the returns from pharmaceutical use on hospital expenses and other outcomes. Lichtenberg hypothesized that if newer drugs are more effective than older ones, then hospital expenses should be lower among those taking newer drugs. He tested the hypothesis with various econometric specifications in both cross-sectional and longitudinal models and found consistent evidence of hospital cost savings associated with newer medications. These are intriguing findings, but leave unanswered the question of why some patients are prescribed newer drugs, while others receive older medications? Moreover, a number of recent publications have demonstrated that in several therapeutic classes, older drugs appear to generate more cost savings than newer compounds (Wertheimer, Levy, and O'Connor 2001; US Congressional Budget Office 2002; Avorn 2004; Duggan 2004; Fischer and Avorn 2004). However, not all of these studies focused on hospital costs.
Other attempts to measure potential cost offsets associated with medication use have focused on the role of prescription coverage. These include the well-known studies by Soumerai et al. (1991, 1994) that attributed increased nursing home admissions and acute mental health services to the imposition of a three-per-month limit on prescriptions in the New Hampshire Medicaid Program. More recent work by Tamblyn et al. (2001) found that increased cost sharing for drug products resulted in higher rates of emergency visits and hospitalizations for elderly and poor recipients of Quebec's provincial health insurance program. Likewise, Christian-Herman, Emons, and George (2004) found that inpatient admissions increased when a Medicare HMO dropped coverage for brand name drugs. However, a larger body of work has failed to find any association between hospitalization rates and prescription coverage or changes in prescription cost sharing (Johnson et al. 1997; Balkrishnan et al. 2001; Motheral and Fairman 2001; Pilote et al. 2002; Fairman, Motheral, and Henderson 2003; Stuart et al. 2004; Briesacher et al. 2005; Stuart et al. 2007a), and one study even found a positive association between insurance coverage and rates of potentially preventable hospitalization (Culler, Parchman, and Przybylski 1998). This lack of consensus is not surprising, considering the wide differences in populations studied, different sample sizes, and the diversity of research designs employed (Rice and Matsuoka 2004; Gibson, Ozminkowski, and Goetzel 2005). It also points up the need for clear theoretical guidance in specifying appropriate empirical models to assess drug-related cost offsets.
Our interest in this article is to determine whether outpatient prescription drug utilization itself is associated with reduced hospitalization costs. Estimates of this effect are important for guiding clinical and behavioral interventions as well as benefit design policies. Drug coverage is important, but by no means the only tool available to influence patient behavior in managing drug therapy. If drug use is found to be an effective means of either preventing unnecessary hospitalizations or reducing the average cost per hospital episode, such findings would provide a powerful incentive for clinicians, patients, and payors alike adopt policies designed to reap the promised returns.
There are three reasons why we would expect drug utilization and hospital costs to be inversely related, other things being equal. First, although some medications are taken to relieve symptoms or treat minor conditions that would not normally result in hospitalization if untreated, a significant share of the medications taken by elderly Medicare beneficiaries is intended as secondary preventive measure for such common chronic conditions such as hypertension, diabetes, coronary artery disease, heart failure, and COPD(chronic obstructive pulmonary disease), where failure to treat may significantly increase the risk of hospitalization (Stuart et al. 2007b). Second, even when drug therapy does not avert hospitalization, it may result in less intense use of hospital services and/or shorter stays, both of which translate to lower hospital costs. The third reason why we would expect an inverse relationship is that in statistical models containing comorbidity control variables, higher aggregate drug use becomes a proxy for better medication adherence; and adherence is a strong predictor of medication effectiveness.
Methods
Data Source
We used data from the 1999 and 2000 Medicare Current Beneficiary Surveys (MCBS) to conduct the analysis. The MCBS is a longitudinal panel survey of a representative national sample of the Medicare population conducted under the auspices of the Centers for Medicare and Medicaid Services (CMS). Approximately 12,000 Medicare beneficiaries are surveyed every year. The MCBS uses a rotating panel design in which a new round of about 4,000 beneficiaries is selected each year from Medicare enrollment files and a prior round of equal size is retired. Respondents are interviewed up to 11 times over a 3.5-year period with computer-assisted personal interviews. The survey instrument includes detailed questions about demographic characteristics, access to care, Medicare supplemental insurance coverage (including questions about the presence and source of prescription benefits), health and functional status, and utilization and spending for all health care services. Respondents maintain logs of prescriptions and keep insurance slips and used medication containers. At the time of the interview, respondents present their medication containers, and the interviewer records each fill or refill as a separate event, noting drug name, strength, dosage, and method of administration. Interviewers also query respondents about medications not mentioned but recorded in previous interviews. The MCBS files contain extracts from Medicare Part A and Part B claims information for each respondent.
Study Sample
Our sample frame comprised community-dwelling MCBS respondents represented in both the 1999 and 2000 survey rounds. From this frame, we selected all Medicare beneficiaries with 24 months of observation and continuous Medicare Part A and Part B coverage. We examined the diagnostic fields in the Medicare claim files for the initial 12 months to assess baseline medical conditions for each sample member. We used the second 12 months to characterize beneficiaries’ utilization of prescription drugs and inpatient hospital expenditures. To improve the precision of our estimates, we restricted the sample with drug coverage to those having it continuously throughout the study period. Likewise, the sample without drug benefits was limited to those with no evidence of coverage at any time during the period. We also excluded beneficiaries enrolled in Medicare+Choice (known now as Medicare Advantage Plans) because these individuals generate no Medicare claims and hence have no diagnostic information. Finally, to avoid bias arising from other insurance effects, both samples were limited to beneficiaries maintaining continuous Medicare supplementation for physician services and hospital care. These selection criteria resulted in a usable sample of 3,101, of whom 2,400 had prescription coverage and 701 did not.
Study Variables
Our dependent variables are the probability of any hospitalization and, for those with one or more inpatient stays, total hospital expenditures based on Medicare Part A claims. The primary independent variable is counts of prescription drug fills. Other independent variables include Medicare entitlement status, age, sex, educational attainment, residence (urban/rural and census region), income, and a risk adjuster to control for underlying differences in morbidity. The risk adjuster is predicted 2000 Medicare spending based on the diagnoses found in Medicare claims from 1999 using the Diagnostic Cost Group/Hierarchical Coexisting Condition or DCG/HCC model. This model was developed by CMS to set capitation rates for Medicare HMOs. The version of the DCG/HCC model that we used creates indicators for the presence of 189 medical conditions based on the diagnoses recorded on beneficiaries’ Medicare claims (Pope et al. 2004). It then applies previously calibrated weights, based on regression coefficients, to create a single risk score (denoted as “Ybase” by CMS). Because the DCG/HCC model captures the prevalence of diseases that affect both drug use and hospital spending, it is a reasonable candidate to control for indication bias. Although the DCG/HCC was designed for payment purposes, it has been widely validated as a measure for controlling confounding in studies of medical and drug use (Wrobel et al. 2003; Pope et al. 2004; Stuart et al. 2004, 2005b 2006, 2007a; Stuart, Simoni-Wastila, and Chauncey 2005a; Doshi, Glick, and Polsky 2006).
Analytic Strategy
Our analytic approach begins with a simple two-part model in which the incidence of hospitalization (H), a binary variable, is regressed via the probit transformation Φ( ) on prescription drug counts (D) and the vector of covariates (X) listed in Table 1 in the first part (equation (1)),
| (1) |
and hospital costs ($H) are regressed on drug use and X in the subsample of beneficiaries with any inpatient stays, via the nonlinear least squares (NLS) method and the exponential functional form in the second part (equation (2)),
| (2) |
where the “δ's” are parameters to be estimated and the “ξ's” denote random error terms.
Table 1.
Characteristics of the Study Sample (N=3,101)
| Characteristics | Percent/Number (SD) |
|---|---|
| Dependent variables | |
| Hospitalized (%) | 20.1 |
| Hospital expense for the sample as a whole (mean/SD) | $2,097 (6,682) |
| Hospital expense for those hospitalized (mean/SD) | $10,425 (11,628) |
| Independent variables | |
| Prescription fills (mean/SD) | 30.1 (27.3) |
| Medicare entitlement status (%) | |
| Aged/no prior disability | 76.8 |
| SSDI disabled (<65) | 16.2 |
| Aged/previously disabled (>65) | 7.0 |
| Age (%) | |
| 65–69 | 12.2 |
| 70–74 | 24.3 |
| 75–79 | 18.8 |
| 80+ | 28.4 |
| Female (%) | 57.1 |
| Marital status (%) | |
| Married | 48.3 |
| Single/widowed/divorced/separated | 51.7 |
| Educational attainment (%) | |
| <High school graduate | 35.7 |
| High school graduate | 64.3 |
| Urban residence (%) | 72.2 |
| Census region (%) | |
| Northeast | 20.5 |
| Midwest | 21.3 |
| South | 40.6 |
| West | 17.6 |
| Annual income (%) | |
| ≤$10,000 | 26.9 |
| $10,001–$20,000 | 26.3 |
| $20,001–$30,000 | 19.9 |
| >$30,000 | 26.9 |
| DCG/HCC risk adjuster | |
| Ybase (mean/SD) | $5,925 (4,911) |
| Instrumental variable | |
| Drug coverage | 77.4 |
Source: 1999 and 2000 MCBS.
The subscript “0” on δ indicates that it is the constant term (intercept) parameter, the subscript “D ” denotes the coefficient parameter for prescription drug usage, the subscript “X” denotes the coefficient parameters for the covariates, the subscript “1” refers to the first part of the two-part model, and the subscript “2” is analogously defined. The probit transformation restricts the regression function to the unit interval in accordance with the binary dependent variable. As recommended by Mullahy (1998), we use the exponential specification, so that the second part regression will conform to the nonnegativity of the expenditure outcome while obviating the need for retransformation. The estimates obtained from equations (1) and (2) are then combined to estimate the average derivative of drug use on hospital spending.1
The covariate-adjusted two-part model given in equations (1) and (2) does not address the possibility that the key explanatory variable—drug use—may be endogenous either because of indication bias or other potential unobserved confounders. Following the argument of Terza, Bradford, and Dismuke (2008), attempting to correct for endogeneity via application of the conventional linear instrumental variable (IV) estimator will be susceptible to bias, owing to the inherent nonlinearity of the two-part model. To address this problem, we implement the two-stage residual inclusion (2SRI) estimator suggested by Terza, Basu, and Rathouz (2008). The 2SRI estimator is a consistent nonlinear extension of the conventional IV method. The instrument we propose for drug use is drug coverage. We consider drug coverage to be a good candidate instrument based on the fact that coverage and benefit design features have been shown to strongly influence drug use (Pauly 2004; Shea et al. 2007) and because there is no theoretic reason to believe that drug coverage per se should affect hospital costs except through the intermediation of drug use. One might argue that beneficiaries who seek drug coverage are likely to be sicker than those who do not (Rice and Matsuoka 2004; Gibson, Ozminkowski, and Goetzel 2005) and thus more likely to be hospitalized. We control for that in two ways: first, by restricting the study sample to beneficiaries who have a Medicare supplemental health insurance policy (which plausibly can affect hospital costs), and second through use of the DCG/HCC risk adjuster. In prior work (Stuart, Simoni-Wastila, and Chauncey 2005a; Shea et al. 2007), we have demonstrated the value of the DCG/HCC risk adjuster in controlling for selection bias in drug coverage. In the present context, while we cannot rule out the possibility of residual confounding, it seems reasonable to believe that the direction of the error would be toward the null; that is, a finding that drug use is positively rather than negatively predictive of hospital cost.
Our 2SRI model has the following three components. The first equation regresses the potentially endogenous drug use variable (D) on the exogenous variables (X) and the IV (C),
| (3) |
where the “α's” are the coefficient parameters to be estimated and ω1 denotes the random regression error terms. The parameters of equation (3) are estimated using the NLS method and the residuals 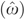 are saved. To complete the estimation, the residuals,
are saved. To complete the estimation, the residuals, 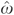 , are entered together with the original drug count variable, D, in a standard two-part expenditure model comprising a probit equation on any hospitalization (equation (4)), and a nonlinear expenditure (equation (5)),
, are entered together with the original drug count variable, D, in a standard two-part expenditure model comprising a probit equation on any hospitalization (equation (4)), and a nonlinear expenditure (equation (5)),
| (4) |
| (5) |
where the “β's” are the coefficient parameters to be estimated and the “ɛ's” denote the random regression error terms, and equation (5) is estimated using the subsample of beneficiaries with any inpatient stay. The residuals play two roles in equations (4) and (5). First, they control for potential endogeneity due to unobserved drug use indications and other latent confounders. Second, their inclusion affords a simple diagnostic tool to statistically test for endogeneity of D. If the coefficient of 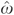 in either equation (4) or (5) is statistically significant, then D is indeed endogenous. If, on the other hand, the coefficient of
in either equation (4) or (5) is statistically significant, then D is indeed endogenous. If, on the other hand, the coefficient of 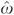 is insignificant, then D is considered exogenous and, consequently, the adjusted model defined in equations (1) and (2) is preferred on efficiency grounds.
is insignificant, then D is considered exogenous and, consequently, the adjusted model defined in equations (1) and (2) is preferred on efficiency grounds.
We favor this nonlinear 2SRI method because it is both appropriate, given the data structure (Terza, Bradford, and Dismuke 2008), and consistent (Terza, Basu, and Rathouz 2008). Moreover, Terza (2006) shows that for models like equations (4) and (5) in which observable (D, X) and unobservable (ω) regressors are given symmetric treatment in the specification, alternative estimators like the generalized method of moments are difficult to implement.
Results
Characteristics of the study sample are summarized in Table 1. Approximately 20 percent of beneficiaries experienced at least one inpatient hospitalization in 2000 with a mean expense of $10,425 per person hospitalized ($2,097 per person averaged over the entire sample). As expected, the distribution of expenses was highly right-skewed, with standard deviations exceeding the mean in both cases. The primary independent variable of interest, counts of prescription fills, was also skewed (mean=30.1, standard deviation=27.3).
Results from the two model approaches are presented in Tables 2–4. The covariate control model results from equations (1) and (2) are summarized in Table 2. The estimated impact of drug use on the probability of hospitalization is small, positive, and highly significant (0.01, p<.001), while that on hospital spending is also small and positive, but insignificant (near zero, p=.95). The average derivative estimated across both parts of the covariate-adjusted model (Table 4) is $15.69 (p<.001).
Table 2.
Results from the Covariate Control Models
| Probit on Any Hospitalization | Nonlinear Least Squares on Hospital Spending (Restricted to Users) | |||
|---|---|---|---|---|
| Variables* | Coefficient | p-value | Coefficient | p-value |
| Counts of drug use | 0.01 | <.001 | 0.0001 | .95 |
| SSDI disabled (<65) | −0.21 | .07 | 0.32 | .13 |
| Aged/previously disabled | 0.26 | .01 | 0.38 | .03 |
| Age | ||||
| 70–74 | −0.10 | .32 | 0.06 | .71 |
| 75–79 | 0.03 | .80 | 0.21 | .29 |
| 80+ | 0.08 | .42 | 0.04 | .82 |
| Married | −0.06 | .34 | 0.09 | .32 |
| Female | −0.13 | .53 | −0.25 | .009 |
| White | 0.03 | .68 | 0.10 | .45 |
| Nonurban area | −0.04 | .53 | −0.01 | .97 |
| High school graduate | 0.13 | .03 | −0.34 | .002 |
| Midwest | 0.06 | .48 | −.53 | <.001 |
| South | 0.02 | .83 | −0.36 | .01 |
| West | 0.01 | .95 | 0.06 | .72 |
| Income | ||||
| $10,001–$20,000 | −0.14 | .07 | −0.16 | .19 |
| $20,001–$30,000 | −0.16 | .08 | −0.41 | .007 |
| >$30,000 | −0.14 | .14 | 0.30 | .04 |
| Ybase | 0.03 | <.001 | 0.14 | <.001 |
| Constant | −1.28 | <.001 | 9.29 | .74 |
Reference groups are as follows: Age 65–69, not formerly disabled, single, male, nonwhite, urban area, East, and income ≤$10,000.
Table 4.
Summary of Estimated Impacts of an Additional Prescription Fill on Hospital Expenditures by Type of Model
| Model | Average Derivative* | p-value† |
|---|---|---|
| Covariate control model | $15.69 | <.001 |
| Residual inclusion IV model | −$104.03 | <.001 |
The derivation of the average derivative and its standard error is described in Note 1.
p-value for Wald statistic for the null that drug use has no effect on hospital expenditures.
Findings from the 2SRI model are presented in Table 3. Results from the NLS estimation of the drug utilization equation (4) indicate that drug coverage is positive and statistically significant (t-value=6.993, p-value<.001), supporting its use as an IV. The probit results for the drug count variable show a small negative impact (−0.01) of marginal significance (p=.09). However, the residuals 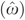 on drug counts derived from equation (5) are positive and highly significant (0.02, p=.008), which is indicative of endogeneity bias in the findings from the covariate control model results shown in Table 2. The results from the second stage of the 2SRI model indicate a significant negative effect (−0.04, p=.01) of drug use on hospital expenditures. The average derivative from combining the two stages (Table 4) is −$104.03 and statistically significant (p<.001).1
on drug counts derived from equation (5) are positive and highly significant (0.02, p=.008), which is indicative of endogeneity bias in the findings from the covariate control model results shown in Table 2. The results from the second stage of the 2SRI model indicate a significant negative effect (−0.04, p=.01) of drug use on hospital expenditures. The average derivative from combining the two stages (Table 4) is −$104.03 and statistically significant (p<.001).1
Table 3.
Results from the Residual Inclusion Instrumental Variable Model
| Nonlinear Least Squares for Rx Use (Equation (4)) | Probit for Any Hospitalization (Equation (5)) | Nonlinear Least Squares for Hospital Spending (Restricted to Users) (Equation (6)) | ||||
|---|---|---|---|---|---|---|
| Variables* | Coefficient | p-value | Coefficient | p-value | Coefficient | p-value |
| Counts of drug use | −0.01 | .09 | −0.04 | .01 | ||
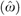 from equation (3)† from equation (3)†
|
0.02 | .008 | 0.04 | .01 | ||
| SSDI disabled (<65) | 0.22 | .01 | −0.07 | .61 | 0.68 | .02 |
| Aged/previously disabled | 0.27 | <.001 | 0.44 | <.001 | 0.75 | .003 |
| Age | ||||||
| 70–74 | −0.04 | .59 | −0.12 | .24 | 0.10 | .60 |
| 75–79 | −0.06 | .39 | −0.02 | .83 | 0.14 | .49 |
| 80+ | −0.04 | .60 | 0.02 | .83 | −0.12 | .60 |
| Married | 0.04 | .32 | −0.04 | .57 | 0.19 | .09 |
| Female | 0.23 | <.001 | −0.01 | .94 | 0.02 | .88 |
| White | 0.01 | .80 | 0.14 | .14 | 0.39 | .05 |
| Nonurban area | −0.08 | .04 | −0.04 | .49 | −0.002 | .99 |
| High school graduate | 0.10 | .06 | 0.09 | .20 | −0.43 | .002 |
| Midwest | 0.02 | .64 | 0.10 | .26 | −0.43 | .01 |
| South | −0.09 | .12 | 0.02 | .80 | −0.31 | .03 |
| West | −0.06 | .27 | −0.04 | .68 | −0.003 | .99 |
| Income | ||||||
| $10,001–$20,000 | −0.10 | .10 | −0.19 | .03 | −0.33 | .05 |
| $20,001–$30,000 | −0.22 | <.001 | −0.23 | .03 | −0.54 | .004 |
| >$30,000 | 0.20 | <.001 | −0.25 | .02 | 0.02 | .92 |
| Ybase | 0.19 | <.001 | 0.44 | <.001 | 0.48 | <.001 |
| Constant | 2.73 | <.001 | −0.98 | <.001 | 9.70 | <.001 |
| Rx coverage | 0.29 | <.001 | ||||
Reference groups are as follows: Age 65–69, not formerly disabled, single, male, nonwhite, urban area, East, and income ≤$10,000.
The residuals represent the difference between individuals’ actual drug counts and predicted drug counts from equation (5).
Discussion
The major empirical finding from this research is that medication use by Medicare beneficiaries is significantly negatively associated with hospital spending. Moreover, the cross-effect is quite large: each additional prescription drug fill reduces hospital costs by slightly more than $100 or about 5 percent measured at the mean level of Medicare payments in 2000 for inpatient hospital services for study subjects. Given that the average price of prescription drugs used by community-dwelling MCBS respondents in 2000 was just under $47, this suggests that drugs are not only cost-effective but actually also cost saving for Medicare beneficiaries. This result is consistent with the findings of Lichtenberg (1996, 2001, 2002) that newer drugs are cost saving, but extends the conclusion to drug use in the aggregate by Medicare beneficiaries. Assuming these findings are replicated in future studies, the implications for Medicare would appear obvious—use whatever policy tools are available to promote appropriate prescription drug use. However, this conclusion should be interpreted in the light of several important caveats relating to our study.
Foremost is the fact that we estimate the average treatment effect across all drugs, irrespective of the indication or mechanism of action by which they could plausibly reduce either the risk of hospitalization or the intensity of service use once hospitalized. Our two-part model approach found that the effect of drug use on the probability of hospitalization was small and marginally significant, whereas the effect of use on spending conditional on hospitalization was large and highly significant. This would suggest that the primary source of hospital cost savings associated with increased drug use is through reduced need of intensive inpatient services or reduced length of stay, perhaps due to less severe illness. However, this supposition needs to be empirically tested.
The second caveat relates to data limitations in the MCBS. Because diagnostic data necessary to compute the DCG/HCC risk adjuster are only available for beneficiaries in the fee-for-service sector, we were unable to include Medicare HMO enrollees in the study sample. In addition, we were also forced to exclude residents in long-term care facilities because prescription drug use statistics are reported only for community-dwelling beneficiaries. Thus, our findings cannot be generalized to these two groups of beneficiaries. Also, it is important to note that the drug service utilization data reported in the MCBS originate from self-reports and may be subject to response bias.
The third caveat relates to the interpretation of study findings in light of the instrument (drug coverage) used in our 2SRI formulation. On the one hand, if the parametric assumptions of the 2SRI model in equations (3)–(5) strictly hold, then all relevant sources of potential heterogeneity in the derivative effects will be appropriately controlled, so that our average derivative estimator is a consistent measure of hospital expenditure effects attributable to any exogenously imposed change in prescription drug usage (see Terza, Basu, and Rathouz 2008). On the other hand, if the parametric assumptions underlying the model are violated, our average derivative estimator may be only “locally” interpretable—i.e., applicable only to the subset of the population who are likely to change their drug utilization patterns as a result of a change in drug coverage. To date, the methodological research on “local” interpretations of IV estimates has been confined to analyses of average treatment effects in the context of linear models. Useful characterizations of the “localness” of nonlinear average derivative estimators (the methodological approach in the present study) have yet to be published. This is an important area for future methodological research.
Future research should also focus on assessing the impact of adherence to recommended secondary preventive medications in specific common chronic conditions such as diabetes, coronary artery disease, heart failure, and COPD. A recent decision analysis concluded that Medicare would save money if beneficiaries with diabetes were given free access to angiotensin-converting enzyme (ACE) inhibitors (Rosen et al. 2005). Another decision analysis concluded that increased adherence to aspirin, beta-blockers, ACE inhibitors, and statins for Medicare beneficiaries with myocardial infarction would be cost-effective (Choudhry et al. 2008). With Medicare Part D claims data soon to be available to researchers, there is an enormous opportunity to conduct empirical research on the economic effectiveness of drug therapy where randomized treatment assignment is either impractical or too limited in scope to produce real-world answers for the Medicare population.
Acknowledgments
Joint Acknowledgment/Disclosure Statement: Research support for this work was provided in part by grants from the Robert Wood Johnson Foundation and the Commonwealth Fund.
Disclosures: None.
Disclaimers: The views presented here are those of the authors and not necessarily those of the Robert Wood Johnson Foundation or the Commonwealth Fund, their directors, officers, or staff.
Note
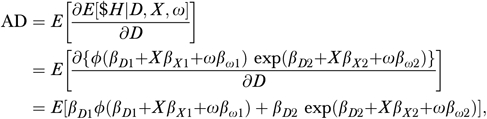 |
Supporting Information
Additional supporting information may be found in the online version of this article:
Appendix SA1: Author Matrix.
Appendix SA2: Other Contributions.
Please note: Wiley-Blackwell is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
References
- Avorn J. Powerful Medicines: The Benefits, Risks, and Costs of Prescription Drugs. New York: Alfred Knopf; 2004. [Google Scholar]
- Balkrishnan R, Byerly W G, Camacho F T, Shrestha A, Anderson R T. Effect of Prescription Benefit Charges on Medical Care Utilization in a Medicare HMO Population. American Journal of Managed Care. 2001;7:1093–100. [PubMed] [Google Scholar]
- Briesacher B, Stuart B, Doshi J, Wrobel M. Medicare Beneficiaries and the Impact of Gaining Prescription Drug Coverage on Inpatient and Physician Spending. Health Services Research. 2005;40(5, part 1):1279–96. doi: 10.1111/j.1475-6773.2005.00432.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choudhry N, Patrick A, Antiman E, Avorn J, Shrank W. Cost-Effectiveness of Providing Full Drug Coverage to Increase Medication Adherence in Post-Myocardial Infarction Medicare Beneficiaries. Circulation. 2008;117(10):1261–8. doi: 10.1161/CIRCULATIONAHA.107.735605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christian-Herman J, Emons M, George D. Effects of Generic-Only Drug Coverage in a Medicare HMO. Health Affairs. 2004;(Web Exclusives):W455–68. doi: 10.1377/hlthaff.w4.455. [DOI] [PubMed] [Google Scholar]
- Culler S D, Parchman M L, Przybylski M. Factors Related to Potentially Preventable Hospitalizations among the Elderly. Medical Care. 1998;36(6):804–17. doi: 10.1097/00005650-199806000-00004. [DOI] [PubMed] [Google Scholar]
- Doshi J, Glick H, Polsky D. Analysis of Cost Data in Economic Evaluations Conducted Alongside Randomized Controlled Trials. Value in Health. 2006;9(5):334–40. doi: 10.1111/j.1524-4733.2006.00122.x. [DOI] [PubMed] [Google Scholar]
- Duggan M. Do New Prescription Drugs Pay for Themselves? Journal of Health Economics. 2004;24:1–31. doi: 10.1016/j.jhealeco.2004.08.001. [DOI] [PubMed] [Google Scholar]
- Fairman K A, Motheral B R, Henderson R R. Retrospective, Long-Term Follow-Up Study of the Effect of a Three-Tier Prescription Drug Copayment System on Pharmocological and Medical Utilization and Costs. Clinical Therapeutics. 2003;25:3147–66. doi: 10.1016/s0149-2918(03)90099-3. [DOI] [PubMed] [Google Scholar]
- Fischer M, Avorn J. Economic Implications of Evidence-Based Prescribing for Hypertension: Can Better Care Cost Less? Journal of the American Medical Association. 2004;291(15):1850–6. doi: 10.1001/jama.291.15.1850. [DOI] [PubMed] [Google Scholar]
- Gibson T B, Ozminkowski R J, Goetzel R Z. The Effects of Prescription Drug Cost Sharing: A Review of the Evidence. American Journal of Managed Care. 2005;11(11):730–40. [PubMed] [Google Scholar]
- Heffler S, Smith S, Keehan S, Borger C, Clemens M, Truffer C. U.S. Health Spending Projections for 2004–2114. Health Affairs. 2005;24(suppl):W5–W74. doi: 10.1377/hlthaff.w5.74. (February) [DOI] [PubMed] [Google Scholar]
- Johnson R E, Goodman M J, Hornbrook M C, Eldridge M B. The Effect of Increased Prescription Drug Cost-Sharing on Medical Care Utilization and Expenses of Elderly Health Maintenance Organization Members. Medical Care. 1997;35:1119–31. doi: 10.1097/00005650-199711000-00004. [DOI] [PubMed] [Google Scholar]
- Lichtenberg F R. Do (More and Better) Drugs Keep People out of Hospitals? American Economic Review. 1996;86(2):384–8. [PubMed] [Google Scholar]
- Lichtenberg F R. Are the Benefits of Newer Drugs Worth Their Cost? Evidence from the 1996 MEPS. Health Affairs. 2001;20(5):241–51. doi: 10.1377/hlthaff.20.5.241. [DOI] [PubMed] [Google Scholar]
- Lichtenberg F R. “Benefits and Costs of Newer Drugs: An Update.” Working Paper 8996. National Bureau of Economic Research. 2002.
- Motheral B M, Fairman K A. Effect of a Three-Tier Prescription Copay on Pharmaceutical and Other Medical Utilization. Medical Care. 2001;39(12):1293–304. doi: 10.1097/00005650-200112000-00005. [DOI] [PubMed] [Google Scholar]
- Mullahy J. Much Ado About Two: Reconsidering Retransformation and the Two-Part Model in Health Econometrics. Journal of Health Economics. 1998;17:247–81. doi: 10.1016/s0167-6296(98)00030-7. [DOI] [PubMed] [Google Scholar]
- Pauly M. Medicare Drug Coverage and Moral Hazard. Health Affairs. 2004;23:113–22. doi: 10.1377/hlthaff.23.1.113. [DOI] [PubMed] [Google Scholar]
- Pilote L, Beck C, Richard H, Eisenberg M J. The Effects of Cost-Sharing on Essential Drug Prescriptions, Utilization of Medical Care and Outcomes after Acute Myocardial Infarction in Elderly Patients. Canadian Medical Association Journal. 2002;167:246–52. [PMC free article] [PubMed] [Google Scholar]
- Pope G, Kautter J, Ellis R, Ash A, Aranian J, Iezzoni L, Ingber M, Levey J, Robst J. Risk Adjustment of the Medicare Capitation Payments Using the CMS-HCC Model. Health Care Financing Review. 2004;25(4):119–41. [PMC free article] [PubMed] [Google Scholar]
- Ramsey S, Willke R, Briggs A, Brown R, Buxton M, Chawla A, Cook J, Glick H, Bengt L, Pettiti D, Reed S. Good Research Practice for Cost-Effectiveness Analysis Alongside Clinical Trials: The ISPOR RCT-CEA Task Force Report. Value in Health. 2005;8(5):521–33. doi: 10.1111/j.1524-4733.2005.00045.x. [DOI] [PubMed] [Google Scholar]
- Rice T, Matsuoka K Y. The Impact of Cost-Sharing on Appropriate Utilization and Health Status: A Review of the Literature on Seniors. Medical Care Research and Review. 2004;61(4):415–52. doi: 10.1177/1077558704269498. [DOI] [PubMed] [Google Scholar]
- Rosen A, Hamel M, Weinstein M, Cutler D, Fendrick A, Vijan S. Cost-Effectiveness of Full Medicare Coverage of Angiotensin-Converting Enzyme Inhibitors for Beneficiaries with Diabetes. Annals of Internal Medicine. 2005;143:89–99. doi: 10.7326/0003-4819-143-2-200507190-00007. [DOI] [PubMed] [Google Scholar]
- Shea D G, Terza J V, Stuart B C, Briesacher B. Estimating the Effects of Prescription Drug Coverage for Medicare Beneficiaries. Health Services Research. 2007;43:933–49. doi: 10.1111/j.1475-6773.2006.00659.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soumerai S B, Ross-Degnan D, Avon J, McLaughlin I T, Choodnovskiy I. Effects of Medicaid Drug-Payment Limits on Admission to Hospitals and Nursing Homes. New England Journal of Medicine. 1991;325(15):1072–7. doi: 10.1056/NEJM199110103251505. [DOI] [PubMed] [Google Scholar]
- Soumerai S B, McLaughlin T, Ross-Degnan D, Casteris C, Bollini P. Effects of a Limit on Medicaid Drug-Reimbursement Benefits on the Use of Psychotropic Agents and Acute Mental Health Services by Patients with Schizophrenia. New England Journal of Medicine. 1994;331(10):650–5. doi: 10.1056/NEJM199409083311006. [DOI] [PubMed] [Google Scholar]
- Stuart B, Briesacher B, Doshi J, Wrobel M, Baysac F. Will Part D Produce Savings in Part A and Part B? The Impact of Prescription Drug Coverage on Medicare Program Expenditures. Inquiry. 2007a;44(2):146–56. [Google Scholar]
- Stuart B, Briesacher B, Shea D, Cooper B, Baysac F, Limcangco R. Riding the Rollercoaster: The Ups and Downs in Out-of-Pocket Spending under the New Medicare Benefit. Health Affairs. 2005b;24(4):1022–31. doi: 10.1377/hlthaff.24.4.1022. [DOI] [PubMed] [Google Scholar]
- Stuart B, Doshi J, Briesacher B, Wrobel M, Baysac F. Impact of Prescription Coverage on Hospital and Physician Costs: A Case Study of Medicare Beneficiaries with Chronic Obstructive Pulmonary Disease. Clinical Therapeutics. 2004;26(10):1688–99. doi: 10.1016/j.clinthera.2004.10.012. [DOI] [PubMed] [Google Scholar]
- Stuart B, Simoni-Wastila L, Baysac F, Shaffer T, Shea D. Coverage and Use of Prescription Drugs in Nursing Homes: Implications for the Medicare Modernization Act. Medical Care. 2006;44(3):243–9. doi: 10.1097/01.mlr.0000199652.15293.fc. [DOI] [PubMed] [Google Scholar]
- Stuart B, Simoni-Wastila L, Chauncey D. Assessing the Impact of Coverage Gaps in the Medicare Part D Drug Benefit. Health Affairs. 2005a;24(suppl 1, Web Exclusives):W5-167–79. doi: 10.1377/hlthaff.w5.167. [DOI] [PubMed] [Google Scholar]
- Stuart B, Simoni-Wastila L, Zuckerman I, Doshi J, Shea D, Shaffer T, Zhao L. Chartbook of Medication Use by Aged and Disabled Medicare Beneficiaries across the Spectrum of Morbidity. Baltimore: The Peter Lamy Center on Drug Therapy and Aging; 2007b. [Google Scholar]
- Tamblyn R, Laprise R, Hanley J, Abrahamowicz M, Scott S, Mato N, Hurley J, Grad R, Latimer E, Perreault R, McLeod P, Huang A, Lavochettle P, Mallet L. Adverse Events Associated with Prescription Drug Cost-Sharing among Poor and Elderly Persons. Journal of the American Medical Association. 2001;285(4):421–9. doi: 10.1001/jama.285.4.421. [DOI] [PubMed] [Google Scholar]
- Terza J, Bradford W D, Dismuke C E. The Use of Linear Instrumental Variables Methods in Health Services Research and Health Economics: A Cautionary Note. Health Services Research. 2008;43:1102–20. doi: 10.1111/j.1475-6773.2007.00807.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terza J, Basu A, Rathouz P. Two-Stage Residual Inclusion Estimation: Addressing Endogeneity in Health Econometric Modeling. Journal of Health Economics. 2008;27:531–43. doi: 10.1016/j.jhealeco.2007.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terza J V. Estimation of Policy Effects Using Parametric Nonlinear Models: A Contextual Critique of the Generalized Method of Moments. Health Services and Outcomes Research Methodology. 2006;6:177–98. [Google Scholar]
- U.S. Congressional Budget Office. Issues in Designing a Prescription Drug Benefit for Medicare. Washington, DC: U.S. Government Printing Office; 2002. [Google Scholar]
- Wertheimer A, Levy R, O'Connor T. Too Many Drugs? The Clinical and Economic Value of Incremental Innovations. Investing in Health: The Social and Economic Benefits of Health Care Innovation. 2001;14:77–118. [Google Scholar]
- White H. Estimation, Inference and Specification Analysis. Cambridge: Cambridge University Press; 1994. [Google Scholar]
- Wrobel M, Doshi J, Stuart B, Briesacher B. Predictability of Drug Expenditures for Medicare Beneficiaries. Health Care Financing Review. 2003;25(2):37–46. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


