Abstract
Interventional, “loopless antenna” MRI detectors are currently limited to 1.5 T. This study investigates whether loopless antennae offer signal-to-noise ratio (SNR) and field-of-view (FOV) advantages at higher fields, and whether device heating can be controlled within safe limits. The absolute SNR performance of loopless antennae from 0.5 to 5 T is investigated both analytically, using electromagnetic (EM) dipole antenna theory, and numerically with the EM method of moments, and found to vary almost quadratically with field strength depending on the medium’s electrical properties, the noise being dominated by direct sample conduction losses. The prediction is confirmed by measurements of the absolute SNR of low-loss loopless antennae fabricated for 1.5, 3, and 4.7 T, immersed in physiologically comparable saline. Gains of 3.8±0.2- and 9.7±0.3-fold in SNR, and approximately 10- and 50-fold gains in the useful FOV area are observed at 3 and 4.7 T, respectively, compared to 1.5 T. Heat testing of a 3 T biocompatible nitinol-antenna fabricated with a redesigned decoupling circuit shows maximum heating of ∼1 °C for MRI operating at high MRI exposure levels. Experiments in the rabbit aorta confirm the SNR and FOV advantages of the 3 T antenna versus an equivalent commercial 1.5 T device in vivo. This work is the first to study the performance of experimental internal MRI detectors above 1.5 T. The large SNR and FOV gains realized present a major opportunity for high-resolution imaging of vascular pathology and MRI-guided intervention.
Keywords: interventional MRI, MRI detectors, high-field MRI, signal-to-noise ratio, safety, MRI devices
INTRODUCTION
Magnetic resonance imaging (MRI)-guided intravascular intervention combines the multifunctional capabilities and inherent high soft-tissue contrast of MRI, with the promise of high-speed, arbitrarily oriented planar or three-dimensional visualization of local tissues, vessels, and targets, without ionizing radiation. This is crucial for navigating interventional devices in vasculatures that are opaque to x-ray fluoroscopy such as the mesenteric venous system1 and arteries that are totally occluded to radio-opaque dye.2 Intravascular ultrasound also permits clinical evaluation of vessel walls and lumens but is limited in sensitivity and efficacy when calcification is present.3, 4, 5 Moreover, MRI-guided procedures promise precise assessment of occlusion regardless of calcification6 and can be combined with the whole range of existing MRI tools for assessing perfusion, function, and biochemistry in the same procedure. With active antenna devices,7, 8 intravascular MRI9 can provide large gains in local signal-to-noise ratio (SNR) over external MRI coils. These gains translate into high-resolution imaging in the 100 μm range, which holds great potential for characterizing the progression and severity of atherosclerotic disease in vessel walls10 and applications to the urethra11 and elsewhere.12
Active intravascular MRI coils are generally of two types: Loop7 and loopless8 antennae. [Although MRI detectors need only be sensitive to the nuclear magnetic field, these detectors are intrinsically sensitive to both electric and magnetic fields and fit the traditional definition of an electromagnetic (EM) antenna.] The small loop-type receivers are commonly embedded inside catheter probes and have high local SNR. The loopless antenna uses a thin flexible coaxial line whose inner conductor is extended by approximately a quarter-wavelength (λm∕4, where λm is the wavelength in the body) at the MRI frequency, to form a “whip” suitable for imaging vessels as small as 1–4 mm in diameter. The coaxial portion is tuned to an integral multiple of a quarter wavelength (λc∕4, in the cable) to transform its impedance. The antenna’s SNR may be improved by dielectric insulation13 and tapering of the whip.14 It has high near-field sensitivity that falls-off approximately as the inverse of radial distance (ρ) from the antenna and can be fabricated with small-diameter superelastic materials that are ideally suited for intravascular applications. Its efficacy has been demonstrated in angioplasty procedures,15, 16, 17 for atherosclerotic plaque characterization,12 and for intrabiliary tumor detection.18 To date, all of these procedures were performed at and limited to, devices working at MRI magnetic field strengths (B0) of 1.5 T or lower, despite the availability of relatively compact clinical 3 T MRI systems.
The potential advantage of higher fields is SNR. The signal voltage is proportional to . For large external loop coils, the sample noise voltage is proportional to B0, and the coil noise is proportional to , so that the realized SNR varies somewhere between , and .19, 20 The coil noise contributions that arise from direct electric (E)-field coupling between the external coil and the sample are either rendered negligible by shielding,20 or by distributing the tuning capacitance,21 or are ignored. Indeed, the intrinsic SNR (ISNR) obtained by setting the coil noise to zero has for many years provided a practical target SNR that might be achievable for a particular coil geometry under optimum conditions.19 Thus, the ISNR and the ultimate ISNR (UISNR), which reflects the best one can do independent of the coil design,22 both vary linearly with B0 provided that the wavelength is not too short.19
In practice, however, real coils have E-fields associated with their conductors, and unfortunately the deployment of shields and distributed capacitance which have successfully minimized direct E-field losses for conventional MRI coils, have practical limitations for internal devices which must be minimally invasive. Consequently, as the size of conventional coils are miniaturized, the noise is increasingly dominated by direct E-field losses in the coil23 and between the coil and the sample. In the case of the loopless antenna, insofar as it can be approximated by a dipole antenna in a lossy medium,24 microwave dipole antenna theory25 suggests that the E-field losses may vary minimally with operating frequency, which might imply a dependence of SNR.
In summary, increasing the field from 1.5 to 3 T anticipates a SNR increase of somewhere between double and perhaps a factor of 4, for equivalent receiver probe designs. The realization of any such gain could benefit spatial resolution and∕or the speed of interventional MRI. Unfortunately, as B0 doubles, the pulsed radio frequency (RF) power transmitted by the body coil for equivalent flip angles and the consequent heating that results from currents induced in the body around the receiving probe, quadruples for the same RF field strength.26 Controlling heating within acceptable limits of less than 2 °C in the vicinity of implanted MRI coils, is already a struggle at 1.5 T.27 The problem was addressed in US Food and Drug Administration (FDA)-approved 1.5 T loopless antennae by providing active decoupling outside the body, at λc∕4 from the junction.7, 8 At 3 T, this solution is compromised by the wavelength being halved, whereupon the cable lengths become too short for practical use inside the body.
Therefore, to determine whether ISNR gains proportional to , , or even , are to be achieved by intravascular loopless antennae detectors above 1.5 T, we apply both analytic EM theory for a half-wave dipole antenna, and the numerical EM method-of-moments (MoM), to compute the absolute SNR of equivalent model loopless antennae over the range 0.5⩽B0⩽5 T. We then test whether experimental loopless MRI detectors can be made for 3 and 4.7 T that can realize the theoretically predicted SNR gains, and whether practical, safe, 3 T intravascular devices with longer electrical lengths are possible. Our analysis predicts surprising SNR gains that are almost quadratic in B0, consistent with detector noise being dominated by direct E-field conduction losses. The SNR predictions are tested experimentally with minimal-loss loopless antennae having the same geometry for 1.5, 3, and 4.7 T MRI, in a saline medium whose measured RF electrical properties approximate those of muscle. Finally, a biocompatible 3 T loopless intravascular antenna is fabricated with a modified decoupling∕balun circuit to control heating. This device is heat-tested at RF power specific absorption rates (SAR) nominally above FDA guidelines for MRI,28 and its SNR performance compared with a substantially equivalent commercial 1.5 T antenna in the same rabbit in vivo.
THEORY
SNR of a half-wave dipole antenna
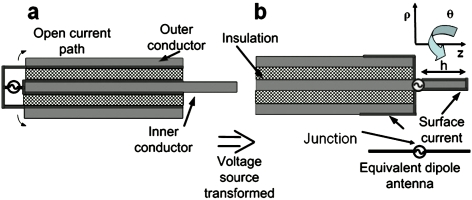
The SNR of the loopless antenna is calculated from the ratio of the transverse RF magnetic field elicited by a 1 A current source applied by the antenna in a biological medium, to the square root of its loaded resistance, in accordance with the principle of reciprocity.29 Because the skin-depth of copper at MRI frequencies above 20 MHz is ⩽40 μm we first assume that the currents on the inner shield and the conductor of the coaxial cable portion of a copper antenna are balanced. In practice this is facilitated by the use of a balun on the cable input. The signal source is then transformed from the antenna end to the whip-cable junction by a λc∕4 tuned transmission line, as shown in Fig. 1.
Figure 1.
(a) Model of actual loopless antenna and (b) corresponding dipole antenna model. The antenna axis is parallel to the B0 field of the MRI system, along the z axis. The tuned cable transforms the voltage source from the cable end in (a), to the whip junction in (b), which excites an equivalent dipole.
The relevant electric (Eρ,Ez) and transverse magnetic (Bθ) fields generated by a balanced half-wave dipole antenna formed by a whip of length h=λm∕4 and a length h=λm∕4 of the surface of the cable shield, immersed in a dissipative biological medium, and excited by a unit current source can be equivalently modeled as30
| (1) |
| (2) |
| (3) |
in cylindrical coordinates z, ρ, θ, where , , and , ω is the angular MRI frequency, and k(ε,σ) is the corresponding complex wave number with ε, σ, and μ as the medium’s the dielectric constant, conductivity, and permeability, respectively. This is a general wave solution of Maxwell’s equations for a dipole antenna unlimited by either frequency-related assumptions or approximations relating to near or far fields. A detailed description of this solution appears elsewhere.31 The loaded resistance of the dipole antenna is calculated by integrating the E-fields over the sample volume
| (4) |
Under fully relaxed conditions, the absolute system SNR (ml−1 Hz1∕2), Ψs, is given by19, 20, 22
| (5) |
where M0=3.111×10−9×B0 J T−1 ml−1 for water32 is the equilibrium nuclear magnetization per unit volume at a specific B0, ∣B+∣ is the magnitude of the circularly polarized transverse magnetic field generated by the antenna with unit current, K is the Boltzmann’s constant, T is the temperature at the whip in K, and NF is the MRI receiver’s noise-figure in dB. For an antenna aligned parallel to B0, ∣B+∣=Bθ∕√2 at the junction [Fig. 1b]. The substitution of Eqs. 1, 4 into Eq. 5 yields the SNR.
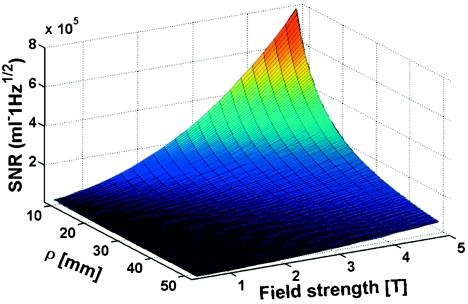
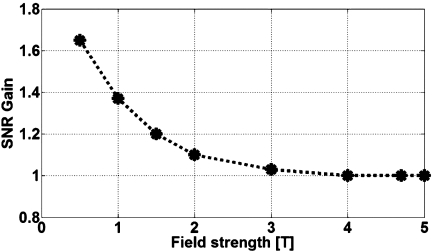
Examination of Eq. 1 reveals that Bθ, and therefore SNR, is maximum at the junction. Moreover, because k is proportional to ω, Eqs. 2, 3 indicate that the frequency dependence of the E-fields in conductive media and, hence, Rload derives mainly from the dispersive electrical properties of the medium, if any. The oscillating functions with arguments in k substantially cancel upon volume integration in Eq. 4. Thus, with Rload in Eq. 4 almost independent of frequency and M0∝ω, Eq. 5 anticipates a near quadratic SNR performance with frequency (or B0). Figure 2 plots the absolute SNR from Eq. 5 as a function of radial distance, ρ, from the antenna in the plane of the junction (z=0) for 0.5 T⩽B0⩽5 T, and NF=0. The plot is obtained by numerical integration of Eq. 4 for a medium with nondispersive ε=80, σ=0.65 S∕m, and μ=1: The SNR varies as for ρ⩽50 mm.
Figure 2.
SNR performance at the antenna junction of a dipole antenna in a lossy medium with of ε=80, σ=0.63 S∕m, as modeled from analytical Eqs. 1, 2, 3, 4, 5 as a function of B0 for different ρ⩽50 mm. Fitting the B0 axis results shows that SNR varies as for ρ⩽50 mm.
This result is very different from the traditional dependence for external loop coils with sample-dominant noise, and a little higher than the dependence predicted for external detectors with dominant coil noise.20 Indeed, this dipole antenna analysis does not actually include the losses in the detector components per se because the E-fields computed from Eqs. 2, 3 correspond to resistive losses in the sample. In addition, the assumption that the loopless antenna is a perfectly balanced dipole is not entirely accurate because the pole on the cable shield is not, in practice, physically confined to h=λm∕4 (Fig. 1), which may result in unbalanced shield currents. Thus, to determine the effects of all of the losses for the loopless antenna, we will resort to a full-wave EM numerical evaluation. This requires as input, the specific details of the antenna configuration and medium.
Medium dielectric constant and conductivity
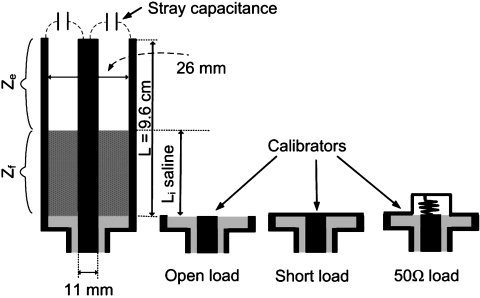
The numerical analysis and subsequent experiments assume a homogeneous 0.35% saline test medium whose electrical properties approximate that of muscle tissue with ε=108–60, and σ=0.65–0.74 S∕m over the frequency range 21–210 MHz33 corresponding to proton (1H) MRI from 0.5 to 5 T. Because the above analysis shows that losses in the medium are central to the SNR analysis of miniature antennae, and because literature values of saline σ and ε are poorly resolved in the MRI frequency range and may vary with solution purity and environment,34 we measure them from 21 to 210 MHz. We use a home-built cylindrical gold-plated copper specimen cell of length L, with a coaxial electrode, as depicted in Fig. 3. The complex impedance of the saline is measured with a Hewlett-Packard HP4395 impedance analyzer. The RF electrical properties are determined using coaxial line impedance equations.35
Figure 3.
Schematic of partially filled coaxial cylindrical transmission line (left) and calibration loads (right) used to measure saline electrical properties with the HP4395 impedance analyzer. The stray capacitance is measured with the device empty.
With the analyzer connected, the cell is first calibrated with short, open and 50 Ω reference loads. The impedance, Zs, of the stray capacitance, Cs, at the cell’s distal end is determined via
| (6) |
where Zm and Ze are the measured and the characteristic impedances of the empty cell, respectively, and γe is its propagation constant. This yields 0.5⩽Cs⩽0.8 pF. The cell is then filled with saline and the impedance, , measured at N different levels Li, at each frequency. Then,
| (7) |
| (8) |
where Zf is the characteristic impedance of the saline-filled fixture. Zf and γf are nonlinear functions of the dielectric medium properties, so the impedance is estimated via an exhaustive search algorithm over a constrained ε (10–150) and σ (0–2 S∕m) space minimizing an error cost function
| (9) |
with measurements recorded at N=13 or 19 different fill lengths.
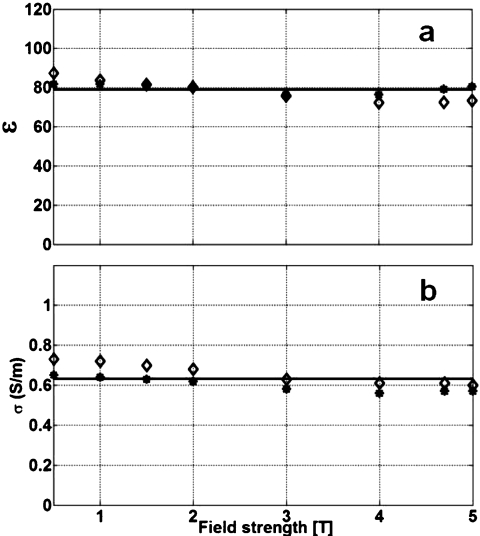
The measurements (Fig. 4) show that the electrical properties of the saline are essentially constant over this frequency range, with a lower variance for the higher N. Therefore the mean values of ε=79 and σ=0.63 S∕m are used, in agreement with the values assumed for the computations. The measured σ is consistent with prior published data on saline with a third of the salt concentration showing three times the σ, and almost identical ε,36 and approximate the values for muscle tissue noted above. However, because the electrical properties of real biological tissue are dispersive26 and the intended application of intravascular antennae involve their contact with blood, SNR analysis is also performed using the electrical properties of blood listed in Table 1.33
Figure 4.
Measured B0 dependence of dielectric constant (a) and conductivity (b) of the 0.35% saline used for SNR experiments. Each point derives from impedance measurements at N=13 (diamonds) and N=19 (stars) different Li values. The mean values (solid lines) are: ε=79±4 and σ=0.63±0.05 S∕m.
Table 1.
Electrical properties of blood used for EM simulations at the frequencies corresponding to the different MRI field strengths investigated.
| Field | 0.5 T | 1 T | 1.5 T | 2 T | 3 T | 4 T | 4.7 T | 5 T |
|---|---|---|---|---|---|---|---|---|
| ε | 148 | 101 | 86.4 | 79.7 | 73.15 | 70 | 68.5 | 68 |
| σ (S∕m) | 1.14 | 1.18 | 1.2 | 1.22 | 1.25 | 1.27 | 1.28 | 1.29 |
Numerical EM computation of loopless antenna SNR
To determine SNR from Eq. 5, ∣B+∣ and Rload are numerically computed from 0.5 to 5 T on an Intel Pentium IV 2.0 GHz personal computer (2048 MB RAM) by the MoM using FEKO, Inc. (South Africa) EM software. The model antennae are comprised of low-loss (copper) semirigid UT-85-C coaxial cable of length λc∕4 with inner and outer conductor diameters of 0.51 and 2.2 mm, and a teflon dielectric (ε=2.2, as will be used in later experiments). The length of the protruding antenna whip is adjusted to resonate when immersed in the 0.35% saline medium. The coaxial cable and whip lengths are listed in Table 2. Because the λc∕4 coaxial cable length is too short (40 cm) at 3 T for practical intravascular applications in humans, the SNR of a 3 T loopless antenna with a 3λc∕4 length coaxial cable length, is also evaluated.
Table 2.
Antenna tuned lengths and impedances in 0.35% saline, the cable attenuation factors used for the EM calculations, and the fraction (%) of the net resistive losses attributable to the radial E-field.
| Field | 0.5 T | 1 T | 1.5 T | 2 T | 3 T | 4 T | 4.7 T | 5 T |
|---|---|---|---|---|---|---|---|---|
| Cable length, λc∕4 (mm) | 2400 | 1200 | 800 | 600 | 400 | 300 | 255 | 240 |
| Attenuation factor, α (dB∕m) | 0.075 | 0.109 | 0.137 | 0.160 | 0.201 | 0.235 | 0.257 | 0.266 |
| Computed resonant whip length, λm∕4 (mm) | 26 | 35 | 39 | 40 | 42 | 40 | 37 | 36 |
| Measured resonant whip length, λm∕4 (mm) | ⋯ | 34 | 37 | 39 | 40 | 39 | 36 | 36 |
| Minimum resistance whip length (mm) | 150 | 110 | 85 | 65 | 43 | 38 | 34 | 29 |
| Computed resistance at resonance (Ω) | 44.2 | 37.5 | 34.8 | 33.4 | 32.3 | 30.8 | 31.1 | 31.0 |
| Measured resonant impedance, Zin (Ω) | ⋯ | 37.0 −0.2j | 34.7 −0.2j | 32.5 +0.1j | 32 +0.1j | 30.3 −0.1j | 29.6 −0.2j | 29.1 |
| Computed minimumR (Ω) | 19.9 | 25.8 | 29.4 | 31.4 | 32.3 | 31 | 29.9 | 29 |
| Rρ∕real(Zin) (%) | 11% | 12% | 14% | 15% | 16% | 18% | 19% | 19% |
The spatial variation of the transverse field, B+(ρ,z) in Eq. 5 is computed by determining the currents on the antenna divided into 2200 elements with sides of length 0.01λ in free space. Rload is corrected for resistive losses in the copper cable portion of the antenna via37
| (10) |
where α is the cable attenuation coefficient (interpolated from the cable data sheet; Table 2) and D is the cable length (λc∕4) at each frequency. R is the input resistance of the loopless antenna with a 1 A current source,13, 37, 38 which is derived from the MoM analysis. The absolute SNR derived from EM theory as applied to the actual device geometry is then numerically computed from Eq. 5 with NF=0.
The resulting SNR in (ml−1 √Hz) computed at ρ=1 cm from the antenna junction in the saline from Fig. 4, is plotted for 0.5–5 T devices in Fig. 5a. A least-squares fit of these data yields a curve proportional to . This result agrees with the above analytic SNR dependence that results from treating the loopless antenna as a dipole (Fig. 2): Indeed the absolute SNR values in (ml−1 √Hz) are quite comparable. The computed SNR with the antenna in blood, is shown in Fig. 5b. This curve is best fit to , illustrating that the frequency dependence of tissue electrical properties does affect SNR performance.
Figure 5.
(a) Absolute SNR (shaded boxes, in ml−1 Hz1∕2) computed by EM MoM at ρ=1 cm from the junction for antennae made with λc∕4 cable portions tuned at 0.5, 1, 1.5, 2, 3, 4, 4.7, and 5 T in the 0.35% saline (squares). Experimental values measured at 1.5, 3, and 4.7 T (stars) are overlaid. The data are best fit to a curve of the form (solid). Experimental data are corrected to eliminate contributions from system noise (NF), but all data include cable losses. The dotted curves show the 95% confidence interval for the fitted curve. (b) Absolute computed SNR performance of the loopless antenna in blood based on the electrical properties in Table 1. This SNR has a 7∕4th power dependence on B0.
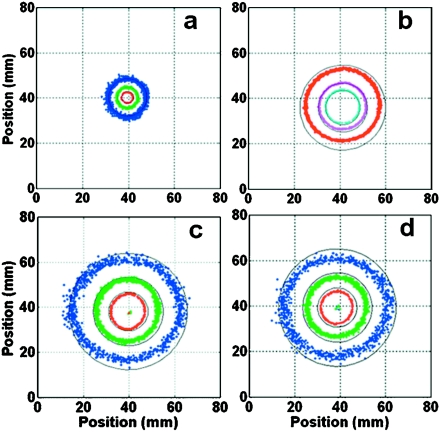
The absolute SNR at different radii in the axial plane at the junction [Fig. 1b] where SNR is highest, are computed for antennae in saline with resonant whips tuned for 1.5, 3, and 4.7 T with cable portions of length λc∕4, and for 3 T with a 3λc∕4 cable. The SNR is plotted as continuous contours that form circles in Fig. 6, and is highest for the 4.7 T probe. The SNR gains versus 1.5 T at ρ=1 cm are slightly over four-fold for 3 T and tenfold for 4.7 T (Table 3), consistent with a dependence. Importantly, these SNR gains result in huge gains in useful field-of-view (FOV) area in the plane of the antenna junction. We define the FOV gain as the ratio of the area of contours at equal values of SNR at the antenna junction, recorded at the different field strengths. The area of the 50 000 and 200 000 ml−1 √Hz contours at 3 T are 9.5- and 10.6-fold larger than at 1.5 T, respectively. The area of the 200 000 ml−1 √Hz contour at 4.7 T is 4.6 times higher than at 3 T, and 49 times higher than the same contour at 1.5 T. The 3 T analysis also shows that there is little difference (<6%) in both the SNR and FOV performance of the probes made with λc∕4 [Fig. 6c] and 3λc∕4 [Fig. 6d] cable lengths at 3 T, illustrating that coaxial cable loss is not a major contributor to SNR in these antennae. Thus, a λ loopless antenna formed from a 3λc∕4 cable instead of a λc∕4 cable has a length suitable for intravascular intervention and, in theory, pays little SNR penalty for it.
Figure 6.
Theoretical (solid, black) and experimental (color, dotted) absolute SNR (ml−1 Hz1∕2) in the plane of the whip junction of the semi-rigid minimal-loss antennae in the 0.35% saline. (a) The 1.5 T antenna made with λc∕4 cable. (b) The 4.7 T antenna made with λc∕4 cable. (c) The 3 T antenna made with λc∕4 and (d) 3λc∕4 cables. The experimental SNR data (blue, 50 000; green, 100 000; red, 200 000; purple, 400 000; cyan, 800 000 ml−1 Hz1∕2) overlap the continuous circular theoretical contours corresponding to the same values. Contributions from the system noise (NF) are subtracted from the experimental data. Theoretical and mean experimental SNR values at a specific location differ by <10% in all cases.
Table 3.
Absolute SNR for the minimal-loss copper loopless antennae at ρ=1 cm, excluding system noise.
| Ψ (104 ml−1 Hz1∕2) | 1.5 T, λ∕4 cable | 3 T, λc∕4 cable | SNR gain 3 T vs 1.5 T, λc∕4 cable | 3 T, 3λc∕4 cable | SNR gain, 3 T vs 1.5 T, 3λc∕4 cable | 4.7 T, λc∕4 cable | SNR gain, 4.7 T vs 1.5 T,λc∕4 cable |
|---|---|---|---|---|---|---|---|
| Computed | 3.99 | 16.8 | 4.21 | 16.5 | 4.11 | 43.0 | 10.77 |
| Measured | 4.04±0.10 | 15.3±0.02 | 3.79±0.15 | 14.6±0.02 | 3.61±0.14 | 39.0±0.03 | 9.65±0.3 |
Predicted impedance and resonant lengths
As a further check on computations, both antenna impedances and resonant lengths of antenna whips are computed and listed in Table 2 for comparison with subsequent experimental measurements. Note that the computed and measured resonant lengths agree within 5%, and vary by ⩽10% for B0⩾1.5 T. The latter is attributable to the effect of the unbalanced pole formed by the cable shield of the antenna, noted above. Previous work reported that SNR performance is optimum when the antenna input resistance (R) is minimum.8 Because minimum-R whip lengths differ from resonant whip lengths, these are also computed at each frequency, and their SNR compared with that of resonant whips.
Table 2 shows that tuning the whip length to minimize the antenna input resistance8 rather than the resonant λm∕4 condition, results in longer whips for probes designed for B0<3 T. However, the resistances of the antennae that result from applying the two criteria do not differ by more than 7% for B0⩾2 T. Figure 7 plots the computed SNR gain that results from using minimum-R whip lengths, as compared with resonant whips. The choice of either criterion for tuning affects SNR by less that 3% for B0⩾3 T (Table 2), but the minimum-R whip length does provide a 20% SNR improvement at 1.5 T, reducing the computed SNR gain versus 1.5 T from 4.2 to 3.5 at 3 T, and the 4.7 T gain from 10.8 to 9. The SNR advantage of using minimum-R whip lengths at B0⩽2 T is attributable to the lower antenna resistances.
Figure 7.
The computed ratio of the SNR of loopless antennae tuned by adjusting the whip length for minimum resistance, to that obtained using a whip length tuned to λm∕4 in the 0.35% saline. As frequency increases both conditions converge, resulting in the same SNR.
Finally, to better understand the sources of the noise detected by the antennae giving rise to the observed B0 dependence, the resistive losses are resolved into components Rz and Rρ, per Eq. 4. Thus, Rz is associated with losses in the axial E-field, Ez, which primarily correspond to the antenna’s return conduction paths through the sample directed parallel to the antenna wire. Rρ is associated with the radial Eρ field reflecting the more conventional “dielectric” losses from E-fields that extend out from the conductor to the sample. The data for Rρ in Table 2 show that the component attributable to Eρ, is only 11%–19% of the total resistance over the frequency range. This indicates that most of the losses are in the return conduction paths which are substantially parallel to the antenna wire, traversing through the sample between the whip and the cable poles.
EXPERIMENT
Experimental minimal-loss loopless antennae
To validate the above analyses, experimental 0.5, 1, 1.5, 2, 3, 4, 4.7, and 5 T loopless antennae were fabricated using the UT-85-C semirigid copper cable (Micro-coax, Inc., Pottstown, PA) as simulated. The semirigid cable is stripped at one end to expose the inner conductor and form one pole (the whip) with the outer shield of the coaxial cable forming the second pole. The resonant whip length and resonant impedance were measured for each device on the HP4395 impedance analyzer for comparison with the computed values. The results summarized in Table 2 show that the computed and measured resistances and lengths of the tuned probes agree within about 1 Ω and 2 mm, respectively. This shows that the EM analysis above accurately predicted the electrical properties of the antennae from which the SNR properties were deduced, at all of these B0 values. MRI scanner availability limited actual SNR testing to the 1.5, 3, and 4.7 T probes, which nevertheless spans a threefold variation in B0.
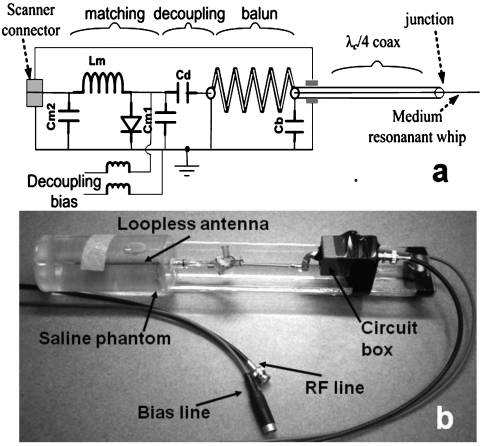
For MRI, the proximal end of the antenna cable is connected to the matching and decoupling circuit shown in Fig. 8. The circuit’s positive-intrinsic-negative (p-i-n)-diode shorts out the connector end of the antenna during MRI excitation when a positive direct current voltage is supplied by the scanner. The short circuit is transformed by the coaxial cable, whose length is an integral multiple of λc∕4, to a high impedance at the antenna junction, thereby minimizing current and heating at the whip end of the device. During reception, the diode is biased off, and the MRI signal is conducted from the antenna to the scanner. Four loopless antennae are fabricated with cable lengths of λc∕4 at 1.5 T, λc∕4 at 3 T, 3λc∕4 at 3 T, and λc∕4 at 4.7 T, as in the EM models. A 3λc∕4 antenna was not fabricated for 4.7 T because the distance to the magnet center was shorter than the cable length (Table 2) and because the 4.7 T studies were performed only as an experimental check of the analysis. Each antenna is matched to 50 Ω in a phantom containing the 0.35% saline mixture.
Figure 8.
(a) Schematic of the loopless antenna with its matching, decoupling and balun circuit. The balun is formed from the coaxial cable tuned with Cb and the center conductor running through to the whip: The outer conductor is grounded at the proximal end. Cd compensates for the balun inductance. (b) Annotated photograph of the 4.7 T experimental setup showing phantom, loopless antenna, and circuit box.
SNR measurements
SNR measurements of 3 T devices are done on a Philips XMR Achieva scanner (Philips Medical Systems, Cleveland, OH), with the decoupling circuit connected to a BNC adaptor and preamplifier. Fully relaxed axial MRI is performed in the saline phantom at the junction of the antenna (Gradient Echo sequence, GRE, 1 echo; echo time TE=6 ms; repetition period, TR=8 s; flip-angle, FA=90°; bandwidth, BW=62.5 kHz; excitations per frame, NEX=1; FOV=8 cm; acquisition matrix=256×256; 3 mm slices; scan time=34.1 min). The 1.5 T loopless antenna is positioned in the same saline phantom and scanned at the same axial locations relative to the antenna junction, in a GE 1.5 T scanner (GE Medical Systems, Milwaukee, WI) using the equivalent GRE sequence parameters. Fermi filtering and gradient unwarping algorithms are turned-off for these acquisitions. The 4.7 T devices [Fig. 8b] are loaded the same, and scanned with equivalent MRI parameters at the same locations relative to the junction on a 4.7 T Bruker Biospin animal scanner (Bruker, Billerica, MA) with a 40-cm long bore.
The root-mean-square (rms) noise at each B0 is measured in images acquired separately with the RF transmitter and MRI gradients turned-off. NF is measured for the GE, Philips, and Bruker systems, at 1.0, 1.1, and 2.2 dB, respectively, using the cold 50 Ω-resistor method.39 The absolute measured SNR in ml−1 √Hz, corrected to eliminate the system noise, is given by
| (11) |
for voxels of volume V in ml, where BW is the receiver bandwidth, Nx and Ny are the number of readout points and phase encoding steps, respectively, and ψ is the peak voxel signal divided by the rms noise. Ψms from Eq. 11 is directly compared to Ψs from Eq. 5 computed with NF=0, but accounting for cable losses via Eq. 10.
The raw measured absolute SNR data for the four experimental antennae are colorized and overlaid on the corresponding EM-computed SNR plots in Fig. 6. These data coincide closely with the theoretical contours at all levels. They demonstrate: (i) That the numerical EM analysis, as implemented, is an excellent predictor of experimental SNR; (ii) that the experimental loopless antennae are performing essentially as well as the design permits, without major defect or deficiency; (iii) that there is little difference in the SNR performance of 3 T probes made with λc∕4 and 3λc∕4 cable lengths, confirming the result from EM analysis that coaxial cable loss is not a key factor in these experimental prototypes; and (iv) relative to 1.5 T, the 3 and 4.7 T antennae offer increases in FOV area of approximately 10- and 50-fold, respectively.
The experimental improvement in SNR for the 3 and 4.7 T antennae at ρ=1 cm from the junction, Ψms is averaged over 0.84⩽ρ⩽1.16 cm, and listed in Table 3 for comparison with the computed gains. The measured SNR gains at 3 and 4.7 T are 3.8 and 9.7 times higher than the 1.5 T probe, respectively, in reasonable agreement with the computed 4.2- and 10.8-fold advantages. The experimental points are added to the fitted curve for SNR in Fig. 5a: They fall within its 95% confidence interval and are therefore consistent with an antenna SNR increasing substantially as the square power of magnetic field.
Performance of biocompatible 3 T intravascular loopless antennae
The semirigid antennae used in phantom experimental models are built from low-loss materials that are easy to fabricate and model by numerical EM analysis. Their low-loss electrical properties serve to demonstrate SNR performance at or near an optimal embodiment of a room-temperature loopless antenna. However, their nonbiocompatibility and semi-rigid mechanical properties render them unsuitable for in vivo intravascular use. Therefore, a biocompatible 3 T intravascular loopless antenna is also constructed to test whether a similar SNR benefit as that achieved with the copper cable antennae can be realized in a practical device. The biocompatible antennae is fabricated by modifying a commercial FDA-approved nitinol λc∕4 1.5 T intravascular MRI coil (Intercept, Surgi-Vision, Inc.; outer diameter, OD=0.76 mm; length 1 m; whip=75 mm) (Although this work is not supported, directed nor done in consultation with Surgi-Vision, Inc., P.A.B. is a cofounder and consultant of Surgi-Vision, Inc., and his ongoing interactions with company are managed by the JHU Office of Policy Coordination.) by cutting the whip portion to 40 mm and extending the nitinol cable portion by 20 cm to 3λc∕4 at 3 T with the same cable. An unaltered 1.5 T Surgi-Vision Intercept intravascular coil serves as an in vivo comparison.
The biocompatible 3 and 1.5 T antennae are first scanned in the same 0.35% saline phantom on the Philips 3 T scanner and the GE 1.5 T scanner with the same parameters used for the semirigid copper cable experiments. The raw image data are extracted from each scanner for SNR analysis, as above. The SNR gain of the 3 T biocompatible nitinol antennae in saline is measured to be 3.53 (±0.3 SD)-fold that of the 1.5 T device. This is consistent with both the experimental and computed SNR gains observed with the low-loss copper antennae (Table 3): the 10% lower experimental gain is possibly attributable to the lower conductivity of nitinol combined the increased length of the 3 T antenna.
Heat testing
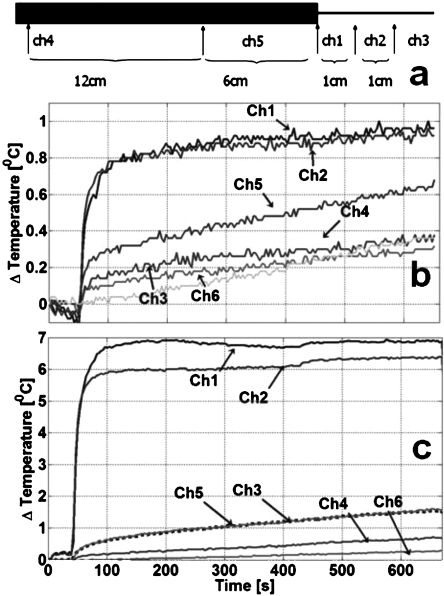
Heat testing is performed with the biocompatible 3 T nitinol intravascular loopless antenna placed in a cylindrical 10.4 kg gel phantom about 1 cm from the phantom edge with the phantom positioned 18 cm away from the edge of the bore of the Philips 3 T scanner. The antenna is instrumented with fiber optic temperature sensors along its length (FISO, Inc., Quebec), as illustrated in Fig. 9a. An additional control probe (Ch6) is placed at the same distance from the bore on the opposite side of the gel in the phantom. The SAR limit is increased by a factor of 2.5 to a nominal value of 10 W∕kg, as reported by the 3 T scanner for a GRE sequence (TE∕TR=2.1∕9.5 ms; 3 mm slice; FA=90°), exceeding the 4 W∕kg FDA guideline for average SAR. Because scanner-reported SAR values are based on model and power loss assumptions that may be conservative or deviate from experiment,40 the applied SAR is also computed from the product of the temperature change measured with the control probe, and the gel’s specific heat.41
Figure 9.
Heat testing of the 3 T biocompatible nitinol loopless antenna. (a) Locations of the fiber optic temperature sensors relative to the cable (thick black section) and whip (thin line). Relative to the whip junction, Ch3 is 2 cm along the whip; Ch2 is 1 cm on the whip; Ch1 is on the junction. Ch5 and Ch4 are at 6 and 12 cm (Ch4) along the cable portion, proximal to the junction. Ch6, located remotely, serves as a control to read the phantom’s normal temperature change. (b) Temperature of the fully decoupled antenna recorded from the sensors over a 10 min period during which MRI is performed at a scanner-estimated 10 W∕kg with a higher, 0.9% saline gel to simulate a worst case heating condition. (c) With the decoupling circuit disconnected, a rapid temperature rise 7 °C is recorded in the first 100 s.
The heat test results for the 3 T biocompatible antenna are plotted in Fig. 9b. Maximum temperature rise occurs on the whip near the junction and is ∼1.0 °C after 10 min. The temperature increase is lower on the cable side of the junction (0.6 °C), and <0.4 °C at all other sites sampled on the antenna, including the whip tip, which exhibits essentially the same temperature increase as the control sensor. If the control sensor’s temperature increase of 0.4 °C is subtracted, the maximum incremental heating at the antenna is ∼0.6 °C. With the decoupling circuit disconnected, MRI at the same SAR produces rapid temperature increases of ⩾7 °C around the junction and whip of the tuned antenna [Fig. 9c].
These data demonstrate that the switching circuitry is effective in decoupling the biocompatible 3 T antennae, and that heating can be kept within safe levels even at high applied SAR levels. The local SAR at the control sensor, as determined from its temperature rise [Fig. 9b], is 3 W∕kg, suggesting that the scanner-reported SAR is overstated.40
In vivo studies
To compare the in vivo SNR performance of the biocompatible intravascular 1.5 and 3 T loopless antennae fabricated with the same materials, high resolution axial images are acquired from the aorta of the same 3.5 kg New Zealand White rabbit at the two field strengths. The protocol is approved by the Johns Hopkins Animal Care and Use Committee. To ensure that axial images taken at the antenna junction correspond to the same anatomical location at 1.5 and 3 T, and to minimize motion artifacts for high resolution MRI, the antennae are immobilized in the aorta using a balloon catheter. The animal is anesthetized and intubated to maintain an open airway, and a 6 Fr (plastic) introducer sheath placed in the femoral artery to provide access. A 5 F balloon catheter (Boston Scientific, Boston, MA; balloon OD, 4 mm; guidewire OD, 0.8 mm) is advanced through the femoral artery into the abdominal aorta 5 cm above the femoral artery bifurcation under x-ray fluoroscopic guidance. Each loopless antenna is inserted through the balloon catheter and positioned with the antenna junction centered in the balloon.
In vivo MRI is conducted on each scanner with comparable fast spin-echo sequences (FSE; TE∕TR=20∕2500; BW=31.25 kHz; NEX=2; FA=90; FOV=40 mm; matrix=256×256; echo-train length, ETL=8; slice thickness, 3 mm with no gap; scan time=2.7 min). Because SNR decreases rapidly as ∼1∕ρ from the loopless antenna, the images are displayed with intensities scaled by ρ, as described earlier.8In vivo images acquired with biocompatible 1.5 and 3 T antenna from the same location within the rabbit aorta are illustrated in Fig. 10, along with a photograph of the 3 T device. The vessel wall and surrounding structures are seen on both images, but the SNR and the FOV advantages of the 3 T versus 1.5 T devices are both clear and large. The SNR of equivalent structures sampled at the same distance from the 3 and 1.5 T wires are 3.5±0.5 (n=10 points) times higher for 3 T. To determine the experimental FOV gain, a threshold is set at image SNR>9 in the 1.5 and 3 T images (with the ρ weighting removed), resulting in a scatter of points that reflects tissue heterogeneity. These are approximated to elliptical contours (Fig. 10) whose areas are measured. The measured FOV area for SNR>9 at 3 T is 8.5 times that at 1.5 T.
Figure 10.
In vivo performance of biocompatible loopless antennae for MRI of the rabbit aorta. (a) The biocompatible, 3λc∕4 cable length, 3 T intravascular loopless antenna with its tuning∕matching∕decoupling box adapted from a Surgi-Vision 1.5 T nitinol MRI antenna. The high resolution (156 μm×156 μm×3 mm) axial MRI acquired at the junction of the 1.5 (b) and 3 T (c) MRI antennae (FSE, TR:2.5 s, TE:20 ms, ETL:8, BW:31.25, FOV:4×4 cm2, ST:3 mm, matrix=256×256, NEX=2, scan time=16 s) are scaled by ρ to compensate for the ∼1∕ρ drop-off in SNR which amplifies noise at large ρ (Ref. 8). The elliptical dashed contour on (b) and (c) enclose comparable FOV areas with SNR>9.
DISCUSSION
We have analyzed, built and demonstrated the first loopless antennae for 3 and 4.7 T MRI, and have reduced the 3 T device to practice in a biocompatible form with a length suitable for in vivo applications. Moreover, we have demonstrated by three independent means: First a theoretical EM analysis of the antenna as a dipole; second, a numerical EM MoM analysis; and third, by direct experimental measurements; the important result that the MRI SNR of loopless antennae scales approximately as the regime 0.5–5 T in nondispersive lossy media. This results in a nearly fourfold SNR gain from 1.5 to 3 T, and an almost tenfold SNR gain at 4.7 T, for devices of equivalent fabrication, with both these findings being confirmed within about 10%, experimentally in phantoms and in vivo at 3 T. A key benefit of these SNR gains is a ∼ ten-fold gain in the useful FOV area for the 3 T antenna versus 1.5 T and a nearly 50-fold gain in FOV area for the 4.7 T antenna, as demonstrated in the numerical EM computations and the experimental phantom data (Fig. 6). In the rabbit, a FOV gain of about 8.5-fold was realized at 3 T versus 1.5 T (Fig. 10). This means that loopless antennae operating at higher fields have a greater range for guiding diagnosis and targeting intervention than present 1.5 T devices. The FOV area gain results from the combined effect of the SNR gain and the antenna’s ∼1∕ρ signal dependence, with FOV area ∼ρ2.
The present findings have important ramifications for the B0 dependence of the SNR of miniature interventional MRI antennae. The generally accepted theory for the dependence of the SNR on field strength or MRI frequency, ν, is captured in Hoult and Lauterbur’s equation for external loop coils20
| (12) |
where α and β are constants, and a and b are measures of loop and sample size, respectively. The first (α) term in the denominator of Eq. 12 represents coil conductive losses and is set to zero when computing the ISNR for the particular detector geometry.19 The remaining second (β) term reflects only those sample losses associated with voltages induced by random magnetic field fluctuations in the sample, and results in the accepted linear dependence of ISNR with frequency or B0.19 Contributions from direct E-field losses are rendered negligible by use of Faraday screens or distributed capacitance20 whose practicality is limited for miniature intravascular antennae. The limitation of ISNR to coil geometry is eliminated by computing the UISNR which expresses the best that can be achieved for external detectors, independent of their geometry.22 For internal coils, the UISNR also varies linearly with field.42 However, arguably, neither the ISNR nor the UISNR may be relevant measures if one cannot come close to realizing them with practical designs.
The essentially quadratic power dependence of SNR for a nondispersive medium demonstrated both theoretically and experimentally here for the first time for the loopless antenna from 0.5 to 5 T is not explained by Eq. 12. However, allowing the α term to dominate yields a 7∕4th power dependence which comes close. Yet the facts that neither: (i) Tripling the 3 T antenna cable length [Figs. 6c, 6d]; or (ii) increasing the whip length (Table 2: Compare SNR of minimum-R versus λ∕4 whips); or (iii) increasing whip conductivity in repeat analysis, negatively impacts the experimental and∕or computed SNR at 3 T and above, suggest that the dominant noise source is primarily not what was meant to be embodied by the α term of Eq. 12.20 The loopless antenna is indeed a different detector than contemplated by Eq. 12, wherein the sample behaves as part of the circuit through which the detector’s return currents pass between the whip and the distal end of the cable. This is evidenced by the result that 80%–90% of the E-field losses are parallel to the antenna axis (Table 2) and are in the sample. These losses are relatively independent of frequency, as evidenced by the analysis of the device as a dipole antenna in a dissipative medium,25 Eqs. 2, 3, Fig. 2, and by both the measured and computed resistances for B0⩾1.5 T in Table 2. With noise being essentially frequency independent, the dependence of the MRI signal translates directly to the dependence of SNR seen with this detector.
True, we also show a 7∕4th power SNR field-dependence for blood [Fig. 5b]. However, this less-than-quadratic performance is entirely attributable to the dispersive nature of blood’s electrical properties,32, 35, 42 as compared with the saline phantom whose σ and ε are essentially constant (Fig. 4). The frequency dependence of tissue electrical properties was not formally incorporated into the traditional Eq. 12 for external coils in the past,20 but clearly affects the E-field losses in general, reducing the SNR B0 dependence for internal coils by a factor of in the case of blood. Note that other normal tissues that are not fluids typically have lower conductivity than both blood and muscle, and hence, lower losses, and that the 1∕√Rload dependence in Eq. 5, renders the effect on SNR of any changes in tissue electrical properties less-than-linear. Tissue heterogeneity affects the integrated losses in a manner that is weighted by the distribution of the lossiest tissues (blood, muscle) as compared to say, adipose which has a 20-fold lower conductivity (σ=0.034–0.38 S∕m).33 Thus, the 3.5-fold SNR gain observed in our in vivo experiments corresponds to a SNR dependence for 1.5–3 T, which is close to that computed for blood.
Note also that because the loopless antenna’s losses are essentially frequency-independent, reflecting a relatively minimal role played by induced currents [the β term in Eq. 12], the present results mean that if the loopless antenna were used as a transmitter,43 SAR levels would not vary as . Instead, transmit SAR should show little or no frequency dependence, reflecting essentially just the dispersive electrical properties of the medium. Having a SAR that is independent of field strength provides, along with the SNR gain, some consolation for using these devices for both transmission and reception at higher MRI fields. Adiabatic pulses might be used to compensate for the highly nonuniform excitation field in such applications.44
Because the dominant losses are all in the sample and demonstrably not in the whip or cable per se, the SNR reported here fits a strict definition of the ISNR.43 To the extent that these losses are intrinsic to the function of the dipole as a MRI detector, and dwarf any cable and conducting losses in the whip, a near-quadratic dependence appears to be the best one can do for the loopless antenna geometry. Nevertheless, the losses are dominated by direct E-field losses, which are conventionally set to zero for determining ISNR.43 Thus, to avoid confusion with the ISNR, it may be appropriate to define a new type of SNR, the design SNR (DSNR), as the best one can do for a given detector design in cases such as these. Unlike both the UISNR and ISNR which have an approximately linear B0 dependence, the DSNR for the loopless antenna varies approximately as from 0.5 to 5 T and is equal to the computed SNR in Figs. 56. The practical utility of the UISNR or ISNR is lessened by the fact that they are not realizable in theory or practice, by this detector design. The irony is that the effect of adding conduction losses that are intrinsic to the loopless antenna, while leading us far from the putative linear dependence of the theoretical UISNR,42 provides a much greater benefit from increasing MRI field strength than if they were absent.
Some benefit obtains from changing the antenna materials, especially the probe diameter, as evidenced by the superior SNR performance of the low-loss copper devices, compared with the smaller diameter biocompatible nitinol probes. Nevertheless, for imaging small vessels such as a coronary artery, miniaturized loopless antennae employing super-elastic materials may be the only choice.45 Our results show that adapting same-diameter biocompatible 1.5 T probes for 3 T using the same materials as for 1.5 T, can deliver essentially the same SNR and FOV area advantages that the analysis predicts, in vivo (Fig. 10).
It is important to note that the realization of optimum or near-optimum SNR from experimental prototypes depends critically and nontrivially on providing effective decoupling of the antenna from an external excitation coil during MRI transmission. Any coupling will, via Lenz’s Law, counter the excitation field near the antenna, and consequently reduce the SNR. Because effective decoupling stops induced currents in the antenna, it also reduces local heating and power deposition during MRI excitation. Thus, the decoupling circuit deployed in the present study [Fig. 8a] is effective in limiting temperature rise to ⩽1 °C in phantoms. Under comparable experimental conditions with the decoupling∕matching∕tuning circuit properly engaged, temperature rise in vivo should thus be limited to a safe 1 °C limit for many applications.
In conclusion, we have introduced interventional loopless antennae for fields of 3 T and above. The 3 T antenna is capable of producing about four times the SNR and ten times the FOV area of an equivalent 1.5 T loopless antenna. Despite the potential for a several-fold increase in heating anticipated at 3 T as compared to 1.5 T with external MRI excitation, temperature increases can be controlled within ranges acceptable to in vivo imaging. Indeed, the same decoupling approaches appear effective up to 4.7 T where further SNR gains consistent with an essentially quadratic power law are achievable. MRI guided intervention at 3 T offers truly new opportunities for high resolution microscopy which should find value in angiography, cardiovascular,46 oncological and other interventions.1
ACKNOWLEDGMENTS
Both A. M. El-Sharkawy and D. Qian contributed equally to this paper. We thank Ergin Atalar at Bilkent University and William Edelstein at Johns Hopkins for useful discussions, V. P. Chacko at Johns Hopkins for help with the Bruker 4.7T experiments, and Michael Schär of Philips Medical Systems for help with the 3T MRI experiments. This work was supported by NIH Grants ROI RR15396 and ROI HL090728.
References
- Arepally A., Karmarkar P. V., Weiss C., and Atalar E., “Percutaneous MR imaging-guided transvascular access of mesenteric venous system: Study in swine model,” Radiology 238, 113–118 (2006). [DOI] [PubMed] [Google Scholar]
- Raval A. N., Karmarkar P. V., Guttman M. A., Ozturk C., Sampath S., DeSilva R., Aviles R. J., Xu M., Wright V. J., Schenke W. H., Kocaturk O., Dick A. J., Raman V. K., Atalar E., McVeigh E. R., and Lederman R. J., “Real-time magnetic resonance imaging-guided endovascular recanalization of chronic total arterial occlusion in a swine model,” Circulation 113, 1101–1107 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaabane L., Canet E., Serfaty J. M., Contard F., Guerrier D., Douek P., and Briguet A., “Microimaging of atherosclerotic plaque in animal models,” MAGMA (N.Y.) 11, 58–60 (2000). [DOI] [PubMed] [Google Scholar]
- Di Mario C., The S. H., Madretsma S., van Suylen R. J., Wilson R. A., Bom N., Serruys P. W., Gussenhoven E. J., and Roelandt J. R., “Detection and characterization of vascular lesions by intravascular ultrasound: An in vitro study correlated with histology,” J. Am. Soc. Echocardiogr 5, 135–146 (1992). [DOI] [PubMed] [Google Scholar]
- Rivas P. A., Nayak K. S., Scott G. C., McConnell M. V., Kerr A. B., Nishimura D. G., Pauly J. M., and Hu B. S., “In vivo real-time intravascular MRI,” J. Cardiovasc. Magn. Reson. 4, 223–232 (2002). [DOI] [PubMed] [Google Scholar]
- Meissner O. A., Rieger J., Rieber J., Klauss V., Siebert U., Tato F., Pfeifer K. J., Reiser M., and Hoffmann U., “High-resolution MR imaging of human atherosclerotic femoral arteries in vivo: Validation with intravascular ultrasound,” J. Vasc. Interv. Radiol. 14, 227–231 (2003). [DOI] [PubMed] [Google Scholar]
- Atalar E., Bottomley P. A., Ocali O., Correia L. C., Kelemen M. D., Lima J. A., and Zerhouni E. A., “High resolution intravascular MRI and MRS by using a catheter receiver coil,” Magn. Reson. Med. 36, 596–605 (1996). [DOI] [PubMed] [Google Scholar]
- Ocali O. and Atalar E., “Intravascular magnetic resonance imaging using a loopless catheter antenna,” Magn. Reson. Med. 37, 112–118 (1997). [DOI] [PubMed] [Google Scholar]
- Settecase F., Sussman M. S., Wilson M. W., Hetts S., Arenson R. L., Malba V., Bernhardt A. F., Kucharczyk W., and Roberts T. P., “Magnetically-assisted remote control (MARC) steering of endovascular catheters for interventional MRI: A model for deflection and design implications,” Med. Phys. 10.1118/1.2750963 34, 3135–3142 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wacker F. K., Hillenbrand C. M., Duerk J. L., and Lewin J. S., “MR-guided endovascular interventions: Device visualization, tracking, navigation, clinical applications, and safety aspects,” Magn. Reson Imaging Clin. N. Am. 13, 431–439 (2005). [DOI] [PubMed] [Google Scholar]
- Quick H. H., Serfaty J. M., Pannu H. K., Genadry R., Yeung C. J., and Atalar E., “Endourethral MRI,” Magn. Reson. Med. 45, 138–146 (2001). [DOI] [PubMed] [Google Scholar]
- Shunk K. A., Garot J., Atalar E., and Lima J. A., “Transesophageal magnetic resonance imaging of the aortic arch and descending thoracic aorta in patients with aortic atherosclerosis,” J. Am. Coll. Cardiol. 37, 2031–2035 (2001). [DOI] [PubMed] [Google Scholar]
- Susil R. C., Yeung C. J., and Atalar E., “Intravascular extended sensitivity (IVES) MRI antennas,” Magn. Reson. Med. 10.1002/mrm.10506 50, 383–390 (2003). [DOI] [PubMed] [Google Scholar]
- Qian D., Karmarkar P. V., and Atalar E., “Loopless antenna with improved distal sensitivity and tapered whip insulation,” Proc. Intl. Soc. Mag. Reson. Med. 13, 195 (2005). [Google Scholar]
- Serfaty J. M., Yang X., Aksit P., Quick H. H., Solaiyappan M., and Atalar E., “Toward MRI-guided coronary catheterization: Visualization of guiding catheters, guidewires, and anatomy in real time,” J. Magn. Reson Imaging 12, 590–594 (2000). [DOI] [PubMed] [Google Scholar]
- Serfaty J. M., Yang X., Foo T. K., Kumar A., Derbyshire A., and Atalar E., “MRI-guided coronary catheterization and PTCA: A feasibility study on a dog model,” Magn. Reson. Med. 49, 258–263 (2003). [DOI] [PubMed] [Google Scholar]
- Yang X. and Atalar E., “Intravascular MR imaging-guided balloon angioplasty with an MR imaging guide wire: Feasibility study in rabbits,” Radiology 217, 501–506 (2000). [DOI] [PubMed] [Google Scholar]
- Arepally A. and Weiss C. R., “Intrabiliary MR imaging,” Magn. Reson Imaging Clin. N. Am. 13, 481–489 (2005). [DOI] [PubMed] [Google Scholar]
- Edelstein W. A., Glover G. H., Hardy C. J., and Redington R. W., “The intrinsic signal-to-noise ratio in NMR imaging,” Magn. Reson. Med. 10.1002/mrm.1910030413 3, 604–618 (1986). [DOI] [PubMed] [Google Scholar]
- Hoult D. I. and Lauterbur P. C., “The sensitivity of the zeugmatographic experiment involving human samples,” J. Magn. Reson Imaging 34, 425–433 (1979). [Google Scholar]
- Edelstein W. A., Hardy C. J., and Mueller O. M., “Electronic decoupling of surface-coil receivers for NMR imaging and spectroscopy,” J. Magn. Reson. (1969-1992) 10.1016/0022-2364(86)90421-X 67, 156–161 (1986). [DOI] [Google Scholar]
- Ocali O. and Atalar E., “Ultimate intrinsic signal-to-noise ratio in MRI,” Magn. Reson. Med. 10.1002/mrm.1910390317 39, 462–473 (1998). [DOI] [PubMed] [Google Scholar]
- Black R. D., Early T. A., Roemer P. B., Mueller O. M., Mogro-Campero A., Turner L. G., and Johnson G. A., “A high-temperature superconducting receiver for nuclear magnetic resonance microscopy,” Science 10.1126/science.8430331 259, 793–795 (1993). [DOI] [PubMed] [Google Scholar]
- Yeung C. J. and Atalar E., “A Green’s function approach to local rf heating in interventional MRI,” Med. Phys. 10.1118/1.1367860 28, 826–832 (2001). [DOI] [PubMed] [Google Scholar]
- Atlamazoglou P. E. and Uzunoglu N. K., “A Galerkin moment method for the analysis of an insulated antennain a dissipative dielectric medium,” IEEE Trans. Microwave Theory Tech. 46, 988–996 (1998). [Google Scholar]
- Bottomley P. A. and Edelstein W. A., “Power deposition in whole-body NMR imaging,” Med. Phys. 10.1118/1.595000 8, 510–512 (1981). [DOI] [PubMed] [Google Scholar]
- Bottomley P. A., Lardo A. C., Tully S., Karmarker P. V., and Viohl I., “Safety and internal MRI coils,” 2001 Syllabus. Special cross-specialty categorical course in diagnostic radiology: practical MR safety considerations for physicians, physicists and technologists (Radiological Society of North America, Oak Brook, IL, 2001), pp. 85–90. [Google Scholar]
- U.S. Department of Health and Human Services, Food and Drug Administration, Center for Devices and Radiological Health, Guidance for the submission of premarket notifications for magnetic resonance diagnostic devices, Rockville, MD, US DHHS FDA; 1998.
- Chen C. N., Sank V. J., Cohen S. M., and Hoult D. I., “The field dependence of NMR imaging. I. Laboratory assessment of signal-to-noise ratio and power deposition,” Magn. Reson. Med. 10.1002/mrm.1910030508 3, 722–729 (1986). [DOI] [PubMed] [Google Scholar]
- King R. and Harrison C., Antennas and Waves: A Modern Approach (IT, Cambridge, MA, 1969). [Google Scholar]
- King R. P. and Iizuka K., “The complete electromagnetic field of a half-wave dipole in a dissipative medium,” IEEE Trans. Antennas Propag. 11, 275–285 (1963). [Google Scholar]
- Chen C. N. and Hoult D. I., Biomedical Magnetic Resonance Technology (A. Hilger, Bristol, 1989), p. 340. [Google Scholar]
- Gabriel C. and Gabriel S., Compilation of the dielectric properties of body tissues at RF and microwave frequencies, Armstrong Laboratory (AFMC), Radiofrequency Radiation Division, http://niremf.ifac.cnr.it, 1996.
- Duck F. A., Physical Properties of Tissue: A Comprehensive Reference Book (Academic, London, 1990), pp. 177–207. [Google Scholar]
- Hayt W. H. and Buck J. A., Engineering Electromagnetics (McGraw-Hill, Boston, 2001), p. 561. [Google Scholar]
- Bottomley P. A., “A technique for the measurement of tissue impedance from 1 to 100 MHz using a vector impedance meter,” J. Phys. E 10.1088/0022-3735/11/5/012 11, 413–414 (1978). [DOI] [PubMed] [Google Scholar]
- Gardiol F. E., Lossy Transmission Lines (Artech House, Boston, 1987), p. 324. [Google Scholar]
- Wright S. M. and Wald L. L., “Theory and application of array coils in MR spectroscopy,” NMR Biomed. 10, 394–410 (1997). [DOI] [PubMed] [Google Scholar]
- Bottomley P. A., “A practical guide to getting NMR spectra in viva.,” in Medical Magnetic Resonance Imaging and Spectroscopy, A Primer, edited by Budinger T. F. and Margulis A. R. (Society for Magnetic Resonance in Medicine, Berkeley, CA, 1986), pp. 81–95. [Google Scholar]
- Stralka J. P. and Bottomley P. A., “A prototype RF dosimeter for independent measurement of the average specific absorption rate (SAR) during MRI,” J. Magn. Reson. Imaging 26, 1296–1302 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeung C. J., Susil R. C., and Atalar E., “RF safety of wires in interventional MRI: Using a safety index,” Magn. Reson. Med. 10.1002/mrm.10037 47, 187–193 (2002). [DOI] [PubMed] [Google Scholar]
- Celik H., Eryaman Y., Altintas A., Abdel-Hafez I. A., and Atalar E., “Evaluation of internal MRI coils using ultimate intrinsic SNR,” Magn. Reson. Med. 52, 640–649 (2004). [DOI] [PubMed] [Google Scholar]
- Yeung C. J. and Atalar E., “RF transmit power limit for the barewire loopless catheter antenna,” J. Magn. Reson. Imaging 12, 86–91 (2000). [DOI] [PubMed] [Google Scholar]
- Sathyanarayana S., Schar M., and Bottomley P. A., “An MRI endoscope?,” Proc. Intl. Soc. Mag. Reson. Med. 15, 492 (2007). [Google Scholar]
- Qiu B., Karmarkar P., Brushett C., Gao F., Kon R., Kar S., Atalar E., and Yang X., “Development of a 0.014-inch magnetic resonance imaging guidewire,” Magn. Reson. Med. 10.1002/mrm.20384 53, 986–990 (2005). [DOI] [PubMed] [Google Scholar]
- Pan L., Stuber M., Kraitchman D. L., Fritzges D. L., Gilson W. D., and Osman N. F., “Real-time imaging of regional myocardial function using fast-SENC,” Magn. Reson. Med. 55, 386–395 (2006). [DOI] [PubMed] [Google Scholar]