Z-matrix formalism for quantitative noise assessment of covariance nuclear magnetic resonance spectra

Abstract

Due to the limited sensitivity of many nuclear magnetic resonance (NMR) applications, careful consideration must be given to the effect of NMR data processing on spectral noise. This work presents analytical relationships as well as simulated and experimental results characterizing the propagation of noise by unsymmetric covariance NMR processing, which concatenates two NMR spectra along a common dimension, resulting in a new spectrum showing spin correlations as cross peaks that are not directly measured in either of the two input spectra. It is shown how the unsymmetric covariance spectrum possesses an inhomogeneous noise distribution across the spectrum with the least amount of noise in regions whose rows and columns do not contain any cross or diagonal peaks and with the largest amount of noise on top of signal peaks. Therefore, methods of noise estimation commonly used in Fourier transform spectroscopy underestimate the amount of uncertainty in unsymmetric covariance spectra. Different data processing procedures, including the Z-matrix formalism, thresholding, and maxima ratio scaling, are described to assess noise contributions and to reduce noise inhomogeneity. In particular, determination of a Z score, which measures the difference in standard deviations of a statistic from its mean, for each spectral point yields a Z matrix, which indicates whether a given peak intensity above a threshold arises from the covariance of signals in the input spectra or whether it is likely to be caused by noise. Application to an unsymmetric covariance spectrum, obtained by concatenating two 2D ¹³C–¹H heteronuclear, single quantum coherence (HSQC) and ¹³C–¹H heteronuclear, multiple bond correlation (HMBC) spectra of a metabolite mixture along their common proton dimension, reveals that for sufficiently sensitive input spectra the reduction in sensitivity due to covariance processing is modest.

INTRODUCTION

Because NMR measurement time is often limited by the achievable sensitivity, careful consideration must be given to the effect of NMR data processing on spectral noise. While for standard Fourier transform (FT) the effect of noise on spectra is well understood,¹ more recent processing methods can have advantages, in particular, when the shortening of measurement time of multidimensional spectra is essential.^{2, 3, 4, 5, 6} However, many of these methods affect the noise signature resulting in changes in both the apparent and the actual sensitivity.^{4, 7}

Due to its linear nature, the FT method converts a free induction decay that includes additive white noise into a spectrum that is superimposed on a homogeneous noise floor. This property allows a straightforward assessment of the signal-to-noise (S∕N) ratio by comparing signal intensities to a summary statistics, such as the standard deviation or the median absolute value of the noise floor in a peak-free region. Nonlinear methods, on the other hand, may affect the noise lying away from a signal peak different from noise on a signal peak itself and thereby they may improve the apparent but not the actual sensitivity.

Covariance NMR is a recently introduced method for spectral resolution enhancement of multidimensional spectra.³ Direct covariance processing endows the indirect (or donor) dimension(s) of a spectrum with the same resolution and spectral width as the corresponding acceptor dimensions, which include the high-resolution detection dimension.^{3, 5, 8} Conversely, indirect covariance maps an indirect dimension of a spectrum onto the direct dimension.⁹ When the covariance spectrum is symmetric, application of the matrix square root strongly attenuates or eliminates artifacts due to relay effects and chemical shift near degeneracy.⁶ In fact, with regularization¹⁰ applied as necessary, the covariance transform followed by a matrix square root leaves the signal-to-noise properties of a spectrum essentially unperturbed.

The covariance NMR concept can be generalized to pairs of spectra, which has been referred to as “unsymmetric” covariance NMR, by multiplying the matrices belonging to two spectra along a common dimension resulting in a spectrum that is generally nonsymmetric.⁷ Unsymmetric covariance NMR has been demonstrated for small molecule NMR where it provides a rapid computational approach to correlate spin resonances for which the experimental measurement of correlations would be very time consuming.^{7, 11, 12, 13} A related concept was introduced in the context of “hyperdimensional” NMR of proteins¹⁴ and extensions have recently been reported for protein backbone assignment, such as COBRA (Ref. ¹⁵) and Burrow–Owl,¹⁶ where pairs of three-dimensional (3D) spectra are combined to four-dimensional (4D) spectra. It should be noted that, despite the covariance name, these spectra generally do not fulfill the mathematical properties of covariance matrices any longer.

Unsymmetric covariance NMR involves the matrix product of two spectra and, thus, is a nonlinear transformation. As a consequence, the propagation of noise through unsymmetric covariance processing is fundamentally different from FT spectroscopy. This paper demonstrates analytically, by simulations and by using experimental data how uniform noise distribution of input FT spectra propagates through unsymmetric covariance processing in an inhomogeneous fashion, thereby endowing different regions of the unsymmetric covariance spectrum with different amounts of noise. The analytical relationships developed here provide a rigorous framework for assessing the sensitivity and experimental statistical errors of peaks in unsymmetric covariance spectra and they are tested both for simulated and experimental spectra. This work does not address the separate issue of systematic errors, for example, due to chemical shift degeneracy, of unsymmetric covariance spectra.

THEORY

Consider two real N₁×N₂ two-dimensional (2D) FT spectra represented by matrices A and B that contain additive noise, where each noise element is an independent, identical distributed (i.i.d.) Gaussian random variable with zero mean and standard deviation σ_A and σ_B, respectively. Unsymmetric covariance processing multiplies the two spectra so that the common ω₁ dimension is contracted,⁷

$$\mathbf{C}={\mathbf{A}}^{\mathrm{T}}\mathbf{B}.$$ (1)

Equation 1 implies that element C_kl is the inner product of column k of A with column l of B, where both of these column vectors have N₁ elements.

To determine the signal-to-noise ratio of C we separately consider a region of signal and different regions of noise. A region of signal around matrix element (i,j) of C arises when columns i and j of A and B have one or several peaks at similar (or identical) positions. The expected signal at point (i,j) is

$$\text{Signal}=C_{ij}=\sum _{k=1}^{N_1}{\widehat{A}}_{ki}{\widehat{B}}_{kj},$$ (2)

where ${\widehat{A}}_{ki}$ and ${\widehat{B}}_{kj}$ denote the noise-free spectral data points belonging to the noise-affected data points A_ki and B_kj, respectively.

Unlike for FT spectra, the amount of noise in C varies depending on the spectral region considered. For a peak-free region around point (p,q) where only noise is multiplied and coadded according to Eq. 1,

$${\text{Noise}}_{\text{free}}=C_{pq}=\sum _{k=1}^{N_1}{A}_{kp}{B}_{kq}.$$ (3)

The elements A_kp and B_kq are i.i.d. Gaussian distributed. While products of Gaussian random variables do not follow the Gaussian distribution,¹⁷ statistical tests of computationally generated samples of sums of products of Gaussian distributed random variables indicate that, for most practical applications, the sum of N₁>25 products is in very good approximation Gaussian distributed.

We find (see EPAPS supporting information¹⁸) that the sum of products of i.i.d. Gaussian variables of mean zero has in very good approximation the variance

$${\mathrm{var}}_{\text{free}}=N_1\cdot {\sigma }_A^2\cdot {\sigma }_B^2.$$ (4)

When Eq. 4 is combined with Eq. 1, one can define a S∕N ratio,

$${(\text{Signal}∕\text{Noise})}_{\mathrm{free}}=\raisebox{1ex}{$\left(\sum _{k=1}^{N_1}{A}_{ki}{B}_{kj}\right)$}\!\left/ \!\raisebox{-1ex}{$\sqrt{N_1}{\sigma }_A{\sigma }_B$}\right.,$$ (5)

for any data point C_ij in a “peak-free” region, which is a region that neither aligns horizontally nor vertically with a cross peak (note that A_ki, B_kj denote noise-affected data points).

However, some regions of C contain noise at a level that is different from the one determined above. These regions originate from the inner product of a column of B(A) that contains one or several signal peaks with a column of A(B) that contains only noise. These regions are located in C along a column (row) that contains a cross peak. The variances of these inner products are given by

$${\mathrm{var}}_{\mathrm{col}}=N_1\cdot {\sigma }_A^2\cdot {\sigma }_B^2+\sum _{k=1}^{N_1}{\widehat{B}}_{kj}^2{\sigma }_A^2\text{and}$$$${\mathrm{var}}_{\text{row}}=N_1\cdot {\sigma }_A^2\cdot {\sigma }_B^2+\sum _{k=1}^{N_1}{\widehat{A}}_{ki}^2{\sigma }_B^2.$$ (6)

It follows that the S∕N of a column and row that belong to a cross peak in C centered around point (i,j) is

$${(\text{Signal}∕\text{Noise})}_{\mathrm{col}j}=\raisebox{1ex}{$\left(\sum _{k=1}^{N_1}{A}_{ki}{B}_{kj}\right)$}\!\left/ \!\raisebox{-1ex}{${\sigma }_A{(N_1\cdot {\sigma }_B^2+\sum _{k=1}^{N_1}{\widehat{B}}_{kj}^2)}^{1∕2}$}\right.,$$$${(\text{Signal}∕\text{Noise})}_{\text{row}i}=\raisebox{1ex}{$\left(\sum _{k=1}^{N_1}{A}_{ki}{B}_{kj}\right)$}\!\left/ \!\raisebox{-1ex}{${\sigma }_B{(N_1\cdot {\sigma }_A^2+\sum _{k=1}^{N_1}{\widehat{A}}_{ki}^2)}^{1∕2}$}\right..$$ (7)

The variance of the cross peak, which is defined as the variance of the peak center over multiple identical experiments, is given by

$${\mathrm{var}}_{\text{peak}}=N_1\cdot {\sigma }_A^2\cdot {\sigma }_B^2+\sum _{k=1}^{N_1}({\widehat{A}}_{ki}^2{\sigma }_B^2+{\widehat{B}}_{kj}^2{\sigma }_A^2).$$ (8)

Accordingly, the S∕N ratio of the peak, defined by the average peak height (i.e., averaged over multiple experiments) divided by its standard deviation, is

$${(\text{Signal}∕\text{Noise})}_{\text{peak}}=\raisebox{1ex}{$\left(\sum _{k=1}^{N_1}{\widehat{A}}_{ki}{\widehat{B}}_{kj}\right)$}\!\left/ \!\raisebox{-1ex}{${[N_1\cdot {\sigma }_A^2\cdot {\sigma }_B^2+\sum _{k=1}^{N_1}({\widehat{A}}_{ki}^2{\sigma }_B^2+{\widehat{B}}_{kj}^2{\sigma }_A^2)]}^{1∕2}$}\right..$$ (9)

It should be noted that Eq. 9 does not only apply to a signal peak at location (i,j), but also to all locations in C where “noise ridges” intersect. The latter are caused by inner products of columns of A and B that contain signal peaks at different locations. Equation 8 subsumes Eqs. 4, 6 when considering that ${\widehat{A}}_{ki}$ and ${\widehat{B}}_{kj}$ are zero in the noise columns and rows, respectively (and are both zero in the baseline noise region). Thus, Eqs. 8, 9 quantify the noise variance and the signal-to-noise ratio for any point in the covariance spectrum. Equations 8, 9, however, assume knowledge of noise-free input spectra, which are experimentally unattainable. Substituting experimentally measured A_ki and B_kj for their noise-free counterparts ${\widehat{A}}_{ki}$ and ${\widehat{B}}_{kj}$ in Eqs. 8 or 9 will thereby result in a biased estimator. On the other hand, an unbiased estimator for Eq. 8 can be derived (see EPAPS supporting information¹⁸)

$${\mathrm{var}}_{\text{unbiased}}=-N_1\cdot {\sigma }_A^2\cdot {\sigma }_B^2+\sum _{k=1}^{N_1}(A_{ki}^2{\sigma }_B^2+B_{kj}^2{\sigma }_A^2),$$ (10)

and the corresponding unbiased S∕N ratio (applicable for any point in the spectrum) is

$$Z_{ij}={(\text{Signal}∕\text{Noise})}_{\text{unbiased}}=\raisebox{1ex}{$\left(\sum _{k=1}^{N_1}{A}_{ki}{B}_{kj}\right)$}\!\left/ \!\raisebox{-1ex}{${[-N_1\cdot {\sigma }_A^2\cdot {\sigma }_B^2+\sum _{k=1}^{N_1}(A_{ki}^2{\sigma }_B^2+B_{kj}^2{\sigma }_A^2)]}^{1∕2}$}\right..$$ (11)

Equation 11 defines a Z matrix whose elements provide a Z score for testing the hypothesis that the intensity at (i,j) arises from a signal∕signal covariance. If the p value, associated with Z_ij via the standard normal distribution, is less than a critical probability α, the intensity C_ij is not likely to arise due to noise but rather due to covariance of input signals. Conversely, if Z_ij is greater than the critical Z value (Z_crit), C_ij likely arises from a covariance of input signals rather than noise. Since this hypothesis test is implicitly done for every point in the spectrum, a modification (see EPAPS supporting information¹⁸) is required to control the false positive rate, such as the Dunn–Sidak correction.¹⁹

Taken together, these results show that the noise distribution in an unsymmetrical covariance spectrum is in good approximation Gaussian with a standard deviation that varies for different spectral regions. Regions that neither align vertically nor horizontally with any signal peak contain less noise than a column or row that contains a peak. Generally,

$${\left(\text{Noise}\right)}_{\text{peak}}>{\left(\text{Noise}\right)}_{\text{row}∕\text{column}}>{\left(\text{Noise}\right)}_{\text{free}},$$ (12)

which implies that the precision of a spectrum is lowest precisely at the positions of the signal peaks and the cross sections between noise ridges. This behavior of unsymmetric covariance processing is in stark contrast to the 2D FT spectrum where random noise is evenly distributed over different regions. The second-most noisy regions are the “noise ridges” that align with peaks either horizontally or vertically (while these features are reminiscent of “t₁ noise” in 2D FT spectra, their origin is entirely different). According to Eq. 6, the presence of a very intense signal in the ith column of A (or the jth column of B) results in increased noise for the ith row (respectively, the jth column) of C, possibly to the point where weaker cross peaks, with their intensities potentially further reduced due to noise [Eqs. 8, 10, 12] in that row (respectively, column), are obscured.

In the remainder of this section, two alternative approaches for the reduction of inhomogeneous noise effects are described, which use either thresholding or maxima ratio scaling.

Thresholding

The thresholding of regions in A and B in which signals are not expected (by removing all points in A and B for which the intensity is close to or below that of the noise floor) eliminates several of the terms in Eqs. 4, 6, 10. Thresholding prior to covariance computation helps to render the baseline noise of covariance spectra uniform and also eliminates the additional noise at the intersection of “noise ridges” where no peak is actually present. This leads to a clear reduction of the inhomogeneity of the noise in the covariance spectrum. However, thresholding will not improve the uncertainty of peak heights due to noise, since it cannot remove the noise superimposed onto the FT peaks that correlate to yield a covariance peak.

Maxima ratio scaling

Thresholding relies on the measurement of the noise level and requires some knowledge about the expected peak heights. Direct multiplication of the input matrices A^T and B according to Eq. 1, on the other hand, leads to the appearance of noise ridges along the rows and columns of all cross peaks. These features are caused by the inner product of a column of A that contains a peak with a column of B that contains only noise or vice versa. To suppress such effects a differential scaling procedure referred to as “maxima ratio scaling” (mrs), can be applied by multiplying each element of C=A^TB by the weighting factor

$$W_{ij}=1∕\exp \left\{\mid \ln ({\max }_k\left(\mid A_{ki}\mid \right)∕{\max }_l\left(\mid B_{lj}\mid \right))\mid \right\}.$$ (13)

The maxima ratio scaled unsymmetric covariance matrix C^mrs has elements

$$C_{ij}^{\mathrm{mrs}}=W_{ij}\sum _{k=1}^{N_1}{A}_{ki}{B}_{kj},$$ (14)

where the weights W_ij reflect the magnitude ratio of columns i and A and j of B. If the columns have a similar maximum value, which is the case if both columns either contain peaks of similar intensity or if both columns contain only noise, W_ij≈1 and therefore $C_{ij}^{\mathrm{mrs}}\approx C_{ij}$. However, if column i contains one or several peaks and column j contains only noise, or vice versa, W_ij⪡1 and $C_{ij}^{\mathrm{mrs}}⪡C_{ij}$, i.e., mrs leads to the desired reduction of the ridges along the columns and rows of a cross peak.

MATERIALS AND METHODS

Simulations

In order to test the equations derived in the Theory section, numerical simulations of model spectra were performed where each spectrum has a statistically independent noise floor and contains a single peak in the same location along the axis concatenated via covariance. The spectral widths of both the direct and the indirect dimensions are 2.5 ppm with N₁=32 and N₂=128 data points. For the present purposes, “signal spectra” with a single diagonal peak at 1 ppm and a full width at half maximum peak height of 12.75 Hz (assuming a 600 MHz resonance frequency to convert from Hz to ppm) were simulated in the program MATLAB.²⁰ Gaussian distributed noise floors were generated in MATLAB and added to the signal spectrum to generate two independent noise and signal spectra to be combined via unsymmetric covariance processing according to Eq. 1.

Experimental

2D ¹³C–¹H–HSQC and ¹³C–¹H–HMBC spectra were recorded at 298 K for a mixture of seven common metabolites at natural ¹³C abundance, namely, D-carnitine, D-glucose, L-glutamine, L-histidine, L-lysine, myo-inositol, and shikimic acid (each at a concentration of 10 mM in D₂O), on a Bruker AVANCE 800 spectrometer equipped with a cryogenic probe. The direct ¹H dimension of each spectrum was acquired with 2048 complex points and a spectral width of 8013 Hz. The indirect ¹³C dimensions were acquired with 1024 complex points. The ¹³C spectral widths of the HSQC and HMBC spectra were set to 50 314 and 32 206 Hz, respectively. For the HMBC spectrum, the “magnitude” spectrum was calculated after FT.²¹

Both data sets were processed using NMRPipe,²² leaving each spectrum unapodized in the direct dimension (to be concatenated via covariance), while the indirect dimensions were subjected to exponential-to-Gaussian apodization. The indirect, unsymmetric covariance calculations, yielding an HMBC-HSQC covariance spectrum,¹² were performed in MATLAB.

RESULTS AND DISCUSSION

Theory

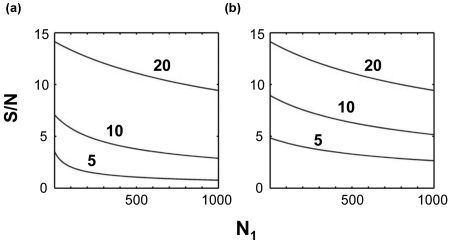
The signal-to-noise ratio of a covariance peak has according to Eq. 9 a characteristic dependence on the S∕N ratio of the input spectra A and B as well as on the size N₁ of the concatenated dimension. Figure 1 shows this dependence for input spectra A and B that have a single peak represented by the Kronecker delta function for variable σ_A and σ_B. In Fig. 1a, σ=σ_A=σ_B takes values 0.05, 0.1, and 0.2 corresponding to S∕N ratios of 20:1, 10:1, and 5:1, respectively. For increasing N₁, the sensitivity decreases with $O(1∕\sqrt{N_1})$. The spectrum with the lowest sensitivity is most strongly affected for increasing N₁, whereas the change in sensitivity of the highest sensitivity spectrum is relatively modest. Figure 1b shows the situation when the sensitivity of spectrum A is constant at 20:1 while the S∕N of spectrum B takes the values 20:1, 10:1, and 5:1. The S∕N of the resulting unsymmetric covariance spectrum C steadily decreases with increasing N₁ and it has a S∕N that is always below that of the less sensitive input spectrum.

Figure 1.

Signal-to-noise (S∕N) ratio of a peak arising from the covariance of a pair of peaks, computed using Eq. 9 as a function of N₁ and the S∕N ratio of the input peaks. (a) S∕N for the covariance between peaks each having the indicated (5, 10, and 20) S∕N values. (b) S∕N for the covariance between a peak with S∕N=20 and a peak with the indicated S∕N. Note that the lower the signal to noise of the weaker peak, the lower the signal to noise of the covariance peak. However, in the limit where the weaker peak is much weaker than the stronger peak, so long as N₁ is small, the signal to noise of the covariance peak approaches that of the weaker peak. The sensitivity of an unsymmetric covariance spectrum, for small values of N₁, is not that much lower than that of the less sensitive of the two spectra subject to covariance with signal-to-noise values decreasing at most by a factor 2^1∕2 from that of the least sensitive of the two input spectra.

Simulations

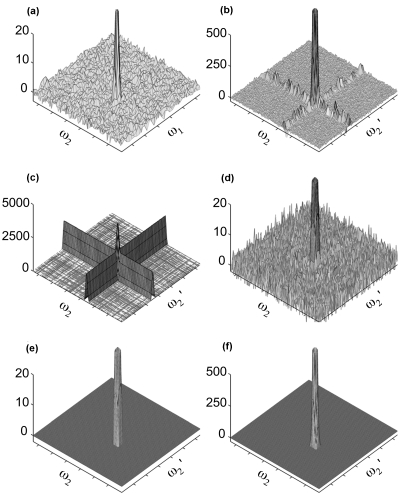
Numerical simulations were performed to test the results presented in the Theory section. The model spectrum A with S∕N=45 [Fig. 2a] was unsymmetrically covariance processed with a spectrum B that has an identical signal peak as spectrum A, but a different random Gaussian noise floor with the same standard deviation. The corresponding unsymmetric covariance spectrum C=A^TB, depicted in Fig. 2b, demonstrates the presence of an uneven noise floor with noise ridges in the same row and column as the signal peak. The variances given in Table 1 quantify the difference between the relatively low variance of baseline noise in covariance spectra and the higher variance in noise intensities in the same column or row as the covariance peak.

Figure 2.

Noise propagation through unsymmetric covariance. (a) Simulated (noisy) input spectrum A with S∕N=45. (b) Covariance spectrum A^TB, where B has the same signal peak as A and the same noise level. (c) The variance calculated using Eq. 10 at each point of the covariance spectrum. (d) Z matrix calculated according to Eq. 11. (e) same as (d) after setting all elements to zero with a S∕N ratio less than Z_crit (4.85), the Z score belonging to the critical p value for which Dunn–Sidak correction yields a spectrum-wide α=0.01. (f) The covariance spectrum produced by thresholding by setting all elements of A and B less than 3σ to zero prior to covariance. In (a), (b), (d), (e), and (f) the cross peak is truncated to highlight noise features: the actual peak heights are 44, 2112, 33, 33, and 2101, respectively.

Table 1.

Variance of noise intensities in a simple unsymmetric covariance spectrum: simulation vs theory.

Locationa	Variance in simulationb			Theoryc
	Mean	Std. dev.	Exampled	Idealized	Mean	Std. dev.
Free (noise)	32.1	1.10	31.3	32	32.1	11.3
Row	2150	265.3	2579	2174	2159	109.5
Column	2167	320.2	1936	2174	2185	93.3
Peak	4341	679.2	0	4316	4315	150.6

^aVariance measures _{var[location]} defined in the Theory section.

^bStatistics given for var_free, var_row, and var_col represent averages over 10 000 simulations.

^cIdealized theory uses the signal spectra to calculate _{var[location]}. Additionally, _{var[location]} is calculated using Eq. 10 and then taking the mean (and standard deviation) for all points in the given location over the simulations performed (100 replications for var_free, var_row, and var_col and 100 rounds of 100 replications for var_peak).

^dVariances for the simulation displayed in Fig. 1.

Table 1 gives both idealized variance estimates, calculated based on Eqs. 4, 6, 8 using noise-free spectra as well as estimates obtained using Eq. 10, which demonstrates the excellent correspondence between theory (both idealized and using unbiased estimators with simulated noisy input data) and simulation. Figure 2c plots the variance predicted by Eq. 10 on a point-by-point basis, displaying the expected “noise ridges” and highest variance at the location of the peak itself. Division of the signal by the predicted variance [Eq. 11] yields a noise floor that, like the noise floor in an FT spectrum, is homogeneous [Fig. 2d]. Figure 2e thresholds Fig. 2d at the critical Z score of 4.85, as adjusted by the Dunn–Sidak correction¹⁹ for 128×128=16 384 hypothesis tests, demonstrating that the Z score is an effective statistic for distinguishing between signal and noise in the covariance spectrum.

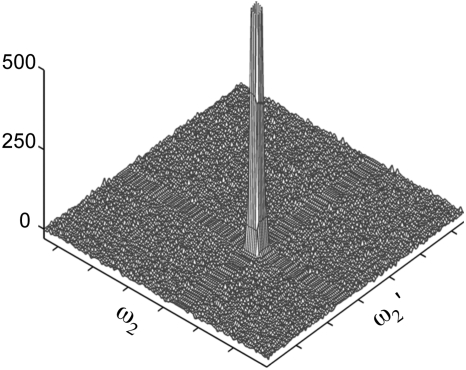
While thresholding eliminates most of the noise along the noise floor, including the noise ridges [Fig. 2f], the variance in peak height, calculated analogously to the corresponding variance reported in Table 1, is 4319 (with a standard deviation of 661) indicating that thresholding does not significantly improve the precision of the covariance peak intensities. For comparison, maxima ratio scaling suppresses noise ridges (Fig. 3) and yields 5687±886 for the corresponding variance in peak height. Thus, the precision of peak intensities produced by the mrs method is only slightly lower than the one obtained by thresholding.

Figure 3.

Covariance of simulated spectra (as described in text) subjected to maxima ratio scaling (mrs). The peak is truncated and has an actual height of 2059.

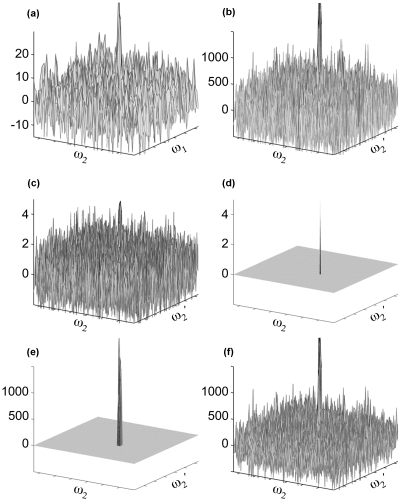
The simulations described above were repeated with a S∕N ratio of 7 for both input spectra (Fig. 4). Because var_free [defined by Eq. 4] scales with ${\sigma }_A^2\cdot {\sigma }_B^2$ while the additional noise present in var_col and var_row scales with ${\sigma }_A^2$ and ${\sigma }_B^2$, respectively, decreased signal-to-noise results in less pronounced noise ridges (Fig. 4b) than are seen in Fig. 2. The chosen S∕N ratio yields a covariance peak with S∕N [estimated by Eq. 11] of 5, which is just above Z_crit [Fig. 4d] and only slightly lower than the input S∕N ratio of 7. The mean local noise estimated by Eq. 10 for var_free, var_row, and var_col are 6.25×10⁴, 1.42×10⁵, and 1.63×10⁵, respectively, which closely match the variances directly calculated from the covariance spectrum (6.21×10⁴, 1.37×10⁵, and 1.94×10⁵, respectively). Together with Table 1, these results demonstrate the applicability of Eqs. 10, 11 in estimating the signal-to-noise ratio of covariance spectra over a wide S∕N range.

Figure 4.

Noise propagation through unsymmetric covariance. (a) Simulated input spectrum A as in Fig. 2 with S∕N=7. (b) Covariance spectrum A^TB, where B has the same signal peak as A and the same noise level. (c) Z matrix calculated according to Eq. 11. (d) same as (c) after setting all elements to zero with a S∕N ratio less than Z_crit (4.85), cf. Fig. 2. (e) The covariance spectrum produced by thresholding by setting all elements of A and B less than 3σ to zero prior to covariance. (f) Covariance of simulated spectra subjected to maxima ratio scaling (mrs). In each panel, the cross peak is truncated to highlight noise features: the actual peak heights are 48, 2387, 5, 5, 2170, and 2246, respectively.

Experiment

The variance of the measured spectral intensities in a peak-free region of the HMBC (A) spectrum is 58.5 while the variance of intensities in a peak free region of the HSQC spectrum (B) is 108.8. Equation 4 predicts a variance of 2.61×10⁷ for regions of the unsymmetric HMBC-HSQC covariance spectrum (C=A^TB) that do not align (either by row or column) to covariance peaks. The region of the covariance spectrum, representing the covariance of the peak free regions of the HSQC and HMBC spectra used to evaluate the noise levels of those input spectra, has calculated intensities with a variance of 2.69×10⁷, which differs by less than 5% from the predicted variance. Such a minor discrepancy may result from “colored noise” effects.²³

Table 2 compares noise variances calculated according to Eq. 10 for two randomly selected covariance peaks, which are (1) the lysine Cγ–Cε cross peak at (24.12,41.76) ppm and (2) the carnitine Cβ–Cα cross peak at (45.66,66.79) ppm. Equation 10 predicts noise generally within 5% of the expected variance in noise intensities. The S∕N values for peaks 1 and 2 roughly correspond to the S∕N values of their associated traces in the FT spectra subject to covariance (Table 3).

Table 2.

Variances of column∕row noise and peak intensity for two covariance peaks.

	Experimenta		Theoryb		Relative error (%)c
	Column	Row	Column	Row	Column	Row
Peak 1d	9.56×109	1.30×1010	7.56×109	1.24×1010	26.5	5.1
Peak 2d	4.63×109	3.32×109	4.69×109	3.44×109	1.4	3.5

^aVariances calculated from intensities (in indicated, peak-free locations relative to the center of the peak at hand) in the covariance spectrum obtained by multiplying an experimentally measured HMBC and with a corresponding HSQC spectrum.

^bValues obtained from Eq. 10.

^cDifference between experiment and theory relative to the theoretical value.

^dPeaks in locations indicated in text.

Table 3.

Expected signal-to-noise ratios for two covariance peaks.

	Covariancea	HSQCb	HMBCb
Peak 1c	437	664	492
Peak 2c	294	346	258

^aExpected S∕N ratio according to Eq. 11.

^bS∕N ratio (peak intensity divided by standard deviation of measured intensities in a representative peak free region) for maximally intense peak contributing to the given covariance peak in the indicated spectrum.

^cPeaks in locations indicated in text.

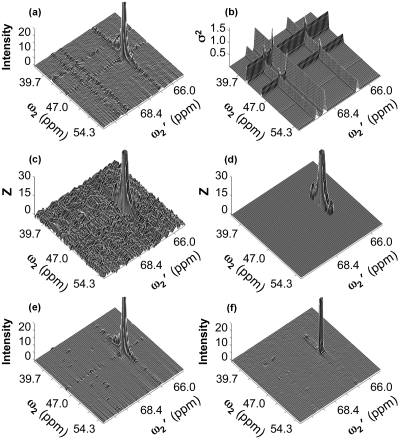
As is the case with simulated data, the increased noise in the same column∕row of covariance peaks is visible upon plotting of covariance spectra [Fig. 5a], which shows the enhancement of noise in the same column and row as the (45.66,66.79) ppm cross peak in the covariance spectra as well as enhanced noise along the same row or the same column as other peaks. Some of the peaks leaving such ridges in the depicted region of the covariance spectrum are located in distal regions of the spectra, which are not displayed in Fig. 5a. [Note that Eqs. 6, 10 do not predict any attenuation of the noise “ridges” with increased distance from a peak along a column or row.]

Figure 5.

Selected spectral region taken from an experimental unsymmetric HSQC-HMBC covariance spectrum of metabolite mixture using different processing schemes. (a) Covariance spectrum computed according to Eq. 1. (b) The variance calculated, by Eq. 10 at each point in the covariance spectrum. (c) Z matrix calculated according to Eq. 11. (d) as (c), after setting all elements to zero having a S∕N ratio less than Z_crit (5.85), the Z score belonging to the critical p value for which Dunn–Sidak correction yields a spectrum-wide α=0.01. (e) Spectrum computed using thresholding at 3σ applied to the input HMBC and HSQC spectra. (f) Spectrum computed using maxima ratio scaling according to Eqs. 13, 14. In (a), (c), (d), (e), and (f), the cross peak (corresponding to peak 2 in text and tables) has been clipped: the maximum amplitude of this peak is 263 [(a) and (e)], 294 [(c) and (d)], and 144 (f).

Consistent with the simulations shown in Figs. 2f, 34e, thresholding the input spectra or maxima ratio scaling during the covariance process strongly suppresses noise ridges as seen in Figs. 5e, 5f. Thresholding does not affect the peak height, while mrs reduces the peak height by a factor (<2), which is much smaller than ridge suppression (<10). The 3σ threshold used in generating the covariance spectrum shown in Fig. 5e is the same as that used in the simulation shown in Figs. 2f, 4e. Increasing this threshold would further attenuate the ridges at the risk of removing true signals from the input spectra and hence attenuate or eliminate true peaks in the resulting covariance spectrum.

Figures 5b, 5c display the variance calculated by Eq. 10 and the Z score calculated by Eq. 11 on a point-by-point basis. Figure 5d thresholds the Z score by its critical value of 5.85, as adjusted via the Dunn–Sidak correction for 2048×2048 hypothesis tests. The only points in the depicted region of the unsymmetric HMBC-HSQC covariance spectrum with signal to noise above the critical value are those associated with peak 2.

CONCLUSION

A chief utility of signal-to-noise comparisons is in determining whether or not a particular intensity is a signal of potential interest or whether it can be explained as random noise. For a Gaussian noise distribution, the signal-to-noise ratio corresponds directly to a Z score for testing such a hypothesis. In Fourier transform spectra, the homogeneity of the noise floor allows for a simple evaluation of the standard deviation of the noise distribution by computing statistics over a spectral region that is void of peak signals. When applied to nonlinearly processed datasets, such as the unsymmetric covariance spectra discussed here, it can lead to spectral distortions and the emergence of false peaks. Such peaks are most likely to occur at the intersection of noise ridges caused by strong signal peaks in the input spectra.

For two FT input spectra A and B whose noise floor standard deviations σ_A and σ_B have been determined by standard methods, an unbiased S∕N ratio matrix Z can be calculated for each point in the unsymmetric covariance spectrum. Because Z has a homogeneous noise distribution, its noise interpretation is analogous to the one of a FT spectrum. In fact, the S∕N ratio of an unsymmetric covariance peak is generally quite close in value to the S∕N ratios of the FT peaks whose covariance gives rise to that covariance peak.

From a statistical perspective, the Z matrix provides a Z score for each spectral point, which translates into a probability that a given Z_ij intensity represents an actual signal as opposed to random noise. This feature puts the unsymmetric covariance Z matrix on the same quantitative footing as its input FT spectra.

Alternatively, the inhomogeneity of the baseline noise in unsymmetric covariance spectra can be eliminated by thresholding, at the risk of eliminating weak cross peaks that are true, or by maxima ratio scaling. Application of the mrs method ensures that the covariance between two columns, one containing a peak and the other containing only noise, is smaller than the covariance between two columns that both contain noise. The mrs method, however, also scales down covariance peak intensities. A strong noise ridge in an unsymmetric covariance spectrum derives from a strong input peak. The mrs method reduces ridge intensity by scaling down such strong input peaks, which also reduces the intensity of covariance peaks associated with strong noise ridges. Thus, to a first approximation, mrs leaves apparent S∕N ratios of peaks unaffected.

Unsymmetric covariance processing has generally limited consequences for the sensitivity. For example, a homonuclear ¹³C or ¹⁵N spectrum obtained via unsymmetric covariance has a sensitivity nearing that of proton-detected NMR rather than the sensitivity experimentally available with ¹³C or ¹⁵N direct detection, confirming previous assessments of indirect∕unsymmetric covariance processing.^{9, 13} In addition, thresholding, maxima ratio scaling, or Z-matrix analysis provide effective means for the suppression of ridge artifacts in the final unsymmetric covariance spectrum based on minimal assumptions, namely, that the Gaussian noise of the spectra subjected to covariance processing are known.

The Z-matrix formalism presented in this work provides a general link between standard multidimensional FT spectroscopy and covariance NMR. It enables one to quantify the sensitivity of covariance spectra and to evaluate whether covariance intensities arise from noise or from covariances between input signals, thereby helping NMR spectroscopists to optimize the acquisition and analysis of datasets subjected to this type of processing.