Abstract
We compared the sampling efficiency of simulated tempering and replica exchange. Our results indicate that simulated tempering is superior to replica exchange if the parameters for temperature transition in simulated tempering are adjusted to be proportional to the partition function. It is shown that, in simulated tempering, the rate of traversing energy space of different temperatures is much higher than that in replica exchange, especially in the case of low tempering frequency and∕or larger temperature separations.
INTRODUCTION
Simulated tempering1 and replica exchange2 are two tempering methods that simultaneously sample a system at different temperatures. The central idea of tempering is to sample the system at multiple temperatures simultaneously. An important advantage of the tempering methods is that they can overcome the problem of broken ergodicity, that is, the system is likely trapped in local configurational space if the simulation is performed only at a low temperature. In the tempering methods, the system can frequently visit higher temperatures where the sampling is ergodic and go back to lower temperatures with a very different configuration. Thus the methods are useful in accelerating samplings at low temperatures and improving the statistics there.
In simulated tempering, the temperature of the system is randomly switched between several predefined values. The frequencies of visiting different temperatures depend on a set of parameters that define the acceptance probability of temperature transitions. The particular set of parameters that result in equal visits to all temperatures comes from the partition function.1 Since the partition function is usually unknown in advance, Park and Pande proposed a method of using short preliminary simulations to estimate the parameters.3 For a complex system where the equilibration time is long, we demonstrated the use of a dynamic updating scheme to obtain a runtime estimate of the partition function.4
In replica exchange, also known as parallel tempering, independent simulations (replicas) at different temperatures are run simultaneously. Two replicas can randomly exchange their temperatures according to certain acceptance rule, which preserves the Boltzmann distribution at each temperature. In this way, the frequencies of visiting different temperatures are always the same.
The performance of the two algorithms was studied by many authors5, 6, 7, 8, 9, 10 focusing on different aspects. Particularly, Park found that the simulated tempering offers a larger acceptance ratio for temperature transitions than replica exchange.8 Sindhikara et al. found that the sampling efficiency increases as one increases the frequency of attempting exchanges in replica exchange.9 In this study, we focus on a measure of tempering efficiency based on the rate of traversing the energy space expanded by all sampling temperatures, which allows us to systematically study the effects of temperature spacing and tempering frequency. We shall demonstrate that a temperature transition is generally more efficient than a temperature exchange under the same conditions.
THEORY AND RESULTS
We first review the acceptance probabilities of simulated tempering and replica exchange. Next, through the autocorrelation function, we define the tempering efficiency, according to which the two tempering methods are compared. Readers familiar with the basics can proceed directly to Sec. 2C.
Acceptance probabilities in simulated tempering and replica exchange
In simulated tempering, several sampling temperatures are defined before simulation. Temperature transitions are randomly proposed to change the system temperature from the current value to another one. The probability of accepting a proposed temperature transition from β to β′ (both β and β′ are expressed in reciprocal temperatures, i.e., β=1∕kBT) is
| (1) |
where E is the current potential energy (we shall drop the adjective “potential” in the following discussion for convenience); Zβ and Zβ′ are the values of the partition function at temperatures β and β′, respectively; and wβ and wβ′ are the weights of visiting temperatures β and β′, respectively. Accordingly, the equilibrium weight of an individual configuration being at β is wβ exp(−βE)∕Zβ; after summing over all configurations, the total weight of visiting β is wβ. The use of the partition function ensures that each sampling temperature is visited by the appropriate weight. In this study, we assume that all wβ’s are the same unless specified otherwise. Previously, we demonstrated the accuracy and efficiency of sampling using these weights on several typical systems.4
In replica exchange, the acceptance probability for an attempted exchange between two replicas with temperatures β and β′ (β>β′) is
| (2) |
where E and E′ are the energy of replicas at temperatures β and β′, respectively.
An important measure is the averaged acceptance probability or the acceptance ratio. It can be calculated in both cases under the Gaussian approximation, where the constant temperature energy distribution pβ(E) is approximated as a Gaussian distribution. Such an approximation is a result of the second order expansion of the entropy, or the logarithm of the density of states: ; the density of states g(E) is related to the energy distribution as pβ(E)∝g(E)exp(−βE). The calculated acceptance ratios are
| (3) |
| (4) |
for simulated tempering7 and replica exchange,5 respectively. Here, is the complementary error function. The relation between the two can be expressed as
| (5) |
which indicates a larger acceptance ratio provided by simulated tempering than by replica exchange. Note that the Gaussian approximation is only correct for large systems. For a small system, however, we have to include higher order terms, such as E3 and E4, in the expansion of the entropy in the energy range of interest, and thus the energy distribution is no longer a Gaussian.5 In such a case, the relation between the two acceptance ratios can deviate from the prediction of Eq. 5. It is worth noting that, although the Gaussian approximation gives a good prediction for the acceptance ratios, caution should be taken when it is used to calculate properties that strongly depend on the distribution tails.5
The above results can be generalized to tempering along several “temperatures” b={βi} instead of one. The partition function of such a generalized canonical ensemble is Z=∑ exp(−b⋅E), where the vector E={Ei} contains energy terms Ei’s corresponding to different βi’s. The acceptance ratios of simulated tempering and replica exchange become
where Δb=b−b′, and A is the curvature matrix of the entropy, i.e., .
An example of the generalized tempering is that along the pressure instead of the temperature, where vector E contains the energy and volume, and b the temperature and pressure. Another example is the tempering along the volume (or the density) of a Lennard–Jones system,4 whose partition function written in the reduced coordinates is
where N is the number of particles and V the volume; the contribution from the ideal gas part is removed. The potential between a particle pair, i and j, with a separation sij is . The repulsive and the attractive energy parts can be collected independently over all particle pairs to form two-energy terms ; the corresponding temperatures are given by b={1∕V4,1∕V2}.
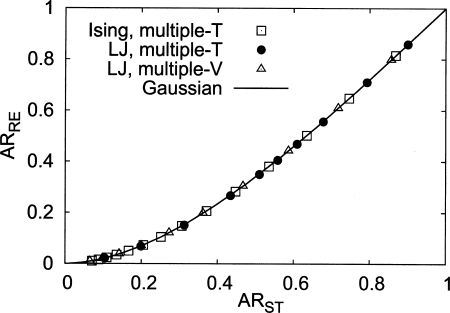
We tested the validity of Eq. 5 on three different systems. The first system was a 32×32 Ising model with two temperatures. The coupling constant is unity. The first temperature was T=3.0. Different choices of the second temperature from 3.05 to 3.70 were used to cover a wide range of acceptance ratios. The second testing system was a 108 particle Lennard–Jones system. The density of the system was set to 0.3. The first temperature was T=2.0, and the second temperature ranged from T=1.0 to 1.9. The third case was the multiple-volume tempering on a 108 particle Lennard–Jones system, where the first density was ρ=0.35, while the other varied from ρ=0.3 to ρ=0.345. The temperature was fixed at T=3.0. In all cases, we used the single particle Metropolis algorithm to generate configurational changes. The results of the three simulations and the prediction from the Gaussian model Eq. 5 are plotted in Fig. 1. A good agreement between the two confirms the validity of the Gaussian model in calculating acceptance ratios. Note that there is generally a significant difference between the two acceptance ratios. For example, at the point where the acceptance ratio of simulated tempering is 15%, that of replica exchange is about 4%. Generally the difference is more prominent as one increases the spacing between the two temperatures (or densities).
Figure 1.
The acceptance ratio of simulated tempering (ST) vs that of replica exchange (RE). The squares are the results from multiple-temperature ensemble simulations on the 32×32 Ising model. The solid circles are those from multiple-temperature ensemble simulations on a 108 particle Lennard–Jones system. The solid triangles are those from multiple-volume ensemble simulations on the same Lennard–Jones system. The solid line is the prediction from the Gaussian approximation.
Transition matrix and correlation function
An accurate measure of tempering efficiency can be established from a transition matrix and its correlation functions. Each step of a Monte Carlo simulation can be viewed as an implementation of a discrete-time master equation. If, at step t, the probability of the system to be in state m (m=1,2,…,M) is given by the mth component of an M-dimensional vector p(t)={pm(t)}, then the probability vector at the next step t+1 is given by
where A is the transition matrix. The largest eigenvector of the transition matrix represents the equilibrium distribution and its eigenvalue is λ1=1.0.11 The other eigenvectors represent directions of fluctuation modes. Starting from an initial distribution p(0), the distribution at time t is p(t)=Atp(0). Then the autocorrelation function for p(0) is defined as
| (6) |
where the contribution from the final distribution p(∞) is removed to make C(∞)=0. Since the vector p(0) can be decomposed to a linear combination of eigenvectors vm’s of the transition matrix as , the autocorrelation function must adopt the form
where 1∕τk=−log(λk)≈1−λk represents the decay rate of the kth fluctuation mode.
Among all fluctuation modes, the second or the slowest mode usually dominates the correlation function of interest, and hence is most important. As long as the mode is retained, it is convenient to define states on a coarse grained level to eliminate irrelevant fluctuation modes and to simplify calculations.
Efficiency of tempering
The main purpose of tempering is to enhance low-temperature sampling by helping the system to overcome high energy barriers. With the help of high temperatures, the system at a low temperature can readily switch between different energy wells. The tempering process therefore can be modeled as a combination of a well-switching process at high temperatures and a tempering process that delivers the system between the highest and the lowest temperatures.
In simulated tempering, a system state can be labeled by the current configuration and the temperature. In replica exchange, such a labeling applies to each individual replica, whose temperature is changed through exchanges with other replicas (however, the configuration of a replica or its energy remains unchanged during an exchange). In this way, each replica acts like a system in simulated tempering; the only difference is that now the acceptance probability of changing the temperature depends on the energy of another replica, as indicated in Eq. 2.
Consider tempering on a double well system with a low temperature β and a high temperature β′ (β>β′). The system state can be categorized into four cases for the system being at (a) temperature β and well 1, (b) temperature β′ and well 1, (c) temperature β′ and well 2, and (d) temperature β and well 2. In each Monte Carlo step at the high temperature β′, the system can switch between wells with a probability p (the probability of well switching at the low temperature is ignored). The transition probability between the two temperatures is P. The transition matrix is
The decay rate is determined by the second largest eigenvalue
This rate represents how fast the system moves in the temperature-energy space and serves as a measure of tempering efficiency. Although derived from the two-temperature case, the model can be approximately used where more than two temperatures are involved. In such a case, β and β′ are interpreted as the lowest and the highest temperatures, respectively, and the well-switching process at a temperature other than β′ is ignored.
Since the well switching rate p at β′ is completely determined by the type of energy move used in simulation, the dependence on temperature transitions can only rest on P, the rate of delivering states between the highest and the lowest temperatures. A tempering method is more efficient if it more frequently shuttles the system state between the energy region of the highest temperature and that of the lowest.
Efficiency of traversing the energy space
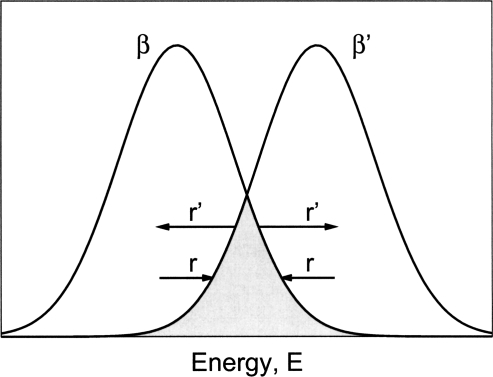
In the case of simulated tempering, consider tempering between two temperatures β and β′. We divide the energy distribution at β into two exclusive parts: an overlapping region with the energy distribution at β′ and the rest, see Fig. 2. A temperature transition from β to β′ is possible if and only if the system resides in the overlapping region. In other words, the overlapping region separates states that are capable of making a temperature transition from those which are not. Accordingly, the acceptance ratio ARST equals the probability of being in the overlapping region (or the fraction of states that are ready to make a transition). We use r′ to denote the transition rate from the overlapping region to the rest part, and r in the reverse direction during constant-temperature sampling at β. The detailed balance condition between the two parts imposes a relation between r and r′: ARSTr′=(1−ARST)r, or
The corresponding division can be made on the energy distribution at β′. For the sake of simplicity, we assume that r′ and r in β′ take the same values as those in the β case.
Figure 2.
The shaded area is the overlapping region. We assume that the system can make a successful temperature transition only when it falls into the region. Constant temperature sampling plays the role of delivering states between the overlapping region and the rest part of the energy distribution. Here, r′ is the transition rate from the overlapping region to the rest part and r is that in the reverse direction.
The above divisions yield four coarse-grained states: (a) being at β but not in the overlapping region, (b) being at β and in the overlapping region, (c) being at β′ and in the overlapping region, and (d) being at β′ but not in the overlapping region. While constant temperature sampling transfers the system between (a) and (b), or (c) and (d), temperature transitions transfer the system between (b) and (c). The transition matrix is
where f is the frequency of attempting temperature transitions. The decay rate of the second largest eigenvalue is
| (7) |
For frequent tempering limit, f⪢r,r′, it becomes r; for infrequent tempering limit, f⪡r,r′, 1∕τ2 is reduced to 2rf∕(r+r′)=2ARSTf.
In the case of replica exchange, we first assume that a temperature exchange is possible if and only if both replicas, I and II, reside in an overlapping region of the two-energy distributions. It is because, if either replica leaves the overlapping region, a large energy difference between the two replicas will effectively inhibit the exchange through the acceptance probability [Eq. 2]. Due to the difference of the acceptance probabilities, the overlapping region here can take a different shape from that in simulated tempering. We now classify states of the system into two categories. In the first category, replica I is at temperature β and II at β′; in the second, I at β′ and II at β. Each category contains three states: neither replica, only one replica, or both replicas being in the overlapping region. Similar to the case of simulated tempering, the rates of moving into or out of the overlapping region are denoted by r and r′, respectively, but they assume slight different values from their counterparts in simulated tempering. The two rates relate to the acceptance ratio as
Assuming both r and r′ are small, the transition matrix is
The decay rate of the second largest eigenvalue is approximately
| (8) |
where
and
It is reduced to in the frequent tempering limit, or 2(r∕(r+r′))2f=2ARREf in the infrequent tempering limit.
In both simulated tempering and replica exchange, the decay rate is proportional to the acceptance ratio in the limit of infrequent tempering; hence simulated tempering is superior over replica exchange because it offers a larger acceptance ratio. This conclusion remains true even in the frequent tempering limit. This can be seen by assuming that the rate r takes a similar value in the two tempering methods and then making an algebraic comparison between the corresponding decay rates. A significant difference can be seen as we separate the two-energy distributions far apart. This leads to a small overlapping region, and r⪡r′. Consequently, the ratio of the decay rate in replica exchange and that in simulated tempering becomes 2r∕(r′+3r), which is much less than 1.
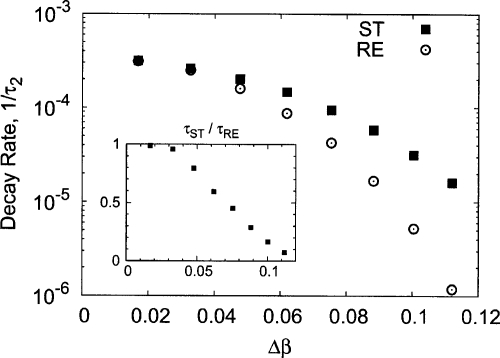
To test this model, a numerical comparison was done on the 32×32 Ising model with two temperatures. The first was fixed at T=1.7 while the second was variable. As before, the setup allowed us to compare the two algorithms at different temperature separations. Since the eigenvalue λ2 corresponds to the slowest mode in the energy space, it can be measured from the longest mode of the energy correlation function, , where is the average energy at the two temperatures. Particularly we focused on the frequent tempering limit where the tempering frequency f is fixed at 1.0 (in the infrequent tempering limit we only need to compare the acceptance ratio directly). In Fig. 3, we show the decay rate 1∕τ2=1−λ2 as a function of the temperature separation. Simulated tempering invariably gives a larger decay rate (or a shorter correlation time) than replica exchange. The difference between the two algorithms is small when the two temperatures are close. With the increase of the separation, the advantage of simulated tempering over replica exchange also becomes apparent, e.g., at the rightmost point, the ratio of the two decay rates is larger than 10.
Figure 3.
The rate of energy space traversing 1∕τ2 (measured from the slowest mode energy correlation function) vs temperature separations Δβ for simulated tempering (ST) and replica exchange (RE). The first temperature is fixed at T=1.7, while the second is variable. The ratio of the two rates is shown in the inset. In both cases, the frequency f=1.0.
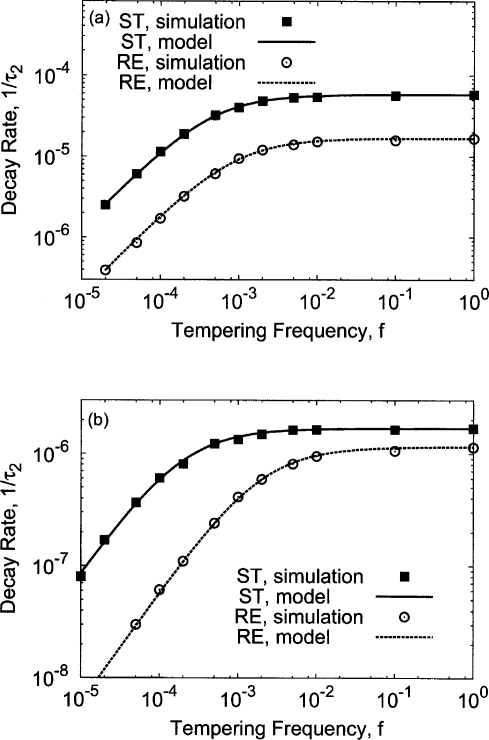
Next, we fixed the second temperature T=2.0, but varied the tempering frequency f from 2×10−5 to 1.0. The acceptance ratios are 6.65% for simulated tempering and 1.03% for replica exchange, respectively. In the frequent tempering limit, the decay rate saturates to 5.8×10−5 for simulated tempering and to 1.7×10−5 for replica exchange. The rates r and r′ can be deduced from the acceptance ratio and the saturated decay rate, and then used in calculating model predictions from Eqs. 7, 8. A good agreement between the simulation results and the model prediction can be seen in Fig. 4a. It is also evident that simulated tempering gives a larger decay rate than replica exchange for any given tempering frequency f.
Figure 4.
The rate of energy space traversing 1∕τ2 vs the frequency of attempting temperature transitions f in simulated tempering (ST) and replica exchange (RE). (a) Two temperatures T=1.7 and 2.0 are used. The prediction from the model is also shown. The model predictions calculated from Eqs. 7, 8 are shown in solid and dashed lines, respectively. (b) Seven temperatures T=1.5, 1.8, 2.0, 2.2, 2.3, 2.4, and 2.6 are used. The solid and dashed lines come from Eq. 9 for simulated tempering and replica exchange, respectively.
A numerical comparison was performed with multiple temperatures on the same Ising model. Seven temperatures were used, T=1.5, 1.8, 2.0, 2.2, 2.3, 2.4, and 2.6. The transition temperature is about 2.27. The results are shown in Fig. 4b, where we also used
| (9) |
to fit the curves. Here, the parameter R0 is the saturated (maximal) decay rate, and f0 is the tempering frequency where the rate drops to half of its maximal value. A good fitting can be seen in both simulated tempering and replica exchange. This is because Eq. 9 is the simplest form that captures the essential features of frequency dependence (for both simulated tempering and replica exchange), that is, a linear dependence in the low frequency limit, and a saturation behavior in the high frequency limit. Note, Eq. 9 can also be treated as a good approximation for the results of the two-temperature case: Eq. 7 is approximately rf∕[f+(r+r′)∕2], while Eq. 8 is roughly C∕(2B). We thus expect that Eq. 9 can be used to approximate the multiple temperature case as well. From Fig. 4b, it can be seen that simulated tempering once again outperforms replica exchange at any given frequency. Note that we used a small separation between neighboring temperature pairs to reduce the difference of the decay rates in the high frequency limit. However, as the frequency is lowered, the difference between the two methods still grows significantly. At the saturated frequency f=1, the decay rate of simulated tempering is about 1.5 times that of replica exchange. At f=10−4, the ratio of the two rises to about 10.
System with a transition temperature
Many systems possess a transition temperature which separates the system between disordered states at high temperatures and ordered states at low temperatures. The energy distribution at the transition temperature becomes a bottleneck region for traversing the energy space. The tempering efficiency can be improved by focusing sampling around the transition temperature to enhance the bridge between the high energy (disordered) states and the low energy (ordered) states.
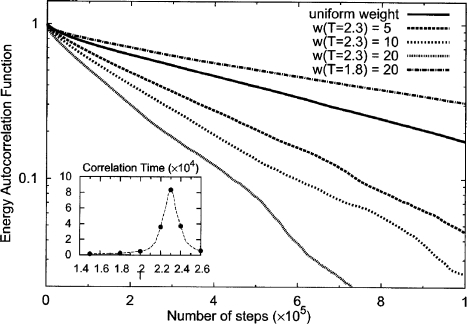
In simulated tempering, we can simply adjust the acceptance probability [Eq. 1] by raising the weight wβ of the transition temperature. The effect of adjusting the weight at the transition temperature can be shown on the 32×32 Ising model. We used the seven-temperature set, T=1.5, 1.8, 2.0, 2.2, 2.3, 2.4, and 2.6. The integrated correlation time (obtained from integrating the normalized autocorrelation function from zero to infinity) at the sampling temperatures are shown in the inset of Fig. 5, where the peak is reached around the transition temperature Tc≈2.3. In Fig. 5, we compared the energy correlation functions in cases where the weight of visiting temperature T=2.3 was adjusted to 1.0, 5.0, 10.0, or 20.0, while the weights of other temperatures were kept at 1.0 (the tempering frequency was f=1 in all the cases). The correlation time was significantly reduced with the increase of the weight, e.g., its value at w=20.0 was less than one-third of that at w=1.0. As a control, we also increased the weight of another sampling temperature T=1.8 to 20.0 while keeping the weights to other temperatures (including T=2.3) unity. From Fig. 5, it is evident that it failed to shorten the correlation time. This indicates that the tempering efficiency can be significantly improved only if the weight of the simulation at the transition temperature is increased.
Figure 5.
The effect of changing the weight to the transition temperature in simulated tempering. Seven temperatures T=1.5, 1.8, 2.0, 2.2, 2.3, 2.4, and 2.6 are used on the 32×32 Ising model. Each temperature has weight of 1.0, except the weight to the temperature T=2.3 is variable: 1.0, 5.0, 10.0, or 20.0. The correlation functions are shown to have a shorter correlation time with the increase of the weight. As a comparison, increasing the weight of T=1.8 to 2.0 fails to shorten the correlation time. The energy autocorrelation time from temperature T=2.0 to 2.5 is shown in the inset (T=2.27 is phase-transition temperature). The correlation time at the transition temperature is much longer than that at a neighboring temperature.
In replica exchange, it is also possible to increase the weight to the simulation at the transition temperature by adding additional replicas there. However, it is usually inconvenient if replicas are distributed in different computer nodes. In the above case, one has to use 19 additional replicas to reach the weight w=20.0. Further, the efficiency can be decreased if an implementation is unable to afford a frequent communication between computer nodes.
Thus, by raising the weight of the transition temperature, we can improve the sampling speed by accelerating the process of traversing the energy space. This in turn leads to a higher rate of switching between local wells, and more accurate statistics for low temperature simulations. A possible side effect is that temperatures other than the transition temperature may receive fewer visits, and thus reduce the total amount of statistics there. However, in a system that manifests a phase transition, it usually takes a long time for the system to switch between different local wells even in the presence of tempering. Thus if we expect that the system can accumulate sufficient statistics on a local well before it transits to another well, such a side-effect is negligible.
CONCLUSIONS AND DISCUSSIONS
We compared the tempering efficiency between simulated tempering and replica exchange. Simulated tempering consistently gives a higher rate of delivering the system between high temperature states and low temperature states as well as a higher rate of traversing the energy space. The difference is especially eminent if the energy distributions of neighboring temperatures are well separated or∕and if the tempering frequency is low. The fundamental feature that makes replica exchange less efficient than simulated tempering is that in replica exchange a successful temperature exchange requires two replicas to be simultaneous in their common energy space, while in simulated tempering a temperature transition can happen whenever the system falls in the region. Besides, it is usually easier for simulated tempering to adopt higher tempering frequency. This is because, in replica exchange, a high tempering frequency requires heavy cost of computer node communication. In addition, simulated tempering is able to concentrate simulation effort on the “bottleneck” temperature to reach the maximal efficiency without adding additional replicas.
In the above discussion, we assumed that the partition function used in simulated tempering is exact. But in reality we usually use an approximated partition function for sampling parameters. In this case, what changes is that each temperature may not receive exactly equal number of visits. To see this, let us assume that the sampling parameter we used is Zβ exp(εβ) instead of Zβ, where εβ represents the error for the sampling temperature β. From Eq. 1, it is clear that using this set of parameters is equivalent to using the exact partition function but with a nonuniform weighting factor wβ≈exp(∼εβ). However, the Boltzmann distribution of each individual sampling temperature is still preserved and thus quantities calculated from each temperature contain no systematic error after equilibration.
However, a sufficiently accurate partition function (e.g., ∣εβ∣<0.5) is still needed for an efficient simulation. Otherwise some temperatures can absorb most of the sampling weights from the rest of the temperatures, which in turn leads to a slower rate of traversing the energy space (with the exception mentioned above where the focused temperature is the transition temperature). For a large and realistic system such as a protein, to obtain an accurate partition function is not trivial, especially for low temperatures where the partition function is dominated by the ground state. In such systems, the technique of using an updating factor to gradually converge the partition function4 is particularly helpful, because the partition function obtained in this way can properly reflect the contribution from low energy states which are usually found in a late stage of simulation. Accordingly we also believe that the updating of the partition function should be used until the system is properly equilibrated.
There are concerns in literature that a high frequency may actually decrease the tempering efficiency in replica exchange.10 This effect is not observed in our model and numerical results. Our results show that the tempering efficiency (measured by the decay rate of traversing energy space) increases monotonically with the frequency of attempting temperature transitions∕exchanges, although it encounters a saturation and the pace of increase slows down significantly when the frequency grows to be comparable with the reciprocal of the autocorrelation time of the energy. The efficiency drop may be due to communications between different replicas or other reasons that escaped our calculation.
ACKNOWLEDGMENTS
The authors acknowledge support from an NIH grant (GM067801-06A1) an NSF grant (MCB-0818353) and a Welch grant (Q-1512).
References
- Marinari E. and Parisi G., Europhys. Lett. 10.1209/0295-5075/19/6/002 19, 451 (1992); [DOI] [Google Scholar]; Lyubartsev A. P., Martsinovski A. A., Shevkunov S. V., and Vorontsov-Velyaminov P. N., J. Chem. Phys. 10.1063/1.462133 96, 1776 (1991). [DOI] [Google Scholar]
- Swendsen R. H. and Wang J. S., Phys. Rev. Lett. 10.1103/PhysRevLett.57.2607 57, 2607 (1986); [DOI] [PubMed] [Google Scholar]; Geyer C. J., Proceedings of the 23rd Symposium on the Interface (American Statistical Association, New York, 1991);; Hukushima K. and Nemoto K., J. Phys. Soc. Jpn. 10.1143/JPSJ.65.1604 65, 1604 (1996); [DOI] [Google Scholar]; Hansmann U. H. E., Chem. Phys. Lett. 10.1016/S0009-2614(97)01198-6 281, 140 (1997). [DOI] [Google Scholar]
- Park S. and Pande V. S., Phys. Rev. E 10.1103/PhysRevE.76.016703 76, 016703 (2007). [DOI] [PubMed] [Google Scholar]
- Zhang C. and Ma J. P., Phys. Rev. E 10.1103/PhysRevE.76.036708 76, 036708 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kofke D. A., J. Chem. Phys. 10.1063/1.1507776 117, 6911 (2002). [DOI] [Google Scholar]
- Kone A. and Kofke D. A., J. Chem. Phys. 122, 206101 (2005); [DOI] [PubMed] [Google Scholar]; Earl D. J. and Deem M. W., J. Phys. Chem. B 10.1021/jp0376626 108, 6844 (2004); [DOI] [Google Scholar]; Earl D. J. and Deem M. W., Phys. Chem. Chem. Phys. 10.1039/b509983h 7, 3910 (2005); [DOI] [PubMed] [Google Scholar]; Zuckerman D. M. and Lyman E., J. Chem. Theory Comput. 10.1021/ct600297q 2, 1693 (2006); [DOI] [PubMed] [Google Scholar]; Nadler W. and Hansmann U. H. E., Phys. Rev. E 10.1103/PhysRevE.76.065701 76, 065701(R) (2007); [DOI] [PubMed] [Google Scholar]; Trebst S., Huse D. A., and Troyer M., Phys. Rev. E 10.1103/PhysRevE.70.046701 70, 046701 (2004); [DOI] [PubMed] [Google Scholar]; Trebst S., Troyer M., and Hansmann U. H. E., J. Chem. Phys. 10.1063/1.2186639 124, 174903 (2006); [DOI] [PubMed] [Google Scholar]; Katzgraber H. G., Trebst S., Huse D. A., and Troyer M., J. Stat. Mech.: Theory Exp. P03018 (2006); [Google Scholar]; Nymeyer H., IEEE Trans. Compon. Packag. Technol. 4, 626 (2008). [Google Scholar]
- Rathore N., Chopra M., and de Pablo J. J., J. Chem. Phys. 10.1063/1.1831273 122, 024111 (2005); [DOI] [PubMed] [Google Scholar]; Nadler W. and Hansmann U. H. E., Phys. Rev. E 10.1103/PhysRevE.75.026109 75, 026109 (2007). [DOI] [PubMed] [Google Scholar]
- Park S., Phys. Rev. E 10.1103/PhysRevE.77.016709 77, 016709 (2008). [DOI] [PubMed] [Google Scholar]
- Sindhikara D., Meng Y. L., and Roitberg A. E., J. Chem. Phys. 10.1063/1.2816560 128, 024103 (2008). [DOI] [PubMed] [Google Scholar]
- Abraham M. J. and Gready J. E., J. Chem. Theory Comput. 10.1021/ct800016r 4, 1119 (2008). [DOI] [PubMed] [Google Scholar]
- Newman M. E. J. and Barkema G. T., Monte Carlo Methods in Statistical Physics (Clarendon, Oxford University Press, Oxford, NY, 1999). [Google Scholar]