An efficient and accurate molecular alignment and docking technique using ab initio quality scoring

Abstract

An accurate and efficient molecular alignment technique is presented based on first principle electronic structure calculations. This new scheme maximizes quantum similarity matrices in the relative orientation of the molecules and uses Fourier transform techniques for two purposes. First, building up the numerical representation of true ab initio electronic densities and their Coulomb potentials is accelerated by the previously described Fourier transform Coulomb method. Second, the Fourier convolution technique is applied for accelerating optimizations in the translational coordinates. In order to avoid any interpolation error, the necessary analytical formulas are derived for the transformation of the ab initio wavefunctions in rotational coordinates. The results of our first implementation for a small test set are analyzed in detail and compared with published results of the literature. A new way of refinement of existing shape based alignments is also proposed by using Fourier convolutions of ab initio or other approximate electron densities. This new alignment technique is generally applicable for overlap, Coulomb, kinetic energy, etc., quantum similarity measures and can be extended to a genuine docking solution with ab initio scoring.

INTRODUCTION

Docking potential drug candidates into active sites of enzymes in receptor based drug design or aligning molecules into abstract external fields or to other molecules in ligand based drug design represents one of the biggest challenges in contemporary in silico drug design. The number of times scoring has to be done is in general very large due to the high number of conformational parameters that need to be examined coupled with the translational and rotational motions of the systems of interest. Accurate, but computationally demanding first principle quantum chemistry calculations are usually not feasible and experimentally or ab initio parametrized model functions represent the best trade off between accuracy and sampling speed for practical docking simulations.^{1, 2, 3, 4, 5, 6, 7, 8, 9} In other areas such as CoMFA and quantum similarity fields there is a relatively new and promising trend to use first principle or at least quantum mechanical based similarity measures.^{10, 11, 12, 13, 14, 15, 16} However, even when quantum mechanical similarity models are used, the molecular alignment, which is an important and vital first step in ligand based modeling, is almost always performed with much simpler techniques based on geometrical, topological, or other empirically obtained information. The solutions obtained in this way are fast but obviously inconsistent with the applied quantum mechanical models. The error due to this inconsistency is poorly understood at this point in time. A new scheme called the quantum similarity superposition algorithm (QSSA) has been introduced recently¹⁷ by using the atomic shell approximation¹⁸ (ASA) for the molecular electronic densities. A validation study of seven different C₄H₆O₂ molecules has been analyzed by performing pair-wise topogeometrical alignment with the topogeometrical superposition approach (TGSA) method¹⁹ as well as QSSA alignments which is computationally expensive but consistent with the applied ASA quantum similarity measures. Significant differences in the resultant similarity matrices have been found.

The goal of this article is to introduce the foundation of a new, affordable, and accurate rigid body molecular alignment algorithm and quantum similarity models based on ab initio wavefunctions. Details of possible extensions for ab initio based docking and molecular flexibility are touched on briefly and more details with applications will be reported on in the future. The combination of two existing techniques is our starting point. The first one is the Fourier transform convolution technique which provides an excellent tool to reduce global optimization problems from six to three dimensions and has been widely applied in areas of numerical image matching and existing molecular alignment and docking methods based on empirical scoring^{20, 21, 22} or experimental data.^{23, 24} In order to obtain ab initio electronic densities in plane wave space the Fourier transform Coulomb^{25, 26, 27} (FTC) method can be used which has been developed as a new solution for linear scaling Coulomb problems in Gaussian based density functional theory (DFT). The FTC technique can evaluate the chemically important “valence” part of the electron density as well as its Coulomb potential on the Fourier grid with high efficiency and with high numerical accuracy. This technique has been applied very successfully to speed up the costly Coulomb matrix evaluations in two modern ab initio packages.^{28, 29, 30, 31}

THEORY

Ab initio quality quantum similarity measures through the use of Fourier transform numerical techniques

The quantum similarity matrix first defined by Carbo et al.³² has the general form of

$$Z_{A,B}={\int }_{-\infty }^{\infty }{\rho }_A\left({\overline{r}}_A\right)\omega ({\overline{r}}_A,{\overline{r}}_B){\rho }_B\left({\overline{r}}_B\right)d{\overline{r}}_{A}d{\overline{r}}_B,$$

where ${\rho }_A\left({\overline{r}}_A\right)$ and ${\rho }_B\left({\overline{r}}_B\right)$ are the electronic densities of systems A and B, respectively, and $\omega ({\overline{r}}_A,{\overline{r}}_B)$ is the similarity operator. One of the most commonly used quantum similarity measures are the overlap and the Coulomb³³ similarities. In the case of overlap similarity,

$$\omega ({\overline{r}}_A,{\overline{r}}_B)=\delta ({\overline{r}}_A,{\overline{r}}_B),$$

and the similarity matrix becomes

$$Z_{A,B}^{\text{overlap}}={\int }_{-\infty }^{\infty }{\rho }_A\left(\overline{r}\right){\rho }_B\left(\overline{r}\right)d\overline{r},$$

while in the case of Coulomb similarity the similarity operator is the Coulomb operator

$$\omega ({\overline{r}}_A,{\overline{r}}_B)=\frac{1}{\mid r_A-r_B\mid },$$

and the similarity matrix can be written in the form of

$$Z_{A,B}^{\text{Coulomb}}={\int }_{-\infty }^{\infty }{J}_A\left(\overline{r}\right){\rho }_B\left(\overline{r}\right)d\overline{r},$$

where $J_A\left(\overline{r}\right)$ is the Coulomb potential of system A,

$$J_A\left(\overline{r}\right)={\int }_{-\infty }^{\infty }{\rho }_A\left({\overline{r}}_A\right)\frac{1}{\mid r_A-r\mid }d{\overline{r}}_A.$$

Evaluations of electron densities and their Coulomb potentials on equally spaced Cartesian grids have proven to be extremely efficient using the FTC method.^{25, 26, 27, 31} Both mathematically and technically the computational steps needed above are very similar or nearly identical to the first and the second SCF iterative steps described by one of us (L.F.-M.) in a paper which deals with the details of the FTC method in the framework of linear scaling DFT algorithms.²⁵ This observation opens a new way to calculate high level ab initio quantum similarity matrices much more efficiently than through the use of analytical integral evaluation techniques especially with high quality Gaussian basis sets.

Adaptive scheme for criteria of expandability

Due to the nature of the Fourier grids, it is not possible to expand all contributions of the electron densities with high accuracy through the use of a computationally tractable number of plane waves. Nonetheless, the valence part of electron density can be expanded with high quality and these are the most important parts for chemical properties, as well, as being the most time consuming calculation using analytical integral evaluation. The success of the FTC technique relies on replacing the most time consuming parts of a computation with efficient numerical techniques while the analytical evaluations for the Coulomb integrals involving the “core” parts of the electron densities have been kept in order to guarantee the traditionally high ab initio integral accuracies. The optimal trade off between efficiency and accuracy is, on the other hand, different in in silico drug design than in the traditional ab initio field. A reasonably good approximation for core parts of the electron density can be introduced and instead of using costly analytical integral evaluations efficient numerical techniques can be used for the entire electronic density, its Coulomb potentials, or other functionals of the density in general. The valence and core words in this article are in quotes because classical chemical meanings were used loosely. More rigorously speaking we define as valence parts of the electron density as those contributions of the density which are expandable at the given accuracy criterion, where at the given quality of plane wave basis sets and the core parts are what remains. The quality of the plane wave space can be characterized with the grid density in coordinate space²⁷ (ρ^grid) which is simply the number of grid points we have along one dimension in each unit (atomic units are used) distance. At any given accuracy criterion, more and more portions of the electron density become expandable by increasing the grid density and at the asymptotic limit the entire electron density would be expandable for any system. To estimate the expansion errors for practical grid densities we introduce the maximum possible momentum (K_lim) of the given grid, which is related to the grid density by the linear relationship K_lim=πρ^grid. The error of the expansion can be estimated by the ratio of finite and infinite integrations in momentum space.³⁴ For instance, using the momentum-space form of an s-type function, the error estimation is

$$\frac{{\int }_{-K_{\lim }}^{K_{\lim }}{\int }_{-K_{\lim }}^{K_{\lim }}{\int }_{-K_{\lim }}^{K_{\lim }}\exp \left(\frac{-(k{x}^2+k{y}^2+k{z}^2)}{4\eta }\right)dkxdkydkz}{{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\exp \left(\frac{-(k{x}^2+k{y}^2+k{z}^2)}{4\eta }\right)dkxdkydkz}=1-\mathrm{erf}{\left(\frac{K_{\lim }}{2\sqrt{\eta }}\right)}^3,$$

where η is the exponent of the Gaussian. Taking into account the angular momentum dependence of the expansion error and with the aim of obtaining a useful approach for shell pairs, the error in general can be approximated as

$$\frac{{\int }_0^{K_{\lim }}{\int }_{-K_{\lim }}^{K_{\lim }}{\int }_{-K_{\lim }}^{K_{\lim }}k{x}^n\exp \left(\frac{-(k{x}^2+k{y}^2+k{z}^2)}{4\eta }\right)dkxdkydkz}{{\int }_0^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }k{x}^n\exp \left(\frac{-(k{x}^2+k{y}^2+k{z}^2)}{4\eta }\right)dkxdkydkz}.$$

Introducing two intermediate variables $a=\mathrm{erf}(K_{\lim }∕2\sqrt{\eta })$ and $b=\exp (K_{\lim }^2∕4\eta )$, the results for up to six degrees of kx (up to the necessary degree for an f-f type of shell pairs) are the following:

$$n=0,1-a^3,$$

$$n=1,\frac{a^2-b{a}^2+b}{b},$$

$$n=2,\frac{b\sqrt{\eta \pi }-a^{3}b\sqrt{\eta \pi }+K_{\lim }{a}^2}{b\sqrt{\eta \pi }},$$

$$n=3,\frac{K_{\lim }^2{a}^2-4\eta b{a}^2+4\eta a^2+4\eta b}{4\eta b},$$

$$n=4,\frac{6K_{\lim }\eta a^2-6b{a}^3{\eta }^{3∕2}\sqrt{\pi }+K_{\lim }^3{a}^2+6b{\eta }^{3∕2}\sqrt{\pi }}{6b{\eta }^{3∕2}\sqrt{\pi }},$$

$$n=5,\frac{8K_{\lim }^2\eta a^2-32b{a}^2{\eta }^2+32a^2{\eta }^2+K_{\lim }^4{a}^2+32b{\eta }^2}{32b{\eta }^2},$$

$$n=6,\frac{K_{\lim }^5{a}^2-60b{a}^3{\eta }^{5∕2}\sqrt{\pi }+60b{\eta }^{5∕2}\sqrt{\pi }+60K_{\lim }{a}^2{\eta }^2+10K_{\lim }^3{a}^2\eta }{60b{\eta }^{5∕2}\sqrt{\pi }}.$$

Once the expandable contributions of the electronic density is determined we approximate the remaining core parts by using expandable s-type Gaussians which can exactly reproduce the missing core charges and which has the maximum possible exponent based on the given accuracy criterion. This approximation was found to be satisfactory for molecular alignments. Approximating the core part of the electron densities makes sense since they play a lesser role in chemistry than the expandable valence densities although the amount of electrons that the core parts hold is very far from negligible. For the purpose of proving this point, a unique series of test results is presented in the Results section below.

The electron charge contributions belonging to the approximate core parts are determined by population analysis using the exact analytic equations at the beginning of the calculations. We should highlight that the effects of using approximate atomic charges for the core electrons are reduced by increasing the grid density and vanishes at the asymptotic limit. Thus checking the convergence of the given property of interest by increasing the grid density provides us information about the quality of the approximations used as well as offering an adaptive tool to determine the optimal balance between efficiency and accuracy under different circumstances.

Alignment

If we consider rigid molecules, the similarity matrix elements are functions of the relative orientations of the molecules towards each other. For an A and B molecule pair one can fix the A molecule, for instance, and introduce translational and rotational vectors of T(X,Y,Z) and R(ϕ,θ,ψ) where the values of all three translational variables X,Y,Z and the three Euler angles ϕ,θ,ψ are relative to a given initial orientation of B. The best alignment has a clear and meaningful mathematical definition, which maximizes the similarity matrix element

$$Z_{A,B}^{\max }(T(X,Y,Z),R(\varphi ,\theta ,\psi ))=\max \left({\int }_{-\infty }^{\infty }{f}_A\left(\overline{r}\right){\rho }_B\left(\overline{r}(T,R)\right)d\overline{r}\right),$$

where, for instance, $f_A\left(\overline{r}\right)$ is the electron density in the overlap similarity case and electronic Coulomb potential of A in the Coulomb similarity case. Note that the form of $f_A\left(\overline{r}\right)$ is defined by the given similarity measure and the best alignment obviously depends on $f_A\left(\overline{r}\right)$. In order to find the best alignment, the global maximum of Z_A,B must be found in a six dimensional space and this has been shown to be a very difficult task¹⁷ even for small molecule pairs and even when using the atomic shell approximation (see also our Results section below). Using accurate ab initio quality electron densities together with analytical integral evaluation techniques is not currently feasible for this task due to the huge numbers of integrals and Z_A,B matrix elements that need to be calculated during the global search in six dimensions. It is, however, possible to reduce the dimensionality of the problem from six to three by decoupling the translational and rotational search using the Fourier convolution technique. For each ϕ,θ,ψ set, the shifted electronic density of system B from its initial position can be written as ${\rho }_B^{\varphi ,\theta ,\psi }(\overline{r}-\overline{T})$. The function to be maximized is then $Z^{\varphi ,\theta ,\psi }\left(\overline{T}\right)={\int }_{-\infty }^{\infty }{f}_A\left(\overline{r}\right){\rho }_B^{\varphi ,\theta ,\psi }(\overline{r}-\overline{T})d\overline{r}$ which is simply the convolution of f_A and ${\rho }_B^{\varphi ,\theta ,\psi }$. Due to the Fourier convolution theorem the function values of $Z^{\varphi ,\theta ,\psi }\left(\overline{T}\right)$ over the entire interesting numerical range of $\overline{T}$ can be obtained by multiplying the f_A and ${\rho }_B^{\varphi ,\theta ,\psi }$ together in momentum space and Fourier transform the product into coordinate space. The global maximum of $Z^{\varphi ,\theta ,\psi }\left(\overline{T}\right)$ can be then obtained with negligible computational effort.

Rotations with ϕ,θ,ψ Euler angles

There is a difficulty arising in the numerical solution due to the rotations. When system B is rotated with R(ϕ,θ,ψ), the numerical values of the ${\rho }_B^{\varphi ,\theta ,\psi }$ density do not belong to the original mesh any more on which the f_A was expanded and on which the Fourier transformation for ${\rho }_B^{\varphi ,\theta ,\psi }$ needs to be performed. This problem is well known and is frequently discussed in the literature in all areas that deal with numerical image matching using Fourier convolutions. The usual solution is to perform interpolation on ${\rho }_B^{\varphi ,\theta ,\psi }$ in order to get its values on the original grid. In the biological area this solution has been applied recently to match numerical electron densities coming from electron microscope and x-ray studies,²⁴ and molecular alignments^{21, 22} based on approximate charge distributions and van der Waals shapes. Using interpolations for this purpose has some disadvantages, however, its accuracy may not be entirely satisfactory by using efficient interpolation schemes and the interpolation could become quite inefficient and the major cost of the calculation when its accuracy is increased. For fully numerical problems there is probably no better alternative solution and the best trade off between accuracy and efficiency needs to be found. For our purpose there is a more attractive solution. The analytical functions of the molecular orbitals are known in our case as linear combination of the given Gaussian basis functions. After each R(ϕ,θ,ψ) rotation, the molecular orbitals of system B can be transformed analytically according to the rotation and its electron density can be built up on the original mesh by using the transformed orbitals. The electronic density of system B needs to build up after every rotation this way. This computational step is, however, just about as costly (i.e., it is fast) as the Fourier transformation itself, which needs to be performed in each rotational steps anyway. Thus, there is no significant performance penalty associated with this analytical transformation and exact molecular orbitals can be used in each rotational step without introducing any error in the model due to the rotations.

Using the z,y^′,z^″ rotational convention for the Euler angles, the R(ϕ,θ,ψ) rotational matrix that transforms the original (x,y,z) axes to their new orientation has the following form:

$$\left(\begin{array}{ccc}\cos \left(\psi \right)\cos \left(\varphi \right)-\cos \left(\theta \right)\sin \left(\varphi \right)\sin \left(\psi \right)& -\sin \left(\psi \right)\cos \left(\varphi \right)-\cos \left(\theta \right)\sin \left(\varphi \right)\cos \left(\psi \right)& \sin \left(\theta \right)\sin \left(\varphi \right)\\ \cos \left(\psi \right)\sin \left(\varphi \right)+\cos \left(\theta \right)\cos \left(\varphi \right)\sin \left(\psi \right)& -\sin \left(\psi \right)\sin \left(\varphi \right)+\cos \left(\theta \right)\cos \left(\varphi \right)\cos \left(\psi \right)& -\sin \left(\theta \right)\cos \left(\varphi \right)\\ \sin \left(\psi \right)\sin \left(\theta \right)& \cos \left(\psi \right)\sin \left(\theta \right)& \cos \left(\theta \right)\end{array}\right).$$

Obviously no transformations are needed for the sphericals parts of the molecular orbital. The p_x,p_y,p_z basis functions transform just like the x,y,z axes. Thus the transpose of the R(ϕ,θ,ψ) matrix can be applied to obtain the p_x,p_y,p_z contributions of the transformed orbital coefficients. The form of the transformation matrix of basis functions with higher angular momentum is the last thing that needs to be derived. Let us denote the matrix element of R(ϕ,θ,ψ) as R_i,j where the i=1⋅⋅3 index belongs to the columns and j=1⋅⋅3 belongs to the rows. One of the convenient choice to define the nonspherical part of the six components of d₆-type basis functions as $(x^2,\sqrt{3}xy,y^2,\sqrt{3}xz,\sqrt{3}yz,z^2)$. In this case the form of the 6×6 transformation matrix is

$$\left(\begin{array}{cccccc}{R}_{1,1}^2& \sqrt{3}{R}_{1,1}{R}_{2,1}& R_{2,1}^2& \sqrt{3}{R}_{1,1}{R}_{3,1}& \sqrt{3}{R}_{2,1}{R}_{3,1}& R_{3,1}^2\\ \frac{2}{3}\sqrt{3}{R}_{1,1}{R}_{1,2}& R_{1,2}{R}_{2,1}+R_{1,1}{R}_{2,2}& \frac{2}{3}\sqrt{3}{R}_{2,1}{R}_{2,2}& R_{1,2}{R}_{3,1}+R_{1,1}{R}_{3,2}& R_{2,2}{R}_{3,1}+R_{2,1}{R}_{3,2}& \frac{2}{3}\sqrt{3}{R}_{3,1}{R}_{3,2}\\ R_{1,2}^2& \sqrt{3}{R}_{1,2}{R}_{2,2}& R_{2,2}^2& \sqrt{3}{R}_{1,2}{R}_{3,2}& \sqrt{3}{R}_{2,2}{R}_{3,2}& R_{3,2}^2\\ \frac{2}{3}\sqrt{3}{R}_{1,1}{R}_{3,1}& R_{1,1}{R}_{2,3}+R_{1,3}{R}_{2,1}& \frac{2}{3}\sqrt{3}{R}_{2,1}{R}_{2,3}& R_{1,1}{R}_{3,3}+R_{1,3}{R}_{3,1}& R_{2,1}{R}_{3,3}+R_{2,3}{R}_{3,1}& \frac{2}{3}\sqrt{3}{R}_{3,1}{R}_{3,3}\\ \frac{2}{3}\sqrt{3}{R}_{1,2}{R}_{1,3}& R_{1,3}{R}_{2,2}+R_{1,2}{R}_{2,3}& \frac{2}{3}\sqrt{3}{R}_{2,2}{R}_{2,3}& R_{1,3}{R}_{2,3}+R_{1,2}{R}_{3,3}& R_{2,3}{R}_{3,2}+R_{2,2}{R}_{3,3}& \frac{2}{3}\sqrt{3}{R}_{3,2}{R}_{3,3}\\ R_{1,3}^2& \sqrt{3}{R}_{1,3}{R}_{2,3}& R_{2,3}^2& \sqrt{3}{R}_{1,3}{R}_{3,3}& \sqrt{3}{R}_{2,3}{R}_{3,3}& R_{3,3}^2\end{array}\right),$$

and its corresponding transpose needs to be used to transform the molecular orbital coefficients.

Quantum chemistry packages often use d₅ type of basis functions. One of the easiest way to implement the necessary 5×5 dimensional transformation matrix is to first transform the basis sets from d₅ to d₆, apply the 6×6 transformation above, and backtransform the resulting vectors from d₆ to d₅. There are also higher polarization functions in larger and more accurate basis sets in ab initio packages. The transformation matrix for f₁₀ type basis functions was also derived.

One of the convenient choice to order the polynomial parts of the f₁₀ basis functions is

$$(x^3,\sqrt{5}{x}^{2}y,\sqrt{5}x{y}^2,y^3,\sqrt{5}{x}^{2}z,\sqrt{15}xyz,\sqrt{5}{y}^{2}z,\sqrt{5}{z}^{2}x,\sqrt{5}{z}^{2}y,z^3).$$

Using this definition a FORTRAN code to obtain the transformation matrix elements of the 10×10 dimensional matrix due to the rotations is provided in the Appendix section and deposited as an Electronic Physics Auxiliary Publication Service (EPAPS) file⁵⁰ in ASCII format.

Looking for the global optimum in ϕ,θ,ψ Euler angles

Looking for global optima in multidimensional spaces is an important area of mathematics in and of itself, which cannot be fully introduced within this article. Good reviews of the current techniques can be found.^{35, 36} Perhaps the simplest and the most commonly used deterministic algorithm for three dimensional (3D) global optimization is to define a three dimensional grid in the ϕ,θ,ψ space and evaluate the function values at each grid point. The art of the global optimization techniques is, however, to find much more economical solutions than this simple scenario. Since the computational efficiency is vital in computational drug design we have utilized the global optimization package called Lipschitz Global Optimizer (LGO) (Ref. ³⁷) which utilizes special deterministic and stochastic approaches. The benefit for doing so can be estimated easily. The results section shows that this optimization package finds the global optimum within about 1000–2000 function calls for all of our test examples. On the other hand, if one allowed, for instance, 10° as the maximum acceptable error in each of the Euler angles and used the simplest grid based solution then 36×18×36=23 328 function calls would be needed. In other words, this approach is an order of magnitude slower than the one we have chosen. The maximum possible 10° error tolerance in the above example is also higher than the error in the result provided by the LGO global optimization packages.

Extension for docking problems

One of the most important advantage of our new technique compared to other alignment solutions is its natural ability for extension to docking problems. The two main source of this advantage is that physically realistic ab initio quality electron densities are used and Coulomb potentials of the electron densities can be evaluated on numerical grids accurately and orders of magnitude more efficiently than traditional ab initio two electron approaches.^{25, 26, 27} If the nuclear charge distributions are added to the electron densities then ${\int }_{-\infty }^{\infty }{J}_A\left(\overline{r}\right){\rho }_B\left(\overline{r}\right)d\overline{r}$, which was defined above as the Coulomb similarity matrix, gives the E_A,B Coulomb interaction energy between the unperturbed A and B systems. (Strictly speaking we need to deduct the Coulomb energies of the separated system A and B to get the correct Coulomb interaction energy. These energies, however, do not depend on the relative orientation of A and B). Thus looking for the minimum of E_A,B (as opposed to the maximum search in molecular alignment) in the relative orientation of A and B leads us to the explicit solution of Coulomb energy based docking problem. All techniques and equations above that were introduced for molecular alignment purposes can be used without modification. In order to consider the total interaction energy of the two systems the kinetic energy contributions as well as the exchange and the correlation contributions, or at least a good approximation of them, need to be added to the Coulomb term. This development is underway in our group and more detailed results for our docking technique will be published later. Since the electron density has ab initio quality this technique has the potential to make significant improvement in the accuracy of current molecular docking packages.

RESULTS AND DISCUSSIONS

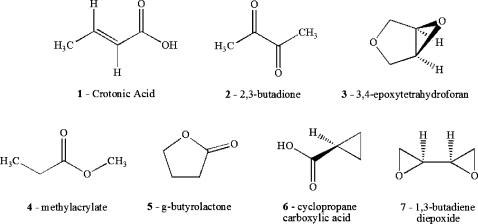
A related algorithm to our alignment scheme is the recently published QSSA method¹⁷ which uses consistent pair-wise alignments and the ASA for the electron density. In order to test out our new technique, study the effect of the approximations made, obtain basic insights into our algorithm, and compare our ab initio based results with the results of QSSA, the same set of seven molecules was chosen as was used in the earlier QSSA study. The two dimensional (2D) structures of these molecules are given in Fig. 1.

Figure 1.

2D structures of seven C₄H₆O₂ isomers. Same molecules with the same order were used in Ref. 17.

Accuracy tests and validations

Table 1 shows the atomic charge contribution from the non expandable core parts of the electron densities. By using the simplest atomic monopole based approximation for these density contributions we have implemented Mulliken and Löwdin charge calculations, however, other atomic charge schemes could be used as well. Note that Löwdin charges obtained from the diagonal elements of the S^1∕2PS^1∕2 matrix, where S is the overlap and P is the density matrix in Gaussian atomic orbital space, are not invariant for molecular rotations when Cartesian d₆ and∕or f₁₀ basis sets are used.^{38, 39} This effect can be corrected by prediagonalization⁴⁰ of the basis functions or using d₅ and f₇ type basis sets. Another complication of the Löwdin charges is that the S (overlap) matrix of the core charges is not guaranteed to be positive definite, and in fact, it is usually not the case when using smaller grid densities. Thus, complex arithmetic needs to be used and all atomic correction charges have a separate real and an imaginary part in general. For simplicity of presentation, only Mulliken atomic charges are used for the results presented in this article.

Table 1.

Contribution of the nonexpandable “core” electron densities to the total atomic charges by varying the grid density.

Grid $\text{density}∕a_0^{-1}$	“Core” electron densitycontributions (%)
1	94
2	53
3	27
4	26

The nonexpandable portion of the electron density contribution to the atomic charges or “correction charges” is summarized in Table 1. As the grid density increases their contribution to the atomic charges is less and less as expected. Their contribution, however, remains far from negligible at all practical grid densities. Since we approximate the true electron densities of these core contributions, it is important to show that they are more or less chemically inert and the correction charges do not change significantly if the chemical environment changes. A good indication for the change of chemical environments is when atomic charges change for the same atoms from one molecule to another. We have introduced a root mean square deviation (RMSD) type of measure of the atomic charges for each pair of molecules. Strictly speaking the RMSD is ill defined in this case since there is more than one atom per atom type. There are four carbon atoms followed by two oxygen atoms and six hydrogen atoms in each of the original downloadable mol files and we define the correspondence between atoms according to their atomic numbers. Note that the RMSD of the atomic charges is overestimated using this approach relative to considering all different possible RMSDs and taking the minimum since the same atom can be in different functional groups. Even with this definition our point is clearly made. Table 2 presents the RMSDs of the atomic charges for each pairs of molecules and Table 3, 4, 5, 6 shows the core electron density contributions to the given RMSD values. As one observes from Table 1, using ${\rho }^{\text{grid}}=1a_0^{-1}$ the correction charges holds about 94% of the atomic charges and from Table 3 that they are responsible for more then 50% of the change of the atomic charges in all cases. Thus, the core contributions to the electronic charges are not chemically inert in these cases and neglecting the changes in those electron density contributions would result in a relatively inaccurate approximation. As the grid density increases, however, the contribution of the correction charges to the RMSDs decreases very rapidly. At ${\rho }^{\text{grid}}=4a_0^{-1}$, despite their 26% contribution to the total charge density, which is still significant, their contributions to the RMSD’s is around 1% on average and there are 9 of the 21 pairs where it is less then 1%. This means that using ${\rho }^{\text{grid}}=4a_0^{-1}$ the nonexpandable contribution of the electron density, which we need to approximate in our method, are more or less constant for all atom types and do not change significantly with changes in chemical environments. The rapid convergence with the grid density also shows that our adaptive scheme to divide the electron densities to expandable and nonexpandable portions works very well in practice. We should note that the results will vary slightly using different ab initio Gaussian basis sets, and that the results in Table 1, 2, 3, 4, 5, 6 belong to the 6-31G^** basis set. We should also note that our purpose of these tests series is to test and validate our adaptive scheme and not to prove that the expandable valence electrons play significantly more important rules in chemistry than the core electrons. The latter fact is well known since the beginning of the modern chemistry and frequently used in computational molecular physics for several decades. A whole area of computational molecular physics by using pseudopotentials are based on that observation^{41, 42, 43} and there are almost countless applications which are published to solve interesting problems in biological and material sciences by using these techniques over the last two decades. When ultrasoft pseudopotentials⁴⁴ are used in those applications then the so called energy cutoff is usually set to about 30–50 Ry which corresponds to about ${\rho }^{\text{grid}}\approx 2a_0^{-1}$ in our nomenclature.

Table 2.

RMSD of the total atomic charges for all 7×7 system pairs.

	1	2	3	4	5	6	7
1	0.00
2	0.19	0.00
3	0.20	0.23	0.00
4	0.11	0.19	0.18	0.00
5	0.09	0.24	0.20	0.11	0.00
6	0.27	0.18	0.19	0.27	0.32	0.00
7	0.20	0.23	0.06	0.16	0.19	0.22	0.00

Table 3.

Percentage contributions of the approximated core parts of electron densities to the RMSD of atomic charges. Grid density=1.0 bohrs⁻¹.

	1	2	3	4	5	6
2	71.98
3	64.43	71.26
4	55.76	78.54	63.45
5	99.22	67.91	67.34	96.66
6	65.87	79.24	67.34	63.65	69.86
7	62.18	63.48	52.39	68.29	68.33	58.96

Table 4.

Percentage contributions of the approximated core parts of electron densities to the RMSD of atomic charges. Grid density=2.0 bohrs⁻¹.

	1	2	3	4	5	6
2	11.47
3	7.53	6.02
4	4.21	12.35	9.07
5	29.31	7.17	11.17	26.66
6	4.79	10.50	4.73	5.32	8.13
7	14.44	5.61	31.83	18.95	12.25	9.89

Table 5.

Percentage contributions of the approximated core parts of electron densities to the RMSD of atomic charges. Grid density=3.0 bohrs⁻¹.

	1	2	3	4	5	6
2	5.39
3	2.38	3.45
4	0.96	5.18	2.34
5	11.81	2.86	4.80	9.74
6	1.32	6.06	2.52	1.35	3.38
7	6.49	1.83	16.82	7.86	4.66	5.97

Table 6.

Percentage contributions of the approximated core parts of electron densities to the RMSD of atomic charges. Grid density=4.0 bohrs⁻¹.

	1	2	3	4	5	6
2	1.52
3	0.75	0.80
4	0.42	1.46	0.86
5	3.81	0.77	1.26	3.10
6	0.74	1.50	0.66	0.79	1.07
7	1.44	0.24	3.02	1.73	1.05	1.16

Similarity matrices based on pair-wise alignments

Alignments for each pair of the seven molecules have been performed based on our ab initio electronic density based technique. The B3LYP exchange-correlation functional and 6-31G^** basis set were used in the calculations. The values of the Carbo indices of the overlap quantum similarity matrix are shown in the Appendix. The optimization of the three Euler angles was performed using the LGO global optimization package.³⁷ Usually between 1000 and 2000 steps were required to find the global minima. Comparing the values of the quantum similarity matrix elements with the published results of QSSA (Ref. ¹⁷) one can find that our values are different and usually a bit higher. The difference could come from two sources. Either our ab initio based pair-wise alignment found better global optima than the QSAA or ab initio electronic density based quantum similarity measures are higher than those based on the ASA approximation. In order to find out the main source of the differences we have implemented our own version of the ASA package based on the tabulated parameters published by Constans⁴⁵ and performed the six dimensional optimization for each molecular pairs. As Bultinck et al.¹⁷ indicated these optimizations are quite difficult to perform due to the presence of numerous local optima. Usually hundreds of thousands of function evaluations and several manual restarts from different starting points were needed for each molecular pair. It should be highlighted that if our ab initio based alignment used analytical integral evaluations without the help of the Fourier transform convolution technique it would share the same difficulties since the optimization must be performed in six dimensions.

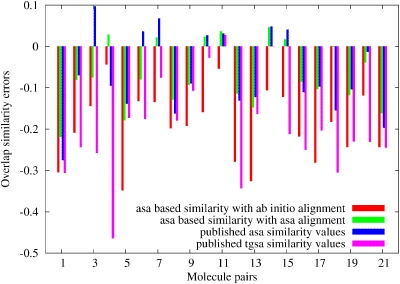
A bar chart of the relative errors (error in the sense that the ab initio value is assumed to be the best value) of the ASA similarities compared to our ab initio based similarity indices are plotted on Fig. 2. Our ASA based similarity values are quite close to the published results in most of the cases but there are some exceptions either due to the different global optimization scheme or due to the slightly different ASA density parameters used. Our implementation used the parameters from Constans⁴⁵ by applying higher number of s functions to make a projection of the same atomic densities based on the 6-311G Hartree–Fock wavefunction. A good example of an exception is the 1,4 matrix element or the fourth entry in Fig. 2, which is higher in our case than the published similarity index value [0.89 (ours) vs 0.75 (published)]. Examining the fourth entry in Fig. 2 we find that our computed ASA value has a positive error compared to the ab initio result with a smaller absolute error than the error of the original published result which is negative in sign. We also found a local optima with a ∼0.70 Carbo index value for this pair and we assume that the aligned geometry of the QSAA work was similar to this orientation. These two different alignments are shown in Figs. 34 as an example. Note that the simple TGSA based alignment with the same ASA based similarity measure resulted in a similarity index value of only 0.40 for this pair¹⁷ which has a significant error compared to both ab initio and ASA based overlap similarity indices. Our chart also shows the errors of similarity indices based on the ASA approximation but using the ab initio pair-wise alignment orientations (ASA-ab initio alignment entries). Since the alignments are the same for all pairs in this case the errors are coming from the differences between the ASA based electronic densities and the ab initio based ones.

Figure 2.

Differences between ASA based quantum similarity Carbo indexes relative to ab initio Fourier transform quantum similarity indices.

Figure 3.

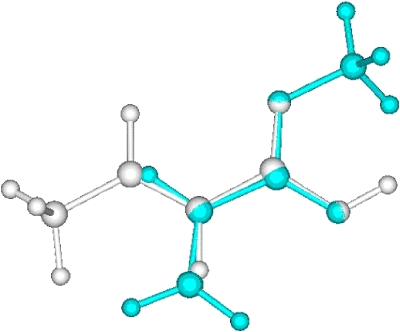
A local optimum in the alignment of methylacrylate to crotonic acid. The color of crotonic acid is set to white.

Figure 4.

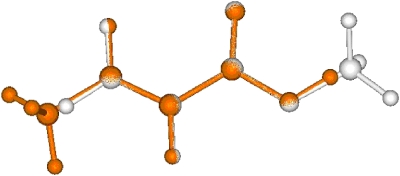
Global optimum in the alignment of methylacrylate to crotonic acid. The color of crotonic acid is set to brown.

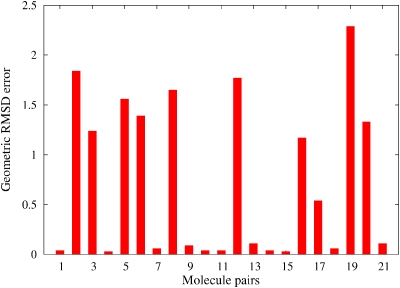
The geometric RMSD error, as one of the simplest similarity measures, is often used in drug design to compare two objects. Figure 5 shows the RMSD errors of our ASA based alignments relative to the aligned geometries of our ab initio based scheme. There are some very small differences but there are many significant differences as well. By analyzing the differences in detail, we found, however, that all ASA based alignments make sense qualitatively and that they are very close to local optima found in the ab initio alignments. Figures 67 show the ab initio and ASA based alignment of 3-4-epoxy THF (3) to crotonic acid (1) as a visual example. One observes that both of them are reasonable and are ultimately very similar alignments and that the main difference between the two is that different oxygen atoms of the 3-4-epoxy tetrahydrofuran (THF) are aligned with the carboxylic acid moiety of crotonic acid. The Carbo index values by using ab initio overlap density similarity are 0.509 and 0.508 at the ab initio and at the ASA based alignment orientations and this small difference is certainly within the accuracy of our model. Thus, the large error in the RMSD observed in Fig. 5 (second molecular pair) is obviously not correlated with the error magnitude of the ASA based alignment relative to the ab initio one. The insight one obtains is that the two alignments have different orientation in 3D space, which is enough to produce a large RMSD, but this does not necessarily lead to a large difference in similarity score.

Figure 5.

Geometric RMSD errors of the ASA alignments relative to the ab initio based alignments.

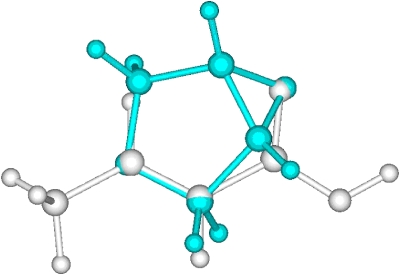
Figure 6.

Ab initio Fourier transform overlap similarity based alignment of 3-4-epoxy THF to crotonic acid.

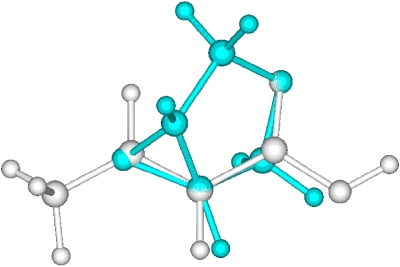
Figure 7.

ASA overlap similarity based alignment of 3-4-epoxy THF to crotonic acid.

It should be noted that at the current stage of development neither the ab initio nor the ASA based molecular alignments are fast enough to perform alignments over large databases of molecules using typical computational resources. Our current ab initio and Fourier transform based alignment, depending on the grid densities and the volume of the molecules, needs about 0.1–2 s per function call on a typical single core CPU and it is still a bit too expensive considering the necessary 1000–2000 function calls that are needed to find the global optimum in the rotational angles by using general global optimization technique and without making any assumption. The six dimensional ASA density based alignment is very time consuming due to the large number of function evaluations needed in the 6D global optimization process.

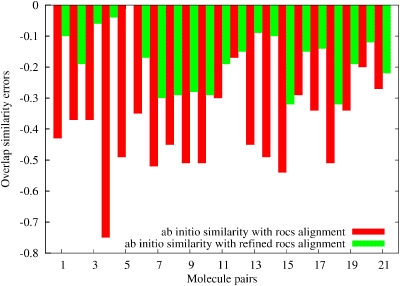
However, a unique combination of these two techniques or a combination with an existing more efficient alignment tool could lead to a very practical and also relatively accurate solution. Herein, we present an example as a first attempt in this direction. We have repeated all pair-wise alignments using the extremely efficient ROCS (Refs. ^{46, 47}) package from OpenEye and recalculated all ab initio overlap similarity indices at the resulting orientations. Note, that ROCS is using shape based alignment technique^{46, 48, 49} which is very close to the ASA scheme since both are using predefined s-type Gaussians to represent the atomic electron densities in molecules. The biggest difference is probably that shape based techniques use usually only one Gaussian function per atom for increasing the efficiency of the calculations. Other technical difference is that modern shape based alignment techniques performs only local optimizations starting from the four initial orientations defined by the eigenvectors of the multipole moment matrix which is significantly more practical and faster but less safe solution than performing the global optimization in 6D in our ASA based implementation.⁵⁰

Figure 8 shows the differences in the Carbo indices which indicate, at first blush, that using modern shape based alignment is a failed strategy for these examples. However, we recognized that the main difference between shape based and ab initio alignments is often in the translational variables. The refinement of shape based alignments in translational variables can be done extremely efficiently even using ab initio methods since our Fourier convolution technique solves it with one function call. Figure 8 also shows our results starting from the shape based alignments and refined with our ab initio translational alignment by using only one function call and without further optimization in the rotational angles. The improvements are very significant for most of the cases. The largest improvement involves the alignment of methylacrylate to 2,3-butadione (fifth entry in Fig. 8) where the shape based alignment difference is completely eliminated after refinement. Figures 910 show shape based and refined shape based alignment results for this molecular pair. We believe that it is possible to refine all shape based alignment solutions this way. Furthermore, the same Fourier convolution based refinement technique can be applied using the expandable contributions of the ASA approximate electronic densities. The advantage of this solution is that it does not require ab initio molecular orbitals or density matrices thus it can be applied effortlessly and efficiently for large databases of molecular geometries in conjunction with modern shape based alignments.

Figure 8.

Differences between ab initio Fourier transform overlap similarity indices using ROCS alignments and quantum mechanical translationally refined ROCS alignments.

Figure 9.

Shape based aligments of methylacrylate to 2,3-butadione.

Figure 10.

Refined shape based aligments of methylacrylate to 2,3-butadione.

We should highlight, that besides accurate pair wise molecular alignments, the most important potential of our new ab initio based numerical scheme is its ability to provide new explicit solution for docking problems, as described above in the Theory section. Other alignment techniques can deal with the docking problems only implicit way via similarity comparisons.

SUMMARY

A new first principle based rigid body alignment and docking solution was presented. The electron densities are efficiently expanded from precomputed ab initio results on numerical Fourier grids. The same grid was also used to decouple the optimizations in translational and rotational coordinates. Analytical transformations for the molecular orbitals were developed to eliminate interpolation errors due to the molecular rotations. Our alignment results for a small test sets of seven molecules are tested in details and compared with other published results. The necessary steps to extend our current alignment program to an explicit and ab initio based docking solution is also described.