Bayesian estimates of free energies from nonequilibrium work data in the presence of instrument noise

Abstract

The Jarzynski equality and the fluctuation theorem relate equilibrium free energy differences to nonequilibrium measurements of the work. These relations extend to single-molecule experiments that have probed the finite-time thermodynamics of proteins and nucleic acids. The effects of experimental error and instrument noise have not been considered previously. Here, we present a Bayesian formalism for estimating free energy changes from nonequilibrium work measurements that compensates for instrument noise and combines data from multiple driving protocols. We reanalyze a recent set of experiments in which a single RNA hairpin is unfolded and refolded using optical tweezers at three different rates. Interestingly, the fastest and farthest-from-equilibrium measurements contain the least instrumental noise and, therefore, provide a more accurate estimate of the free energies than a few slow, more noisy, near-equilibrium measurements. The methods we propose here will extend the scope of single-molecule experiments; they can be used in the analysis of data from measurements with atomic force microscopy, optical, and magnetic tweezers.

INTRODUCTION

A central endeavor of thermodynamics is the measurement of entropy and free energy changes, for which the principal experimental methods are based on the Clausius inequality.¹ One starts with a system equilibrated in one thermodynamic state, A, and then perturbs the system, following some explicit protocol, until the control parameter corresponds to a new thermodynamic state, B. If the temperature T of the surroundings is fixed, the change in entropy, ΔS=S_B−S_A, is related to the flow of heat Q into the system:

$$\Delta S\ge \beta ⟨Q⟩,$$ (1)

where β=1∕k_BT and k_B is the Boltzmann constant. Note that we are using natural units of entropy in which the change in entropy, ΔS, is dimensionless. Equivalently, the free energy difference ΔF=F_B−F_A=Δ⟨U⟩−ΔS∕β is related to the work W done on the system:

$$\Delta F\le ⟨W⟩.$$ (2)

Here, we use the sign convention ΔU=Q+W. The angular brackets indicate an average over many repetitions of the same experiment. In macroscopic systems, individual observations do not differ significantly from the mean. However, for a microscopic system, the fluctuations from the mean can be large and the inequality only holds on average (i.e., not for individual measurements).

It was recently discovered that equilibrium free energy differences can also be determined by measuring the work performed during irreversible transformations, using the Jarzynski^{12, 13, 14, 15} and work fluctuation relations.^{16, 17} These theoretical insights have been used to determine the unfolding free energy of a RNA hairpin^{2, 3, 4, 9, 18} from finite-time, nonequilibrium experiments, as described in Figs. 1 and 2. We consider a protocol (labeled as Λ) that starts with an equilibrated system and then transforms an external control parameter from an initial value A to a final value B in a finite time. (In the RNA hairpin unfolding experiments, the control parameter is the distance between the center of the optical trap and the center of the fixed bead.) This perturbation drives the system out of equilibrium. Once the protocol ends, the control parameter is fixed and the system can relax back to thermal equilibrium. One can also run the protocol in reverse, starting with a system equilibrated with the control parameter at B, and then transform the system through the reverse sequence of intermediate control parameters to A. We label this conjugate protocol $\tilde{\Lambda }$. Due to the reversibility of the microscopic dynamics, the probability P( W∣ΔF_Λ,Λ) of measuring a particular value of the work during protocol Λ is related to the work probability density of the conjugateprotocol $\tilde{\Lambda }$ by the following work fluctuation symmetry:^{2, 4, 16, 17, 19, 20, 21, 22}

$$\frac{P\left(\phantom{|}+W|\Delta F_{\Lambda },\Lambda \right)}{P\left(\phantom{|}-W|\Delta F_{\tilde{\Lambda }},\tilde{\Lambda }\right)}=e^{+\beta W-\beta \Delta F_{\Lambda }},$$ (3)

with ΔF_Λ$\left(=-\Delta F_{\tilde{\Lambda }}\right)$ the change in free energy associated with the change in the external control parameter in protocol Λ $\left(\tilde{\Lambda }\right)$. This relation immediately implies the Jarzynski equality^{12, 13, 14, 15, 16, 23}

$$⟨e^{-\beta W}⟩=\int dWP\left(\phantom{|}+W|\Delta F_{\Lambda },\Lambda \right)e^{-\beta W}=\int dWP\left(\phantom{|}-W|\Delta F_{\tilde{\Lambda }},\tilde{\Lambda }\right)e^{-\beta \Delta F}=e^{-\beta \Delta F}.$$ (4)

In other words, a Boltzmann weighted average of the irreversible work recovers the equilibrium free energy difference from a nonequilibrium transformation. The Clausius relation follows by an application of Jensen’s inequality, ln⟨exp(x)⟩≥⟨x⟩.

Figure 1.

Nonequilibrium work measurements for folding and unfolding a RNA hairpin (Ref. ²). A single RNA molecule is attached between two beads via hybrid DNA∕RNA linkers. One bead is captured in an optical laser trap that can measure the applied force on the bead. The other bead is attached to a piezoelectric actuator, which is used to irreversibly unfold and refold the hairpin (Refs. ², ³, ⁴, ⁵, ⁶, ⁷, ⁸, ⁹, ¹⁰, ¹¹).

Figure 2.

Typical force-extension curves in the unfolding (solid lines) and folding (dashed lines) of a 20 base pairs RNA hairpin. Different colors correspond to different unfolding-folding cycles. The rip in force observed around 15 pN corresponds to the cooperative unfolding∕folding transition. The area below the force-extension curve is equal to the mechanical work done on the RNA hairpin. Because the transformations are irreversible, the work performed varies from one unfolding or refolding measurement to the next. Drift effects observed in force-extension curves arise from different causes, including air currents, mechanical vibrations, and temperature changes.

Given the above thermodynamics preamble, we can rephrase the problem of measuring the free energy as follows: How do we calculate the most accurate, least biased estimate of the free energy given a finite number of irreversible work measurements?^{3, 17, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37} We consider both the statistical error due to limited data and, for real experiments, the additional error due to measurement noise. Furthermore, we may wish to simultaneously combine the data from multiple protocols connecting the same thermodynamic states.³⁸ For example, in the single-molecule experiment described in Fig. 1, the same RNA hairpin was unfolded at three different rates, with each data set providing a different compromise between statistical and experimental errors.

The Clausius relations are exact equalities only for infinitely slow, thermodynamically reversible transformations, where the irreversible dissipation is zero. A transformation that occurs in a finite time provides only an upper bound to the free energy and a lower bound to the entropy change. [Since entropy and free energy are state variables, the reverse transformation, from thermodynamic state B back to A, provides a lower (upper) bound to the same free energy (entropy) change.] One approach in analyzing irreversible transformations is to directly apply the Jarzynski relation.^{3, 13, 18, 39} However, this identity strictly holds only in the limit of an infinite number of repeated experiments. For a finite number of measurements, we again obtain an inequality that only holds on average,¹² and the free energy estimates tend to be strongly biased.^{25, 30, 32, 33, 36, 40, 41, 42, 43} Because the magnitude of the bias depends on the protocol, one cannot reliably combine data from different protocols.⁴⁴ Moreover, the Jarzynski relation is sensitive to measurement noise and variations in the experimental setup (e.g., heterogeneity in the attachments and variable length of tethers). Broadening of the work distribution leads to a bias in the estimated free energy since smaller work values contribute more than larger work values in the exponential average of Eq. 4.

Bennett⁴⁵ laid the foundations for the solution to this problem in his development of the acceptance ratio method for free energy perturbation calculations (a technique for computing free energy changes by simulating infinitely fast transformations). He realized that an optimal solution requires combining work measurements from both forward and reverse switches. The acceptance ratio method was later extended to finite-time switches,¹⁷ shown to a maximum likelihood free energy method,^{28, 46} related to the problem of logistic regression,^{28, 38, 47, 48} and extended to a network of thermodynamic states connected with many protocols.³⁸ In this paper, we develop a Bayesian formalism that extends these results to provide not only a reliable estimate of the free energy but also reliable estimates of the statistical uncertainty. In this formalism, it is straightforward to incorporate additional prior information about the experiment into the analysis. In particular, we show how to allow for experimental measurement noise. The magnitude of the noise can be determined from the data and an error-corrected free energy estimate recovered. We use this approach to reanalyze a recent experiment in which a single RNA hairpin was unfolded and refolded at three different rates using optical tweezers.²

POSTERIOR FREE ENERGY ESTIMATE

Formally, we require the probability that the free energy change ΔF has a particular value, given a collection of work measurements W, the protocol used for each measurement (either Λ or $\tilde{\Lambda }$), and the (fixed) temperature of the environment T. Initially, we consider the simplest case, in which there are two protocols that are conjugate to each other, so that the work distributions are related by the fluctuation relation Eq. 3. We also assume, for now, that the measurements are error-free.

The essential element in solving this problem is to treat both the work and the protocol as random variables that are uncorrelated from one observation to the next.²⁸ We rewrite the free energy probability density given a single measurement in terms of these variables using Bayes’ rules, P(A∣B)=P(B∣A)P(A)∕P(B),

$$\phantom{|}P\left(\Delta F_{\Lambda }\right|W,\Lambda )=\frac{\phantom{|}P\left(W,\Lambda \right|\Delta F_{\Lambda })P\left(\Delta F_{\Lambda }\right)}{P\left(W,\Lambda \right)}.$$ (5)

Since a priori the free energy could be positive or negative and of any magnitude, the prior distribution of free energy P(ΔF_Λ) can be reasonably taken as uniform (see Kass and Wasserman⁴⁹ for an in-depth discussion of priors). The denominator, which does not depend on ΔF_Λ, can be absorbed into a normalization constant.

The distribution P(W,Λ∣ΔF_Λ) is the final undetermined factor on the right-hand side of Eq. 5. In the absence of detailed knowledge about the work likelihood for the system under investigation, we should choose a maximally uninformative, system independent distribution. If the work were not conditional on the free energy, we could again assign a uniform distribution, since a single work measurement could be positive or negative and of any magnitude. However, we expect that the work will probably (but not certainly) be larger than that value of the free energy. Concretely, any work probability distribution must satisfy the work fluctuation symmetry [Eq. 3]. We can satisfy this constraint by first considering the symmetrized distribution $P(W,\Lambda \mid \Delta F_{\Lambda })+P(-W,\tilde{\Lambda }\mid \Delta F_{\tilde{\Lambda }})$. The work value in this averaged distribution has no a priori preference to be larger or smaller than the value of the free energy and, therefore, we can assign a maximally uninformative improper prior:

$$\phantom{|}P\left(W,\Lambda \right|\Delta F_{\Lambda })+P\left(\phantom{|}-W,\tilde{\Lambda }|\Delta F_{\tilde{\Lambda }}\right)=\text{const}$$ (6)

However, the work fluctuation relation implies that

$$\frac{\phantom{|}P(+W,\Lambda |\Delta F_{\Lambda })}{P\left(\phantom{|}-W,\tilde{\Lambda }|\Delta F_{\tilde{\Lambda }}\right)}=e^{\beta W-\beta \Delta F_{\Lambda }+M_{\Lambda }},$$ (7)

where $M_{\Lambda }=\ln P(\Lambda \mid \Delta F_{\Lambda })∕P(\tilde{\Lambda }\mid \Delta F_{\tilde{\Lambda }})$. It follows that

$$\phantom{|}P\left(W,\Lambda \right|\Delta F_{\Lambda })\propto \frac{1}{1+e^{-\beta W+\beta \Delta F_{\Lambda }-M_{\Lambda }}}.$$ (8)

Note that Eq. 6 is a constraint imposed only to derive a reasonable, uninformative free energy prior [Eq. 5]. Therefore, the constraint need not be respected in practice, else all work distributions would be logistic [Eq. 8]. The prior is used to describe our state of knowledge about the behavior of the system before we perform any work measurements. Once we have information about the work distribution, the posterior free energy distribution becomes peaked and will converge to a delta function centered at the correct value, assuming sufficient data and adequate sampling. When the posterior is sharply peaked, any smooth variation in the prior will not change the posterior distribution by any significant amount, and the exact form of the prior becomes largely irrelevant. Equation 8 was derived in Ref. 28 starting from a different set of assumptions.

Together with an uninformative free energy prior, we finally obtain

$$\phantom{|}P\left(\Delta F_{\Lambda }\right|W,\Lambda )\propto P\phantom{|}\left(W,\Lambda \right|\Delta F_{\Lambda })\propto f\left(\beta W-\beta \Delta F_{\Lambda }+M_{\Lambda }\right),$$ (9)

where f(x) is the logistic function (Fig. 3), the cumulative distribution function of the standard logistic distribution (see the Appendix0, Fig. 4)

$$f\left(x\right)=\frac{1}{1+e^{-x}}.$$ (10)

Essentially, each measurement of the work provides a soft upper bound to the free energy change. Measurements made on the conjugate protocol provide soft lower bounds to the same free energy. Therefore, combining measurements from conjugate protocol pairs provides reliable but fuzzy free energy bounds. This is in contrast to the Clausius inequality [Eq. 2] where the average work provides a hard bound to the free energy change.

Figure 3.

The standard logistic function, f(x)=1∕(1+e^−x).

Figure 4.

The approximation of the standard logistic distribution by the Gaussian distribution with zero mean and standard deviation $\sqrt{8∕\pi }$.

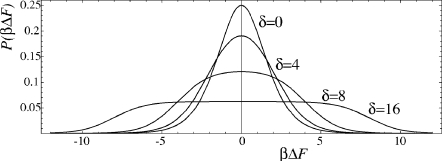
Figure 5 illustrates the posterior distribution resulting from combining two work measurements, one from each of a conjugate protocol pair, where the measured values are βW=±1∕2δ. If the work values are widely separated, then the posterior free energy distribution is broad and flat. We only obtain a tight constraint on the free energy if the separation is less than about 4k_BT. The minimum uncertainty for a single pair of measurements is σ≈1.8k_BT, which occurs when δ=0.

Figure 5.

Posterior free energy given two work measurements, one from each of two conjugate protocols with values βW=±1∕2δ. The posterior variance, π²∕3+δ²∕12, is minimized when the rectified work variables coincide and increases quadratically with separation.

Assuming that each measurement of the work is independent, we can combine measurements by multiplying the separate posterior distributions together. So far, we have been considering a single pair of conjugate protocols switching between two thermodynamic states. However, it was recently demonstrated that we can combine measurements from many different protocols connecting many different thermodynamic states in a network of transformations.³⁸ Each measurement provides a single soft constraint [Eq. 9], which we can combine by multiplying the different posterior distributions:

$$\phantom{|}P\left(\mathbf{F}\right|\mathbf{W},\mathbf{\Lambda })=\frac{1}{\mathcal{C}}\prod _{k=1}^{N}f\left(\beta W_k-\beta \Delta F_{{\Lambda }_k}+M_{{\Lambda }_k}\right),$$ (11)

where W_k is the work measured in the kth experiment, performed with protocol Λ_k, ΔF_Λk is the free energy change associated with that protocol, C is a normalization constant, and N is the total number of measurements. In the simplest case, we have only a single conjugate protocol pair, forward and reverse. In general, we can have many different protocols (for example, pulling a molecule apart at different loading rates), and different protocols could connect different thermodynamic states.³⁸ In the equation above, F={F₁,F₂,F₃,…} are the free energies of the initial and final states of these transformations. At least one free energy F_i is fixed at zero, or some other convenient reference point, since only differences in free energy are significant.

The M_Λk terms compensate for a difference in the probability of observing a forward or reverse protocol from a conjugate protocol pair. In the absence of detailed prior information about the work distributions, it is best to pick each member of a conjugate pair equally often.⁴⁵ However, the difficulties of real world experiments may result in unequal numbers of forward and reverse measurements. In such cases, we can estimate a reasonable value for M_Λk from the number of observations, N_Λ, obtained from each protocol:

$$M_{\Lambda }=\text{ln}\frac{\phantom{|}P\left(\Lambda \right|\Delta F_{\Lambda })}{P\left(\phantom{|}\tilde{\Lambda }|\Delta F_{\tilde{\Lambda }}\right)}\approx \text{ln}\frac{N_{\Lambda }+1}{N_{\tilde{\Lambda }}+1}.$$ (12)

The additional “+1” is a pseudocount which regularizes the frequency estimate. It can be justified as a Laplace prior on the probabilities.^{50, 51} Note that without this regularization, Eq. 12, and thus also Eq. 11, would become invalid in the single sample limit. With the addition of the pseudocount, the probability distribution in Eq. 11 may still only produce one-sided bounds (for example, when there is no protocol that ends in a certain state, one has, at best, an upper bound for the free energy of that state). However, we could recover a finite free energy posterior distribution if we were to use a more informative free energy prior in Eq. 11.

The experimental measurements of the work values can typically be considered to be uncorrelated. However, when the measurements or simulation results are correlated, the maximum likelihood or Bayesian estimates may need to be modified to result in an optimal estimate of the free energy.⁴⁸ In the absence of a general-purpose formulation for correlated work measurements, the estimators discussed in this paper are likely to underestimate the errors.

The Bayesian free energy posterior is an optimal estimate in the sense that it uses all of the available data and makes the fewest possible assumptions. We can, in principle, improve the estimate by incorporating additional information either by using more informative priors or by adding additional assumptions, for example, by assuming that the work distribution is smoothly varying,⁴⁵ or that it can be parametrized in terms of a particular functional form.⁵²

In many practical cases, the posterior distribution of ΔF quickly converges to a normal one as a consequence of the central limit theorem. We can summarize this posterior distribution with a point estimate and reasonable error bounds, for example, the posterior mean free energy and 95% confidence intervals. The posterior mean will coincide with the maximum likelihood, and the confidence interval will be ±2 standard deviations.

EXPERIMENTAL ERRORS

The preceding analysis does not include the possibility of experimental errors, an omission that we now address, since real experiments are not ideal and real measurements can be inaccurate.

We initially assume that the instrument error can be adequately described as additive white noise with zero mean and standard deviation σ. Since we do not know the magnitude of the noise, we estimate the joint distribution of the free energy and the noise, then integrate out the noise to obtain a final free energy estimate:

$$\phantom{|}P\left(\Delta F_{\Lambda }\right|W,\Lambda )=\int P\phantom{|}\left(\Delta F_{\Lambda },\sigma \right|W,\Lambda )d\sigma .$$ (13)

Let us write W=w+ϵ, where W is the observed work value, w is the true work, and ϵ is the measurement error. Using Eq. 9, we get

$$\phantom{|}P\left(\Delta F_{\Lambda },\sigma \right|W,\Lambda )\propto {\int }_{-\infty }^{+\infty }f\left(\beta W-\beta ϵ-\beta \Delta F_{\Lambda }+M_{\Lambda }\right)\mathcal{N}\left(ϵ;0,\sigma \right)dϵ.$$ (14)

Here, N(x;μ,σ) is a Gaussian distribution with mean μ and standard deviation φ [see Eq. A3].

This convolution of a logistic function and a Gaussian distribution generates a new sigmoidal function, illustrated in Fig. 6. This function does not have a simple closed form, but fortunately, it can be closely approximated by a reparametrized logistic distribution,

$$\phantom{|}P\left(\Delta F_{\Lambda },\sigma \right|W,\Lambda )\propto f\left(\frac{1}{\gamma }\left(\beta W-\beta \Delta F_{\Lambda }+M_{\Lambda }\right)\right),$$ (15)

where the parameter $\gamma =\sqrt{1+\pi {\beta }^2{\sigma }^2∕8}$ essentially acts as a correction factor to the work fluctuation symmetry. (The mathematical details are given in the Appendix0.)

Figure 6.

The approximation of the sigmoidal function g(x;α,σ) [Eq. A1] by the logistic function f(x;γ)=1∕[1+exp(−x∕γ)], where $\gamma =\sqrt{1+\pi {\sigma }^2∕8}$ [Eq. A7]. The absolute difference between the functions is always less than 0.02.

Having proceeded this far, we no longer need to assume that the errors are a result of white noise. Instead, we will treat γ as the principal experimental error factor directly, without reference to an explicit error model or to the standard deviation of the noise, σ. For example, a systematic miscalibration of the work measurement or an incorrect thermostat would also result in a nonunit γ. In such cases, γ could be less than 1. Therefore, we allow γ to be any positive number. We introduce an uninformative prior for γ, P(γ)=1∕γ. This distribution is scale invariant and follows given only that γ is positive and a priori of unknown magnitude.⁵⁰ We can now average over the free energy to obtain the posterior distribution of the error correction factor γ or average over the error correction factor to obtain the posterior free energy estimate corrected for instrument error,

$$\phantom{|}P\left(\Delta F_{\Lambda }\right|W,\Lambda )=\frac{1}{{\mathcal{C}}^{\prime }}{\int }_0^{+\infty }\frac{1}{\gamma }\prod _{k}f\left(\frac{1}{\gamma }\left(\beta W_k-\beta \Delta F_{\Lambda }+M_{\Lambda }\right)\right)d\gamma ,$$ (16)

where C^′ is a normalization constant. Note that instrument error, and thus, the distribution of γ, will vary with the protocol. One could construct a complex hierarchical prior⁴⁸ for the experimental error factors that would feed information about the typical scale of the errors from one protocol to the next. In this work, we find it sufficient to estimate γ independently for each protocol and obtain a final posterior:

$$\phantom{|}P\left(F\right|W,\Lambda )=\prod _{\Lambda }P\left(\phantom{|}\Delta F_{\Lambda }|W,\Lambda \right).$$ (17)

Here, as in Eq. 11, F={F₁,F₂,F₃,…} are the free energies of the initial and final thermodynamic states.

Another potential source of errors arises from unintended variations in the experimental procedure from one measurement to the next. For example, we may intend to forcibly unfold a RNA hairpin in a particular time, but each experimental run may be slightly faster or slower than another. Instead of an experiment being described by a single protocol, each measurement is made with a similar but slightly different procedure (e.g., due to hysteresis effects of the actuators on the mechanical response). However, if a protocol variation has the same probability both forward and reverse, then the factor M_Λ [Eq. 12] does not change. Consequently, if the variations in protocol are statistically the same for the conjugate forward and reverse protocol pairs, then that variation has no effect on the free energy estimate.

APPLICATION AND DISCUSSION

Figure 7 shows the result of applying the Bayesian free energy estimate to data from the single-molecule RNA pulling experiments reported in Ref. 2, both with and without noise correction. This data set is particularly useful to illustrate the previous analysis, since it represents three distinct protocols; i.e., the same RNA hairpin is unfolded at three different rates: slow, medium, and fast. The free energy change is the same in each case; we can see that this is qualitatively true by noting that the forward-reverse work histograms all cross at roughly the same value of the work. The experimental noise is expected to accumulate during a single experiment, and so we expect the data from the fastest pulling rate to be contaminated with the least measurement error. This is indeed what the Bayesian error analysis finds: γ approaches 1 as the pulling rate increases.

Figure 7.

(a) Histograms of work measurements for folding and unfolding an RNA hairpin at three different rates. Observations are binned into integers centered at 1k_BT intervals. These data correspond to Fig. 2 of Collin et al. (Ref. ²) Note that Eq. 3 predicts that the folding and unfolding work distributions cross at the free energy change. (b) The posterior distribution of the error correction factor γ [Eq. 16]. (c) Posterior free energy derived from the data in (a), both with [solid line, Eq. 16] and without [dashed line, Eq. 11] correction for measurement noise. Notice that the correction is substantial for the slowest experiment (1.5 pN∕s) and minor for the intermediate rate, and the corrected and uncorrected posteriors are indistinguishable (at this scale) for the fastest rate. The most reliable free energy estimate is obtained by combining the three separate noise-corrected free energy posterior distributions.

Qualitatively, the effect of instrument noise is to broaden both the forward and reverse work distributions. This broadening tends not to significantly change the crossing point, but it does increase the overlap between the conjugate distributions. Therefore, ironically, the instrument error does not greatly change the free energy estimate, but it does significantly (and erroneously) reduce the calculated error bars. Fortunately, the noise invalidates the fluctuation theorem, and the magnitude of that violation allows us to estimate the magnitude of the instrument errors and to extract noise-corrected free energy estimates with meaningful error bounds.

A useful feature of this error analysis is that we can use the correction parameter γ as a measure of how well the experiments have confirmed the work fluctuation relation [Eq. 3]. For the fastest pulling, highest quality data, we find that γ=1±0.14; in other words, the fluctuation relation is confirmed to within 14% at the 95% confidence limit. Although more accurate constraints can be obtained by performing experiments on systems with simple potentials,^{39, 53, 54, 55, 56, 57} this is the best available experimental data for irreversibly switching a complex system.^{2, 58} We can also use the interrelation between the noise and the correction factor $(\gamma =\sqrt{1+\pi {\beta }^2{\sigma }^2∕8})$ to estimate the measurement accuracy needed to improve this result. For example, if we wish to confirm the fluctuation relation to better than 1%, then the work must be measured to better than ≈1∕4k_BT accuracy, which is well within the limits of modern optical tweezer instruments.

The quantitative effect of the noise corrections to ΔF can be seen in Fig. 7c and Table 1. The noise correction makes a substantial difference to the free energy confidence interval for the slowest data, but very little difference to the posterior mean free energy or the error bounds for the faster data. Note that the free energy considered in this analysis includes unfolding the RNA hairpin and stretching the DNA∕RNA handles; deconvoluting the contributions of the handles introduces additional uncertainty not considered here.^{2, 3, 18} Having applied the instrument noise correction, we can safely combine the posterior free energy estimates from the three different protocols to obtain a combined estimate of ΔF=110.1±k_BT. This result is a substantial improvement over the best, single protocol, maximum likelihood estimate, ΔF=110.2±0.6k_BT, extracted from the same data.²

Table 1.

Summary of results graphed in Fig. 7. N_U and N_R: number of unfolding and refolding work measurements at each pulling rate, respectively. ΔF: posterior mean free energy estimate with 95% confidence intervals, both corrected and uncorrected for measurement error. γ: posterior mean estimate of the noise correction factor, with 95% confidence intervals.

	NU	NR	ΔF(uncorrected)	ΔF(corrected)	γ
1.5 pN/s	127	129	109.8±0.4	109.8±0.8	2.70±1.00
7.5 pN/s	384	383	110.3±0.3	110.3±0.3	1.11±0.17
20 pN/s	699	696	110.0±0.3	110.0±0.3	1.00±0.14
Combined				110.1±0.2

In summary, we have presented a Bayesian formalism for estimating free energy changes from nonequilibrium work measurements. The formalism compensates for instrument noise and combines results from multiple experimental protocols. The method is widely applicable and could be used in the analysis of single-molecule experimental data from optical tweezers, atomic force microscopy, or magnetic tweezers. Together with advances in single-molecule traps and use of multiple experimental setups (e.g., changing bead sizes, trap power, or the length of the handles), it will aid in extending the scope of single-molecule experiments.

APPENDIX: APPROXIMATE CONVOLUTION OF A LOGISTIC FUNCTION WITH A GAUSSIAN DISTRIBUTION

We are interested in the function

$$g\left(x;\alpha ,\sigma \right)={\int }_{-\infty }^{+\infty }f\left(x+ϵ;\alpha \right)\mathcal{N}\left(ϵ;0,\sigma \right)dϵ,$$ (A1)

the convolution of a logistic (or Fermi) function

$$f\left(x;\alpha \right)=\frac{1}{1+e^{-x/\alpha }}=\frac{1}{2}+\frac{1}{2}\text{tanh}\frac{x/\alpha }{2},$$ (A2)

with a Gaussian (or normal) distribution with zero mean and standard deviation σ:

$$\mathcal{N}\left(x;\mu ,\sigma \right)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\text{exp}\left(-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}\right).$$ (A3)

The function g(x;α,σ) does not have a simple, closed form. However, as is illustrated in Fig. 6, it can be reasonably approximated by a reparametrized logistic function:

$$g\left(x;\alpha ,\sigma \right)\approx f\left(x;\gamma \right),$$ (A4)

where γ is a function of α and σ. We fix γ by requiring equality of the derivative at the origin, since, for our purposes, it is more important to minimize the errors around the origin than elsewhere. The value of g(x;α,σ) at the origin is 1∕2, the same as f(0;γ). Note that

$${\phantom{|}\frac{d}{dx}f\left(x;\gamma \right)|}_{x=0}={\phantom{|}\frac{1}{2\gamma +2\gamma \text{cosh}\left(x/\gamma \right)}|}_{x=0}=\frac{1}{4\gamma },$$ (A5)

and, therefore,

$${\gamma }^{-1}={\phantom{|}4\frac{d}{dx}g\left(x;\alpha ,\sigma \right)|}_{x=0}=4{\int }_{-\infty }^{+\infty }\left({\phantom{|}\frac{d}{dx}f\left(x+ϵ;\alpha \right)|}_{x=0}\right)\mathcal{N}\left(ϵ;\sigma \right)dϵ=4{\int }_{-\infty }^{+\infty }\left(\frac{1}{2\alpha +2\alpha \text{cosh}ϵ/\alpha }\right)\mathcal{N}\left(ϵ;\sigma \right)dϵ.$$ (A6)

The expression inside the bracket is a logistic distribution, which is closely approximated by the Gaussian distribution $\mathcal{N}(ϵ;0,\alpha \sqrt{8∕\pi })$ (see Fig. 4). These parameters ensure that the two distributions agree exactly at the origin. Therefore, our problem reduces to a straightforward Gaussian integral:

$${\gamma }^{-1}\approx 4{\int }_{-\infty }^{+\infty }\mathcal{N}\left(ϵ;0,\alpha \sqrt{\frac{8}{\pi }}\right)\mathcal{N}\left(ϵ;0,\sigma \right)dϵ,$$ (A7)

$$\gamma =\sqrt{1+\frac{\pi }{8{\alpha }^2}{\sigma }^2}.$$

For α=−1∕β, we recover the case of white noise discussed in the main text.