Diffusion in linear porous media with periodic entropy barriers: A tube formed by contacting spheres

Abstract

The problem of transport in quasi-one-dimensional periodic structures has been studied recently by several groups [D. Reguera et al., Phys. Rev. Lett.96, 130603 (2006); P. S. Burada et al., Phys. Rev. E75, 051111 (2007); B. Q. Ai and L. G. Liu, ibid.74, 051114 (2006); B. Q. Ai et al., ibid.75, 061126 (2007); B. Q. Ai and L. G. Liu, J. Chem. Phys.126, 204706 (2007); 128, 024706 (2008); E. Yariv and K. D. Dorfman, Phys. Fluids19, 037101 (2007); N. Laachi et al., Europhys. Lett.80, 50009 (2007); A. M. Berezhkovskii et al., J. Chem. Phys.118, 7146 (2003); 119, 6991 (2003)]. Using the concept of “entropy barrier” [R. Zwanzig, J. Phys. Chem.96, 3926 (1992)] one can classify such structures based on the height of the entropy barrier. Structures with high barriers are formed by chambers, which are weakly connected with each other because they are connected by small apertures. To escape from such a chamber a diffusing particle has to climb a high entropy barrier to find an exit that takes a lot of time [I. V. Grigoriev et al., J. Chem. Phys.116, 9574 (2002)]. As a consequence, the particle intrachamber lifetime τ_esc is much larger than its intrachamber equilibration time, τ_rel, τ_esc⪢τ_rel. When the aperture is not small enough, the intrachamber escape and relaxation times are of the same order and the hierarchy fails. This is the case of low entropy barriers. Transport in this case is analyzed in the works of Schmid and co-workers, Liu and co-workers, and Dorfman and co-workers, while the work of Berezhkovskii et al. is devoted to diffusion in the case of high entropy barriers.

In this paper we study diffusion in a tube formed by periodic contacting spherical cavities of radius R (Fig. 1) over the entire range of the entropy barrier height. On times when the mean squared displacement of a diffusing particle is much greater than the tube period l, the particle motion can be characterized by an effective diffusion constant D_eff, which is smaller than the particle diffusion constant D in space with no constrains. When the tube period increases, the radius a of the circular aperture connecting neighboring cavities decreases, $a=\sqrt{R^2-(l^2∕4)}$, 0<l<2R. As a result, the entropy barrier increases, and the ratio D_eff∕D gets smaller. One can find D_eff analytically for high and low entropy barriers. For high entropy barriers D_eff has been derived in Ref. 1. Here we derive D_eff for low entropy barriers. We also run Brownian dynamics simulations to find D_eff as a function of the ratio a∕R and to compare the numerical results with those predicted by different analytical expressions. The major goal of our analysis is to establish the range of applicability of different approximate expressions for D_eff.

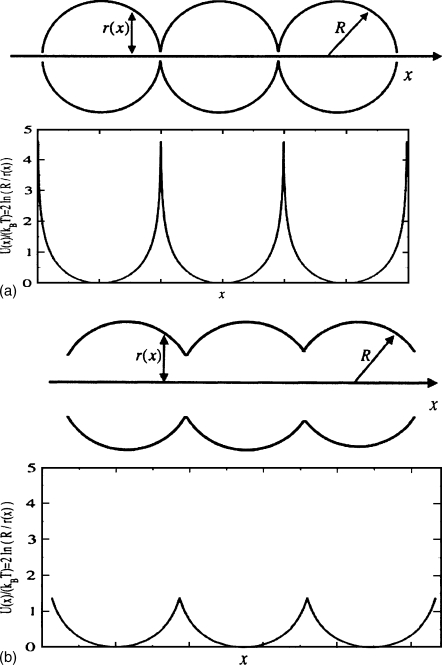
Figure 1.

Entropy potential for tubes with (a∕R)=0.1 [panel (a)] and (a∕R)=0.5 [panel (b)]. The dimensionless heights of the entropy barriers are ΔU∕(k_BT)=2 ln 10=4.6 [panel (a)] and ΔU∕(k_BT)=2 ln 2=1.4 [panel (b)].

For high entropy barriers (small apertures, a⪡R) Berezhkovskii, Zitserman, and Shvartsman (BZS) derived the following expression for the effective diffusion constant:

$$D_{\mathrm{eff}}^{\mathrm{BZS}}=\frac{6Da}{\pi R}.$$ (1)

In the opposite limiting case of low entropy barrier, i.e., when (R−a)⪡R, one can find D_eff by approximately reducing the three-dimensional problem of diffusion in the tube of varying cross section to an effective one-dimensional problem of diffusion along the tube axis. Significant progress in understanding the reduction has been made in recent years.^{2, 3, 4, 5} Directing the x-axis along the center line of the tube, one can write an approximate one-dimensional effective diffusion equation as

$$\frac{\partial c(x,t)}{\partial t}=\frac{\partial }{\partial x}\left\{D\left(x\right)A\left(x\right)\frac{\partial }{\partial x}\left[\frac{c(x,t)}{A\left(x\right)}\right]\right\},$$ (2)

where D(x) is a position-dependent diffusion coefficient, A(x)=π[r(x)]² is the cross-section area of the tube of radius r(x), and c(x,t) is the effective one-dimensional concentration of the diffusing particles at given x, which is related to the three-dimensional concentration C(x,y,z,t) by

$$c(x,t)={\int }_{A\left(x\right)}C(x,y,z,t)dydz.$$ (3)

Equation 2 with position-independent diffusion coefficient, D(x)=D, is known as the Fick–Jacobs (FJ) equation.⁶ Zwanzig (Zw) derived an expression for D(x) assuming that the tube radius r(x) is a slowly varying function, ∣r^′(x)∣⪡1,²

$$D_{\mathrm{Zw}}\left(x\right)=\frac{D}{1+r^{\prime }{\left(x\right)}^2∕2}.$$ (4)

Reguera and Rubí (RR) generalized this result.³ Based on heuristic arguments they suggested

$$D_{\mathrm{RR}}\left(x\right)=\frac{D}{\sqrt{1+r^{\prime }{\left(x\right)}^2}}.$$ (5)

Equation 2 can be considered as the Smoluchowski equation for diffusion in the entropy potential U(x) defined as

$$U\left(x\right)=-k_{B}T\ln \frac{A\left(x\right)}{A\left(x_0\right)},$$ (6)

where k_B and T are the Boltzmann constant and the absolute temperature, and U(x) at x=x₀ is taken to be zero, U(x₀)=0. Potentials U(x) with high and low entropy barriers are shown in Fig. 1. Since our system is periodic, it follows from Eqs. 4, 5, 6 that both U(x) and D(x) are periodic functions of x, U(x+l)=U(x) and D(x+l)=D(x). Therefore, we can find D_eff using the Lifson–Jackson formula,⁷ which is an exact result for the one-dimensional Smoluchowski equation with periodic U(x) and D(x). According to this formula D_eff is given by

$$D_{\mathrm{eff}}^{-1}=⟨{\left[D\left(x\right)A\left(x\right)\right]}^{-1}⟩⟨A\left(x\right)⟩,$$ (7)

where $⟨f\left(x\right)⟩=(1∕l){\int }_0^{l}f\left(x\right)dx$. We use Eq. 7 to obtain three different expressions for D_eff.

Assuming that D(x)=D we find $D_{\mathrm{eff}}^{\mathrm{FJ}}$, which corresponds to the FJ equation

$$\frac{D}{D_{\mathrm{eff}}^{\mathrm{FJ}}}=⟨\frac{1}{A\left(x\right)}⟩⟨A\left(x\right)⟩=\frac{2+{(a∕R)}^2}{6\sqrt{1-{(a∕R)}^2}}\ln \frac{1+\sqrt{1-{(a∕R)}^2}}{1-\sqrt{1-{(a∕R)}^2}}.$$ (8)

Using D_Zw(x) [Eq. 4], we obtain $D_{\mathrm{eff}}^{\mathrm{Zw}}$ given by

$$\frac{D}{D_{\mathrm{eff}}^{\mathrm{ZW}}}=\frac{D}{D_{\mathrm{eff}}^{\mathrm{FJ}}}+\frac{1}{2}⟨\frac{r^{\prime }{\left(x\right)}^2}{A\left(x\right)}⟩⟨A\left(x\right)⟩=\frac{2+{(a∕R)}^2}{12}[\frac{1}{{(a∕R)}^2}+\frac{3}{2\sqrt{1-{(a∕R)}^2}}\ln \frac{1+\sqrt{1-{(a∕R)}^2}}{1-\sqrt{1-{(a∕R)}^2}}].$$ (9)

Respectively, D_RR(x) in Eq. 5 leads to $D_{\mathrm{eff}}^{\mathrm{RR}}$ given by

$$\frac{D}{D_{\mathrm{eff}}^{\mathrm{RR}}}=⟨\frac{\sqrt{1-r^{\prime }{\left(x\right)}^2}}{A\left(x\right)}⟩⟨A\left(x\right)⟩=\frac{2+{(a∕R)}^2}{3(a∕R)}.$$ (10)

The results in Eqs. 8, 9, 10 were obtained assuming that the entropy barrier is low and the difference R−a is small compared to R. It is interesting to compare the behavior predicted by these equations in the opposite limit when a→0 and the entropy barrier is high, with $D_{\mathrm{eff}}^{\mathrm{BZS}}$ in Eq. 1, which is asymptotically exact in this limit. Comparison shows that $D_{\mathrm{eff}}^{\mathrm{FJ}}∕D_{\mathrm{eff}}^{\mathrm{BZS}}\to \infty$, $D_{\mathrm{eff}}^{\mathrm{Zw}}∕D_{\mathrm{eff}}^{\mathrm{BZS}}\to 0$, $D_{\mathrm{eff}}^{\mathrm{RR}}∕D_{\mathrm{eff}}^{\mathrm{BZS}}\to \pi ∕4$. Thus, $D_{\mathrm{eff}}^{\mathrm{RR}}$ in Eq. 10 is a good candidate for a unique formula that covers the entire range of a∕R, 0<a∕R<1, while both $D_{\mathrm{eff}}^{\mathrm{FJ}}$ and $D_{\mathrm{eff}}^{\mathrm{Zw}}$ fail as a∕R→0.

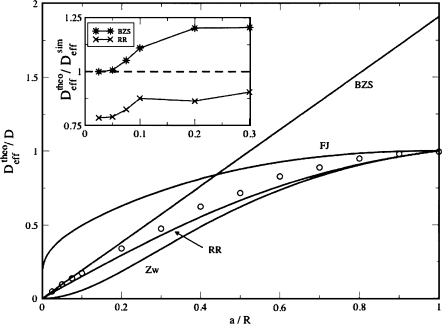
We compare different expressions for D_eff [Eqs. 1, 8, 9, 10], with $D_{\mathrm{eff}}^{\mathrm{sim}}$ found in Brownian dynamics simulations. Numerically we compute the mean squared displacement along the channel axis of 2.5×10⁴ particles as a function of time, ⟨Δx²(t)⟩=⟨[x(t)−x(0)]²⟩, assuming that the particle starting points are uniformly distributed over the cavity. We determine $D_{\mathrm{eff}}^{\mathrm{sim}}$ from the long-time behavior of ⟨Δx²(t)⟩. The results presented in Fig. 2 show that $D_{\mathrm{eff}}^{\mathrm{sim}}$ is in excellent agreement with $D_{\mathrm{eff}}^{\mathrm{BZS}}$ for a∕R<0.1, reasonably well described by both $D_{\mathrm{eff}}^{\mathrm{BZS}}$ and $D_{\mathrm{eff}}^{\mathrm{RR}}$ for a∕R=0.2, and close to $D_{\mathrm{eff}}^{\mathrm{RR}}$ for a∕R⩾0.3.

Figure 2.

Effective diffusion constants found numerically (circles) and predicted by Eqs. 1, 8, 9, 10 (solid curves). The inset shows the ratio of $D_{\mathrm{eff}}^{\mathrm{BZS}}$ and $D_{\mathrm{eff}}^{\mathrm{RR}}$ predicted by Eqs. 1, 10, respectively, to $D_{\mathrm{eff}}^{\mathrm{sim}}$ from (a∕R)=0.025 to (a∕R)=0.3.

To summarize, $D_{\mathrm{eff}}^{\mathrm{RR}}$ in Eq. 10 found on the basis of the generalized Fick–Jacobs equation [Eq. 2] with D(x) given by the RR formula [Eq. 5] provides a reasonably good approximation for D_eff over the entire range of the size of the aperture. For small windows (high entropy barriers) $D_{\mathrm{eff}}^{\mathrm{sim}}$ found numerically is in excellent agreement with $D_{\mathrm{eff}}^{\mathrm{BZS}}$ in Eq. 1. We hope that the results of our analysis will be of use when interpreting experiments on controlled drug release and migration in porous media.