Magnetization transfer proportion: a simplified measure of dose response for polymer gel dosimetry

Abstract

The response to radiation of polymer gel dosimeters has most often been described by measuring the nuclear magnetic resonance transverse relaxation rate as a function of dose. This approach is highly dependent upon the choice of experimental parameters, such as the echo spacing time for Carr-Purcell-Meiboom-Gill-type pulse sequences, and is difficult to optimize in imaging applications where a range of doses are applied to a single gel, as is typical for practical uses of polymer gel dosimetry. Moreover, errors in computing dose can arise when there are substantial variations in the radiofrequency (B₁) field or resonant frequency, as may occur for large samples. Here we consider the advantages of using magnetization transfer imaging as an alternative approach and propose the use of a simplified quantity, the magnetization transfer proportion (MTP), to assess doses. This measure can be estimated through two simple acquisitions and is more robust in the presence of some sources of system imperfections. It also has a dependence upon experimental parameters that is independent of dose, allowing simultaneous optimization at all dose levels. The MTP is shown to be less susceptible to B₁ errors than are CPMG measurements of R₂. The dose response can be optimized through appropriate choices of the power and offset frequency of the pulses used in magnetization transfer imaging.

1. Introduction

Polymer gel dosimeters comprise an aqueous matrix in which various monomers are uniformly distributed. The monomers convert to polymers upon irradiation, so that various local properties are modified in a dose-dependent fashion. The resulting spatial pattern of dose deposition can be read out using one of several methods, including magnetic resonance imaging (MRI) (Maryanski et al 1993) and optical (Gore et al 1996) and X-ray computed tomography methods (Hilts et al 2000). Most practical applications to date have used MRI, and the dose response has usually been described in terms of the transverse relaxation rate, R₂ (Maryanski et al 1994). Alternative imaging metrics have also been investigated, including magnetization transfer (MT) imaging (Lepage et al 2002). MT imaging is sensitive to the exchange of magnetization between proton pools in a sample that results from chemical exchange or through-space dipolar interactions (Wolff and Balaban 1989, Henkelman et al 1993). In a simple model that may be appropriate for polymer gels, two distinct proton populations are considered to be coupled together. One pool corresponds to the mobile solvent protons, and a second pool corresponds to hydrogen nuclei that are relatively immobile, associated with the polymer in some way, and have different relaxation times or different resonant frequencies because of chemical-shift effects. The integrated signal from both pools is measured after the application of an appropriate saturating RF pulse at a frequency that is off-resonance to the free water. The magnetization transfer ratio (MTR) has often been used as an index of the degree of MT. It is defined as

$$\mathrm{MTR}=\frac{M_0-M_{\mathrm{sat}}}{M_0},$$ (1)

where M₀ is the signal of the sample acquired without off-resonance saturation and M_sat is the signal acquired with saturation. Gel dosimetry measurements of MT have used slightly different assessments of the magnetization measured with and without saturation. For example, De Deene et al (2006b) proposed the ‘true magnetization transfer ratio’ which incorporates the direct effect of the saturating irradiation on the free water. This ratio is given by

$$\mathrm{MT}=\frac{M_{{\mathrm{H}}_2\mathrm{O}}-M_{\mathrm{sat}}}{M_0}=\mathrm{MTR}-\frac{M_{\mathrm{dir}}}{M_0},$$ (2)

where M_H2O is the experimentally measured magnetization of water after a saturation pulse has been applied and M_dir is described by the authors of the work to be the ‘direct effect contribution which is due to the saturation of the water proton pool’. Other studies have published values for the specific parameters that contribute to MT for different types of polymer gel dosimeters as a function of dose (Gochberg et al 2001, 2003).

The aim of this paper is to provide a theoretical and experimental basis for using a slightly different ratio of MT measurements for gel dosimetry that results in a linear response of this quantity with dose in the range of 0–20 Gy. This approach will be compared to the more traditional transverse relaxation rate measurement for dosimetry gels. In particular, the relative sensitivities of the MT and transverse relaxation dose responses to the effects of imperfections in imaging, including errors in the amplitudes of the radiofrequency pulses used, are evaluated.

2. Theory

2.1. Dose response

Traditional transverse relaxation rate measurements of polymer gel dosimeters are performed using spin–echo imaging. Assuming that the system is not saturated (i.e. TR ≫ T₁), the signal at echo time TE is given by

$$S=M_0{\mathrm{e}}^{-R_2\mathrm{TE}}.$$ (3)

In a region of linear dose response,

$$R_2=R_{2,0}+\alpha D,$$ (4)

where α and R_2,0 are the slope and intercept, respectively. The signal difference generated by any small dose increment ΔD is then

$$\Delta S=-\alpha \cdot \mathrm{TE}\cdot S\cdot \Delta D.$$ (5)

This has a maximum value when TE = 1/R₂, when the signal change is

$$\Delta S=-0.37\frac{\alpha }{R_{2,0}+\alpha D}\Delta D\cdot M_0,$$ (6)

and decreases with dose D. For the most sensitive PAG and MAGIC gels, α is 0.19 and 0.503, and R_2,0 is 0.9 and 7.653, respectively (De Deene et al 2006a, Luci et al 2007). Thus, compared to the signal of an unirradiated dosimeter, a dose of 1 Gy will decrease the gel MRI signal by 0.064M₀ and 0.151M₀ initially for PAG and MAGIC gels, respectively, but this decreases to only 0.011M₀ and 0.015M₀, respectively, when comparing doses at 20 Gy, even at the optimal echo spacing for that dose. The situation is further compromised because R₂ may vary throughout the gel so no single choice of TE is then optimal for all regions. Thus, even without considering errors inherent in calculating values of R₂ from multiple echo data, the signal changes available for discriminating regions of similar doses are small. A further complication occurs in multi-echo sequences, which can produce maps of R₂ from a single acquisition but are sensitive to RF and static field inhomogeneities (Majumdar et al 1986a, 1986b), and the precise value of T₂ may depend on the echo spacing (Baldock et al 2001).

A simple method using only two images, and from which a quantity that varies approximately linearly with dose can be easily extracted, would be attractive. A simple MT-sensitive imaging sequence is one that incorporates an off-resonance saturating pulse immediately prior to imaging. The off-resonance pulse can be designed to saturate the immobile or chemically shifted protons and to not affect the free water resonance directly. MT effects alone then cause the signal from the mobile protons to decrease. This approach is the conventional MT imaging option available on commercial MRI systems.

The effect of the off-resonance saturating irradiation is to reduce the signal of the mobile water from M₀ to M_sat. The residual MRI signal is given by (Henkelman et al 1993)

$$\frac{M_{\mathrm{sat}}}{M_0}=\frac{R_{1,m}{k}_{fm}+R_{1,f}{R}_{\mathit{rf},m}+R_{1,f}{R}_{1,m}+R_{1,f}{k}_{\mathit{mf}}}{(R_{1,f}+R_{\mathit{rf},f}+k_{\mathit{fm}})(R_{1,m}+R_{\mathit{rf},m}+k_{\mathit{mf}})-k_{\mathit{mf}}{k}_{\mathit{fm}}}.$$ (7)

In this model, suppose the subscript ‘f’ stands for the free water pool and ‘m’ for a second proton pool which has more efficient relaxation and a broader resonance or is chemically shifted. This pool represents the polymerized product of irradiation and increases in direct proportion to the degree of polymerization and dose, a linear approximation to an exponential change (Lepage et al 2001). R₁ is the longitudinal magnetization rate constant, k_mf and k_fm are the rates of MT from the polymer pool to the free pool and vice versa, respectively, and R_rf,i is the rate of loss of longitudinal magnetization in either the free or other pool. If we take R_rf,f to be zero and R_rf,m to be much greater than all other rates, as is the case in an ideal MT experiment, equation (7) becomes

$$\frac{M_{\mathrm{sat}}}{M_0}=\frac{R_{1,f}}{R_{1,f}+k_{\mathit{fm}}}.$$ (8)

For the rest of the discussion, R_1,f and k_fm will be referred to as R₁ and k, respectively, to simplify notation. M_sat and M₀ can be rearranged to give

$$\frac{M_0-M_{\mathrm{sat}}}{M_{\mathrm{sat}}}=\frac{k}{R_1}.$$ (9)

We will call the ratio $\frac{M_0-M_{\mathrm{sat}}}{M_{\mathrm{sat}}}$ the magnetization transfer proportion (MTP). The MTR is related to the MTP:

$$\mathrm{MTR}=\frac{M_0-M_{\mathrm{sat}}}{M_0}=\frac{k}{R_1+k};\mathrm{MTP}=\frac{\mathrm{MTR}}{1-\mathrm{MTR}}.$$ (10)

The rate constant k will increase with dose in proportion to the amount of polymer produced, as has been shown to be the case for methacrylic-based dosimeter gels in the dose range of 0–20 Gy (Gochberg et al 2003). We therefore may write

$$k=k_0+\beta D.$$ (11)

We then have

$$\mathrm{MTP}=k_0{T}_1+\beta T_{1}D.$$ (12)

To calculate the MTP, two images (M₀, M_sat) must be measured, which then can be combined to produce a quantity that should vary linearly with dose. The slope of this dose response is

$$\beta T_1=\frac{\beta }{R_1}.$$ (13)

The ratio of the slope to the intercept of the dose response is a useful indicator of sensitivity when considering the detectibility of small changes in dose (Fong et al 2001); for the MT measure this is $\frac{\beta }{k_0}$, compared with $\frac{\alpha }{R_{2,0}}$ for methods measuring transverse relaxation.

Equation (9) may also be derived by considering the relationship of M_sat to M₀ as given by (Wolff and Balaban 1989)

$$M_{\mathrm{sat}}=M_0(1-k{T}_{1\mathrm{sat}}),$$ (14)

where T_1sat is the spin lattice relaxation time of the mobile water in the presence of the RF irradiation and is given by

$$\frac{1}{T_{1\mathrm{sat}}}=\frac{1}{T_1}+k.$$ (15)

A manipulation of the quantities M_sat and M₀ results in the same relationship found in equation (9).

Equations (9) and (10) illustrate an advantage in calculating the effect of MT in terms of the MTP: if k is linear in dose (as given in equation (11)), so is MTP, but not MTR, even though fundamentally it contains the same information.

The interpretation of the MT–dose relationship can be further understood by considering a two-pool model of MT in more detail, such as that suggested by the results of measurements by Gochberg et al (2003). We can then write the second population as

$$p_m=p_m^0+\gamma D,$$ (16)

where p_m is the size of the relevant polymer proton pool after irradiation, $p_m^0$ is the size of this second pool in the unirradiated dosimeter, D is the absorbed dose and γ is the slope of the pool size versus dose relationship. The MT rate constant, in the nomenclature introduced by Gochberg et al (2003), is then

$$k=k_{\mathit{mf}}\frac{p_m}{p_f}=k_{\mathit{mf}}\frac{p_m^0+\gamma D}{p_f},$$ (17)

ignoring the (insignificant) changes in p_f. Thus the slope of MTP versus D, as given in equation (9) and incorporating equation (17), is $\frac{k_{\mathit{mf}}\gamma }{p_f{R}_1}$. We may also note that for a two-pool exchange model of transverse relaxation

$$R_2=R_{2f}+k_{\mathit{mf}}\frac{p_m}{p_f}.$$ (18)

Thus for this model, α, the slope of the R₂ versus dose line, is $\frac{k_{\mathit{mf}}\gamma }{p_f}$; thus the ratio $\frac{\alpha }{R_{2,0}}=\frac{k_{\mathit{mf}}\gamma }{p_f{R}_{2,0}}$. We see that mapping R₂ and the MTP are fundamentally related, both reflecting increases in the contribution of the fraction of polymer gel. However, the fractional increase in R₂ per dose is smaller than the increase in MTP by the ratio $\frac{R_2}{R_1}$, which can be as large as 10. Moreover, the slope-to-intercept ratio for the MT-based approach is $\frac{\gamma }{p_m^0}$ whereas for the conventional R₂ method it is $\frac{\gamma }{p_m^0+\frac{p_f{R}_{2f}}{k_{\mathit{mf}}}}$, which is clearly smaller.

2.2. Effects of B₁ inhomogeneities

Both quantitative R₂ imaging and MTP imaging are vulnerable to variations and inaccuracies in the RF (B₁) field. Significant variations of the B₁ amplitude occur within large samples, especially at higher fields, so the flip angle experienced by any part of the sample may be in error from the ideal intended value. The sensitivity of multi-echo measurements of R₂ to such errors has been well documented (Majumdar et al 1986b, Sled and Pike 2000a). When the refocusing pulses in a CPMG sequence are not precisely 180°, the percent deviation in estimating T₂ is a function of T₂ itself; i.e. samples with higher T₂ value (and lower R₂) experience higher fractional deviations in T₂ (and thus, dose extracted from a calibration curve) for a given error in B₁ than samples of lower T₂. These inaccuracies in transverse relaxation time estimates can result in an apparent nonlinearity of R₂ versus dose and miscalibration of the dose response curve.

The susceptibility of MT measurements to variations in B₁ has not been as thoroughly explored. In practice, the RF pre-pulse may produce incomplete saturation of the broad component and/or partial saturation of the narrow water resonance. An apparent linear dependence of the MTR on variations in B₁ has previously been reported (Samson et al 2006). We therefore have evaluated the effects of B₁ errors on estimates of dose in polymer gels for both the MTP and R₂ approaches.

3. Methods

3.1. Gel preparation and irradiation

MAGIC (9% methacrylic acid) and MAGIC-2 gel dosimeters were produced as previously described (Fong et al 2001, Luci et al 2007). The components of the two formulations are the same but in different proportions, as the MAGIC-2 formulation has been optimized for measurement of the transverse relaxation rate in the 0–20 Gy dose range. The manufacturing process was as follows: a Pyrex beaker containing the water for the desired volume of gel was placed in a water bath, along with a magnetic stirrer, on a hot plate. The desired quantity of gelatin was added and allowed to bloom. The temperature of the system was brought to 45 °C, at which point the water–gelatin solution was in liquid form. The monomer, ascorbic acid and cupric sulfate were added and the system was stirred for approximately 3 min. The solution was poured into 14 mL Pyrex screw-top test tubes and placed in a refrigerator until irradiation. Samples were brought to room temperature, immersed in a water bath and irradiated with 6 MV photons with a dose rate of 2.84 Gy min⁻¹. Total dose increments of 2 Gy were applied in a parallel-opposed fashion in sub-increments of 1 Gy each, in a range of 0–20 Gy. A single gel dosimeter from each formulation was removed after each application of 2 Gy of irradiation to create the set of gels in the desired range and dose separation. Samples were returned to refrigeration after irradiation. The MAGIC gels were manufactured 48 h before irradiation, and the MAGIC-2 gels were manufactured 24 h before irradiation.

3.2. Imaging measurements

After a refrigeration period of 9 days following irradiation, samples were allowed to come to room temperature and imaged at 4.7 T using a 31 cm bore Varian Inova (Varian Inc., Palo Alto, CA, USA) spectrometer using a 63 mm quadrature coil. The imaging matrix was 64 × 64, the field of view was 70 × 70 mm and the slice thickness was 4 mm. All samples from a given formulation were imaged together. MT imaging was performed with a MT-prepared spoiled gradient echo sequence (Sled and Pike 2000b), as this method is relatively fast and does not have the potential disadvantage of heating of the samples. To prevent stimulated echoes, spoiler gradients and rf spoiling were used to disperse transverse magnetization, and complete spoiling was assumed. A 10 ms Gaussian MT pulse was applied at 30 offset frequencies logarithmically distributed between 100 and 200 000 Hz for three different nominal MT pulse angles (283°, 566° and 849°), as well as at power levels of ±5 and 10% from each of these three powers. These powers are equivalent to 4.44, 8.88 and 13.32 μT, respectively (Tozer et al 2003, Tofts et al 2005). These powers were chosen to be representative of the strength of MT pulses available on clinical scanners. The signal was acquired via a 7° excitation sinc pulse. The TR was 25 ms and TE was 4 ms, and the data from two acquisitions were averaged together for each measurement.

Transverse relaxation measurements were made with a 32 echo CPMG-type pulse sequence with TR of 15 s and TE of 10 ms. The transverse relaxation time was estimated using a pixel-by-pixel fit (using Matlab's ‘robustfit’ function) of the log of the data to a linear model (see equation (3)). Transverse relaxation rate maps were measured as a negative slope of the linear fit to the data for each pixel. One acquisition was taken for each measurement.

Reported values for MTP and R₂ were taken as the average value of pixels from a circular region (radius of 3 pixels) of interest for each sample.

4. Results

4.1. Magnetization transfer proportion measurements

Figure 1 displays an example MTP image of the data acquired from the MT experiment for the MAGIC-2 dosimeter. The image was created by applying equation (10) to images acquired for power of 8.88 μT at 200 000 Hz off-resonance (M_sat) and 1375 Hz off-resonance (M₀).

Figure 1.

Example MTP image for the MAGIC-2 dosimeter, acquired at 8.88 μT calculated from images acquired at 200 000 and 1375 Hz off-resonance. The dose values are, beginning at the top left and reading left to right, (row 1) 2, 10, 4 Gy; (row 2) 6, 12, 9, 14 Gy; (row 3) 18, 8, 16 Gy and (row 4) 20 Gy. The dark space to the left of the 20 Gy dosimeter is a small vial of water used for location reference purposes.

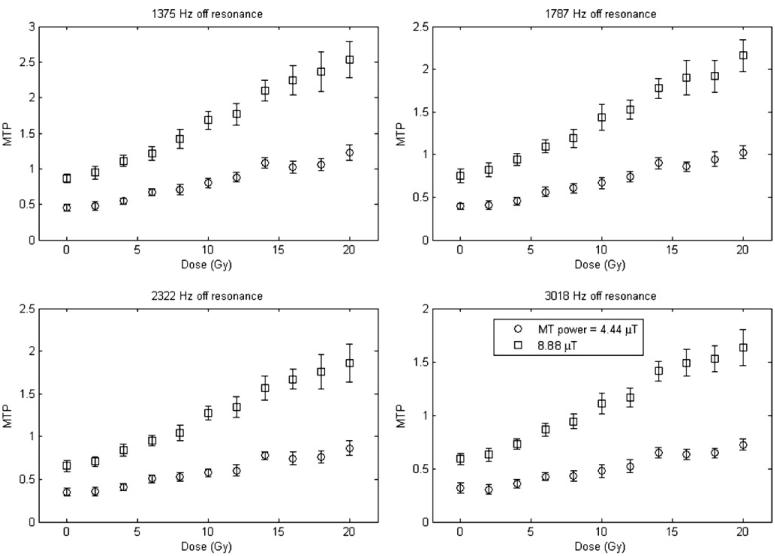
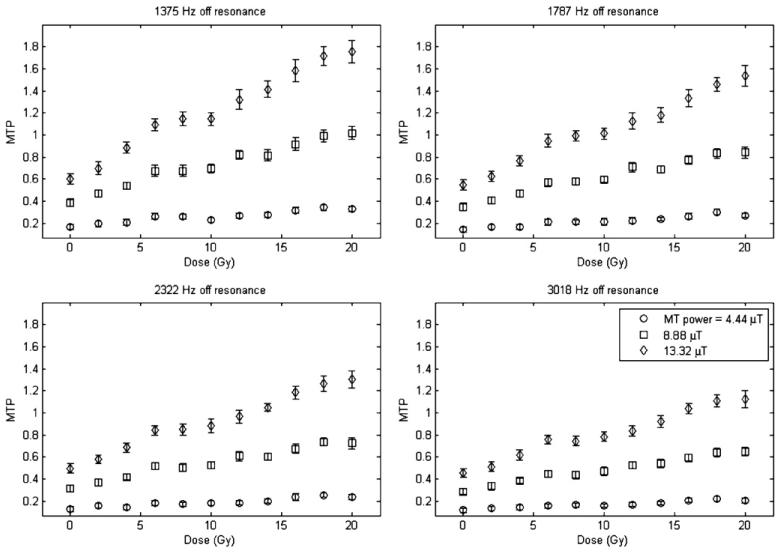
Figures 2 and 3 plot the measurement of the MTP for both types of MAGIC gel over a range of dose values, at four different offset frequencies and different MT powers. Each data point is the mean of a region of interest for each dosimeter, and the standard deviation is the standard deviation of those pixels in the region of interest.

Figure 2.

MTP versus dose for the MAGIC dosimeter.

Figure 3.

MTP versus dose for the MAGIC-2 dosimeter.

There are a few important features to note from figures 2 and 3. Sensitivity, defined as the slope of the MTP versus dose, varies with the offset frequency and power of the MT pulse. At low powers and larger offsets the polymer pool is not fully saturated so the effects of MT are reduced. Additionally, there is a strong dependence of the intercept on the offset frequency and power chosen due to the direct effect of saturation on water, since it increases at small offsets, where the direct effect is strongest. This issue is addressed more fully in section 5. Given this lack of full saturation of the immobilized pool, we do not expect equation (9) or equation (14) to be valid at all offsets and powers. Indeed, in section 5, we consider how the theoretical expression for MTP should be modified under these circumstances. Nonetheless, our experimental data do in fact show linear responses, though with a slope and offset that depends upon the offset and power (in disagreement with equation (12), but as predicted below). In order to maximize dose sensitivity for MT measurements, the appropriate offset frequency and MT power should be chosen, as will be elaborated in section 5.

Tables 1 and 2 show values of the linear correlation coefficients R², a measure of how well these data are represented by a linear relationship, as a function of both offset frequency and power of the B₁ pulse, for the least-squares fit of MTP versus dose for MAGIC and MAGIC-2 dosimeters.

Table 1.

R² for the measurement of the linearity of MTP versus dose, for the MAGIC gel dosimeter.

Offset frequency	MT power = 4.44 μT	MT power = 8.88 μT
1375	0.969	0.989
1787	0.979	0.988
2322	0.961	0.990
3018	0.962	0.985

Table 2.

R² for the measurement of the linearity of MTP versus dose, for the MAGIC-2 gel dosimeter.

Offset frequency	MT power = 4.44 μT	MT power = 8.88 μT	MT power = 13.32 μT
1375	0.894	0.976	0.982
1787	0.925	0.975	0.983
2322	0.896	0.966	0.982
3018	0.923	0.981	0.976

The slope and intercept of the dose response relationships can be combined to provide an assessment of dose response sensitivity (Fong et al 2001). Experimental values for these parameters for MTP are reported below. To aid in assessment of the performance of the MTP in the face of B₁ errors, the results acquired with the known B₁ error are also reported.

Tables 3 and 4 display the slope and intercept values calculated from a linear fit of the data acquired at different powers and a range of ±10% from the nominal powers, for the MAGIC-2 dosimeter. Values for the MAGIC dosimeter vary similarly.

Table 3.

Measured slope of the MTP versus dose line for a variety of MT powers and offset frequencies for the MAGIC-2 dosimeter.

		Error in B1 pulse angle
Offset frequency		−10%	−5%	No error	+5%	+10%
MT power = 4.44 μT
	1375	0.0070	0.0071	0.0081	0.0089	0.0116
	1787	0.0056	0.0054	0.0069	0.0070	0.0093
	2322	0.0043	0.0044	0.0058	0.0055	0.0072
	3018	0.0032	0.0034	0.0047	0.0042	0.0061
MT power = 8.88 μT
	1375	0.0254	0.0291	0.0308	0.0335	0.0361
	1787	0.0205	0.0228	0.0247	0.0279	0.0299
	2322	0.0170	0.0186	0.0209	0.0237	0.0248
	3018	0.0140	0.0153	0.0178	0.0185	0.0207
MT power = 13.32 μT
	1375	0.0521	0.0537	0.0580	0.0621	0.0677
	1787	0.0425	0.0461	0.0480	0.0520	0.0578
	2322	0.0341	0.0382	0.0399	0.0443	0.0467
	3018	0.0294	0.0314	0.0338	0.0377	0.0409

Table 4.

Measured intercept of the MTP versus dose line for a variety of MT powers and offset frequencies for the MAGIC-2 dosimeter.

		Error in B1 pulse angle
Offset frequency		−10%	−5%	No error	+5%	+10%
MT power = 4.44 μT
	1375	0.1467	0.1639	0.1790	0.1944	0.1776
	1787	0.1273	0.1448	0.1505	0.1704	0.1635
	2322	0.1233	0.1270	0.1323	0.1549	0.1408
	3018	0.1086	0.1130	0.1221	0.1427	0.1273
MT power = 8.88 μT
	1375	0.3656	0.3825	0.4207	0.4388	0.4621
	1787	0.3252	0.3530	0.3730	0.3904	0.4173
	2322	0.2875	0.3254	0.3367	0.3546	0.3825
	3018	0.2668	0.2986	0.3051	0.3285	0.3428
MT power = 13.32 μT
	1375	0.5549	0.6145	0.6343	0.6519	0.6899
	1787	0.5121	0.5400	0.5681	0.5757	0.6068
	2322	0.4718	0.4948	0.5196	0.5256	0.5704
	3018	0.4247	0.4572	0.4718	0.4783	0.5083

Tables 5 and 6 display the calculated change in the slope-to-intercept ratio for the measured MTP of the MAGIC and MAGIC-2 dosimeter. With the exception of the MTP acquired for the MAGIC-2 dosimeter at the lowest power, the slope-to-intercept ratio of the MTP has a range of approximately ±15% for a range of −10 to +10% error in B₁ power.

Table 5.

Measured percent change in the slope-to-intercept ratio of the MTP versus dose line for a variety of MT powers and offset frequencies for the MAGIC dosimeter. For most powers and offset frequencies, the slope-to-intercept ratio does not vary more than 10% for even a 10% error in B₁ pulse angle.

		Error in B1 pulse angle
Offset frequency		−10%	−5%	No error	+5%	+10%
MT power = 4.44 μT
	1375	−0.61%	−1.73%	0.0941	−1.39%	10.05%
	1787	−12.68%	−11.43%	0.0941	−0.92%	5.96%
	2322	−3.80%	0.87%	0.0815	6.87%	18.92%
	3018	−11.07%	−6.75%	0.0766	12.06%	13.41%
MT power = 8.88 μT
	1375	−6.17%	0.42%	0.1151	5.51%	3.11%
	1787	6.16%	5.15%	0.1058	10.53%	14.42%
	2322	−5.31%	4.14%	0.1087	0.45%	12.76%
	3018	−3.03%	−4.00%	0.1051	8.16%	8.78%

Table 6.

Measured percent change in the slope-to-intercept ratio of the MTP versus dose line for a variety of MT powers and offset frequencies for the MAGIC-2 dosimeter. With the exception of the values acquired at the lowest power, the slope-to-intercept ratio does not vary more than 10% for even a 10% error in B₁ pulse angle.

		Error in B1 pulse angle
Offset frequency		−10%	−5%	No error	+5%	+10%
MT power = 4.44 μT
	1375	5.93%	−4.48%	0.0452	1.38%	44.15%
	1787	−3.49%	−19.47%	0.0459	−10.51%	23.44%
	2322	−19.66%	−20.44%	0.0436	−18.69%	17.91%
	3018	−24.73%	−22.81%	0.0386	−23.05%	24.66%
MT power = 8.88 μT
	1375	−5.16%	4.06%	0.0732	4.20%	6.86%
	1787	−5.21%	−2.57%	0.0663	7.60%	7.87%
	2322	−4.26%	−7.91%	0.0619	7.88%	4.58%
	3018	−9.82%	−12.34%	0.0584	−3.33%	3.40%
MT power = 13.32 μT
	1375	2.64%	−4.54%	0.0915	4.04%	7.18%
	1787	−1.66%	0.97%	0.0845	6.83%	12.74%
	2322	−5.67%	0.57%	0.0767	10.00%	6.81%
	3018	−3.25%	−3.92%	0.0715	10.06%	12.34%

4.2. Transverse relaxation simulation and measurement

The effect of B₁ errors on measurements of transverse relaxation has been well characterized in the literature. The observed value of R₂ due to a given error in B₁ power can be related as (Sled and Pike 2000a)

$$R_{2,\mathrm{obs}}=R_2-\frac{\ln f}{\tau },$$ (19)

where f is an attenuation factor and τ is the echo spacing of the CPMG-type experiment. The attenuation factor f incorporates the effect of errors due to imperfect B₁ pulses, and for a hard pulse sequence, assuming no error in B₀, is given by

$$f=\frac{\cos \left(\delta \right)}{2}-\cos \left(\delta \right)+\frac{1}{2},$$ (20)

where δ is the degree of the refocusing B₁ pulse. Note that this derivation assumes that complete spoiling occurs of any transverse magnetization produced by incomplete nutations and stimulated echoes. Using experimental values for R₂ for the MAGIC and MAGIC-2 gel dosimeters and the above relationship, the expected deviation in R₂ due to a given error in B₁ can be calculated and the effect on the dose response can be estimated. The values used for the dosimeter from the experiment described above were 5.00 and 14.40 s⁻¹ for the MAGIC dosimeter at 0 and 20 Gy, respectively, and 6.29 and 17.69 s⁻¹ for the MAGIC-2 dosimeter. These values were calculated from a linear fit of the R₂ data acquired in the above experiment to simulate the kind of values that would be taken from a calibration curve. Figure 4 displays the expected variation in R_2,obs for a given error in B₁ power for the MAGIC dosimeter as measured via a CPMG-type experiment using hard pulses.

Figure 4.

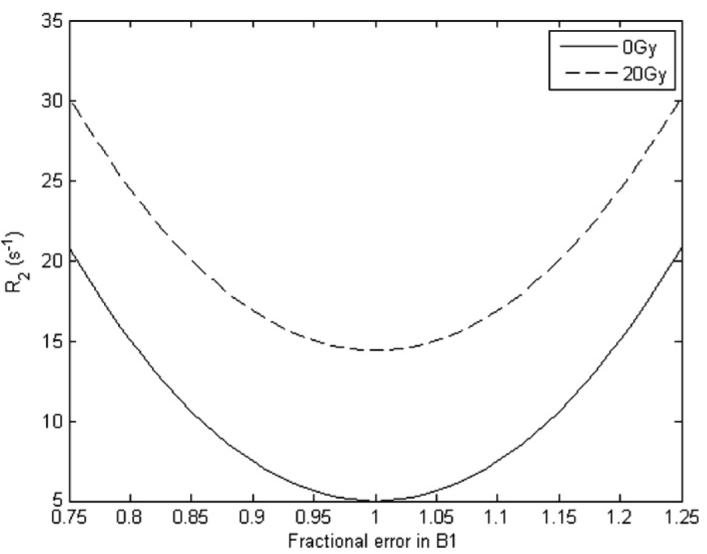
Expected variation in R₂ for a given error in B₁ angle for the MAGIC dosimeter.

The simulation shows that while the slope of the R₂ versus dose line remains the same (as indicated by the B₁-independent difference in R₂ between 20 and 0 Gy), the intercept (the value of R₂ at 0 Gy) will change significantly over a range of errors in B₁. Table 7 lists the expected percent change in the slope, intercept and slope–intercept ratio of R₂ versus dose for hypothetical errors in B₁ power.

Table 7.

Expected change in the slope, intercept and slope–intercept ratio of R₂ versus dose for inclusion of B₁ angle error. Negative percent error in B₁ angle is not included as the result is symmetrical about zero percent error in B₁.

		Percent error in B1 angle
		0%	5%	10%
MAGIC
	Slope (s−1 Gy−1)	0.470	0.470	0.470
	Intercept (s−1)	5.000	5.618	7.4778
	Slope–intercept ratio	0.094	0.0834	0.063
	Percent change in the	–	−10.99%	−33.13%
	slope–intercept ratio
MAGIC-2
	Slope (s−1 Gy−1)	0.570	0.570	0.570
	Intercept (s−1)	6.290	6.908	8.768
	Slope–intercept ratio	0.091	0.083	0.066
	Percent change in the	–	−8.94%	−28.26%
	slope–intercept ratio

4.3. Comparison of the effect of B₁ errors on dose estimates

Finally, a useful measure of the effect an error in B₁ power has on a measurement is to consider the apparent dose that would be calculated in the event of a specific B₁ variation. When polymer gel dosimeters are used for radiation field assessment, a calibration curve is created from dosimeters to which known doses are applied. The form of this line is

$$X=\mathit{aD}+b,$$ (21)

where X is the measured value, such as R₂ or MTP; a is the slope of the line and b is the intercept. Once the desired measurement is made of the dosimeter to be assessed for dose, the following equation is used to back-calculate to the apparent dose D_app:

$$D_{\mathrm{app}}=\frac{X-b}{a}.$$ (22)

If the parameter, be it MTP or R₂, has been mis-measured due to B₁ errors, the apparent dose will be different than its true dose. This effect was investigated for the MTP and R₂ measurements in the MAGIC and MAGIC-2 dosimeters. The slope and intercept of the calibration curves for MTP data acquired with no B₁ error (the nominal B₁ powers referenced above) were applied to MTP values measured with a manually adjusted power with known error (±5 and 10% of the nominal B₁ power) using equation (22). Additionally, the slope and intercept calculated for the R₂ values were applied to simulated R₂ values acquired with a 5 and 10% B₁ error. The percent error in apparent dose was calculated as

$$\frac{D_{\mathrm{app}}-D}{D}\times 100.$$ (23)

Figure 5 displays representative data of the percent error in apparent dose acquired in both MTP and R₂ measurements, as a function of applied dose. The data show that at lower dose levels, on the order of that which most radiation therapy dose fractionations deliver, measurements of MTP with a 10% error in B₁ show much less error in apparent dose than measurements of R₂.

Figure 5.

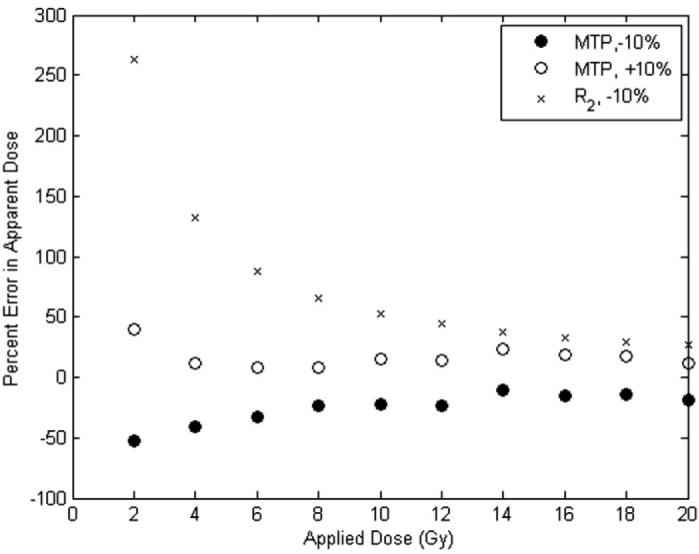
Percent error in the apparent dose for MTP measurements at ±10% B₁ error and R₂ measurements at 10% error in the MAGIC gel dosimeter. The MTP data were acquired at MT power 7.92 (−10% error) and 9.68 (+10% error) μT and offset frequency 1375 Hz. The R₂ data were calculated by simulation using data from figure 4. Corresponding data for the MAGIC-2 dosimeter show an expected percent error in apparent dose for R₂ at 2 Gy to be approximately 217%, while the percent error for the MTP was an average of 96%. At 4 Gy, the percent error in R₂ was approximately 109%, while the percent error for the MTP was an average of 54%. With a few exceptions, the data followed this trend for all offset frequencies investigated (1375, 1787, 2322 and 3018 Hz off-resonance).

5. Discussion

5.1. Saturation of the two pools

MT measurements of the dose response of gel dosimeters are potentially less dependent upon errors in B₁ power than traditional multi-echo measurements of the transverse relaxation rate. In principle, once sufficient B₁ power is applied off-resonance, complete saturation of the broad resonance can be achieved, and using larger powers will have little effect as long as direct saturation of the narrow water line is avoided.

At the powers and offsets shown in this work, complete saturation of the bound pool was not achieved, which may be more typical of conditions when using clinical scanners. The effect of incomplete saturation of the bound pool in the experiment can be estimated by adding a correction factor to equations (8) and (9), which were derived by taking R_rf,m to be much greater than k, k_mf, R₁ and R_1,m. A first-order correction for incomplete macromolecular saturation can be derived by instead assuming that R_rf,m and k_mf are much greater than k, R₁ and R_1,m. This gives

$$\frac{M_{\mathrm{sat}}}{M_0}=\frac{R_1}{R_1+k\left(1-\frac{k_{\mathit{mf}}}{R_{\mathit{rf},b}+k_{\mathit{mf}}}\right)}.$$ (24)

The quantity $1-\frac{k_{\mathit{mf}}}{R_{\mathit{rf},b}+k_{\mathit{mf}}}$ can be interpreted as a measure of the effect incomplete saturation has on measurements of MT. For the MTP, the inclusion of this error results in

$$\mathrm{MTP}=\frac{k}{R_1}\left(1-\frac{k_{\mathit{mf}}}{R_{\mathit{rf},b}+k_{\mathit{mf}}}\right).$$ (25)

Equation (25) is strictly linear in dose only if k_mf is independent of dose, which is true for BANG gels (Gochberg et al 2001) but not MAGIC gels (Gochberg et al 2003). Hence, achieving complete saturation of the macromolecular pool would be ideal. Using published values for R₁, k and k_mf for the MAGIC gel dosimeter, the level of saturation (M_sat/M₀) achieved in our experiments can be estimated via equation (24). These estimated values for dosimeters irradiated to 0 Gy are on the order of 84%, 65% and 53% saturation for the three powers (4.44, 8.88 and 13.32 μT, respectively) of the MT pulse in the experiment, while values for 20 Gy dosimeters are on the order of 76%, 49% and 33% for the three powers. The experiment was designed to perform the MT experiment at power levels similar to those available on clinical scanners, but the significant dependence of M_sat/M₀ on the rf power is due to incomplete saturation of the macromolecular pool.

It would be ideal to use known values for R₁, k and k_mf to estimate the appropriate MT power strength and offset frequency to use in MTP experiments. Such prior knowledge could aid in ensuring that the assumptions behind equations (9) and (11) are fully met. For example, prior work (Gochberg et al 2003) has estimated that for the MAGIC gel dosimeter, R₁, k and k_mf for dosimeters at 20 Gy are approximately 1 Hz, 7.2 Hz and 122 Hz, respectively. To estimate the range of powers and offsets for which R_rf,f is much less than and R_rf,m is much greater than any other rate, these values can be calculated using lineshape assumptions for the system in question and compared for the regime in which equations (9) and (11) are valid. Figure 6 displays calculations of the saturation of the free and bound pools and an assessment for whether or not the assumptions behind equations (9) and (11) were met. Values for R_rf,f were calculated by assuming a Lorentzian lineshape for the free pool and using the relationship

$$R_{\mathit{rf},f}=\frac{{\omega }_1^2{T}_{2,f}}{1+{\left(2\pi \Delta T_{2,f}\right)}^2},$$ (26)

where T_2,f is the transverse relaxation time of the water pool, Δ is the offset frequency of the saturation and ω₁ is the strength of the MT pulse in rad s⁻¹. Values for R_rf,m were calculated by assuming that the bound pool could be characterized by a Gaussian lineshape and using the relationship

$$R_{\mathit{rf},m}={\omega }_1^2{T}_{2,m}\sqrt{\frac{\pi }{2}}{T}_{2,m}{\mathrm{e}}^{-\frac{{\left(2\pi \Delta T_{2,m}\right)}^2}{2}},$$ (27)

where T_2,m is the transverse relaxation time of the bound pool. For this value, an estimated value of 10 μs was used.

Figure 6.

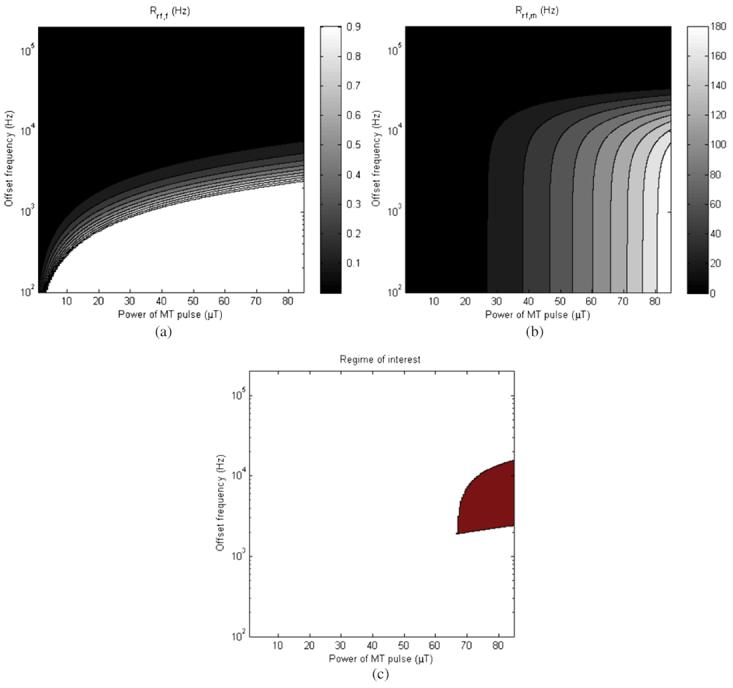
(a) R_rf,f for a 20 Gy MAGIC gel dosimeter, (b) R_rf,m and (c) region for which the two criteria (R_rf,f much less than all other rates, R_rf,m much more than all other rates) overlap.

In figure 6(a), R_rf,,f is displayed as a function of both MT pulse power and frequency. Values greater than 1, approximately R₁ (the lowest rate of concern), are not plotted to preserve the scale of interest. Figure 6(b) displays R_rf,m. Figure 6(c) is displayed by evaluating at each offset frequency and MT power whether or not the criteria of R_rf,f ⪡ all other rates and R_rf,m ⪢ all other rates are valid, and the shaded area indicates the values for which the criteria are met.

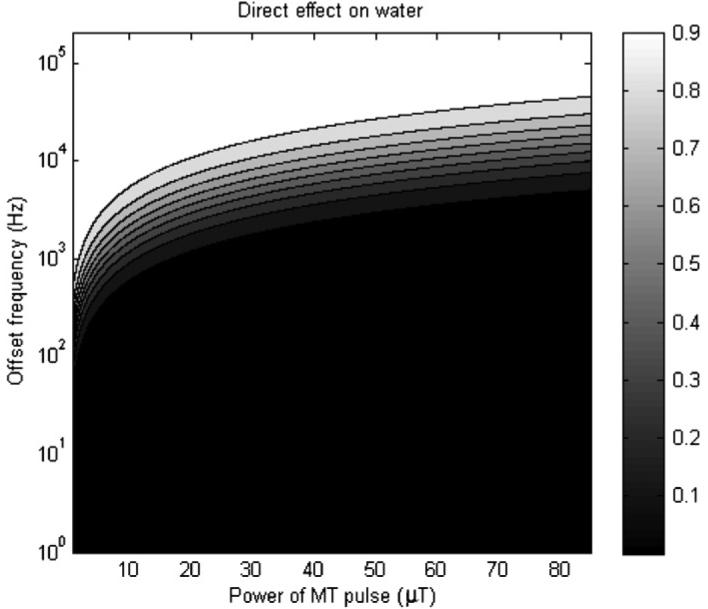
A similar analysis can be used to appreciate the direct effect on the free water line. Assuming steady state conditions, the solution for the uncoupled Bloch equations for the transverse magnetization of the water is given by

$$\frac{M_{\mathrm{sat}}}{M_0}=\frac{1+{\left(\Delta T_{2,f}\right)}^2}{1+{\left(\Delta T_{2,f}\right)}^2+{\left(\frac{{\omega }_1}{2\pi }\right)}^2{T}_{1,f}{T}_{2,f}}.$$ (28)

Using values of T_2,f of 1/14.4 Hz and assuming that R₁ is on the order of 1 Hz for polymer gel dosimeters at 4.7 T, the direct effect on the free water line can be estimated. Results for a range of frequency offsets and MT powers are displayed in figure 7.

Figure 7.

Simulation of the direct effect on water for a range of offset frequencies and MT powers.

It can be estimated from figure 7 that at the offset frequencies and powers in this work, there was some level of direct effect on the water (M_sat/M₀ having a range of approximately 40–70%), and this is likely another reason why our measurements of the MTP dose response intercept vary at the different offset frequencies.

These simulations suggest that while an appropriate range of offset frequencies was used for the measurement of MTP as displayed in figures 2 and 3, the MT power strength was less than ideal for a dosimeter with these specific relaxation properties. However, our results show that for clinically feasible implementation of MT experiments, where the power of the MT pulse may not be able to be increased by much or the user may only be able to set a nominal maximum power level, a linear dose response can still be attained. These results suggest that complete saturation of the macromolecular pool and a priori knowledge of the sample parameters are not necessary to achieve linearity in dose.

5.2. Comparison of dose measurement in the presence of B₁ errors

The change in the slope-to-intercept ratio for the measurement of the MTP in MAGIC-type gel dosimeters was approximately ±15%, while the value of the slope-to-intercept ratio for R₂ could be expected to deviate by as much as 33% for 10% error in B₁ power.

The estimated (apparent) dose at dose levels used in most fractionation schemes varies with B₁, but for the range of changes considered here the MTP appears less susceptible to errors in apparent dose than are measurements of R₂.

While the measurement of the MTP is linear in dose for a wide range of MT pulse powers and offset frequencies, it is important to note that the sensitivity can be maximized by the appropriate choice of these two variables. A priori knowledge of the MT rates for a particular type of dosimeter can be used to estimate the appropriate values for MT power and offset frequency, but as has been shown is not necessary to achieve a linear dose response of MTP.

The MTP approach has not been tested in polyacrylamide-type (PAG) polymer gel dosimeters. Some studies (Gochberg et al 2001, 2003) have suggested that MT may behave differently in PAG versus methacrylic acid-based dosimeters, which may affect the measurement of the MTP versus dose in PAG. Note also that the MTP is proportional to k (equation (9)) and inversely proportional to p_f, the size of the free pool (equation (17)), so efforts to change these may result in greater sensitivity. Sensitivity should also differ between dosimeters with different amounts of MT present due to formulation, as k_mf is dependent upon the amount of monomer. We have assumed, based on expectations and some experimental data, that k_mf is not dose dependent. In some conditions, this may no longer be valid (Gochberg et al 2003), such that k_mf = k_mf,0 + mD. Then, the MTP has both a linear and a quadratic term in terms of D. However, it will still appear linear until mD ≥ k_mf,0.

The MTP has been described before in the imaging literature, using the name ‘equivalent cross-relaxation rate (ECR)’ (Sogami et al 2001), for imaging studies for breast cancer. However, the term ‘cross-relaxation’ has usually been reserved in nuclear magnetic resonance to denote dipolar cross-relaxation, whereas MT includes chemical exchange and other effects. We therefore feel it is not appropriate to use the ECR name and propose MTP for this quantity.

5.3. Other concerns

Image resolution should not significantly affect these types of measurements unless regions of interest are drawn such that partial volume effects are present in the measurement of the MTP. Creating regions of interest that are well within the boundaries of the samples will ensure that this error is avoided.

6. Conclusion

This work has shown that the measurement of the MTP in methacrylic acid-type gel dosimeters is linear with dose and shows promise as a measure of dose response in polymer gel dosimeters. The method has been validated at powers and offset frequencies similar to those used in clinical applications, and prior knowledge of magnetization transfer quantities, while desirable to maximize contrast, is not necessary to acquire useful dose response data. The method is less susceptible to calibration errors than transverse relaxation rate measurements in the presence of B₁ inhomogeneities.