Mechanism of Spectral Tuning Going from Retinal in Vacuo to Bovine Rhodopsin and its Mutants: Multireference ab initio Quantum Mechanics/Molecular Mechanics Studies

Abstract

We have investigated photoabsorption spectra of bovine rhodopsin and its mutants (E122Q and E113Q) by hybrid quantum mechanical/molecular mechanical (QM/MM) calculations as well as retinal in vacuo by pure QM calculations, employing multireference (MR) ab initio and TD-B3LYP methods. The sophisticated MR-SORCI+Q and MRCISD+Q methods extrapolated with respect to adopted approximations can reproduce the experimental absorption maxima of retinal very well. The relatively inexpensive MR-DDCI2+Q method gives absorption maxima blue-shifted by ca. 65 nm from experimental values; however, this error is systematic and thus MR-DDCI2+Q can be used to estimate spectral shifts. In MR calculations, the ground state energy of retinal at B3LYP geometry is significantly lower than that at CASSCF geometry. Therefore, B3LYP geometry is more reliable than CASSCF geometry, which has blue-shift error as large as 100 nm in the gas phase. The effect of ground state geometry on the excitation energies is less critical in the polarizing field of protein environments. At the B3LYP geometry, there is no significant charge transfer upon vertical excitation to the S₁ excited state either from Glu113 to retinal or from Schiff-base terminal to β-ionone ring through the polyene chain. All-trans to 11-cis isomerization of retinal in the gas phase has no influence on the calculated S₁ absorbing state, in agreement with experiment. The shoulder of the experimental absorption spectrum of retinal in vacuo at the S₁ absorbing band appears to be the second electronic transition (S₂) in our calculations, contrary to previous tentative assignment to vibrational state of S₁ or to the S₁ band of a retinal isomer.

I. Introduction

Rhodopsin (Rh) is responsible for the dim-light vision in vertebrate eyes and belongs to the G-protein-coupled receptor family.^1,2 It is activated by the light-induced 11-cis to all-trans isomerization of protonated Schiff-base retinal (PSBR). While the retinal in vacuo absorbs light at 610 nm,³ the retinal in bovine Rh absorbs at 500 nm.^1,2 Despite extensive mutagenesis and computational analyses in the last two decades (see ref 2 and references therein), the molecular basis of spectral tuning, e.g., how environments of retinal modulate its absorption maximum in the UV-visible spectrum, remains unclear.

In general, computation of the absorption maxima for retinal proteins is a very challenging problem. Our recent ONIOM quantum mechanical/molecular mechanical (QM/MM) calculations on bovine Rh, employing density functional theory (DFT), show that the effects of amino acids other than Glu113 on the first (S₁) vertical excitation energy of retinal tend to cancel to each other.⁵ Analogously, the protein environment of retinal and Glu113 represented with several point charge models contributes up to ±20 nm at CASPT2/ANO level.⁶ However, the protein environment around retinal and Glu113 red-shifts the S₁ excitation energy by 110 nm at (aug-MCQDPT2/cc-pVDZ)/EFP level, where EFP is an effective fragment potential method for calculating QM/MM interaction.⁷ Glu113 blue-shifts the S₁ excitation energy in the gas phase by ca. 60, 150 and 210 nm at TD-B3LYP/6-31G*,⁴ CASPT2/(ANO or 6-31G*)^6,8 and aug-MCQDPT2/cc-pVDZ⁷ levels, respectively. Although this varying Glu113 effect is well captured at those levels where its atoms are represented with point charges rather than included in the QM model system, SACCI/D95(d) calculations find a significant blue-shift (ca. 100 nm) charge-transfer contribution of Glu113.⁹

The computed gas-phase excitation energies of all-trans and 11-cis retinals also vary quite a lot.^2,5 For example, the errors in the S₁ excitation energy of all-trans retinal (experiment:^3,4 610 nm) are -100/-50 nm (TD-B3LYP/6-31G* at B3LYP and complete active space self-consistent field [CASSCF] geometries, respectively),^10,11 -65 nm (CASPT2/6-31G* at CASSCF geometry),¹² -10/-40 nm (OM2-MRCI at B3LYP and CASSCF geometries, respectively),¹¹ 25/-20 nm (spectroscopy-oriented configuration interaction [SORCI]/6-31G* at B3LYP and CASSCF geometries, respectively)¹¹ and more than 200 nm (SACCI/D95(d) at B3LYP geometry).¹⁴ However, CASPT2 calculations with a large ANO basis set at MP2 geometry (606 nm)^6,15 reproduce the experiment (610 nm).

In our previous study,⁵ we investigated absorption spectra of bovine rhodopsin and its mutants by time-dependent (TD)-DFT QM/MM calculations in ONIOM scheme and reproduced the experimental absorption maxima within 10 nm. In this study, we employ high-level multireference (MR) ab initio QM/MM calculations on retinal to pinpoint origins of differences among various calculations and to provide computational strategies for accurately calculating its absorption spectra in the gas phase as well as in the protein environments of bovine rhodopsin and its mutants.

II. Computational Details

For bovine Rh and its mutants (E122Q and E113Q), ONIOM(B3LYP/6-31G*:AMBER)-optimized structures with electronic embedding (EE) are used in this study (see ref 5). All single-point ab initio QM/MM calculations on these structures were carried out with ORCA 2.6.19 program package¹⁶ using an EE scheme,¹⁷ in which fixed MM point charges are included in the one-electron QM Hamiltonian and the QM/MM electrostatic interactions are evaluated from the QM electrostatic potential and the MM atomic charges. Although this EE scheme¹⁷ is slightly different from the ONIOM-EE,^5,18 they result in identical excitation energies at given Rh geometries in our test calculations. Therefore, ONIOM-EE geometries can be used for QM/MM excitation energy calculations with the ORCA program package that has many MR methods implemented. No cutoffs were introduced for the nonbonding MM and QM/MM interactions. Hydrogen link atoms¹⁹ were used at the QM/MM boundary along with a charge shift model.²⁰

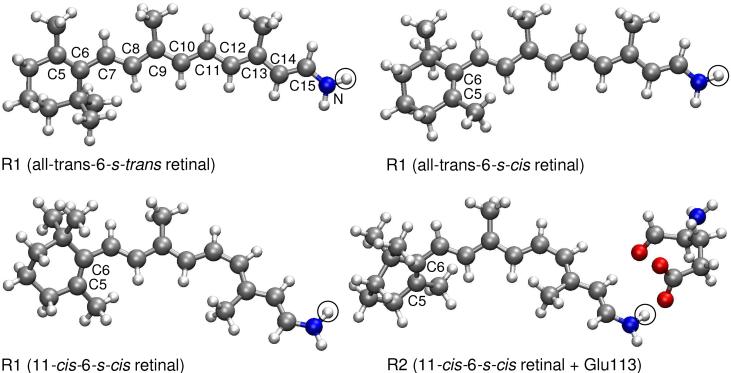
We employed two QM regions shown in Figure 1: (i) R1, including the full retinal along with covalently bound N/NH moiety of Lys296 for deprotonated/protonated Schiff-base (SB) linkage, which results in total of 50/51 atoms. We do not extend this QM region to C_ε atom of Lys296 since it red-shifts the S₁ excitation energy only 10 nm in TD-DFT⁵ and CASPT2¹² studies. (ii) R2, consisting of R1 region plus full Glu113, which results in total of 68 atoms when either retinal or Glu113 side chain is protonated. The gas-phase QM calculations on the bare R1 and R2 regions at the QM/MM geometries will be called as QM-none. Unless stated otherwise, our calculations were performed for PSBR modeled as R1 and using 6-31G* basis set.²¹ In order to assess the basis set dependence of computed excitation energies, we also used VDZP (known also as SV(P)),²² VTZP,²² TZVP,²³ double-ξ {BNANO-DZP: (33s12p3d) → [3s2p1d] for N, (32s12p3d) → [3s2p1d] for C and (4s1p) → [2s1p] for H} and triple-ζ {BNANO-TZ2P: (44s18p6d) → [4s3p2d] for N, (43s18p6d) → [4s3p2d] for C and (5s2p) → [3s2p] for H} type ANO basis sets from the ORCA library.^16,24 Auxiliary basis sets used to speed-up the ab initio calculations are SV/C and TZV/C for double-ζ and triple-ζ quality basis sets, respectively.²⁵ The calculated excitation energies are not affected by the use of auxiliary basis sets for the current system.

Figure 1.

QM models and atom numbering of PSBR. SBR corresponds to removing the hydrogen circled or transferring it to Glu113 carboxylic oxygen.

We applied CASSCF²⁶ theory for obtaining zero-order wave function of all MR ab initio calculations. CASSCF captures a major part of static correlation by mixing the active-space configurations at the full configuration interaction (CI) level. The largest 6-root CASSCF(12/12) calculations include all valance π-electrons of the polyene chain of R1 from C5 to the SB terminal. For the extensive post-CASSCF calculations at SORCI and MRCISD levels, we had to use 3-root CASSCF(6/6). For R2 with Glu113 in the QM region, we performed 6-root CASSCF(12/12) calculations including π-electrons of Glu113 in the active space.

Subsequent post-CASSCF MR calculations on the CASSCF reference wave function were performed at several CI levels. As cost-effective post-CASSCF methods, we applied difference dedicated CI (DDCI) methods DDCI2 and DDCI3.²⁷ These methods use a CI expansion aimed at improving energy difference between individual states rather than their absolute correlation energies. Whereas the DDCI2 method includes double excitations which involve either two particles in the inactive empty orbitals or two holes in the inactive occupied orbitals in addition to all single excitations, the DDCI3 method also includes out of the active-space configurations with two holes and one particle or two particles and one hole.^27-29 The effects of excitations higher than doubles (i.e., disconnected quadruple excitations) were estimated with the a posteriori MR Davidson +Q term, which corrects the energy but not the expansion coefficients of the correlated wavefunction.³⁰ To assess the effect of size-consistency error in DDCI type methods more accurately, we applied a slightly modified version of MR averaged coupled pair functional ACPF/2³⁰ procedure to DDCI2 excitations, leading to the size-consistent DDACPF/2a-2 method implemented in ORCA.

We also applied the SORCI method,²⁸ which performs a DDCI3 calculation in a truncated basis of approximate average natural orbitals (AANOs) obtained from a DDCI2 calculation. In the DDCI3 step of SORCI, AANOs with an occupation number less than a threshold T_nat are rejected while those with an occupation number larger than 2.0-T_nat are frozen.

Finally, we also applied the most straightforward MRCISD approach including all single and double excitations^32,33 to benchmark the validity of results obtained with the lower level DDCI2, DDCI3 and SORCI methods. For accounting size-consistency error, +Q correction was also calculated for SORCI and MRCISD results.

To enhance computational efficiency, the ORCA thresholds T_nat (used only for SORCI), T_pre and T_sel were set to 10^-6, 10^-4 and 10^-6 E_h, respectively.^11,28,13 The present DDCI2 and SORCI calculations on retinal in vacuo and the previous SORCI calculations on model retinal systems (see Supporting Information of ref 13) show that looser ORCA thresholds of T_sel and T_nat result in the significant loss of accuracy. Improved virtual orbitals were not used. Core orbitals with energies of less than -4 E_h were frozen, and no virtual orbitals were neglected. In all perturbative treatments, a level shift of 0.4 E_h was applied in order to avoid intruder state problems.

III. Results

A. Protonated Schiff-Base Retinal (PSBR) in Vacuo

In this section, we mainly discuss the calculated first (S₁) and second (S₂) singlet vertical excitation energies of PSBR.

Basis Set Dependence

The improvement of the 6-31G* basis set to aug-cc-pVTZ red-shifts the S₁ vertical energy of PSBR by only 10 nm in DFT calculations.⁵ As the correlated ab initio calculations converge to the basis set limit slower than DFT calculations, it is necessary to investigate the basis set effect on the excitation energies of PSBR for MR ab initio treatments. Indeed, for a small model of PSBR (without β-ionone ring), the S₁ and S₂ vertical energies were found to red-shift by ca. 20 nm when 6-31G* basis set is improved to aug-cc-pVTZ at the SORCI level (see Supporting Information of ref 13). To assess the basis set effect further on the full all-trans retinal, we performed 6-root DDCI2+Q(12/12) calculations at the gas-phase B3LYP/6-31G* geometry of all-trans-6-s-trans retinal, as shown in Table 1. When the double-ζ quality basis sets were improved to TZVP, the S₁ excitation energy red-shifts by ca. 20 nm. However, with the largest basis set considered (BNANO-TZ2P), it comes back and gives only 5 nm blue-shifted result relative to the 6-31G*. This ANO basis set gave slightly better agreement with experiment than the aug-cc-pVTZ basis set in previous test calculations.²⁴ As to the S₂ excitation energy, 6-31G* and VDZP basis sets give ca. 20 nm blue-shift compared with the larger basis sets, which is similar to the results on model systems.¹³ In the following, we will use the cost-effective 6-31G* basis set that contains ca. 5 (20) nm blue-shift error for the S₁ (S₂) excitation energy of full PSBR.

Table 1.

Basis set dependence of the S₁ (S₂ in parentheses) vertical excitation energy (nm) of PSB all-trans-6-s-trans retinal in vacuo at the 6-root CASSCF(12/12) and DDCI2+Q(12/12) level at the B3LYP/6-31G*-optimized geometry

Basis Set	Basis Set Size	CASSCF(12/12)	DDCI2+Q(12/12)
6-31G*	354	553 (404)	545 (416)
VDZP [or SV(P)]	444	566 (405)	555 (420)
BNANO-DZP	444	559 (405)	555 (437)
TZVP	579	572 (406)	570 (438)
VTZP	600	572 (406)	563 (441)
BNANO-TZ2P	753	552 (404)	550 (437)

The Effects of Several Computational Settings

We have investigated the effects of several computational settings (approximations) at the DDCI2+Q/6-31G* level on the excitation energies of PSB all-trans-6-s-trans retinal, as shown in Table 2. The number of roots has no significant effect on the computed excitation energies. Reducing CASSCF(12/12) to CASSCF(6/6) introduces a large blue-shift error of ca. 160 (60) nm in the CASSCF S₁ (S₂) vertical excitation energy. CI calculations substantially reduces the error due to small active space; the DDCI2+Q S₁ (S₂) excitation energy error due to the reduction of the active space is ca. 15 (30) nm to red (blue). Tightening T_sel from 10^-6 E_h to 10^-7 E_h blue-shifts the S₁ (S₂) DDCI2+Q excitation energy by ca. 15 (5) nm whereas tightening T_pre = 10^-4 has no notable effect, a situation similar to SORCI calculations on model systems.¹³ In an overall assessment, CI calculations with T_sel = 10^-6 using CASSCF(6/6) wave function have a net error of ca. +15 (-55) nm in S₁ (S₂) excitation energy, arising from T_sel [+15 (-5) nm], active space size [+15 (-30) nm], basis set [-5 (-20) nm] and the use of NH₂ terminal rather than NHCH3 [-10 (0) nm¹¹].

Table 2.

The effects of active space size, the number of roots and T_sel (E_h) in post-CASSCF/6-31G* calculations on the computed S₁ (S₂) vertical excitation energy (nm) of PSB all-trans-6-s-trans retinal in vacuo optimized at B3LYP/6-31G* level

	6-root CAS(12/12)	3-root CAS(12/12)	3-root CAS(6/6)	3-root CAS(6/6)
CASSCF	553 (404)	548 (391)	382 (334)	382 (334)
Tsel	10-6	10-6	10-6	10-7
DDCI2+Q	545 (416)	544 (412)	559 (385)	545 (379)

Accuracy of Several CI Levels

Experimental absorption spectra of PSBR (both all-trans and 11-cis conformations) have absorption bands peaking at 610 nm and ca. 390 nm.^3,4 These bands were assigned previously to S₁ and S₂ transitions, respectively.^3,4 The band at 610 nm has a shoulder at around 540 nm.^3,4 This shoulder was tentatively assigned either to the S₁ state of an all-trans retinal isomer or to a vibrational state of the electronic S₁ state.^3,4 The results of several CI calculations are given in Table 3. From the error estimates in the previous section, one should subtract 15 nm from S₁ and add 55 nm to S₂ excitation energies given in Table 3 when CI results using CASSCF(6/6)/6-31G* are compared with experiment. The magnitude of +Q correction for the S₁ (S₂) excitation energy is sizable and depends on the applied CI level: -26 (-33) nm, 42 (0) nm, 47 (5) nm and -73 (-280) nm at DDCI2, DDCI3, SORCI and MRCISD levels, respectively. Therefore, we consider the results only with Q correction.

Table 3.

S₁ and S₂ vertical excitation energies (nm) for PSB all-trans-6-s-trans retinal in vacuo at various CI/6-31G* levels along with CASSCF and TD-B3LYP results at the B3LYP/6-31G*-optimized geometry

Method	S1	S2
TD-B3LYP	501	380
CASSCF(12/12)a	553	404
CASSCF(6/6)	382	334
DDCI2+Q(12/12)a	545	416
DDCI2+Q(6/6)	559	385
DDACPF/2a-2(12/12)a	527	394
DDCI3+Q(6/6)	640	474
SORCI+Q(6/6)	626	491
MRCISD+Q(6/6)	604	458

^a6-root CAS(12/12) results are given for comparison.

As already found in the previous section, CI calculations improve the poor performance of small CASSCF(6/6) and make the results comparable to the CI results based on CASSCF(12/12). Our lowest level post-CASSCF calculation (DDCI2+Q) corrects the TD-B3LYP S₁ excitation energy by ca. 50 nm. DDCI2+Q and size-consistent DDACPF/2a-2 results agree within 20 nm. DDCI3+Q, SORCI+Q and MRCISD+Q methods improve DDCI2+Q energies significantly, making the S₁ excitation energies agree with experiment within ±20 nm (including 15 nm correction). Natural orbital iteration at SORCI+Q level further improves the S₁ DDCI3+Q excitation energy toward experiment by ca. 15 nm.

As to the S₂ excitation energy, when the DDCI3+Q, SORCI+Q and MRCISD+Q S₂ excitation energies based on CASSCF(6/6) are corrected with our error estimate of 55 nm, we obtain values (513-546 nm) that are close to the 540 nm shoulder of S₁ band rather than to the 390 nm absorption band assigned to S₂ in the experimental spectrum.^3,4 At the B3LYP-optimized geometry, the calculated oscillator strengths f of S₁ and S₂ excitation for the 6-s-trans/6-s-cis conformation are around 1.8/1.8 and 0.03/0.14, respectively. As these oscillator strengths are significantly different than zero, we assign the shoulder of the S₁ band to the S₂ band of ground-state 6-s-cis conformation (see Table 4 for the results on this species), rather than a vibrational splitting or S₁ of a local minimum. The difference between the S₁ and third (S₃) excitation energies in DDCI2+Q(12/12)/6-31G* (not listed in Table 3, see Supporting Information) is 237 nm; which agrees reasonably well with the difference (225 nm) in the experimental absorption maxima of 610 and 385 nm bands of all-trans retinal. Therefore, we assign the band peaking at 385 nm in the experimental spectrum as the S₃ band, contrary to the previous assigned S₂.^3,4 The appearance of three absorption bands in the absorption spectrum of PSB all-trans retinal in vacuo is in agreement with two-photon spectroscopy of PSB all-trans retinal in the protein environment of bacteriorhodopsin (568 nm, 488 nm and 410 nm).³⁴

Table 4.

Geometry dependence of the S₁ (S₂) excitation energy of PSB retinal in vacuo in MR calculations with 6-31G* basis set based on 3-root CAS(6/6) or 6-root CAS(12/12) levels

	CASSCF(12/12)	CASSCF(6/6)	DDCI2+Q(12/12)	SORCI+Q(6/6)	MRCISD+Q(6/6)
all-trans-6-s-trans
CASSCF geometrya	526 (345)	421 (295)	539 (360)	565 (395)	603 (412)
B3LYP geometry	553 (404)	382 (334)	545 (416)	626 (491)	604 (458)
all-trans-6-s-cis
CASSCF geometryb,c	457 (312)	415 (328)	470 (361)	505 (396)	546 (421)
B3LYP geometryd	545 (391)	467 (350)	551 (412)	610 (475)	604 (493)
11-cis-6-s-cis
B3LYP geometry	535 (383)	362 (313)	541 (403)e	625 (473)	601 (454)

^aCoordinates taken from ref 13. C5-C6 dihedral angle was fixed to its HF value as it relaxed to 6-s-cis minimum.

^bCoordinates taken from ref 12.

^c3-root CASPT2(12/12)/6-31G*: 534 (353) nm¹²

^d6-root CASPT2(12/12)/ANO at MP2 geometry: 606 (436) nm⁶

^e3-root DDCI2+Q(6/6)/6-31G*: 556 (370) nm

Geometry Effect at Several CI Levels

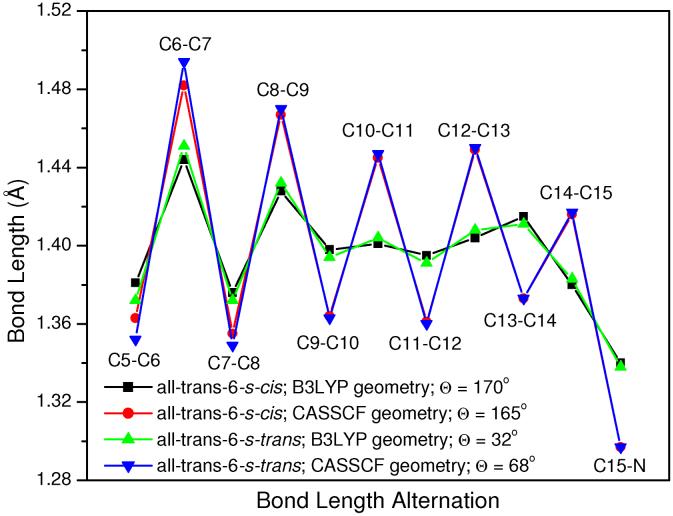
As shown in Figure 2, CASSCF single and double bonds are on average 0.04 Å longer and 0.03 Å shorter than B3LYP distances, respectively. In the SORCI+Q and MRCISD+Q calculations, the B3LYP geometry of PSB all-trans retinal (both 6-s-trans and 6-s-cis) is at least 8 kcal/mol more stable than the CASSCF geometry. Therefore, the B3LYP ground-state geometries (incorporating both static and dynamical correlations) are more appropriate for retinal systems than CASSCF ones (incorporating only static correlation and unbalanced). B3LYP, MP2 and CASPT2 geometries have been shown to be almost the same on small PSBR models, whereas HF (no electron correlation) and CASSCF (incorporating only static correlation) methods overestimate bond length alternation (BLA) of the polyene chain.^5,35-37 As discussed earlier, the clear BLA pattern of PSBR in rhodopsins is the result of the polarizing field of protein environments.⁵ Therefore, it is not expected to have a significant BLA in gas-phase retinal systems.

Figure 2.

Bond length alternation of polyene chain of PSB all-trans retinal at B3LYP/6-31G* and CASSCF/6-31G* levels along with C5-C6-C7-C8 tilt angle of β-ionone ring (Θ)

CASSCF and B3LYP geometries are both used extensively in literature for retinal systems. However, going from CASSCF geometries to B3LYP ones in the present post-CASSCF calculations, the S₁ and S₂ excitation energies improve up to 100 nm and reach to the range of experimental value at SORCI+Q and MRCISD+Q levels, as shown in Table 4. An analogous geometry effect was also seen in the previous SORCI,¹³ SACCI calculations^9,14 and some lower level calculations.¹³ For example, going from HF geometries of retinal proteins (being similar to CASSCF geometries) to B3LYP ones (being similar to CASPT2 geometries), the S₁ SACCI excitation energy red-shifts by ca. 100 nm.^9,14 Remembering the basis set effect on the S₁ and S₂ excitation energies of PSBR is small, the difference between the previous CASPT2 excitation energies of all-trans-6-s-cis retinal with the 6-31G* basis set at CASSCF geometry (534 nm for S₁ and 353 nm for S₂)¹² and with an ANO basis set at MP2 geometries (606 nm for S₁ and 436 nm for S₂)⁶ should also mainly arise from such geometry effects. Actually, these CASPT2 S₁ excitation energies are almost the same as our MRCISD+Q results at CASSCF (546 nm) and B3LYP (604 nm) geometries. However, the S₂ excitation energy calculated at the CASPT2 level (353 nm¹² and 436 nm⁶) is ca. 60 nm blue-shifted than that at the MRCISD+Q level (421 and 493 nm).

The SORCI+Q and MRCISD+Q S₁ excitation energies of 6-s-cis and 6-s-trans conformations at B3LYP geometries (calculated: 604 nm; estimate with 15 nm corrrection: 589 nm) agree with experiment^3,4 reasonably well. The calculated S₂ excitation energies are more sensitive to the conformational changes. Including the error estimate of 55 nm in our post-CASSCF(6/6) S₂ excitation energy calculations, the maximum of the shoulder at the S₁ band of experimental spectrum (ca. 540 nm),^3,4 e.g., S₂ band in our new assignment discussed above, is reproduced at SORCI+Q (530 nm) and MRCISD+Q (548 nm) levels using the B3LYP geometry of 6-s-cis conformation. However, it is ca. 30 nm blue-shifted at the MRCISD+Q level for the 6-s-trans conformation (513 nm). Hence, the absorption spectrum of all-trans retinal recorded in vacuo³ should belong mainly to the 6-s-cis conformation. This conformation is at least 3 kcal/mol more stable than the 6-s-trans one at SORCI+Q and MRCISD+Q levels.

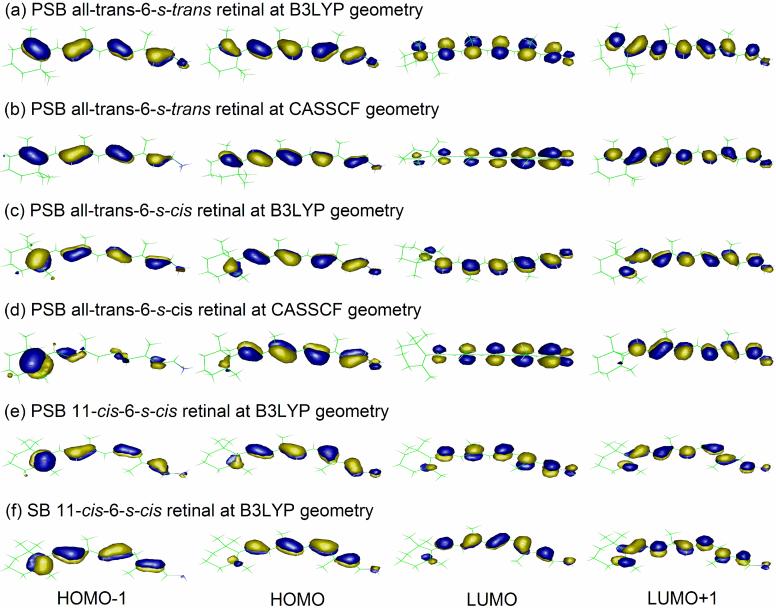
11-cis-retinal with 6-s-cis conformation is ca. 6 kcal/mol above the ground-state all-trans-6-s-cis retinal in all of our MR calculations at the B3LYP geometry. Its frontier orbitals (Figure 3) and calculated excitation energies are very similar to those for all-trans retinal (Table 4). Therefore, 11-cis ↔ all-trans isomerization is not expected to affect the S₁ excitation energy much in protein environments.

Figure 3.

The key 6-root CASSCF(12/12) orbitals of retinal in vacuo.

Dominant configurations in S₀, S₁, and S₂ states are the closed-shell singlet, the HOMO to LUMO single excitation, and the HOMO-1 to LUMO single excitation, respectively (see Figure 3).³⁸ If HF or CASSCF geometry with overestimated polyene chain BLA is used, LUMO is artificially destabilized and thus S₁ and S₂ transitions shift to blue. At the B3LYP geometries, HOMO-1 or HOMO to LUMO double excitation contributes significantly in the S₂ transition since LUMO becomes stable enough with the decreased BLA. In other words, the decreased (increased) BLA results in the red (blue) shift in the S₁ and S₂ excitation energies.

At the CASSCF geometries, half of the positive charge located on the CNH₂ moiety moves toward the β-ionone ring upon S₁ excitation, consistent with previous studies.^8,39 This originates from the nature of the LUMO, whose π-electron density decreases from the SB terminal to β-ionone ring (Figure 3). However, there appears to be no such charge transfer at B3LYP geometries. Therefore, the charge transfer effect seen at CASSCF geometries upon the S₁ transition is artificial and arises from the overestimation of BLA.

B. Deprotonated SBR in Vacuo

The conjugation scheme in the frontier orbitals of the charged PSBR (Figure 3a-e) and neutral SBR (Figure 3f) is different from each other. The effects of computational approximations used for reducing computational cost in CI calculations may thus be different between the two systems. This leads us to investigate several computational factors in accessing the error in post-CASSCF(6/6)/6-31G* calculations of deprotonated SB 11-cis-retinal with T_sel = 10^-6 E_h, as shown in Table 5. These analyses are especially important for estimating the error in ab initio QM/MM calculations of visual pigments with deprotonated SBR, such as E113Q mutant of rhodopsins.

Table 5.

The effect of active space size, basis set and T_sel (Eh) in CASSCF and CI calculations on the computed S₁ and S₂ (in parentheses) vertical excitation energy (nm) of deprotonated SB 11-cis-6-s-cis retinal in vacuo optimized at B3LYP/6-31G* level

Number of Roots	6	6	6	3	3	3
CAS Size	CAS(12/12)	CAS(10/10)	CAS(10/10)	CAS(6/6)	CAS(6/6)	CAS(6/6)
Basis Set	6-31G*	6-31G*	BNANO-TZ2P	6-31G*	BNANO-TZ2P	6-31G*
CASSCF	285 (231)	285 (230)	285 (230)	246 (231)	247 (235)	246 (231)
Tsel	10-6	10-6	10-6	10-6	10-6	10-7
DDCI2+Q	310 (309)	299 (292)	320 (294)	283 (274)	298 (278)	282 (269)

Reducing the CAS(12/12) to CAS(6/6) blue-shifts the CASSCF S₁ excitation energy of SBR by ca. 40 nm, whereas the CASSCF S₂ excitation energy is not affected. It also has 27 (35) nm blue-shift effect for the S₁ (S₂) DDCI2+Q excitation energy. Tightening T_sel from 10^-6 to 10^-7 E_h does not have much influence on the S₁ or S₂ excitation energies. Although the S₁ and S₂ CASSCF as well as the S₂ DDCI2+Q excitation energies are not affected much by the basis set extension from 6-31G* to BNANO-TZ2P, the S₁ DDCI2+Q excitation energy blue-shifts by 21 and 15 nm at CAS(10/10) and CAS(6/6) levels, respectively. With the summation of these error estimates, our practical DDCI2+Q(6/6)/6-31+G* calculations are expected to have a blue-shift error of ca. 50 (35) nm for the S₁ (S₂) excitation energy of SBR relative to the DDCI2+Q(12/12)/BNANO-TZ2P.

C. Bovine Rhodopsin and its Mutants

Bovine Rh and its mutants with PSBR have two absorption maxima at around 500 nm and 380 nm. In our SORCI+Q/MM and MRCISD+Q/MM calculations, S₁ is an absorbing state (f = 1.2-2.0) whereas S₂ is a nonabsorbing state with f ~ 0 due to structural distortions in the protein environment. Therefore, the S₂ state in these calculations cannot be assigned to the experimental absorption band at around 380 nm. As the spectral tuning of visual pigments is mainly discussed on the S₁ absorbing state, we will not address the tuning of the second absorbing state, which will require an extension of the present 3-root calculations. For deprotonated SBR, the S₁ and S₂ states are very close in energy (within 10-20 nm), and S₂ may become absorbing rather than S₁ depending on the computational settings; here we only discuss the absorbing state (f = 1.4-2.0) in relating the calculations to the experiments.

The Effects of Protein Environment

The QM part used in the QM/MM calculation in this section is R1, the full 11-cis-retinal along with covalently bound N/NH moiety of Lys296 for deprotonated/protonated SB linkage. Geometries were obtained by ONIOM(B3LYP:AMBER)-EE optimization. QM/MM excitation energy calculations with TD-B3LYP, SORCI+Q and MRCISD+Q reproduce experimental absorption maximum of WT bovine Rh perfectly (experiment: 500 nm), as shown in Table 6. In the present QM/MM calculations with TD-B3LYP, DDCI2+Q, SORCI+Q and MRCISD+Q, the experimental spectral shift of -20 nm with E122Q mutation^2,5 is also reproduced within 10 nm. Hence, all of these methods can be used in evaluating QM/MM spectral shifts of PSBR with mutations.

Table 6.

The calculated excitation energy (nm) of the absorbing state for the WT bovine Rh and its E122Q and E113Q mutants at protein geometries in the absence (QM-none) and presence (QM/MM) of protein environments (QM region: R1; basis set: 6-31G*)^a

Structure [Experiment]	WT Rh [500 (0)]		E122Q [480 (-20)]		E113Q[384 (-116)]
Retinal Protonation	PSBR		PSBR		SBR
QM Method	QM-none	QM/MM	QM-none	QM/MM	QM-none	QM/MM
TD-B3LYP	560 (0)	503 (0)	566 (6)	492 (-11)	398 (-162)	409 (-94)
DDCI2+Q(12/12)	527 (0)	435 (0)	522 (-5)	427 (-8)	310 (-217)	320 (-115)
SORCI+Q(6/6)	616 (0)	495 (0)	586 (-30)	462 (-33)	327 (-289)	330 (-165)
MRCISD+Q(6/6)	626 (0)	499 (0)	584 (-42)	490 (-9)	323 (-303)	322 (-177)

^aNumbers (nm) in parentheses are spectral shifts relative to the WT bovine Rh. The calculated QM and QM/MM shifts are relative to the QM-none and QM/MM results of WT Rh.

The polarizing protein environment induces an increased BLA for the polyene chain.⁵ This BLA increase is more significant with B3LYP (ca. 0.03 Å⁵) than with CASSCF (ca. 0.01 Å⁸). Thus, CASSCF geometries in protein environments are more similar to B3LYP ones and more reliable than those in the gas phase. Actually, previous CASPT2/MM S₁ excitation energies at CASSCF/AMBER and DFTB (being similar to B3LYP one, see ref 5) geometries are very similar to each other (480 and 506 nm, respectively) for bovine Rh.^8,39

In our previous TD-B3LYP/MM study,⁵ we reproduced experimental spectral shifts due to mutations on bovine Rh within 10 nm except for E113Q mutant. Here we reinvestigate the E113Q mutant with SBR by using MR methods. As our post-CASSCF calculations are expected to have ca. 15 (50) nm red (blue) shift error for the absorbing state of PSBR (SBR), our MR calculations with present settings should overestimate the spectral shift going from WT Rh to E113Q mutant by ca. 65 nm. As expected, SORCI+Q(6/6)/MM and MRCISD+Q(6/6)/MM shifts are ca. 65 nm larger than the experimental shift.⁴⁰ Whereas DDCI2+Q/MM reproduces the SORCI+Q/MM and MRCISD+Q/MM excitation energies of SBR (Table 6), its result for S₁ of PSBR is ca. 65 nm blue-shifted since some contributing double excitations are ignored. Therefore, going from PSBR to SBR, the error arising from our computational settings (ca. 50 nm red shift with CAS(12/12)) and the intrinsic error of DDCI2 for S₁ of PSBR (ca. 65 nm blue shift) tend to cancel to each other. Hence, DDCI2+Q(12/12)/MM reproduces the experimental shift due to error cancellation without applying any correction.

The Effects of Glu113 Counterion and Retinal Protonation

DDCI2+Q reproduces the experimental shifts reasonably well with the current settings as a result of error cancellation. Therefore, we will assess the effect of Glu113 counterion on the absorbing state of 11-cis-retinal with 6-root DDCI2+Q(12/12)/6-31G* calculations, as shown in Table 7.

Table 7.

Gas-phase QM-none (e.g., QM at protein geometry) and QM/MM excitation energies (nm) for the absorbing state of bovine Rh in the absence (R1) and presence (R2) of Glu113 in the QM region and the effect retinal protonation (basis set: 6-31G*) along with QM and QM/MM spectral shifts with deprotonation of retinal (in parentheses) and with inclusion of Glu113 in the QM model (△)

Protonation State	Method	QM region = R1 (without Glu113)	QM region = R2 (with Glu113)	△ = E(R2) - E(R1)
QM=TD-B3LYP
PSBR (deprotonated Glu113)	QM-none	560 (0)	500 (0)	-60
	QM/MM	503 (0)	499 (0)	-4
SBR with protonated Glu113	QM-none	408 (152)	423 (77)	15
	QM/MM	429 (74)	435 (64)	6
SBR with deprotonated Glu113	QM-none	396 (164)	380 (120)	-16
	QM/MM	380 (123)	382 (117)	-2
QM=DDCI2+Q(12/12)
PSBR (deprotonated Glu113)	QM-none	527 (0)	395 (0)	-133
	QM/MM	435 (0)	432 (0)	-2
SBR with protonated Glu113	QM-none	318 (209)	309 (86)	-9
	QM/MM	336 (99)	337 (95)	1
SBR with deprotonated Glu113	QM-none	313 (214)	298 (97)	-15
	QM/MM	309 (126)	294 (138)	-15

When Glu113 is included in the gas-phase QM model of PSBR at the protein geometry, the S₁ excitation energy blue-shifts at DDCI2+Q level by ca. 130 nm. This shift agrees with previous CASPT2 results within 30 nm.^6,8,39,41,42 The remaining protein environment red-shifts the S₁ excitation energy by ca. 35 nm, similar to a previous CASPT2/ANO study at DFTB geometry.⁶ This shift is significantly larger (ca. 100 nm) in CASPT2 studies at CASSCF gas phase geometry,^8,39 which should not be used because of overestimated BLA. The calculated S₁ excitation energy of PSBR at TD-B3LYP/MM and DDCI2+Q/MM levels does not depend on the presence or absence of Glu113 in the QM region (R1 vs R2). Hence, Glu113 contributes to the S₀ and S₁ states equally and the Glu113 point-charge model can be safely used in calculating the S₁ excitation energy of retinal.

Although previous SACCI/AMBER⁹ and aug-MCQDPT2/EFP⁷ calculations reproduce the experimental absorption maximum of bovine Rh, their energy contributions are somewhat different to each other and from the other studies. First, concerning the SACCI/AMBER result, inclusion of Glu113 in the QM region, e.g. R2, is necessary to reproduce experimental S₁ absorption maximum. It blue-shifts the SACCI/AMBER S₁ excitation energy by ca. 100 nm.⁹ However, such a charge transfer effect from Glu113 to retinal has not been found in the present ab initio MR-QM/MM and the previous TD-B3LYP/MM calculations. Furthermore, the SACCI S₁ excitation energy with R1 has a large error of more than 200 nm in the gas phase. The source of errors in the SACCI and SACCI/MM excitation energies with R1 remains a puzzle.^9,13 Next, concerning the aug-MCQDPT2/EFP⁷ result, the protein environment around retinal and Glu113 (an R2-like QM region) red-shifts S₁ excitation energy (QM-none = 388 nm vs. QM/MM = 515 nm) more than 100 nm.⁷ However, all previous calculations with R2 (TD-B3LYP,⁵ CASPT2⁶ and the present DDCI2+Q) find a small contribution from the protein environment. It seems that this discrepancy comes from significant blue-shift error in the gas-phase aug-MCQDPT2 result.⁷

TD-B3LYP has a significant error of 110 nm for the S₁ excited state of protonated R1 in the gas phase (Table 3) as a result of the use of nonlocal exchange functionals.¹³ The gas phase TD-B3LYP S₁ excitation energy of protonated R1 at the protein geometry has a smaller error of ca. 60 nm, i.e. the difference between TD-B3LYP gas-phase spectral shifts relating to R1 with the corresponding DDCI2+Q shifts in Table 7. The inclusion of the effect of Glu113 fixes the error in TD-B3LYP calculations significantly. Hence, TD-B3LYP can be useful for estimating excitation energies in protein environments both with R1 and R2 QM regions as well as in the gas phase with R2 (but not with R1). This means that the conclusions of the previous TD-B3LYP/AMBER study remain true although the gas phase results with R1 are blue-shifted.⁵

Deprotonation of retinal blue-shifts the absorption maximum by ca. 90 nm (Table 7). The inclusion of Glu113 in the QM region and/or of the protein environment does not affect the SBR excitation energies much in both TD-B3LYP and DDCI2+Q calculations (less than 20 nm, see ref 5 for detailed discussions). When the interaction between SBR and its counterion is weakened, the absorbing state blue-shifts, as seen from the comparison of the results with the protonated and deprotonated Glu113.

IV. Discussion and Conclusions

We have investigated vertical excitation energies of retinal in vacuo and bovine Rh along with its E122Q and E113Q mutants by using MR ab initio methods in combination with the QM/MM method in order to clarify the origins of differences among various previously published calculations and to provide computational strategies for accurately calculating absorption spectra. MR excitation energy calculations are too demanding with sufficiently large QM regions, active spaces, basis sets and configuration selections. Therefore, we need to adjust these computational settings looser than desired, to a certain extent. Taking each of the settings at a desired level while all of the remaining ones are fixed at lower levels, we roughly estimated the errors in reducing computational accuracy. For example, the post-CASSCF(6/6)/6-31G* calculations with T_sel = 10^-6 E_h has a red-shift (blue-shift) error of ca. 15 (50) nm for the S₁ absorbing state of PSBR (SBR). Applying these error corrections to SORCI+Q(6/6)/6-31G* and MRCISD+Q(6/6)/6-31G* excitation energies with T_sel = 10^-6 E_h, the experimental absorption maxima are reproduced quite well.

The relatively inexpensive DDCI2+Q method has an intrinsic blue-shift error of ca. 65 nm in calculating the S₁ excitation energy of PSBR in the gas-phase and protein environment as a result of the ignored double excitations. As this error is constant, (a) absolute values of excitation energies of PSBR can be estimated from the calculated DDCI2+Q excitation energies and (b) DDCI2+Q reproduces experimental spectral shifts of PSBR due to mutation reasonably well. The absorbing excitation energy of SBR calculated with DDCI2+Q is almost the same as that with higher level SORCI+Q and MRCISD+Q calculations, e.g. ca. 60 nm blue-shifted compared with experiment due to computational settings. As this error in SBR and the intrinsic error in PSBR DDCI2+Q excitation energies are almost the same, the experimental spectral shift due to deprotonation of retinal can be reproduced well by using the bare DDCI2+Q results.

The TD-B3LYP S₁ excitation energy of retinal in the gas phase has a significant blue-shift error arising from the use of nonlocal exchange functionals.¹³ The net error in the excitation energy calculations with TD-B3LYP diminishes significantly when including the effect of H-bonding counterion (Glu113) of retinal.

The level of ground-state geometry optimization has a large impact on the computed vertical excitation energies. In the post-CASSCF excitation energy calculations, B3LYP geometries give results that are consistent with experiment both in the gas phase and in the protein environment. S₁ may have up to 100 nm blue-shift error in the gas phase if the CASSCF structure with overestimated BLA is used. However, at CASSCF/MM geometries, the error in the post-CASSCF/MM excitation energies is small since polarizing field of protein environment makes the CASSCF structure closer to the B3LYP structure. Our calculations indicate that the large error in the previous CASPT2 S₁ excitation energy in vacuo¹² arises mainly from the use of an inappropriate CASSCF geometry.

The previous^8,39 and present calculations at CASSCF geometries find that half of the positive charge located on the SB terminal moves toward β-ionone ring upon S₀ to S₁ excitation. However, there appears to be no such charge transfer at the more appropriate B3LYP geometries.

All-trans to 11-cis isomerization of retinal has no significant effect on the S₁ excitation energy in our MR calculations, in agreement with experiments,^3,4 showing almost the same absorption spectra for both isomers. The 6-s-cis conformer of all-trans retinal is more stable than the 6-s-trans one in the present MR calculations. Moreover, its calculated S₂ excitation energy is more consistent with the experimental value. Therefore, experimental spectra of all-trans retinal^3,4 belong mainly to the 6-s-cis conformer, in agreement with ground state energetics. Our calculations also suggest that the shoulder of the experimental absorption spectrum of retinal in vacuo at the S₁ absorbing band belongs to the second electronic transition (S₂), contrary to previous tentative assignment to vibrational state of S₁ or to the S₁ band of a retinal isomar.

Glu113 has a blue-shift effect of ca. 130 nm on the S₁ excitation energy of PSBR whereas it has almost no effect on that of SBR. The net Glu113 effect for PSBR is mainly electrostatic in the present MR and the previous TD-B3LYP⁵ calculations. In other words, S₀ to S₁ excitation does not involve any charge transfer from Glu113 to retinal. Thus, it is appropriate to place Glu113 in the MM part of QM/MM calculations. The protein environment of retinal other than Glu113 has small effect on the S₁ excitation energy. Deprotonation of retinal may play an important role in the UV vision of vertebrates. It blue-shifts the S₁ excitation energy by ca. 90 nm.

In summary, the present calculations pinpoint the origin of most of the conflicting issues in literature and thus enhance significantly our understanding on spectral tuning mechanism in retinal systems. The relatively inexpensive DDCI2+Q method can be used in calculating spectral shifts. TD-B3LYP is also useful in calculating the S₁ excitation energy shifts in protein environments.