Abstract
How the axonal distribution of Na+ channels affects the precision of spike timing is not well understood. We addressed this question in auditory relay neurons of the avian nucleus magnocellularis. These neurons encode and convey information about the fine structure of sounds to which they are tuned by generating precisely timed action potentials in response to synaptic inputs. Patterns of synaptic inputs differ as a function of tuning. A small number of large inputs innervate high- and middle-frequency neurons, while a large number of small inputs innervate low-frequency neurons. We found that the distribution and density of Na+ channels in the axon initial segments varied with the synaptic inputs, and were distinct in the low-frequency neurons. Low-frequency neurons had a higher density of Na+ channels within a longer axonal stretch, and showed a larger spike amplitude and whole-cell Na+ current than high/middle-frequency neurons. Computer simulations revealed that for low-frequency neurons, a large number of Na+ channels were crucial for preserving spike timing because it overcame Na+ current inactivation and K+ current activation during compound EPSPs evoked by converging small inputs. In contrast, fewer channels were sufficient to generate a spike with high precision in response to an EPSP induced by a single massive input in the high/middle-frequency neurons. Thus the axonal Na+ channel distribution is effectively coupled with synaptic inputs, allowing these neurons to convey auditory information in the timing of firing.
Sounds are represented in the temporal firing patterns of neurons with remarkable precision in the auditory nervous system. This representation is based on the ability of auditory neurons to generate spikes whose timing reflects the phase of sound waveforms (Kiang, 1965). Neurons in nucleus magnocellularis (NM) of birds relay the temporal information with submillisecond precision from the auditory nerve fibres to binaural coincidence detectors for sound source localization in nucleus laminaris (Sullivan & Konishi, 1984; Warchol & Dallos, 1990). NM neurons are tuned to a specific frequency of sound (characteristic frequency), and arranged tonotopically along a rostro-medial (high frequency) to caudo-lateral (low frequency) axis (Rubel & Parks, 1975). The temporal precision of auditory nerve activity decreases toward the low frequency (Hill et al. 1989; Koppl, 1997; Fukui et al. 2006); the jitter, defined as the standard deviation (s.d.) of spike timing, increases from 0.1 ms at the high frequency to 0.3 ms at the low frequency in the chicken. Correspondingly, NM neurons differ in the synaptic inputs as a function of the frequency to which they are tuned. High- and middle-frequency neurons receive a massive EPSP from one or a few end-bulb terminals (Parks & Rubel, 1978; Jhaveri & Morest, 1982; Carr & Boudreau, 1991; Fukui & Ohmori, 2004), any of which is robust enough to drive a spike (Trussell, 1999). On the other hand, low-frequency neurons require summation of converging EPSPs from multiple-bouton terminals to generate spikes (Carr & Boudreau, 1991; Koppl, 1994; Fukui & Ohmori, 2004). It has been proposed that the summation of EPSPs made by multiple inputs corrects for variability in the timing of each input and thus reduces the temporal dispersion in postsynaptic spiking (Rothman et al. 1993; Joris et al. 1994; Xu-Friedman & Regehr, 2005; Fukui et al. 2006; Joris & Smith, 2008).
Temporal coding mechanisms in NM neurons have been explored in synaptic transmission (Trussell, 1999) and the role of postsynaptic K+ channels underlying low-voltage-activated (IKLVA) and high-voltage-activated (IKHVA) K+ currents; expression of such currents increases toward the high frequency (Reyes et al. 1994; Koyano et al. 1996; Rathouz & Trussell, 1998; Parameshwaran et al. 2001; Fukui & Ohmori, 2004). On the other hand, the precision of spike timing is also influenced by the distribution and the properties of voltage-gated Na+ (Nav) channels. In particular, NM neurons differ in the number and the size of synaptic inputs depending on their tuning frequency and Nav channels likely play a role in converting synaptic inputs to precisely timed action potentials.
In the present study in slices, we separated NM neurons into three groups along the tonotopic axis, and examined the distribution and the properties of Nav channels and their contributions to the temporal coding of NM neurons. We found that Nav channels at the axon initial segment were more abundant in the low-frequency neurons than in the higher-frequency neurons.
Methods
Electrophysiology
The care of experimental animals was in accordance with the guidelines of Kyoto University. Chicks (P3–8) were deeply anaesthetized with halothane (Fluothane, Takeda, Japan), and coronal brain slices (250 μm) were obtained after decapitation (Kuba et al. 2003). During experiments, slices were perfused with an artificial cerebrospinal fluid (ACSF, concentrations in mm: 125 NaCl, 2.5 KCl, 26 NaHCO3, 1.25 NaHPO4, 2 CaCl2, 1 MgCl2 and 17 glucose, pH 7.4). Recordings were made using a patch-clamp amplifier (Axopatch 200B, Axon Instuments, Union City, CA, USA) (Kuba et al. 2003). Recording temperature was 40°C, the body temperature of birds, for current clamp and 20°C for voltage clamp, unless otherwise stated. Pipettes for whole-cell recordings had a resistance of 3–4 MΩ (3 μm tip diameter) when filled with a KCl-based solution (160 KCl, 0.2 EGTA, 10 Hepes-KOH, pH 7.4) for current clamp (Figs 1,2,7 and 10) and a CsCl-based solution (150 CsCl, 10 NaCl, 0.2 EGTA, 10 Hepes-CsOH, pH 7.4) for voltage clamp (Figs 5 and 6). In whole-cell voltage-clamp recordings, [Na+]o was decreased to 72.3 mm (Fig. 5A, ENa=+51.0 mV) or 27.3 mm (Fig. 6A and C, ENa=+25.8 mV) by isotonic replacement of Na+ with TEA+, and 4-aminopyridine (0.2 mm) and Cs+ (5 mm) were added to the bath. In cell-attached recordings, pipettes were 2–3 MΩ (5 μm tip diameter, Fig. 5B), and ACSF containing 4-aminopyridine (0.2 mm), TEA (3 mm) and Cs+ (5 mm) was used in the pipettes and in the bath. With this external solution and the KCl-based internal solution, the resting potential measured under the whole-cell condition was −53.3 ± 0.8 mV (n= 4) and −49.3 ± 0.9 mV (n= 3) for the high/middle-frequency and low-frequency neurons, respectively. Therefore, the resting potential during cell-attached recordings was assumed to be −50 mV (Fig. 5B). Care was taken to optimize the space clamp when Na+ currents were recorded, and we reduced the driving force of Na+ current and minimized the series resistance (described above), and slowed the Na+ current time course by lowering the recording temperature (20°C). The Na+ current densities in the soma membrane were calculated with the surface areas of the soma (about 900 μm2) for whole-cell clamp and the patch membrane (about 13 μm2) for cell-attached clamp, which were obtained from the morphology of labelled NM neurons (long and short axis of 20 and 16 μm, see Kuba et al. 2005 for calculation) and the diameter of recording pipettes, respectively (Fig. 5D). Antidromic spikes were evoked with a bipolar tungsten electrode placed medially to NM in the presence of 40 μm bicuculline (Sigma) and 40 μm 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX; Tocris) (Figs 1 and 2). Peak amplitude of orthodromic and antidromic spikes was measured between the baseline and the peak (Fig. 1D). Half-amplitude widths were measured at the midpoint between the threshold and the peak for orthodromic spikes, and between the baseline and the peak for antidromic spikes (Fig. 1F). When EPSPs were evoked with a bipolar tungsten electrode or glass capillaries filled with ACSF, postsynaptic Na+ currents were blocked by filling 5–10 mm QX314 (Alomone) in the recording pipette (Fig. 7). Pipettes were coated with a silicone resin (Sylgard, Dow Corning Asia), and were fire polished before use. The electrode capacitance and series resistance (3–10 MΩ) were estimated and compensated electronically up to 99%. The liquid junction potential (3.1–8.0 mV) was corrected after the experiments (Kuba et al. 2003). Data were sampled at 20–100 kHz, and were low-pass filtered at 10 kHz. Statistical significance was tested with Student's t test for paired or unpaired data, while one-way ANOVA and post hoc test (Sheffe's F test) were used for multiple data. Values are presented as means ± standard error of the mean (n= number of cells).
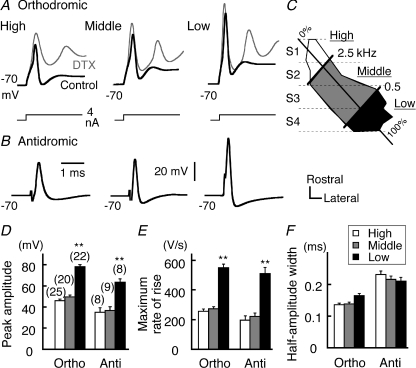
Figure 1. Spike amplitude is largest in low-frequency neurons.
A and B, orthodromic (A) and antidromic (B) spikes were induced by injecting a depolarizing current into the soma and by stimulating the axon, respectively (see Methods). Gray traces in A were recorded under the block of IKLVA with dendrotoxin (DTX, 80 nm). C, NM neurons were classified into three frequency groups, according to the medio-lateral position in each slice (see Methods). Four coronal slices (S1–S4) were obtained across NM. D–E, peak amplitude (D), maximum rate of rise (E) and half-amplitude width (F) of spikes. Here and in the following figures, error bars indicate standard error of the mean. The numbers in parenthesis are the number of cells. **P < 0.01 and *P < 0.05. Comparisons were made against middle frequency in Figs 1–5. Resting membrane potential was maintained at −70 mV with a constant current in current clamp recordings.
Figure 2. Antidromic spikes during somatic depolarization.
A, antidromic spikes were induced at various timings against somatic depolarization. Eight traces were superimposed. B, antidromic spikes before and during depolarization. C, the amplitude was reduced during depolarization to a similar extent across NM.
Figure 7. Low-frequency neurons receive multiple small Inputs.
A, EPSPs recorded under the block of Na+ current with QX314 (5–10 mm). An increase in the stimulus intensity evoked large EPSPs in an all-or-none manner at high/middle frequency, while EPSPs were small and graded at low frequency. B–D, amplitude (B), maximum rate of rise (C) and 10–90% rise time (D) of minimum EPSPs (arrows).
Figure 10. Slow rise of depolarization reduces maximum rate of rise of spikes and increases the threshold in actual low-frequency NM neurons.
Spikes (upper) were induced by a rectangular current (0.5 ms duration, A) or a ramp current (1 ms duration, B). Lower traces are the time derivatives. Threshold current was larger by 11.2 ± 0.3% (n= 9, P < 0.01), threshold potential was higher by 1.5 ± 0.6 mV (n= 9, P < 0.05, arrows), and maximum rate of rise of spikes was smaller by 19.7 ± 3.1% (n= 9, P < 0.05) for the ramp current compared with the rectangular current.
Figure 5. Whole-cell but not cell-attached Na+ current is large in low-frequency neurons.
A and B, ensemble averaged Na+ current in NM neurons. A, whole-cell and B, cell-attached conditions. C, amplitude of whole-cell Na+ current measured at −30 mV ([Na+]o of 72.3 mm, see Methods). D, Na+ current density calculated on the assumption that Nav channels exist only on the somatic membrane (see Methods). Recordings were made from 10 cells in the high/middle-frequency neurons, and from 9 cells in the low-CF neurons. Among them, only 5 cells and 3 cells, respectively, showed Na+ current in the patch membranes. Large discrepancies between the two recording conditions indicate that Nav channels are present predominantly in the axon.
Figure 6. Inactivation of Na+ current is not different across frequencies.
A, Na+ currents with a 10 ms prepulse from −90 mV to −30 mV. B, voltage dependence of Na+ current inactivation. C, pair of Na+ currents induced at different time intervals (1–8.5 ms). D, recovery time course of Na+ current inactivation. Recovery time course was fitted with a double exponential function (see Results). [Na+]o was 27.3 mm (see Methods).
Classification of NM neurons
We classified NM neurons into three frequency groups, as previously described (Fukui & Ohmori, 2004): high (2.5–4 kHz), middle (0.5–2.5 kHz) and low (0.1–0.5 kHz) frequency neurons. Briefly, the outline of NM was reconstructed (see Fig. 1C), and was superimposed on a linear function between the characteristic frequency and the anteromedial–caudolateral position of neurons (Rubel & Parks, 1975). A distance of 25% from the rostromedial edge would correspond to characteristic frequencies of 2.5 kHz, and that of 75% to 0.5 kHz. We obtained four coronal slices (S1–S4) of 250 μm thicknesses across NM; the classification was made according to the medio-lateral position in each slice (see Fukui & Ohmori, 2004).
Immunohistochemistry
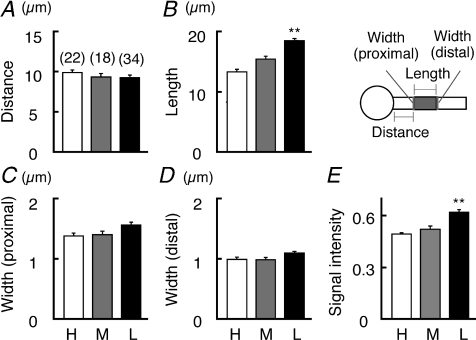
Guinea pig anti-chick Pan-Nav polyclonal antibody (0.65 μg ml−1), Nav1.6 polyclonal antibody (0.49 μg ml−1) (see Kuba et al. 2006), and mouse monoclonal Pan-Nav antibody (5 μg ml−1, Sigma) were used for immunohistochemistry. Pre-adsorption of the antibodies with corresponding peptides (20 μg ml−1) blocked the staining in the chicken brain sections. Detailed immunostaining procedures were previously described (Kuba et al. 2005). Briefly, chicks (P3–8) were perfused transcardially with periodate–lysine–paraformardehyde fixative (ml (g body weight)−1): 2% (w/v) paraformardehyde, 2.7% (w/v) lysine HCl (Nacalai, Japan), 0.21% (w/v) NaIO4, 0.1% (w/v) Na2HPO4. The brainstem was postfixed for 4 h at 4°C. After cryoprotection with 30% (w/w) sucrose in phosphate buffered saline (PBS), coronal sections (20–30 μm) were obtained. The sections were incubated overnight with the primary antibodies, then with Alexa594-conjugated secondary antibodies (10 μg ml−1, Molecular Probes) for 2 h, and were observed under a confocal laser-scanning microscope (FV1000, Olympus). NM neurons were retrogradely labelled by stereotaxic injection of Alexa488-conjugated dextran (Molecular Probes; Mr 10 000, 10% in PBS) into NL of P3–6 chicks under anaesthesia. Two days after the surgery, sections were prepared for immunohistochemistry. The geometry and signal intensity of Nav channel clusters (Fig. 4) were measured as follows. The distance was between the proximal end of the cluster and the soma, the length was between the proximal and distal end, the widths were at both proximal and distal ends, and the intensity was along the cluster. The intensity did not vary within the cluster, when measured separately at the proximal and distal sides. The signal intensity of the cluster was normalized to that of adjacent nodes of Ranvier (dot-like structures). Signal intensity of the nodes did not vary along the tonotopic axis, when calibrated with the nodes in the medial vestibular nucleus in each slice.
Figure 4. Nav channels are abundant at the axon initial segment in low-frequency neurons.
Distance (A), length (B), width at the proximal (C) and distal (D) ends, and signal intensity (E) of Nav channel cluster (see Methods). Schema indicates geometric definition of Nav channel cluster (grey). Measurements were made from 5 chicks.
Computational model
Neuronal modelling and simulation were performed with NEURON 5.8. The model was modified from that reported previously (Kuba et al. 2006), on the basis of the morphological and electrophysiological data of the chick NM neurons in the low-frequency region (Fukui & Ohmori, 2004). The model consisted of multiple sections: a soma (16 μm in length and diameter); and an axon with a non-myelinated axon hillock (10 μm length), a non-myelinated initial segment (20 μm length), 10 myelinated internodes, and 10 nodes of Ranvier. Hodgkin–Huxley type Na+ current (Rothman & Manis, 2003), IKLVA and IKHVA (Rathouz & Trussell, 1998; Simon et al. 1999) followed the web-accessible Model DB (Hines et al. 2004). Activation and inactivation parameters of the Na+ current were modified according to the observations in NM neurons (Fig. 6); V1/2 and slope factor were −39 mV and 5 mV for activation and −58 mV and 5 mV for inactivation, respectively. Na+ current and IKLVA and IKHVA were incorporated in soma, initial segment and nodes. gNa (0.01 S cm−2), gKLVA (0.005 S cm−2) and gKHVA (0.015 S cm−2) in the soma were determined according to the experimental observations (Fukui & Ohmori, 2004). gNa (3 S cm−2), gKLVA (0.1 S cm−2) and gKHVA (1.5 S cm−2) in the axon were determined in order to simulate the spike shape of low-frequency neurons, with the arrangement of an initial segment of 20 μm length at a 10 μm distance (see Supplemental Fig. 3). Temperature was 40°C and Q10 was 3.0. Differences in the temperature dependence of IKLVA and IKHVA were not incorporated (Cao & Oertel, 2005). Time step of calculation was 12.5 μs. Synaptic conductance has a time profile of an α function (=gsynt/τsynexp(1 –t/τsyn)) with a time constant (τsyn) of 0.3 ms, corresponding to that of EPSCs in low-frequency neurons (Fukui & Ohmori, 2004). The minimum synaptic conductance (4 nS, Figs 8, 9 and 11) was determined to induce an EPSP amplitude comparable to that observed in low-frequency neurons (around 5–10 mV).
Figure 8. Synaptic convergence Improves temporal coding.
Spikes induced by either single input (A) or multiple inputs (B) of equal strength in a model neuron. Aa and Ba, raster plots of individual inputs during 50 cycles; Ab and Bb, time histogram of individual inputs during 50 cycles; Ac and Bc, spikes during 10 cycles; Ad and Bd, time histogram of outputs during 50 cycles. Sound waveforms of 200 Hz were overlaid on the raster. Insets in Ac and Bc are spikes aligned at the first EPSP onset (vertical broken lines) to show the spike induction at a short and constant latency in single input neuron. Scale bar in inset, 0.5 ms. Number of inputs at each cycle (SynNo) and unitary conductance (SynG) were adjusted so that the total conductance (SynNo × SynG) became 1.3 times of threshold conductance (see below); SynG = 44 nS for single input, while SynNo = 16 and SynG = 4 nS for multiple inputs. Individual inputs were normally distributed with a s.d. of 0.3 ms (input jitter, see Results) in this and following figures. Spontaneous activity was not included for simplicity. C, output jitter (see Results) as a function of SynG and SynNo. Subthreshold responses were indicated as a shaded area. Output jitter (D) and firing probability (E) plotted against the total synaptic conductance. Threshold conductance was defined as total synaptic conductance to induce firing probability above 0.2 (horizontal broken line in E), and N denotes below threshold conductance here and in Fig. 11.
Figure 9. Synaptic convergence slows EPSP, activates IKLVA and Inactivates Na+ current.
A and B, EPSPs under the block of spike induction by setting Na+ conductance (gNa) to 0 S cm−2. A, a single input (SynG = 44 nS); B, multiple inputs (SynNo = 16, SynG = 4 nS). Aa and Ba, time histogram of input conductance; Ab and Bb, EPSPs (black); Ac and Bc, time derivatives (black); Ad and Bd, inactivation of Na+ current (hNa, black) and activation of IKLVA (nKLVA, grey). Time course of unitary input is shown in inset (top). Truncated grey traces (Ab, Ac, Bb, Bc) are spike responses with control gNa (3 S cm−2). Two vertical broken lines indicate the onset of EPSPs and spikes. Increase in the input jitter decreased maximus rate of rise of EPSPs (C) and hNa (D), and increased nKLVA (E). In C–E, SynNo was adjusted to induce EPSPs of similar amplitudes, and was 11, 13 and 16 for s.d. of 0, 0.15 and 0.3, respectively. Note that threshold potential (arrows) is increased in multiple inputs (Bb).
Figure 11. Large Na+ conductance is crucial for precise and reliable firings during synaptic convergence.
A, output jitter (upper) and firing probability (lower) plotted against gNa in the axon. B, 10 superimposed EPSPs induced by inputs in A. Traces are the same as those in Fig. 8, but the spike induction was blocked by setting gNa to 0 S cm−2. Upper, single input neuron (SynG = 44 nS); lower, multiple input neuron (SynNo = 16, SynG = 4 nS). Small circles indicate onsets of spike induction in neurons with control (×1, 3 S cm−2, grey) and large gNa (×4, 12 S cm−2, white) in B and C. Arrows indicate the spike thresholds. C, an example of EPSP (upper) and its time derivative (lower) in multiple input neuron (gNa of 0 S cm−2). Large gNa shortens the spike onset latency and increases the slope of EPSP at the point. Overlaid grey traces are responses with control and large gNa. Large gNa increased hNa (D) and decreased nKLVA (E) at the spike onset, and reduced the fluctuation in onset-to-peak time of spike (F).
Results
Spike amplitude differs along the tonotopic axis
Spikes were compared among the three frequency groups in NM (see Fig. 1C and Methods). Both orthodromic and antidromic spikes (see Methods) showed a difference in the peak amplitude among the three frequency groups, being the largest in the low-frequency neurons (P < 0.01 by ANOVA) (Fig. 1A black, B and D), while the time courses were not different across NM (Fig. 1F). The change in amplitude was paralleled by a difference in the maximum rate of rise (Fig. 1E), suggesting the greatest Na+ conductance in the low-frequency neurons. Alternatively, the dendrotoxin (DTX)-sensitive IKLVA might shape the difference in spike amplitude. Because of its rapid activation kinetics (Rathouz & Trussell, 1998), the IKLVA would counterbalance the inward Na+ current and reduce the spike amplitude. Nevertheless, under the blockade of IKLVA by DTX (80 nm), the amplitude and maximum rate of rise of orthodromic spike in the high- and middle-frequency neurons were still far smaller than those in the low-frequency neurons (Fig. 1A grey): the maximum rate of rise in DTX was 330.5 ± 17.0 V s−1 (n= 10), 370.4 ± 16.3 V s−1 (n= 11), 604.4 ± 79.1 V s−1 (n= 3) for high-, middle- and low-frequency neurons, respectively (P < 0.01 by ANOVA). The tonotopic differences in the amplitude and maximum rate of rise of spikes were not affected by TEA (5 mm, blocker of IKHVA) (data not shown). Thus, the Na+ conductance is distinct at the low-frequency region of NM.
Site of spike generation would be close to the soma in NM
Another possible explanation for the tonotopic difference in the spike amplitude is that the distance between the soma and the spike generation site in the axon varies tonotopically, as shown in NL neurons (Kuba et al. 2006). To examine this possibility, antidromic spikes were induced at various times relative to the subthreshold somatic depolarization (5–10 mV, Fig. 2A). If the spikes are generated near the soma, somatic depolarization would be expected to increase inactivation and to reduce the antidromic spike height (Kuba et al. 2006). The peak of antidromic spikes was gradually decreased during the somatic depolarization (Fig. 2A, grey circles 2–4) compared with the control (black circles) to an extent similar in the three frequency regions (Fig. 2B and C). The results suggest that Nav channels are located near or at the soma irrespective of tuning frequency.
Nav channels accumulate most abundantly at the axon initial segment of low-frequency neurons
The analysis of spikes indicated that Nav channels are arranged near or at the soma of NM neurons and are the most abundant in low-frequency neurons. We examined the density and the locus of Nav channels in NM neurons with immunohistochemistry using an antibody that recognizes all known Nav channels (Pan Nav, see Methods). In NM, strong immunoreactivity for Nav channels appeared as either fibre-like (red arrowheads) or small dot-like structures (yellow arrowheads) (Fig. 3B). These two types of structure were also immunopositive for Nav1.6 (Supplemental Fig. 1A and B). These observations are the same as in NL, where the fibre-like structures were at axon initial segments of NL neurons, while the dot-like structures were at nodes of Ranvier (Kuba et al. 2006).
Figure 3. Distribution of Nav channels in NM neurons.
Aa–c, retrogradely labelled NM neurons. Note that projection fibres from contralateral NM are anterogradely labelled in NL (Aa). Ba–c, immunosignals of Pan-Nav channels (red and yellow arrowheads). Ca–c, Nav channels (red) were localized on the proximal axon of retrogradely labelled NM neuron (green). A series of 3–4 confocal images were stacked with an axial distance of 440 nm in C. A rail-track-like pattern of Nav signals indicates their localization on the axonal membrane (double arrowheads).
To determine the subcellular localization of the fibre-like structures, we labelled NM neurons by injecting a retrograde tracer into the contralateral NL (Fig. 3A, see Methods), and stained with the Pan Nav antibody (Fig. 3C). Double staining revealed that the fibre-like Nav-channel clusters (red) were on the proximal axon of labelled NM neurons (green), presumably the axon initial segment (see also Supplemental Fig. 1C and D), suggesting that the cluster is the site of spike generation. The clusters were located close to the soma, and the distance from the soma was not different in the three frequency regions (less than 10 μm, Fig. 4A). The width of clusters at the proximal end was slightly higher at the low frequency (P= 0.04 and P= 0.11 compared with the high and middle frequencies, respectively) (Fig. 4C), while that at the distal end was not different (Fig. 4D). In contrast, the length of clusters varied among the frequency regions, being significantly longer at the low-frequency regions (Fig. 4B). Furthermore, the intensity of Nav immunosignals in the clusters was greatest for low-frequency neurons (Fig. 4E, see Methods), indicating the highest Nav channel density. Therefore, more Nav channels accumulated at the axon initial segment in low-frequency neurons than in high- and middle-frequency neurons.
Axonal component of Na+ current is the largest at low frequency
We tested the conclusion from immunohistochemical findings that Nav channels are more abundant in low-frequency NM neurons by recording Na+ currents (Fig. 5). The whole-cell or cell-attached clamp was applied to the cell soma at 20°C in the presence of intracellular Cs+ and reduced extracellular Na+ to achieve a better space clamp (see Methods). The whole-cell recording showed an inward Na+ current during a depolarizing pulse to −30 mV (Fig. 5A). However, their amplitudes differed. At [Na+]o of 72.3 mm, the amplitude in the low-frequency neurons was about 1.3–1.5 times larger than that in high- and middle-frequency neurons (Fig. 5C), while their membrane capacitances were not different: 22 ± 1.2 pF (n= 7), 21.6 ± 1.4 pF (n= 8), and 20.5 ± 1.1 pF (n= 8) for high-, middle-, and low-frequency neurons, respectively (P= 0.69 by ANOVA). Na+ current amplitude in these regions also differed in reduced [Na+]o of 27.3 mm (P < 0.05), which should improve the voltage clamp further (see Fig. 6A and C). In contrast, Na+ currents recorded from the cell-attached patch membranes of cell soma had similar amplitudes in both high/middle-frequency and low-frequency neurons (Fig. 5B). They were 13.1 ± 1.5 pA (5 cells out of trials in 10 cells, see legend of Fig. 5) and 13.7 ± 0.4 pA (3 out of 9 cells) (P= 0.78), respectively, in response to depolarization to −10 mV (estimated potential: see Methods). Na+ current densities (see Methods) were 7–9 times larger for the whole-cell clamp (light grey columns) than for the cell-attached clamp (dark grey columns) in both high/middle-frequency and low-frequency neurons (Fig. 5D), indicating that the whole-cell Na+ current must mostly reflect that in the axon. Thus, the greatest whole-cell Na+ current in the low-frequency neurons indicates that the axonal Na+ conductance is the largest in the low-frequency neurons, consistent with the immunohistochemical findings (Figs 3 and 4).
Voltage dependence and kinetics of Na+ current inactivation are not different throughout NM
The biophysical properties, as well as the number and the location, of Nav channels are crucial for spike generation. The inactivation of Nav channels in particular should critically affect the precision of firing (Torkkeli & French, 2002; Leao et al. 2005). We therefore examined the characteristics of the inactivation of Na+ current in NM neurons at the three frequency regions (Fig. 6). The voltage dependence of steady-state inactivation (hNa) was measured with a depolarizing pulse to −30 mV following a prepulse potential ranging from −90 mV to −30 mV (Fig. 6A). The Na+ current progressively inactivated as the prepulse depolarized in both types of neurons. The voltage dependence of hNa was not different between the high/middle- and low-frequency neurons (Fig. 6B): V1/2 was −57.5 ± 1.1 mV (n= 7) for the high/middle-frequency neurons and −57.9 ± 0.6 mV (n= 7) for the low-frequency neurons (P= 0.74), while slope factor was 4.8 ± 0.3 mV and 4.6 ± 0.5 mV, respectively (P= 0.73). This indicates that about 6% of Nav channels are inactivated at −70 mV (around the resting membrane potential) in NM neurons. The voltage dependence of activation was not different among the frequency regions either: V1/2 was −39.5 ± 0.4 mV (n= 5) for the high/middle-frequency neurons and −38.6 ± 1.3 mV (n= 6) for the low-frequency neurons (P= 0.56), while slope factor was 4.4 ± 0.3 mV and 4.1 ± 0.1 mV (P= 0.36), respectively.
The recovery from inactivation was studied with a standard double-pulse protocol (Fig. 6C). Na+ currents were inactivated after the first pulse and recovered partially after 8 ms at −80 mV; 66 ± 2% (n= 10) for the high/middle-frequency neurons and 65 ± 3% (n= 11) for the low-frequency neurons (P= 0.79). The time course of recovery was fitted by a double exponential function, and the time constants were also similar at both frequencies: fast and slow components were 3.3 ± 0.2 ms and 75.7 ± 3.6 ms (% fast of 79.5 ± 0.9%, n= 10), and 3.2 ± 0.3 ms and 71.5 ± 7.1 ms (% fast of 77.2 ± 1.0%, n= 11) (P > 0.1) for the high/middle- and low-frequency neurons, respectively (Fig. 6D). Similar time constants were reported in neurons of mammalian medial nucleus of trapezoid body (MNTB): fast and slow time constants were 1.7 ms and 77.7 ms at −100 mV, respectively (Leao et al. 2005). The fast component of recovery time course was dependent on the membrane potential, and was slightly accelerated with hyperpolarization (Supplemental Fig. 2). When experiments were made at the physiological temperature of birds (40°C), the fast time constant was reduced to 0.5 ± 0.1 ms (n= 4) at −80 mV, corresponding to Q10 of about 2.5 (data not shown).
Number and strength of synaptic inputs differ along the tonotopic axis
NM neurons differ in the number of synaptic inputs and their strength (the quantal content of transmitter released by a single impulse) depending on the tuning frequency (Fukui & Ohmori, 2004). EPSPs were recorded under the block of Na+ current with QX314 (10 mm) (Fig. 7). Consistent with the previous reports (Fukui & Ohmori, 2004), a gradual increase in the stimulus intensity induced an EPSP in an all-or-none manner in the high/middle-frequency neurons (Fig. 7A). The amplitude and maximum rate of rise of the minimal EPSP, which probably reflects the activity of a single auditory nerve fibre, were quite large (Fig. 7B and C) and even larger than those of spikes (Fig. 1A–E), indicating that the synaptic current predominates over the Na+ current in these neurons. In the low-frequency neurons, on the other hand, the EPSPs increased in a stepwise manner (about 4–6 mV), and the minimum amplitude (arrows) was below the spike threshold (−47.1 ± 0.9 mV, n= 22, see Fig. 1A), indicating that the convergence of multiple inputs is required for the spike induction (see Fukui & Ohmori, 2004). The 10–90% rise time of EPSPs was slightly greater in the low-frequency neurons (Fig. 7D), presumably because of the high input resistance of these neurons (Fukui & Ohmori, 2004).
Synaptic convergence improves precision of spike timing
What is the role of the specialized distribution of Nav channels in the temporal coding of NM neurons? In the high/middle-frequency neurons, the robust synaptic conductance enables neurons to preserve the presynaptic spike timing with small temporal jitter. In low-frequency neurons, on the other hand, the convergence of multiple small inputs has been proposed to improve the postsynaptic spike timing (Rothman et al. 1993; Joris et al. 1994; Fukui & Ohmori, 2004; Xu-Friedman & Regehr, 2005; Fukui et al. 2006). To test whether the large Na+ conductance in the low-frequency NM neurons contributes to this improvement, we constructed a multiple-compartment model of low-frequency NM neurons (Supplemental Fig. 3, see Methods). We assigned either a single input of a large conductance (44 nS) or multiple inputs of a small conductance (16 inputs, 4 nS) to the model neuron (see Fig. 8Aa, Ab, Ba and Bb; see also legends and Methods for determination of SynNo and SynG), and examined the effects of Na+ conductance on the spike timing during the two patterns of synaptic inputs (Figs 8, 9 and 11). The timing of individual inputs was randomly varied with a s.d. of 0.3 ms for each cycle of sound wave (input jitter, see Methods), mimicking that observed in the low-frequency auditory nerve fibres in vivo (200–400 Hz, Fukui et al. 2006).
We first examined the contributions of synaptic input patterns to the timing of postsynaptic spiking (Fig. 8). In the model neuron of a single input, a spike was induced at a uniform timing with a short latency (on average, 0.50 ms) in response to each input, whereas a spike was generated with a longer latency (0.86 ms) of a larger variability (0.13 ms) to the first EPSP in the multiple input neurons (Fig. 8Ac and Bc insets). When the phase responsiveness of spikes among each cycle was compared, however, the multiple input neurons showed higher phase responsiveness than that of the single input neurons (Fig. 8Ac and Bc); vector strength (Goldberg & Brown, 1969) was 0.99 and 0.93, respectively, at 200 Hz. The jitter of outputs, defined as the s.d. of spike peak time, in the multiple input neurons, was far smaller (0.14 ms) than that of the inputs (Fig. 8Bd). By contrast, the jitter of output was the same (0.3 ms) as that of inputs in the single input neurons (Fig. 8Ad). Thus, the synaptic convergence averaged the timing of spike inductions by summating temporally dispersed EPSPs in the multiple input neurons, whereas the input jitter remained in the single input neurons because of the short and constant latency (see also Fig. 8C). This distinction of output jitter in the two types of synaptic inputs was also seen in its dependence on the total synaptic conductance (SynNo × SynG). The jitter was reduced with an increase in SynNo in the multiple input neurons (filled squares in Fig. 8D), while it was unchanged as a function of SynG in the single input neurons (open circles). Thus, multiple small inputs must be crucial to improve the spike timing, especially for neurons that receive inputs with a large temporal jitter.
Synaptic convergence reduces the excitability of neurons
The multiple small inputs could reduce the temporal jitter as the result of summating EPSPs. However, the multiple inputs required a larger synaptic conductance to induce a spike (Fig. 8D filled squares, 56 nS) than the single input (open circles, 40 nS). In fact, the firing probability of the multiple input neurons increased more moderately with an increase in the total synaptic conductance (SynNo × SynG) than that of the single input neurons (Fig. 8E). This reduction of firing probability in the multiple inputs could be related to a longer latency of spike induction from the summated EPSP (Fig. 8Ac and Bc insets). Then, we compared EPSPs under the block of spike induction between these two patterns of inputs (Fig. 9).
As expected, the rate of rise of the summated EPSPs was 2.3 times smaller and the rise time was 1.9 times greater in the multiple input neuron than in the single input neuron; the 10–90% rise time was 0.50 and 0.26 ms, respectively, although the EPSPs had similar amplitudes (Fig. 9Ab, Ac, Bb and Bc). This slower rising phase of the summated EPSPs provided time for the inactivation of Na+ current (hNa, black) and the activation of IKLVA (nKLVA, grey) to grow (Fig. 9Ad and Bd). An increase in the input jitter reduced the maximum rate of rise of EPSPs (Fig. 9C), thereby inactivating Na+ current and activating IKLVA more extensively (Fig. 9D and E). Accordingly, the maximum rate of rise of spikes was smaller and the threshold of spike was higher for the multiple inputs than for the single input: 494 V s−1 and 541 V s−1 (Fig. 8Ac and Bc), while −43.1 mV and −44.9 mV (Fig. 9Ab and Bb, arrows, see also overlaid grey traces showing spikes with the control gNa), respectively.
The growth of the inactivation of Na+ current and the activation of IKLVA during the slow rise of depolarization was also confirmed in the actual low-frequency NM neurons (Fig. 10). The ramp current (1 ms duration) mimicked the slow depolarization, reduced the maximum rate of rise of spikes, and increased both threshold current and threshold potential compared with the rectangular current (0.5 ms duration). Similar effects were observed in neurons of the mammalian ventral cochlear nucleus (Ferragamo & Oertel, 2002; McGinley & Oertel, 2006).
High density of Nav channels augments reliability and precision of firing during synaptic convergence
The foregoing results suggest that the convergence of multiple small inputs slows the rising phase of EPSPs, which increases the spike threshold and reduces the firing probability. This drawback might be compensated for in the low-frequency NM neurons by the large Na+ conductance (Figs 1–5), and also by the small IKLVA conductance (Fukui & Ohmori, 2004). We confirmed this mechanism in simulation (Fig. 11). As expected, an increase in the Na+ conductance overcame the activation of IKLVA and the inactivation of Na+ current (which occurred during the synaptic convergence: see Fig. 9), thus increasing the firing probability in the multiple input neurons (Fig. 11A lower, filled squares). Under this condition, the synaptic conductance required for spiking was reduced (Supplemental Fig. 4) so that a spike was generated at the lower threshold potential with a shorter latency (Fig. 11B black arrows and white circles). This reduction of threshold yielded another advantage for the multiple input neurons, which was a decrease in the output jitter (from 0.14 ms to 0.1 ms, Fig. 11A upper, filled squares). The reduction of jitter was accomplished because lowering the threshold induced a spike at the steeper rising phase of summated EPSPs (Fig. 11C), which reduced the fluctuation of spike onset time (from 0.12 ms to 0.09 ms, Fig. 11B lower). The slope was about 1.3 times steeper in neurons with large Na+ conductance (43.4 V s−1, white circles) than those with the control Na+ conductance (32.6 V s−1, grey circles). In addition, the shorter latency of spike induction by the large Na+ conductance reduced the growth of Na+ current inactivation and K+ current activation before firing (Fig. 11D and E, see also Fig. 9Bd), thereby minimizing the variability in onset-to-peak time of spikes (0.05 ms to 0.02 ms, Fig. 11F). In the single input neurons, on the other hand, increasing the Na+ conductance did not reduce the output jitter (Fig. 11A upper, open circles). This was because individual EPSPs had identical shapes, and a change in the threshold did not affect the fluctuations of spike onset time and of onset-to-peak time in the single input neuron (Fig. 11B upper). Thus, the high membrane excitability caused by an increase in the Na+ conductance was particularly important in the multiple input neurons for the precise temporal coding. The idea was further supported by the findings that a decrease in the IKLVA conductance at the soma increased the precision and reliability of firing during the synaptic convergence (Supplemental Fig. 5).
In the simulation, we also examined the effects of the length and the distance of Nav channel cluster on the temporal coding (see Figs 3 and 4). These factors, however, had little effect on the output jitter in both types of neurons having the same channel conductance (Supplemental Fig. 6, see legends). An increase in the distance moderately reduced the firing probability during the multiple inputs, because the distance increased the dissipation of charges along the axon.
Discussion
We have shown that the Na+ conductance at the axon initial segment of individual NM neurons differs along the tonotopic axis; the conductance is smaller in high/middle-frequency neurons than in low-frequency neurons. In low-frequency neurons, converging synaptic inputs reduce the temporal jitter of spike induction. However, synaptic convergence reduces the firing probability due to the Na+ current inactivation and K+ current activation, which occurs during the slow rise of summating EPSPs of multiple inputs. The greater Na+ current compensated for this reduction of membrane excitability, thus enabling the low-frequency neurons to further increase the precision of firing.
Coupling of synaptic inputs and Na+ current size for precise temporal coding in NM neurons
Sound waves are represented as receptor potentials in hair cells, which can evoke spikes in the auditory nerve that are phase-locked to the sound stimulus (Pfeiffer & Molnar, 1970; Palmer & Russell, 1986). The variability (jitter) of spike timing in the auditory nerve is small at the high/middle-frequency region (Hill et al. 1989; Koppl, 1997; Fukui et al. 2006). The high-frequency NM neurons receive the small number of inputs, each having a large quantal content, and generate high-fidelity one-to-one synaptic transmission that preserves information contained in the presynaptic timing of firing (Trussell, 1999; Fukui & Ohmori, 2004). Accordingly, an EPSP induced by a single presynaptic terminal is sufficiently large to generate a spike safely even with a relatively small Na+ conductance (Figs 1–5) and large IKLVA conductance (Fukui & Ohmori, 2004). The large IKLVA conductance shortens the EPSP time course and contributes further to increase the precision of spike timing (Reyes et al. 1994; Koyano et al. 1996; Rathouz & Trussell, 1998; Trussell, 1999; Fukui & Ohmori, 2004). In fibres tuned to lower frequencies, the temporal jitter of auditory nerve activity is higher (Hill et al. 1989; Koppl, 1997; Fukui et al. 2006). In NM neurons tuned to the lowest frequencies, the number of inputs is greatest and the quantal content of individual presynaptic terminals is smallest (Fukui & Ohmori, 2004), thereby allowing the neuron to compensate for the large jitter through summation of EPSPs in an input-number-dependent manner (see Fig. 8D filled squares). Moreover, the large Na+ conductance in the low-frequency NM neurons (Figs 1–5) ensures reliable firing during the summated EPSPs, and further improves the precision of spike timing (Fig. 11). Thus, the tonotopic variation of the number and the size of inputs effectively couples with that of the axonal Na+ conductance to improve the temporal coding in NM neurons. This should contribute to increase the acuity of binaural coincidence detection at nucleus laminaris for sound source localization (Carr & Konishi, 1990; Oertel, 1999; Kuba et al. 2003).
The coupling between the axonal Na+ conductance and the synaptic inputs is also strategic in an economical sense. In the high/middle-frequency neurons, the small Na+ conductance reduces unnecessary Na+ influx, which should be particularly beneficial for these neurons because they suffer a vast Na+ influx through the postsynaptic AMPA receptors during synaptic inputs. The results may also raise a possibility that AMPA receptors and Na+ channels contribute differently to the total Na+ influx in NM neurons between high/middle- and low-frequency regions. Recently, contributions of Na+/K+-ATPase to the reliable and precise firing are reported in the rat MNTB (Kim et al. 2007; Leao et al. 2008). Therefore, the distribution of Na+/K+-ATPase in NM neurons would be also an important issue to be examined.
Rapid inactivation kinetics of Na+ current in NM neurons
Fast inactivation kinetics of Na+ current are required for high-frequency firing of neurons; a rapid inactivation shortens the spike duration, while a rapid recovery from inactivation reduces the refractory periods (Torkkeli & French, 2002; Leao et al. 2005). In the rat MNTB, Na+ current shows a rapid recovery from inactivation in both presynaptic terminals and postsynaptic neurons (Leao et al. 2005), thus enabling neurons to follow afferent fibre stimulation rates of 800 Hz (Taschenberger & von Gersedorff, 2000). In the present study, Na+ current in both high/middle- and low-frequency NM neurons also showed a rapid recovery time course, and the fast time constant (3.2 ms at −80 mV, 20°C) was similar to that observed in MNTB (2.4 ms at −80 mV, 22–24°C; Leao et al. 2005). The time constant was reduced to 0.5 ms at the physiological temperature of birds (40°C), which enables the high-frequency firing of NM neurons up to 500 Hz in vivo (Warchol & Dallos, 1990; Fukui et al. 2006). However, the rapid inactivation kinetics could reduce the available Na+ current for spike generation and impair the firing in neurons that receive an EPSP with a slow rising phase. It seems that low-frequency NM neurons increase the number of Nav channels in the axon to overcome this disadvantage (Figs 3 and 4).
Cell-specific Nav-channel distribution in the axon initial segment
In general, an action potential is initiated at the axon initial segment (Stuart et al. 1997; Khaliq & Raman, 2006; Palmer & Stuart, 2006; Shu et al. 2007), which is classically defined as the unmyelinated region adjacent to the axon hillock (Palay et al. 1968). The axon initial segment has several advantages for effective induction of spikes. First, the site is relevant for reducing the magnitude of a local current for spike induction due to its being a small compartment (Stuart et al. 1997). Second, a high density of Nav channels (Komada & Soriano, 2002; Inda et al. 2006; Kole et al. 2008) and/or those having a low threshold for activation (Colbert & Pan, 2002) at the axon initial segment reduce the spike threshold. Third, its fast membrane properties are suitable for generating spikes at high frequency, as expected in neurons of mammalian medial superior olive (Scott et al. 2007).
In the previous study in nucleus laminaris, the next order nucleus to NM, we have shown that patterns of Nav-channel distribution in the axon are more specific than those described above, which ensures the accurate binaural synaptic coincidence detection over a wide range of sound frequency (Kuba et al. 2006). In nucleus laminaris, the location of Nav channels in the axon varies depending on the frequency of synaptic inputs along the tonotopic axis; the location is more distant from the cell soma in the higher-frequency neurons. In NM, on the other hand, the number and density of Nav channels at the axon initial segment are optimized depending on the tuning of synaptic inputs, thereby enabling the precise encoding of auditory temporal information at each frequency. In spherical bushy cells of ventral cochlear nucleus, a mammalian homologue of NM neuron, a similar tuning frequency-dependent variation in the synaptic inputs is reported to increase the precision of temporal coding (Joris et al. 1994), suggesting that a corresponding variation in the channel expression might exist in these neurons. In octopus cells of mammalian ventral cochlear nucleus, spikes are unusually small (less than 20 mV), and some specializations in the axonal Nav channels are also expected (Golding et al. 1999). Thus, the variation of Nav-channel distribution should play a critical role in serving the specific function of each type of auditory neuron. The findings of the tuning frequency-dependent Nav-channel distribution in auditory neurons may suggest that the distribution of Nav channels in other central neurons is also determined in a cell-specific manner depending on their synaptic inputs and functions.
Acknowledgments
We thank Professor L. O. Trussell, Drs T. Ishii, I. Fukui and R. Yamada for critical reading of this manuscript. This work was supported by Grants-in-aid (18019016 and 19680021 to H.K. and 17023027 to H.O.) from the Ministry of Education, Science and Technology.
Supplemental material
Online supplemental material for this paper can be accessed at:
http://jp.physoc.org/cgi/content/full/jphysiol.2008.162651/DC1
References
- Cao X-J, Oertel D. Temperature affects voltage-sensitive conductances differentially in octopus cells of the mammalian cochlear nucleus. J Neurophysiol. 2005;94:821–832. doi: 10.1152/jn.01049.2004. [DOI] [PubMed] [Google Scholar]
- Carr CE, Boudreau RE. Central projection of auditory nerve fibers in the barn owl. J Comp Neurol. 1991;314:306–318. doi: 10.1002/cne.903140208. [DOI] [PubMed] [Google Scholar]
- Carr CE, Konishi M. A circuit for detection of interaural time differences in the brain stem of the barn owl. J Neurosci. 1990;10:3227–3246. doi: 10.1523/JNEUROSCI.10-10-03227.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colbert CM, Pan E. Ion channel properties underlying axonal action potential initiation in pyramidal neuron. Nat Neurosci. 2002;5:533–538. doi: 10.1038/nn0602-857. [DOI] [PubMed] [Google Scholar]
- Ferragamo MJ, Oertel D. Octopus cells of the mammalian ventral cochlear nucleus sense the rate of depolarization. J Neurophysiol. 2002;87:2262–2270. doi: 10.1152/jn.00587.2001. [DOI] [PubMed] [Google Scholar]
- Fukui I, Ohmori H. Tonotopic gradient of membrane and synaptic properties for neurons of the chicken nucleus magnocellularis. J Neurosci. 2004;24:7514–7523. doi: 10.1523/JNEUROSCI.0566-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukui I, Sato T, Ohmori H. Improvement of phase information at low sound frequency in nucleus magnocellularis of the chicken. J Neurophysiol. 2006;96:633–641. doi: 10.1152/jn.00916.2005. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol. 1969;32:613–636. doi: 10.1152/jn.1969.32.4.613. [DOI] [PubMed] [Google Scholar]
- Golding NL, Ferragamo MJ, Oertel D. Roles of intrinsic conductances underlying responses to transients in octopus cells of the cochlear nucleus. J Neurosci. 1999;19:2897–2905. doi: 10.1523/JNEUROSCI.19-08-02897.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill KG, Stange G, Mo J. Temporal synchronization in the primary auditory response in the pigeon. Hear Res. 1989;39:63–74. doi: 10.1016/0378-5955(89)90082-8. [DOI] [PubMed] [Google Scholar]
- Hines ML, Morse T, Migliore M, Carnevale NT, Shepherd GM. Model DB: a database to support computational neuroscience. J Comput Neurosci. 2004;17:7–11. doi: 10.1023/B:JCNS.0000023869.22017.2e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inda MC, DeFelipe J, Munoz A. Voltage-gated ion channels in the axon initial segment of human cortical pyramidal cells and their relationship with chandelier cells. Proc Natl Acad Sci U S A. 2006;103:2920–2925. doi: 10.1073/pnas.0511197103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jhaveri S, Morest DK. Neuronal architecture in nucleus magnocellularis of the chicken auditory system with observations on nucleus laminaris: a light and electron microscope study. Neuroscience. 1982;7:809–836. doi: 10.1016/0306-4522(82)90045-8. [DOI] [PubMed] [Google Scholar]
- Joris PX, Carney LH, Smith PH, Yin TCT. Enhancement of neural synchronization in the anteroventral cochlear nucleus. I. Responses to tones at the characteristic frequency. J Neurophysiol. 1994;71:1022–1036. doi: 10.1152/jn.1994.71.3.1022. [DOI] [PubMed] [Google Scholar]
- Joris PX, Smith PH. The volley theory and the spherical cell puzzle. Neuroscience. 2008;154:65–76. doi: 10.1016/j.neuroscience.2008.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khaliq ZM, Raman IM. Relative contribution of axonal and somatic Na channels to action potential initiation in cerebellar Purkinje neurons. J Neurosci. 2006;26:1935–1944. doi: 10.1523/JNEUROSCI.4664-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiang NYS. Discharge Pattern of Single Fibers in the Cat's Auditory Nerve. Cambridge, MA, USA: MIT Press; 1965. [Google Scholar]
- Kim JH, Sizov I, Dobretsov M, von Gersedorff H. Presynaptic Ca2+ buffers control the strength of a fast post-tetanic hyperpolarization mediated by the a3 Na+/K+-ATPase. Nat Neurosci. 2007;10:196–205. doi: 10.1038/nn1839. [DOI] [PubMed] [Google Scholar]
- Kole MHP, Ilschner SU, Kampa BM, Williams SR, Ruben PC, Stuart GJ. Action potential generation requires a high sodium channel density in the axon initial segment. Nat Neurosci. 2008;11:178–186. doi: 10.1038/nn2040. [DOI] [PubMed] [Google Scholar]
- Komada M, Soriano P. βIV-spectrin regulates sodium channel clustering through ankyrin-G at axon initial segments and nodes of Ranvier. J Cell Biol. 2002;156:337–348. doi: 10.1083/jcb.200110003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koppl C. Auditory nerve terminals in the cochlear nucleus magnocellularis: differences between low and high frequencies. J Comp Neurol. 1994;339:438–446. doi: 10.1002/cne.903390310. [DOI] [PubMed] [Google Scholar]
- Koppl C. Phase locking to high frequency in the auditory nerve and cochlear nucleus magnocellularis of the barn owl, Tyto alba. J Neurosci. 1997;17:3312–3321. doi: 10.1523/JNEUROSCI.17-09-03312.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koyano K, Funabiki K, Ohmori H. Voltage-gated ionic currents and their roles in timing coding in auditory neurons of the nucleus magnocellularis of the chick. Neurosci Res. 1996;26:29–45. doi: 10.1016/0168-0102(96)01071-1. [DOI] [PubMed] [Google Scholar]
- Kuba H, Ishii TM, Ohmori H. Axonal site of spike initiation enhances auditory coincidence detection. Nature. 2006;444:1069–1072. doi: 10.1038/nature05347. [DOI] [PubMed] [Google Scholar]
- Kuba H, Yamada R, Fukui I, Ohmori H. Tonotopic specialization of auditory coincidence detection in nucleus laminaris of the chick. J Neurosci. 2005;25:1924–1934. doi: 10.1523/JNEUROSCI.4428-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuba H, Yamada R, Ohmori H. Evaluation of the limiting acuity of coincidence detection in nucleus laminaris of the chicken. J Physiol. 2003;552:611–620. doi: 10.1113/jphysiol.2003.041574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leao RM, Kushmerick C, Pinaud R, Renden R, Li G-L, Taschenberger H, Spirou G, Levinson R, von Gersedorff H. Presynaptic Na+ channels: locus, development, and recovery from inactivation at a high-fidelity synapse. J Neurosci. 2005;25:3724–3738. doi: 10.1523/JNEUROSCI.3983-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leao RN, Leao RM, da Costa LF, Rock Levinson S, Walmsley B. A novel role for MNTB neuron dendrites in regulating action potential amplitude and cell excitability during repetitive firing. Eur J Neurosci. 2008;27:3095–3108. doi: 10.1111/j.1460-9568.2008.06297.x. [DOI] [PubMed] [Google Scholar]
- McGinley MJ, Oertel D. Rate thresholds determine the precision of temporal integration in principal cells of the ventral cochlear nucleus. Hear Res. 2006;216–217:52–63. doi: 10.1016/j.heares.2006.02.006. [DOI] [PubMed] [Google Scholar]
- Oertel D. The role of timing in the brain stem auditory nuclei of vertebrates. Annu Rev Physiol. 1999;61:497–519. doi: 10.1146/annurev.physiol.61.1.497. [DOI] [PubMed] [Google Scholar]
- Palay SL, Sotelo C, Peters A, Orkand PM. The axon hillock and the initial segment. J Cell Biol. 1968;38:193–201. doi: 10.1083/jcb.38.1.193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer AR, Russell IJ. Phase-locking in the cochlear nerve of the guinea-pig and its relation to the receptor potential of inner hair-cells. Hear Res. 1986;24:1–15. doi: 10.1016/0378-5955(86)90002-x. [DOI] [PubMed] [Google Scholar]
- Palmer LM, Stuart GJ. Site of action potential initiation in layer 5 pyramidal neurons. J Neurosci. 2006;26:1854–1863. doi: 10.1523/JNEUROSCI.4812-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parameshwaran S, Carr CE, Perney TM. Expression of the Kv3.1 potassium channel in the avian auditory brainstem. J Neurosci. 2001;21:485–494. doi: 10.1523/JNEUROSCI.21-02-00485.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parks TN, Rubel EW. Organization and development of the brain stem auditory nuclei of the chicken: primary afferent projections. J Comp Neurol. 1978;180:439–448. doi: 10.1002/cne.901800303. [DOI] [PubMed] [Google Scholar]
- Pfeiffer RR, Molnar CE. Cochlear nerve fiber discharge patterns: relationship to the cochlear microphonic. Science. 1970;167:1614–1616. doi: 10.1126/science.167.3925.1614. [DOI] [PubMed] [Google Scholar]
- Rathouz M, Trussell L. Characterization of outward currents in neurons of the avian nucleus magnocellularis. J Neurophysiol. 1998;80:2824–2835. doi: 10.1152/jn.1998.80.6.2824. [DOI] [PubMed] [Google Scholar]
- Reyes AD, Rubel EW, Spain WJ. Membrane properties underlying the firing of neurons in the avian cochlear nucleus. J Neurosci. 1994;14:5352–5364. doi: 10.1523/JNEUROSCI.14-09-05352.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothman JS, Manis PB. The roles potassium currents play in regulating the electrical activity of ventral cochlear nucleus neurons. J Neurophysiol. 2003;89:3097–3113. doi: 10.1152/jn.00127.2002. [DOI] [PubMed] [Google Scholar]
- Rothman JS, Young ED, Manis PB. Convergence of auditory nerve fibers onto bushy cells in the ventral cochlear nucleus: implications of a computational model. J Neurophysiol. 1993;70:2562–2583. doi: 10.1152/jn.1993.70.6.2562. [DOI] [PubMed] [Google Scholar]
- Rubel EW, Parks TN. Organization and development of the brain stem auditory nuclei of the chicken: tonotopic organization of N. magnocellualris and N. laminaris. J Comp Neurol. 1975;164:411–434. doi: 10.1002/cne.901640403. [DOI] [PubMed] [Google Scholar]
- Scott LL, Hage TA, Golding NL. Weak action potential backpropagation is associated with high-frequency axonal firing capability in principle neurons of the gerbil medial superior olive. J Physiol. 2007;583:647–661. doi: 10.1113/jphysiol.2007.136366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shu Y, Duque A, Yu Y, Haider B, McCormick DA. Properties of action-potential initiation in neocortical pyramidal cells: evidence from whole-cell axon recording. J Neurophysiol. 2007;97:746–760. doi: 10.1152/jn.00922.2006. [DOI] [PubMed] [Google Scholar]
- Simon JZ, Carr CE, Shamma SA. A dendritic model of coincidence detection in the avian brainstem. Neurocomputing. 1999;26–27:263–269. [Google Scholar]
- Stuart G, Spruston N, Sakmann B, Hausser M. Action potential initiation and backpropagation in neurons of the mammalian CNS. Trends Neurosci. 1997;20:125–131. doi: 10.1016/s0166-2236(96)10075-8. [DOI] [PubMed] [Google Scholar]
- Sullivan WE, Konishi M. Segregation of stimulus phase and intensity coding in the cochlear nucleus of the barn owl. J Neurosci. 1984;4:1787–1799. doi: 10.1523/JNEUROSCI.04-07-01787.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taschenberger H, von Gersedorff H. Fine-tuning an auditory synapse for speed and fidelity: developmental changes in presynaptic waveform, EPSC kinetics, and synaptic plasticity. J Neurosci. 2000;20:9162–9173. doi: 10.1523/JNEUROSCI.20-24-09162.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torkkeli PH, French AS. Simulation of different firing patterns in paired spider mechanoreceptor neurons: the role of Na+ channel inactivation. J Neurophysiol. 2002;87:1363–1368. doi: 10.1152/jn.00440.2001. [DOI] [PubMed] [Google Scholar]
- Trussell LO. Synaptic mechanisms for coding timing in auditory neurons. Annu Rev Physiol. 1999;61:477–496. doi: 10.1146/annurev.physiol.61.1.477. [DOI] [PubMed] [Google Scholar]
- Warchol ME, Dallos P. Neural coding in the chick cochlear nucleus. J Comp Physiol A. 1990;166:721–734. doi: 10.1007/BF00240021. [DOI] [PubMed] [Google Scholar]
- Xu-Friedman MA, Regehr WG. Dynamic clamp analysis of the effects of convergence on spike timing. I. Many synaptic inputs. J Neurophysiol. 2005;94:2512–2525. doi: 10.1152/jn.01307.2004. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.