Rate-sensitive contractile responses of lymphatic vessels to circumferential stretch

Abstract

Phasic contractile activity in rat portal vein is more sensitive to the rate of change in length than to absolute length and this response is widely assumed to be a general characteristic of myogenic behaviour for vascular smooth muscle. Previously, we found that rat lymphatic vessels exhibit phasic contractile behaviour similar to that of portal vein. In the present study, we hypothesized that lymphatic muscle would exhibit rate-sensitive contractile responses to stretch. The hypothesis was tested on rat mesenteric lymphatics (90–220 μm, i.d.) using servo-controlled wire- and pressure-myograph systems to enable ramp increases in force or pressure at different rates. Under isometric conditions in wire-myograph preparations, both the amplitude and the frequency of phasic activity were enhanced at more optimal preloads, but superimposed upon this effect were bursts of contractions that occurred only during fast preload ramps. In such cases, the ratio of contraction frequency during the ramp to that at the subsequent plateau (at optimal preload) was > 1. Further, the frequency ratio increased as a function of the preload ramp speed, consistent with a rate-sensitive mechanism. In contrast, the amplitude ratio was < 1 and declined further with higher ramp speeds. Downward preload ramps produced corresponding rate-sensitive inhibition of contraction frequency but not amplitude. Similar findings were obtained in pressurized lymphatics in response to pressure ramps and steps. Our results suggest that lymphatics are sensitive to the rate of change in preload/pressure in a way that is different from portal vein, possibly because the pacemaker for generating electrical activity is rate sensitive but lymphatic muscle is not. The behaviour may be widely present in collecting lymphatic vessels and is probably an important mechanism for rapid adaptation of the lymphatic pump to local vascular occlusion.

Phasic contractile activity of smooth muscle in rat portal vein is known to be more sensitive to the rate of change in length than to the absolute length (Johansson & Mellander, 1975). Under isometric conditions, the longitudinal muscle layer of portal vein exhibited spontaneous contractile activity that was superimposed on, and modulated by, the level of passive force (preload). When preload was elevated gradually from suboptimal to optimal level, large amplitude (AMP), high frequency (FREQ) contraction bursts were evident in the force recordings (Johansson & Mellander, 1975). The most prominent contraction bursts occurred just before and just after passive force reached a plateau at a more optimal preload. During the plateau, both AMP and FREQ declined somewhat to values that were still higher than their respective values at the original (suboptimal) preload. Thus, the values of both AMP and FREQ were larger during the force ramp than at the higher, plateau level associated with a more optimal preload. Portal vein also exhibited the opposite response to reduction in preload: during a declining force ramp, inhibition of both AMP and FREQ occurred, with the effect again most prominent at the end, or just after the end, of a downward force ramp. The rate-sensitive aspect of this behaviour became particularly apparent when the changes were analysed as a function of the rate of the preload ramp (mN s⁻¹). As the speed of the ramp increased, the bursting responses became more prominent. Positive force ramps up at a rate of 3% length s⁻¹ produced maximum AMP and FREQ responses, whereas declining force ramps up at a rate of –3% length s⁻¹ produced contractions with AMP and FREQ values that were disproportionately smaller than those at the final force (Johansson & Mellander, 1975; Sigurdsson et al. 1977).

The physiological impact of rate-sensitive changes in portal vein contractility remains unclear. What changes in portal vein diameter and/or length would be associated with the observed rate-sensitive changes in contraction AMP in response to vessel lengthening? Could the associated diameter/length changes alter portal vein resistance to a significant degree? Despite these unanswered questions about relevance, the rate-sensitive behaviour of portal vein to stretch has been inferred to be a general characteristic of all myogenically active blood vessels (Grände et al. 1977; Sigurdsson et al. 1977; Grände & Mellander, 1978; Johnson, 1981; Björnberg et al. 1988). A presumed correlate to this behaviour was noted by Sparks (1964) in isometric human umbilical artery, where secondary force development was observed after initial stretch and stress-relaxation and that response was evident only after a 25% stretch, not after a 10% stretch. Conceptually, rate-sensitive myogenic behaviour of peripheral arteries/arterioles could be homeostatically advantageous by allowing those vessels to respond to rapid changes in local vascular pressure associated with postural shifts or local occlusions. Evidence to support that possibility was deduced from whole-organ resistance changes (Grände et al. 1977; Grände & Mellander, 1978) and microvascular diameter changes (Borgstrom & Grande, 1979) in response to controlled rates of change in perfusion pressure; however, the interpretation of that data is highly controversial because of difficulties in distinguishing pressure-dependent and -independent effects in vivo (Davis & Sikes, 1989, 1990; Davis & Meininger, 1993; Davis & Hill, 1999).

Few, if any, arteries/arterioles exhibit the same type of spontaneous contractions as portal vein; however, the behaviour is well documented in most collecting lymphatic vessels (McHale & Roddie, 1976; McHale & Meharg, 1992; Crowe et al. 1997; Gashev et al. 2002; Gashev et al. 2004). In the lymphatic circulation, phasic activity serves as an essential pump mechanism to propel lymph uphill against a hydrostatic pressure gradient from peripheral lymphatics through lymph nodes into the thoracic duct (Szabo & Magyar, 1967; Hargens & Zweifach, 1976; Zweifach & Lipowsky, 1984). In the course of a recent study of rat mesenteric lymphatic vessels (Zhang et al. 2007b), we observed that rapid preload or pressure steps were associated with contraction bursts, i.e. behaviour reminiscent of that in portal vein. Therefore, the objective of the present study was to systematically test if lymphatic vessels exhibit rate-sensitive contractile responses to controlled changes in circumferential length.

Methods

Vessel isolation

Male Sprague–Dawley rats (170–260 g) were anaesthetized with Nembutal (60 mg kg⁻¹, i.p.) and a loop of intestine from each animal was exteriorized through a midline abdominal incision. All animal protocols were approved by the University of Missouri Animal Care and Use Committee and conformed to the Public Health Service Policy for the Humane Care and Use of Laboratory Animals (PHS Policy, 1996). Collecting lymphatic vessels (90–180 μm inner diameter, by 1–2 mm in length) were dissected away from their paired mesenteric small arteries/veins in Mops-buffered, albumin-supplemented PSS (APSS) at room temperature. After clearing connective tissue and fat, each vessel was transferred to a wire- or pressure-myograph chamber for respective isometric or isobaric studies. The animal was subsequently killed with Nembutal (120 mg kg⁻¹, i.c.).

Solutions

APSS contained (in mm): 145.0 NaCl, 4.7 KCl, 2.0 CaCl₂, 1.2 MgSO₄, 1.2 NaH₂PO₄, 0.02 EDTA, 5.0 glucose, 2.0 sodium pyruvate, 3.0 Mops and 0.5 g per 100 ml purified bovine serum albumin (pH 7.4 at 37°C). The composition of Ca²⁺-free APSS was identical except that 3.0 mm EDTA was substituted for CaCl₂. All chemicals were from Sigma (St Louis, MO, USA) except albumin (U.S. Biochemicals no. 10856).

Wire myograph methods

To study isometric contractions, each vessel was cannulated with two 40 μm stainless steel wires and mounted in a small vessel wire myograph (Danish Myo Technology; Aarhus, Denmark). The rate of change in passive force was controlled using an Inchworm piezo actuator (EXFO, Fishers, NY, USA). The direct force output of the myograph was amplified and filtered (NPI Electronic; Tamm, Germany) before digitization at 20 Hz with a PCI 6030e A–D interface (National Instruments, Austin, TX, USA) in a Pentium 4 computer. The Inchworm was controlled using GPIB and serial commands (IW800 controller, EXFO Burleigh, Fishers). Images of the mounted vessel were acquired at 100× magnification using a Leica DM IL inverted microscope, Sony X-55 CCD camera, and video acquisition card (PCI 1409, National Instruments). Servo-control, acquisition and analysis routines were written in LabView and IMAQ Vision (National Instruments). Igor (Wavemetrics, Lake Oswego, OR, USA) was used for data display.

Pressure myograph methods

To study isobaric contractions, mesenteric lymphatic segments (12 mm in length) were cannulated with glass micropipettes on a Burg-style V-track system (Duling et al. 1981) and pressurized on the stage of an inverted microscope. The vessel segments used for these protocols had at most one valve to ensure adequate pressure control in the entire segment. Pressure was initially set to 3 cmH₂O for a 30–60 min equilibration period. To control the rate of change in intraluminal pressure, the pipette connections were switched from the reservoirs to a servo-controlled pressure system (Davis et al. 2007). Servo-null style shaker pumps (Ling Dynamic Systems, Royston, UK) connected to the pipettes were driven by a hardware-based servo controller through unitary-gain power amplifiers (Cardiovascular Research Institute, Texas A & M University). The controller compared the output signal from low-pressure transducers (CyQ model 104; Cybersense, Nicholsville, KY, USA) to reference voltages specified by a computer and adjusted the pump voltages accordingly. Diameter and pressure signals were recorded using a PCI 6030e A–D/D–A interface (National Instruments). Diameter changes were continuously tracked by computer by digitizing the image using a 1632 × 1234 pixel firewire camera (Basler AG model A641FM, Ahrensburg, Germany) and processing it as previously described (Davis, 2005). All diameters reported in this study represent internal diameters.

Isometric force ramp protocols

Each vessel was equilibrated for 30–60 min at 36–37°C, with preload fixed at the optimal level (0.3 mN) until a stable contraction pattern developed. The force transducer was then re-zeroed and preload set to the minimum, passive (isometric) force at which spontaneous contractions developed (0.02–0.05 mN), typically at a rate of 2–5 contractions min⁻¹. The servo-controlled wire-myograph permitted the generation of constant speed, ramp increases in passive force to test whether rate-sensitive changes in the AMP and/or FREQ of spontaneous lymphatic contractions occurred. To test for a possible rate-sensitive reaction to stretch, the ramp speed was altered in increments between 0.3 and 7 × 10⁻³ mN s⁻¹, from a constant initial preload (F_i) of ∼0.02 mN to a more optimal preload (F_o) of 0.3 mN (optimal preload was typically 0.3 mN). In force ramp protocols, internal diameter changed as needed to permit precise force control. The computer algorithm for controlling the ramp detected the initiation of each spontaneous contraction and temporarily disabled the servo control until that contraction was complete; otherwise the servo system would have interfered with the amplitude and duration of the force transient (Davis et al. 2007). Ramp speeds were selected empirically, with the lowest speed producing minimal or no rate-sensitive effect, and the highest rate being sufficiently long to permit multiple contractions (otherwise FREQ determinations could not be made with confidence). Ultimately, five to six different ramp speeds were selected and we attempted to perform ramps of each speed on each vessel in a pseudo-randomized order.

Isometric diameter ramp protocols

Responses to controlled, ramp changes in vessel diameter were also tested using the wire myograph. This mode more closely simulated previous studies on portal vein where the rate of change in longitudinal length was controlled (Johansson & Mellander, 1975; Sigurdsson et al. 1977). Here, the associated change in force was slightly different from a force ramp, due to stress relaxation and the elastic properties of the vessel. As diameter changed at a constant rate, force rose slowly at first and then accelerated near the end of the ramp. The diameter ramp protocol also permitted us to test lymphatic responses to declining preload ramps, which was not possible with the force ramp protocol due to difficulties in designing an appropriate algorithm (Davis et al. 2007). For diameter ramps, an initial test on each vessel measured the optimal diameter (D_o) associated with a stable passive force at F_o (optimal preload). Passive force was then set at the minimal force (F_i) and corresponding diameter (D_i) that produced regular contractions (0.02–0.05 mN). Internal diameter (the outer edge of the wires) was continuously measured by tracking the inside edges of the wires and adjusting for constant wire thickness. Once D_i and D_o were determined, diameter ramps at varying speeds were imposed on the vessel. Internal diameter was increased to D_o using a ramp waveform, with force increasing as needed for precise diameter control. A range of ramp speeds was chosen to closely match those used in the force ramp protocols. In some cases (as noted in figures), a low dose of substance P (SP) was applied to increase basal contraction frequency.

Isobaric protocols

Rate-sensitive AMP and FREQ responses were also tested in pressurized mesenteric lymphatics. During the initial equilibration period, a stable contraction pattern typically developed at 36–37°C. Pressure was then lowered from 3.0 to 0.5 cmH₂O until a new contraction pattern developed.

In the first protocol, pressure ramps from 0.5 to 3 cmH₂O at different rates were imposed while continuously tracking internal diameter. The range of pressures was selected because (1) 0.5 cmH₂O is the minimum pressure at which spontaneous contractions persist in most vessels (Gashev et al. 2001), (2) optimal pumping occurs at 3–5 cmH₂O (Gashev et al. 2004), and (3) during lymphatic systole intraluminal pressure in rat mesenteric lymphatics increases by 3–4 cmH₂O on average (Benoit et al. 1989). After each ramp was complete, pressure was returned to 0.5 cmH₂O until the basal contraction pattern recovered. Pressure ramps lasting 30, 15, 6, 3 or 1.5 min were imposed, with each ramp speed tested in each vessel, if possible. To account for differences in baseline and peak FREQ that typically occurred from vessel to vessel, the values of FREQ and AMP were normalized according to the following equation:

(1)

An analogous equation was used to calculate normalized AMP. Using this procedure, FREQ and AMP for each vessel varied between 0 and 1 for a given series of ramps and steps. As an alternative analysis method, FREQ and AMP ratios (ramp/plateau) were computed as described above for isometric protocols.

In the second protocol, rapid pressure steps were used to test the pressure range over which rate-sensitive responses occurred. The vessel was equilibrated at a low pressure (1 cmH₂O) and then rapidly stepped to a higher pressure (3, 5, 7 or 9 cmH₂O). Pressure steps were ∼90% complete within 200 ms without any overshoot or artifacts that might otherwise trigger extra contractions. Positive pressure steps were always initiated when the vessel was in diastole. After 1–2 min at the higher pressure (allowing for at least 25 contraction cycles), pressure was rapidly returned to the baseline value, with the pressure drop always being initiated in systole.

At the end of the isobaric protocols, the bath solution was replaced with Ca²⁺-free APSS at a pressure of 5 cmH₂O. After allowing ∼30 min for equilibration, pressure was lowered to 0.5 cmH₂O for 1 min and then set at 1 cmH₂O for 1 min, after which a pressure ramp or pressure steps were imposed, to the same pressures used previously in that experiment.

Data analysis

After completion of an experiment, custom analysis routines were used to detect the amplitudes and frequencies of the individual contractions prior to, during and following the preload or pressure ramps/steps. AMP was taken as the difference between the peak force/diameter of the spontaneous contraction and the preload/pressure immediately prior to the contraction. Frequency was computed on a contraction-by-contraction basis.

The data were analysed using JMP 5.1 (SAS, Cary, NC, USA). For tests on contraction parameters, one-way ANOVAs were performed, with pressure or preload designated as the independent variable. Tukey–Kramer or Dunnett's post hoc tests were used to test for significant within-group variation. Significance was defined as P < 0.05.

Results

Positive preload ramps

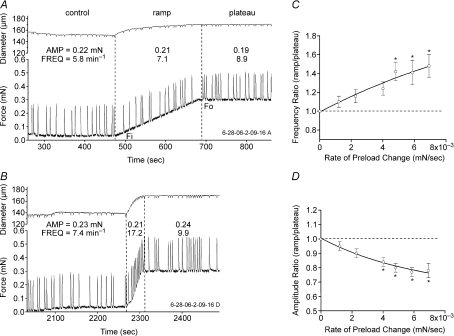
To test for rate-sensitive contractile responses to stretch, preload was increased from ∼0.03 to 0.3 mN at varying rates. Figure 1 shows two examples of the lymphatic response to preload ramps using the wire myograph. With preload set to 0.02 mN, FREQ averaged 5.8 min⁻¹ (measured over a 3 min control period; Fig. 1A). At t= 475 s, a preload ramp was initiated. During the ramp (using a low speed of 1.3 × 10⁻³ mN s⁻¹), FREQ increased to 7.1 min⁻¹ and then to 8.9 min⁻¹ after a plateau was reached at 0.3 mN passive force (t∼ 690 s). AMP was virtually unchanged during the control, ramp and plateau periods. Figure 1B shows the response of the same vessel to a faster ramp (6.1 × 10⁻³ mN s⁻¹) in which FREQ was almost double during the ramp compared to its value during the plateau at the more optimal preload. Notably, a comparable enhancement in AMP did not occur.

Figure 1. Lymphatic vessel responses to preload ramps.

A, after equilibration at an initial (suboptimal) preload of 0.02 mN, passive force was increased to 0.3 mN (the optimal preload for this vessel) at a ramp speed of 1.3 × 10⁻³ mN s⁻¹. B, same vessel as in A with same initial and final preloads but at a ramp speed of 5.8 × 10⁻³ mN s⁻¹. Note the relatively high contraction FREQ during the ramp compared to the subsequent FREQ at optimal preload. The small periodic deflections in the diameter trace correspond to contractions (i.e. slight departures from truly isometric contractions). C, plot of the FREQ ratio (average FREQ during the ramp divided by average FREQ during the plateau) as a function of ramp speed for 6 vessels. D, plot of AMP ratio versus ramp speed for the same vessels. Lines represent exponential fits of the data points. Error bars are ±s.e.m. An asterisk indicates a significant difference from the value at the lowest rate. Force ramp speeds corresponded to rates of 0.09 ± 0.01, 0.19 ± 0.03, 0.35 ± 0.03, 0.55 ± 0.05, 0.83 ± 0.07, and 0.82 ± 0.08 in percentage lengths s⁻¹, respectively, from the slowest to fastest ramps.

Substantial changes in baseline FREQ sometimes occurred from vessel to vessel and even for a given vessel over the time period required to test the response to an entire set of preload ramps (∼1 h). To normalize for these differences, the AMP and FREQ data for each vessel were expressed in terms of the ratio of the average value during the ramp to the average value during the plateau. We previously documented that both AMP and FREQ increase over the preload range 0.03–0.3 mN (Zhang et al. 2007b) so that, in the absence of a rate-sensitive mechanism, AMP and FREQ ratios (ramp/plateau) < 1 would be predicted. For the recordings in Fig. 1, the FREQ ratio was 0.80 for the slower ramp compared to 1.74 for the faster ramp; the AMP ratios were 1.14 and 0.88, respectively, for the two ramps. Thus, rate-sensitive enhancement in FREQ was characterized by a ratio > 1 (reflecting a burst of contractions during the faster ramp). The results from eight lymphatic vessels subjected to preload ramps at six different speeds are summarized in Fig. 1C and D, where the FREQ and AMP ratios, respectively, are plotted as a function of ramp speed. The dotted lines in the two panels indicate boundaries (where ratios were > 1) for the appearance of rate-sensitive enhancement with this protocol. Clearly, the FREQ ratio exceeded 1 regardless of the ramp speed, and the ratio increased with increasing ramp speed to a value of ∼1.5 for the fastest ramp. A value > 1 for the FREQ ratio (1.1) at the lowest ramp speed suggests even that speed was associated with a slight, rate-sensitive enhancement of FREQ. In marked contrast, the average AMP ratio was always < 1 and progressively declined with increasing ramp speed, suggesting that contraction AMP was not enhanced by stretch in a rate-sensitive manner. Indeed, in force ramp protocols, we never observed any AMP responses that resembled those reported in portal vein (i.e. Figs 1 and 2 in Johansson & Mellander, 1975).

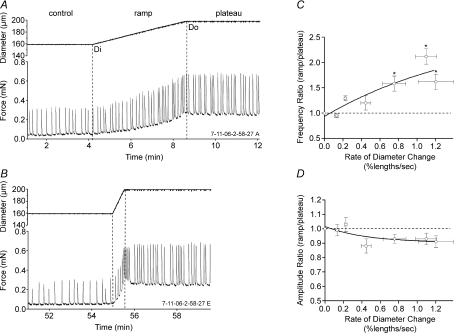
Figure 2. Lymphatic vessel responses to diameter ramps.

A, initially, the diameters at 0.02 mN (D_i) and 0.3 mN (D_o) passive force were measured; subsequently, diameter was ramped from D_i to D_o at a constant speed of ∼0.15% lengths s⁻¹. B, same vessel as in A with same initial and final preloads and diameters but with a ramp speed of ∼1.1% lengths s⁻¹. Note the relatively high contraction FREQ near and just after the end of the ramp. C, plot of the FREQ ratio as a function of ramp speed for 11 vessels. D, plot of AMP ratio versus ramp speed for the same vessels. Lines represent exponential fits of the data points. Error bars are ±s.e.m. An asterisk indicates a significant difference from the value at the lowest rate.

The eight vessels used for the analysis in Fig. 1 comprised a subset of a larger group (15 total experiments) studied using the same protocol. In about half of the experiments, the baseline contraction FREQ was too low to permit the full range of ramp speeds to be tested. For example, if baseline contraction FREQ was such that only one contraction occurred during a high speed ramp, then determination of FREQ on a contraction-by-contraction basis was impossible. Likewise, we were concerned that only two to three contractions during a fast ramp might not give an accurate indication of FREQ (see example in Fig. 3). For this reason, we used only vessels for the analysis shown in Fig. 1 that had a minimum of six contractions during the fastest ramp. It should be noted, however, that rate-sensitive FREQ responses were not limited to the specific conditions described above. For example, in vessels with a low baseline contraction FREQ, a low dose (< 3 × 10⁻⁸m) of substance P (SP) could be added to the bath to increase baseline FREQ, and subsequent elevation of preload at an appropriately high rate then evoked a rate-sensitive FREQ response (not shown, but see Fig. 3 below). This effect occurred as long as baseline FREQ was well below the maximum value of ∼50 min⁻¹ (induced by a high dose of SP). However, the group data analysed in Fig. 1C and D were collected from vessels in the absence of SP stimulation.

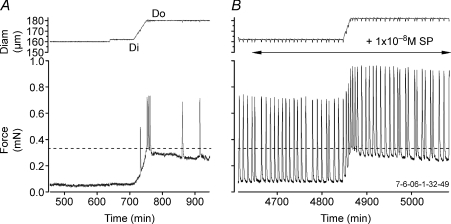
Figure 3. Examples of the responses of a lymphatic vessel to a relatively fast diameter ramp in the absence (A) and presence (B) of 1 × 10⁻⁸m substance P.

A, bursting is evident near the end of the ramp in the absence of SP even though the vessel had no spontaneous contractions at low preloads. B, in the presence of SP, a regular pattern of spontaneous contractions was established and typical contraction bursts were evident during a relatively high speed diameter ramp.

Positive diameter ramps

To ensure that rate-sensitive contractile responses were not unique to force-ramp protocols, we performed an alternative ‘diameter ramp’ protocol in which vessel diameter, rather than passive force, was servo-controlled (Fig. 2). This protocol more closely matched that used previously on portal vein, where the rate of change in longitudinal length was controlled (Johansson & Mellander, 1975). To impose a diameter ramp, the on-line diameter tracking signal obtained from the video image was used in the software-based loop to control the rate of diameter change (note the well-defined ramp shape of the diameter traces in Fig. 2A and B). Because preload under these conditions needed to approach but not exceed its optimal value in the plateau phase of the protocol, it was first necessary to determine D_i, the diameter associated with a minimal preload that produced a regular contraction pattern, and D_o, the diameter associated with optimal preload (∼0.3 mN). Once D_i and D_o were determined for each vessel, a ramp was imposed such that diameter changed at a constant rate. Figure 2 shows two representative examples of the lymphatic response to a slow (Fig. 2A) and a fast (Fig. 2B) diameter ramp. For the slow ramp, the AMP ratio (ramp/plateau) was 0.9 and the FREQ ratio was 1.3. A pattern often observed with fast diameter ramps was the appearance of a contraction burst immediately at the end of the ramp (Fig. 2B) that persisted into the beginning of the plateau period (a similar pattern was also evident in portal vein (Fig. 1 in Johansson & Mellander, 1975). Because this contractile pattern was consistently observed, the data used for analysis of the ramp period included the entire contraction burst. The end of the burst was defined as the time when diastolic force returned to the plateau level (lasting 2–15 s after the end of the ramp). For the faster ramp shown in Fig. 2B, the AMP ratio (ramp/plateau) was 0.8 and the FREQ ratio was 1.7. The viscoelastic properties of the wall were apparent in that relatively large increases in diameter typically occurred before there were substantial increases in preload, after which preload increased rapidly near the end of the diameter ramp (Fig. 2A). An analysis of the diameter ramp data from 11 vessels, with each vessel subjected to four to six different ramp speeds, is shown in Fig. 2C and D. The rate of the diameter change (dL/dt) is expressed as percentage length ((D_o–D_i)/D_i) × 100, per unit time. The diameter was altered at each of six standard rates for each vessel but since the vessels were of different sizes, the actual rate, in percentage lengths s⁻¹ varied slightly between vessels. Nevertheless, the average response patterns were very similar to those shown with force ramps, with the FREQ ratio increasing approximately 2-fold at the highest ramp speed without a corresponding increase in the AMP ratio (the average response was a slight but not significant decrease with increasing ramp speed). The maximum FREQ ratio increases were higher for diameter ramps than for force ramps probably because we were able to increase diameter at faster rates than in the first protocol where force ramp speeds corresponded to rates of 0.09 ± 0.01, 0.19 ± 0.03, 0.35 ± 0.03, 0.55 ± 0.05, 0.83 ± 0.07 and 0.82 ± 0.08 in percentage lengths s⁻¹ from the slowest to fastest ramps (Fig. 1C).

The same response pattern was also observed after stimulation of the vessel with low doses of SP to increase baseline FREQ. Figure 3 shows an example of a vessel that initially did not show spontaneous contractions at D_i. Subsequently, the vessel exhibited a few contraction bursts in response to a relatively fast diameter ramp (Fig. 3A). The dotted horizontal line shows the target force associated with D_o. In the right panel of Fig. 3, the same vessel is shown after application of SP (1 × 10⁻⁸m). Baseline FREQ increased from 0 to 16 min⁻¹ (AMP increased ∼2-fold) and the vessel again exhibited contraction bursts during and immediately following a diameter ramp of approximately the same speed. It should be noted, however, that the group data analysed in Fig. 2C and D were collected from vessels in the absence of SP stimulation.

We also tested if an apparent rate-sensitive effect of stretch on FREQ could be observed with the stretch protocol recently used on stomach smooth muscle by Won et al. (2005). In that study, tissue length was increased at constant rate only until length reached an optimal value, after which stress-relaxation was allowed to occur during the plateau phase. Supplemental Fig. 1 shows a representative trace of a lymphatic vessel subjected to two force ramps at different speeds. At the end of each ramp, servo control was disabled, allowing a variable amount of stress-relaxation to occur (compare passive force in the plateau phase with that in Fig. 1). As before, a slow ramp evoked only a slight rate-sensitive FREQ response (FREQ ratio = 1.05), while a faster ramp evoked a greater response (FREQ ratio = 1.33). Interestingly, the corresponding behaviour (i.e. rate-sensitive FREQ bursts) was not evident in visceral smooth muscle (see Figs 1, 3, 4, 5 and 6 in Won et al. 2005).

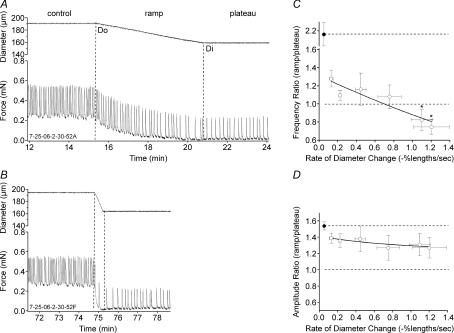
Figure 4. Lymphatic vessel responses to negative diameter ramps.

The diameters associated with the optimal (D_o) and minimal (D_i) preloads were determined, after which slow or fast diameter ramps were imposed in the negative direction. A, a slow ramp (0.06 lengths s⁻¹; 5.6 μm min⁻¹; 0.04 mN min⁻¹) was associated with a gradual decline in AMP and FREQ. B, a faster ramp (0.72 lengths s⁻¹; −81.1 μm min⁻¹; –0.54 mN min⁻¹) produced a variable period of contraction inhibition (i.e. a disproportionately low FREQ but not AMP) at the end of the ramp (same vessel as in A). C and D, summary of changes in FREQ ratio and AMP ratio as a function of the rate of diameter change for 14 vessels. Error bars are ±s.e.m. An asterisk indicates a significant difference from the value at the lowest rate. Filled symbols indicate the average values of the ratio control/plateau from the combined data for all of the ramps.

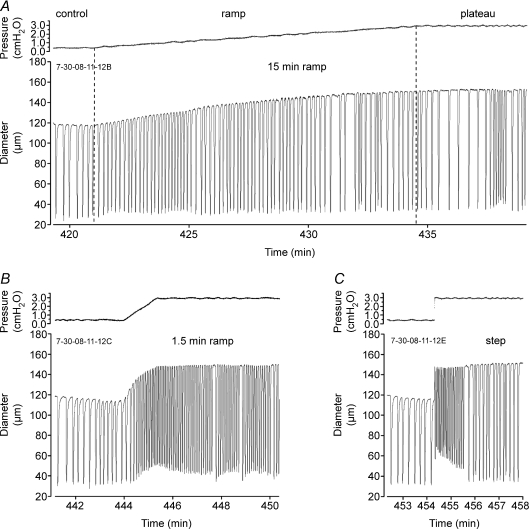
Figure 5. Lymphatic responses to pressure ramps.

A, a ∼15 min ramp from 0.5 to 3 cmH₂O was associated with a gradual rise in FREQ and AMP of spontaneous contractions, interspersed with pauses and slight bursts (typical for long records even at constant pressure). B, a ∼1.5 min pressure ramp over the same pressure range in the same vessel produced a high-frequency contraction burst in the latter half of the ramp, compared to the FREQ after a few minutes at 3 cmH₂O; AMP during the ramp was slightly reduced compared to the average AMP at 3 cmH₂O. C, the response of the same vessel to a rapid pressure step from 0.5 to 3 cmH₂O. The time axes of all three graphs are equally scaled.

Figure 6. Analysis of pressure ramp data.

A and B, contraction-by-contraction analysis of FREQ and AMP changes for the records shown in Fig. 5, plotted as a function of pressure. This method of presentation clearly shows the higher FREQ and lower AMP values associated with the faster pressure ramp. C and D, summary analysis of FREQ and AMP changes for 15 min and 1.5 min pressure ramps from 0.5 to 3 cmH₂O for 6 vessels (both ramp speeds performed in each vessel). The first few points after a pressure step from 0.5 to 3 cmH₂O are shown for reference. For statistical analysis and plotting, the data were binned according to pressure, in 10 bins from 0.4 to 3.2 cmH₂O. Error bars are ±s.e.m. Asterisks indicate a significant difference from the value for the other ramp rate at the same pressure level.

Downward diameter ramps

Portal vein also exhibited rate-sensitive inhibition of both AMP and FREQ when passive force was lowered at a constant rate (Johansson & Mellander, 1975), such that faster reductions in passive force produced disproportionate inhibition of both parameters. In our system, servo control of passive force in the downward direction was not feasible due to interference by the algorithm used to detect and temporarily disable the servo control during spontaneous contractions (Davis et al. 2007). However, contraction FREQ inhibition was consistently noted when preload was rapidly stepped down from progressively higher initial preloads. In this protocol the duration of the force step was constant so that the rate of force decline progressively increased with higher levels of initial force. Supplemental Fig 2 shows an example of this behaviour in which there was a progressively longer delay in the redevelopment of contractions after the largest downward step in passive force. This vessel also exhibited typical rate-sensitive contraction bursts in response to positive preload steps, consistent with the results shown in Figs 1–3.

To systematically test for rate-sensitive inhibition of contraction, vessel diameter (rather than passive force) was servo-controlled in the downward direction (from D_o to D_i) at various rates. Figure 4 shows examples of a lymphatic responding to diameter ramps between ∼0.3 and ∼0.03 mN, where diameter was lowered at two different rates. In Fig. 4A, a slow ramp produced a gradual reduction in both AMP and FREQ, with both parameters declining gradually to stable but lower values at the minimal preload associated with D_i. The FREQ and AMP ratios for this record were 1.29 and 1.28, respectively. However, as shown in Fig. 4B, a faster, declining diameter ramp was associated with an initial low contraction frequency (i.e. contraction inhibition) at the target diameter (D_i) that gradually increased with time after the diameter had stabilized at the lower level. The FREQ and AMP ratios for this record were 1.13 and 1.25, respectively. Figure 4C and D summarizes the data for downward diameter ramps at six different ramp speeds, with ramp speeds plotted in percentage lengths s⁻¹ as described above. There was no significant change in the AMP ratio with faster (downward) diameter ramps; however, the FREQ ratio progressively declined with increasing ramp speed. For reference, the respective FREQ and AMP ratios for the control period relative to the plateau are also shown (filled symbols); FREQ was ∼2.2 times higher at D_o than at D_i and AMP was ∼1.6 times higher. Each of these points represents the upper limit of the possible ramp/plateau ratio, whereas a value of 1 indicates the lower limit that would occur in the absence of rate-sensitive inhibition. Clearly, the AMP ratio curve lies within these bounds, whereas the FREQ ratio curve does not.

Pressure ramps and steps

It is possible that the rate-sensitive contractile responses shown in Figs 1–3 were artifacts of vessels studied under isometric conditions in the wire myograph. The cross-sectional geometry of a wire-mounted vessel is elliptical rather than circular, and the wires contact only a small portion of the vessel wall. Under such conditions, the stress on the lymphatic muscle layer is predicted to be highly non-uniform (Zhang et al. 2007a). For this reason, we developed methods to test for analogous, rate-sensitive behaviour of pressurized lymphatic vessels.

Previously, when pressurized lymphatics were exposed to a slowly rising (> 10 min in length) pressure ramp between 0.5 and 10 cmH₂O, a gradual and progressive increase in FREQ and AMP occurred as pressure was elevated (Zhang et al. 2007b; Davis et al. 2008). AMP increased over the pressure range 0.5–3 cmH₂O and then progressively declined at higher pressures; FREQ increased over the pressure range 0.5–5 cmH₂O and then plateaued above 5 cmH₂O. Thus, the product AMP × FREQ, an index of pumping ability, was optimal at 3–5 cmH₂O (Davis et al. 2008). Based on that information, we performed controlled pressure ramps from 0.5 to 3 cmH₂O at different rates. From initial trials, we found that ramps lasting 15–30 min were required in order not to produce rate-sensitive increases in FREQ. Subsequently, pressure ramps were imposed at five different rates associated with ramp times of 30 min, 15 min, 6 min, 3 min and 1.5 min. Faster ramps were not practical because in many vessels a low basal FREQ at the lower end of the pressure range resulted in only 1–3 contractions during the ramp, leading to inconsistent analysis of the actual FREQ associated with faster ramps. In each vessel, we also tested the response to a rapid step change in pressure from 0.5 to 3 cmH₂O, which usually provided the upper limit of the rate-sensitive response at 3 cmH₂O.

Figure 5 shows representative recordings from one lymphatic vessel responding to pressure ramps at two different rates (lasting 15 and 1.5 min), along with the response to a rapid pressure step. The slow pressure ramp in Fig. 5A was associated with a nearly continuous and progressive rise in both AMP and FREQ, interspersed with typical periods of slight bursts and pauses; a very similar pattern occurred in response to a 30 min ramp (not shown). In contrast, the same vessel responded to a 10-fold faster ramp with a relatively high FREQ during the later part of the ramp, which then declined after pressure reached 3 cmH₂O (Fig. 5B). Lastly, a step change in pressure produced an even more dramatic effect, with FREQ rising immediately after the step to a high value and then gradually declining (Fig. 5C).

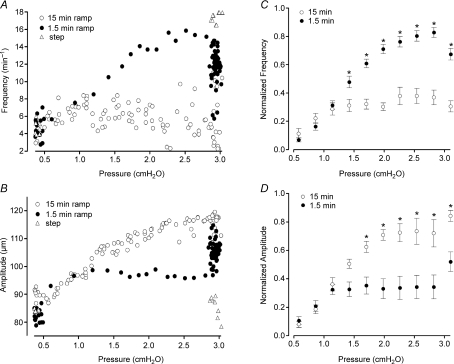
To analyse and compare data collected in response to pressure ramps at different rates, the FREQ and AMP data associated with each spontaneous contraction were plotted against pressure. Figure 6A and B represents the data analysis for the traces in Fig. 5. During the 15 min ramp, FREQ rose gradually with pressure from 4 to 6 contractions min⁻¹ (averaged over the control and plateau periods shown). During the 1.5 min ramp, FREQ rose to ∼16 min⁻¹ during the ramp and then declined after pressure reached 3 cmH₂O. Clearly, there were substantial differences between the FREQ values over the pressure range 1.5–3.0 cmH₂O at the two ramp speeds. Likewise, there were substantial differences between the AMP values over the same pressure range for the two ramp speeds, but AMP was consistently lower during the faster ramp, suggesting that a rate-sensitive enhancement occurred only in FREQ. The graphs in Fig. 6C and D summarize the data for six vessels subjected to the pressure ramp protocol. To account for substantial differences in basal contraction FREQ and AMP that occurred from vessel to vessel, the values for each vessel were normalized to their respective maximum values that occurred during the ramp or step (see Methods). The data were binned according to pressure so that statistical comparisons could be made between the different groups. The average response of the six vessels shown in Fig. 6C and D was quite similar to the single vessel shown in Fig. 6A and B. Significantly higher FREQ values were achieved when pressure was raised from 0.5 to 3 cmH₂O at the higher rate. Concomitantly, contraction AMP was significantly reduced during the faster ramp. Eventually (> 5 min at 3 cmH₂O), the two data sets in each graph converged (not shown).

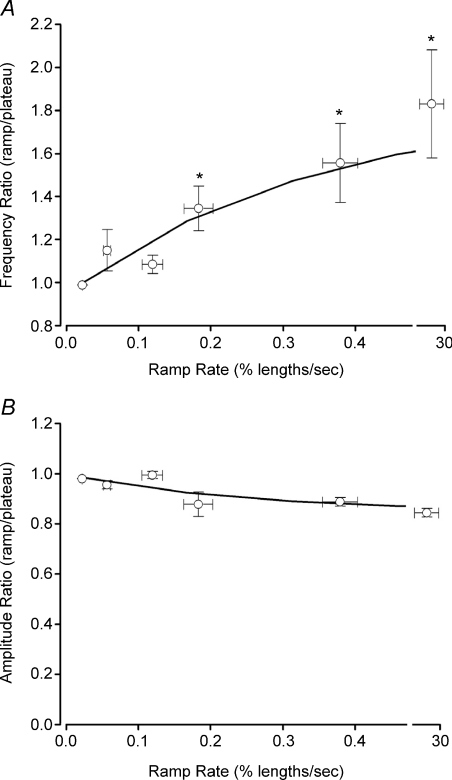
For comparison with the data sets obtained in isometric preparations, FREQ and AMP ratios (ramp/plateau) were also determined for pressure ramp protocols. Figure 7 summarizes the responses of seven vessels to pressure ramps at four different speeds, with ramp speed expressed in percentage lengths s⁻¹, calculated from the rate of pressure rise (in cmH₂O min⁻¹) and the actual diameter change (D_o–D_i)/D_o. The fifth point represents the rate associated with a pressure step from 0.5 to 3 cmH₂O, which was complete in < 200 ms. As in previous protocols, there is a clear, graded increase in FREQ with increasing rate of pressure change, with the highest three rates being statistically significantly different from the lowest rate. In contrast, there is a trend for AMP to decline slightly with ramp speed, but none of the AMP values are significantly different from each other.

Figure 7. Summary analysis of FREQ (A) and AMP (B) for pressure ramps at different rates.

Ramp rates were 30, 15, 6, 3 and 1.5 min; pressure steps were from 0.5 to 3 cmH₂O. Error bars are ±s.e.m. An asterisk indicates a significant difference from the value at the lowest rate.

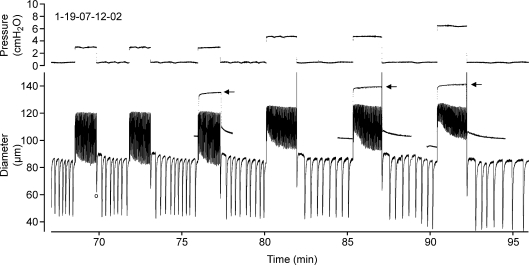
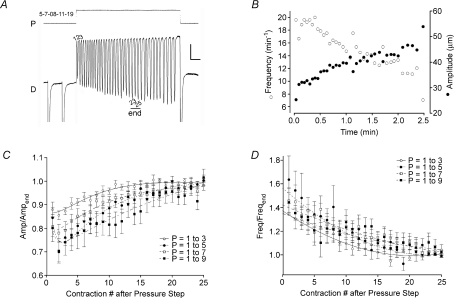
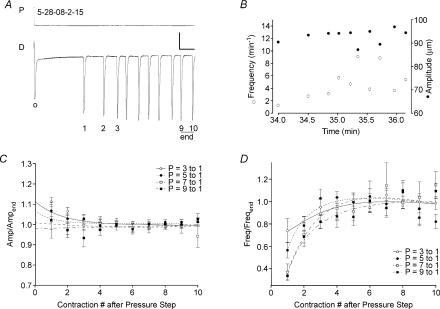
Having established that rate-sensitive contractile responses occur in pressurized lymphatics, we tested whether this effect was limited to a specific pressure range. An example of the lymphatic response to pressure steps of increasing magnitude is shown in Fig. 8. An increase in contraction FREQ occurred after each positive pressure step and a decrease in FREQ following each step reduction in pressure. Correspondingly, AMP was initially reduced compared to the AMP at 0.5 cmH₂O but then progressively increased with time at the elevated pressure, due mostly to a decline in end-systolic diameter. However, because of the compressed time scale, changes in FREQ that occurred while pressure was elevated are not apparent (but see Fig. 9A). The time-dependent AMP effect was progressively greater as the magnitude of the pressure step increased. Note also the slight decline in end-diastolic diameter (a slight myogenic constriction) at the higher pressures, although myogenic constrictions were not observed in all vessels. For reference, the passive responses of the same vessel to identical pressure steps (performed at the end of the protocol in Ca²⁺-free PSS) are superimposed on the trace for pressure steps to 3, 5 and 7 cmH₂O (denoted by arrows).

Figure 8. Diameter recording from a pressurized lymphatic vessel in response to rapid intraluminal pressure steps.

The record is too compressed to distinguish individual contractions at the higher pressures (but see Fig. 9 for example). The first (blunted) contraction on each downward step is associated with a pressure change (marked by ‘o’ at time = 70 min), and therefore is not an isobaric contraction. Arrows indicate the passive responses of the same vessel recorded at the end of the experiment in Ca²⁺-free solution (and then overlayed onto the active diameter responses).

Figure 9. Summary of lymphatic vessel responses to upward pressure steps.

A, expanded view of the diameter (D) response to a single positive pressure (P) step. Calibration bar: 12.5 cmH₂O, 20 μm for y-axes; 15 s for time axis. The first 10 contractions are numbered, along with the last three contractions (23–25) for which the average AMP and FREQ served as a reference to normalize the earlier contractions. B, subsequent analysis of contraction FREQ and AMP for the record in panel A. C and D, analysis of relative FREQ and AMP for the first 25 contractions after a positive pressure step with the magnitude of the step (in cmH₂O) indicated in the legend; n= 8 vessels. AMP or FREQ values > 1 are indicative of rate-sensitive enhancement. Error bars are ±s.e.m.

The changes in FREQ that occurred over time immediately after pressure elevation are shown more clearly in Fig. 9A, with the calculated values of FREQ and AMP plotted for that recording (Fig. 9B). FREQ typically was higher immediately following the pressure step than after ∼2 min at the higher pressure. In contrast, the AMP of the first few contractions was low and progressively increased toward the end of the trace. For statistical analyses, the AMP and FREQ changes were analysed on a beat-to-beat basis, with each parameter normalized to the average value for contractions numbered 23–25, to account for differences in the baseline parameters at different pressure levels. Peaks 23–25 were selected as a reference because in most vessels the contraction pattern stabilized after about 20 contractions. Figure 9C and D represents the contraction-by-contraction analysis for each of four successively greater positive pressure steps from a baseline pressure of 1 cmH₂O. In each case, the average AMP ratio for the first ∼10 contractions was < 1, i.e. less than the average AMP for contractions 23–25 (Fig. 9C). There was also a trend for AMP over the first few contractions to be smaller with larger pressure steps. In contrast, the average FREQ for the first ∼15 contractions after a positive pressure step was 1.4–1.6 times greater than the average FREQ at contractions 23–25 (Fig. 9D). However, the FREQ response was not substantially different between any the four different pressure steps.

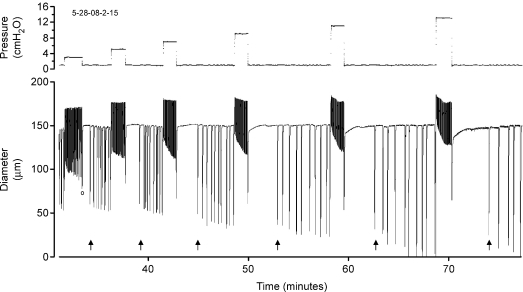
Figure 10 shows a recording from another lymphatic vessel, highlighting the pattern of diameter changes in response to downward pressure steps. After stepping pressure down to 1 cmH₂O (note the blunted contraction associated with each pressure step), there was a substantial delay until the first full contraction at the lower pressure. The delay was quite consistent if the same pressure step was repeated multiple times (e.g. the first 3 pressure steps in Fig. 8), but progressively increased with larger pressure steps, as denoted by the arrows in Fig. 10. A similar pattern is evident in Fig. 8 (and also in Suppl. Fig. 2 for isometric contractions), although it is not as dramatic. Subsequently, the diameter responses to downward pressure steps (i.e. negative dP/dt) were analysed in the manner used previously (Fig. 11A and B). In response to downward pressure steps, the contraction pattern typically stabilized after five to seven contractions, and therefore the AMP and FREQ values averaged over contractions 9 and 10 were used to calculate the relative AMP or FREQ for each contraction. The FREQ and AMP data for this recording are plotted in Fig. 11B and the average data sets for 11 vessels are plotted in Fig. 10C and D. There was a slight but consistent increase in the relative AMP of the first contraction after a downward pressure step, which then declined over subsequent contractions. The changes in FREQ over time were much more substantial, with the relative FREQ on the first contraction being ∼75% for a pressure step from 3 to 1 cmH₂O. Furthermore, the magnitude of this apparent inhibition was 55%, 37% and 35% with pressure steps from 5, 7 and 9 cmH₂O, respectively.

Figure 10. Diameter response of a pressurized lymphatic vessel to sequentially larger pressure steps.

Time scale emphasizes the contraction inhibition in response to falling pressure. Note that the time between the blunted contraction associated with each downward pressure step (marked by ‘o’ on the first pressure step) and the first full contraction (arrows) becomes progressively greater with increasing magnitude of the pressure step.

Figure 11. Summary of lymphatic vessel responses to downward pressure steps.

A, expanded view of the diameter response to a downward pressure step. Calibration bar: 8 cmH₂O, 15 μm for y-axes; 15 s for time axis. The blunted contraction associated with the pressure step is marked by ‘o’. B, subsequent analysis of contraction FREQ and AMP for the record shown in panel A. C and D, analysis of relative FREQ and AMP for the first 25 contractions after a negative pressure step with the magnitude of the step (in cmH₂O) indicated in the legend; n= 10 vessels. AMP or FREQ values < 1 would be indicative of rate-sensitive inhibition. Error bars are ±s.e.m.

Thus, the AMP ratio was consistently ≥ 1 and the FREQ ratio was consistently < 1 immediately after a downward pressure step.

Discussion

Rate-sensitive responses to stretch were observed using three different experimental methods in both wire-mounted and pressurized lymphatic vessels isolated from rat mesentery. In wire-mounted preparations, fast but not slow ramp increases in passive force elicited increases in contraction FREQ that were greater during the ramp than when passive force had plateaued at a higher, more optimal level. Contraction bursts were often evident during the ramps. The FREQ responses became progressively greater when the vessels were subjected to higher-speed force ramps. Similar behaviour was recorded in response to ramp increases in vessel diameter rather than passive force. In both protocols, contraction AMP did not change in an analogous fashion, but merely showed a graded increase with preload. Furthermore, increasing the ramp speed caused a slight decrease rather than an increase in the AMP ratio. In pressurized lymphatics, slow pressure ramps from 0.5 to 3 cmH₂O were associated with gradual increases in both FREQ and AMP, whereas faster ramps over the same pressure range produced much larger increases in FREQ and decreases in AMP. FREQ bursts were often evident for the first 1–2 min after rapid pressure elevation and contraction inhibition occurred after rapid pressure reduction. Rate-sensitive FREQ changes occurred over a relatively wide range of intraluminal pressures from normal physiological values to pressures associated with lymphoedema (Zaugg-Vesti et al. 1993; Gretener et al. 2000). The redundancy and consistency of these findings suggests that rate-sensitive FREQ responses of lymphatics to circumferential stretch are robust and consistent between vessels and preparations. Unlike previous findings in blood vessels, FREQ but not AMP exhibited rate–sensitive enhancement in response to stretch. It is likely that the behaviour described in the present study is a general characteristic of lymphatics and may allow the lymphatic pump to compensate for impaired flow during/after partial occlusion of the outflow tract.

Differences between portal vein and mesenteric lymphatics

Like the longitudinal smooth muscle layer of rat portal vein (Johansson & Mellander, 1975), rate-sensitive enhancement in FREQ was consistently demonstrated in lymphatic vessels in response to increases in length. The FREQ of spontaneous force transients in lymphatic vessels was higher during an increasing preload ramp than after the vessel reached optimal preload; furthermore, the FREQ ratio increased with the speed of the ramp (Fig. 1). The pattern of lymphatic FREQ responses under isometric conditions was strikingly similar to that of rat portal vein, but in contrast to portal vein, the AMP of lymphatic force transients was always lower during a rising preload ramp compared to the stable AMP value at optimal preload; furthermore, the lymphatic AMP ratio fell further as the rate of change in preload increased (Fig. 1). In most cases, the AMP values during the ramp were intermediate between those at the initial preload and those at the optimal preload (particularly evident in Fig. 2A), suggesting that AMP was determined simply by the instantaneous preload value prior to each contraction. The dramatic difference in the AMP response of lymphatics compared to portal vein is evident from the raw recordings in Johansson & Mellander (1975), which show a clear enhancement in AMP during/after positive length ramps as well as inhibition of AMP after negative ramps. Our estimates of AMP and FREQ ratios from portal vein data (calculated from traces shown in Fig. 1 in Johansson & Mellander, 1975) indicate that both ratios were greater than 1 for positive length ramps (AMP ratio = 1.4, FREQ ratio = 3.5 for dL/dt=+3% lengths s⁻¹). In contrast, for the lymphatic vessels shown in Fig. 2, comparable calculations yielded an AMP ratio ∼0.9 and FREQ ratio ∼1.5 when diameter was increased at +1.1% lengths s⁻¹ (the peak FREQ response in Fig. 2C). This degree of stretch of portal vein produced ∼2-fold increase in FREQ (Fig. 3 in Johansson & Mellander, 1975), which is very close to what we observed in lymphatics. We were unable to determine whether lymphatic vessels would have further increased their FREQ at higher rates of stretch due to an insufficient number of contractions during faster force ramps. However, occasional examples of the lymphatic response to force steps suggest that FREQ could potentially increase up to 4-fold (e.g. Suppl. Fig. 2), closer to the maximum value observed in portal vein.

Rate-sensitive changes in contraction FREQ were also recorded in pressurized lymphatic vessels, indicating that the phenomenon was not limited to wire-mounted or isometric preparations. Transient, high-frequency contraction bursts were consistently noted in response to rapid pressure elevation (Figs 5C and 9A) and to pressure ramps lasting 1.5–3.0 min (Fig. 6). Furthermore, the relationship between the FREQ ratio and the ramp speed (Fig. 7A) had a very similar appearance to that recorded in wire-mounted vessels (Figs 1C and 2C). In contrast, there was not a substantial or significant change in the AMP ratio with increasing ramp speed (Fig. 7B).

Lymphatic vessels appeared to be more sensitive to stretch than portal vein. From Fig. 3 in Johansson & Mellander (1975) the threshold for a rate-sensitive FREQ response was ∼+0.6% lengths s⁻¹ compared to isometric lymphatic vessels where the threshold was ∼+0.2% lengths s⁻¹; however, the lowest significant increase in lymphatic FREQ ratio occurred at a ramp rate of ∼0.8% lengths s⁻¹ (Fig. 2C). In pressurized lymphatics, the threshold for an increase in the FREQ ratio appeared to be even lower (∼0.05% lengths s⁻¹), with the lowest statistically significant value occurring at a ramp rate of ∼+0.2% lengths s⁻¹ (Fig. 7A). These comparisons suggest either that lymphatics are 2- to 3-fold more sensitive to stretch than portal vein or that pressurized vessels may be more sensitive to stretch than wire-mounted vessels, possibly due to a more uniform force distribution in the former.

Mechanisms underlying rate-sensitive contractions

Our finding that rat lymphatics exhibit rate-sensitive enhancement in FREQ but not AMP to stretch, unlike rat portal vein, is consistent with a previous assertion that lymphatic muscle is not typical vascular smooth muscle but exhibits biochemical characteristics of both vascular and striated muscle (Muthuchamy et al. 2003). Although the mechanism underlying rate-sensitive FREQ modulation is unknown, preliminary observations rule out a few possibilities. First, rate-sensitive FREQ enhancement does not require an intact endothelium, since the endothelial layer was disrupted in many of our isometric protocols (e.g. Figs 1–4) in the process of sliding wires into the vessel lumen; also, in preliminary experiments (not shown), rate-sensitive responses continued in the presence of the cyclooxygenase inhibitor indomethacin (10 μm; n= 5) to block the possible action of endothelial-derived prostanoids. Second, the mechanism does not appear to involve the release of SP or other tachykinins from nerve endings (Widdicombe, 2003) that are present on the outside of the vessels because rate-sensitive responses also persist in the presence of neurokinin receptor blocker with spantide (1 μm; n= 2) or WIN57108 (10 μm; n= 5; not shown). Mediation of rate-sensitive FREQ responses by SP is also unlikely given the fact that SP is known to modulate both FREQ and AMP (Davis et al. 2008).

A possible explanation for a differential effect of stretch on lymphatic FREQ but not AMP is that an electrical pacemaker in the wall is rate-sensitive but lymphatic muscle is not. This distinction points to a possible neural mechanism, given the fact that rate-sensitive characteristics are well-documented in certain mechanoreceptors (Widdicombe, 2003). Although the mechanism of pacemaker activity has not yet been definitively resolved in either portal vein or lymphatic vessels, recent studies have implicated interstitial cells of Cajal (ICC). ICC are present in many hollow organs (Pucovsky et al. 2007) but have been characterized best in the gastrointestinal system as networks of pacemaker cells connecting enteric neurons to circular and longitudinal smooth muscle cells (Sanders & Ward, 2008); ICC are strongly implicated in the generation and propagation of gastrointestinal slow waves (Ordog et al. 1999) in addition to mediating inhibitory and excitatory neurotransmission (Hirst et al. 2002). Intramural ICC in murine gastric muscle can function as stretch receptors to regulate pacemaker activity, but do not appear to show bursting in response to ramp increases in passive force (Won et al. 2005).

A specialized population of ICC-like cells has been suggested to be involved in the generation of pacemaker activity and basal tone of blood vessels and lymphatics (McCloskey et al. 2002; Harhun et al. 2005), but that remains a controversial issue (Pucovsky et al. 2007). Rat mesenteric lymphatics have only 1–2 layers of muscle cells, making it difficult to envision how a discrete ICC layer could be present, particularly between the endothelium and smooth muscle (McCloskey et al. 2002). However, the sparse, longitudinally orientated cells located in the outer medial layer (Crowe et al. 1997) could possibly function as ICC to generate pacemaker signals and transduce stretch. Resolution of these issues will likely require the application of electrophysiological methods to the mechanical protocols described here.

Physiological significance

The behaviour of lymphatic vessels described here is not specific to isolated mesenteric lymphatics because we have observed similar rate-sensitive stretch responses in femoral lymphatics and thoracic duct of the rat (unpublished observations). Moreover, an analysis of the lymphatic literature yields anecdotal evidence for rate-sensitive stretch responses in other types/species of lymphatic vessels. Despite numerous published examples of lymphatic diameter recordings at various steady-state levels of intraluminal pressure (Mizuno et al. 1997; Zhang et al. 2007b), only a few continuous records of lymphatic vessel responses during changes in pressure/preload appear in the literature. In one prominent example (Fig. 8 in McHale & Roddie, 1976), an isolated bovine mesenteric lymphatic did not exhibit obvious bursting after positive pressure steps but did show slight contraction inhibition after negative pressure steps. In a similar preparation, Ohhashi et al. showed a recording of the response of a two-lymphagion segment to sinusoidal pressure (Fig. 7B in Ohhashi et al. 1980) in which the downstream segment may have exhibited modest bursting on the rising phase of the pressure wave. Orlov and Lobacheva published a single recording from a goat mammary gland lymphatic in response to changes in pressure at two different rates (4 or 0.5 mmH₂O s⁻¹), in which the vessel was pressurized from one end while axial tension was recorded at the other end. In response to pressure elevation, the otherwise quiescent vessel showed a large increase in passive (axial) tension followed by the development of contractions in which both the FREQ and AMP were higher when pressure was increased at the higher rate (Orlov et al. 1983). In this regard the vessel behaved more like portal vein (Johansson & Mellander, 1975) than the lymphatics described in the present study, pointing to the possibility that the circular and longitudinal muscle layers in lymphatics (and portal vein?) may respond differently to rapid stretch, with the longitudinal layer exhibiting rate-sensitive changes in both AMP and FREQ with axial stretch but the circular layer showing changes only in FREQ with circumferential stretch. In spite of this evidence in isolated vessels, we were unable to find in vivo evidence in the literature for rate-sensitive lymphatic responses. Downstream microocclusion of rat mesenteric lymphatics in vivo led consistently to elevated pressure and elevated contraction FREQ (Hargens & Zweifach, 1977) but methodological limitations resulted in only very slow and delayed intraluminal pressure changes; not surprisingly, no rate-sensitive effects in FREQ or AMP were apparent in the records. Collectively, these reports suggest that the behaviour of the rat mesenteric lymphatics described here may be a general characteristic of collecting lymphatic vessels, if the experiments are performed under the appropriate conditions.

A rate-sensitive change in FREQ to rapid circumferential stretch is more likely to be physiologically important in lymphatic vessels than in portal vein. The longitudinal muscle layer of rat portal vein shows rate-sensitive AMP and FREQ responses when that vessel is stretched axially, but the impact of such changes on portal vein diameter or resistance to flow has not been established – nor are such changes likely to be substantial. In lymphatics, however, rate-sensitive FREQ responses occur at intraluminal pressure levels associated with normal states of hydration (Hargens & Zweifach, 1977; Benoit et al. 1989) as well as at elevated pressures that are characteristic of patients with lymphoedema (Zaugg-Vesti et al. 1993; Gretener et al. 2000). In rat mesenteric lymphatics, optimal pumping occurs at 3–5 cmH₂O (Gashev et al. 2004) and the AMP × FREQ product, which is an index of pumping ability, would be dramatically altered by rate-sensitive changes in FREQ immediately after a pressure change, because FREQ is typically the more dominant of the two terms (Gashev et al. 2004; Zhang et al. 2007b; Davis et al. 2008). A rate-sensitive change in FREQ potentially would allow the lymphatic pump to compensate for impaired flow during and/or after sudden, partial occlusions of the outflow tract. In addition, it might enhance mesenteric lymphatic pump function during an initial, postprandial period of increased lymph flow.

Supplemental material

Online supplemental material for this paper can be accessed at:

http://jp.physoc.org/cgi/content/full/jphysiol.2008.162438/DC1