Abstract
Finger tapping involves 3 important features: time, spatial amplitude, and frequency. In classical analysis, investigators examine timing parameters; in spectral analysis, they examine frequency parameters. Both types of analysis are based on stationary tap information. The authors propose that time–frequency analysis is a useful tool for analyzing nonstationary finger tapping. They describe the method and give examples of frequency modulation, age difference, and speed transition that demonstrate additional insights one can gain by using this analysis.
Keywords: finger tapping, fast Fourier transform (FFT), time–frequency
One method of assessing the integrity of the neuromuscular system and examining motor control issues is to measure individuals’ ability to tap their finger. Finger tapping has the advantage of being a relatively pure neurologically driven motor task because the inertial and intersegmental interactions are so small that biomechanical influences on movement are reduced (Collyer, Broadbent, & Church, 1994). Stable finger tapping is also relatively uninfluenced by cognitive and perceptual demands or by cultural experience, although musical and keyboard influences can be present. In addition, developmental trends and clinical impairments are readily apparent, making changes in the behavior a clear signal of changes in some aspect of the neuromotor system. How the characteristics of tapping relate to underlying neuromotor processes, then, is an important question. In this note, we propose that the classical methods of measuring finger tapping in either the time or the frequency domain could be supplemented or possibly replaced by a time–frequency analytical method that may provide additional insight into the underlying processes.
Historically, the measured characteristics of repetitive unilateral tapping have been rate and consistency. Rate is typically measured as the mean intertap or interresponse interval (ITI or IRI, respectively) between successive taps across a trial. Consistency is measured as the coefficient of variation or the standard deviation of mean ITI (e.g., CV ITI, SD ITI). A second classical method of describing finger tapping is spectral analysis of the kinematics time series, which exposes the different frequency components of tapping. In that approach, one decomposes a signal into different frequency components by using the fast Fourier transform (FFT) to compute the discrete Fourier transform (DFT) needed to obtain the spectrum of frequency components. In both types of analysis, the spectrum of a given signal is presented as though finger tapping were time-invariant (i.e., spectral characteristics do not change over time). In reality, however, neuromotor signals are under the influence of many intrinsic and extrinsic constraints that may cause rapid and abrupt changes in the signal that one should not ignore or smooth as noise.
Our purpose in this note is twofold. First, we describe the two classical methods of analysis and show the derivation of time–frequency tools that can be applied to finger-tapping data. Second, we illustrate the potential usefulness of the time–frequency method in single-trial analyses across different experimental conditions and populations.
Description of Measurement Methods
Time-Domain Analysis
In the most fundamental approaches to finger-tapping analysis, investigators have focused on timing and consistency of timing as measured by a discrete event, usually the moment of surface contact, to denote the boundary between one tap cycle and the next. One method of decomposing variability of timing was originally proposed by Wing and Kristofferson (1973), who used the autocorrelation of ITI to decompose total observed tapping variance into central clock versus peripheral motor sources (see Wing & Kristofferson for details). It should be noted that, quite often, the assumptions of the Wing and Kristofferson model are not met (particularly in children) because the model requires stationary data. Nonstationarity of tapping has long been recognized as a problem for analysis. Mean data are very likely to misrepresent the real performance. An alternative method of dealing with nonstationarity is to perform adjustments through post hoc processing. For example, there are various methods of detrending the data, usually involving the fitting of a linear or curvilinear function to the data (Robertson et al., 1999).
Frequency-Domain Analyses
FFT methods have long been a standard tool for identifying the dominant frequencies within stationary periodic signals (Oppenheim & Schafer, 1989). The FFT is the basis for a spectral analysis that provides a valuable window on repetitive tapping behavior, revealing the presence of frequency components that are not necessarily at the main driving frequency of the finger tapping and that would not be detected by time-domain measures alone. Although the FFT is computationally simple and fast, its performance is quite inefficient, with bias for short data sequences and a “leakage effect,” even with the help of advanced windowing techniques (Welch, 1967). Furthermore, its removal of the time domain precludes the potential insights that may be derived from the linking of spectral information to the time course of the tapping behavior. It would therefore be valuable to have a method that merges time and spectral analyses so that changes of frequency decomposition across a trial can be seen.
Time–Frequency Analysis
In the time–frequency analysis technique, nonstationary signals are tolerated; one can therefore use it to quantify changes in the spectral characteristics of a signal over time (time-variant). Two widely used time–frequency representations are the short time Fourier transform (STFT) and the generalized time–frequency distribution (TFD) approaches (Cohen, 1989).
The STFT is simply the result of multiplying the time series by a short time window and then performing a FFT. The action of that window is to quantify spectra within narrower epochs of the behavior, resulting in a series of local spectra that are determined for all time. A display of local power spectra is referred to as a spectrogram. That windowing scheme can be described as constant width windowing. The time resolution is the same for all spectral components. The magnitude for any given spectral component of the TFD gives the average over the windowed time series. The choice of window size is somewhat arbitrary. One sometimes must perform two STFTs with different window sizes to achieve adequate time and frequency resolution. In the choice of window size, however, the investigator will trade off time resolution and frequency resolution. Cohen’s (1989) class of time–frequency analysis is a more precise approach that overcomes the window size problem.
Cohen’s (1989) class is a very general approach toward devising a joint function of time and frequency that will describe the energy density or intensity of a signal simultaneously in time and frequency. In this article, we investigate the application of the Choi–Williams (1989) transformation as the kernel for analyzing finger-tapping data. The most important property of Cohen’s class is the bilinear time–frequency transformation that is time- and frequency-shift invariant—which brings up the limitation of that class, referred to as interference term or cross-term. In this study, we used the Hilbert transformation function (Oppenheim & Schafer, 1989) to transform our kinematic data of finger-tapping movement to an analytic signal. An analytic signal is defined as a complex signal whose spectrum is identical to the real signal’s spectrum for positive frequencies and is zero for the negative frequencies. One of the major reasons to use the analytic signal in TFD is that it does not contain negative frequency components; there are no cross-terms generated as interference between the negative frequency and the positive frequency components; thus, the pattern of TFD is more readable and clear. It should be noted that there are several kernels. For example, we compared the Choi–Williams kernel with the cone-shaped kernel (Zhao, Atlas, & Marks, 1990) and found that the use of the analytic signal was sufficient to eliminate the cross-terms and the associated artifact. Furthermore, the comparison between kernels did not make a real difference for those tapping data. We therefore performed offline analysis by using MATLAB with the signal processing tool-box (The MathWorks, Natick, MA) and the Choi–Williams kernel (Auger, Flandrin, Goncalves, & Lemoine, 1996).
Demonstration of the FFT and the TFD: Analysis of Sine Waves
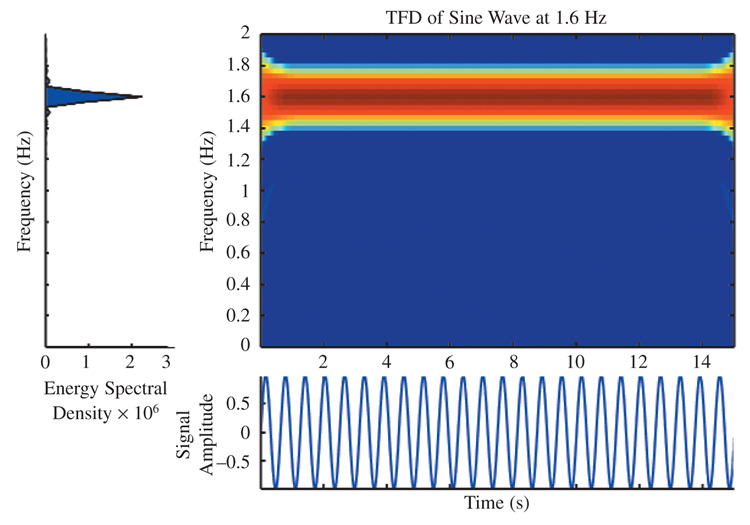
To illustrate the relationships and differences between time, frequency spectrum, and time–frequency approaches, we first present a demonstration on an artificially generated sine wave signal at a frequency of 1.6 Hz over 15 s. The sine wave approximates the time–space pattern of a continuous finger-tapping signal in space. A sine wave is a stationary signal if its fundamental frequency is constant over time.
The sine wave generated by MATLAB and the FFT and TFD of the sine wave are shown in Figure 1. The FFT of the sine wave shows that the peak power of the spectrum corresponded to 1.6 Hz, as is also shown in the TFD of the sine wave. That observation confirms that the sine wave has a constant frequency.
FIGURE 1.
Computer-generated sine wave at 1.6 Hz, fast Fourier transform (FFT), and generalized time–frequency distribution (TFD) of that sine wave. The magnitude of power of TFD is illustrated by the color gradient, with red and blue denoting the highest and lowest powers, respectively.
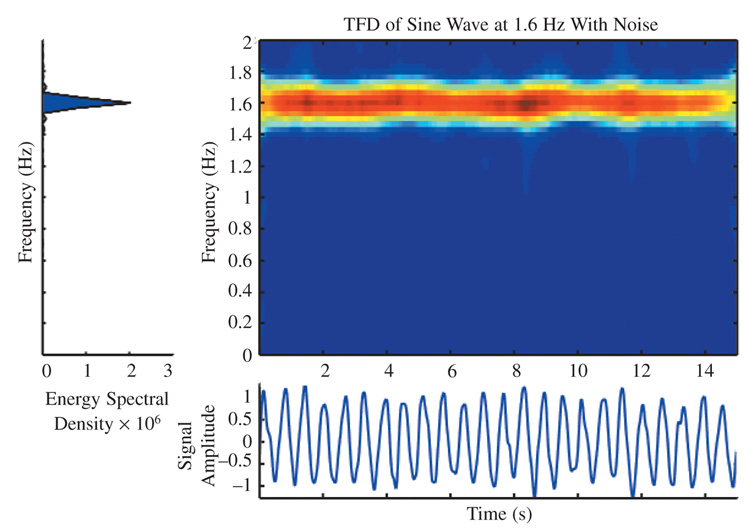
To illustrate the robustness of the TFD algorithms to additive noise, we added random noise to the original 1.6-Hz sine wave signal generated from MATLAB. The FFT and TFD results are shown in Figure 2. The FFT of the sine wave still shows that the peak power of the spectrum corresponded to 1.6 Hz, but more frequency components are distributed along the frequency axis. The TFD of the sine wave also shows a stronger frequency band at 1.6 Hz along the time axis. That finding confirms that when one uses the TFD approach, the sine wave has a relatively constant frequency when noise is added. Although that example over-simplifies the probable nature of noise in finger tapping, it does illustrate the capability of the algorithm to deal with random noise.
FIGURE 2.
Computer-generated sine wave at 1.6 Hz obtained by adding random noise, and FFT and TFD of that sine wave with random noise; note that the frequency scale of the FFT matches that of the TFD. FFT = fast Fourier transform; TFD = generalized time–frequency distribution.
Demonstration of Time–Frequency Analysis on Individual Finger-Tapping Trials
Method
For all trials, we measured finger tapping with the Motion Monitor system (Innsport, Chicago, IL), a magnetic tracking system that provides three-dimensional spatial position data. Motion data of the dominant index finger were sampled at 100 Hz for 15 s. Trials were either performed at preferred speed or paced by auditory signals produced via a Hewlett Packard waveform generator (set to 0.4, 1.2, and 1.6 Hz) attached to an amplifier and speaker. Data are presented from adult participants (n = 3) and a typically developing child (n = 1). The participants were taking part in an experiment that was approved by the University of Maryland’s Institutional Review Board; either they or their parent or caregiver had signed a consent form.
Example 1: TFD of an Adult’s Finger Tapping at 1.6 and 0.4 Hz
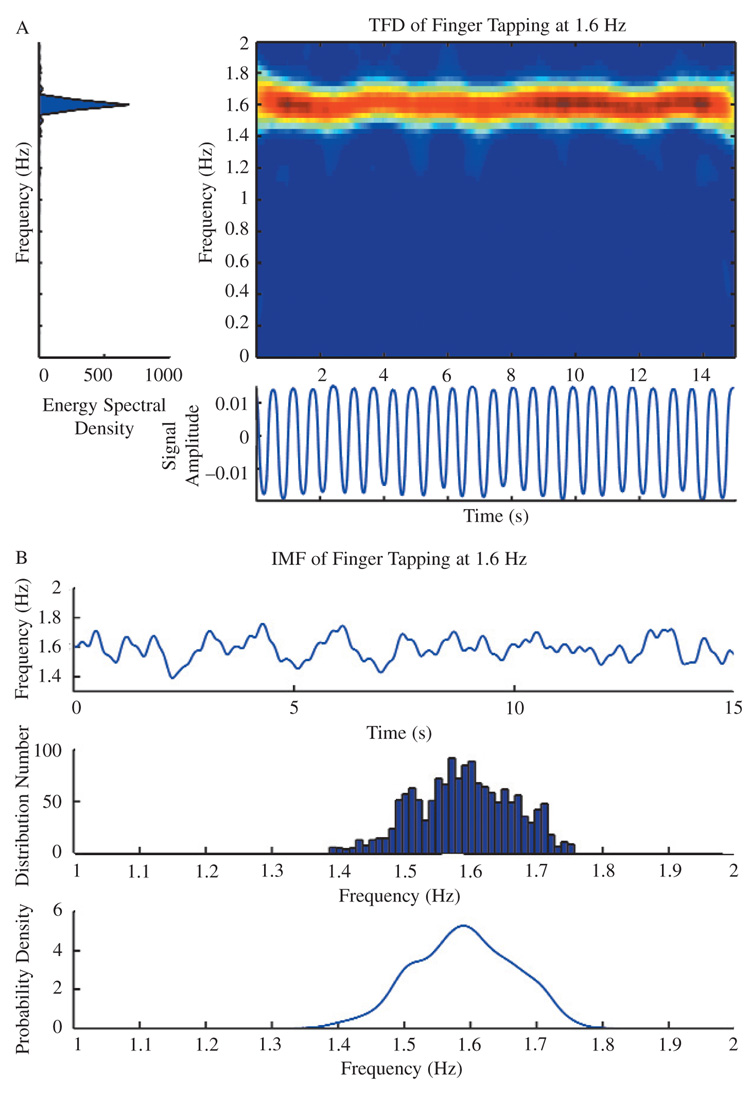
For demonstration purposes, the spatiotemporal data, FFT, and TFD of finger tapping for trials performed by a healthy adult participant at 1.6 Hz are shown in Figure 3A. At that speed, TFD of finger tapping shows a bandwidth from 1.5 to 1.8 Hz over the time, and variability of frequency change over time is shown as well in Figure 3. Compared with Figure 1, the TFD shows a frequency bandwidth pattern change over time, indicating control that differs from a machine-like finger (Deutsch & Newell, 2003; Riley & Turvey, 2002; Sternad, Dean, & Newell, 2000) producing a sine wave motion. In contrast to common spatiotemporal output, we see in the figure evidence of variability typically associated with human movement.
FIGURE 3.
Adult’s finger tapping at 1.6 Hz. (A) FFT and TFD of finger tapping. (B) Histogram and kernel density function estimation of IMF. FFT = fast Fourier transform; TFD = generalized time–frequency distribution; IMF = instantaneous mean frequency.
In addition to seeing time and frequency components on one plot, we extracted two parameters to quantify the TFD of finger tapping. The TFD(t, f) is a three-dimensional matrix that includes time index, frequency index, and magnitude of power. Frequency component changes over time or the magnitude of power changes over time are two ways of decomposing that three-dimensional matrix. The calculation of instantaneous mean frequency (IMF) is a standard way of decomposing TFD(t, f) (Choi & Williams, 1989), and it provides more insight on spectrum parameter changes over time. An additional way of portraying the IMF signal is to display it as a histogram and as a smoothed approximation, which one can obtain by using a kernel density estimation (Bowman & Azzalini, 1997).
We show the IMF in Figure 3B. The histogram and kernel density function estimation in Figure 3B indicated a unimodal distribution pattern, with the peak corresponding to 1.6 Hz and a high probability that the frequency would match the external driving signal.
Results from 0.4-Hz tapping from the same adult are shown in a similar format in Figure 4A and B. An interesting difference is that at the slow speed, the TFD of finger tapping was not simply a scaled-down map of the same structure from the fast speed; rather, it showed a distinct signature for slow finger tapping, with a wide bandwidth. From the histogram and kernel density function estimation in Figure 4B, we see indications of a bimodal pattern with two peaks (0.20 and 0.70 Hz) and one valley (0.45 Hz). That observation suggests that at the lower tapping frequency, there is a high probability that spectral components will not completely match the external driving signal. Indeed, there is one major frequency component in addition to the external frequency. One can speculate that the complexity of frequency components at a slow speed is a function of the dwell time between taps. The presence of a bimodal as opposed to a unimodal pattern indicates possible differences in control strategies for the two frequencies. However, we cannot make an inference about the linearity or nonlinearity of the underlying control process.
FIGURE 4.
Adult’s finger tapping at 0.4 Hz. (A) FFT and TFD of finger tapping. (B) Histogram and kernel density function estimation of IMF. FFT = fast Fourier transform; TFD = generalized time–frequency distribution; IMF = instantaneous mean frequency.
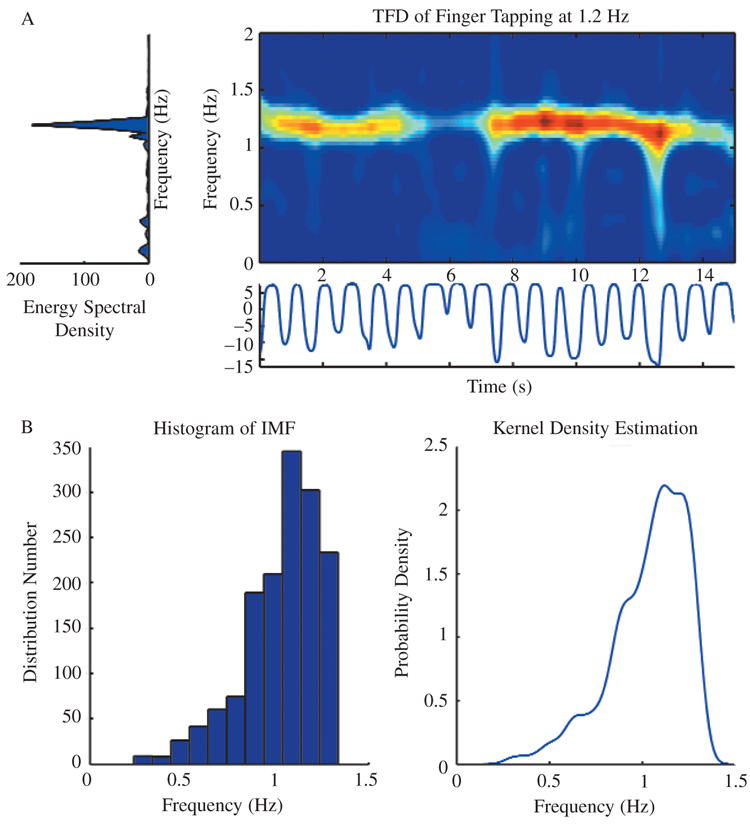
Example 2: TFD of an Adult’s and a Child’s Finger Tapping at 1.2 Hz
The time–space data, FFT, and TFD of finger tapping for trials from adult and child participants are shown in Figure 5A and Figure 6A. The IMF data for the same trials are shown in Figure 5B and Figure 6B. We selected those trials because a time-based analysis of the trials showed that they had the same ITI (0.83 s) and CV ITI (6.96 adult; 6.39 child). That is, a time-based analysis would not reveal differences between the adult and the child; but we can see from the TFD analysis the different patterns at similar ITI and CV ITI conditions. Specifically, when we compared the mean of IMF over time, the adult’s finger tapping showed a stable pattern (1.19 ± 0.05 Hz), whereas the child’s finger tapping showed an unstable pattern (1.04 ± 0.20 Hz). In addition, the probability of IMF was different. Those differences illustrate the potential for using IMF as quantitative changes in individual performance that could be used for future statistical analysis. It is also feasible to set criteria based on power level so that one can detect the difference in the spread of the bandwidth, as is shown in Figure 5A and Figure 6A.
FIGURE 5.
Finger tapping at 1.2 Hz for an adult. (A) FFT and TFD of finger tapping. (B) Histogram and kernel density function estimation of IMF. FFT = fast Fourier transform; TFD = generalized time–frequency distribution; IMF = instantaneous mean frequency.
FIGURE 6.
Finger tapping at 1.2 Hz for a child. (A) FFT and TFD of finger tapping. (B) Histogram and kernel density function estimation of IMF. FFT = fast Fourier transform; TFD = generalized time–frequency distribution; IMF = instantaneous mean frequency.
Example 3: TFD of Adult’s Finger Tapping With Midtrial Change of Frequency
In this example, the participant was asked to tap the right index finger in synchrony with an auditory signal under two conditions: (a) a sudden shift from a slow (0.667 Hz) to a fast (2.8 Hz) rate and (b) a sudden shift from a fast (2.8 Hz) to a slow (0.667 Hz) rate. The time–space data, FFT, and TFD of finger-tapping trials of changing from slow to fast pacing, and vice versa, are shown in Figure 7A and Figure 8A. The IMF data for the same trials are shown in Figure 7B and Figure 8B. In this case, the TFD provided insight into how intentional changes were made within a trial. As expected, relatively constant frequency was maintained within each period of constant pacing. Between those steady-state epochs, the TFD illustrates how the finger adapted to the sudden change of the auditory driving signal. The patterns of frequency adaptation revealed subtle differences in how the participant responded to the shift in externally driven timing constraints. The fast-to-slow transition appears as a smoother and more stable pattern in the TFD, in contrast to the more disjointed pattern during the slow-to-fast transition. The TFD analysis can therefore reveal the features of the transition, and in this case it suggests that the increase in period contains more frequency components than does the decrease in period. Those features may illustrate characteristics of the hysteresis effect in bidirectional frequency scaling.
FIGURE 7.
Finger tapping with midtrial change of frequency in an adult (from slow to fast speed). (A) FFT and TFD of finger tapping. (B) Histogram and kernel density function estimation of IMF. FFT = fast Fourier transform; TFD = generalized time–frequency distribution; IMF = instantaneous mean frequency.
FIGURE 8.
Finger tapping with midtrial change of frequency in an adult (from fast to slow speed). (A) FFT and TFD of finger tapping. (B) Histogram and kernel density function estimation of IMF. FFT = fast Fourier transform; TFD = generalized time–frequency distribution; IMF = instantaneous mean frequency.
Discussion
We have demonstrated how one can use a time–frequency analysis to potentially aid in the understanding of the neuromotor process underlying repetitive finger tapping. The strength of that approach is simply that the frequency components of the movement are captured over time, eliminating the need for stationary data. First, during different frequency protocols, the analysis of IMF showed us a unimodal pattern at 1.6 Hz and a bimodal pattern at 0.4 Hz. Second, with a similar ITI and CV ITI condition, an adult showed a different TFD pattern than did a child. Third, we detected in that approach subtle differences in transition under the period shift conditions.
To illustrate, we used single-trial data, but it would also be possible to average the continuous spatiotemporal data and then display the TFD of a group. One limitation of this approach is that computation is longer than it is for either a time or a frequency analysis. In the future, one can extend that approach to analyze two-finger tapping by looking at coherence in the TFD domain. One can also use TFD analysis to look at the ongoing electromyographic signal of finger taps, which provides a method of combining behavior and muscle activity.
Time–frequency analysis has been used in other motor domains, including muscle fatigue during dynamic contraction (Bonato & Knaflitz, 1999) and balance control (Schumann, Redfern, & Furman, 1995). To our knowledge, this is the first time investigators have used it to illustrate repetitive finger-tapping data. In summary, the main benefit of this approach is its capacity to detect subtle changes caused by a signal based on a nonstationarity, which allows one to gain more information from the signal.
ACKNOWLEDGMENT
Grants from the National Institute on Disability and Rehabilitation Research (H133G10111) awarded to Jill Whitall, from VA RR&D (#B3390K) awarded to Larry Forrester, and from the National Institute on Aging (P60AG12583) awarded to Jill Whitall and Larry Forrester supported this study.
APPENDIX
Temporal Analysis
Consider the time-domain analysis of finger tapping. The measures mean ITI and CV ITI are denoted by the following equations:
| (A1) |
| (A2) |
where N is the number of taps and i is the index of the individual tap.
Consider the decomposing of variability of timing; the method was originally proposed by Wing and Kristofferson (1973), who used the autocorrelation of ITI to decompose total observed tapping variance. The equation is
| (A3) |
where C is timekeeper interval, I is interresponse interval, and j is an index of the individual tap.
Frequency Spectrum Analyses
Consider the frequency spectrum analysis of finger tapping. The Fourier transform is the basis for spectral analysis; it relates the frequency domain (Equation A4) and the time domain (Equation A5).
| (A4) |
| (A5) |
where H(f ) is the Fourier series in the frequency domain, h(t) denotes the signal in the time domain, t is the time index, and f is the frequency index.
When dealing with an actual discrete time series, the equation is modified as the discrete Fourier transform (DFT), as follows:
| (A6) |
| (A7) |
where N is the number of points in the time series, and T is the sampling interval.
Time–Frequency Analysis
Consider the time–frequency analysis of finger tapping; two widely used time–frequency representations are the short time Fourier transform (STFT) and the generalized time–frequency distribution (TFD) approaches (Cohen, 1989). The STFT is the most common time–frequency representation.
| (A8) |
The one-dimensional sequence h[n] is converted into a two-dimensional function of the time variable n, which is discrete. The frequency variable λ is continuous, whereas w[m] is a window sequence that limits the extent of the sequence to be transformed so that the spectral characteristics are reasonably stationary over the duration of the window.
Cohen’s class is a very general approach for devising a joint function of time and frequency that will describe the energy density or intensity of a signal simultaneously in time and frequency. That joint function can be obtained from Cohen’s general formulation:
| (A9) |
TFD(t, f ) is the Cohen’s class time–frequency spectrum, x(t) is the real signal, x*(t) is a complex conjugate of x(t), t is the time index, f is the frequency index, τ is the time-lag,θ is the frequency lag, and ϕ(θ,τ) is called the kernel. Different selections of a kernel can have different properties of distribution of TFD. In this note, we have investigated the application of the Choi–Williams (1989) transformation as the kernel for analyzing finger-tapping data. The kernel of Choi-Williams is defined as
| (A10) |
Decomposition of Time–Frequency Distribution
Consider the decomposition of time–frequency distribution; IMF and kernel density estimation are defined as follows in Equation A11 and Equation A12, respectively:
| (A11) |
| (A12) |
Kernel density estimation is a nonparametric technique for density estimation in which one averages a known density function (the kernel) across the observed data points to create a smooth approximation. In kernel density estimation, xi (from x1 to xn) are n independent observations from the random variable x, K(●) denotes a so-called kernel function, and h denotes the bandwidth.
REFERENCES
- Auger F, Flandrin P, Goncalves P, Lemoine O. Time–frequency toolbox—For using with MATLAB, reference guide. Paris, France: Centre National de la Recherche Scientifique; 1996. [Google Scholar]
- Bonato P, Knaflitz M. Time–frequency methods applied to muscle fatigue assessment during dynamic contractions. Journal of Electromyography and Kinesiology. 1999;9:337–350. doi: 10.1016/s1050-6411(99)00009-7. [DOI] [PubMed] [Google Scholar]
- Bowman AW, Azzalini A. Applied smoothing techniques for data analysis. Oxford, England: Oxford University Press; 1997. [Google Scholar]
- Choi HI, Williams WJ. Improved time–frequency representation of multicomponent signals using exponential kernels. IEEE Transactions on Acoustics, Speech, & Signal Processing. 1989;37:862–871. [Google Scholar]
- Cohen L. Time–frequency distribution: A review. Proceedings of the IEEE. 1989;77:941–981. [Google Scholar]
- Collyer CE, Broadbent HA, Church RM. Preferred rates of repetitive tapping and categorical time production. Perception & Psychophysics. 1994;55:443–453. doi: 10.3758/bf03205301. [DOI] [PubMed] [Google Scholar]
- Deutsch KM, Newell KM. Deterministic and stochastic processes in children’s isometric force variability. Developmental Psychobiology. 2003;43:335–345. doi: 10.1002/dev.10140. [DOI] [PubMed] [Google Scholar]
- Oppenheim AV, Schafer RW. Discrete-time signal processing. Upper Saddle River, NJ: Prentice-Hall; 1989. [Google Scholar]
- Riley MA, Turvey MT. Variability and determinism in motor behavior. Journal of Motor Behavior. 2002;34:99–125. doi: 10.1080/00222890209601934. [DOI] [PubMed] [Google Scholar]
- Robertson SD, Zelaznik HN, Lantero DA, Bojczyk KG, Spencer RM, Doffin JG, et al. Correlations for timing consistency among tapping and drawing tasks: Evidence against a single timing process for motor control. Journal of Experimental Psychology: Human Perception and Performance. 1999;25:1316–1330. doi: 10.1037//0096-1523.25.5.1316. [DOI] [PubMed] [Google Scholar]
- Schumann T, Redfern M, Furman J. Time–frequency analysis of postural sway. Journal of Biomechanics. 1995;28:603–607. doi: 10.1016/0021-9290(94)00113-i. [DOI] [PubMed] [Google Scholar]
- Sternad D, Dean WJ, Newell KM. Force and timing variability in rhythmic unimanual tapping. Journal of Motor Behavior. 2000;32:249–267. doi: 10.1080/00222890009601376. [DOI] [PubMed] [Google Scholar]
- Welch PD. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Transactions on Audio and Electroacoustics. 1967;AU-15:70–73. [Google Scholar]
- Wing AM, Kristofferson AB. Response delays and the timing of discrete motor responses. Perception & Psychophysics. 1973;14:5–12. [Google Scholar]
- Zhao Y, Atlas LE, Marks RJ. The use of cone-shaped kernels for generalized time–frequency representations of nonstationary signals. IEEE Transactions on Acoustics, Speech, & Signal Processing. 1990;38:1084–1091. [Google Scholar]