Angiotensin-converting enzyme inhibitor-enhanced MR renography: repeated measures of GFR and RPF in hypertensive patients

Abstract

This study aims to assess the feasibility of a protocol to diagnose renovascular disease using dual MR renography acquisitions: before and after administration of angiotensin-converting enzyme inhibitor (ACEi). Results of our simulation study aimed at testing the reproducibility of glomerular filtration rate (GFR) and renal plasma flow demonstrate that for a fixed overall dose of 12 ml gadolinium-based contrast material (500 mmol/l), the second dose should be approximately twice as large as the first dose. A three-compartment model for analyzing the second-injection data was shown to appropriately handle the tracer residue from the first injection. The optimized protocol was applied to 18 hypertensive patients without renovascular disease, showing minimal systematic difference in GFR measurements before and after ACEi of 0.8 ± 4.4 ml/min or 2.7 ± 14.9%. For 10 kidneys with significant renal artery stenosis, GFR decreased significantly after ACEi (P < 0.001, T value = 3.79), and the difference in GFR measurements before and after ACEi averaged 8.3 ± 6.9 ml/min or 26.2 ± 43.9%. Dual-injection MRI with optimized dose distribution appears promising for ACEi renography by offering measures of GFR changes with clinically acceptable precision and accuracy.

renovascular disease (RVD) is the most common curable form of hypertension and renal insufficiency in humans. Of the 60 million Americans estimated to have hypertension, ∼1–5% have RVD. For the diagnosis of RVD, renal scintigraphy is typically performed following an angiotensin-converting enzyme inhibitor (ACEi) such as captopril. In kidneys with significant renal artery stenosis (RAS), glomerular filtration rate (GFR) is often preserved because activation of the renin-angiotensin system leads to efferent arteriolar vasoconstriction and increased pressure at the glomerulus. The ACEi reverses efferent arteriolar vasoconstriction and leads to a decrease in GFR. GFR reduction of more than 10% indicates high probability of renovascular hypertension (RVH) (25, 26, 29). The ACEi-induced change in renal perfusion such as renal plasma flow (RPF) could serve a complementary role (25), although the significance of change in RPF due to ACEi as measured in renal scintigraphy is controversial (7, 17, 21, 29). Such protocol has been proposed as a predictor of successful revascularization among patients with RAS as the cause of hypertension (4, 7, 11, 15, 21, 25, 26, 28, 29).

The protocol for dual-injection scintigraphy using Tc^99m-MAG3 or Tc^99m-DTPA pre- and post-ACEi has been extensively studied (25, 26). When performed on the same day, standard protocol calls for the second dose of radioactive tracer to be 5–10 times larger than the first one (1 vs. 5–10 mCi) (24–26) and for a 40- to 60-min delay between the first and the second injection to minimize the residual activity from the baseline scan (25). Alternatively, the two scans can be performed on 2 separate days.

Dynamic contrast-enhanced MRI is an alternative diagnostic procedure that allows a comprehensive exam of both renal vascular disease with MR angiography (MRA) and renal function with MR renography (MRR) in a single session (19). The commonly used tracer Gd-based contrast agent (gadopentetate dimeglumine or gadoteridol) is freely filtered at the glomerulus and does not experience reabsorption or secretion along tubules. With appropriate image segmentation (20) and tracer kinetic modeling (2, 6, 8, 12, 30), multiple parameters associated with perfusion, filtration, and tubular function can be identified. Using MRR in a swine model, Prasad et al. (19) demonstrated delay in tracer washout (due to reduced GFR) after the administration of captopril in kidneys with significant RAS.

This study investigates the feasibility of a single examination in which baseline and post-ACEi MRR are performed in quick succession, followed by contrast-enhanced MRA. To diagnose RVD and predict response to therapy, the goal is to measure single-kidney GFR before and after the ACEi with sufficient precision that changes in GFR in the presence of RVD can be detected. The overall dose of the injected tracer is limited because of the risk of nephrogenic systematic fibrosis (NSF) and the nonlinear and nonmonotonic relationship between Gd contrast concentration and signal intensity, where at high concentrations, signal loss may occur due to transverse relaxation time (T₂) effects. Therefore, we sought to determine, for a given total Gd chelate dose, the optimal distribution of that dose across two injections (d₁ and d₂). Our outcome measure is the precision of measured changes in renal function between the two injections.

In the first part of this paper, we use simulation techniques to evaluate the precision of two consecutive RPF and two GFR measurements and their changes using MRR. We also analyze the effects of the presence of residual tracer from the first injection on the post-ACEi results. A conventional “background subtraction” method is used where the residual is subtracted from the second-injection data to reset baseline for the second MRR concentration curves to zero. As an alternative to this approach, we present a procedure based on modeling the residual concentration from the first injection in the analysis of the second injection and demonstrate reduced error for the new procedure. Furthermore, to validate our simulations, we report the initial results from a clinical dual-injection MRR study. We studied hypertensive subjects referred for evaluation of RAS. In those without RAS, we hypothesized that the ACEi should have minimal effect on renal function, and therefore used changes in GFR and RPF measurements obtained pre- and post-ACEi as an estimate of reproducibility (precision) in dual-injection MRR. We also compared repeat measurements of GFR in these patients with the values obtained in a subset of patients with significant RAS. Since prior work established that significant RAS is associated with a decrease in GFR after ACEi (3, 19), to validate dual-injection MRR we tested the sensitivity of GFR decrease in separating the kidneys with significant RAS from those without RAS.

MATERIALS AND METHODS

MRR Technique

All Monte Carlo simulations and clinical examinations using MRR were based on a standard MR protocol performed on a 1.5 T MR system using a body phased array coil.

Serial coronal three-dimensional (3D) spoiled gradient recalled echo (GRE) images were acquired at 1.5 T (Avanto, Siemens Medical Solutions, Erlangen, Germany) using the following parameters: TR/TE/flip angle = 2.84 ms/1.05 ms/12°, partition matrix 161 × 256 × 20 interpolated to 256 × 256 × 40, field of view 400 × 400 × 100 mm, voxel size 1.6 × 1.6 × 2.5 mm, parallel imaging acceleration factor of 3, acquisition time 3 s. Before contrast administration, five 3D images were acquired during one 15-s breath-hold, to obtain a reliable precontrast signal for measurement of tracer concentration. A bolus injection of 4 ml Gd-based contrast agent was intravenously administered, followed by a 20-ml saline flush at 2 ml/s (Simulation Studies explains how we arrived at the dose distribution). Eight seconds following the start of Gd-DTPA injection, 10 3D acquisitions were repeated continuously for 30 s, during which time the subject was asked to suspend respiration for as long as possible. Sixteen additional 3D images were acquired during separate 3-s breath-holds for ∼10 min thereafter.

About 3 min before the end of the first MRR acquisition, an ACEi enalaprilat (0.04 mg/kg, up to 2.5 mg) was administered intravenously over 3 min. Typically, 7–10 min after the baseline scan ended, the post-ACEi scan started. For the post-ACEi scan, an 8-ml bolus of Gd-based contrast agent was injected. The MRR imaging protocol was the same as for the baseline scan.

Semiautomated image registration and segmentation of the 3D MRR data sets were performed to produce aortic, renal cortical, and renal medullary signal intensity vs. time curves (20). These signal curves were converted to concentration vs. time curves for the renal cortex and renal medulla and aorta, as previously reported (1). Briefly, the relationship between T₁ and signal intensity (SI) for the gradient echo MRR sequence is expressed as

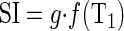(1)

where g is a scaling term that depends on a variety of factors, such as subject habitus, system gain, and coil sensitivity, and f(T₁) is a function that depends only on sequence parameters. Function f can be derived analytically or empirically by phantom experiments (1). With known f, g can be determined for each region (aorta, cortex, and medulla) using precontrast T₁ value (T₁⁰). For any contrast-enhanced SI value from dynamic images, the corresponding postcontrast T₁ value can be estimated using equation 1. The concentration ([Gd]) of the tracer that induces the change in T₁ value can be further estimated as

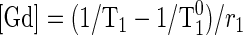(2)

where r₁ is the relaxivity of gadolinium contrast (4.5 mM⁻¹·s⁻¹). For conversions in the simulations, T₁⁰ values for aorta, renal cortex, and medulla were set at 1,200, 880, and 1,160 ms, respectively, and g at 2,800. All values are typical for our patient cases and MR system.

For patient study, the converted concentration vs. time curve for aorta, termed AIF, may be problematic due to several MR artifacts such as inflow effect. We normalized the AIF for the second injection assuming that patient's cardiac output Q remains constant throughout the exam. The procedure consists of two steps: 1) estimate Q with the first dose d₁ and the AIF for the first injection, based on the dye dilution principle (16); and 2) scale the AIF for the second injection using the estimated Q and the known dose d₂.

The concentration curves were subjected to the parameter-fitting procedure described below to derive renal functional parameters such as RPF and GFR.

Analysis of Renal Function using Tracer Kinetic Model

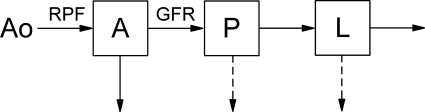
A previously validated three-compartment model was used for data analysis (12, 30). Briefly, from the abdominal aorta (Ao) the tracer transits through renal vascular pathway (A, arterioles and vasa recta), tubules (P), and loops of Henle (L; Fig. 1). RPF represents the flow into compartment A, and GFR the flow from A to P. Compartment A is distributed in both renal cortex and medulla, compartment P in renal cortex, and L in medulla. Hence, tracer retention curves of renal cortex and medulla (M_Cx and M_Med) can be expressed as

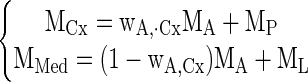(3)

where w_A,Cx is the volume fraction of A in renal cortex, and M_A, M_P, and M_L are the compartmental retentions.

Fig. 1.

Schematic diagram of 3-compartment model. A, intrarenal arteries; P, proximal tubule; L, loop of Henle. Renal plasma flow (RPF) represents the flow rate into A, and glomerular filtration rate (GFR) the flow rate from A to P. Solid arrow denotes tracer flow, and dashed arrow denotes water reabsorption.

The dynamics of tracer propagation in each compartment are characterized by the compartmental impulse retention function R_i(t). This function depicts tracer retention following an idealized scenario of a direct application of a unit impulse, i.e., the instantaneous bolus injection of unit dose of tracer. Given Ao, the aortic input function measured in units of tracer concentration, the tracer retention in the A compartment, M_A, is (30)

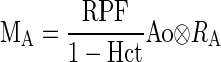(4)

where Hct is the hematocrit, R_A is the tracer retention in the vascular compartment, and ⊗ denotes convolution.

To compute retention in P and L compartments based on the input function Ao, we need to know the retention function R_i(t) that reflects the indirect (distal) tracer input. In a previous paper (30), we showed how to derive R_i(t) for P and L compartments. Using these derivations, we have

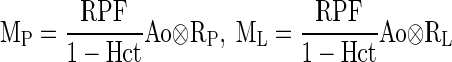(5)

We can express the regional tracer retentions (M_Cx and M_Med) by aortic input (Ao) and the model parameters including GFR, RPF, mean transit times, and washout rates for each of the three compartments (A, P, L) (30). The model parameters can be identified by minimizing the residual discrepancy (root mean square difference) between the measured retentions (M_Cx and M_Med) and the model-constructed ones. This is implemented using the iterative Levenberg-Marquardt minimization algorithm (13). We previously showed that GFR and RPF have sufficient sensitivity to measured data as to be reliably identified by the three-compartmental renal model (12, 30). We also showed that 3D image segmentation of MRR data into renal cortex and renal medulla is relatively accurate and segmented curves provide valid measure of renal function by this model (20).

Analysis of post-ACEi MRR: Residual Tracer from pre-ACEi Injection

The biological half-life of Gd-DTPA in the kidney is ∼1∼2 h and even longer for patients with renal dysfunction. In double-injection MRR, residual tracer from the baseline scan is present in the kidney at the time the second dose of tracer (for the post-ACEi scan) is injected. We examined two methods for accounting for residual tracer in the analysis of the post-ACEi scan: the baseline subtraction method and a model-derived initial value method.

Baseline subtraction method.

In the conventional method (25), residual Gd tracer in renal cortex and medulla from the end of the first MRR study (pre-ACEi) is subtracted from the cortical and the medullary curves for the second-injection data. Resulting curves for post-ACEi data have zero Gd retentions at the start of the second injection and are fitted with the same model as for the first-injection data.

Model-derived initial value method.

For the alternative method, the analysis of the post-ACEi data considers separately the tracer kinetics of the contrast material in each injection. The residual contrast from the first injection is taken as the initial value for the second injection, and modeled as an impulse input presented directly into the compartment. This impulse input transits through the originating compartment and then through the subsequent ones (Fig. 1). Take compartment P as an example. Tracer retention in P during the second MRR study is the sum of tracer from three sources: aortic input (Ao₂), tracer residue in compartment A that then transits through P, and residue in P itself. Note that Ao₂ also contains the tracer residue in the aorta from the first injection. The compartmental retentions during post-ACEi scan, M_i2 (i = A, P, or L), are expressed as

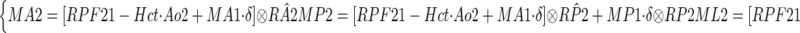(6)

The tracer residues from first injection, denoted as M_i1 (i = A, P, or L), can be estimated by sampling compartmental curves just before the start time of the post-ACEi scan. R_PL2 represents the tracer retention in L compartment as a function of time, induced by unit impulse at P compartment. δ is a unit impulse function.

Substituting the compartmental retentions shown in equation 6 into equation 3 gives the three-compartment model used in fitting the second-injection data. As in fitting of the baseline curves, functional parameters RPF₂, GFR₂, etc. are obtained by minimizing the residual discrepancy between the model-constructed retentions and the measured ones.

Simulation Studies

Our analysis of dual-injection MRR assumes that the total tracer dose d₀ is given. Using simulation techniques, we investigate different subdivisions of d₀ into the first-injection dose d₁ and the second dose d₂ (= d₀ − d₁), where each injection is performed under the same physiologic conditions so that we expect GFR₁ = GFR₂ and RPF₁ = RPF₂. We fix d₀ = 12 ml Gd-DTPA (with standard concentration of 500 mmol/l). We assume that the measurements of kidney function (such as GFR or RPF) are the main diagnostic interest and assess differences in estimates based on two separate injections, using doses d₁ and d₂. Our simulations vary the distribution d₁ and d₂; the precision of GFR₂ − GFR₁ and that of RPF₂ − RPF₁ are taken as the main outcome.

We began by generating a representative and low-noise arterial input function A₀(t), for a single injection. A₀ was obtained by averaging arterial concentrations in 24 subjects, after aligning the time axis to match the time of arterial peaks. The concentrations were derived from single-injection 10-min exams. A₀ was extrapolated to 30 min by assuming a biexponential behavior of the arterial concentration curve beyond 5 min. A representative arterial input in a dual-injection experiment was simulated as

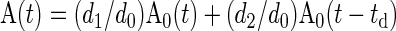(7)

where t_d is the time delay between the two injections. In all experiments below we assume t_d of 20 min, which is sufficient to administer ACEi challenge.

Tracer concentration vs. time curves for renal cortex and medulla were then constructed by convolving A(t) with impulse retention functions based on equations 3-5. The temporal resolution of MRR was assumed equal to 3 s/frame. Since each MRR exam extends over 10 min, with a 10-min delay between them, the total acquisition time for the simulated dual-injection experiment was 30 min. For addition of noise, we converted the concentrations (aorta, cortex, and medulla) to signal intensities, and added random noise (1). The level of noise was chosen to be 5% of precontrast cortical signal intensity. The noisy signal intensity vs. time curves were converted to concentration vs. time curves as described in MRR Technique.

The concentration vs. time curves for aorta, cortex, and medulla were separated into the first data set (the first 10 min) and the postchallenge data set (the last 10 min). Both data sets were then subjected to the parameter-fitting procedure. The Monte-Carlo process of adding random data noise was repeated n_trials times. The value of n_trials was determined by analyzing the convergence rate of observed standard deviations of all relevant functional parameters provided by the model. In all scenarios, n_trials = 1,000 was sufficient for ±3% accuracy.

For each simulation scenario, we assume no RVD so that GFR₁ = GFR₂. Two scenarios were considered, reflecting different functional status for the kidney: 1) normal where GFR₁ = GFR₂ = 58 ml/min, RPF₁ = RPF₂ = 168 ml/min and 2) dysfunctional where GFR₁ = GRF₂ = 24 ml/min, RPF₁ = RPF₂ = 76 ml/min. In the simulation, five combinations of d₁ and d₂ (2 + 10, 4 + 8, 6 + 6, 8 + 4, 10 + 2 ml) were compared for each scenario. The mean and SD for these four parameters (GFR₁, GFR₂, RPF₁, and RPF₂) and their differences, GFR₂ − GFR₁ and RPF₂ − RPF₁ were calculated over n_trials simulations. The SD indicates the precision of the parameters, and the deviation of the mean value from the value assumed in simulation experiments indicates the measurement bias. The optimal dose distribution should result in high precision and low bias for GFR₂ − GFR₁ and RPF₂ − RPF₁.

To compare the conventional background subtraction method with the initial value method for addressing residual gadolinium from the first injection at the time of the second injection, data from Monte Carlo trials were processed with both methods. This analysis focused on comparing the deviation of parameters GFR₂ and RPF₂ from their true value. Deviations obtained with the conventional and initial value methods were compared using paired t-test. Statistical significance was assumed for P < 0.05.

Patient Study

A patient study was carried out to assess the feasibility of double-injection MRR using the optimized doses, to evaluate the precision of GFR and RPF estimates, and to test the sensitivity of the proposed method in separating kidneys with significant RAS from nonstenotic kidneys. The Health Insurance Portability and Accountability Act (HIPAA)-compliant protocol was approved by the local institutional review board, and written informed consent was obtained from all subjects.

From n = 31 consecutive patients examined with MRR and MRA between 2004 and 2008 for evaluation of hypertension, we identified two groups based on the results of renal angiography (Table 1). For each patient, MRA was performed on the same day after dual-injection MRR. The percentage of RAS was measured from source data viewed in multiplanar reconstruction mode on a commercial workstation (Multimodality Workplace, Siemens Medical Solutions) by three radiologists independently, and a consensus interpretation was obtained. In Table 1, group A consisted of all patients classified as non-RAS (n = 18). Group B consisted of all patients with significant RAS (>50% stenosis in at least one renal artery; n = 8). Patient characteristics of these two groups were compared using unequal variance t-test. Statistical significance was assumed at P < 0.05. Patients with mild RAS (n = 5) were excluded because ACEi-induced renal response in these patients would be difficult to interpret.

Table 1.

Demographic and functional characteristics of the study population

Characteristic	Patients without RAS (Group A)	Patients with RAS (Group B)	P Unequal Variance t-test
No. of patients	18	8
Sex (M + F)	11 + 7	2 + 6
Age, yr	51.1±18.0	80.4±9.2	0.001
Weight, kg	83.8±18.9	64.0±8.5	0.001
Systolic pressure, mmHg	149.7±22.2	159.0±29.2	0.437
Diastolic pressure, mmHg	85.1±10.5	82.6±11.6	0.611
Creatinine level, mg/dl	1.6±1.1	2.0±1.2	0.361
Baseline eGFR, ml·min·1.73 m2	68.9±31.6	38.0±16.1	0.003

Values are means ± SE. RAS, renal artery stenosis; M, male; F, female; eGFR, estimated glomerular filtration rate.

All subjects underwent MRR before and after intravenous enalaprilat, according to the protocol described above. Based on the results of simulation, the injected tracer doses for pre- and postenalaprilat MRR were set as d₁ = 4 ml and d₂ = 8 ml. For three kidneys from three different patients in group A, image segmentation could not be done because of either multiple large cysts or severe motions during scans. For the other 33 kidneys in group A and 10 stenotic kidneys in group B, GFR and RPF for both pre- and post-ACEi studies were successfully measured using the proposed analysis methods described above.

To support the validity of the GFR measurement by MRR, the estimated GFR (eGFR) by the Modification of Diet in Renal Disease equation (MDRD) was computed (14). Single-kidney GFR estimates from pre-ACEi MRR for the two kidneys of each patient were summed to obtain a total GFR (tGFR). Correlation coefficient was used to compare eGFR and tGFR for all the subjects.

Pre-ACEi GFR values for the 33 nonstenotic kidneys in group A were compared with those for the 10 stenotic kidneys in group B, using unequal variance t-test. Similar comparison was done for pre-ACEi RPF. Statistical significance was assumed for P < 0.05.

For the kidneys in group A (without RAS), the two estimates for each parameter (GFR or RPF) obtained at baseline and after ACEi were taken as a reflection of the reproducibility or reliability of our measurement technique and were compared using paired t-test, Pearson's correlation coefficient, and a Bland-Altman plot. SD of the changes in each parameter (e.g., GFR₂ − GFR₁) across the nonstenotic kidneys was calculated as a measure of the reproducibility of the proposed method. For the stenotic kidneys in group B, correlation coefficient and linear regression were used to evaluate the possible change in GFR and RPF due to ACEi. We also tested the sensitivity and the specificity of relative or percentage GFR decrease, i.e., (GFR₁ − GFR₂)/GFR₁, in discriminating nonstenotic and significantly stenotic kidneys.

RESULTS

Simulations

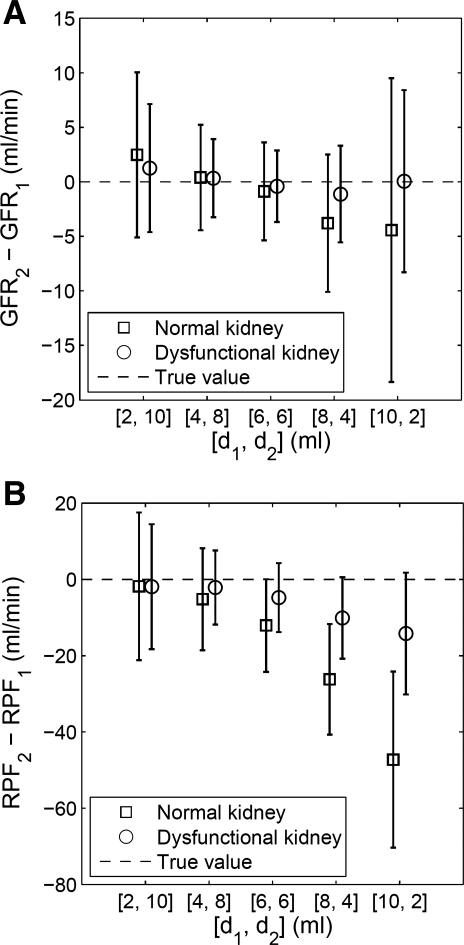
Figure 2 plots the distribution of GFR₂ − GFR₁ and RPF₂ − RPF₁. As the dose for the first injection (d₁) increased from 2 to 10 ml, the SD of GFR₂ − GFR₁ (reflecting its precision) first decreased then increased, for both the normal and the dysfunctional kidney scenarios. The minimum SD occurs for d₁ = 4 ml and d₂ = 8 ml. The same behavior of SD is observed for RPF (Fig. 2B). At d₁ = 4 ml and d₂ = 8 ml, GFR₂ − GFR₁ has comparable and minimal bias, <1 ml/min for both normal and dysfunctional cases. The biases for RPF₂ − RPF₁ at d₁ = 4 ml are about half of those at d₁ = 6 ml. Overall, the optimal dose distribution appears to be d₁ = 4 ml and d₂ = 8 ml.

Fig. 2.

Monte Carlo simulated estimates of renal function expressed as differences in renal function between first and second MR renography (MRR) acquisitions using d₁ for the first injection and assuming a total dose of 12 ml (d₂ = 12 ml − d₁). Plots show the simulated changes in renal function: GFR₂ − GFR₁ (A) and RPF₂ − RPF₁ (B) for each combination of doses and for 2 scenarios, a normally functioning kidney and a dysfunctional kidney. In this simulation, the true values of GFR₂ − GFR₁ and RPF₂ − RPF₁ are 0. Error bars denote mean value ± SD.

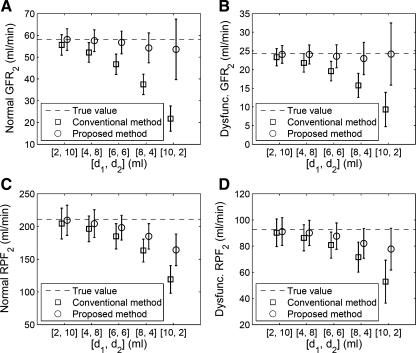
Figure 3 compares two methods of correcting for the residual tracer from the first MRR injection when analyzing second MRR acquisition data. With the initial value method, the systematic error in GFR₂ is less than 8% across all dose distributions (Fig. 3, A and B). The conventional subtraction method underestimates GFR₂ by an amount that progressively increases as d₁ increases, reaching an error larger than 60% for d₁ of 10 ml (Fig. 3, A and B). At d₁ of 4 ml, the accuracy of GFR₂ estimates by the proposed method is significantly better than that by the conventional method (P < 0.001).

Fig. 3.

Monte Carlo simulated estimates of renal function parameters (mean ± SD) for the second of 2 MRR acquisitions. A and B: GFR₂ of the normal and the dysfunctional kidneys. C and D: RPF₂ of the normal and the dysfunctional kidney. Two methods of correcting tracer residue from the first injection are tested: conventional background subtraction method (shown as squares) and initial value method described by equation 6 (circles). Results show consistently lower bias using the initial value method. Dashed lines are true values for the parameters in the simulation. At dose distribution (d₁, d₂) of 4 and 8 ml, the proposed initial value method reduces measurement bias while preserving the precision of GFR and RPF.

For both the conventional subtraction and proposed initial value methods, the systematic error in RPF₂ estimates increases as d₁ increases (Fig. 3, C and D). At every dose distribution, this systematic error by the proposed method is roughly half that by the conventional method. At the optimal dose distribution of d₁ = 4 ml and d₂ = 8 ml, the accuracy of RPF₂ estimates by the proposed method is significantly better than that by the conventional method (P < 0.001).

Patient Study

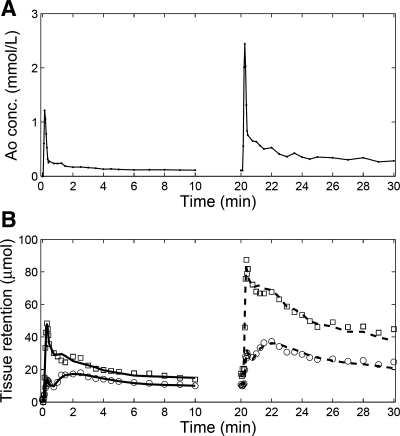
Tracer retention curves from a representative kidney, together with the model fits, are shown in Fig. 4. Two MRR acquisitions were performed, first using d₁ = 4 ml and the second, starting 10 min after the conclusion of the first, using d₂ = 8 ml. For both cortex and medulla, the retention curves from the second-injection data are higher than those from the first injection because of the residual contrast from the first injection as well as because of the larger dose used for the second injection (8 vs. 4 ml). Tracer residues in both renal cortex and medulla are little changed between the tail of the first injection (10 min) and the beginning (before) of the second injection (20 min). With the residues appropriately handled by the initial value model (equation 6), the cortical and medullary concentration vs. time curves from the second MRR acquisition were well fitted, with relative root mean square (RMS) error 7.0% for cortex and 8.0% for medulla.

Fig. 4.

Measured double-injection MRR data and model fits for a representative kidney. A: tracer concentrations measured from an aortic region of interest. B: tracer retention in cortex is represented by squares and that from medulla by circles. The first-injection data (0–10 min) were fitted using the model described by equations 3-5 (solid lines), with results GFR₁ = 43.8 ml/min, RPF₁ = 208.4 ml/min. The second-injection data (20–30 min) were fitted using the model described in equations 3 and 6 (dashed lines), with results GFR₂ = 44.9 ml/min, RPF₂ = 177.6 ml/min. In this case, GFR₂ − GFR₁ = 1.1 ml/min, while RPF₂ − RPF₁ = −30.8 ml/min. In the absence of renovascular disease, the expected GFR₂ − GFR₁ value is 0.

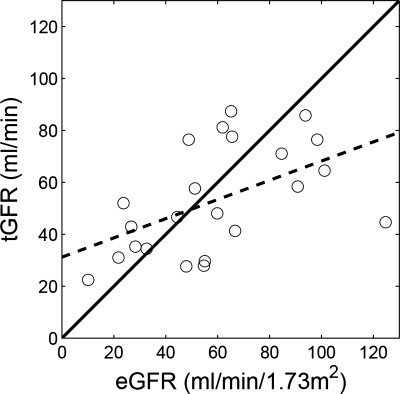
In total, 43 kidneys from 26 subjects were examined using the dual-injection protocol and curve fitting for the first MRR acquisition resulted in relative RMS averages of 11.8 ± 4.0% for cortex and 13.1 ± 5.0% for medulla. For second MRR acquisitions, the fits were better, with relative RMS errors averaging 6.8 ± 2.2% for cortex and 7.5 ± 2.9% for medulla. Total GFR by our MR approach correlated moderately with eGFR from MDRD formula (r = 0.522, P = 0.011; Fig. 5).

Fig. 5.

Correlation of estimated GFR (eGFR; by MDRD) and total GFR (tGFR; sum of the single-kidney GFRs by MRR). Regression equation is tGFR = 0.37 eGFR + 31.2, and correlation coefficient r = 0.522 (P = 0.011). Solid line is identity line and dashed line is regression line.

Derived in baseline MRR without ACEi, RPF₁ estimates for the 33 kidneys without RAS in group A were significantly higher than those for the 10 kidneys with significant RAS in group B (Table 2). Similarly, GFR₁ estimates for the non-RAS kidneys were significantly higher than those for the RAS kidneys, but the difference was not as large as that in RPF (Table 2).

Table 2.

Comparison of pre-ACEi GFR and RPF for nonstenotic kidneys and significantly stenotic kidneys in patient study

	Kidneys without RAS	Kidneys with RAS	Unequal Variance t-test
RPF, ml/min	150.6±70.1	68.3±33.4	P=0.0001
GFR, ml/min	30.7±11.1	20.9±11.9	P=0.037

Values are means ± SE. ACEi, angiotensin-converting enzyme inhibitor; RPF, renal plasma flow.

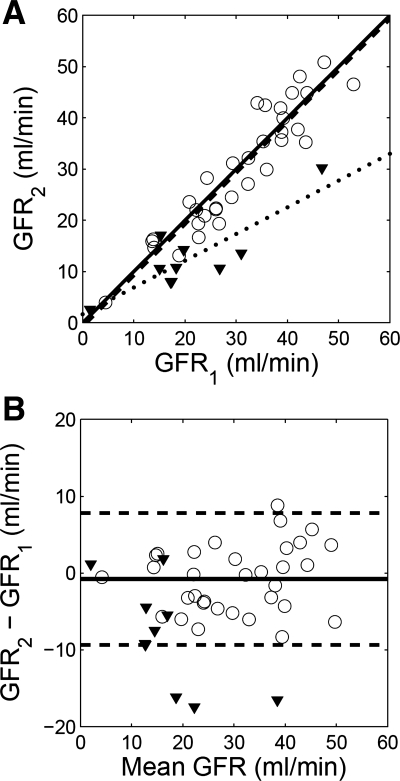
In the 33 kidneys without RAS (group A), GFR₁ estimates correlated well with GFR₂ estimates (Fig. 6A, regression equation GFR₂ = 1.00 GFR₁ − 0.77 and correlation coefficient 0.931). Bland-Altman plot shows that the differences GFR₂ − GFR₁ averaged −0.8 ± 4.4 ml/min (or −2.7 ± 14.9% of GFR₁) with 95% confidence interval between −9.3 and 7.8 ml/min (Fig. 6B). Paired t-test indicated no significant difference between the two estimates (paired t-test, T = 0.99, P = 0.33). In contrast, GFR₂ estimates for the 10 kidneys of significant RAS in group B were significantly lower than GFR₁ (paired t-test, T = 3.79, P = 0.004), and regression equation was GFR₂ = 0.52 GFR₁ + 1.67 (Fig. 6A). The difference GFR₂ − GFR₁ averaged −8.3 ± 6.9 ml/min (or −26.2 ± 43.9% of GFR₁). A cutoff value of 27.6% for (GFR₂ − GFR₁)/GFR₁ resulted in 80% sensitivity and 94% specificity for detecting significant RAS.

Fig. 6.

Comparison of baseline GFR (GFR₁) and second-injection GFR (GFR₂) measured using a dual-injection MRR protocol. A: correlation plot and linear regression. For the nonstenotic kidneys (displayed as circles), correlation coefficient is 0.931, and regression line y = 1.00x − 0.77 (dashed line); for the stenotic kidneys (triangles), correlation coefficient is 0.870, and regression line y = 0.52x + 1.67 (dotted line). The solid line is the identity line. B: Bland-Altman plot. Difference between the 2 GFR estimates for the nonstenotic kidneys (displayed as circles) averaged −0.8 ml/min with 95% confidence interval between −9.3 and 7.8 ml/min (dashed lines). Differences between the 2 GFR estimates for the stenotic kidneys are shown as triangles.

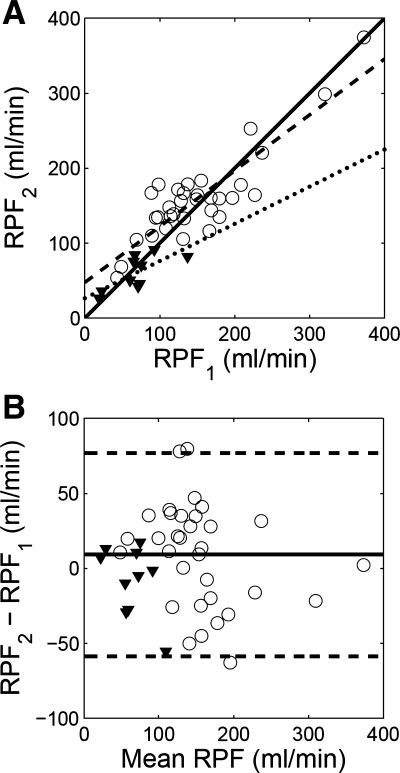
RPF estimates of the nonstenotic patients in group A show a correlation coefficient 0.870 before and after ACEi (Fig. 7A; regression equation, RPF₂ = 0.75 RPF₁ + 47.5). Differences between the two RPF estimates (RPF₂ − RPF₁) averaged 9.2 ± 34.6 ml/min (or 13.6 ± 28.7% of RPF₁) with 95% confidence interval between −58.6 and 76.9 ml/min (Fig. 7B). No significant difference was observed between RPF₁ and RPF₂ (paired t-test, T = 1.52, P = 0.14). Similarly for the kidneys with significant RAS in group B, there was no significant difference between RPF₁ and RPF₂ (paired t-test, T = 1.1, P = 0.30). Regression equation for RPF₁ and RPF₂ was RPF₂ = 0.50 RPF₁ + 26.3. The difference RPF₂ − RPF₁ averaged −8.0 ± 23.1 ml/min (or −0.50 ± 34.7% of RPF₁).

Fig. 7.

Comparison of baseline RPF (RPF₁) and second-injection RPF (RPF₂) measured using a dual-injection MRR protocol. A: correlation plot and linear regression. For the nonstenotic kidneys (displayed as circles), correlation coefficient is 0.870, and regression line y = 0.75x + 47.5 (dashed line); for the stenotic kidneys (triangles), correlation coefficient is 0.870, and regression line y = 0.50x + 26.3 (dotted line). The solid line is the identity line. B: Bland-Altman plot. Difference between the 2 RPF estimates for the nonstenotic kidneys (displayed as circles) averaged 9.2 ml/min with 95% confidence interval between −58.6 and 76.9 ml/min (dashed lines). Differences between the 2 RPF estimates for the stenotic kidneys are shown as triangles.

DISCUSSION

ACEi-enhanced MRR offers the opportunity to improve the diagnosis of RVD by providing functional information to complement vascular imaging using MRA. MRR can be performed before and after an ACEi and changes in GFR can be used to diagnose RVD. According to a previous consensus report (25), a decrease in GFR larger than 10% (for example, a decrease of 6 ml/min for GFR 60 ml/min) after ACEi indicates high probability of RVH. In our study, we sought to determine the optimal dose distribution for pre- and post-ACEi MRR protocols and to analyze precision and accuracy in measuring GFR and RPF before and after ACEi. We also tested this protocol in a small sample of subjects referred for evaluation of RVD.

Our simulations show that approximately twice as large a dose should be given for the second injection than for the first injection. In our simulation and patient protocol, the time interval between the start of the two injections was set at 20 min to keep the MRR portion of study within 30 min. Hence, a significant amount of tracer from the baseline study was retained in the kidney at the time of the second injection. We found that a larger dose given in the second study helps minimize the relative effect of the residue, thereby balancing the precision of the serial parameter estimates of GFR₁ and GFR₂. Balancing the precision appears to maximize the precision of the difference measure GFR₂ − GFR₁.

One challenge in analyzing dual-injection data is the handling of the residual contrast material in the kidney at the time of the second injection. During the second scan, the residue diminishes due to continuous excretion of the kidney. However, using the conventional background subtraction method, residues are assumed constant during the second scan. The simulations revealed a significant artifactual bias associated with background subtraction. At optimal dose distribution (d₁ = 4 ml, d₂ = 8 ml) the second GFR is systematically underestimated by 7.4∼8.9% (8.9 ± 8.6% for the normal kidney and 7.4 ± 15% for the dysfunctional one). Given that a threshold of ∼10% decrease in GFR may be used to diagnose RVD, this underestimation may possibly lead to false positives or misdiagnoses. Using our initial value method for analyzing the second-injection data, our simulations predicted negligible ∼1% (0.7 ± 8% for normal and 1.2 ± 14.8% for dysfunctional kidney) systematic error in GFR₂. The magnitude of the residue during the second scan depends on the filtration rate and is different for the normal and the dysfunctional kidneys. However, for the simulated normal and dysfunctional kidneys, the errors in GFR₂ were comparable (0.4 ± 4.6 vs. 0.3 ± 3.5 ml/min), supporting the validity of the proposed method.

In our patient study, tGFR derived by MRR (baseline values before ACEi) correlated only moderately with the eGFR by the formula of MDRD (r = 0.522). This may be due to the fact that serum creatinine level does not reliably reflect renal function in elderly patients (23).

Our study of patients without RAS (group A) confirmed good agreement between GFR₁ and GFR₂, with correlation coefficient of 0.931 and GFR₂ − GFR₁ averaging −0.8 ± 4.4 ml/min or 2.7 ± 14.9% of GFR₁. These results are promising for the application of this technique to the diagnosis of RVD. For one preliminary group of kidneys with RAS (≥50%), a significant decrease in GFR was observed after ACEi, with GFR₂ − GFR₁ averaging −8.3 ± 6.9 ml/min (or −26.2 ± 43.9% of GFR₁).

Based on current study, the estimated SD of the difference GFR₂ − GFR₁ in the nonstenotic kidneys is 4.4 ml/min. Assuming that ACEi had no physiologic effect in these kidneys, the relative reproducibility of GFR change was 14.9% of GFR₁ (multiple patients in this study had low GFR₁). This level of precision compares favorably with plasma clearance methods in nuclear medicine. Using multiple sample method, Piepsz et al. (18) measured a precision of 9.0 ml·min⁻¹·1.73 m² for ⁵¹Cr-EDTA clearance, and a precision of 53.7 ml·min·1.73 m² for ^99mTc-MAG3 clearance. Clearly, the precision of these clearance measurements would be worse for single kidneys.

Both simulations and the patient study suggest relatively poor reproducibility of RPF, with coefficient of variability in the 15–20% range. Several explanations for this can be proposed: invalid treatment of vascular pool in the three-compartmental model, insufficient temporal resolution to measure RPF with accuracy, and random errors in arterial input function. In addition, the variability in RPF could be possibly due to the short-term (cycle length ∼40 s) oscillation in renal blood flow in patients with essential hypertension, as suggested by previous studies (9, 10). While resolution of this issue will require further work, it should be noted that GFR measures may be clinically more relevant than measurements of perfusion.

The study has several limitations. First, the simulation study only simulated random noise (thermal MRI noise). In reality, the data are contaminated with physiological noise (e.g., patient motion). Nevertheless, we found good agreement between simulations and patient estimates of precision. Second, in our patient study, we had so far only eight subjects with RAS. More cases are needed for validating the proposed method.

Gadolinium-based contrast agents, especially gadodiamide (Gd-DTPA-BMA) and to a lesser extent gadopentetate dimeglumine (Gd-DTPA), may cause NSF in patients with renal insufficiency, and the risk of NSF seems to be dose dependent (5, 22, 27). In our study, we used low dose of Gd-DTPA (12 ml for both injections combined). Even with Gd-MRA using a single dose, the total dose is <0.2 mmol/kg. No NSF symptom has been reported for our patients. To minimize the risk of NSF, our new protocol uses gadoteridol (Gd-HP-DO3A). Based on current data, Gd-HP-DO3A is considered to be significantly safer than Gd-DTPA because of its stable macrocyclic structure (22).

In summary, dual-injection MRR with optimized dose distribution appears promising for ACEi renography by offering reliable and reproducible measures of GFR, with acceptable precision and accuracy. Studies to validate our dual MRR approach as a diagnostic tool for RVD in conjunction with renal MRA are underway.

GRANTS

This work was supported in part by National Institute of Diabetes and Digestive and Kidney Diseases Grants DK-063183 and DK-061599.