Frequency discrimination in rats measured with tone-step stimuli and discrete pure tones

Abstract

Two modified go/no-go tasks are compared for the measurement of frequency discrimination in albino rats. The first task required detection of an instantaneous, phase-matched frequency change, called a “tone-step,” within a continuous reference tone. The more traditional second task required detection of a frequency change between repetitions of a reference sequence of repeating discrete tones. For each task frequency difference limens were measured over a range of reference frequencies from 2.31 to 27.7 kHz at 60 dB sound pressure level, with both upward and downward frequency shifts. All 24 subjects quickly learned the “tone-step” task to criterion, but only 13 could also learn the discrete tone task. Subjects’ performance at either task generally improved with increasing reference frequency, and in both tasks upward frequency change thresholds were significantly higher than thresholds for downward changes. Overall mean Weber ratios were 1.73±0.27% for the “tone-step” task and 2.76±0.29% for the discrete tone task. However, subjects’ performance on the “tone-step” task was not correlated with subsequent performance on the discrete tone task. We suggest that the lack of correspondence between tasks might be due to frequency discrimination processes interacting with short-term memory traces during inter-tone intervals in the discrete tone task.

1. Introduction

Rats are a commonly used animal model in neurophysiological studies of the auditory system, but they are relatively underrepresented in behavioral studies of frequency discrimination. This disparity may stem from Fay’s 1974 review that showed they had relatively poor acuity, based on Kelly’s early data (1970), compared to other mammals and might therefore be a poor choice for related research. More recent studies in the rat have found rats’ frequency discrimination ability is on par with other mammals (Syka et al., 1996; Talwar and Gerstein, 1998; Talwar and Gerstein, 1999). To complement neurophysiological studies it would be desirable to continue accumulating a large body of literature on rat frequency discrimination, but behavioral studies can often be prohibitively time-consuming. Of the many paradigms that have been developed which minimize training time in animals by simplifying task requirements, the “repeating standard” paradigm has been shown to work well for testing frequency discrimination in rodents (Prosen et al., 1989; Sinnott et al., 1992; Talwar and Gerstein, 1998). In a “repeating standard” task subjects must detect a change in frequency within a sequence of repeating discrete tones. While this type of task has demonstrated advantages in efficiency of training, would it be possible to simplify the task, and further reduce training time and perhaps increase the proportion of subjects able to successfully acquire the task, while continuing to reliably measure frequency discrimination?

Detection of linear frequency modulation sweeps or glides between two constant frequency tones has previously been used as a measure of frequency discrimination in humans (Shower and Biddulph, 1931; Lyzenga et al., 2004). As glide durations decrease and overall stimulus duration increases, thus lengthening the constant frequency components, measured frequency difference limens (FDLs) approach frequency discrimination thresholds for separated pure tones (Nabelek and Hirsh, 1969; Arlinger, 1977; Sek and Moore, 1999; Lyzenga et al., 2004). For very rapid glides, listeners apparently rely mainly on detection of the difference between the constant frequencies of the bounding tones and not detection of the glide itself (Arlinger, 1977). Therefore, a task that requires detection of a fast frequency transition connecting two tones of different frequency may measure frequency discrimination comparable to tasks that require comparison of two distinct tones separated in time. In a study on human temporal acuity, Wier and Green (1975) found that discrimination of the frequency change direction within two-frequency tones containing an instantaneous, phase-matched frequency shift also approximately measured frequency discrimination. Despite this seemingly close correspondence, the only study, to our knowledge, that has used detection of instantaneous, phase-matched frequency transitions as a measure of frequency discrimination was Roverud’s study in the lesser bulldog bat (1999), which reported FDLs comparable to other bat studies.

This study investigates the use of two paradigms for measuring frequency discrimination ability in rats. In the first task subjects must detect an abrupt change in frequency within a continuous reference tone. We will borrow terminology from Roverud (1999) and refer to this type of stimulus as a “tone-step.” The second task uses a more traditional paradigm in which subjects must detect a change in the frequency of a sequence of pure tones separated in time, which we will refer to as “discrete” tones. Our pilot studies showed that these two tasks represent markedly different levels of difficulty for rats. Only roughly half of subjects were able to learn the discrete tone task to criterion, while all subjects were able to quickly and successfully learn the tone-step task. If the tone-step task provides a reliable measurement of frequency discrimination ability comparable to the discrete tone task, then use of the tone-step paradigm may make for more efficient and conscientious use of animals. In this study we compare FDLs measured with a tone-step detection task against FDLs measured in a more traditional discrete tone task to determine if the tone-step task provides a measurement of frequency discrimination, and in testing with both tasks we attempt to add to the body of data on rat frequency discrimination ability.

2. Materials and Methods

2.1. Subjects

A total of 24 female Sprague-Dawley albino rats were used as subjects in this study over a period of 2 years. Subjects began training at ages of 3-6 months and initially weighed 200-300 g. Subjects were housed singly or in pairs, depending on size, within a vivarium on a 12:12 light-dark cycle. Subjects had free access to water, but were food restricted. Food was removed 24 hours before training or testing began, and subjects were then maintained at or above 85% of pre-training weight. Subjects were trained to detect a difference in tone frequency to receive a 45 mg food chocolate-flavored reward (BioServ). Subjects that did not obtain enough food during training or testing were given supplemental rat chow to maintain body weight. Training and testing lasted for 2-4 months for each subject with sessions 5-7 days per week. On days when subjects were neither tested nor trained, they were given supplemental food. The care and use of animals in this study conformed to NIH guidelines and were in accordance with the University of Oklahoma Laboratory Animal Resources and Institutional Animal Care and Use Committee (IACUC) regulations.

2.2. Apparatus

Subjects were trained and tested in an acrylic cage inside a double-walled, anechoic acoustic chamber. The acrylic cage had a machined octagonal top and bottom, with walls constructed of round acrylic rods, designed to minimize acoustic reflection and electrical noise for subsequent neurophysiological studies. Integrated in the back wallpiece was an infrared sensor-monitored nosepoke, also made from machined acrylic, centered ~7 cm above the cage floor. Two acrylic feeder trays were integrated into the orthogonal wallpieces on each side of the nosepoke, just above the cage floor. A piezoelectric loudspeaker (CTS Powerline KSN-1165) was attached to the cage top, ~35 cm above the cage floor, and approximately centered above the body position of a rat engaging the nosepoke (see supplementary material for a illustration of the test set-up). The behavioral chamber was lighted by two small, direct-current light bulbs above the cage top that could be turned on or off to indicate session initiation or negative reinforcement “time-outs”.

Sessions were controlled by custom MatLab software on a PC computer interfacing with an external real-time digital-to-analog processor (RP2.1; Tucker-Davis Technologies). The real-time processor continuously monitored the nosepoke sensor and controlled the cage lights. Pure tone stimuli were generated digitally in MatLab at a sampling rate of 100 kHz for each trial as sine waves of desired frequency and duration with 5 ms onset and offset cosine ramps. Stimuli were uploaded to the real-time processor between trials for conversion to analog voltage and playback at the initiation of the next trial.

2.3. Calibration

Tone amplitude for all stimuli in this study was set to 60 dB sound pressure level (SPL), relative to a 20 μPa (RMS) standard, using a voltage-intensity calibration function specific to the loudspeaker. Subjects were required to engage and hold in the nosepoke during trials, so calibration was carrried out with a 1/4 in. ACO Pacific condenser microphone placed in the approximate center of the stereotyped head position. Calibration functions were derived for discrete frequencies by measuring SPL for the middle segments of ramped sine-wave tones generated digitally in MatLab, uploaded to the real-time processor, and played from the loudspeaker. Test tone output voltage amplitudes ranged logarithmically from 0.01 to 2 V or until SPL exceeded 80 dB, with measurements repeated 3-5 times. For each frequency the calibration function was determined by a logarithmic regression curve iteratively fit to the measured SPL values, rejecting outliers with residuals greater than twice the standard deviation. Calibration functions were determined for 533 frequencies spanning a range from 1 to 40 kHz with 0.01 octave spacing, a resolution finer than any frequency difference used in any subsequent behavioral test. Calibration of the loudspeaker resulted in a flat frequency response at 60 dB (±0.55 dB) SPL between 2 and 32 kHz. For any arbitrary stimulus used in behavioral training or testing that had a frequency not explicitly calibrated for, the voltage amplitude for 60 dB SPL was linearly interpolated from voltage-intensity functions of the two nearest calibration frequencies. Adjusting for the albino rat audiogram, 60 dB SPL is approximately 40-60 dB above hearing threshold (Kelly & Masterton, 1977; Borg, 1982) within the tested frequency range of 2 to 32 kHz, with an effective sound level at those endpoints of ~40 and ~55 dB, respectively.

2.4. Tone-Step Task

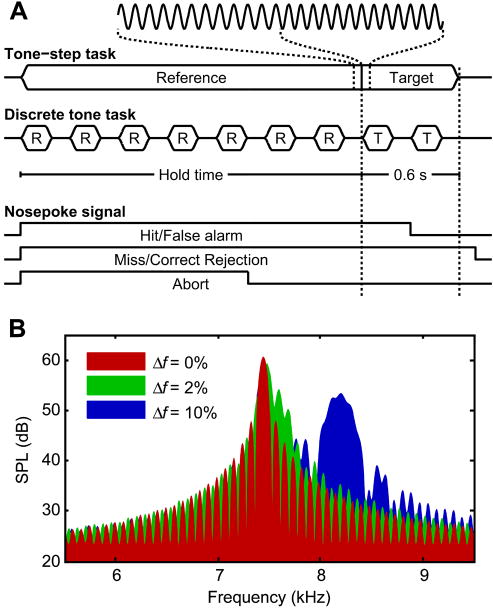
In their first session food-deprived subjects received a 45 mg food pellet for any engagement of the nosepoke. Starting with the second session, subjects were required to detect changes in the frequency of a continuous reference tone in order to receive the food reward. A time diagram of the tone-step task is shown Fig. 1A. Trials began when subjects nosed and held in the central nosepoke, immediately triggering the presentation of the continuous reference. After a randomly-preset hold time, the frequency of the continuous tone would be abruptly changed to a target frequency, and subjects would indicate detection by withdrawing from the nosepoke. The transition was phase-matched to minimize transients, and any differences in the calibrated voltage amplitude of the reference and target sinusoids was smoothed with a 5 ms cosine ramp on the higher-voltage side of the transition. Despite the instant change in frequency at the transition, this method of joining reference and target tones resulted in relatively little spectral splatter compared to control “transitions” with no frequency change (0%), as seen in discrete Fourier transforms of signal snippets, centered around the transition, recorded at a 100 kHz sampling rate with a 1/4 in. ACO Pacific condenser microphone (Fig. 1B).

Fig. 1.

(A) Schematic representation of the tone-step and discrete tone tasks with corresponding scoring for nosepoke withdrawal scenarios. The waveform cut-out at top shows an example of phase-matching at the reference-target transition of a +15% Δf tone-step stimulus. (B) Examples of acoustic spectra from three 12 ms tone-step signal snippets centered around the tone-step frequency transition for a 7.44 kHz reference with Δfs of 0% (catch trial), 2% (f_TAR = 7.58 kHz), and 10% (f_TAR = 8.20 kHz). Note that the ~6dB difference in peak height between the 0% and 10% transitions represents the expected 50% decrease in signal strength caused by halving the 7.44 kHz contribution to the snippet.

If subjects withdrew from the nosepoke within 600 ms of a frequency change the trial was scored as a hit. Failure to withdrawal within 600 ms was scored as a miss. Catch trials in which continuous tone frequency did not change at the transition were included to estimate false alarm rate (~6% of all trials). A nosepoke withdrawal during a catch trial within 600 ms following the “transition” was scored as a false alarm. A catch trial was scored as a correct rejection when a subject held in the nosepoke longer than 600 ms after the “transition.” If a subject withdrew from the nosepoke at any time before the frequency transition, the trial was scored as an abort. Hits were rewarded with 45 mg food pellets. Misses, false alarms, and aborts resulted in 5-10 second time-outs in which the cage lights were turned off and the program was paused. Correct rejections were neither rewarded nor punished, but subjects had to disengage and then re-engage the nosepoke in order to initiate a new trial.

In all tone-step training and testing sessions, reference frequency was randomly varied between trials over 18 frequencies ranging from 2.31 to 27.66 kHz in 0.21 octave steps. The difference between reference and target frequency was randomly varied, both with upward and downward frequency changes (Δfs), between a range of 0 to 0.281 octaves in 0.0140 octave steps, which approximately correspond to Weber fraction steps of 1% when calculated with the direction-insensitive equation: Δf = 2·|(f_reference-f_target)|/(f_reference+f_target). In initial training sessions Δfs were ±5-20% while subjects were trained to hold in the nosepoke for increasing hold times. Subjects graduated to testing when they showed detection for all |Δf| ≥ 5% with a d’ signal detection index of >1.96 (Green & Swets, 1966) and could hold for as long as 20 seconds before a frequency transition, although hold times were shorter during testing.

Tone-step frequency difference limens (FDLs) were tested by the method of constant stimuli. The stimulus set contained all 378 combinations of the 18 reference frequencies noted above with upward Δfs of 1 to 10% and downward Δfs of -1 to -10% in ±1% steps and catch trials with 0% change. Reference frequency and upward-downward frequency change direction were varied in every test session, such that FDLs reflected general frequency discrimination acuity. The stimulus set was randomized at the beginning of testing and was re-randomized after all stimuli had been presented in a completed trial. A completed trial was defined as a trial scored as a hit, miss, false alarm, or correct rejection. Stimuli from aborted trials were added to the end of the stimulus set for retesting. Hold time was randomly set for between 2 to 7 seconds during testing and was not reset with the stimulus following aborts, so that subjects were required to complete trials with the full range of hold times. Single sessions would typically yield ~300 completed trials, less than one full stimulus set. Any remaining untested stimuli in the stimulus set were saved for presentation in the next session, and the stimulus set was regenerated and re-randomized when completed mid-session. Subjects completed 6-12 repetitions of the stimulus set over the course of multiple daily sessions.

2.5. Discrete Tone Task

All subjects were first trained on the tone-step task before beginning training on the discrete tone task. In pilot studies subjects universally failed to conceptualize the task when trained with discrete tones at the outset, but most subjects could generalize learned tone-step task requirements to the discrete tone task. For discrete tone training the reference and target tones were 200 ms in duration with 5 ms onset and offset cosine ramps, with a 100 ms inter-tone interval (ITI). The discrete task was similar to the tone-step task in nearly all aspects, except that it used discrete tones, the frequency change occurred in the ITI between tones, and the number of reference tones was randomly set between 7 and 23, generating discrete nosepoke hold times in multiples of the 300 ms tone/ITI period. The 600 ms response period began at the onset of the first of two tones at the target frequency. Definitions of a hit, miss, false alarm, correct rejection, or abort were the same as in the tone-step task (Fig. 1A).

Reference frequency in training and testing was varied between the same 18 frequency values used in the tone-step task and Δfs also varied within the same octave range with the same 0.0140 octave (~1%) steps. Subjects were again first trained with ±5-20% Δfs while required nosepoke hold times were incrementally increased. For the discrete tone task, subjects graduated to testing when they showed detection for all |Δf| ≥ 10% with a d’ index of >1.96 and could hold for as long as 20 seconds before presentation of the target frequency, although again hold times were shorter during testing.

Discrete tone task testing consisted of two phases, each testing by the method of constant stimuli. In the first phase all tones were 200 ms in duration with a 100 ms ITI. The stimulus set consisted of all 558 combinations of the 18 reference frequencies with upward and downward Δfs of ±1-15% in ±1% steps and 0% change catch trials. Preliminary results showed that discrete tone FDLs might be larger than tone-step FDLs, so the tested Δf range was increased from ±10% to ±15%. In the second phase of testing tone duration was varied, with values of 10, 20, 50, 100, and 200 ms, and ITI was increased accordingly to maintain a tone+ITI period of 300 ms. For this phase only three of the standard reference frequencies were used: 4.15, 8.61, and 17.85 kHz. The stimulus set for the second phase consisted of 465 combinations of duration, reference frequency, and Δf. Both phases were otherwise similar to tone-step testing. Aborted trials were added to the end of the stimulus set for retesting. Hold times were randomly set between 2-7 seconds and were not reset by aborts. Subjects completed 10-15 repetitions of the stimulus set over multiple daily sessions.

2.6. Analysis

Catch trials were inserted into the stimulus set to estimate false alarm rate during sessions, but true false alarm rate was used in all final analyses. In “repeating standard” paradigms, the long reference tone or tone sequence can be divided into contiguous response windows, within which an abort should technically be classified as a false alarm and a sustained nosepoke hold should be classified as a correct rejection. True false alarm rate (F) can be calculated by summing the number of estimated false alarms and the number of aborts, and dividing by the number of actual and “virtual” catch trials. Hit rate (H) was calculated for all non-catch trial stimuli by dividing the number of hits by the number of completed trials for that stimulus. Hit rates were corrected for false alarm rate prior to FDL measurements using Heffner and Heffner’s (1988) commonly-used correction formula: H_c = H·(1-F), in which H_c is corrected hit rate. For each reference frequency (and tone duration for the discrete tone task) FDLs were then determined from performance curves plotting H_c versus Δf, defined as the Δf value for the point the curves cross 50% performance. Note here that the 0.0140 octave spacing for Δf used is actually equivalent to 0.97% spacing, whereas a 0.0145 octave spacing would have been more precisely equivalent to 1% spacing. The 0.0140 octave spacing was chosen to agree with stimuli from other concurrent experiments, and the true 0.97% Δf spacing is used in all FDL calculations.

Since both negative-going (downward) and positive-going (upward) Δfs were tested, there are two respective FDLs measured from each v-shaped performance curve for each reference frequency (and tone duration for the discrete tone task). In some parts of the analysis, FDLs are calculated without respect to reference frequency or upward versus downward direction.

This study uses false alarm-corrected hit rate to determine FDLs similar to most previous studies to allow easy comparison. More recent studies have used signal detection theory to control for response bias (Talwar and Gerstein, 1998; Talwar and Gerstein, 1999). For this study, a concurrent signal detection analysis was carried out using the nonparametric index A’ (Grier, 1971). Signal detection FDLs and resultant trends closely corresponded to corrected hit rate results, so only the corrected hit rate results are presented here. Subjects’ discrete tone FDLs determined with A’ are listed in the supplementary tables.

3. Results

3.1. Tone-step task

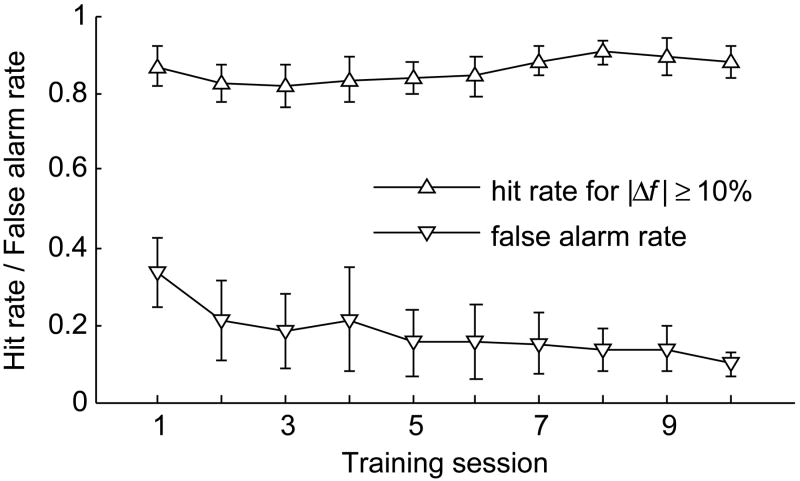
All 24 subjects were first trained on the tone-step task following one session of nosepoke training. Mean hit rates and false alarm rates for the first 10 tone-step training sessions are shown in Fig. 2. Subjects quickly associated nosepoke withdrawals in response to frequency changes with feeding, and hit rates were >80% even in the first session. Training improved performance mainly by decreasing false alarm rate. All but 3 subjects reached the performance criterion required to graduate to tone-step testing, a d’ of 1.96 for |Δf|s ≥ 5%, in 10 sessions or less (median = 6 sessions). The remaining 3 subjects graduated to testing after 12, 14, and 15 tone-step training sessions, respectively.

Fig. 2.

Mean hit rate and false alarm rate from all subjects (N = 24) during training on the tone-step task as a function of training session. Error bars show 95% confidence intervals.

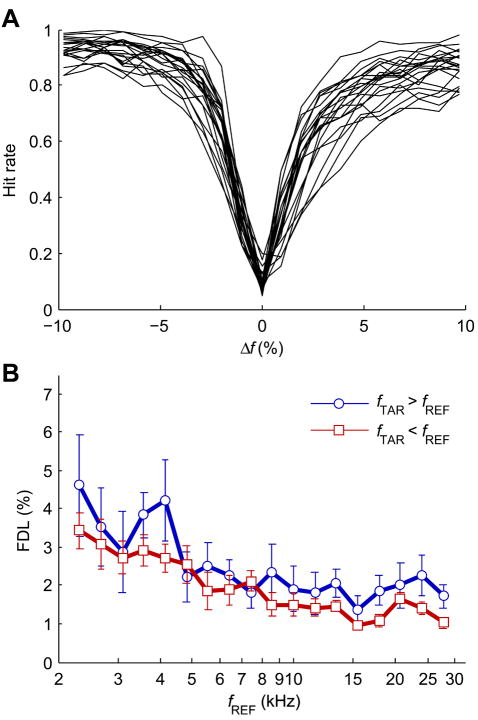
FDLs for the tone-step task were determined from false alarm-corrected hit rate for 22 subjects at 18 reference frequencies and for upward and downward frequency changes. Subjects completed a minimum of 6 repetitions of the stimulus set (median = 10 repetitions) for a minimum total of 2268 tested stimuli. Data were combined across sessions, with subjects completing trials for a median of 297 stimuli per session, over the course of a median of 11 tone-step testing sessions. Uncorrected hit rate curves for each subject, combined across all reference frequencies, are shown in Fig. 3A. Overall false alarm rates in the tone-step were between 0.05 and 0.2 (median = 0.084). Hit rate curves were approximately v-shaped, but did not appear symmetrical for upward and downward Δfs, with noticeably poorer performance for upward Δfs.

Fig. 3.

(A) Psychometric functions of hit rate for the tone-step task as a function of Δf for all subjects (N = 22) that completed tone-step testing, with hit rate combined across all reference frequencies. (B) Population mean tone-step FDLs for all upward (f_TAR > f_REF) and downward (f_TAR < f_REF) Δfs at each reference frequency. Error bars show 95% confidence intervals.

Tone-step FDLs are shown in Fig. 3B as a function of reference frequency and frequency change direction. A 3-way ANOVA on FDLs showed significant main effects of subject (F_21,786 = 18.00, p < 0.0001), reference frequency (F_17,786 = 35.18, p < 0.0001), and frequency change direction (F_1,786 = 75.68, p < 0.0001). There was also significant interaction between all groups (subject and reference frequency: F_357,786 = 1.54, p < 0.0001; subject and frequency change direction: F_21,786 = 3.55, p < 0.0001; reference frequency and frequency change direction: F_17,786 = 2.84, p = 0.0002). Differences in tone-step FDLs between reference frequencies were quite large compared to differences between upward and downward frequency changes at each reference frequency. In general, tone-step FDLs decreased with increasing reference frequency from ~4% to ~2%. Tone-step FDLs for upward frequency changes were larger than those for downward at most reference frequencies by 0.55% on average. Directional difference trends were also most consistent for reference frequencies above 8 kHz. Overall mean FDLs, irrespective of reference frequency and frequency change direction, for the tone-step task were 1.73 ±0.27%.

Since subjects typically did not complete testing on a full stimulus set in one session, it was only possible to determine FDLs within a single session by ignoring reference frequency and frequency change direction. To determine whether tone-step FDLs showed improvement between sessions during testing, session FDLs for each subject were tested for a decreasing trend with a Spearman rank correlation (α = 0.05). Only 4 of the 22 subjects showed a significant negative rank correlation between tone-step FDL and session number, and no subjects showed significant positive correlations that might indicate worsening performance. Presumably most subjects’ thresholds had reached an asymptotic level during training prior to tone-step testing.

3.2. Discrete tone task

Of an initial group of 20 subjects that completed tone-step testing, 11 were able to successfully transition to the discrete tone task. To see if tone-step testing resulted in over-training that inhibited learning of the discrete tone task, the final 4 subjects were transitioned directly from tone-step training to discrete tone training without undergoing tone-step testing. Only 2 of the 4 subjects were able to learn the discrete tone task to criterion. Those 2 subjects of the final 4 that couldn’t learn the discrete tone task were transitioned back to the tone-step task, which they successfully completed testing on. Successful learning of the discrete tone task appears to be more dependent on subjects’ individual abilities than on the training order. For the 13 subjects that did successfully learn the discrete tone task, most reached performance criterion, a d’ of 1.96 for |Δf| ≥ 10%, in less than 10 discrete tone training sessions (median = 8 sessions).

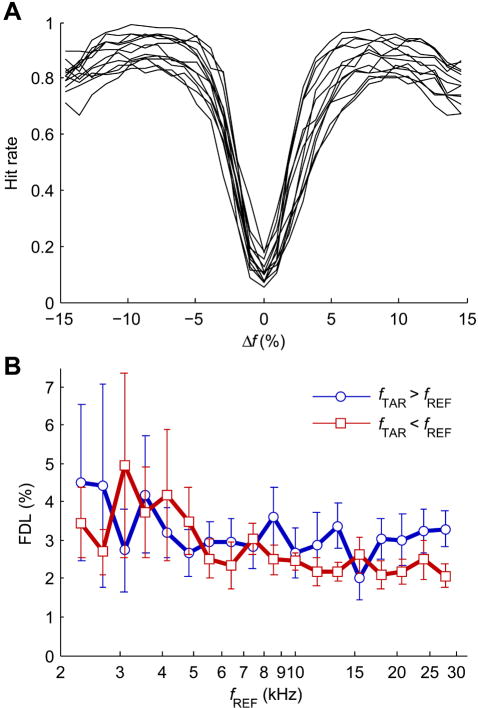
In the first phase of discrete tone testing, tone duration was held to 200 ms while reference frequency and frequency change direction were varied. Data were again combined across sessions, with subjects completing testing in a median of 14 sessions. Uncorrected hit rate curves for each subject in the discrete tone task, for 200 ms tones combined across all reference frequencies, are shown in Fig. 4A. Overall false alarm rates were similar to the tone-step task, ranging between 0.05 and 0.2 (median = 0.101). Hit rate curves were less sharply v-shaped, rounded by lower hit rates for -1% and 1% Δfs. The asymmetry for frequency change direction was also less pronounced than in the tone-step task. Interestingly, all subjects showed better performance for nearer-threshold 8-10% |Δf|s than for larger 13-15% |Δf|s. After correcting for false-alarm rate, mean hit rate for 8-10% |Δf|s were significantly greater than mean hit rate for 13-15% |Δf|s (paired t-test, p < 0.0001). Therefore, subjects performed significantly better for near-threshold frequency changes than for large, perhaps “obvious” changes, although for both |Δf| ranges performance was certainly suprathreshold.

Fig. 4.

(A) Psychometric functions of hit rate for the discrete tone task as a function of Δf for all subjects (N = 13) that completed discrete tone testing, with hit rate combined across all reference frequencies. (B) Population mean discrete tone FDLs for all upward (f_TAR > f_REF) and downward (f_TAR < f_REF) Δfs at each reference frequency. Error bars show 95% confidence intervals.

Discrete tone task FDLs for 200 ms duration tones are shown in Fig. 4B (and listed in supplementary Table S1) as a function of reference frequency and frequency change direction. A 3-way ANOVA showed significant main effects of subject (F_12,461 = 16.39, p < 0.0001), reference frequency (F_17,461 = 6.11, p < 0.0001), and frequency change direction (F_1,461 = 14.26, p = 0.0002), again with significant interaction between all groups (subject and reference frequency: F_204,461 = 1.53, p = 0.0014; subject and frequency change direction: F_12,461 = 2.58, p = 0.0034; reference frequency and frequency change direction: F_17,461 = 4.73, p < 0.0001). Differences in FDLs dependent on reference frequency were less pronounced than in the tone-step task, decreasing from ~4% to ~3% as reference frequency increased. The greater variability in FDL for frequencies below 5 kHz is largely attributable to 2 subjects that showed much larger FDLs at those frequencies than did other subjects. Differences between upward and downward Δfs were somewhat smaller than in the tone-step task, with upward FDLs about 0.35% larger than downward FDLs on average. Again, the directional difference trends were most consistent for the higher reference frequencies. Overall mean FDLs for the discrete tone task were 2.76 ±0.29%, disregarding reference frequency and frequency change direction.

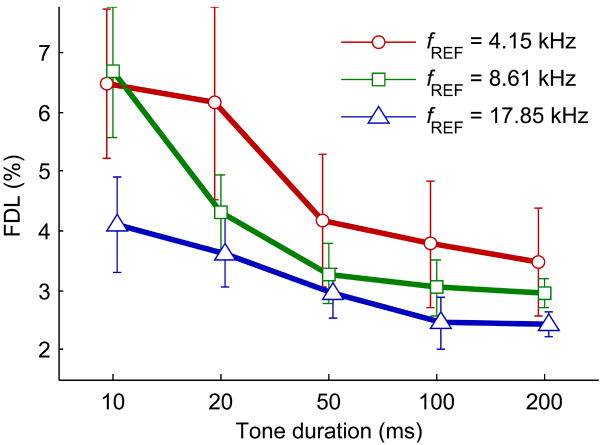
In the second phase of discrete tone testing, tone duration was varied between 10, 20, 50, 100, and 200 ms while reference frequency was varied over a more restricted set of 4.15, 8.61, and 17.85 kHz. Direction-irrespective FDLs are shown as a function of tone duration in Fig. 5. A 4-way ANOVA showed a significant main effect of duration (F_4,383 = 53.10, p < 0.0001) along with expected significant main effects of subject, reference frequency, and frequency change direction (α = 0.05). There was significant interaction between tone duration and reference frequency (F_8,383 = 3.19, p = 0.0018), but not between tone duration and subject (F_48,383 = 0.67, p = 0.95) or tone duration and frequency change direction (F_4,383 = 0.69, p = 0.60). FDLs decreased with increasing tone duration overall, but decreases were more pronounced for the two lower reference frequencies as tone duration increased. When FDLs are calculated for each tone duration without respect to reference frequency and plotted versus tone duration (not shown), the trend of increasing FDL with decreasing tone duration shows a strong negative slope below 50 ms and seems to asymptotically approach a constant threshold at durations greater than ~100 ms.

Fig. 5.

Population mean discrete tone task FDLs plotted as a function of tone duration for the three tested reference frequencies. FDLs shown are determined irrespective of frequency change direction. Plots for each reference frequency are slightly offset to better show error bars, which represent 95% confidence intervals.

3.3. Tone-step vs. discrete tone task

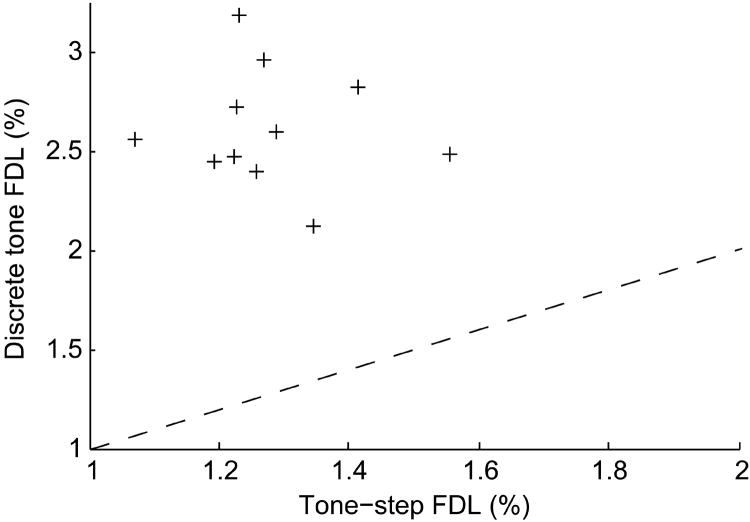
Overall tone-step FDLs and discrete tone FDLs, calculated irrespective of reference frequency and frequency change direction over a frequency range for which FDLs were relatively uniform (8.61 to 27.65 kHz), from the 11 subjects that underwent testing in both tasks are plotted versus each other in Fig. 6. Discrete tone FDLs are consistently higher than corresponding tone-step FDLs, but there is no significant correlation (R = -0.10, p = 0.76). Subjects’ tone-step FDLs do not appear to be predictive of their subsequent discrete tone FDLs.

Fig. 6.

Overall FDLs, calculated irrespective of reference frequency and frequency change direction over a frequency range for which FDLs were relatively uniform (8.61 to 27.65 kHz), measured with the tone-step task are plotted against those measured with the discrete tone task for the 11 subjects that completed testing on both tasks.

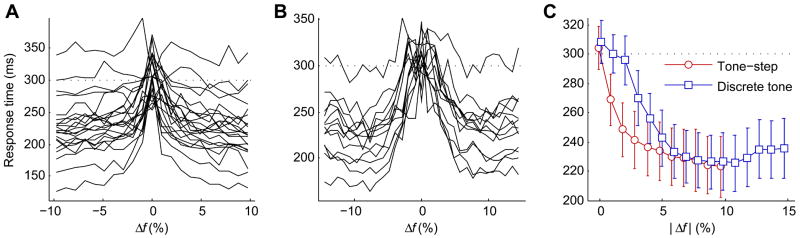
The absence of correlated FDLs from the tone-step task and discrete tone task might suggest that the two tasks depend on different detection abilities, a difference that might also manifest in a comparison of response times for hit trials. Nosepoke withdrawal responses were monitored at a sampling rate of 100 kHz within the 600 ms response window. Plots of hit trial response time versus Δf for the tone-step and discrete tone tasks are shown in Figs. 7A and 7B, respectively. Mean population hit trial response times are shown as a function of absolute frequency change for both the tone-step and discrete tone task in Fig. 7C. Plots of response time have the appearance of inverted hit rate performance curves, which is due to strong correlations between reaction time and false alarm-corrected hit rate in both tasks. In the tone-step task mean reaction time and hit rate were negatively correlated in all 22 subjects, 21 of which were significant correlations (α = 0.05). In the discrete tone task all 13 subjects showed significant, negative correlations (α = 0.05). If the processing of tone-step and discrete tone stimuli are the same, reaction times should be equivalent for equivalent hit rates regardless of the frequency change. However, for the 11 subjects that completed both tasks, linear regressions fit to reaction time versus hit rate were significantly different for all subjects (ANCOVA, α = 0.05). Assuming equal slope in the regressions and controlling for false alarm-corrected hit rate, discrete tone task response times were on average 18 ms slower than those for the tone-step task.

Fig. 7.

Mean hit trial/false alarm trial response times are plotted versus Δf for all subjects in the tone-step task (A) and discrete tone task (B). Population mean response times, irrespective of reference frequency and frequency change direction, for the tone-step and discrete tone tasks are shown in (C). The dashed line at 300 ms in each plot represents expected mean response time for purely guessing behavior within the 600 ms response window. Plots are slightly offset to better show error bars, which show 95% confidence intervals.

To briefly examine the possibility that spectral splatter in the tone-step task served as cues, two subjects that had completed testing on the discrete tone task, RN23 and RN24, were further tested to compare FDLs for tone durations of 200 ms and 300 ms. The tone+ITI period was fixed at 300 ms for both tone durations, such that the ITI for 300 ms tone sequences was zero, which approximated a continuous tone except where the 5 ms offset and onset ramps from consecutive tones met. A single reference frequency of 17.85 kHz was used for these tests. FDLs calculated irrespective of frequency change direction for the 300 ms/no ITI tones were 2.00% and 2.32% for subjects RN23 and RN24, respectively, which are approximately in the range of tone-step FDLs. The FDLs measured for 200 ms tones in the same stimulus set were 2.49% and 2.75% for RN23 and RN24, respectively. Although the small sample size prevents any statistical analysis or conclusions, the difference in measured FDLs suggest that increasing tone separation from 0 to 100 ms may have a significant effect on frequency discrimination.

3.4. Effects of reference duration

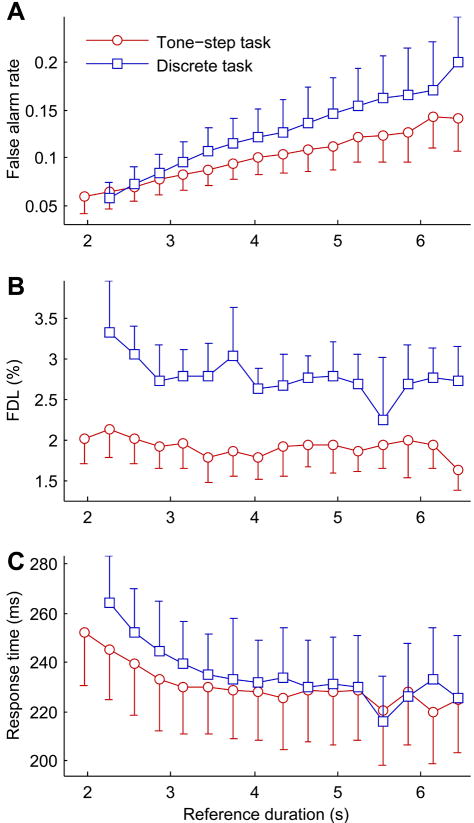
It is possible in “repeating standard” paradigms for subjects to gain an advantage by dynamically adjusting their detection strategies based on the relationship between time held in the nosepoke and target probability. During testing on either the tone-step or discrete tone task, the required hold time before a target presentation is randomly set between bounds of 2 and 7 seconds. Therefore the longer a subject holds before being presented a target, the higher the probability that a target is about to occur. To determine if subjects’ detection strategies varied with reference duration, false alarm rate was determined within 300 ms time bins from 1.8 to 6.9 seconds, corresponding to tone+ITI periods in the discrete tone task. Subjects appeared to recognize increasing target probability and showed increasing false alarm rates with increasing hold time (Fig. 8A). Differences in false alarm rate with reference duration were significant for both the tone-step (ANOVA; F_15,351 = 5.62, p < 0.0001) and the discrete tone task (F_15,207 = 7.71, p < 0.0001). The trend was distinctly linear, with subjects showing false alarm rates of ~0.05 when hold time was 2 seconds up to false alarm rates of ~0.15 when hold time was 7 seconds.

Fig. 8.

(A) False alarm rate, (B) overall population mean FDL, and (C) hit trial response time as a function of time held in the nosepoke, calculated for time bins of 300 ms from 1.8 to 6.9 seconds, for the tone-step task (circles) and the discrete tone task (squares). Error bars show 95% confidence intervals.

To determine if increasing false alarm rates affected FDLs, FDLs were calculated irrespective of reference frequency or frequency change direction as a function of hold time within 300 ms bins from 1.8 to 6.9 seconds from the start of the trial. FDLs are shown as a function of hold time in Fig. 8B. There was no significant effect of hold time on FDLs for either the tone-step (ANOVA; F_15,350 = 0.59, p = 0.884) or discrete tone task (F_14,191 = 1.23, p = 0.255). Subjects’ increasing “go” biases, evidenced in increasing false alarm rates, did not apparently confer any detection advantage. Similarly, the increasing “go” bias did not confer any significant advantage in response time. Although response times appear to decrease regularly with increasing hold time (Fig. 8C), changes were not significant for either the discrete tone task (ANOVA; F_14,194 = 1.58, p = 0.088) or the tone-step task (F_15,351 = 0.73, p = 0.7578).

4. Discussion

4.1. Tone-step task FDLs

In this study we compared frequency discrimination in the rat measured with a tone-step task that required detection of an abrupt frequency change in a continuous tone and with a discrete tone task that required detection of a frequency change in a sequence of discrete pure tones. We found little evidence to suggest that the two tasks were measuring precisely the same behavioral ability. Overall FDLs measured with the tone-step task (mean 1.93 ±0.27%) were significantly lower than FDLs measured with the discrete tone task (mean 2.78 ±0.29%) and FDLs from the two tasks were not correlated in subjects that completed testing on both. Furthermore, when hit rate was controlled for, response times in hit trials were 18 ms (~10%) faster on average for the tone-step task, indicating that tone-step detection may require less processing time.

The tone-step task investigated in this study is somewhat unique in its use of an abrupt, phase-matched frequency change, which to our knowledge was used in only one previous study on the lesser bulldog bat (Roverud, 1999). The bat’s specialized auditory system makes any comparison with the present study in rats difficult. Apart from Roverud’s study, the tone-step task might be most comparable to frequency discrimination studies that use detection of frequency modulation (FM). Much like our results, studies directly comparing FM detection FDLs and two-tone discrimination FDLs in humans find that the two tasks seemingly measure different abilities (Jesteadt and Sims, 1975; Moore, 1976; Sek and Moore, 1995). However, the relationship between FM detection FDLs and discrete tone frequency discrimination FDLs in humans (Sek and Moore, 1995) appears to be quite different from the relationship between tone-step detection FDLs and discrete tone FDLs seen in this study. The tone-step FDLs seen here were consistently lower than corresponding discrete tone FDLs, but FM detection FDLs were shown to be higher than discrete tone FDLs over much of the tested frequency range in humans. Therefore, while FM detection FDLs and tone-step detection FDLs both differ from discrete tone frequency discrimination, it’s likely they differ by separate means.

One obvious distinction of the tone-step task from frequency discrimination or FM detection tasks is that frequency changes are instantaneous, which could create detectable spectral splatter for subjects to use as a cue. However, examination of the acoustic spectra at the frequency change (Fig. 1B) shows little spectral splatter relative to catch trial stimuli (Δf = 0%), especially near FDL thresholds (Δf = 2%). Roverud (1999) similarly saw little evidence of spectral splatter being used as a cue for tone-step detection. Aside from spectral splatter, the only cue available for subjects to detect in the tone-step stimulus is the frequency change, which would require frequency discrimination. Perhaps tone-step FDLs are not correlated with discrete tone FDLs because a common frequency discrimination process is confounded by processes of auditory short-term memory. In the discrete tone task subjects must retain frequency information throughout silent intervals separating tones. Talwar and Gerstein (1998) showed that FDLs in the rat did not increase when ITIs were varied between 0.1 to 2.1 seconds, a range for which humans also show no notable decrement (Harris, 1952; Clement et al., 1999). However, Lyzenga et al. (2007) found that decreasing silent ITI from 200 ms to 0 ms significantly improved detection of frequency differences between tones for humans, with an effect size similar to the FDL improvements we saw in two rats when ITI was reduced from 100 ms to 0 ms in the discrete tone task. In a neurophysiological study in cat auditory cortex, Ulanovsky et al. (2004) found multiple concurrent timescales of adaptation for tracking auditory stimulus history, the two shortest having time constants of ~6.6 ms and ~150 ms. Perhaps FDLs from the tone-step task and the discrete tone task are statistically unrelated because the auditory system stores frequency information in different-timescale memory stores which interact nonlinearly with processes of frequency discrimination, a possibility which could be investigated in future studies by testing short ITIs between 0 and 100 ms.

4.2. Comparison to previous studies

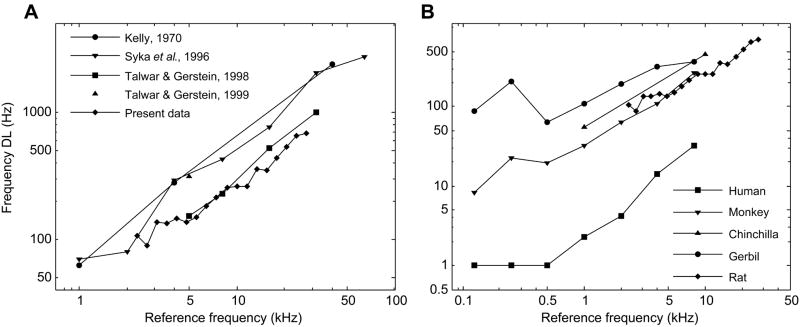
Regardless of the uncertain relationship between the tone-step and discrete-tone tasks, FDLs from the more traditional discrete tone task can be readily compared to existing literature on frequency discrimination in the rat. A graphical comparison of the discrete tone results of this study are shown versus FDLs measured in other studies on the rat in Fig. 9A and versus FDLs measured for other mammals in Fig. 9B. Overall, the mean FDLs from our data appear to be considerably smaller than those measured for the rat by Kelly (1970), Syka et al. (1996), or Talwar and Gerstein (1999), but are comparable to Talwar and Gerstein’s 1998 results. Tawlar and Gerstein’s 1998 study used a “repeating standard” paradigm very similar to that used in this study, which they suggested results in lower measured FDLs due to a difference in task requirements. They argue that a “repeating standard” paradigm presents a “detection” problem and two-tone stimulus, go/no-go trial paradigms, as used in other studies, present an “identification” problem, supported by evidence of different cortical processing pathways in frequency discrimination experiments in cats (Thompson, 1960; Cranford, 1978). Conceptually, however, the distinction between “detection” and “identification” seems marginal in go/no-go tasks that do not require directional classification of frequency differences. A more conspicuous difference between “repeating standard” paradigms and two-tone go/no-go tasks is the long iso-frequency tone sequence prior to target presentation. In human subjects isofrequency tone sequences can induce a bias towards perceiving two auditory “streams” in subsequent alternating tone sequences, whereas without the inducing sequence subjects will perceive only a single stream (Rogers and Bregman, 1993; Beauvois and Meddis, 1997). Perhaps the FDLs measured with “repeating standard” paradigms are smaller due to the priming of the auditory system with isofrequency sequences which have been shown to improve perception and segregation of frequency differences.

Fig. 9.

(A) A comparison of the FDLs for the rat measured in this study to previous studies in the rat. (B) A comparison of FDLs measured for five mammalian species using “repeating standard” frequency discrimination tasks: Human, Monkey, Gerbil (Sinnott et al., 1992), Chinchilla (Prosen et al., 1989), and Rat (present data).

Effects of reference frequency and tone duration in our discrete tone results were consistent with previous studies in the rat. We used a larger set of reference frequencies, but tested within the same relative range, and our data show FDLs to be relatively flat for frequencies from 5 to 27.66 kHz. There was a small trend for FDLs to increase with decreasing frequency below 5 kHz, but this might be an artifact stemming from the use of a constant SPL intensity over a frequency range for which rat audibility thresholds increase by perhaps as much as 10 dB with decreasing frequency (Jamison, 1951; Gourevitch & Hack, 1966; Kelly & Masterton, 1977; Borg, 1982). In studies that explicitly adjusted intensity relative to rats’ hearing thresholds there was no decreasing trend for FDLs with increasing reference frequency in the same range (Kelly, 1970; Syka et al., 1996). However, increasing intensity from 30 to 50 dB above hearing threshold has also been shown to have little effect on rat FDLs (Syka et al., 1996). In the second phase of discrete tone testing in which tone duration was varied, FDLs increased with decreasing tone duration, with an apparent inflection point around 50 ms equivalent to previous reports in the rat (Talwar and Gerstein, 1998) and relatively similar to FDL-duration functions in humans (Moore, 1973; Hall and Wood, 1984; Freyman and Nelson, 1986). The common effect of tone duration on frequency discrimination between rats and humans suggests that despite considerable differences in sensitivity (Fig. 9B), mammals may share a common process underlying frequency discrimination.

Response times in hit trials in this study had a more linear relationship to hit rate than that reported by Talwar and Gerstein in the rat (1998). Although they did see significant differences in response latency between threshold-level hit trials and suprathreshold-level hit trials, plots of response latency against frequency difference did not appear as the inverse of hit-rate curves (1998). Strong negative correlations between response time and hit rate should be expected, however, under B.F. Skinner’s (1938) law of latency: response latency is inversely proportional to the salience of the stimulus. The strong correlations seen in this study relative to previous studies is most likely due to the higher temporal precision of monitoring nosepoke withdrawal responses, i.e. much less movement by the animal is required to signal a decision. Nosepoke holding is also advantageous in auditory paradigms such as this because the stereotyped head position tends to standardize subjects’ orientation to the sound source.

Despite general agreement with previous studies on the rat, our data present two unique results that bear future study. First, FDLs differed significantly with frequency change direction, showing lower thresholds overall for downward (−Δf) changes. Syka et al. (1996) found no significant effect of frequency change direction in pigmented rats, but for a relatively small sample size of three rats. The one other study in the rat with sample sizes comparable to our data (Talwar and Gerstein, 1998) only tested with upward (+Δf) frequency differences. Results from some studies in other animals show similar magnitude directional differences, but without consensus as to the preferred direction. Cats (Brown et al., 2004), Cercopithecus monkeys, and one rhesus monkey (Sinnott et al., 1987) show lower FDLs for downward shifts similar to this study, but Japanese macaques and humans have shown lower FDLs for upward shifts (Sinnott et al., 1987). North American blackbirds show both upward and downward shift preference dependent on reference frequency (Sinnott et al., 1980). Our analysis found a similar significant interaction between direction and reference frequency and between direction and subject. Procedural differences between studies or within-species subject selection could perhaps account for conflicting results. Inclusion of both upward and downward frequency changes and multiple reference frequencies in the stimulus sets of future frequency discrimination studies could help clarify directional effects. Second, subjects appeared to dynamically adjust their decision strategies within trials to the increasing probability of a target presentation, evidenced by significantly increasing mean false alarm rate. Rats have been shown to significantly adjust their decision strategies trial-to-trial in a two-tone go/no-go task (Talwar and Gerstein, 1999), but in the only previous “repeating standard” frequency discrimination study in rats subjects did not appear to adjust decision strategies within trials based on time held (Talwar and Gerstein, 1998). However, Talwar and Gerstein’s (1998) hold times were considerably longer (5-35 s) than those used in this study (2-7 s), so the probability of a target presentation increased at a faster rate and subjects may have been better able to track time held over the shorter reference durations. Future “repeating standard” studies could likely avoid dynamic adjustments in decision strategies by using longer reference durations than those used here.

To summarize, this study found that the auditory sensitivity measured with a tone-step detection paradigm is not predictive of frequency discrimination ability measured with a more traditional discrete tone paradigm. Differences may be due in part to frequency discrimination processes interacting with short-term memory traces during inter-tone intervals, but until this interaction is investigated further, a discrete tone paradigm would likely provide measurements more comparable to previous studies in rats. The discrete tone task data from this study supports frequency- and duration-dependent trends in FDLs seen in previous rat studies, but also finds significant frequency change direction-dependence in FDLs and target-probability-dependent decision strategies for the first time in the rat.