The Relation Between Color Discrimination and Color Constancy: When Is Optimal Adaptation Task Dependent?

Abstract

Color vision supports two distinct visual functions: discrimination and constancy. Discrimination requires that the visual response to distinct objects within a scene be different. Constancy requires that the visual response to any object be the same across scenes. Across changes in scene, adaptation can improve discrimination by optimizing the use of the available response range. Similarly, adaptation can improve constancy by stabilizing the visual response to any fixed object across changes in illumination. Can common mechanisms of adaptation achieve these two goals simultaneously? We develop a theoretical framework for answering this question and present several example calculations. In the examples studied, the answer is largely yes when the change of scene consists of a change in illumination and considerably less so when the change of scene consists of a change in the statistical ensemble of surface reflectances in the environment.

1 Introduction

Color vision supports two distinct visual functions: discrimination and constancy (Jacobs, 1981; Mollon, 1982). Color discrimination, the ability to determine that two spectra differ, is useful for segmenting an image into regions corresponding to distinct objects. Effective discrimination requires that the visual response to distinct objects within a scene be different. Across changes in scene, adaptation can improve discrimination by optimizing the use of the available response range for objects in the scene (Walraven, Enroth-Cugell, Hood, MacLeod, & Schnapf, 1990).

Color constancy is the ability to identify objects on the basis of their color appearance (Brainard, 2004). Because the light reflected from an object to the eye depends on both the object’s surface reflectance and the illumination, constancy requires that some process stabilize the visual representation of surfaces across changes in illumination. Early visual adaptation can mediate constancy if it compensates for the physical changes in reflected light caused by illumination changes (Wandell, 1995).

Although there are large theoretical and empirical literatures concerned with both how adaptation affects color appearance and constancy on the one hand (Wyszecki, 1986; Zaidi, 1999; Foster, 2003; Shevell, 2003; Brainard, 2004), and discrimination on the other (Wyszecki & Stiles, 1982; Walraven et al., 1990; Hood & Finkelstein, 1986; Lennie & D’Zmura, 1988; Kaiser & Boynton, 1996; Eskew, McLellan, & Giulianini, 1999), it is rare that the two functions are considered simultaneously. Still, it is clear that they are intimately linked since they rely on the same initial representation of spectral information. In addition, constancy is useful only if color vision also supports some amount of discrimination performance; in the absence of any requirement for discrimination, constancy can be achieved trivially by a visual system that assigns the same color descriptor to every object in every scene.¹ The recognition that constancy (or its close cousin, appearance) and discrimination are profitably considered jointly has been exploited in a few recent papers (Robilotto & Zaidi, 2004; Hillis & Brainard, 2005).

Here we ask whether applying the same adaptive transformations to visual responses can simultaneously optimize performance for both constancy and discrimination. If the visual system adapts to each of two environments so as to produce optimal color discrimination within each, what degree of constancy is achieved? How does this compare with what is possible if adaptation is instead tailored to optimize constancy, and what cost would such an alternative adaptation strategy impose on discrimination performance?

To address these questions, we adopt the basic theoretical framework introduced by Grzywacz and colleagues (Grzywacz & Balboa, 2002; Grzywacz & de Juan, 2003; also Brenner, Bialek, & de Ruyter van Steveninck, 2000; von der Twer & MacLeod, 2001; Foster, Nascimento, & Amano, 2004; Stocker & Simoncelli, 2005) by analyzing task performance using explicit models of the visual environment and early visual processing. Parameters in the model visual system specify the system’s state of adaptation, and we study how these parameters should be set to maximize performance, where the evaluation is made across scenes drawn from a statistical model of the visual environment (see Grzywacz & Balboa, 2002; Grzywacz & de Juan, 2003). Within this framework, we investigate the trade-offs between optimizing performance for discrimination and for constancy. We begin in section 2 with consideration of a simple one-dimensional example that illustrates the basic ideas and then generalize in section 3. The work presented here complements our recent experimental efforts directed toward understanding the degree to which measured adaptation of the visual pathways mediates judgments of both color discrimination and color appearance (Hillis & Brainard, 2005).

2 Univariate Example

We begin with the specification of a model visual system, a visual environment, and performance measures. The basic structure of our problem is well illustrated for the case of lightness/brightness constancy and discrimination, and we begin with a treatment of this case.

2.1 Visual Environment

The model visual environment consists of achromatic matte surfaces lit by a diffuse illuminant. Each surface j is characterized by its reflectance r_j, which specifies the fraction of incident illumination that is reflected. Each illuminant is specified by its intensity e_i. The intensity of light c_i,j, reflected from surface j under illuminant i is thus given by

$$c_{i,j}=e_i{r}_j.$$ (2.1)

At any given moment, we assume that the illuminant e_i is known and that the particular surfaces in the scene have been drawn from an ensemble of surfaces. The ensemble statistics characterize regularities of the visual environment. In particular, we suppose that

$$r_j\sim \overline{N}({\mu }_r,{\sigma }_r^2),$$ (2.2)

where ~ indicates “distributed as” and N̄(μ_r, ${\sigma }_r^2$) represents a truncated normal distribution with mean parameter μ_r and variance parameter ${\sigma }_r^2$. The overbar in the notation indicates the truncation, which means that the probability of obtaining a reflectance in the range 0 ≤ r_j ≤ 1 is proportional to the standard normal density function, while the probability of obtaining a reflectance outside this range is zero. The truncated distribution is normalized so that the total probability across all possible values of r_j is unity.

We are interested in (1) how well a simple model visual system can discriminate and identify randomly chosen surfaces viewed within a single scene and (2) how well the same visual system can discriminate and identify randomly chosen surfaces viewed across different scenes where the illumination, surface ensemble, or state of adaptation has changed.

2.2 Model Visual System

The model visual system has a single class of photoreceptor. At each location, the information transmitted by this photoreceptor is limited in two ways. First, the receptor has a limited response range. We capture this by supposing that the deterministic component of the response to surface j under illuminant i is given by

$$u_{i,j}=\frac{{(g{c}_{i,j})}^n}{{(g{c}_{i,j})}^n+1},$$ (2.3)

where u_i,j represents the visual response, c_i,j represents the intensify of incident light obtained through equation 2.1, g is a gain parameter, and n is a steepness parameter that controls the slope of the visual response function. For this model visual system, the adaptation parameters g and n characterize the system’s state of adaptation. Across scenes, the visual system may set g and n to optimize its performance.

The second limit on the transmitted information is that the responses are noisy. We can capture this by supposing that the deterministic component of the visual responses is perturbed by zero-mean additive visual noise, normally distributed with variance ${\sigma }_n^2$.

2.3 Discrimination Task and Performance Measure

To characterize discrimination performance, we need to specify a discrimination task. We consider a same-different task. On each trial, the observer sees either two views of the same surface (same trials) or one view each of different surfaces (different trials), all viewed under the same light e_i. The observer’s task is to respond “same” on the same trials and “different” on the different trials. On same trials, a single surface is drawn at random from the surface ensemble and viewed twice. On different trials, two surfaces are drawn independently from the surface ensemble. Independently drawn noise is added to the response for each view of each surface. This task is referred to in the signal detection literature as a roving same-different design (Macmillan & Creelman, 2005). The observer’s performance is characterized by a hit rate (fraction of “same” responses on same trials) and a false alarm rate (fraction of “same” responses on different trials).

It is well known that the hit and false alarm rates obtained by an observer in a same-different task depend on both the qualify of the information supplied by the visual responses (i.e., signal-to-noise ratio) and how the observer chooses to trade off hits and false alarms (Green & Swets, 1966; Macmillan & Creelman, 2005). By tolerating more false alarms, an observer can increase his or her hit rate. Indeed, by varying the response criterion used in the hit-false alarm trade-off, an observer can obtain performance denoted by a locus of points in what is referred to as a receiver operating characteristic (ROC) diagram (see Figure 1 and its caption). A standard criterion-free measure of the quality of information available in the visual responses is A′, the area under the ROC curve (Green & Swets, 1966; Macmillan & Creelman, 2005). In this letter, we use A′ as our measure of performance for both discrimination (as is standard) and constancy (see below).

Figure 1.

ROC diagram. The ROC (receiver operating characteristic) diagram plots hit rate versus the false alarm rate. An observer can maximize hit rate by responding “same” on every trial. This will lead to a high false alarm rate, and performance will plot at (1,1) in the diagram. An observer can minimize false alarms by responding “different” on every trial and achieve performance at (0,0). Varying criteria between these two extremes produces a trade-off between hits and false alarms. The exact locus traced out by this trade-off depends on the information used at the decision stage. Better information leads to performance curves that tend more toward the upper left of the plot (the solid curve indicates better information than the dashed curve.) The area under the ROC curve, referred to as A′, is a task-specific measure of information that does not depend on criterion. The hatched area is A′, for the dashed ROC curve. The ROC curves shown were computed for two surfaces with reflectances r₁ = 0.15 and r₂ = 0.29 presented in a roving same-different design. The illuminant had intensity e = 100, and the deterministic component of the visual responses was computed from equation 2.3 with g = 0.02 and n = 2. The solid line corresponds to σ_n = 0.05 and A′ = 0.85, and the dashed line corresponds to σ_n = 0.065 and A′ = 0.76. Hit and false alarm rates were computed using the decision rule described in section 2.4.

2.4 Effect of Adaptation on Discrimination

To understand the effect of adaptation, we ask how the average A′ depends on the adaptation parameters, given the surface ensemble, illuminant, and noise. For a roving design, a near-optimal strategy is to compute the magnitude of the difference between the visual responses for two surfaces and compare this difference to a criterion C (Macmillan & Creelman, 2005). The intuition is that when the visual responses to the two surfaces are similar, the observer should say “same.” Let u_i,j be the visual response to one surface under the given illuminant e_i, u_i,k to the other surface. The observer responds “same” if the squared response difference $\mathrm{\Delta }{u}_{i,jk}^2=\parallel u_{i,j}-u_{i,k}\mid {\mid }^2$ is less than C and “different” if $\mathrm{\Delta }{u}_{i,jk}^2\ge C$.

For any pair of surfaces r_j and r_k, we can compute the values of the deterministic component of the corresponding visual responses (u_i,j and u_i,k), once we know the illuminant e_i and the adaptation parameters g and n. Because of noise, the observed response difference $\mathrm{\Delta }{u}_{i,jk}^2$ varies from trial to trial. If the variance of the noise is ${\sigma }_n^2$, the distribution of the quantity ${(\mathrm{\Delta }{u}_{i,jk}^{\prime })}^2={(\mathrm{\Delta }{u}_{i,jk}/\sqrt{2}{\sigma }_n)}^2$ is noncentral chi-squared with 1 degree of freedom and noncentrality parameter ${(\mathrm{\Delta }{u}_{i,jk}/\sqrt{2}{\sigma }_n)}^2$.² Because scaling the visual response for both same and different trials by a common factor $1/\sqrt{2}{\sigma }_n$ does not affect the information contained in these responses, a decision rule based on comparing ${(\mathrm{\Delta }{u}_{i,jk}^{\prime })}^2$ criterion C′ = C/2σ² leads to the same performance as one that compares $\mathrm{\Delta }{u}_{i,jk}^2$ to C. Thus, the known noncentral chi-square distributions on same and different trials may be used, along with standard signal detection methods, to compute hit and false alarm rates for a set of criteria. The resultant ROC curve may then be numerically integrated to find the value of $A_{i,jk}^{\prime }$.

To evaluate overall discrimination performance, we compute $A_{i,jk}^{\prime }$ for many pairs of surfaces drawn according to the surface ensemble and compute an aggregate measure. Figure 2 illustrates how the gain parameter g affects discrimination performance for a single illuminant and surface ensemble, when the steepness parameter is held fixed at n = 2. The top shows histograms of $A_{i,jk}^{\prime }$ for two choices of gain. As the gain parameter is changed from g = 0.010 (solid bars) to g = 0.021 (hatched bars), the values of $A_{i,jk}^{\prime }$ increase, with fewer values near 0.5 and more values near 1.0.

Figure 2.

Effect of gain and noise on discrimination performance. (Top) Histograms of the discrimination measure $A_{i,jk}^{\prime }$ for two values of the gain parameter (solid bars, g = 0.010; hatched bars, g = 0.021). In the calculations, we set σ_n = 0.05, n = 2, μ_r = 0.5, σ_r = 0.3, and e = 100. Calculations were performed for 500 draws from the surface ensemble, and $A_{i,jk}^{\prime }$ was evaluated for all possible 124,750 surface pairs formed from these draws. (Bottom) The mean of the $A_{i,jk}^{\prime }$ (denoted by ) as a function of the gain parameter for four noise levels.

To study how performance varies parametrically with changes in gain, we need a measure that summarizes the change in the distribution of the $A_{i,jk}^{\prime }$. In this letter, we use the mean of the $A_{i,jk}^{\prime }$ for this purpose. For simplicity of notation, we denote this value by the symbol (script “D” for discrimination). The bottom panel of Figure 2 shows how varies with gain for four noise levels. There is an optimal choice of gain for each noise level (cf. Brenner et al., 2000), and the optimal gain does not vary appreciably with noise level. To provide some intuition about the state of the model visual system when the gain is optimized, the top right panel of Figure 3 shows the response function obtained for the optimal choice of gain when σ_n = 0.05. The histogram below the x-axis of this panel shows the distribution of reflected light intensities, while that to the left of the y-axis shows the distribution of visual responses. The histogram of responses appears more uniform than the histogram of light intensities. This general effect is expected from standard results in information theory, where maximizing the information transmitted by a channel occurs when the distribution of channel responses is uniform (Cover & Thomas, 1991). The response histogram is not perfectly uniform because varying the gain alone cannot produce this result and because our performance measure is rather than bits transmitted. Figure 6 below shows response histograms when both gain and steepness parameters are allowed to vary.

Figure 3.

State of model visual system for optimal choice of gain. The top right panel shows the response function for the optimal choice of gain (g = 0.021) when the noise is σ_n = 0.05. Below the response function is a histogram of the light intensities c_i,j reaching the eye, while to the left is a histogram of the resultant visual responses. Calculations were performed for 500 draws from the surface ensemble. Choices of gain less than or greater than the optimum would shift the response function right or left. For these nonoptimal choices, visual responses would tend to cluster nearer to the floor or ceiling of the response range, resulting in poorer discrimination performance.

Figure 6.

Adaptation to surface ensemble change for discrimination. Numerical search was used to optimize for two visual environments characterized by a common illuminant but different surface ensembles (surface ensemble 1 and surface ensemble 2). The illuminant intensity was 100. In surface ensemble 1, μ_r = 0.5 and σ_r = 0.3. In surface ensemble 2, μ_r = 0.7 and σ_r = 0.1. The histogram under the graph shows the distributions of reflected light intensities for the two ensembles. The graph shows the resultant visual response function for each case. The solid line corresponds to surface ensemble 1 and the dotted line to surface ensemble 2. The histogram to the left of the graph shows the response distribution for surface ensemble 1 under the surface ensemble 1 response function, while the histogram to the right shows the response distribution for surface ensemble 2 under the surface ensemble 2 response function. All calculations done for σ_n = 0.05 and e = 100. In evaluating for surface ensemble 1, performance was averaged over draws from surface ensemble 1; in evaluating for surface ensemble 2, performance was averaged over draws from surface ensemble 2. The dashed lines show how the visual response to the light intensity reflected from a fixed surface varies with the change in adaptation parameters. (Since the illuminant is held constant, a fixed surface corresponds to a fixed light intensity.)

2.5 Effect of Illuminant Change on Discrimination

We can also investigate the effect of illumination changes on performance and how adaptation can compensate for such changes. First, consider the case where the adaptation parameters are held fixed. We can compute the performance measure for any visual environment. The filled circles and solid line in Figure 4 plot as a function of the illuminant intensity when the adaptation parameters, noise, and surface ensemble are held fixed. Not surprisingly, performance falls off with the change of illuminant: increasing the illuminant intensity pushes the intensity of the reflected light toward the saturating region of the visual response function and compresses the response range used.

Figure 4.

Effect of illuminant change on discrimination and constancy performance. The filled circles and solid line show how discrimination performance decreases when the illuminant intensity is changed and the adaptation parameters are held constant. Here the x-axis indicates the single scene illuminant intensity used in the calculations for the corresponding point. The open circles and dashed line show how constancy performance decreases when the test illuminant intensity is changed and the adaptation parameters are held fixed across the change. Here the x-axis indicates the test illuminant intensity, with the reference illuminant intensity held fixed at 100. All calculations performed with adaptation parameters held fixed (g = 0.021, n = 2) and for σ_n = 0.05. The surface distribution had parameters μ_r = 0.5 and σ_r = 0.3.

The effect of increasing the illuminant intensity is multiplicative, so this effect can be compensated for by decreasing the gain (which also acts multiplicatively) so as to keep the distribution of responses constant. Perfect compensation is possible in this example because of the match between the physical effect of an illuminant change (multiplication of all reflected light intensities by the same factor) and the effect of a gain change (also multiplication of the same intensities by a common factor). In general, such perfect compensation is not possible.

2.6 Constancy

Suppose that instead of discriminating between surfaces seen under a common illuminant, we ask the question of constancy: How well can the visual responses be used to judge whether two surfaces are the same, when on each trial one surface is viewed in a reference environment and the other is viewed in a test environment? On same trials of the constancy experiment, the observer sees a surface in the reference environment and the same surface in the test environment. On different trials, the observer sees one surface in the reference environment and a different surface in the test environment. As in the discrimination experiment, the observer must respond “same” or “different.” The test and reference environments can differ through a change in illuminant, a change in surface ensemble, a change in adaptation parameters, or all of these.

We assume that the observer continues to employ the same basic distance decision rule applied to the visual responses, with the decision variable evaluated across the change of environment: $\overrightarrow{\mathrm{\Delta }}{u}_{jk}^2=\parallel u_{\mathit{ref},j}-u_{\mathit{test},k}\mid {\mid }^2$. On same trials, the expression is evaluated for a single surface across the change (r_k = r_j), and on different trials, the expression is evaluated for two draws from the surface ensemble. In the notation, the arrow indicates that the response difference is evaluated across the change from reference to test environment. Basing the decision rule on the response difference models the fact that in our framework, the observer has no explicit knowledge of the illuminant, surface ensemble, or state of adaptation—all effects of adaptation on performance are modeled explicitly with a change in adaptation parameters.³

The quantity A′ remains an appropriate measure of performance across a change in visual environments, as it continues to characterize how well hits and false alarms trade off as a function of a decision criterion. For any pair of surfaces, we denote the value of A′ obtained across the change as ${\overrightarrow{A}}_{jk}^{\prime }$. We obtain an aggregate performance measure by computing the mean of the ${\overrightarrow{A}}_{jk}^{\prime }$. To emphasize the fact that the performance measure for constancy is computed across a change in visual environments, we denote this measure by the symbol (script “C” for constancy) rather than overloading the meaning of the symbol . Evaluating requires specification of the illuminant and adaptation parameters for both test and reference environments, as well as the surface ensemble and noise level over which the ${\overrightarrow{A}}_{jk}^{\prime }$ are evaluated. Note that may be regarded as a special case of when the illumination, surface, and adaptation parameters are all held fixed, so that the test and reference environments are identical.

As an example, the open circles and dashed line in Figure 4 show how constancy performance falls off with a change in test illuminant when there is no compensatory change in adaptation parameters. The reference illuminant had intensity 100, and the x-axis provides the intensity of the test illuminant. Constancy performance was evaluated across draws from the surface ensemble common to the reference and test environments.

As with the effect of the illuminant change on within-illuminant discrimination performance, the deleterious effect of the illuminant change on constancy may be eliminated if an appropriate gain change occurs between the test and reference scenes. This is because changing the gain with the illumination can restore the responses under the test light back to their values under the reference light.

2.7 Trade-offs Between Discrimination and Constancy

When the adaptation parameters include a gain change, adaptation can compensate perfectly for changes in illumination intensity so that discrimination performance (obtained in a discrimination experiment) remains unchanged and constancy performance (obtained in a constancy experiment with a change of illuminant intensity and a gain change that compensates for it) is at ceiling given discrimination. More generally, there will be cases where the adaptation parameters available within a given model visual system are not able to compensate completely for environmental changes. This raises the possibility that the adaptation parameters that optimize discrimination may differ from those that optimize constancy.

Consider the case of an illuminant change where the gain parameter is held fixed and the steepness parameter n is allowed to vary between test and reference environments. Each connected set of solid circles in the left panel of Figure 5 plots against for various choices of the steepness parameter. The five different sets shown were computed for different levels of noise. The point at the lower right of each set indicates performance when the steepness parameter was chosen to maximize for the test illuminant, while the point at the upper left plots performance when the steepness parameter was chosen to maximize , evaluated across the change from reference to test illuminant. The points between these two extremes represent performance obtained when the steepness parameter was chosen to maximize either the expression − w( − ₀)² or the expression − w( − ₀)² Maximizing these expressions pushes the value of the leading measure as high as possible while holding the value of the other measure close to a target value. Which expression was used, as well as values of w, ₀, and _0, were chosen by hand so that the trade-off curve represented by each connected set was well sampled. Values of w and ₀ or ₀ were held fixed during the optimization for individual points on the trade-off curves. All optimizations were performed in Matlab using routines from its Optimization Toolbox (Version 3).

Figure 5.

Trade-off between discrimination and constancy. (Left) Each set of connected solid circles shows the trade-off between and for various optimizations of the steepness parameter n (see the text). Each set is for a different noise level (σ_n = 0.01, 0.025, 0.05, 0.075, 0.10), with the set closest to the upper right of the plot corresponding to the lowest noise level. The reference illuminant had intensity e_ref = 100, and the test illuminant had intensity e_test = 160. The surface ensemble was specified by μ_r = 0.5 and σ_r = 0.3 and was common to both the reference and test environments. Both and were evaluated with respect to draws from this surface ensemble. The gain parameter was held fixed at g = 0.02045. The steepness parameter for the reference environment was n = 4.5. Parameters g = 0.02045 and n = 4.5 optimize discrimination performance for the reference environment when σ_n = 0.05. The open circles connected by the dashed line show the performance points that could be obtained for each noise level if there were no trade-off between discrimination and constancy. (Right) Equivalent trade-off noise plotted against visual noise level σ_n. See the discussion in the text.

Figure 5 shows that there is a trade-off between the two performance measures—optimizing for constancy results in decreased discrimination performance and vice versa. Indeed, the open circles connected by the dashed line show the performance points that could be obtained for each noise level if there were no trade-off between discrimination and constancy. These were obtained as the points ( _max, _max) where the maxima were obtained over the trade-off curves for each noise level.

Although the trade-off curves do not include the open points, the distance between each trade-off curve and its corresponding no-trade-off point is not large. One way to quantify this distance is to ask, for each trade-off curve, how much the visual noise would have to be reduced so that performance at the no-trade-off point was feasible. We call this noise reduction the equivalent trade-off noise. To find its value, we treat each solid point as a triplet (, σ_n) and use bilinear interpolation to find σ_n as a function of and . We then identify the value of σ_n corresponding to each ( _max, _max). For the trade-off curve corresponding to visual noise level σ_n = 0.10 (the lowest left curve in the left panel of Figure 5), for example, the noise level corresponding to ( _max, _max) is 0.092, leading to an equivalent trade-off noise value of 0.008. The right panel of Figure 5 plots the equivalent tradeoff noise versus noise level σ_n.⁴ The mean value was 0.005 ± 0.003 S.D. If there were no trade-off, performance at the point ( _max, _max) would be possible for each noise level, but to achieve each ( _max, _max) requires, on average, a reduction of the visual noise by 0.005.

2.8 Intermediate Discussion

The example above illustrates our basic approach to understanding how adaptation affects both discrimination and constancy. The example illustrates a number of key points. First, as is well known, adaptation is required to maintain optimal discrimination performance across changes in the state of the visual environment (Walraven et al., 1990). Second, adaptation is also necessary to optimize performance for constancy, when we require that surface identity be judged directly in terms of the visual responses. The link between adaptation and constancy has also been explored previously (Burnham, Evans, & Newhall, 1957; D’Zmura & Lennie, 1986; Wandell, 1995). What is new about our approach is that we have set our evaluations of both discrimination and constancy in a common framework by using an A′ measure for both. This allows us to ask questions about how any given adaptation strategy affects both tasks and whether common mechanisms of adaptation can simultaneously optimize performance for both. The theory we develop is closely related to measurements of lightness constancy made by Robilotto and Zaidi (2004), who used a forced-choice method to measure both discrimination within and identification across changes in illuminant. Our theory allows us to quantify the trade-off between constancy and discrimination, either by examination of the shape of trade-off curves or through the equivalent trade-off noise concept.

2.9 Contrast Adaptation

Changing the illuminant is not the only way to change the properties of the environment. Within the context of the univariate case introduced above, we can also vary both the mean and variance of the surface ensemble. Such variation might occur as a person travels from, say, the city to the suburbs during an afternoon commute. There is good evidence that the visual system adapts to changes in the variance of the reflected light. This is generally called contrast adaptation (Krauskopf, Williams, & Heeley, 1982; Webster & Mollon, 1991; Chubb, Sperling, & Solomon, 1989; Zaidi & Shapiro, 1993; Jenness & Shevell, 1995; Schirillo & Shevell, 1996; Brown & MacLeod, 1997; Bindman & Chubb, 2004; Chander & Chichilnisky, 2001; Solomon, Peirce, Dhruv, & Lennie, 2004). Here we expand our analysis by considering changes to the mean and variance of the surface ensemble and explore the effect of adaptation to such changes on both discrimination and constancy, using the approach developed above.

Given a particular illuminant, we used numerical search to find the values of g and n that optimized for two visual environments that differed in terms of their surface ensembles (surface ensemble 1 and surface ensemble 2). The illuminant was held constant across the change in visual environment. This calculation tells us how the adaptation parameters should be chosen under a discrimination criterion. Figure 6 shows the results. We see in the middle panel in the top row that the visual response function under surface ensemble 2 has shifted to the right and become steeper. The effect of this adaptation is to distribute the visual responses fairly evenly across the available response range for each ensemble (cf. Fairhall, Lewen, Bialek, & de Ruyter van Steveninck, 2001). The gain and steepness parameters that optimize discrimination for surface ensemble 1 and surface ensemble 2 are different.

Suppose now that we evaluate constancy by computing across the change in visual environment and adaptation parameters required to optimize discrimination for the two surface ensembles.⁵ The lower right points on each of the trade-off curves in Figure 7 plot this value of against the corresponding value of for five different noise levels. The resultant value is very low (see Figure 7). This low value occurs because the change in adaptation parameters remaps the relation between surface reflectance and visual response (see the dashed lines in the response function panel of Figure 6).

Figure 7.

Trade-off between discrimination and constancy for change in surface ensemble. (Left) The plot shows the trade-off between C versus in the same format as the left panel of Figure 5. When the adaptation parameters are chosen to optimize discrimination () for the test environment (surface ensemble 2), constancy performance () is poor (lower right end of each set of connected dots). When the adaptation parameters are chosen to optimize constancy, discrimination performance is poor (upper left end of each set.) The connected sets of dots show how performance on the two tasks trades off for five noise levels σ_n = 0.01, 0.025, 0.05, 0.075, 0.10. Surface ensemble parameters and illuminant intensty are given in the caption for Figure 6. In evaluating , the adaptation parameters used for computing responses in the reference environment (surface ensemble 1) were held fixed at g = 0.02045 and n = 4.5. These parameters optimize discrimination performance for the reference environment when σ_n = 0.05. (Right) Equivalent trade-off noise plotted against noise level σ_n.

Rather than choosing adaptation parameters for the test environment to optimize discrimination performance , one can instead choose them to optimize constancy performance . This choice leads to quite different adaptation parameters and to different values of and . Here the best adaptation parameters for surface ensemble 2 are very similar (but not identical) to their values for surface ensemble 1⁶ and constancy performance is better (upper left points on the trade-off curves shown in Figure 7). Discrimination performance suffers, however.

More generally, the visual system can choose adaptation parameters that trade off against . This trade-off is shown in Figure 7 in the same format as Figure 5.⁷ If there were no trade-off, each set of connected dots would pass through the corresponding open circle. We quantify the deviation as before, using the equivalent trade-off noise. The right panel of Figure 7 plots equivalent trade-off noise against visual noise. The average value is 0.029 ± 0.012 SD, larger than the average value of 0.005 obtained for the illuminant change example.

The comparison shows that adapting to optimize discrimination in the face of changes in the distribution of surfaces in the environment is not always compatible with adapting to maximize constancy across the same change in surface ensemble. The intuition underlying this result is relatively straightforward: changing the surface ensemble affects the optimal use of response range and hence leads to a change in adaptation parameters for optimizing discrimination, but it does not affect the mapping between surface reflectance and receptor response. Thus, any change in adaptation parameters perturbs the visual response to any fixed surface.

3 Chromatic Adaptation

The univariate example presented above illustrates the key idea of our approach. In this section, we generalize the calculations to a more realistic trichromatic model visual system and a more general parametric model of adaptation. In addition, in comparing adaptation to changes in illumination and changes in surface ensemble, we develop a principled method of equating the magnitude of the changes. The overall approach, however, is the same as for the univariate example.

We begin with a standard description (Wandell, 1987; Brainard, 1995) of the color stimulus and its initial encoding by the visual system. Each illuminant is specified by its spectral power distribution, which we represent by a column vector e. The entries of e provide the power of the illuminant in a set of N_λ discretely sampled wavelength bands. Each surface is specified by its spectral reflectance function, which we represent by a column vector s. The entries of s provide the fraction of incident light power reflected in each wavelength band. The light reflected to the eye has a spectrum described by the column vector

$$\mathbf{c}=\mathbf{diag}(\mathbf{e})\mathbf{s},$$ (3.1)

where diag() is a function that returns a square diagonal matrix with the elements of its argument along the diagonal. The initial encoding of the reflected light is the quantal absorption rate of the L-, M-, and S-cones. We represent the spectral sensitivity of the three cone types by a 3 × N_λ matrix T. Each row of T provides the sensitivity of the corresponding cone type (L, M, or S) to the incident light. The quantal absorption rates may then by computed as

$$\mathbf{q}=\mathbf{Tc}=\mathbf{Tdiag}(\mathbf{e})\mathbf{s},$$ (3.2)

where q is a three-dimensional column vector whose three entries represent the L-, M-, and S-cone quantal absorption rates. We used the Stockman and Sharpe (2000) estimates of the human cone spectral sensitivities (2 degree), and we tabulate these in the supplemental material (http://color.psych.upenn.edu/supplements/adaptdiscrimappear/).

As with the univariate example, we model visual processing as a transformation between cone quantal absorptions (q) and visual responses. Here we model the deterministic component of this transformation as

$$\mathbf{u}=\mathbf{f}(\mathbf{M}{\mathbf{D}}_{\mathbf{q}-{\mathbf{q}}_0}),$$ (3.3)

where u is a three-dimensional column vector representing trivariate visual responses, D is a 3 × 3 diagonal matrix whose entries specify multiplicative gain control applied to the cone quantal absorbtion rates, M is a fixed 3 × 3 matrix that describes a postreceptoral recombination of cone signals, q₀ is a three-dimensional column vector that describes subtractive adaptation, and the vector-valued function f() applies the function f_i() to the ith entry of its vector argument. Because incorporation of subtractive adaptation allows the argument to the nonlinearity to be negative, we used a modified form of the nonlinearity used in the univariate example:

$$f_i(x)=\{\begin{array}{ll}\frac{{(x+1)}^{n_i}}{{(x+1)}^{n_i}+1}\hfill & x>0\hfill \\ 0.5\hfill & x=0\hfill \\ 1-\frac{{(1-x)}^{n_i}}{{(1-x)}^{n_i}+1}\hfill & x<0\hfill \end{array}.$$ (3.4)

This nonlinearity maps input x in the range [−∞, ∞] from the real line into the range [0,1]. We allow the exponent n_i to vary across entries. The matrix M was chosen to model, in broad outline, the postreceptoral processing of color information (Wandell, 1995; Kaiser & Boynton, 1996; Eskew et al., 1999; Brainard, 2001):

$$\mathbf{M}=\left[\begin{array}{lll}0.33\hfill & 0.33\hfill & 0.33\hfill \\ 0.5\hfill & -0.5\hfill & 0\hfill \\ -0.25\hfill & -0.25\hfill & 0.5\hfill \end{array}\right].$$ (3.5)

This choice of M improves discrimination performance by approximately decorrelating the three entries of the visual response vector prior to application of the nonlinearity and the injection of noise (Buchsbaum & Gottschalk, 1983; Wandell, 1995).

As with the univariate example, we assume that each entry of the deterministic component of the visual response vector is perturbed by independent zero-mean additive visual noise that is normally distributed with variance ${\sigma }_n^2$.

We characterized the reference environment surface ensemble using the approach developed by Brainard and Freeman (Brainard & Freeman, 1997; Zhang & Brainard, 2004). We assumed that the spectral reflectance of each surface could be written as a linear combination of N_s basis functions via

$$\mathbf{s}={\mathbf{B}}_s{\mathbf{w}}_s.$$ (3.6)

Here B_s is an N_λ × N_s matrix whose columns provide the basis functions, and w_s is an N_s-dimensional vector whose entries provide the weights that describe any particular surface as a linear combination of the columns of B_s. We then assume that surfaces are drawn from an ensemble where w_s is drawn from a truncated multivariate normal distribution with mean vector w̄ and covariance matrix K_w. The truncation is chosen so that the reflectance in each wavelength band lies within the range [0, 1]. We obtained B_s by computing the first eight principal components of the reflectance spectra measured by Vrhel, Gershon, and Iwan (1994). We obtained w̃ and by K_w taking the mean and covariance of the set of w_s required to best approximate each of the measured spectra with respect to B_s. Computations were run using an ensemble consisting of 400 draws from this distribution.⁸ The 400 reflectances in the reference environment surface ensemble are tabulated in the online supplement (http://color.psych.upenn.edu/supplements/adaptdiscrimappear/), and we refer to this ensemble below as the baseline surface ensemble.

Given the visual system model and surface ensemble defined above, we can proceed as with the univariate case and ask how the adaptation parameters affect and , the discrimination and constancy performance measures, respectively. The only modification required is that the decision rule now operates on the difference variable $\mathrm{\Delta }{u}_{i,jk}^2=\parallel {\mathbf{u}}_{i,j}-{\mathbf{u}}_{i,k}\mid {\mid }^2$, and this variable is distributed as a noncentral chi-squared distribution with 3 degrees of freedom rather than 1. The adaptation parameters are the three diagonal entries of D, the three entries of q₀, and the three exponents n_i.

Figure 8 shows how , and trade off when the illuminant is changed from CIE illuminant D65 to three separate changed illuminants. Each of the changed illuminants was constructed as a linear combination of the CIE daylight basis functions. We refer to the three changed illuminants as the blue, yellow, and red illuminants, respectively. Their CIE u′v′ chromaticities are provided in Table 1, and their spectra are tabulated in the supplemental material (http://color.psych.upenn.edu/supplements/adaptdiscrimappear/). The relative illuminant spectra are essentially the same as the neutral (here D65), Blue_60 (here blue), Yellow_60 (here yellow), and Red_60 (here red) illuminants used by Delahunt and Brainard (2004) in a psychophysical study of color constancy. The changes between D65 and the blue and yellow illuminants are typical of variation in natural daylight (see Delahunt & Brainard, 2004). The change between D65 and the red illuminant has a similar colorimetric magnitude but is atypical of variation in daylight. For the calculations here, the units of overall illuminant intensity are arbitrary; the four illuminant spectra were scaled to have the same CIE 1931 photopic luminance. Figure 8 shows that discrimination and constancy are highly compatible here.

Figure 8.

Chromatic example, illuminant change results. Trade-off between discrimination and constancy for illuminant change. Each pair of horizontally aligned panels is in the same format as Figure 5. (Left panels) versus trade-off curves with respect to illuminant changes. The reference environment illuminant was D65; the test environment illuminants were (from top to bottom) the blue, yellow, and red illuminants. The reference and test environment surface ensembles were the baseline surface ensemble in each case. The individual sets of connected points show performance for noise levels σ_n,, = 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50. In evaluating , the adaptation parameters for the reference environment were those that optimized discrimination performance in the reference environment. These parameters were optimized separately for each noise level. (Right panels) Equivalent tradeoff noise plotted against noise level σ_n.

Table 1.

Illuminant Chromaticities

Illuminant	CIE u′	CIE v′
D65	0.198	0.468
Blue	0.185	0.419
Yellow	0.226	0.508
Red	0.242	0.450

Notes: CIE u′v′ chromaticity coordinates of the four illuminants used in the trichomatic calculations. Chromaticity coordinates were computed over the wavelength range 390 nm to 730 nm, which is the range for which we had surface reflectance data from the Vrhel et al. (1994) data set.

We also investigated discrimination constancy trade-offs for the color case when the surface ensemble is changed. An issue that arises is how to produce a surface ensemble change whose magnitude is commensurate with that of the illuminant changes. We did not treat this magnitude issue in the univariate example above. Here we created three changed surface ensembles (the blue, yellow, and red ensembles) so that the cone responses to each changed ensemble under the reference illuminant were exactly the same as those of the baseline surface ensemble under the corresponding changed illuminant. For example, the 400 triplets of LMS cone responses from the blue ensemble under illuminant D65 were exactly the same as the 400 triplets of LMS cone responses from the baseline ensemble under the blue illuminant. Construction of changed surface ensembles such that they have this property is straightforward using the type of linear-model-based colorimetric calculations developed by Brainard (1995). We constrained the reflectance functions in the changed ensemble to be a linear combination of the first three columns of the matrix B_s that was used to construct the baseline ensemble. We also required that all of the surfaces in all four ensembles have reflectance functions with values between 0 and 1. This required rejecting some draws from the truncated normal distribution used to define the baseline ensemble at the time the ensembles were constructed. The supplemental material (http://color.psych.upenn.edu/supplements/adaptdiscrimappear/) tabulates the changed surface ensembles, as well as the baseline surface ensemble.

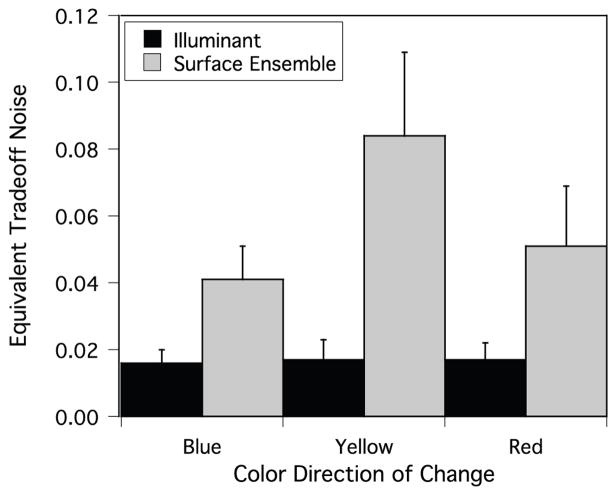
Figure 9 shows the results from the surface ensemble change calculations, in the same format as Figure 8. Direct examination of both the trade-off curves and the summary provided by the equivalent trade-off noise measure indicate that constancy and discrimination are considerably less compatible in the surface ensemble change case than in the illuminant change case. This difference is summarized in Figure 10, where the mean equivalent trade-off noise is shown for each of the changes reported in Figures 8 and 9.

Figure 9.

Chromatic example, surface ensemble change results. Trade-off between discrimination and constancy for surface ensemble changes. Same format as Figure 8. The reference and test environment illuminants were D65, the reference environment surface ensemble was the baseline esemble, and the test environment surface ensembles were (from top to bottom) the blue, yellow, and red ensembles. The individual sets of connected points in the left panels show performance for noise levels σ_n = 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50. In evaluating , the adaptation parameters for the reference environment were those that optimized discrimination performance in the reference environment. These parameters were optimized separately for each noise level.

Figure 10.

Summary of equivalent trade-off noise for the chromatic example. The solid black bars show the mean equivalent trade-off noise (+/− one standard deviation) for the three illuminant changes reported in Figure 8. The solid gray bars show the corresponding values for the three surface ensemble changes reported in Figure 9. In each case, the mean and standard deviation were taken over visual noise levels (that is, over the values shown in each of the right-hand panels in Figures 8 and 9.)

4 Summary and Discussion

The theory and calculations presented here lead to several broad conclusions. First, we note that constancy cannot be evaluated meaningfully without considering discrimination. By using a signal detection theoretic measure (A′) to quantify constancy, we explicitly incorporate discrimination into our treatment of constancy.

When the environmental change is a change in illuminant, then the dual goals of discrimination and constancy are reasonably compatible for the cases we studied: a common change in adaptation parameters comes close to optimizing performance for both our discrimination and constancy performance measures. To be more precise about the meaning of “reasonably compatible” and “comes close,” we turn to the quantification in terms of the mean equivalent trade-off noise, which was less than 2% for each of the changes we studied in the chromatic example (see Figure 10). For applications where an increase in 2% in visual noise relative to the baseline visual noise (10–50% across the trade-off curves we computed) is deemed to be large, one could revise the verbal descriptions accordingly.

When the environmental change is a change in the surface ensemble, discrimination and constancy were less compatible. As measured by the mean equivalent trade-off noise, the incompatibility between constancy and discrimination is approximately two to four times larger for surface ensemble changes than for the corresponding illuminant changes, under conditions where the physical effect of the corresponding illuminant and surface ensemble changes on the LMS cone responses between reference and test environments was equated. Thus, the analysis suggests that stimulus conditions where the surface ensemble changes may provide psychophysical data that are most diagnostic of whether the early visual system optimizes for discrimination, for constancy, or whether it has evolved separate sites that mediate performance on the two tasks. We have started to develop an experimental framework for approaching this question (see Hillis & Brainard, 2005; see also Robilotto & Zaidi, 2004).

As noted in the introduction, our approach is similar to that of Grzywacz and colleagues (Grzywacz & Balboa, 2002; Grzywacz & de Juan, 2003; see also Foster et al., 2004). Previous authors have considered the adaptation of the visual response function required to optimize discrimination performance (Laughlin, 1989; Buchsbaum & Gottschalk, 1983; Brenner et al., 2000; von der Twer & MacLeod, 2001; Fairhall et al., 2001), as well as the nature of adaptive transformations that can mediate constancy (von Kries, 1970; Buchsbaum, 1980; West & Brill, 1982; Brainard & Wandell, 1986; D’Zmura & Lennie, 1986; Maloney & Wandell, 1986; Foster & Nascimento, 1994; Foster et al., 2004; Finlayson, Drew, & Funt, 1994; Finlayson & Funt, 1996). Here the two tasks are analyzed in a unified manner using the theory of signal detection. The work provides both a framework for a fuller theoretical exploration of adaptation across different models of adaptation and environmental changes and an ideal observer benchmark against which future experimental results may be evaluated.