Abstract
One of the most critical challenges in systems neuroscience is determining the neural code. A principled framework for addressing this can be found in information theory. With this approach, one can determine whether a proposed code can account for the stimulus-response relationship. Specifically, one can compare the transmitted information between the stimulus and the hypothesized neural code with the transmitted information between the stimulus and the behavioral response. If the former is smaller than the latter (i.e., if the code cannot account for the behavior), the code can be ruled out.
The information-theoretic index most widely used in this context is Shannon’s mutual information. The Shannon test, however, is not ideal for this purpose: while the codes it will rule out are truly nonviable, there will be some nonviable codes that it will fail to rule out. Here we describe a wide range of alternative indices that can be used for ruling codes out. The range includes a continuum from Shannon information to measures of the performance of a Bayesian decoder. We analyze the relationship of these indices to each other and their complementary strengths and weaknesses for addressing this problem.
1 Introduction
Information-theoretic analysis is a powerful tool to illuminate how neurons represent the sensory world. A fundamental reason for this is that the classic information measure, Shannon’s mutual information, places a limit on the number of possible stimuli that can be distinguished from the output of a neural channel. Thus, measuring mutual information can serve as a way to determine whether the activity of a channel can account for behavioral performance in a sensory discrimination task.
For example, suppose one wanted to determine which features of the activity (e.g., firing rate, interspike intervals) are critical for performing the task. One can measure the mutual information between a given feature and the stimulus set in the task. If the mutual information between the feature and the stimulus set is less than the mutual information between the stimulus set and the behavioral performance, then one can deduce that that feature is insufficient to account for the behavior. That is, one can rule out a neural code based solely on that feature.
Mutual information, though, is not perfect, that is, it is not a highly stringent test. While any code that fails this test is guaranteed to be nonviable, there are conditions in which nonviable codes can pass. The basic reason for this is that information is lost when neural activity is converted into a behavioral response (response discretization). By not taking this loss into account, mutual information can fail to exclude codes that are, in fact, nonviable for producing behavior.
Like mutual information, the best performance of a Bayesian decoder is an index that can be used to test the viability of neural codes in a rigorous fashion. This index takes into account the above information loss and might therefore appear to be a more universal test. However, this measure is highly sensitive to assumptions about the decision criterion used in performing the behavioral task. Consequently, it also can fail to exclude nonviable codes under some situations, but these situations are distinct from those in which mutual information fails.
Here we show that these indices are but two of many possible choices. In particular, they represent the extremes of a continuum of indices that provide rigorous tests of neural codes. However, these indices differ in their ability to test codes for a range of reasons, including differences in their sensitivity to decision criterion, differences in their sensitivity to response discretization, and differences in their bias and variance characteristics. In this article, we analyze the properties of these indices, their relationships to each other, and their complementary strengths and weaknesses.
In the main section of this article, we approach the problem of ruling codes out assuming no knowledge of what the subject is thinking, that is, what the subject’s priors and decision rules are. The Data Processing Inequality (DPI) justifies this, since it places absolute limits on the behaviors a code can support. Thus, any code that is ruled out by these indices is truly ruled out. In the appendixes, we show how priors and decision rules can be taken into account to allow still more codes to be ruled out.
2 Results
This article has two main components: one that focuses on general indices of information and one that focuses on using these indices to test coding hypotheses.
In the first component, the ideas build on the central notion that information represents a reduction in uncertainty. Uncertainty can be formalized as the extent to which a probability distribution is dispersed. We therefore begin by recognizing that there are many ways of quantifying dispersion. We then show that for every way of quantifying dispersion, there is a corresponding generalized index of transmitted information. The corresponding index is the extent to which a distribution becomes less dispersed by making an observation. These general indices of information include the familiar Shannon mutual information, the performance of the best Bayesian decoder, and many others. All of these indices satisfy the DPI and therefore provide means to test coding hypotheses.
Then we show how these indices can be used to test coding hypotheses. We consider several examples that illustrate how the indices differ and identify their complementary strengths and weaknesses.
2.1 Indices of Concentration
Let P denote a probability distribution. To quantify its dispersion, we consider its opposite, namely concentration, as this will enable us to make use of the properties of convex functions. We define an index of concentration f to be a convex function on a probability distribution P and denote this by f(P).1
The range of indices of concentration is captured by two well-known examples:
| (2.1) |
and
| (2.2) |
where P is a probability distribution on L symbols and pi is the probability associated with the ith symbol. The first index, equation 2.1, is associated with a Bayesian measure of information, as we show in the text following equation 2.4.2 The second index, equation 2.2, is the negative of the Shannon entropy, the quantity associated with Shannon mutual information.
These two indices have quite different properties: the Bayes index fmax, equation 2.1, depends on only the largest probability, while the Shannon index, equation 2.2, depends smoothly on all of the probabilities. These dependencies put them at two ends of a continuum. Indices along the continuum have intermediate dependence on the nonpeak probabilities. This viewpoint is useful not only conceptually but also practically: these intermediate indices can, under some circumstances, have advantages over either the Bayes or Shannon indices (as we will show in the second half of section 2).
To display formally that the Bayes and Shannon indices constitute the ends of a continuum, we consider the function fα(P) defined by
| (2.3) |
This function is convex and thus is an index of concentration.3 As α → ∞, fα is progressively dominated by the single largest probability and approaches the Bayes index fmax, equation 2.1. As α →1, (fα − 1)/(α − 1) approaches the negative of the Shannon entropy, equation 2.2.4
2.2 For Every Index of Concentration, There Is a Generalized Index of Transmitted Information
To construct an index of transmitted information, If, from any index of concentration f, we generalize the relationship between Shannon mutual information and Shannon entropy. As is well known, Shannon mutual information is the difference between an a priori entropy and an a posteriori entropy, for example, the difference between the entropy of a stimulus distribution and the entropy of that distribution conditional on observing a response. By generalizing this relationship, we show that any index of concentration f can be turned into an information-theoretic quantity and can therefore be used to test codes. As we will also show, the new indices have distinct properties that make them useful for analyzing different kinds of behavioral experiments.
To generalize the Shannon construction, consider two random variables X (with distribution PX) and Y (with distribution PY). We will think of X as the stimulus set and Y as the response set. X assumes values i ∈ {1, …, M} with probability pX;i = xi, and Y assumes values j ∈{1, …, N} with probability pY;j = yj. (Here and below, we use upper-case letters such as X to denote a random variable, PX to denote its associated probability distribution, and pX;i, to denote the probability that X assumes a specific value i.)
We construct an index If (X, Y) that tells us to what extent observation of response variable Y narrows the possibilities for X. That is, to what extent does the a priori concentration f(X) increase when a response is observed? The index If (X, Y) is given by
| (2.4) |
where PX|Y=j is the conditional distribution of X, given the observation Y = j.
Note that for f = −H1, equation 2.4 is the familiar Shannon mutual information, which we will denote IShannon. The first term is the expected concentration of the stimulus distribution X, given the benefit of an observation in Y. The second term is the a priori concentration of the stimulus distribution. For f(P) = max(pi), equation 2.4 is a corresponding Bayesian measure. In this case, the first term of equation 2.4 is the expected fraction correct of the Bayesian decoder that has the benefit of an observation in Y. The second term is the fraction correct that could be achieved by choosing the a priori most likely symbol. So, in both cases, equation 2.4 is the increase in concentration that is achieved on the basis of the observations Y. Since the two indices of concentration f represent the ends of a continuum, so do their corresponding indices of transmitted information If, with α →; ∞ yielding a Bayes measure and α →1 yielding a Shannon information.5
2.3 Properties of Indices of Transmitted Information
Here we show that several key properties of Shannon information extend to all of the indices If (X, Y) as defined by equation 2.4. These properties are important because they show the indices If (X, Y) behave in a manner that merits the designation “transmitted information” and because they will allow us to use these indices to test coding hypotheses. The properties are (1) nonnegativity: If (X, Y) ≥ 0, with strict inequality implying that X and Y are dependent, and If (X, Y) = 0 whenever X and Y are independent; (2) refinement (Rényi, 1961): If (X, Y) should behave in a lawful manner if the response variable Y is refined into a more detailed representation; and (3) the DPI: stimulus-independent processing of the response variable Y should not increase If (X, Y). In this section, we show that all of the If (X, Y) have these properties.
In addition, statistical properties of estimates of If (X, Y) are important to consider, because in laboratory applications, the indices must be estimated from a finite amount of data. As is well known, naive estimates of the Shannon mutual information are upwardly biased. Naive estimates of the general indices If (X, Y) are also biased. However, the nature of this bias depends on f, as does the variance of the estimates, as we discuss at the end of this section.
Finally, we mention that there are several properties of Shannon mutual information that do not generalize, but these properties are not essential to our purpose, ruling out codes. First, Shannon information is symmetric in X and Y, but this is not true of If in general. For this reason, we use the term transmitted information for If rather than mutual information. Second, the channel coding theorem and Sanov’s theorem (large deviation approximation) (Cover & Thomas, 1991; Rieke, Warland, de Ruyter van Steveninck, & Bialek, 1997) do not apply to the other indices. While these properties of Shannon information are at the foundation of classical information theory and formalize its privileged place as a tool for characterizing codes and analyzing information flow, they are not required for eliminating codes.
2.3.1 Nonnegativity
Convexity of f guarantees that If (X, Y) ≥ 0. To see this, we first observe that the unconditional distribution PX is a mixture of the conditional distributions PX|Y=j. That is, , where yj is the probability of the jth symbol in Y. The convexity property states that the concentration of their mixture is no greater than the weighted sum of the concentrations of the individual components. That is, for any set of N distributions Pn and any set of mixing weights (real numbers λn ∈ [0, 1] that sum to 1),
| (2.5) |
The conclusion that If (X, Y) ≥ 0 follows from equation 2.5 by choosing λj = yj. The minimum value If (X, Y) = 0 is achieved when X and Y are independent (so PX|Y=j = PX).
2.3.2 Refinement
The generalized transmitted information If obeys a refinement rule (Rényi, 1961) that governs its behavior when the response variable Y is “refined” into a more detailed representation Z. Suppose that we initially analyze the relationship between a stimulus set X and a response set Y and only later realize that the final value Y = N actually represents R distinguishable responses. The refinement rule dictates how the unrefined information If (X, Y) and the refined information If (X, Z) are related:
| (2.6) |
This relationship follows from the definition 2.4 of If, as we now show. When Y takes on one of its first N − 1 values, then Z = Y. That is, for the unrefined symbols j ≤ N − 1, pZ|y=k;j = δ(j, k) and PX|Y=j = PX|Z=j. When Y takes on the final value Y = N, Z can take any value in {N, N + 1, …, N + R − 1}. For the symbols r ∈{N, N + 1, …, N + R − 1} generated by this refinement, pZ|y=N;r = pZ;r/pY;N, and pZ|y=k;r is zero for k < N. Therefore,
2.3.3 Data Processing Inequality
The DPI, an important property of Shannon mutual information, states that stimulus-independent transformation of the response variable Y into another variable Z cannot increase the amount of information. This property is shared by the generalized transmitted information If. More formally, if X →Y →Z form a Markov chain, then
| (2.7) |
We remark that if both X →Y →Z and X →Z →Y are Markov chains, then the DPI implies that If (X, Z) = If (X, Y), since, in addition to equation 2.7, If (X, Y) ≤ If (X, Z) must hold.
To demonstrate the DPI, we first observe that any transformation from Y to Z can be achieved by a sequence of simple steps Y = Y0, Y1, …, Yk, … Ys = Z, where each step consists of one of the following kinds of transformations: (1) symbols in Yk are relabeled in Yk+1; (2) a symbol a in Yk splits into one of two new symbols b or c in Yk+1; or (3) two distinct symbols in Yk, say g and h, are merged into a new symbol u in Yk+1.
We now proceed to show that none of these transformations can increase If (X, Yk). The relabeling transformation (transformation 1) does not affect If, since it merely reorders the terms in the sum of equation 2.4. The splitting transformation (transformation 2) does not affect If for the following reason. The assumption that X, Y, and Z form a Markov chain implies that the choice of b versus c is independent of X. Therefore, the a posteriori distributions PX|Yk=a, PX|Yk+1=b and PX|Yk+1=c are identical. Moreover, since b and c arise only from a, the marginal probabilities pYk+1;b and pYk+1;c must sum to pYka. Together, these observations imply that transformation 2 does not affect If (see equation 2.4). Finally, the merging transformation, transformation 3, may affect If, but the convexity property, equation 2.5, implies that If cannot increase, as the following calculation shows. Since u can arise only from g or h,
| (2.8) |
and
| (2.9) |
Thus, the conditional probability PX|Yk+1=u is a mixture of the conditional probabilities PX|Yk=g and PX|Yk=h, with mixing weights λ1 = pYk;g/(pYk;g + pYk;h) and λ2 = 1 − λ1 in equation 2.5. The convexity property shows that the contribution of the terms of If that involve g and h cannot increase when they are merged into the new symbol u.
In sum, the above paragraph emphasizes the importance of convexity for the DPI, that is, it implies the DPI. Conversely, the DPI implies convexity. More formally, if (for an arbitrary f) an expression of the form of equation 2.4 satisfies the DPI, then the function f must be convex. To demonstrate equation 2.5, create random variables X and Y for which PY=yn = λn and PX|Y=yn = Pn. “Processing” Y by merging all of its symbols into a single symbol Z sets up a situation in which If (X, Z) = 0, and If (X, Y) ≥ 0 is equivalent to equation 2.5.
2.3.4 Bias and Variance of Naive Estimates of the Indices
To apply the indices If (X, Y) to an experiment, they must be estimated from a finite quantity of laboratory data. Therefore, we consider the bias and variance properties of simple estimates of the indices If (X, Y). These are the naive (plug-in) estimates, which consist of inserting the observed frequencies of joint observations of X and Y into the definition of If (X, Y), equation 2.4. As we show, these naive estimates of If (X, Y) tend to be overestimates; they are upwardly biased. However, depending on the choice of the concentration index f, bias affects some kinds of data sets more than others. For Bayes-like indices, bias is most severe when performance is at threshold (chance performance) and minimal when performance is far from threshold (close to perfect). For Shannon-like indices, bias is independent of the level of performance to a first approximation.
To see how the bias properties of the indices If (X, Y) emerge, we make use of the fact that they are sums of indices of concentration, f. We therefore begin by discussing the statistical behavior of estimates of f.
It is well known that the naive estimate of the Shannon entropy is down-wardly biased (Carlton, 1969; Miller, 1955; Treves & Panzeri, 1995; Victor, 2000). Consequently, naive estimates of its negative, the Shannon index of concentration f = −H1, are upwardly biased. As we show in appendix C, naive estimates of all indices of concentration are upwardly biased, and, moreover, as the sample size increases, the bias decreases monotonically. The proof hinges on the convexity of the index of concentration, along with the following observation: a probability distribution estimated from the frequencies encountered in a data set containing N observations is a mixture of probability distributions estimated from the N data sets, each of size N − 1, in which one of the observations is omitted.
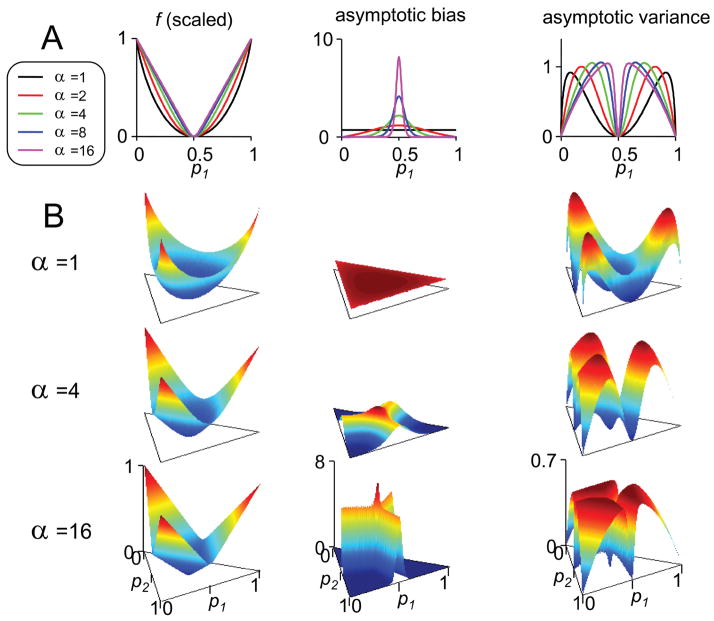
The specific bias behavior of the naive estimate of an index of concentration depends in a systematic fashion on the form of the index. To illustrate this, we consider the bias behavior of fα for a range of values of the parameter α. Figure 1A considers the case of two symbols, with probability p1 and p2 = 1 − p1. The left panel shows how the true value of fα depends on p1. For all values of α, the minimum concentration occurs when the probabilities are equal ( ). As α increases, this minimum becomes progressively sharper, approaching a singularity as α → ∞ (here, α = 16).
Figure 1.
Behavior of bias and variance of naive estimates of indices of concentration fα. (A) Two symbols, with probabilities p1 and p2 = 1 − p1. (B) Three symbols, with probabilities p1, p2, and p3 = 1 − p1 − p2. Column 1: fα, linearly rescaled into the range [0, 1]. Column 2: the coefficient of 1/N in the asymptotic bias (same normalization as column 1). Column 3: the coefficient of 1/N in the asymptotic variance (same normalization as column 1).
Column 2 of Figure 1A shows how the expected bias in the naive estimate of fα depends on p1. As shown in appendix C, this expected bias is asymptotically proportional to 1/N; we plot the proportionality constant in the figure. In the Shannon limit (α = 1), bias is independent of p1, as is well known (Carlton, 1969; Miller, 1955; Treves & Panzeri, 1995; Victor, 2000). For large α, there is a large bias when the probabilities are nearly equal (near ) and little bias when the probabilities are very unequal.
The behavior of bias of estimates of fα can be understood intuitively as follows. Two factors need to be considered: first, the variability in the estimate of p, and second, how the naive estimate of fα depends on the estimate of p. The variability in the estimate of p is determined by multinomial statistics and is independent of α (i.e., it is the same for all of the indices), so we focus on the second factor, the shape of fα. We consider first the peak in the bias near for large α. The origin of this peak is that fα is sharply curved at this point. In particular, as α → ∞, fα approaches fmax. In this limit, fmax is V-shaped at this point, because it is determined by whichever symbol happens to have the highest frequency in the data sample. Thus, any fluctuation away from equal occurrences of the two symbols will produce a naive estimate that is higher than the correct value. Consequently, the bias is large. However, if p1 is far from , fluctuations in the number of occurrences of the two symbols are just as likely to lead to an overestimate of fmax as an underestimate. Consequently, the bias in the estimate of fmax is minimal. For small α, the sharpness of the trough of fα is progressively smaller, and the peak in the bias is progressively smaller and broader.6 Note that although the expected bias of naive estimators of the indices fα is generally less than that of the Shannon entropy (α = 1) when the probabilities are far from equality, the naive estimate of the Shannon entropy is asymptotically less biased than that of the other indices near .
The third column of Figure 1A shows how the variance of the naive estimate of fα depends on p1. For all indices fα, variance is smallest when fα has its extreme values: at , where fα is minimum, and at p1 =0 and p1 = 1, where fα is maximum. However, the range of values of p1 at which the variance in the estimate of fα is largest depends strongly on α, with p1 near associated with the largest variances for large α and p1 near 0 or 1 associated with the largest variances for small α.
Intuitively, the behavior of the variance can be understood as the net result of two factors. One factor is the local slope of the index fα (see Figure 1A, column 1). A large slope implies a high sensitivity to errors in the estimates of p1, while a small slope implies insensitivity to errors in the estimates of p1. The slope is 0 at , and this accounts for the trough of the variance at this point. The second factor is the behavior of the variance of binomial distributions, which determines how accurately one can estimate p1 from a finite sample. For N samples, the variance is given by Np1(1 − p1), indicating that estimates of p1 are least variable at the extremes of its range. This accounts for the minima of the variance at p1 = 0 and p1 = 1.
The case of three symbols (see Figure 1B) shows how the observations of Figure 1A (two symbols) extend to the general case. For large α, fα has a trough where the two largest probabilities are equal (e.g., p1 = p2 = 2/5, p3 = 1/5), and a sharp minimum where these troughs converge (p1 = p2 = p3 = 1/3). This leads to local maxima in the bias of the naive estimator along these troughs and a global maximum at their convergence. As α decreases, the sharpness of the bias distribution is blunted, attaining uniformity in the Shannon (α = 1) case. As in the two-symbol case, the variance of the naive estimator has a minimum at the point of equal probabilities and at the extremes, and the largest variances occur near the point of equal probabilities when α is large.
The properties of estimates of generalized transmitted information If are consequences of the bias properties of estimates of the underlying index of concentration f. In the typical laboratory situation, the input symbols X can be chosen by the experimenter, so that the frequencies encountered after N trials exactly match those of the true distribution PX. In this case, only the conditional probabilities PX|Y=j in equation 2.4 must be estimated. Naive estimates of If thus decrease monotonically with N, since they inherit the monotonically decreasing behavior of estimates of f (see appendix C). For large α, this bias will be large when the conditional distributions have nearly equal probabilities, while for α = 1, the bias will depend only on the number of symbols in X and Y (Treves & Panzeri, 1995).
We caution that the above analysis hinges on the assumption that the input distribution PX is known. If PX must also be estimated, then estimates of If may approach the true value from below rather than from above. For example, consider estimates of Ifmax in a scenario in which each of the symbols of X occurs with equal probability and each is signaled reliably by a corresponding symbol in Y. That is, the probabilities in the a posteriori distributions PX|Y= j are unequal, but the probabilities in the a priori distribution PX are equal. Consequently, naive estimates of fmax(PX|Y= j) are nearly unbiased, but naive estimates of fmax(PX) have a large upward bias. Therefore, their difference, the naive estimates of the Bayesian index Ifmax, has a downward bias. This bias behavior for Ifmaxcontrasts with the bias behavior naive estimates of IShannon, which is always upward if all of the co-occurrence probabilities of symbols in X and Y are nonzero (Treves & Panzeri, 1995).
2.4 Using Indices of Concentration to Test Coding Hypotheses
Now that we have constructed a variety of indices of transmitted information and shown that they share many of the properties of Shannon information, we describe how they can be used to test hypotheses about neural codes. We consider a generic behavioral task consisting of presentation of input symbols that elicit observable behavioral responses. We assume that we have recorded from all of the neurons that provide the sensory signals relevant to this task and that we have hypothesized a “neural code,” that is, a way to represent these neural signals by instances of some random variable. The question to be asked is, can the neural activity as represented in this fashion account for the behavioral performance? If the answer to the question is no, then (since we have assumed that we have recorded from all the relevant neurons), we have rigorously ruled out a neural code (Nirenberg et al., 2006). This strategy, which seeks to determine whether specific statistical features of neuronal activity are insufficient to support a behavior, stands in contrast to the more standard approach (Bialek, Rieke, de Ruyter van Steveninck, & Warland, 1991; McClurkin, Optican, Richmond, & Gawne, 1991; Victor & Purpura, 1996) of identifying statistical features that might support a behavior.
2.5 Setup
The question of whether a neural code can support a stimulus-behavior linkage is equivalent to the question of whether the stimulus set, the neural representation, and the behavior constitute a Markov chain. In the analysis below, the stimulus is a random variable X assuming one of L discrete values, characterized by a distribution PX. The neural code is represented by a random variable Y, whose relationship to X is characterized by the conditional distributions PX|Y=y. Like the stimulus X, the behavioral response Z is a discrete random variable; its relationship to X is characterized by PX|Z=z. Our question is whether the neural code Y can account for the observed dependence of the behavior Z on the stimulus X. That is, we want to determine whether PX|Y=y and PX|Z=z are consistent with a Markov chain X →Y →Z, and to do so from two sets of joint measurements: stimulus and code (PX|Y=y) and stimulus and behavior (PX|Z=z). According to the DPI, a necessary condition is that X →Y →Z constitute a Markov chain that
| (2.10) |
for every generalized transmitted information If. However, for different choices of the index of concentration f, the above inequality places different conditions on the neural activity Y. Our goal is to analyze this situation, comparing the utility of different choices of If. The main points are evident even in the simplest scenario: two stimuli and two behavioral responses. We thus analyze this scenario first and then describe how the analysis generalizes to scenarios in which there are multiple stimuli or behavioral responses.
2.6 Two Stimuli, Two Responses: The Indices Are Inequivalent
We focus on the two-stimulus, two-response case in which both stimuli are equally probable. This case illustrates the complementary properties of the constraints (see equation 2.10) for different choices of the indices If. In our first example, the Shannon index is generally stronger. In the second example, the Bayes index is generally stronger. But no index is guaranteed to be the stronger in either case. The subsequent examples examine the basis for this complementarity.
2.6.1 Example 1: Shannon Index Is Superior
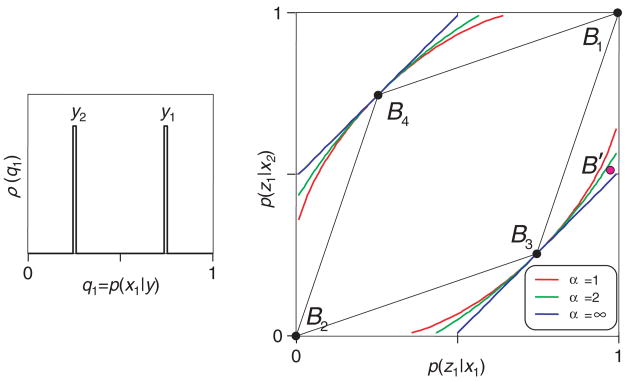
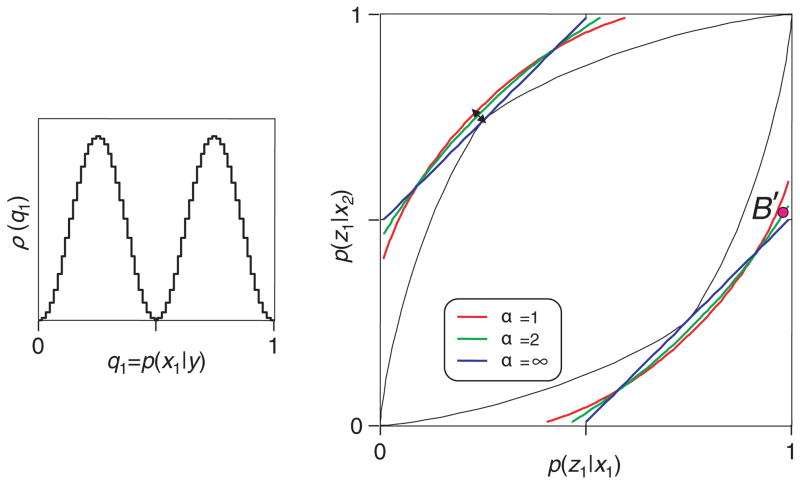
In our first example (see Figure 2) we analyze a scenario in which there are only two words in the neural code Y, each of which signals the two stimuli with moderate reliability. For one of the code words (say, y1) the a posteriori probabilities of the stimuli x1 and x2 are given by 0.75 and 0.25; for the other code word (say, y2), the a posteriori probabilities of the stimuli are given by 0.25 and 0.75.
Figure 2.
Testing a neural code in a scenario in which the Shannon index has the advantage. The neural code has two words: y1, for which the a posteriori probabilities of the stimuli x1 and x2 are given by 0.75 and 0.25, and y2, for which the a posteriori probabilities of the stimuli are given by 0.25 and 0.75 (inset). The diamond-shaped region in the main graph shows the range of behaviors that can be supported by the code and the bounds provided by several different indices of transmitted information. The Shannon bound (α = 1) is tighter than the Bayes bound (α =∞). For further details, see the text.
The inset in Figure 2 illustrates the relationship between the stimulus and the code. Each code word y is associated with an a posteriori probability of the two stimuli, q1 = p(x1 | y) and q2 = p(x2 | y). One can describe the relationship between stimuli and code words by tabulating how often a code word has a particular pair (q1, q2) of a posteriori probabilities. Since q1 + q2 = 1 (i.e., the a posteriori probabilities for all of the stimuli must sum to 1), for this tabulation we need to consider only q1. We call this density ρ(q1), and it is the ordinate of the inset.
The main portion of Figure 2 illustrates the range of possible behaviors that is supported by code diagrammed in the inset. Since there are two stimuli and two behavioral responses, the stimulus-response behavior is completely specified by the probabilities that each of the two stimuli (x1 and x2) will elicit the behavior z1. These probabilities, p(z1 | x1) and p(z1 | x2), are the two axes of the main plot. There are four ways that the subject could use these two neural responses; we refer to them as decision rules:
For any code word y, always respond with z1. That is, p(z1 | x1) = p(z1 | x2) = 1. This results in the behavior plotted at point B1.
For any neural code word y, always respond with z2. That is, p(z1 | x1) = p(z1 | x2) = 0. This results in the behavior plotted at point B2.
When (and only when) y1 is present, respond with z1. That is, p(z1 | x1) = 0.75 and p(z1 | x2) = 0.25. This results in the behavior plotted at point B3.
When (and only when) y2 is present, respond with z1. That is, p(z1 | x1) = 0.25 and p(z1 | x2) = 0.75. This results in the behavior plotted at point B4.
The general calculation of the above probabilities from the density ρ(q1) is detailed in appendix D.
These four behaviors (B1, …, B4) are the corners of a diamond-shaped region. The interior of this diamond represents all of the behaviors that can be supported by the code Y. The reason that the interior points are included is that they correspond to behaviors that can be achieved by mixing the behaviors at the corners, that is, by applying one decision rule on one trial and another decision rule on another trial. Appendix D shows that no other behaviors are possible.
Now that we have delineated all possible behaviors that can be supported by the code Y, we can show how the different indices allow us to test whether this code is viable. For each index If, we can calculate the transmitted information available in the code Y, If (X, Y). The data processing inequality (see equation 2.10) requires that for any behavior derived from this code, If (X, Z) ≤ If (X, Y). Therefore, for each index If, we plot the locus of behaviors for which If (X, Z) = If (X, Y). If we observe a behavior outside this locus, it would allow us to rule out that code. In other words, that particular code Y did not carry enough information to account for that particular behavior Z.
Note that the bounds are different for the different indices Ifα. We show the Shannon bound (α = 1) in red, the Bayes bound (α = ∞) in blue, and the bound determined by an intermediate index (α = 2) in green. Importantly, these bounds are not only distinct but also differ in strength.
Here is an example that illustrates this point that the bounds provided by the different indices are both distinct and differ in strength. Suppose that we made the assumption that only spike count matters, but in reality, behavior makes use of spike timing. That is, our assumed code Y is insufficient, and the observed behavior B′ is outside the diamond of supportable behaviors, as in Figure 2. But although B′ cannot be supported by Y, it is inside the bounds of the Bayes index (α = ∞, blue). Hence, had we analyzed the experiment using the Bayes index, the code Y would appear to be a viable code. Importantly, though, B′ is outside the bounds of the Shannon index (α = 1, red). In other words, in this example, the Shannon index does rule out the code Y, even though the Bayes index does not. Indices that are intermediate between the Shannon and Bayes indices (e.g., α = 2) have intermediate behavior: they succeed in ruling out the code Y for some of the behaviors, but not for all of them.
2.6.2 Example 2: Bayes Index Is Superior
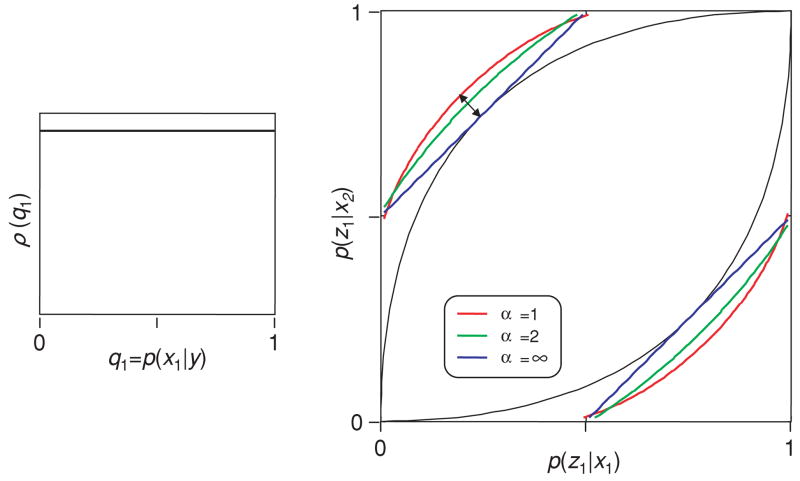
In the first example (see Figure 2), the Shannon index provided a stronger test of the neural code Y than the Bayes index. That is, the region of behaviors within the bounds for α = 1 (red) was smaller than the region of behaviors within the bounds for α = ∞ (blue). Here we set up a situation in which the opposite is true.
In this example, the neural code Y has many code words y (see Figure 3, inset). Specifically, code words with all a posteriori probabilities q1 = P(x1 | y) are represented, and all are equally likely (i.e., the density ρ(q1) is constant). Any a posteriori probability q1 can serve as the cutoff for a decision rule. For example, a typical decision rule chooses behavior z1 if the a posteriori probability of x1 is sufficiently high. This decision rule is characterized by a cutoff criterion qcut, along with the policy of choosing behavior z1 if q1 ≥ qcut. These decision rules correspond to the behaviors that form the curved black trajectory below the diagonal in Figure 3. There are also behaviors that form a curved trajectory above the diagonal. These correspond to decision rules that choose the behavior z1 if the a posteriori probability of x1 is sufficiently low, that is, q1 ≤ qcut. All possible behaviors that can be supported by Y are mixtures of these behaviors and correspond to points that lie within the lens-shaped region bounded by these two curves (proof is in appendix D).
Figure 3.
Testing a neural code in a scenario in which the Bayes index has the advantage. The neural code words cover the entire range of a posteriori probabilities (see inset). The lens-shaped region in the main graph shows the range of behaviors that can be supported by the code, and the bounds provided by several different indices of transmitted information. The Bayes bound (α = ∞) is tighter than the Shannon bound (α = 1). For further details, see the text.
In contrast to the situation of Figure 2, the bounds associated with the Bayes index (blue) are tighter than the bounds associated with the Shannon index (red).
Note that from the insets of Figures 2 and 3, it might appear that the critical difference between these two examples is that the former has a discrete set of code words and the latter has a continuum of code words. However, the critical factor is not the discreteness of the code itself. Rather, the critical difference is that the range of certainties associated with the code words is wider in Figure 3 than Figure 2, combined with the fact that the behavior is discrete. We show two more examples that illustrate this point and then turn to why it is the case.
2.6.3 Further Examples: The Range of Certainty Is Crucial
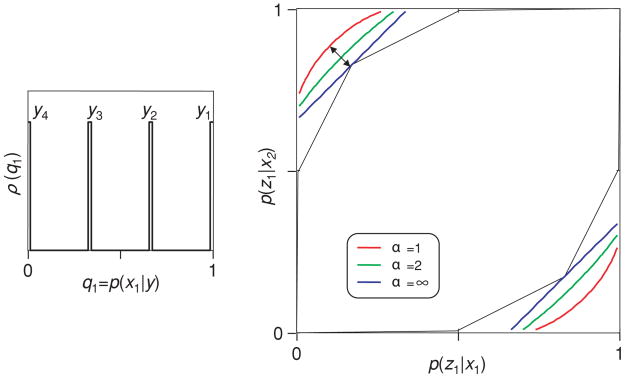
To see that the critical factor is the range of certainty (rather than whether the code has a continuum of words), we consider a code with four code words, covering a range of certainties. Specifically, in the code illustrated in the inset of Figure 4, Y consists of four code words y1, y2, y3, and y4, with a posteriori likelihoods q1 = P(x1 | y) of 1, 2/3, 1/3, and 0. That is, y1 and y2 indicate that stimulus x1 was probably present, while y3 and y4 indicate that stimulus x2 was probably present. However, y1 and y4 are reliable, while y2 and y3 are ambiguous.
Figure 4.
The range of uncertainties affects the choice of indices. The neural code (see inset) has four words y1, y2, y3 and y4, two of which have high certainty (y1 and y4) and two of which have low certainty (y2 and y3). The polygonal region in the main graph shows the range of behaviors that can be supported by the code and the bounds provided by several different indices of transmitted information. The Bayes bound (α = ∞) is tighter than the Shannon bound (α = 1). For further details, see the text.
As in Figure 2, the set of supported behaviors forms a polygonal region. The corners of this region correspond to decision rules in which one set of code words {y1, …, yc } elicits one behavior, and the complementary set {yc+1, …, y4} elicits the alternative behavior. However, unlike Figure 2, the bounds associated with the Bayes index (blue) are tighter than the bounds associated with the Shannon index (red).
In the final example, Figure 5, the code words form a continuum (as in Figure 3), but the certainties are tightly clustered. This happens because the density ρ(q1) is bimodal, with modes at 0.25 and 0.75.
Figure 5.
Complementary strengths of the Bayes and Shannon indices. The neural code words cover the entire range of a posteriori probabilities but are bimodally distributed (see inset). The lens-shaped region in the main graph shows the range of behaviors that can be supported by the code and the bounds provided by several different indices of transmitted information. The Bayes bound (α = ∞) is tighter than the Shannon bound (α = 1) near its the point of tangency to the range of supportable behaviors, but the Shannon bound is tighter than the Bayes bound away from this point. For further details, see the text.
As in the uniformly distributed example in Figure 3, the region of supportable behaviors forms a lens-shaped region. However, in contrast to the uniformly distributed example, the Bayes index does not always provide the strongest test. Rather, there are behaviors (e.g., B′) that will result in excluding the code only if the Shannon index is used.
Comparing the above examples suggests that the difference in performance of the indices depends primarily on the range of certainty of the code words. We now discuss why this is the case by focusing on the geometry of the bounds corresponding to the Bayes and Shannon indices.
There are two interacting factors: the relative positions of the Bayes and Shannon bounds and their shapes. We first consider their positions. The Bayes bound will always make contact with the region of behaviors that the code can support (e.g., at points B3 and B4 in Figure 2 and at the inner arrowhead in Figure 3.) This is because the Bayes bound can always be attained by a decision rule that maximizes the fraction of correct responses (this decision rule chooses the stimulus with the maximum a posteriori probability). In contrast, the Shannon bound need not make contact with the region of supportable behaviors (see Figures 3–5). This is because converting the neural code to a binary behavioral response causes a loss of information about the level of certainty. In other words, the code has a greater Shannon information than the subject can possibly transmit with a binary behavioral decision. The difference between the Shannon information transmitted by the code and the maximum Shannon information that can be transmitted by processing the code into a binary behavior results in a gap between the Shannon bound and the region of supportable behaviors (see the arrows in Figures 3–5). This gives an advantage to the Bayes index, whose bound is always in contact with the region of supportable behaviors.
We next consider the shapes of the bounds. The Bayes bound will always be a straight line, since it is determined by linear functions of the probabilities p(z1 | x1) and p(z1 | x2). In contrast, the Shannon bound will always be curved, since it is determined by a nonlinear function of these probabilities. Consequently, the Shannon bound will curve inward toward the region of supportable behaviors, while the Bayes bound departs from it at a tangent. Because the Shannon bound curves inward toward the region of supportable behaviors, it can be stronger than the Bayes bound away from the point at which the subject chooses a decision rule that maximizes the fraction of correct responses. That is, the Shannon bound is less sensitive to the decision criterion.
In sum, the bottom line can be stated simply: the Shannon index is weakened by fact that information is lost when a code is converted to a behavior, while the Bayes index is weakened if the decision rule is not known. However, the Bayes index can be readily pushed further, since its bound always comes into contact with the region of supportable behaviors. For further discussion, see appendix A.
2.7 Multiple Stimuli, Multiple Responses
The above examples considered scenarios with two stimuli and two behavioral responses. Here we show the implications of the analysis for scenarios in which there are more than two stimuli or more than two behavioral responses. As in the above analysis, the first step is to construct the set of supportable behaviors. When there are L stimuli and N behaviors, this is a space of (L − 1)N dimensions. This is because each of the N behaviors corresponds to an a posteriori distribution of the L stimuli, for which there are L − 1 degrees of freedom (dimensions). Above, L = N = 2, so the supportable behaviors constituted a region in the plane. But here, the space of supportable behaviors has a higher dimension.
As in the simpler L = N = 2 scenario, the set of supportable behaviors must be a convex region within this space. Its boundary will have a more complex shape, parameterized by partitions of the space of a posteriori probabilities (this characterization is demonstrated in appendix D).
The Shannon index provides a bound that is curved inward and thus has the potential to follow the boundary of the complex shape closely. However, it is typically offset from the supportable behaviors because of conversion of the code into one of N possible behaviors.
In contrast, the Bayes index provides a bound that is a hyperplane tangent to the set of supportable behaviors. It is thus optimal at this point of tangency, but it is increasingly suboptimal away from that point.
Thus, as in the two-stimulus, two-response case, the Shannon index is weakened by the loss of information about certainty when the code is reduced to a behavior, while the Bayes index is weakened if the decision rule is not known exactly.
It is therefore straightforward to construct examples in which the Bayes index fails, or the Shannon index fails, or both. For larger values of L (the number of stimuli) and N (the number of behavioral responses), there are separate factors that favor each of the two kinds of indices, so their complementary nature persists. As L increases, a factor that favors the Bayes index is that the dimensionality of the set of a posteriori probabilities associated with each code word is L − 1. Thus, there is an increasing information loss resulting from discretization of this high-dimensional characterization of uncertainty to one of N discrete responses. This loss due to discretization puts the Shannon index at an increasing disadvantage. But other factors favor Shannon-type indices. As N increases, the effect of response discretization decreases because more responses are available. Moreover, as both L and N increase, the variety of decision rules increases (see appendix D). Thus, sensitivity to the decision rule (which weakens the Bayes index) is an increasingly important factor. Related to this, as L or N increases, the possibility of near misses increases—that is, the possibility that a subject responds with an answer that is close to the correct answer but wrong. The Bayes index gives no credit for these close answers, only for correct answers. The Shannon index (as well as the intermediate indices) gives credit for answers that are systematic but wrong. When wrong answers are systematic, Shannon-like indices can provide a stronger test of a coding hypothesis than Bayes-like indices.
2.8 Other Indices of Concentration and Transmitted Information
Above, we have focused on the Shannon index, the Bayes index, and a natural continuum of indices for which they represent the extremes. However, this continuum does not exhaust the realm of useful indices. Moreover, these other indices have specific behavioral interpretations and are particularly useful when the subject’s decision rule is known (see appendix A).
Any index of concentration can be modified by applying a nonnegative set of weights w⃗ = (w1, …, wL) to the probabilities. That is, if f (P) = f (p1, …, pL) is an index of concentration, then so is
| (2.11) |
In the Bayes limit (w⃗fmax), the index of transmitted information corresponding to equation 2.11 measures the improvement in performance of a decoder that associates unequal values with each stimulus.
A second kind of generalization is useful for multi-alternative behavioral paradigms. When there are three or more possible behaviors (N ≥ 3 in the above), a subject’s pattern of errors may indicate a greater level of knowledge about the stimulus than merely the fraction of correct responses (Thomson & Kristan, 2005). This kind of systematic behavior captured by the index of concentration is , the sum of the k largest values of pi:
| (2.12) |
In particular, the index of transmitted information corresponding to equation 2.12 is the improvement in the performance of a Bayesian decoder that is allowed k attempts at a correct answer.
3 Discussion
Information theory has been enormously useful for characterizing spike trains and proposing neural codes (reviewed in Dayan & Abbott, 2001; Rieke et al., 1997). Any feature of neural responses that depends systematically on the stimulus is a carrier of information and, in principle, a candidate neural code. Given that the ultimate goal is to reduce the space of candidate codes, that is, to close in on which codes the animal could actually be using, a logical next step is to consider whether any of these candidates can be eliminated (Nirenberg et al., 2006). Shannon’s information works for this, but it is a loose bound, and it turns out that there are many related quantities that can be tighter bounds—that is, they can rule out more codes than can be eliminated by Shannon information. This is the focus of our article: the existence of these measures, their relationships to each other, and their properties for eliminating codes.
It is worth mentioning that using information to eliminate codes is distinct from using it to identify and characterize candidate codes. As a result, the properties that the indices must have are different. This is why the indices we discuss lack some of the properties of Shannon information associated with characterizing codes (Cover & Thomas, 1991; Rieke et al., 1997). However, these indices all retain one key property: the DPI. Consequently, they provide equally valid tests for the elimination of a code as provided by Shannon information, and in some cases, stronger tests.
3.1 Complementary Strengths and Weaknesses
We have shown that the indices we describe have complementary strengths and weaknesses: Shannon-like indices fail to exclude nonviable codes in scenarios in which the neural code words differ substantially in certainty, because these differences are suppressed (i.e., information is lost) when the code is reduced to a behavior (see Figures 3 and 4). Bayes-like indices yield stronger tests than Shannon-like indices in these scenarios, but the advantage may depend on knowing the decision rule precisely (see Figure 5). In addition, Bayes-like indices cannot take into account systematic error patterns. Systematic error patterns are particularly important in behavioral paradigms with multiple stimuli and multiple behaviors (Thomson & Kristan, 2005), such as the near misses that are likely to occur with reaching and eye movement tasks, or letter identification.
3.2 Indices Differ in Statistical Properties
The focus of this article is on the idealized case—that is, on the performance of an index when there are sufficient data so that its value can be determined exactly. In this limit, using the index to test a code based on the DPI is rigorous, and the properties of the index depend in a simple way on the distribution of certainty of the responses, the number of behaviors, and the range of likely decision rules. In application to laboratory data, this limit may not be reached, and the statistical properties (i.e., the bias and variance of estimates of these indices) must also be taken into account. We do not analyze this in detail here because of the variety of approaches available to estimate information-theoretic quantities (Kennel, Shlens, Abarbanel, & Chichilnisky, 2005; Nemenman, Bialek, & de Ruyter van Steveninck, 2004; Nirenberg, Carcieri, Jacobs, & Latham, 2001; Paninski, 2004; Shlens, Kennel, Abarbanel, & Chichilnisky, 2007) and the many kinds of behavioral scenarios in which they might be applied. However, we do point out (see Figure 1) that these indices differ systematically in their bias and variance properties when naive (i.e., plug-in) estimates are used. Estimates of Bayes-like indices tend to have greater bias and variance for close-to-threshold responses than Shannon-like indices (see Figure 1), but smaller bias and variance away from threshold.
3.3 Eliminating Codes Versus Inferring Interaction Networks
A comparison of the problem studied here to the general problem of identifying interaction networks among several variables (Nemenman, 2004) provides further insight into the reason that non-Shannon quantities are useful for eliminating codes. For the problem of inferring interaction networks among genes, an approach based on Shannon mutual information outperforms Bayesian methods (Margolin et al., 2006). Yet for eliminating codes, Bayes-like indices can outperform Shannon-like indices.
There are two reasons for this difference: the goal of the analysis and the nature of the data. In the analysis of interaction networks, the goal is to identify the simplest, or most likely, relationship graph. Here, we have a different goal: in effect, we ask whether a particular relationship graph can be excluded. The second difference is that our problem lacks some of the symmetry of the interaction network problem: the three variables play distinguishable roles. The stimulus variable X is distinguished in that we know how it is correlated with each of the other two variables, but we do not necessarily know how the other two variables are correlated with each other. Moreover, the code variable Y and the behavior variable Z are distinguished from each other in that we are interested in whether the code can account for behavior, not vice versa. These asymmetries lead to the utility of measures If (X, Y) and If (X, Z) that are not symmetric in their arguments.
Acknowledgments
We thank Ifije Ohiorhenuan and Rebecca Jones for comments on the manuscript. S.N. is supported by EY12978. J.V. is supported by EY9314, by MH68012 (to Dan Gardner), and by EY09314 (to Jonathan Victor).
Appendix A: Taking into Account What the Subject Knows About the Task
In the main section of this article, we approached the problem of ruling out neural codes without making assumptions as to what the subject is thinking (e.g., what priors it is using for the task and what rules it is using for making decisions). The DPI allows us to do this, since it places absolute limits on performance: any code that is ruled out by one of the indices If is truly ruled out, provided, of course, that the estimated value of the index If is accurate. However, it is intuitive that knowledge of the decision rule can allow us to take this approach a step further and allow even more codes to be ruled out. (This makes direct contact with ideal observer analysis; Geisler, 1989). Here, we show how this can be done. As in the main text, we focus on the two-stimulus, two-response scenario that we used in the examples of Figures 2 to 5. A hypothetical code Y has a limited range of behaviors that it can support: the diamond- or lens-shaped region in the main portion of each figure. Our task is to determine whether an observed behavior is inside this region. If it is not, our assumed code can be ruled out. That is, for a code to be viable, the observed behavior must be inside all of the tangents to this region.
We begin by showing that the tangents represent decision rules, and that each tangent also corresponds to a weighted Bayesian index (see equation 2.11). Thus, if the subject’s decision rule is known, we can choose a specific index that is optimal for testing codes. To show this, we start by specifying the decision rule itself. Suppose that the subject makes a decision—to optimize the expected value of a response. So he assigns a value v(xj, zk) to producing a behavior zk in response to a stimulus xj. The expected value is a linear combination of the quantities v(xj, zk), each weighted by the probability p(xj, zk) that the combination of the stimulus xj and the behavior zk occur together. Since p(xj, zk) = p(zk | xj) p(xj) and p(xj) is constant, the expected value is a linear function of the coordinates p(z1 | xj). That is, the points that share the same expected value,
| (A.1) |
fall on a line in the (p(z1 | x1), p(z1 | x2))-plane, and the lines corresponding to different values of E are parallel. The line that maximizes E must be tangent to the region of supportable behaviors, since if it entered the interior of this region, then another line with a higher value of E could be positioned between this line and the boundary.
We next show that each such tangent line corresponds to a DPI test for an index w⃗Imax, where w⃗Imax is the index of transmitted information that corresponds to a weighted Bayes-like index of concentration w⃗ fmax (see equation 2.11). To accomplish this, we first find a set of weights w⃗ for which the index w⃗ Imax is constant on line segments parallel to the desired tangent, and then we show that the criterion line w⃗Imax(X, Z) = w⃗ Imax(X, Y) contacts the region of behaviors that can be supported by the code.
To determine the weights w⃗ for an index that is constant on lines parallel to a given tangent, we use definition 2.4 to write out the index w⃗ Imax corresponding to w⃗ fmax:
| (A.2) |
With the usual rules for conditional probabilities and p(z2 | xj) = 1 − p(z1 | xj), this can be rewritten as
| (A.3) |
Equation A.3 is a piecewise linear function of the coordinates p(z1 | xj). When p(z1 | x1) is sufficiently large and p(z1 | x2) is sufficiently small (or vice versa), it is constant along a line of slope m = w1 p(x1)/w2 p(x2). Thus, to ensure that the locus for which w⃗ Imax(X, Z) = C contains a line segment of the desired slope m, we choose the weights so that w1/w2 = mp(x2)/p(x1). To see that this segment is tangent to the region of supportable behaviors (i.e., that w⃗ Imax(X, Z) = w⃗ Imax(X, Y) can be achieved), we choose a decision rule that selects z1 whenever w1 p(x1 | y) ≥ w2 p(x2 | y), and z2 otherwise. This is the decision rule that an ideal observer would use to maximize the expected value (see equation A.1) with priors p(x1) = p(x2) and v(xj, zk) = δjk wj.
In sum, then, what we have shown are three related facts: (1) the tangents represent decision rules; (2) when we know a decision rule, we know what the ideal observer would do, given that decision rule; and (3) the tangents also correspond to weighted Bayesian indices. Thus, if we known the subject’s decision rule, we can choose the index corresponding to ideal observer’s behavior.
The significance of this is that when we know the decision rule, we do not have to deal with the problem of using many indices and face the potential problems of multiple comparisons—instead we can cut to the chase and choose the index that compares behavior with the ideal observer limit. Note that in the main text, we avoid the multiple-comparison problem by other means—choosing a test that leads to a curved bound; here we are describing how knowledge of the decision rule also provides a way to avoid the problem.
Finally, when there are multiple stimuli and multiple behavioral responses, the correspondence between ideal-observer analysis and tests based on indices becomes more complex. There are two reasons for this. First, there are extreme behaviors (i.e., points on the boundary of the set of supportable behaviors) that do not correspond to optimal decision rules for any set of values. This is shown in appendix D. Second, the set of optimal decision rules is larger. As a consequence, one must look beyond the weighted Bayesian indices to find the equivalent test based on the DPI. For example, a decision rule that maximizes the expected value of a second guess requires an index derived from equation 2.12 to provide the equivalent DPI test.
Appendix B: The Direct Approach: The Problem of Multiple Comparisons
The reader may wonder why we do not take a more direct approach to the problem of ruling out codes. By “direct,” we mean the following: having determined the range of behaviors that can be supported by a code (as in Figures 2–5), why not simply ask whether the observed behavior lies within this convex set?
While at first glance the direct approach might appear the most straightforward, it in fact has a substantial disadvantage: it leads to a problem of multiple comparisons. To be sure that a behavior is inside the convex set, one must test whether it is on the correct side of each tangent to the set (as discussed in appendix A). Each tangent therefore corresponds to a separate statistical test that must be satisfied. That is, determining “directly” whether a behavior can be supported by a code is, implicitly, a multiple-comparison problem. This problem is exacerbated when there are more than two behaviors or more than two stimuli, since the region of supportable behaviors is high-dimensional (see appendix D).
The multiple-comparison problem is particularly difficult because the individual comparisons are highly interdependent but nevertheless distinct. That is, most, but not all, of the codes that are excluded by one test are also excluded by another. In the main text, we circumvent the multiple-comparison problem by choosing a single index. When this strategy is taken, Shannon-like indices, which do not correspond to any decision rule, can be more effective than Bayes-like indices (e.g., Figures 2 and 5), since their bounds curve inward. In appendix A, we describe another way to solve the multiple-comparison problem: if the subject’s decision rule is known, then a single Bayes-like index becomes more effective: in fact, it becomes nearly ideal.
One might also hope to avoid the multiple-comparisons problem by formulating a single “compound” hypothesis to test whether the behavior lies within the convex set supported by a putative code. That is, if we had a priori knowledge of the shape of the convex set, we could formulate a single test statistic that would accurately indicate whether the behavior was inside the convex set. The problem with this approach is that in typical experimental situations, the shape of the convex set is not known in advance. Rather, as illustrated in Figures 2 to 5, its shape is determined by the fraction of code words y with each ratio of a posteriori probabilities p(x1 | y)/p(x2 | y). Thus, a multiple-comparisons problem has been avoided, but it has been replaced by an equivalent problem: the estimation of the number of code words with each a posteriori probability ratio.
Appendix C: Properties of Naive Estimators of Indices of Concentration and Transmitted Information
In this appendix, we (1) show that naive estimators of indices of concentration are upwardly biased, (2) show that the bias decreases monotonically as sample size increases, (3) develop asymptotic expressions for their bias and variance, and (4) discuss how these results extend to estimators of transmitted information. The analysis of the bias of naive estimates of indices of concentration hinges on the convexity property, equation 2.5.
C.1 Upward Bias of Naive Estimates of Indices of Concentration
The naive estimate is formed in the following way. Suppose that N observations x⃗ = (x1,…, xN) are drawn from a discrete distribution P on L symbols Each of the samples of x⃗ is one of the discrete symbols 1,…, L. From the set of observations x⃗, we construct an empirical distribution Px⃗, in which the probabilities match the observed frequencies in x⃗. That is, in Px⃗, the probability assigned to the kth symbol (1 ≤ k ≤ L) is ck (x⃗)/N, where ck (x⃗) is the count of occurrences of the symbol k in x⃗. By definition, the naive estimate of f(P) is f(Px⃗).
The expected value of the naive estimate from data sets of size N is
| (C.1) |
where P(x⃗) denotes the probability of the set of observations x⃗ in the true distribution P:
| (C.2) |
The true distribution P is a mixture of the empirical distributions Px⃗, each weighted by their probabilities P(x⃗):
| (C.3) |
Therefore, with weights λ chosen to be the probabilities P(x⃗), the convexity property, equation 2.5, implies that EN( f) ≥ f(P). That is, that the expected value of the naive estimator is greater than the true value of the index of concentration.
C.2 Expected Values of Estimators Decrease Monotonically with Sample Size
Having shown that naive estimates are upwardly biased, we now prove the stronger statement that as the number of observations N increases, the expected value of the naive estimate descends monotonically to its finalvalue. Specifically, we show that EN( f), equation C.1 is a nonincreasing function of N.
The argument hinges on the observation that an empirical probability distribution Px⃗ derived from N observations x⃗ is a mixture of probability distributions derived from N − 1 observations, that is, probability distributions with one observation missing. We use x⃗ (n) to denote the sequence of observations of x⃗ with the nth observation missing, namely, x⃗ (n) = (x1,…, xn−1, xn+1,…, xN). Then,
| (C.4) |
where Px⃗ is the empirical probability distribution formed from the full data set, and Px⃗ (n) is the empirical probability distribution formed from the data set with the nth observation missing.
Equation C.4 follows from a simple counting argument. The probability assigned to the kth symbol in Px⃗ is Px⃗ (k) = ck (x⃗)/N, where ck (x⃗) is the count of occurrences of the symbol k in x⃗. The probability assigned to the kth symbol in Px⃗ (n) is Px⃗ (n)(k) = ck (x⃗ (n))/(N − 1). After multiplication by N(N − 1), equation C.4 is equivalent to
| (C.5) |
Equation C.5 holds because each occurrence of k in the full data set x⃗ (say, xr = k) corresponds to an occurrence in all of the missing-observation data sets x⃗ (n) except x⃗ (r). So each contribution to ck (x⃗) is counted N − 1 times.
Combining the convexity property equation 2.5 (with λn = 1/N) and equation C.4 yields
| (C.6) |
The right-hand side of equation C.6 is EN(f). We will show that the left-hand side is EN−1(f). To do this, we simplify the left-hand side by (1) interchanging the order of summation, (2) breaking the sum over x⃗ into a component that depends on only the N − 1 retained observations x⃗ (n) and an inner sum that depends on only the value of missing observation k = xn, (3) noting that if the omitted nth value xn is k, then P(x⃗) = pk P(x⃗ (n)), and (4) noting that . That is,
| (C.7) |
The final expression of equation C.7 is a sum over N replicas of the same quantity, since, across all full data sets x⃗, the collection of omitted-sample data sets will be independent of which sequential sample n is omitted. Thus,
| (C.8) |
Finally, combining equations C.6 and C.8 yields
| (C.9) |
Moreover, the above argument shows that inequality C.9 is strict (i.e., that the sequence EN(f) is strictly decreasing) whenever there is at least some pair of distributions Px⃗ and Py⃗ for which the inequality of equation C.6 is strict. This is typical of any nontrivial index of concentration.
For the indices of concentration considered in the main text, it is straightforward to show that the expected value of the naive estimate EN(f) converges to the true value f(P).
C.3 Asymptotic Analysis
We can gain insight into the qualitative behavior of the bias of naive estimates by expanding f(Q) = f(q1,…, qL) as a Taylor series for Q = Px⃗ near P:7
| (C.10) |
Here, qk is the naive estimate of pk derived from the observations x⃗ = (x1,…, xN). That is, qk = ck (x⃗)/N, where ck (x⃗) is the number of occurrences of the symbol k in x⃗. The first-derivative term does not contribute to the bias, since the expected value of qk is pk. Bias arises from the second term, since the covariance of two estimates qk and qm is nonzero. In particular, from just a single trial (N = 1), the covariances of the counts ck (x⃗) are
| (C.11) |
Since successive observations are independent, the covariance matrix of the counts on N trials is C N, and the covariance matrix of the probability estimates qk = ck (x⃗)/N is C N/N2 = C/N. It now follows from equation C.10 that the bias of EN(f) = 〈f (Q)〉 may be estimated by
| (C.12) |
For fmax,
| (C.13) |
so the asymptotic bias, equation C.12, is zero when all of the pk ’s are distinct. In the Shannon limit, (see equation 2.2),
| (C.14) |
This recovers from equation C.12 the well-known result (Carlton, 1969; Miller, 1955; Treves & Panzeri, 1995; Victor, 2000) that the bias is asymptotically independent of the probabilities pk:
| (C.15) |
The customary factor of log 2 is missing from the denominator since the quantities are calculated with natural logs, not bits.
The Taylor expansion, equation C.10, also provides an asymptotic estimate for the variance of the estimate EN(f):
| (C.16) |
Figure 1 shows the behavior of the coefficient of 1/N in the bias (see equation C.12) and variance (see equation C.16) of estimators of indices fα (see equation 2.3).
C.4 Estimators of Generalized Transmitted Information
The analysis in sections C.1 and C.2 extends to the first term in the definition (see equation 2.4) of the transmitted information If, namely, the sum over the conditional probabilities:
| (C.17) |
As above, we relate estimates from a data set containing N observations to estimates from N data sets containing N − 1 observations. To do this, we drop the rth observation from the larger data set and compare the estimates of expression C.17 to the estimates obtained from the resulting smaller data sets. Say that for the rth observation, y⃗r = k. Dropping this observation does not change any of the estimates involving the probabilities conditioned by the other values j ≠ k in Y. That is, estimates of f(PX|Y= j) are unchanged, for j ≠ k. For f(PX|Y=k), the above arguments (applied to the subset within the N observations that have Y = k) imply that the bias of this term is positive and decreases when the rth observation with y⃗r = k is included. Thus, estimators of expression C.17 have a positive bias that decreases monotonically with sample size.
However, If (X, Y) is the difference between expression C.17 and the concentration f(X). If X is known exactly, then so is f(X), and the statistical properties of estimators of If(X, Y) are determined by the properties of estimators of expression C.17 as described in the above paragraph. But if X must be determined from the sample, the statistics of estimators of f(X) also have to be considered. In this case, the bias of naive estimates If(X, Y) are not guaranteed to be monotonic decreasing.
Appendix D: The Range of Behaviors That Can Be Supported by a Neural Code
In this appendix, we determine the range of stimulus-behavior relationships that can be supported by a given neural code. We show that the stimulus-behavior relationships that can be supported by a code form a convex set (as illustrated in Figures 2–5), and we characterize the boundary of this set in terms of the decision rules that generate these behaviors—the “extreme” decision rules. Surprisingly, although many extreme decision rules can be described in terms of optimizing the “value” of a behavior, not all extreme decision rules can be described in this fashion when the number of stimuli and behaviors is sufficiently large.
D.1 Extreme Decision Rules Correspond to Convex Polyhedral Partitions
We consider scenarios in which the stimulus set X has L discrete elements, and the behavioral response set Z has N discrete elements. The neural code Y can be either discrete or continuous. Our goal is to determine the range of stimulus-behavior relationships PZ|X that can be supported by a given X, Y, and PX|Y=y.
A stimulus-behavior relationship is the net result of an encoding process that transforms the stimuli X into the neural code Y and a decision rule that generates behaviors Z from the code words of Y. In general, the decision rule may be probabilistic, that is, it is specified by the conditional probability distributions PZ|Y. The decision rule PZ|Y and the encoding process PY|X together determine the stimulus-behavior relationship PZ|X:
| (D.1) |
Equation D.1 states that the stimulus-behavior relationship PZ|X is a linear transformation of the decision rule PZ|Y.
Note that even though individual decision rules may be highly nonlinear, decision rules can be considered to combine in a linear fashion—by mixture. That is, a mixture of two decision rules is a decision rule in which the subject uses one decision rule on some fraction of the trials and another decision rule on the rest of the trials. In this sense, decision rules form a convex set.
Because decision rules form a convex set, the linearity of equation D.1 implies that the set of supportable stimulus-behavior relationships is also convex. We therefore focus on determining the boundaries of this set. These are the “extreme” stimulus-behavior relationships—those for which there is no (nontrivial) decomposition as a mixture:
| (D.2) |
The linear relationship D.1 maps a mixture of decision rules into a mixture of behaviors. Therefore, extreme stimulus-behavior relationships must have extreme decision rules—decision rules that are not mixtures of other rules.
Extreme decision rules must be deterministic. This is because nondeterministic decision rules are mixtures of deterministic ones. To see this, suppose that some code word y0 can lead to several behaviors z1,…, zm, each with nonzero probability pZ|Y = y0;zn. These nonzero probabilities can be viewed as weights λn = pZ|Y= Y0;zn which express PZ|Y as a convex mixture of rules PZn|Y that are deterministic for y = y0 and match PZ|Y for y ≠ y0. Conversely, a decision rule that is deterministic for code word y cannot be a nontrivial mixture (since the mixing process implies that a single neural symbol y ∈ Y can map to more than one behavior in Z).
To sum up, all supportable behaviors are mixtures of extreme behaviors, and extreme behaviors correspond to extreme decision rules, which are necessarily deterministic. We now show that it suffices to consider only a small subset of deterministic rules.
To determine this subset, we introduce a parameterization of decision rules. A decision rule (the probability of choosing a behavior z, given the code word y) can be thought of as acting on the a posteriori distribution PX|Y=y rather than on the identity y of the code word. A decision rule is therefore characterized by the (possibly stochastic) mapping from each a posteriori distribution q⃗ to the behaviors in Z. We denote this mapping by r(q⃗, z), where q⃗ ranges over all a posteriori distributions PX|Y=y, and z ranges over all behaviors Z. That is, given a code word y with a posteriori distribution q⃗ = PX|Y=y, r(q⃗, z) is the probability that the behavioral outcome is z. When there are L input symbols, an a posteriori distribution PX|Y=y is a list of L probabilities, that is, a vector q⃗ = (q1,…, qL) whose components are nonnegative and sum to 1. A decision rule is completely described by mappings from such vectors to behaviors in Z, namely, r(q⃗, z).
We next rewrite equation D.1, the stimulus-behavior relationship, in terms of r(q⃗, z). To do this, we introduce ρY|X= xj (q⃗) to represent the probability that a trial with stimulus xj will produce any code word in Y for which PX|Y=y =q⃗. Since all of these symbols lead to behaviors as determined by r(q⃗, z), we may rewrite equation D.1 as
| (D.3) |
where J is the space of a posteriori probabilities, q⃗ = (q1,…, qL) When the set of code words Y is discrete, then so is the density ρY|X=xj (q⃗), and the integral, equation D.3, becomes a sum.
Equation D.3 can be put into a form that avoids the stimulus conditioning in the density ρY|X=xj (q⃗). To begin, let ρY(q⃗) be the probability that any trial will produce a code word y for which PX|Y=y = q⃗. (In the text examples, ρY(q⃗) = ρ(q1), the quantity plotted in the insets of Figures 2–5.) We now relate ρY(q⃗) to ρY|X = xj (q⃗). The joint probability of a stimulus xj and a (3 code word y ∈ Y with PX|Y=y = q⃗ is ρY(q⃗) · qj, since this expression is the probability that such a code word y was present (ρY(q⃗)), times the conditional probability of xj given this code word (qj). But this joint probability can also be calculated from the product of the conditional density ρY|X=xj (q⃗) and the a priori probability of xj (pj). Thus,
| (D.4) |
Substitution of equation D.4 into equation D.3 yields
| (D.5) |
The above equations are linear in r(q⃗, z), so linear combinations of r correspond to linear combinations of the stimulus-behavior relationship. We are now set up to characterize the extreme stimulus-behavior relationships in terms of r.
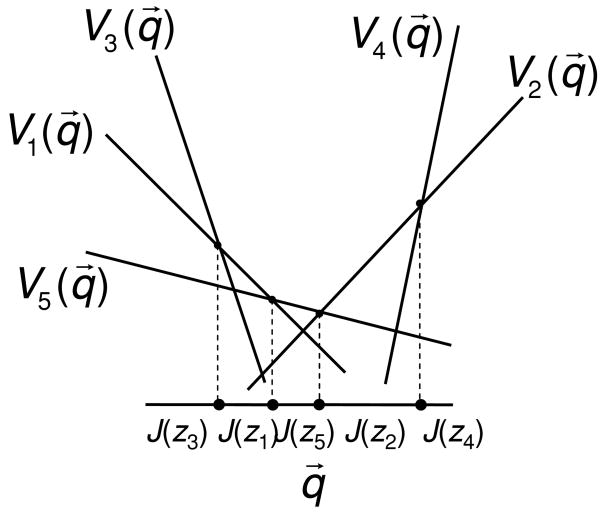
As we have seen above, for extreme stimulus-behavior relationships, the decision rule is deterministic. For a deterministic rule, r(q⃗, z) is concentrated on a single value in Z for each q⃗ ∈ J. We use J(z) to denote the “indicator region” for z, namely, the region of J for which r(q⃗, z) = 1. Equation D.5 can be then be rewritten as
| (D.6) |
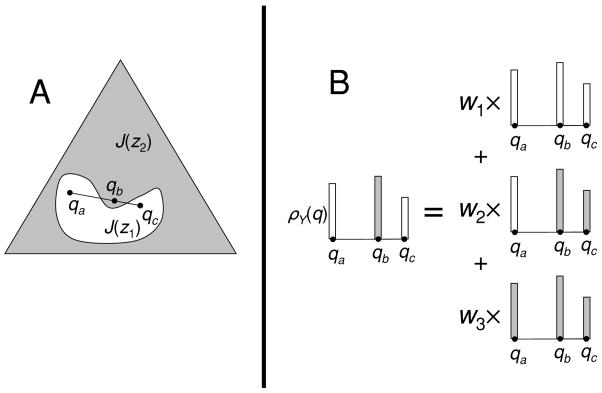
Appendix E shows, based on this representation, that any extreme stimulus-behavior relationship is the result of a rule in which each J(z) is convex. That is, extreme stimulus-behavior relationships correspond to partitions of the space J into convex indicator regions J(z). In the main portions of Figures 2 to 5, the region of behaviors that can be supported by each code is derived from equation D.6, with indicator regions J(z1) and J(z2) that consist of partitions of the interval [0, 1] into disjoint convex sets, namely, [0, q) and [q, 1].
The partitioning of the domain J into convex regions J(zj) has an intuitive interpretation. Imagine that on a single trial, the decision process is uncertain as to whether a trial resulted in neural symbol ya or yc (with a posteriori probabilities q⃗a = PX|Y=ya and q⃗c = PX|Y = yc), but that both neural symbols are in the same indicator region J(zj). Even though the subject is uncertain about the a posteriori probabilities, the subject is nevertheless sure that they lie somewhere on the line between q⃗a and q⃗c. The convexity property states that under these circumstances, the decision rule yields the output symbol zj. That is, if the subject is uncertain as to which of two neural symbols was present but either would have resulted in the same behavior zj, then that behavioral response will always be produced.
Since any two adjacent indicator regions J(zj) and J(zk) within this partition are both convex, their mutual border must be flat (e.g., a straight line segment or a region of a hyperplane). Consequently, for any extreme decision rule, the domain J is partitioned into convex polyhedrons J(zj), one for each output symbol zj. This is a much stronger condition than merely requiring that r is deterministic, since deterministic rules can have arbitrary shapes for the indicator regions J(z).
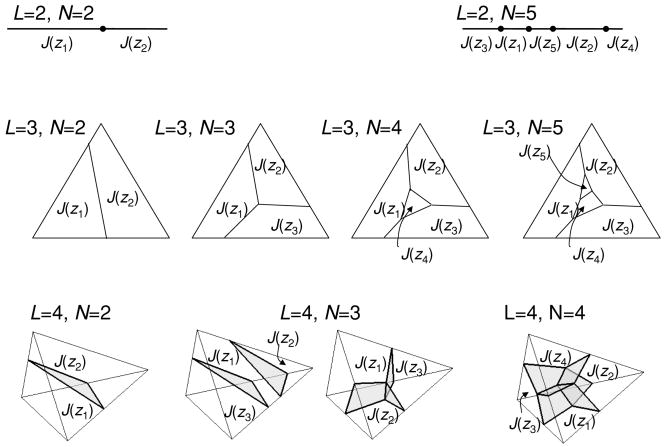
In sum, the boundary of the stimulus-behavior relationships PZ|X that can be supported by a neural code Y is determined by the “extreme” decision rules, which are in turn parameterized by the partitions of the space J of a posteriori probabilities into convex polyhedral indicator regions J(zj). Examples of partitions of J with L stimuli in X and N behaviors in Z are shown in Figure 6.
Figure 6.
Geometric characterization of extreme stimulus-behavior relationships in scenarios with L stimuli and N behavioral responses. The extreme stimulus-behavior relationships are parameterized by the partitions of the L – 1–dimensional space of a posteriori probabilities into N convex subsets.
D.2 Optimal Decision Rules
The above framework readily provides for a characterization of “optimal” decision rules: decision rules that maximize the expected value of a behavior. But as the examples below will show, extreme decision rules need not be “optimal” in this sense. This somewhat surprising result underscores the point that the range of systematic strategies that a subject might choose is very large.
Optimal decision rules are characterized by convex polyhedral indicator regions. We consider an optimal decision rule for a set of values v(xj, zk) associated with producing a behavior zk when the stimulus is xj. Given a neural response y with a posteriori probabilities q⃗, the expected value Vk (q⃗) associated with a behavior zk is
| (D.7) |
Maximizing the expected value of the behavior corresponds to choosing the behavior zk that maximizes Vk (q⃗).
Each Vk (q⃗) is a linear function on the domain J of q⃗. At a typical point q⃗ in J, one of the Vk (q⃗) will be larger than all other Vm(q⃗). For each k, the set of points for which Vk (q⃗) is larger than all other Vm(q⃗) constitutes the interior of J(zk), the indicator region of J on which the response symbol zk is chosen. The boundary between two indicator regions is the points of J at which two (or more) of the Vk (q⃗) are identical. Since Vk (q⃗) = Vm(q⃗) is a linear relationship among the q⃗’s, these boundaries will be flat.
D.3 Examples
We now consider how this analysis applies to scenarios in which there are a specific number of stimuli L in X and a specific number of behaviors N in Z. When there are only two stimuli, or only two behaviors, the optimal decision rules and the extreme decision rules are identical. But in general, there are extreme decision rules that do not correspond to any optimal decision rule.
The set J of all possible a posteriori probabilities q⃗ consists of all L- element vectors q⃗ = (q1,…, qL) with nonnegative components that sum to 1. For example, with L = 2 symbols, J is a line segment. With L = 3 stimuli, J is the set of three-element vectors q⃗ = (q1, q2, q3) in the triangle with vertices at (0, 0, 1), (0, 1, 0), and (1, 0, 0). To characterize the extreme stimulus-behavior relationships, we need to determine the ways that we can partition this space into N convex subsets.
D.3.1 Two Stimuli, Two or More Responses
For two stimuli (L = 2), J is the set of two-element vectors q⃗ = (q1, q2) on the line segment from (0, 1) to (1, 0), Convex subsets of J consist of shorter segments that it contains. Therefore, extreme decision rules with N behavioral responses correspond to partitions of the unit line segment into N smaller segments (see Figure 6, top row). Any such partition corresponds to a choice of N − 1 cutpoints, followed by an assignment of the resulting N segments to the N behavioral responses. Note that the symbols can be assigned in any order (as illustrated in the example for L = 2, N = 5). For any such partition, it is possible to find a corresponding set of stimulus-behavior values v(xj, zk)—a set of values v(xj, zk) for which the corresponding expected values Vk (q⃗) (see equation D.7) intersect at these cutpoints, as illustrated in Figure 7.
Figure 7.
Correspondence between extreme rules and optimal rules for scenarios with L = 2 stimuli. The case of N = 5 behavioral responses is shown. The expected value associated with each behavior z1,…, z5 is a linear function V of the a posteriori probabilities q⃗. Each of these linear functions is maximal over a different interval of the range of a posteriori probabilities.
Note that for all values of N, many choices of the values v(xj, zk) will lead to the same cutpoints, since the cutpoints are determined solely by the values of q⃗ at which the Vk (q⃗) intersect. The slopes of the successive Vk (q⃗) must be monotonically increasing, but they are otherwise free to vary.
D.3.2 Two Responses, Two or More Stimuli
For L stimuli, J is a simplex of dimension L − 1 with vertices at (1, 0,…, 0),…, (0,…, 0, 1). Extreme decision rules with N = 2 behavioral responses correspond to partitions of J into two convex sets—to all the hyperplanes that intersect J (first column of Figure 6). As in the above case of two stimuli, it is possible to find many sets of stimulus-behavior values v(xj, zk) that lead to this partition. To do this, it suffices to choose v(xj, zk)so that the equation of the separating hyperplane between J(z1) and J(z2) is given by
| (D.8) |
D.3.3 More Than Two Stimuli and More Than Two Behavioral Responses
This situation is noteworthy because it is no longer the case that partitions of J into N convex sets necessarily correspond to an optimal decision rule for some set of values v(xj, zk). To demonstrate this, we show that there are more degrees of freedom required to specify the partition than can be supported by the number of degrees of freedom provided by choices of the values v(xj, zk). Let us assume that any partition can be generated by optimizing the expected value Vk (q⃗) derived from some set of values. Consider the partitions for (L = 3, N = 3) and (L = 3, N = 4) in Figure 6. For the (L = 3, N = 3) partition, the boundaries between each pair of indicator regions correspond to the condition that two expected values are equal: V1(q⃗) = V2(q⃗), V1(q⃗) = V3(q⃗), and V2(q⃗) = V3(q⃗). The point at which all three indicator regions meet is determined by V1(q⃗) = V2(q⃗) = V3(q⃗). The configuration shown for (L = 3, N = 4) is derived from the configuration from (L = 3, N = 3) in the following manner. First, the point at which the three indicator regions meet is replaced by a small triangle, J(z4). Second, the line segments that form the boundaries of the first three indicator regions are shifted by arbitrary small amounts, since (because of the presence of J(z4)) they are no longer constrained to meet at a point. Thus, the (L = 3, N = 4) configuration has four more degrees of freedom than the (L = 3, N = 3) configuration: for (L = 3, N = 4), the coordinates of the corners of J(z4) must be specified (6 degrees of freedom), while for the (L = 3, N = 3) configuration, the coordinates of vertex common to J(z1), J(z2), and J(z3) must be specified. This process can be continued indefinitely, adding an indicator region by replacing a vertex with a triangle and allowing the positions of its corners to vary slightly. Each new indicator region thus adds 4 degrees of freedom. However, adding a new behavior allows only three additional values: v(x1, zN), v(x2, zN), and v(x3, zN). Consequently, for a sufficiently large number of behaviors N, at least some configuration cannot be realized as any optimal decision rule. For L = 3, this point is reached at N = 4, since 9 degrees of freedom are required to specify a polygonal partition (2 degrees of freedom for each of the three internal intersections, 1 degree of freedom for each of the points on the edges), while at most L N − L − 1 = 8 degrees of freedom are available from the choices of values.8
The existence of extreme decision rules that are not optimal decision rules also occurs for L > 3 stimuli. Once a sufficient number of indicator regions are present, addition of a new indicator region (a new behavior) replaces a point common to L indicator regions with a small new simplex. The L vertices of the new simplex can be independently specified in the (L − 1)-dimensional domain J, gaining L(L − 1) degrees of freedom. But since the new simplex covered up the common point, the L − 1 degrees of freedom required to specify the coordinates of the common point are lost. Thus, there is a net gain of L(L − 1) − (L − 1) = (L − 1)2 degrees of freedom. Since adding a new behavior allows only L additional values v(xj, zN+1), the number of degrees of freedom required to specify a convex partition will eventually exceed the number of degrees of freedom available to specify an optimum decision rule via a set of values.
Appendix E: Convexity of Indicator Regions for Extreme Decision Rules
Here we prove, as required for appendix D, that any extreme stimulus-behavior relationship can be represented by a decision rule in which each J(z) is convex. We argue by contradiction. Assume we have an extreme stimulus-behavior relationship for which the sets J(z) that characterize the deterministic rule are not convex. We show how this implies that the behavior is a nontrivial mixture. In particular, assume that we have a rule described by a deterministic r(q⃗, z) with a nonconvex indicator region J(z1) (see Figure 8). That is, we assume that there are points q⃗a and q⃗c in J(z1) and an intermediate point q⃗b in a distinct region J(z2). We will construct a mixture of a trio of deterministic rules r[m](q⃗, z) (m = 1, 2, 3) that yields the same behavior as r(q⃗, z) via equation D.5. The strategy is to shift some of the mass in J(z2) at q⃗b to one of the flanking points q⃗a or q⃗c (see Figure 8).
Figure 8.
Diagram illustrating shifting of mass for proof of characterization of extreme decision rules (see appendix E). (A) A decision rule r with a nonconvex indicator region J(z1). (B) At the code words with a posteriori probabilities q⃗a, q⃗b, and q⃗c, r can be represented as a weighted sum of three decision rules r[1], r[2], and r[3]. The heights of the bars indicate the density ρ(q⃗), and the shading indicates assignment to J(z1) (open) or J(z2) (filled).
Since the behaviors corresponding to the rulesr[m](q⃗, z) (via equation D.5) are distinct, we have exhibited the assumed extreme behavior r(q⃗, z) as a mixture—and therefore have derived a contradiction from the assumed existence of an intermediate point q⃗b in a distinct region J(z2).
In order for this shift to leave the stimulus-behavior linkage unchanged, r[m](q⃗, z) and their mixture weights wm (with ) need to satisfy
| (E.1) |
where r(q⃗a, z1) = 1 and r(q⃗c, z1) = 1 (since q⃗a and q⃗c are in J(z1)), and r(q⃗b, z2) = 1 (since q⃗b is in J(z2)), and all other r(q⃗h, z) = 0. This follows from the discrete version of equation D.6.
At all points z other than z1 or z2, equation E.1 is readily satisfied by choosing r[m](q⃗, z) = 0 unless z = z1 or z = z2. For z = z1 or z = z2, equation E.1 represents L pairs of equations, with one pair for each coordinate j in Q:
| (E.2) |
and
| (E.3) |
However, these L pairs of equations are highly degenerate because q⃗b is between q⃗a and q⃗c on a line. That is, we can write qh, j = qa, j + μ(qc, j − qa, j), with μ= 0 for q⃗a, μ = 1 for q⃗c, and some μ = λ for q⃗b, with 0 < λ < 1. With these substitutions and matching the coefficients of μ0 and μ1, the L pairs of equations, E.2 and E.3 (one for each j), reduce to four equations:
| (E.4) |
| (E.5) |
| (E.6) |
| (E.7) |
Without loss of generality, we may assume that
| (E.8) |
since if not, it suffices to reverse the roles of a and c.
To find weights in [0, 1] that solve equations E.4 to E.7, we make the following assignments for the deterministic rules r[m](q⃗, z): r[1] chooses response z1 at all q⃗h, r[2] chooses response z1 at q⃗a but z2 at q⃗b and q⃗c, and r[3] chooses z2 at all q⃗h (see the shading in Figure 8B). That is,
| (E.9) |
with all other values r[m](q⃗h, z) = 0. These choices reduce equations E.4 to E.7 to
| (E.10) |
| (E.11) |
| (E.12) |
| (E.13) |
Straightforward algebra verifies that the choices
| (E.14) |
satisfy equations E.10 through E.13 and that . Since (via equation E.8) all of the wm ≥ 0, it also follows that wm ≤ 1.
Footnotes
The convexity property (made explicit in equation 2.5) states that f never increases when distributions are mixed—that the concentration of a weighted average of distributions is no greater than the weighted average of the concentrations. This justifies the use of the term index of concentration for f.
In the ecology literature, this is the Berger-Parker (1970) diversity index.
Convexity of equation 2.3 is a straightforward consequence of the Minkowski inequality (Abramowitz & Stegun, 1970). Although equation 2.3 might suggest otherwise, we cannot create indices of concentration fg(P) = g−1(Σi g(pi)) from any convex function g. For example, g(p) = − log(p) leads to fg(P) = Πpi, which is not convex. Necessary and sufficient conditions of g for convexity of fg are given in Zhao, Fang, and Li (2005). We thank Liam Paninksi for pointing us to this literature.
The indices fα are monotonically related to the generalized entropies of Rényi (1970) and Tsallis (1988), but there are important distinctions that justify our focus on fα. The negative of the Rényi entropy is not convex (Wehrl, 1978) and is therefore not an index of concentration. The negative of the Tsallis entropy, while convex (as shown in appendix B), is limited because of its bias properties. Specifically, since the negative of the Tsallis entropy is a linear transformation of (fα)α (a concave-up function), its estimators will have greater upward bias than corresponding estimators of fα.
Although the intermediate indices of concentration fα are monotonically related to the generalized entropies of Renyi (via an exponential transformation) and Tsallis (via a power law transformation), the corresponding indices of transmitted information If are not monotonically related to these entropies, because values of fα are combined by addition in equation 2.4.
It is generally stated that the bias properties of the Renyi entropies are more favorable than that of the Shannon entropy. For example, Strong, Koberle, de Ruyter van Steveninck, and Bialek (1998) used the Ma bound (α = 2) because of this property. However, the indices fα are exponential functions of the Renyi entropies, which makes their bias behavior less favorable. Additionally, as Figure 1 shows, the bias behavior depends strongly on the range of probabilities, with relatively greater bias for the Shannon entropy when the probabilities are unequal.
For the Taylor expansion, we consider the arguments q1,…,qL of f to be independent, not constrained to sum to unity. This constraint is expressed by the fact that the covariance matrix, equation C.11, is singular.
The array of values v(xj, zk) has NL parameters, but some sets of values result in the same decision rules. This results in a loss of L + 1 degrees of freedom for the decision rules: the hyperplanes determined by equation D.8 are unchanged if an arbitrary constant cj is added to each v(xj, zk) or if all of the v(xj, zk) are multiplied by a positive constant. Thus, at most NL − L − 1 degrees of freedom are available for the number of optimal decision rules.
Contributor Information
Jonathan D. Victor, jdvicto@med.cornell.edu, Department of Neurology and Neuroscience and Institute for Computational Biomedicine, Weill Cornell Medical College, New York, NY 10065, U.S.A
Sheila Nirenberg, shn2010@med.cornell.edu, Department of Physiology and Biophysics and Institute for Computational Biomedicine, Weill Cornell Medical College, New York, NY 10065, U.S.A.
References
- Abramowitz M, Stegun IA. Handbook of mathematical functions. New York: National Bureau of Standards; 1970. [Google Scholar]
- Berger WH, Parker FL. Diversity of planktonic foraminifera in deep-sea sediments. Science. 1970;168(3937):1345–1347. doi: 10.1126/science.168.3937.1345. [DOI] [PubMed] [Google Scholar]
- Bialek W, Rieke F, de Ruyter van Steveninck RR, Warland D. Reading a neural code. Science. 1991;252(5014):1854–1857. doi: 10.1126/science.2063199. [DOI] [PubMed] [Google Scholar]
- Carlton AG. On the bias of information estimates. Psychol Bull. 1969;71:108–109. [Google Scholar]
- Cover TM, Thomas JA. Elements of information theory. New York: Wiley; 1991. [Google Scholar]
- Dayan P, Abbott LF. Theoretical neuroscience: Computational and mathematical modeling of neural systems. Cambridge, MA: MIT Press; 2001. [Google Scholar]
- Geisler W. Ideal observer theory in psychophysics and physiology. Physica Scripta. 1989;39:153–160. [Google Scholar]
- Kennel MB, Shlens J, Abarbanel HD, Chichilnisky EJ. Estimating entropy rates with Bayesian confidence intervals. Neural Comput. 2005;17(7):1531–1576. doi: 10.1162/0899766053723050. [DOI] [PubMed] [Google Scholar]
- Margolin AA, Nemenman I, Basso K, Wiggins C, Stolovitzky G, Dalla Favera R, et al. ARACNE: An algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics. 2006;7:S7. doi: 10.1186/1471-2105-7-S1-S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClurkin JW, Optican LM, Richmond BJ, Gawne TJ. Concurrent processing and complexity of temporally encoded neuronal messages in visual perception. Science. 1991;253(5020):675–677. doi: 10.1126/science.1908118. [DOI] [PubMed] [Google Scholar]
- Miller GA. Note on the bias on information estimates. Information Theory in Psychology: Problems and Methods, II-B. 1955:95–100. [Google Scholar]
- Nemenman I. Information theory, multivariate dependence, and genetic network inference, (Tech. Rep. NSF-KITP-04-54) Santa Barbara: Kavli Institute for Theoretical Physics, University of California, Santa Barbara; 2004. [Google Scholar]
- Nemenman I, Bialek W, de Ruyter van Steveninck R. Entropy and information in neural spike trains: Progress on the sampling problem. Phys Rev E Stat Nonlin Soft Matter Phys. 2004;69(5 Pt 2):056111. doi: 10.1103/PhysRevE.69.056111. [DOI] [PubMed] [Google Scholar]
- Nirenberg S, Carcieri SM, Jacobs AL, Latham PE. Retinal ganglion cells act largely as independent encoders. Nature. 2001;411(6838):698–701. doi: 10.1038/35079612. [DOI] [PubMed] [Google Scholar]
- Nirenberg S, Jacobs A, Fridman G, Latham P, Douglas R, Alam N, et al. Ruling out and ruling in neural codes. Journal of Vision. 2006;6:889a. doi: 10.1073/pnas.0900573106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paninski L. Estimating entropy on m bins given fewer than m samples. IEEE Trans Inf Theory. 2004;50:2200–2203. [Google Scholar]
- Rényi A. Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability. Vol. 1. Berkeley: University of California Press; 1961. On measures of entropy and information; pp. 547–561. [Google Scholar]
- Rényi A. Probability theory. Amsterdam: Elsevier North-Holland; 1970. [Google Scholar]
- Rieke F, Warland D, de Ruyter van Steveninck RR, Bialek W. Spikes: Exploring the neural code. Cambridge, MA: MIT Press; 1997. [Google Scholar]
- Shlens J, Kennel MB, Abarbanel HD, Chichilnisky EJ. Estimating information rates with confidence intervals in neural spike trains. Neural Comput. 2007;19(7):1683–1719. doi: 10.1162/neco.2007.19.7.1683. [DOI] [PubMed] [Google Scholar]
- Strong SP, Koberle R, de Ruyter van Steveninck RR, Bialek W. Entropy and information in neural spike trains. Phys Rev Lett. 1998;80(1):197–200. [Google Scholar]
- Thomson EE, Kristan WB. Quantifying stimulus discriminability: A comparison of information theory and ideal observer analysis. Neural Comput. 2005;17(4):741–778. doi: 10.1162/0899766053429435. [DOI] [PubMed] [Google Scholar]
- Treves A, Panzeri S. The upward bias in measures of information derived from limited data samples. Neural Comput. 1995;7:399–407. [Google Scholar]
- Tsallis C. Possible generalization of Boltzmann-Gibbs statistics. J Stat Phys. 1988;52:479–487. [Google Scholar]
- Victor JD. Asymptotic bias in information estimates and the exponential (Bell) polynomials. Neural Comput. 2000;12(12):2797–2804. doi: 10.1162/089976600300014728. [DOI] [PubMed] [Google Scholar]
- Victor JD, Purpura KP. Nature and precision of temporal coding in visual cortex: A metric-space analysis. J Neurophysiol. 1996;76(2):1310–1326. doi: 10.1152/jn.1996.76.2.1310. [DOI] [PubMed] [Google Scholar]
- Wehrl A. General properties of entropy. Reviews of Modern Physics. 1978;50(2):221–260. [Google Scholar]
- Zhao Y-B, Fang S-C, Li D. Constructing generalized mean functions using convex functions with regularity conditions. 2005 Available online at http://www.optimization-online.org/DBFILE/2005/06/1164.pdf.