Experimental Evidence for Hydrogen Tunneling when the Isotopic Arrhenius Prefactor (A_H/A_D) is Unity

Abstract

The temperature dependence of the kinetic isotope effect (KIE) is one of the major tools used for the investigation of hydrogen tunneling in condensed phase. Hydrogen transfer reactions displaying isotopic Arrhenius prefactor ratios (A_H/A_D) of unity are generally ascribed to a semi-classical mechanism. Here, we have identified a double mutant of soybean lipoxygenase (SLO-1, an enzyme previously shown to follow quantum mechanical hydrogen tunneling), that displays an A_H/A_D of unity and highly elevated (non-classical) KIEs. This observation highlights the shortcoming of assigning a hydrogen transfer reaction to a semi-classical model based solely on an Arrhenius prefactor ratio.

Elevated values for primary deuterium kinetic isotope effects (k_H/k_D),¹ deviations of the temperature dependence of k_H/k_D from semi-classical predictions¹ and the breakdown of multiple isotope effects from simple reduced mass relationships (Swain-Schaad relationship)^2,3 have been used extensively in the detection of hydrogen tunneling near room temperature. In particular, the temperature dependence of k_H/k_D has emerged as an important diagnostic of H-tunneling, with isotopic Arrhenius prefactor ratios (A_H/A_D) that are distinct from unity providing strong evidence for tunneling. However, the case is ambiguous when the value of A_H/A_D approaches unity (range of 0.8 to 1.4) and is generally interpreted as a reaction involving no tunneling.¹ Herein, we report experimental evidence for an isotopic Arrhenius prefactor ratio of unity in an enzymatic reaction that undergoes extensive tunneling of both protium and deuterium. Such an observation has been predicted within the environmentally coupled tunneling model put forth by Knapp et al.⁴

According to a Bell tunneling model,¹ all three hydrogen isotopes can cross a reaction barrier at some point below the classical transition state. Protium, with the longest de Broglie wavelength, can cross the barrier at a much lower and wider point than deuterium or tritium. A major consequence of this tunneling mechanism is an inflated deuterium kinetic isotope effect (KIE) that exceeds the semi-classical limit of ∼7. At or near room temperature, where the majority of biological catalysts operate, this type of tunneling leads to the trend: E_a(H) < E_a(D) < E_a(T), and the corresponding trend in Arrhenius pre-factors: A_H < A_D < A_T. There are a number of enzymatic reactions where the temperature dependence of experimental KIEs has been found to produce A_H/A_D, A_H/A_T and/or A_D/A_T ≪ 1.⁵

Arrhenius behavior deviations such that E_a(H)−E_a(D) ≈ 0, leading to temperature-independent KIEs with A_H/A_D ≫ 1, have also been observed for enzymes that transfer hydride, hydrogen atom and proton.⁶ These surprising, temperature-independent KIEs in enzyme-catalyzed reactions, together with the observation of Swain-Schaad deviations that cannot be accommodated within a Bell model,⁷ have led to new theories for H-transfer in condensed phase that are much closer to Marcus models for electron transfer.^4,8

The enzyme soybean lipoxygenase-1 (SLO-1) catalyzes the regio- and stereospecific conversion of linoleic acid (9,12-(Z,Z)-octadecanoic acid) (LA) to produce 13(S)-hydroperoxy-9(Z),11(E)-octadecadienoic acid [13-(S)HPOD]. The first part of this process is a proton-coupled electron transfer where the proton is transferred to the oxygen of the Fe³⁺–OH and the electron is transferred to the iron center,⁹ Scheme 1. Published kinetic data for wild-type (WT) SLO-1 indicate an extremely large KIE on k_cat (k_H/k_D = 81), a small Arrhenius prefactor and activation energy, together with experimental KIEs that are largely temperature-independent.¹⁰ The crystal structure of SLO-1¹¹ indicates a substrate binding site lined by hydrophobic side chains, with the residues Leu⁵⁴⁶ and Leu⁷⁵⁴ in the vicinity of the active site cofactor Fe³⁺–OH. A previous study demonstrated that single mutations, Leu⁵⁴⁶Ala and Leu⁷⁵⁴Ala, lead to a moderately temperature-dependent KIE and an elevated E_a in comparison to WT, whereas the more distal mutation, Ile⁵⁵³Ala, exhibits an enhanced temperature-dependent KIE with an inverse Arrhenius prefactor ratio.⁴ A regular increase in the temperature dependence of the KIE following a progressive decrease in the bulkiness of the side chain at residue 553 was subsequently reported.¹²

Scheme 1.

Mechanism of H• abstraction catalyzed by SLO-1.

The observation that the weakly temperature-dependent KIE of WT SLO-1 becomes more temperature-dependent upon the introduction of mutations at or near the active site has been explained within a Marcus-like, full tunneling model that allows for distance sampling (gating) between the H-donor and acceptor.^4,8

$$k_{\text{tun}}=(\text{const}.)\text{exp}\left\{\stackrel{-{(\Delta G°+\lambda )}^2}{}/\underset{(4\lambda RT)}{}\right\}{\int }_{r_1}^{r_0}\text{exp}\left\{\stackrel{-m_H{\omega }_H{r}_H^2}{}/\underset{2\hslash }{}\right\}\text{exp}\left\{-E_X/k_{b}T\right\}dX$$ (1)

As represented in eq (1), the efficiency of hydrogen transfer is dependent upon three major factors: (1) A Marcus term that contains λ, the sum of outer and inner sphere reorganization to the reaction barrier, and ΔG°, the reaction driving force; this term is temperature dependent but only weakly isotope independent; (2) the Franck-Condon overlap, that defines the probability of wave function overlap between the H–donor and acceptor as a function of the mass (m), frequency (ω), and distance traveled (r) by the transferred hydrogen, and is strongly mass dependent; and (3) a donor/acceptor distance sampling (gating) term that reflects the barrier encountered, E_x, in reducing the distance between the H–donor and acceptor. The third exponential term connects both temperature and mass dependencies within a single function. Under this model, a close approach between the H–donor and acceptor distance, that ensures efficient wave function overlap for both protium and deuterium transfer, leads to similar enthalpies of activation for H• and D• transfer. However, when the donor/acceptor distance deviates from its optimal position, gating will impact the rate of D• transfer to a greater extent due to its smaller wavelength and subsequent poorer wave function overlap. This situation is especially apparent in the Ile⁵⁵³Gly mutant of SLO-1 where A_H/A_D = 0.027 and the observed KIE is increased 2-fold from that of the WT at 30 °C.¹²

In the case of WT SLO-1, the magnitude and nearly temperature-dependent KIEs implicate an optimized active site with a fixed and weakly-modulated donor/acceptor distance that results from a relatively high gating frequency.^4,12 Introduction of active site packing defects, via deletion of large hydrophobic side chains, alters the initial H–donor/acceptor distance as well as the oscillator frequency for distance modulation, causing enhanced temperature dependencies for the KIE.^12,13 Under this premise, two active site residues, Leu⁵⁴⁶ and Ile⁵⁵³, have now been simultaneously mutated to Ala, and the corresponding hydrogen transfer parameters investigated.

Table 1 contains a summary of the kinetic data for the double mutant Leu⁵⁴⁶Ala/Ile⁵⁵³Ala, in relation to the respective single mutants Leu⁵⁴⁶Ala and Ile⁵⁵³Ala, as well as WT SLO-1. The overall rate of catalysis (k_cat) of the double mutant Leu⁵⁴⁶Ala/Ile⁵⁵³Ala is decreased one hundred fifty-fold from that of WT and the single mutant Ile⁵⁵³Ala, and two-fold from the single mutant Leu⁵⁴⁶Ala. The rate of catalysis for the double mutant Leu⁵⁴⁶Ala/Ile⁵⁵³Ala between 15 and 50 °C is shown in Figure 1. The temperature dependencies of k_cat for both H• and D• abstraction were fitted to the empirical Arrhenius equation to yield E_a and the Arrhenius prefactor, A. This double mutant exhibits a more temperature-dependent isotope effect than WT or the single mutant Leu⁵⁴⁶Ala but less than the single mutant Ile⁵⁵³Ala. A particularly significant observation with this double mutant is that the magnitude of A_H/A_D is reduced to unity (1.05), an observation normally attributed to semi-classical hydrogen transfer. At the same time the experimental KIEs remain exceedingly large at all temperatures, at values much larger than permitted within a semi-classical H–transfer model. These observations show the difficulty of accommodating the experimental observations for the double mutant Leu⁵⁴⁶Ala/Ile⁵⁵³Ala using either semi-classical transition state theory or a Bell tunneling model.

Table 1.

Kinetic parameters for SLO-1 and mutants in 0.1 M borate buffer (pH 9.0)^a

Enzyme form	kcatb (s-1)	KIEc	Ea(H) (kcal/mol)	ΔEad (kcal/mol)	AH (s-1)	AH/AD	kcat/KM (μM-1s-1)
WT-SLOe	297 (12)	81 (5)	2.1 (0.2)	0.9 (0.2)	9 × 103 (2× 103)	18 (5)	11 (1)
546Ae	4.8 (0.6)	93 (9)	4.1 (0.4)	1.9 (0.6)	4 × 104 (3× 104)	4 (4)	0.33 (0.1)
553Af	280 (10)	93 (4)	1.9 (0.2)	4.0 (0.3)	7 × 103 (2× 103)	0.12 (0.06)	12 (1)
546A/553Ag	2.21 (0.09)	128 (3)	3.8 (0.4)	2.8 (0.4)	1.1 × 103 (5 × 102)	1.05 (0.45)	0.11 (0.02)

^aData were collected from 15 to 50 °C.

^bThe rate constants are reported for 30 °C.

^cKIE = ^Dk_cat = k_cat(H)/k_cat(D).

^dThis is the isotope effect on E_a, ΔE_a = E_a(D) − ΔE_a(H).

^eRef (10a).

^fRef (4a).

^gThis work.

Figure 1.

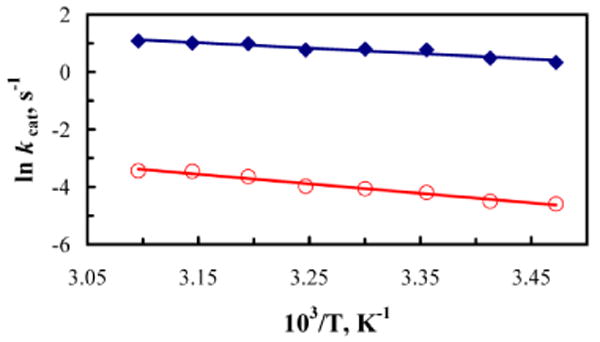
Arrhenius plot of kinetic data for Leu⁵⁴⁶Ala/Ile⁵⁵³Ala SLO-1 double mutant. Data points for protio-linoleic acid [blue filled diamond (◆)] and dideutero linoleic acid [red open circle (○)]. Linear fits to the Arrhenius equation are shown as solid lines; error bars are obscured by the symbol.

By contrast, the environmentally coupled tunneling model, equation (1) requires, at some point, that A_H/A_D = 1, as a transition between a rigid optimized active site (E_a(D) − E_a(H) ≈ 0, A_H/A_D ≫ 1) and a site that has been compromised to the extent that extensive distance sampling becomes necessary to achieve a close enough distance between the H–donor and acceptor for efficient tunneling to occur (E_a(D) > E_a(H), A_H/A_D ≪ 1). To our knowledge, the data presented herein provide the first unambiguous evidence for the involvement of full quantum mechanical hydrogen tunneling for both protium and deuterium, where the isotopic Arrhenius prefactor ratio is unity. These results have important consequences for many reactions where the observation of A_H/A_D ≈ 1 has been automatically attributed to reaction via a semi-classical transition state. As an alternative, we posit that, within a given enzyme reaction, the trends of A_H/A_D provide a measure of the degree to which the H–donor/acceptor can achieve an optimal configuration for protium and deuterium wave function overlap. A range of A_H/A_D value may be expected that will fall between ≫ 1 and ≪ 1 depending on the impact of the environment on the tunneling efficiency. The behavior reported herein is expected to apply equally well to reactions characterized by relatively small isotope effects, as seen, for example in numerous enzyme-catalyzed hydride transfer reactions.^{14, 6(d), 15-17}

Supplementary Material

1_si_001. Supporting Information Available.

Experimental procedures: preparation of mutant enzyme, protein isolation and details of enzymatic assay. This information is available free of charge via the Internet at http://pubs.acs.org.