Abstract
Estimation of the energy from a given Boltzmann sample is straightforward since one just has to average the contribution of the individual configurations. On the other hand, calculation of the absolute entropy, S (hence the absolute free energy F) is difficult because it depends on the entire (unknown) ensemble. We have developed a new method called, “the hypothetical scanning molecular dynamics” (HSMD) for calculating the absolute S from a given sample (generated by any simulation technique). In other words, S (like the energy) is “written” on the sample configurations, where HSMD provides a prescription of how to “read” it. In practice, each sample conformation, i is reconstructed with transition probabilities and their product leads to the probability of i, hence to the entropy. HSMD is an exact method where all interactions are considered and the only approximation is due to insufficient sampling. In previous studies HSMD (and HS Monte Carlo – HSMC) has been extended systematically to systems of increasing complexity, where the most recent is the 7-residue mobile loop, 304–310 (Gly-His-Gly-Ala-Gly-Gly-Ser) of the enzyme porcine pancreatic α-amylase modeled by the AMBER force field and AMBER with the implicit solvation GB/SA (paper I). In the present paper we make a step further and extend HSMD to the same loop capped with TIP3P explicit water at 300 K. As in paper I, we are mainly interested in entropy and free energy differences between the free and bound microstates of the loop, which are obtained from two separate MD samples of these microstates. The contribution of the loop to S and F is calculated by HSMD and that of water by a particular thermodynamic integration procedure. As expected, the free microstate is more stable than the bound microstate by a total free energy difference, Ffree − Fbound = −4.8 ± 1, as compared to −25.5 kcal/mol obtained with GB/SA. We find that relatively large systematic errors in the loop entropies, Sfree(loop) and Sbound(loop) are cancelled in their difference which is thus obtained efficiently and with high accuracy, i.e. with a statistical error of 0.1 kcal/mol. This cancellation, which has been observed in previous HSMD studies, is in accord with theoretical arguments given in paper I.
I. Introduction
I.1. The difficulty in calculating the absolute entropy
The commonly used simulation methods, Metropolis Monte Carlo (MC)1 and molecular dynamics2,3 (MD) enable one a direct calculation of quantities such as the energy Ei that are “written” on a simulated configurations i. However, these methods (due to their dynamic character) do not provide the absolute entropy S (hence the absolute Helmholtz free energy F, F=E−TS, where T is the absolute temperature) in a straightforward manner. More specifically, , where kB is the Boltzmann constant and is the Boltzmann probability of configuration i
| (1) |
However, depends not only on i but also on the whole ensemble through the partition function Z, (Z=Σexp[−Ei/kBT]), which cannot be obtained directly from a finite sample. Therefore, in spite of the progress achieved during the years, calculation of S from a single MC or MD sample still remains a difficult problem.
In recent years we have developed a new method for calculating the absolute S and F from a single sample called the hypothetical scanning Monte Carlo (HSMC) (or HSMD, where MD is used). HSMC(D) is based on ideas of previous methods suggested by Meirovitch, the local states (LS)4–6 and the hypothetical scanning (HS).7–9 HSMC(D) has been developed systematically as applied to liquid argon, TIP3P water,10,11 self-avoiding walks on a square lattice,12 and peptides,13–15 where for the first three models HSMC(D) results have been found to agree within error bars to thermodynamic integration results obtained by extensive MC or MD simulations. Also, for polyglycine molecules differences ΔFmn and ΔSmn for α-helix, extended, and hairpin microstates were calculated very reliably by HSMC118–120 (IV.C–E).
Very recently HSMD has been applied successfully to a mobile loop of the protein α-amylase, 16 where the system was modeled by the AMBER96 force field17 alone and the AMBER96 force field with the GB/SA implicit solvent of Still and coworkers;18 this paper (Ref. 16) is referred here as paper I. In the present paper we make a step further in the development of HSMD, where GB/SA is replaced by explicit water, i.e., the same loop is capped with TIP3P19 water molecules.
I.2. Microstates of biological macromolecules
Before discussing the loop and HSMC(D) further, one should emphasize the importance of the free energy in structural biology as a criterion of stability. Bio-macromolecules such as proteins have rugged potential energy surface, E(x) (x is the 3N-dimensional vector of the Cartesian coordinates of the molecule’s N atoms), which is “decorated” by a tremendous number of localized wells and “wider” wells, defined over regions, Ωm, which we call microstates; thus, each microstate consists of many localized wells (an example for a microstate is the α-helical region of a peptide). A microstate Ωm, which typically constitutes only a tiny part of the entire conformational space Ω, can be represented by a sample (trajectory) generated by a local MD simulation starting from a structure that belongs to Ωm. MD studies have shown that a molecule will visit a localized well only for a very short time [several femtoseconds (fs)] while staying for a much longer time within a microstate,20,21 meaning that the microstates are of a greater physical significance than the localized wells (see also I.4 below).
A central aim of computational structural biology is to identify the most stable microstates, i.e., those with the largest conformational partition function Zm (or equivalently with lowest Helmholtz free energy, Fm)
| (2) |
where the integration is carried out over the limited microstate Ωm, rather than over Ω (for simplicity we shall denote in most cases a microstate Ωm by m). Thus, the protein folding problem is the notoriously difficult task of identifying the microstate with the global minimum Fm, which practically might be achieved by two challenging stages: (1) identifying an initial set of microstates with expected high stability (e.g., based on an energetic criterion), and (2) calculating their relative populations, pm/pn [pm = exp[−Fm/kBT]/Z, which leads to minimum Fm,
| (3) |
where ΔFmn= Fm−Fn.
Calculation of relative populations is also required in problems which are less challenging than protein folding, i.e., in cases of intermediate flexibility, where a flexible protein segment (e.g., a side chain or a surface loop), a cyclic peptide, or a ligand bound to an enzyme populates significantly several microstates in thermodynamic equilibrium. It is of interest to know whether the conformational change adopted by a loop (a side chain, ligand, etc.) upon binding has been induced by the other protein (induced fit 22,23) or alternatively the free loop already interconverts among different microstates where one of them is selected upon binding (selected fit24). This analysis requires calculating pm values, which are also needed for a correct analysis of NMR and x-ray data of flexible macromolecules.25–28 Calculation of F is essential in many other biological processes. Thus, F determines the binding affinities of protein-protein interactions, it is an important factor in enzymatic reactions, electron transfer, and ion transport through membranes, and it leads to the solubilities of small molecules.
I.3. Advantages of the absolute F and S
The examples discussed above require calculating only the difference in free energy ΔFmn (rather than the absolute F) which can be obtained, in principle, by applying thermodynamic integration (TI) techniques or a counting method which leads to ΔFmn= − kBTln[(#m)/(#n)], where #m (#n) are the populations of m and n obtained from a long MD trajectory.29–35 In paper I16 we discuss these methods, emphasizing their limitations where m and n are separated by high energy barriers, which demonstrates the need for methods for calculating the absolute Fm from a given sample; with such methods, one will be able to carry out (only) two separate local MD simulations of microstates m and n, calculating directly the absolute Fm and Fn hence their difference ΔFmn = Fm − Fn, where the complex TI process or the long runs needed for the counting method are avoided.
The absolute S and F can be calculated by the harmonic36–38 and quasi-harmonic39 approximations and can also be obtained by TI provided that a reference state R with known FR is available and an efficient integration path R→m can be defined. However, for non-homogeneous systems such integration might not be trivial, and in models of peptides and proteins defining adequate reference states is a difficult problem (for further discussions on these and other methods, see paper I16 and Ref.35).
With the LS, HS and HSMC(D) techniques mentioned earlier, each conformation i of a sample (generated by MC MD or any other technique) is reconstructed step-by-step (from nothing) using transition probabilities (TPs). The product of these TPs leads to an approximation for the correct Boltzmann probability (eq 1) from which various free energy functionals can be defined. The TPs of HSMC(D) are stochastic in nature calculated by MC or MD simulations, where all interactions are taken into account. From this respect HSMC(D) (unlike HS and LS) can be viewed as exact;10 the only approximation involved is due to insufficient MC(MD) sampling. HSMC(D) has unique features: it provides rigorous lower and upper bounds for F, which enable one to determine the accuracy from HSMC(D) results alone without the need to know the correct answer. Furthermore, F can be obtained from a very small sample and in principle even from any single conformation (e.g., see results for argon in Ref. 10).
I.4. Problems to define microstates by computer simulation
Thus far we have dealt with microstates (and their populations) without providing a practical definition for them This, however, is not a straightforward task which has been ignored to a large extent in the literature but has been given considerable thoughts by us in the course of the years.5,6,26,40–43 (see also paper I16). To illustrate the problem assume a peptide model based on constant bond lengths and bond angles in a helical microstate Ωh, i.e., the dihedral angles φi and ψi are expected to vary within relatively small ranges Δφi and Δψi around φi = −60° and ψi = −50° (we ignore for a moment the side chains). However, the correct limits of Ωh in terms of [φi, ψi] are unknown because the strongly correlated angles define a complicated narrow “pipe” within the region, Δφ1×Δψ1×Δφ2×Δψ2·····ΔφN ×ΔψN. Obviously, these correlations are taken into account by an exact simulation method and thus, in practice, Ωh can be defined (or more correctly, represented) by a local MC (MD) sample of conformations initiated from an α-helical structure.
However, this definition should be used with caution. Thus, a short simulation will span only a small part of Ωh and this part will grow constantly as the simulation continues; correspondingly, the calculated average potential energy, Eh and the entropy Sh (obtained by any method) will both increase and the free energy, Fh is expected to change as well. As the simulation time is increased further, side chain dihedrals will “jump” to different rotamers, which according to our definition should also be included within Ωh; for a long enough simulation the peptide is expected to ”leave” the α-helical region moving to a different microstate. Thus, in practice, the microstate size and the corresponding thermodynamic quantities depend on the simulation time t. Therefore, in practice there is always some arbitrariness in the definition of a microstate, which affects the calculated averages. This arbitrariness is severe with some methods and can be controlled (minimized) by others.
Because the size of m (n) depends on t, calculation of differences Sm − Sn (Fm − Fn) from their absolute values [with QH, LS, or HSMC(D)] will depend on t as well where (as mentioned above) typically m and its energy and entropy all grow with t. To be able to carry out reliable estimation of ΔSmn (ΔFmn, etc.) we simulate both m and n for the same t looking for a range of t values where ΔFmn(t), ΔSmn(t) and ΔEmn(t) are stable within the statistical errors [due to simultaneous increase of Em(t), En(t), etc.]. With HSMC(D) one can calculate a series of improving approximations denoted SA(tr) by increasing the reconstruction time tr which leads to improving differences [and ]; if these differences converge within the statistical errors, the converged values are considered to be the correct differences due to cancellation of equal systematic errors in and (a similar procedure is applicable with LS) (see a detailed discussion in II.10 of paper I16).
Obviously, if m is less stable than n the t values should be adjusted (i.e., decreased) to fit the stability of m. If m is significantly larger than n, tm should be large enough to allow an adequate coverage of m However, if ΔSmn(t) increases monotonically it constitutes a lower bound. If the microstate is restrictive, e.g., side chains should populate a single rotamer, the MD sample can be composed of several smaller samples each starts from the same structure with a different set of velocities. One should always verify that the samples remain in the original microstates and have not “escaped” to neighbor ones. We have developed methods for analyzing the stability of a microstate by calculating distribution profiles of dihedral angles.26,41,43
I.5. A mobile loop in porcine pancreatic α-amylase
As in paper I16, we apply HSMD to two structures (microstates) of the flexible surface loop 304–310 (Gly-His-Gly-Ala-Gly-Gly-Ser) of the enzyme porcine pancreatic α-amylase (PPA). PPA is a single polypeptide chain of 496 amino acid residues44–47 consisting of three structural domains, domain A (residues 1–99, 170–404), domain B (residues 100–169) and domain C (residues 405–496). Domain A adopts a (β/α)8 barrel structure and contains the three catalytic residues Asp197, Glu233 and Asp300. A deep cleft in this domain is accepted to be the substrate-binding site.44–50 An essential chloride ion and a calcium ion are located closer to this V-shaped depression and have been suggested to enhance the catalytic activity.50–53 (for more details about PPA see Paper I).
In the crystal structures of the free protein (PPA I44 and II47 which differ by two residues) the above loop has larger B-factors than the average B-factors of the atoms in the protein. However, in the crystal structures of PPA I complexed with acarbose45 and PPA II complexed with V-153247 the B-factors of this loop are close to the average value in the protein where the loop has moved toward the active site. The maximum main-chain movement is ~5 Å at His305, which approaches the inhibitor from the solvent side to make a hydrogen bond with a glucose residue. The outcome of this movement is an apparent closure of the surface edge of the cleft.45 Subsequently, several hypotheses have been put forward with respect to the function of the mobile loop in α-amylases, such as providing assistance in holding the glucose residues in a favorable orientation during catalysis,45 or assisting in the transition state,54 or inducing a trap-release mechanism of substrate and products.55
In paper I we carried out two MD simulations, starting from the x-ray structures of the free and complexed PPA II, 1pif and 1pig, respectively,47 which spanned the corresponding microstates and the entropy and free energy was calculated by HSMD. In this initial study the loop was modeled by the AMBER96 force field17 alone (where solvation effects are not considered) and by the AMBER96 and the highly approximate GB/SA implicit solvent.18. In the present work we make an additional step in the development of HSMD by extending it to the above loop capped by TIP3P water molecules.19
II. Theory and methodology
II.1. The loop and the protein’s template
As was pointed out above we study the 7-residue loop, 304–310 of PPA in two microstates related to the free and bound loop structures; the starting point is the available crystal structures of PPA II, 1pif and 1pig,47 respectively. Because the structures of these proteins are almost identical, we have chosen (as in paper I) to carry out the calculations with the 1pif structure, where the loop structure of 1pig is attached to the 1pif structure by superimposing the structure of 1pig on that of 1pif (the ligand was discarded). This might indicate whether the transition of the loop to the bound microstate constitutes a selected fit, i.e., whether this microstate is reachable in the free protein. PPA is a relatively large protein and it would be computationally unfeasible to include all of its atoms in the calculations. Therefore, exactly as in paper I, we consider only a template of 700 atoms (the same atoms for the bound and free structures) that are close to the loop where the rest of the protein’s atoms are ignored. Using the same template as in paper I will allow comparing the present results to those obtained in paper I with implicit solvent. The construction of the template is described in some detail below.
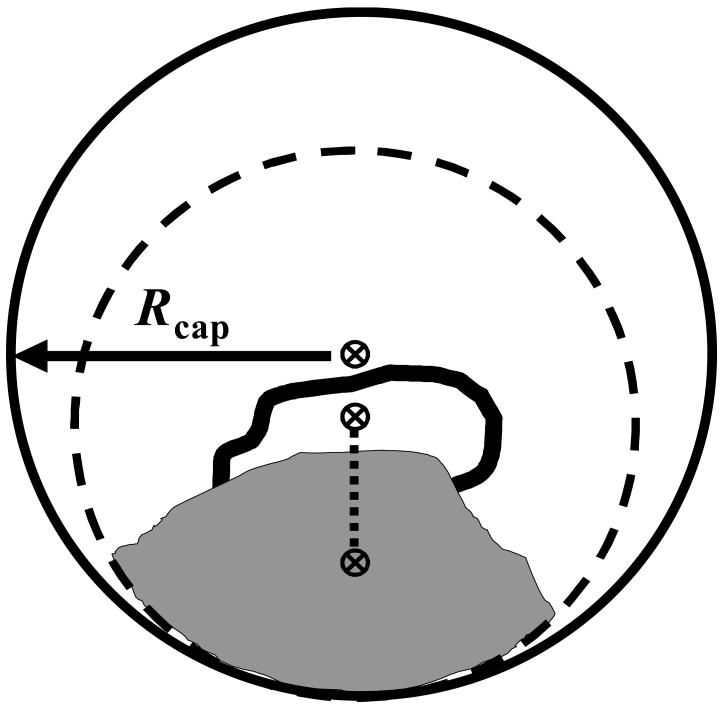
Thus (see Figure 1 and Ref. 56), the center of mass of the loop backbone atoms (in the x-ray structure of 1ipf) is calculated as a reference point denoted xcmb. A distance (Rtemp) is chosen such that if the distance of any atom of a residue from xcmb is less than Rtemp, the entire residue is included in the template. Otherwise, the residue is eliminated. As in paper I, Rtemp =12 Å (which leads to a template of 700 atoms). Then, the loop and template atoms are relaxed to a nearby geometry. This minimization is carried out using harmonic positional restraints with force constant of 5 kcal mol−1Å−2, which are applied to all heavy atoms. This eliminates bad atomic overlaps and strains in the original structure, while keeping the atoms still reasonably close to the PDB coordinates. All these procedures are exactly the same as in paper I.
Figure 1.
A two dimensional diagram of the spherical water restraining region. The loop is represented as the heavy black curve, and the protein template is the region shown in gray. The dashed circle (radius = Rtemp), defines the edge of the template Three positions are marked with the symbol, ⊗, in the figure. These are, starting from the bottom, xcm, xcmb, and xsph. xcm is the center of mass of the loop and template atoms, while xcmb is the center of mass of the loop backbone. xcm and xcmb are connected by a dotted line which defines the vector direction (pointing from xcm to xcmb) that is used to determine the position of xsph. (That is, xsph is shifted away from the template by rshift, see eq 4.) Water molecules are contained within a spherical region defined by the distance, Rcap, measured from xsph. This containment region is represented by the large outer circle. Note that generally, Rcap > Rtemp, and therefore the edge of this circle (sphere in 3D) is shifted to keep the water molecules on the “loop side” of the model system.
The treatment of water has been discussed in Ref. 56, where the effect of minimalist explicit solvation models for surface loops in proteins has been studied, following the original work of Steinbach and B. Brooks.57 In Ref. 56 we performed MD simulations of surface loops capped by TIP3P water,19 in the presence of fixed templates, where the prime focus of the study was to check the performance of the small numbers (e.g., ~100) of water molecules employed. The number of water molecules, N was systematically varied, and convergence with large N was monitored to reveal the minimum number required for the loop to exhibit realistic (fully hydrated) behavior. It was found that the loop backbone can stabilize with a surprisingly small number of water molecules (as low as 5 molecules per amino acid residue). The side chains require somewhat larger N, roughly 12 water molecules per residue. The importance of this result lies in the fact that at this hydration level, computational times are comparable to those required for GB/SA,18 while the “minimalist explicit models” are expected to provide a viable and potentially more accurate alternative. In the present paper we have chosen to apply initially N=70 due to the fact that five out of the seven residues are Gly and Ala, which practically are without side chains. However, we have also carried out calculations using N=120 (see III.4).
To hold these waters around the loop they are restrained with a flat-welled half-harmonic potential (a force constant of 10 kcal mol−1Å−2), based on the distance from the “center” of the loop region. That is, the distance of each water molecule (in practice, the oxygen atom) is measured from a restraining center denoted xsph. If this distance is greater than a prescribed distance, Rcap, a harmonic restoring force is applied, otherwise the restraining force is zero. A reasonable restraining center could be, for example, the center of mass of the loop backbone atoms (i.e. xsph = xcmb). However, we have found that our template is too “thin” and during MD simulations water molecules percolate through cavities in the template to its “back side”. To avoid this undesired situation we have chosen Rcap=14 Å (i.e. Rcap is larger than Rtemp) and as suggested in Ref 56, xsph was defined by,
| (4) |
where xcm is the overall center of mass of the loop-template system. Here, the effect is to shift the center of the restraining sphere (xsph) toward the “loop side” of the loop-template system by rshift Å (see Figure 1). However, because changing rshift affects the energy of the system one would seek to adopt its smallest value that still avoids the percolation of water. We carried out several MD simulations (500 and 1000 ps long) for Rcap=14 Å and rshift = 2 – 7, 9, 15, and 25 Å calculating the various energy components; it has been found that water seeping is eliminated for rshift ≥ 4 Å, but as a step of precaution have decided to use rshift=5 Å, for which the energy results are similar to those obtained with rshift = 4 Å.
As in paper I, the potential energy is defined by the AMBER96 force field,17 the His residue is protonated in the free and bound states. The reconstruction of the loop structure is carried out in internal coordinates, therefore, the conformations simulated by MD should be transferred from Cartesians to the dihedral angles φi, ψi, and ωi (i=1,N=7), the bond angles θi,l (i=1,N, l=1,3), the side chain angles χ and the corresponding bond angles. As in paper I we consider only three χ angles two of His and one of Ser, while the contribution of the side chain of Ala is ignored. Also, because the side chains are much shorter than the backbone and are not restricted by the loop closure condition, the effect of their bond angles on entropy differences is expected to be small and is thus ignored; we have argued in paper I that to a good approximation bond stretching can be ignored as well. For convenience, these angles (ordered along the backbone) are denoted by αk, k=1,45=K. The MD runs are carried out with the package TINKER,58 where the loop and the capped TIP3P waters are free to move while the template is kept fixed in its x-ray coordinates and the total potential energy E is
| (5) |
where Eloop includes the loop-loop and loop-template potential energy and Ewater consists of the water-water, water-loop, and water-template interactions (the template-template energy is constant and thus is ignored).
II.2. Statistical mechanics of a loop in internal coordinates
The partition function of the loop/water system Z (eq 1) is an integration of exp-[E/kBT] with respect to xloop, the Cartesian coordinates, of the loop and xN, the 3N coordinates of the N water molecules over a microstate m (for brevity we omit the letter m in most equations). However, it is convenient to change the variables of integration from xloop to internal coordinates, αk, k=1,K which makes the integral dependent also on a Jacobian, J, which for a linear chain has been shown to be a simple function of the bond angles and bond lengths independent of the dihedral angles.36,37,39 This transformation is applied under the assumption that the potentials of the bond lengths (“the hard variables”) are strong and therefore their average values can be assigned to J, which to a good approximation can be taken out of the integral (however, see a later discussion in this section). For the same reason one can carry out the integration over the bond lengths (assuming that they are not correlations with the αk) and the remaining integral becomes a function of the K dihedral and bond angles (αk) 36,37,39 and a Jacobian that depends only on the bond angles; the partition function is
| (6) |
where [αk] = [α1,…αK]. D is a product of the integral over the bond lengths and their Jacobian J. The Jacobian [Πj sin(θj)] of the bond angles, θj that should appear under the integral is omitted for simplicity (However, in paper I we have shown that the Jacobian cancels out in entropy and free energy differences; therefore, we shall discard the Jacobian from future discussions.) We assume D to be the same (i.e., constant) for different microstates of the same loop and therefore lnD cancels and can be ignored in calculations of free energy and entropy differences. The Boltzmann probability density corresponding to Z (eq 6) is (E is defined in eq 5)
| (7) |
and the exact entropy S and exact free energy F (defined up to an additive constant) are
| (8) |
and
| (9) |
It should be pointed out that the fluctuation of the exact F is zero;59 thus (provided that the above assumptions about the bond lengths are correct) one can substitute the expression for ρB ([αk], xN) (eq 7) inside the curly brackets of eq 9 to obtain,
| (10) |
i.e. the expression in the curly brackets is constant and equal to F for any set ([αk], xN) within m. This means that the free energy can be obtained from any single conformation if its Boltzmann probability density is known. However, the fluctuation of an approximate free energy (i.e., which is based on an approximate probability density) is finite and it is expected to decrease as the approximation improves.9,40,59–61 Because HSMC(D) provides an approximation for ρB ([αk], xN), it enables one, in principle, to estimate the free energy of the system from any single structure [Notice, however, that calculation of ρB ([αk], xN) for a single conformation depends on the entire microstate as is also evident from the HSMC(D) procedure discussed later].
With MD the bond stretching energy is taken into account in eq 9 (and in free energy functionals defined later) while the corresponding entropy is ignored. The contribution of this energy to the free energy becomes an additive constant if one accepts the assumptions about the stretching energy and the corresponding Jacobian made prior to eq 6. This is a very good approximation; however, if the bond stretching entropy should be considered, we have argued in paper I, II.6 that it can be estimated approximately within the framework of HSMD.
II.3. Exact future scanning procedure
HSMC(D) (as well as HS and LS) is based on the ideas of the exact scanning method where a system is constructed (from nothing) step-by-step using transition probabilities (TPs). The product of these TPs is equal to the Boltzmann probability (eqs 1 and 7) from which the entropy and free energy can be calculated. Practically, a loop/water configuration is generated by initially building a loop structure followed by the construction of a configuration of the water molecules. In this way a sample of statistically independent system configurations can be obtained.
For simplicity this construction is described for a loop consisting of M Gly residues (with dihedral and bond angles denoted αk,1≤ αk ≤ 6M=K) in microstate m; the loop is surrounded by N water molecules moving within the volume defined by the sphere of radius Rcap, the template, and the loop. Starting from nothing, a conformation of the loop is built first by defining the angles αk step-by-step using transition probabilities (TPs) and adding the related atoms;62 for example, the angle φ determines the coordinates of the two hydrogens connected to Cα, while the bond angle N-Cα-C′ determines the position of C′. Thus, at step k, k−1 angles α1,···,αk−1 have already been determined; these angles and the related structure (the past) are kept constant, and αk is defined with the exact TP density ρ(αk|αk−1···α1),
| (11) |
where Zfuture (αk, ···,α1) is a future partition function. The term “future” indicates that the integration defining Zfuture is carried out over the variables αk +1, ···,αK and the 3N coordinates xN of the water molecules which will be determined in future steps of the build-up process. In this integration the atoms treated in the past are held fixed in their coordinates (which are determined by α1 ···αk), while αk+1,···,αK are varied in a restrictive way where the corresponding conformations of the “future” part of the loop remain in microstate m. Thus
| (12) |
where E (eq 5) is the total potential energy of the loop/template/water system, which also imposes the loop closure condition. The product of the TPs (eq 11) leads to the (Boltzmann) probability density of the entire loop conformation,
| (13) |
After the loop structure has been constructed a configuration of water molecules is generated step-by-step, where the TP density for placing water molecule k at xk is
| (14) |
where the loop conformation is kept constant and the k−1 water molecules that have already been treated are fixed at their coordinates, xk−1 and the summation in Z(xk) is over the as yet undecided N−k+1 water molecules. (Notice that xk denotes the 3 Cartesian coordinates of water molecule k, while xk denotes the set of Cartesian coordinates of the k molecules 1,2,….,k). The Boltzmann probability density of the water is
| (15) |
and the probability density of the loop/water configuration is,
| (16) |
where Zfuture (α1)(= Z) is the partition function of the entire loop/water system for microstate m. Because ρB ([αk], xN) is known one can obtain the free energy from any single loop/water configuration (see eq 10). In addition to S (eq 8), one can define for m “the loop entropy of mean force”, Sloop,
| (17) |
where d[αk] ≡ dα1 ···dαK; Sloop is defined up to an additive constant. Extending the exact scanning procedure to side chains is straightforward.
This construction procedure (which is not feasible for a large loop/water system) provides the theoretical basis for HSMC(D). Thus, the exact scanning method is equivalent to any other exact simulation technique (in particular Metropolis MC and MD) in the sense that large samples generated by such methods lead to the same averages and fluctuations. Therefore, one can assume that a given MC or MD sample has rather been generated by the exact scanning method, which enables one to reconstruct each conformation i by calculating the TP densities that hypothetically were used to create it step-by-step; this is the basis for HSMC(D) (as well as the HS and LS methods).
II.4. The HSMC(D) method
The theory of HSMD is again described as applied loop consisting of Gly residues. One starts by generating an MD sample of microstate m with water molecules; the conformations are then represented in terms of the dihedral and bond angles αk,1≤αk ≤ 6N=K, and the variability range Δαk is calculated,
| (18) |
where αk(max) and αk(min) are the maximum and minimum values of αk found in the sample, respectively. Δαk, αk(max), and αk(min) enable one to verify that the sample spans correctly the microstate m.
System configuration ([αk], xN) (denoted i for brevity) is reconstructed in two stages, where the loop structure is reconstructed first followed by the reconstruction of the water configuration. Thus, at step k of stage 1, k−1 angles αk−1···α1 have already been reconstructed and the TP density of αk, ρ(αk|αk−1,···, α1) is calculated from an MD sample of nf conformations (generated in Cartesian coordinates), where the entire future of the loop and water is moved [i.e., the loop atoms defined by αk, ···, αK and the water coordinates (xN)] while the past (the loop atoms defined by α1, ···, αk−1) are held fixed at their values in conformation i. A small segment (bin) δαk is centered at αk(i) and the number of visits of the future chain to this bin during the simulation, nvisit, is calculated; one obtains,
| (19) |
where ρHS(αk|αk−1,···,α1) becomes exact for very large nf (nf → ∞) and a very small bin (δα → 0). This means that in practice ρHS(αk|αk−1,···,α1) will be somewhat approximate due to insufficient future sampling (finite nf), a relatively large bin size δαk, an imperfect random number generator, etc. This equation is suitable for HSMC. However, for practical reasons, with HSMD a pair of angles should be treated simultaneously, where each pair consisting of a dihedral angle and its successive bond angle (e.g., φ and the bond angle N-Cα-C′). Thus, at each step both αk and αk+1 are considered and nvisit is increased by 1 only if αk and αk+1 are located within the limits of δαk and δαk+1, respectively; therefore eq 19 becomes
| (20) |
where in paper I we have shown that δαk and δαk+1can be optimized. Notice that with HSMD the future loop conformations generated by MD at each step k remain in general within the limits of m, which is represented by the analyzed MD sample. The corresponding probability density is
| (21) |
where in the product only odd values of k are used. ρHS ([αk]) defines an approximate entropy functional, denoted which can be shown using Jensen’s inequality to constitute a rigorous upper bound for Sloop (eq 17),10
| (22) |
(eq 13) is the Boltzmann probability density of [αK] in m. Thus, for microstate m, can be estimated from a Boltzmann sample (of size ns) generated by MD using the arithmetic average,
| (23) |
where ρHS (t, m) is the value of ρHS ([αk]) obtained for configuration t of the sample of m. constitutes a measure of the loop flexibility of a pure geometrical character, i.e. with no direct dependence on the interaction energy. We denote the difference in the loop entropies obtained for a specific set of parameters by but the converged difference, which is expected to be exact within the statistical errors, is denoted by ΔSloop
| (24) |
In the same way one calculates the arithmetic averages of the energies over the ns system configurations
| (25) |
where Eloop (t, m) is the loop-loop and loop-template interaction energy of loop conformation t. The corresponding difference is,
| (26) |
One can also define a free energy difference, ΔFloop for the loop,
| (27) |
To reconstruct the water configuration one can use the HSMC(D) procedure for fluids developed previously, which would lead to [as an approximation for (eq 15)] and then to the contribution of the water configuration to the free energy . However, this procedure for fluids has not been optimized yet and it is relatively time consuming. Alternatively, one can obtain Fwater([αk], xN) by a thermodynamic integration (TI) procedure, where the water molecules are integrated from an ideal gas to their TIP3P form within the spherical volume (Rcap) and the presence of constant template and loop structure; however, this would be a complex procedure as well. Since the free and bound loop structures have the same template and because we are mainly interested in free energy differences, we have applied a much simpler TI procedure based on the same reference state for the two microstates. In this state the water-water and water-template interactions are preserved but the (fixed) loop structure [αk] does not “see” the surrounding waters, i.e. the loop-water interactions (electrostatic and Lennard Jones) are switched off. These interactions are gradually increased (from zero) during an MD simulation of water [while the loop structure remains fixed at ([αk])]; For [αk] of microstate m one obtains from the integration which is then averaged over the ns sample configurations (see eq 23),
| (28) |
and the difference in the free energy of water between m and n denoted ΔFwater is
| (29) |
In the same way one calculates the arithmetic averages of the water energy over the ns system configurations
| (30) |
where Ewater (t, m) is the water-water, water-template, and water-loop interaction energy of system configuration t. The corresponding differences are,
| (31) |
and
| (32) |
The difference in the total free energy between microstates m and n is
| (33) |
The difference in the water entropy between m and n is
| (34) |
where the corresponding difference in the total entropy is
| (35) |
It should be pointed out again that the dependence of ΔFtotal (eq 33) (and TΔStotal, eq 35) on the bond stretching energy is through Eloop while this interaction is ignored in (eqs 22 and 23). However, under the assumptions leading to eq 6 this is not expected to affect differences in free energy which are our main interest; see also paper I (II.6).
II.5. The reconstruction procedure with HSMD
The HSMD reconstruction procedure needs further discussions. Thus, the MD simulation of the future chain at step k starts from the reconstructed conformation i, and every g fs the current conformation is considered, where the ninit initial considered conformations are discarded for equilibration. The next nf (considered) future conformations are represented in internal coordinates and their contribution to nvisit (eq 20) is calculated. An essential issue is how to guarantee an adequate coverage of microstate m, i.e., that the future chains will span its entire region (in particular the side chain rotamers) while avoiding their “overflow” to neighboring microstates, conditions that will occur for a too small and a too large nf, respectively. (Note that even at step k, where the “past” of the loop is kept fixed, the (future) unfixed part can leave the microstate during long MD simulations. Such “overflow” is more likely to happen for small residues such as Gly and for small k.) To be able to control the extent of coverage of m the following procedure has been applied: nf has been divided into several (j) shorter repetitive procedures (“units”), each based on n′f < nf conformations where nf=jn′f, and each unit starts from the reconstructed structure i with a different set of velocities followed by equilibration of size, ninit; obviously, one would seek to determine the minimal values for n′f, j, and ninit, which would keep the future chains within m while allowing its adequate sampling. A similar procedure was first suggested by Brady & Karplus63 within the framework of the quasi-harmonic method, and was also used in implementations of the LS method to peptides.26,41
In paper I (II.6) we have discussed (and applied) several measures which enable one to estimate the extent of coverage of the reconstructed samples of the future chains. Because the present Δαk values are smaller than those in paper I (see Table 1) and we use the same nf values, we did not consider it necessary to apply these measures here. However, it should be emphasized again that we are interested in an entropy difference, between two microstates, where is considered to be reliable (i.e., to lead to ΔSloop, eq 24) if its results are found to be stable for a large range of the parameters ninit, n′f, and j. From now on we shall replace in most cases n′f by the word unit.
TABLE 1.
Two sets of differences Δαk (in degrees) between the minimum and maximum values of dihedral angles in the free and bound samplesa
| Explicit Solvent | Implicit solvent | |||||||
|---|---|---|---|---|---|---|---|---|
| Free | Bound | Free | Bound | |||||
| Reidue | Δφ | ΔΨ | Δφ | ΔΨ | Δφ | ΔΨ | Δφ | ΔΨ |
| Gly 1 | 47 | 90 | 75 | 121 | 76 | 153 | 92 | 148 |
| His 2 | 86 | 104 | 107 | 70 | 139 | 130 | 125 | 105 |
| Gly 3 | 83 | 99 | 173 | 177 | 175 | 124 | 80 | 95 |
| Ala 4 | 133 | 87 | 96 | 132 | 131 | 94 | 143 | 288 |
| Gly 5 | 73 | 88 | 95 | 88 | 107 | 100 | 199 | 360 |
| Gly 6 | 133 | 98 | 116 | 81 | 126 | 109 | 285 | 267 |
| Ser 7 | 65 | 59 | 84 | 71 | 83 | 64 | 243 | 109 |
| χ1 (His) | 78 | 89 | 55 | 53 | ||||
| χ2(His) | 107 | 106 | 130 | 108 | ||||
| χ1 (Ser) | 166 | 163 | 317 | 321 | ||||
Δαk are defined in eq 18. The explicit solvent results were calculated in the present study based on a sample of ns=600 configurations of the loop and 70 TIP3P water molecules using the AMBER force field. The implicit solvent results have been obtained in paper I16 from the entire sample of 500 conformations using the AMBER force field and the GB/SA implicit solvent.
II.6. The Local States (LS) and the quasi-harmonic (QH) methods
With the LS method4–6 (applied to an N-residue polyglycine with 6N=K backbone angles, αk) the ranges Δαk (eq 18) are divided into l equal segments, where l is the discretization parameter. These segments are denoted by νk, (νk=1,l), where an angle αk is represented by the segment νk to which it belongs, and a conformation i is expressed by the corresponding vector of segments [ν1(i), ν2(i), …,νK (i)]. The TP ρ(αk|αk−1···α1) can be estimated only approximately by n(νk, ···, νk−b)/{n(νk−1, ···, νk−b)[Δαk/l]}, where n(νk, ···, νk−b) is the number of times the local state [i.e., the vector (νk,···, νk−b)] appears in the sample; b is the correlation parameter. One obtains the approximate probability density, , the larger are b and l the better the approximation (for enough statistics). ρi (b, l) defines a rigorous upper bound, (eq 22) where ρi (b,l) replaces ρHS; can be estimated by eq 23.
With the QH method introduced by Karplus and Kushick,39 the Boltzmann probability density of structures defining a microstate is approximated by a multivariate Gaussian. Thus,
| (36) |
where the covariance matrix, σ, is obtained from a local MD (MC) sample and N is (usually) the number of internal coordinates. Clearly, SQH constitutes an upper bound for S since correlations higher than quadratic are neglected; also, an-harmonic contributions are ignored, and QH is not suitable for diffusive systems such as water. While QH has been used extensively during the years, a systematic study of its performance has been carried out only recently by Gilson’s group64 who have found that the performance of QH deteriorates significantly in Cartesian coordinates and when applied to more than one microstate.35
III. Results and discussion
III.1. Simulation details
We carried out two MD simulations at T=300 K starting from the free and bound PDB structures (which were capped by 70 TIP3P waters); by considering a structure every 0.5 ps these simulations led to stable samples of ns=600 conformations. These simulations and the reconstruction simulations (for generating the future samples) were carried out with the velocity-Verlet algorithm65 based on a time step of 2 fs, where bonds involving hydrogens (including those of water) were frozen to their ideal values by the RATTLE algorithm;65 the Berendsen65 heat bath controlled the temperature. Cut-offs on long-range interactions were not imposed, and in the reconstruction process a structure was added to the sample every g=10 fs, where the ninit=250 initial structures (2.5 ps) were discarded for equilibration. The future samples were generated for four bin sizes, δ= Δαk/45, Δαk/30, Δαk/15, and Δαk/10, centered at αk (i.e., αk ±δ/2) (eqs 19 and 20). If the counts of the smallest bin are smaller than 50 the bin size is increased to the next size, and if necessary to the next one, etc. In the case of zero counts, nvisit is taken to be 1; however, zero counts is a very rare event.
To obtain the loop entropy, (eq 23) the calculations are based on unit n′f=250 (2.5 ps) and future sample sizes nf =250 (j=1), 500 (j=2), 750 (j=3), and 1250 (j=5). To examine the convergence of the results for (eq 24) we have extracted from the main samples (of the free and bound microstates) two sets (pairs) of partial samples. One set, which consists of ns=100, was obtained by selecting every 6th conformation of the main samples; the corresponding conformations were reconstructed (as above) with nf = 250, 500, 750, and 1250. The second partial set (which was selected in a similar way) consists of ns=40 but its conformations were reconstructed more extensively again with unit n′f=250 (2.5 ps) but nf =1250 (j=5), 2500 (j=10), 5000 (j=20), and 104 (j=40).
III.2. Results for the loop entropy
In Table 1 we present the values of Δαk (eq 18) for the free and bound microstates obtained from the corresponding MD samples (of size 600). These values suggest that the two samples indeed are concentrated in conformational space, and the corresponding values for the χ angles of the two microstates are comparable. For comparison we also provide the corresponding values obtained in paper I (Table 6) for the same loop in the GB/SA implicit solvent. The present results, in most cases, are larger than those obtained in paper I for the loop in vacuum (not shown) but are smaller (and in some cases considerably smaller) than results obtained with implicit solvent as Table 1 reveals. Larger Δαk values are expected to correlate with higher entropy and indeed the results for in Table 2 are smaller than those of paper I obtained with implicit solvent, as discussed below.
TABLE 2.
HSMD results (in kcal/mol) for the entropy, (eqs 22 and 23) at T=300 K for the free and bound microstatesa
| Free loop | Bound loop | ||||
|---|---|---|---|---|---|
| Bin size | nf (j) | ||||
| Δαk/15 | 250 (1) | 67.18 (4) | 68.72 (4) | ||
| “ | 500 (2) | 66.48 (7) | 67.86 (8) | ||
| “ | 750 (3) | 66.17 (4) | 67.58 (8) | ||
| “ | 1250 (5) | 65.74 (4) | 67.19 (8) | ||
| “ | 1250 (2) | 69.9 (1) | 70.3 (2) | ||
| Δαk/30 | 250 (1) | 67.04 (9) | 68.61 (7) | ||
| “ | 500 (2) | 66.22 (7) | 67.61 (7) | ||
| “ | 750 (3) | 65.77 (4) | 67.15 (8) | ||
| “ | 1250 (5) | 65.19 (4) | 66.49 (3) | ||
| “ | 1250 (2) | 69.4 (1) | 69.8 (2) | ||
| Δαk/45 | 250 (1) | 67.03 (4) | 68.60 (5) | ||
| “ | 500 (2) | 66.17 (7) | 67.56 (7) | ||
| “ | 750 (3) | 65.69 (4) | 67.08 (8) | ||
| “ | 1250 (5) | 65.06 (4) | 66.36 (8) | ||
| “ | 1250 (2) | 69.4 (2) | 69.7 (2) | ||
| TSQH | 78.6 (1) | 87 (6) | |||
| TSLS | 87.4 (1) | 90 (7) |
The bin sizes are δ = Δαk/l. nf denotes the sample size of the future chains used in the reconstruction process, nf = unit×j, where j is the number of simulations of unit size applied at each reconstruction step. Generation of the samples (of ns=600 conformations) and their reconstruction is based on the AMBER force field17 and 70 TIP3P water molecules.19 However, the underscored results for nf=1250 (2) (unit=650) were obtained in paper I from samples of 200 conformations using the AMBER force field and the GB/SA implicit solvation. The statistical error in the last significant digit is given in parentheses, e.g., 65.06 (4) = 66.06 ± 0.04. SQH (eq 36) is the quasi-harmonic entropy and SLS is obtained by the local states method using b=2 and the discretization parameter, l=10 (see II.6); these results were obtained from larger samples (see text for details). The entropy is defined up to an additive constant that is the same for both microstates.
Table 2 contains results for the entropy, (eq 23) for the free and bound microstates. The statistical errors were obtained from the fluctuations and results obtained for partial samples. For comparison we have added in Table 2 results for nf=1250 (appear with an underscore) obtained in paper I for a loop in implicit solvent. These results are larger (by ~4.2 and ~3.2 kcal/mol for the free end bound microstates) than the results for nf=1250 obtained with explicit water, which is in accord with Δαk(implicit) being larger in most cases than Δαk(explicit) in Table 1.
Being an upper bound, one would expect to decrease with decreasing bin size and increasing nf – an expectation which is fully satisfied. Also, results for the same n for Δαk/30 and Δαk/45 are almost converged; thus, for both microstates, which is close to the statistical errors. On the other hand, results of the same bin (obtained for different nf values) are not converged. The computer time required to reconstruct a loop structure capped with 70 water molecules using nf=500 is ~1.6 h CPU on a 2.1 GHz Athlon processor, which is smaller than 3.6 h CPU required for reconstructing a structure in implicit solvent in paper I
The HSMD results for the entropy are compared in the table to those obtained with the LS and QH methods from larger MD samples of 25,000 loop-water configurations. These samples were obtained from 2.5 ns trajectories where a configuration is retained every 0.1 ps (where the 20 ps initial trajectory is discarded for equilibration). The central values of (eq 36) exceed the HSMD results (for ns =600) by ~14 and ~20 kcal/mol for the free and bound microstates, respectively, while the corresponding LS results (eq 23, using b=1, l=10, see II.6) are even higher, exceeding the HSMD results by ~22 and ~24 kcal/mol. These elevated results are in accord with both and being upper bounds; however, they might also be affected by the longer MD trajectories generated for QH and LS than for HSMD, as discussed in the I.4. SLS > SQH was also found in previous studies.13–15
III.3. Differences in loop entropy
In paper I and ref 16 converging results for TΔSA were obtained already for unit 2.5 ps and nf ≥ 500 (and even for smaller nf values using optimized bins). Because the Δαk values for a loop in explicit water are smaller than those obtained with implicit solvent (Table 1) we have applied unit =2.5 ps and nf =250–1250 also in the present study and to examine the convergence of the results for of for smaller samples, we present in Table 3 also results for ns=200, 100, and 40 as discussed in III.1. The results in the table are given for the two smallest bins of Δαk/30 and Δαk/45.
TABLE 3.
Entropy differences, (in kcal/mol) at T=300 K between the free and bound microstates obtained by HSMD for different samples in explicit watera
| Bin size | nf | nf | ||||||
|---|---|---|---|---|---|---|---|---|
| ns = 600 | ns = 200 | ns = 100 | ns = 40 | |||||
| Δαk/30 | 250 | − 1.6 | −1.5 (1) | −1.1 (2) | 1250 | −0.9 (3) | ||
| “ | 500 | −1.4 | −1.3 (1) | −1.0 (2) | 2500 | −0.9 (4) | ||
| “ | 750 | −1.4 | −1.4 (1) | −1.1 (2) | 5000 | −0.9 (2) | ||
| “ | 1250 | −1.3 | −1.3 (1) | 0.9 (2) | 104 | −1.0 (2) | ||
| Δαk/45 | 250 | −1.6 | −1.5 (1) | −1.1 (2) | 1250 | −0.9 (3) | ||
| “ | 500 | −1.4 | −1.3 (1) | −1.0 (2) | 2500 | −0.9 (3) | ||
| “ | 750 | −1.4 | −1.4 (1) | −1.1 (2) | 5000 | −0.9 (2) | ||
| “ | 1250 | −1.3 | −1.3 (1) | 0.9 (2) | 104 | −1.0 (2) | ||
is defined in eq 24 and its results are given only for the two smallest bins, δ = Δαk/30 and δ = Δαk/45, using unit=2.5 ps. The table consists of two parts. The results in the left-hand part are based on 250 ≤ nf ≤ 1250 and are presented for the entire (two) samples (ns=600), for the samples’ first 200 conformations, and for ns=100 by considering every 6th conformation of the entire sample. The results in the right-hand part are based on 1250 ≤ nf ≤ 104 using samples of ns=40 by considering every 15th conformation of the entire sample. The statistical error is defined in Table 2; for ns=600 it is smaller than ±0.1. Results for TΔSQH and TΔSLS are not given due to their low accuracy (see Table 2). All calculations were carried out with the AMBER96 force field and 70 TIP3P water molecules.
The statistical errors of the results for are not larger than ±0.06 kcal/mol and to simplify the comparison are not presented in the table. All the results for nf ≥ 500 converge to −1.3 kcal/mol within ±0.1 kcal/mol, and even those for nf =250 (−1.6 kcal/mol) deviate only by 0.3 – 1.3 kcal/mol; furthermore, the results for Δαk/15, which are not provided in Table 3 are very good, −1.4 and −1.5 kcal/mol. This extent of convergence is comparable to that obtained in previous HSMD studies.15,16 Notice that the results for the first 200 conformations of the samples are equal to those based on ns=600 (while providing a factor of 3 reduction in computer time). On the other hand, the results obtained for ns =100 and 40 are higher by 0.3–0.4 kcal/mol above the ns=600 values. Still the merit of such calculations (that might provide further reduction in computer time) depends on the errors caused by the other components, i.e., the total energy and the water contribution to the entropy. It should be pointed out that for a loop in implicit solvent (paper I) , while in explicit water the loop entropy of the free microstate is lower than that of the bound microstate.
This convergence of entropy differences stems from the cancellation (in ) of approximately equal systematic errors in and as discussed in detail in section II.10 of paper I. Thus, Table 2 shows that the worst approximations that still lead to a good value differ from the best ones by for the free and bound microstates, respectively; these differences constitute lower bounds because the correct TSloop values might be significantly smaller than . The large errors in the results for LS and QH do not allow calculating meaningful differences.
III.4. Thermodynamic integration of water
As described earlier, in the TI process the interaction energy [electrostatic and Lennard Jones (LJ)] between a fixed loop structure and the (moving) water molecules is decreased gradually to zero (rather than increased from zero) at constant T and V, where the water-water and water-template potential energy is unchanged. For the (LJ) potential we have used the shifted scaling potential, introduced by Zacharias et al.,66
| (37) |
where the shift parameter, δ=2 Å2, prevents the divergence of the potential (and its derivative) at small pair separations; a similar scaling function is used for the electrostatic interactions. The free energy derivatives with respect to λ, ∂F/∂λ is
| (38) |
where the derivative of the energy is calculated analytically. The integration with respect to λ is carried out by dividing the range [1,0] into 16 equal integration bins Δ λi. The (λ=1 → λ=0) integration of the electrostatic interactions is carried out first (in the presence of intact LJ interactions) followed by a λ =1→0 integration of the LJ interactions. Thus, the entire two-stage process is based on 32 ∂F/∂λi integration steps.
The MD simulation consists of a 2 fs integration step, where every 20 fs the current water configuration is added to the sample. For each (Δλi) step the initial simulation (5 ps) is used for equilibration and is thus discarded; the following 20 ps (1000 configurations) are used for evaluating <∂F/∂λi>. Notice that in spite of the advanced scaling function (eq 37), in the last steps of the LJ integration (i.e., λ close to zero) the results always increased strongly; therefore, we have adopted the results integrated up to λ=0.25. For a single loop structure this free energy integration requires ~5 h CPU on a 2.1 GHz Athlon processor. As shown in Table 4, the free energy integrations over the two samples have given and 35.5 kcal/mol. (eq 28) for the free and bound microstates, respectively, thus leading to ΔFwater = − 4.4±0.7 kcal/mol (eq 29), i.e., the water provides higher stability to the free microstate. To check whether computer time can further be decreased, we also calculated by considering the contribution of only 100 configurations of each sample (i.e., every 6th configuration was considered) obtaining ΔFwater = − 5.0 kcal/mol, which is within the error bars of the result based on the entire samples, while computer time is reduced by a factor of 6.
TABLE 4.
Energy and free energy averages for the loop and water obtained from the samples (ns=600) of the free and bound microstates at T=300 Ka
| Ēloop(m) | Ēwater (m) | Ētotal (m) | |||
|---|---|---|---|---|---|
| Free | −108.3 ± 2 | −1021.9 ± 2 | −1130.8 ± 0.5 | 31.2 ± 0.5 | |
| Bound | −106.6 ± 0.7 | −1016.5 ± 1.5 | −1123.0 ± 1.5 | 35.5 ± 0.4 | |
| Free-Bound | ΔEloop | ΔEwater | ΔEtotal | ΔFwater | |
| −1.7 ± 0.9 | −5.4 ± 2.5 | −7.2 ± 1.2 | −4.4 ± 0.7 |
Ēloop(m) (eq 25) is the loop-loop and loop-template average energy for microstate m, Ēwater(m) (eq 30) is the water-water, water-loop, and water-template average energy for m where Ē total (m) is their sum. (eq 28) is the average free energy of water for fixed loop structures. The corresponding differences are ΔEloop (eq 26), ΔEwater (eq 31), ΔEtotal (eq 32), and ΔFtotal (eq 33). All results are in kcal/mol, where is defined up to an additive constant which is the same for both microstates.
It should be pointed out that unlike an NVT system of pure water under periodic boundary conditions, the water system here is not homogeneous. Computer graphics has shown that the water molecules cover the loop and parts of the template while the outer region of the spherical volume is predominately vacant. Indeed, a crude calculation shows that the empty volume is ~5000 Å3 which would require ~160 water molecules to obtain the experimental density of water. Thus, crevices in the template might remain empty or become occupied by waters for long simulation time, which leads to increased fluctuations of thermodynamic parameters. Therefore, a systematic improvement in the integration parameters (i.e., using up to 64 Δλi steps and longer simulations for each TI step) has not decreased these fluctuations. We expect this picture to improve as the number of waters, N increases, and the effect of various minimalist models studied. We have already carried out preliminary simulations with N=120, but could not reach definite conclusions due to the dependence of the results on the parameters rshift and Rcap. This problem will be studied systematically in the future by considering a larger template, where using rshift might not be needed, because the percolation of water will be avoided.
In Table 4 we provide results for the free and bound microstates obtained for Ēloop(m) (eq 25), Ēwater(m) (eq 30), their sum, Ētotal(m) and (eq 28); we also provide the corresponding differences (free-bound), where the errors were estimated from results obtained for partial samples. It is of interest to point out that the results for Ēloop(m) ~ −108 and −106 for the free end bound microstates are in the same range of ~ −137 and −99 kcal/mol, respectively obtained in paper I for a loop in vacuum; however, the difference here ΔEloop = −1.7 is much smaller than in paper I (~ −38 kcal/mol) due to the effect of water. This low ΔEloop (eq 26) together with a small entropy contribution, TΔSloop = −1.3 leads to ΔFloop= −0.4 ± 1 kcal/mol (eq 27), i.e., the loop contributes very little to the higher stability of the free microstate (see Table 5 where all the various differences are summarized).
TABLE 5.
Summary of energy, entropy, and free energy differences (in kcal/mol) for the free and bound microstates at T=300 Ka
| ΔFwater | ΔEwater | TΔSwater | ΔEloop | TΔSloop | ΔFloop |
|---|---|---|---|---|---|
| −4.4 ± 0.7 | −5.4 ± 2.5 | −1.0 ± 2 | −1.7 ± 0.9 | −1.3 ± 0.2 | −0.4 ± 1 |
| ΔFtotal | ΔEtotal | TΔStotal | |||
| −4.8 ± 1 | −7.2 ± 1.2 | −2.3 ± 2 |
Differences (free-bound) in the following quantities: free energy of water, ΔFwater (eq 29), energy of water, ΔEwater (eq 31), energy of loop, ΔEloop (eq 26), entropy of water, TΔSwater (eq 34), entropy of loop, TΔSloop (eq 24), total free energy, ΔFtotal (eq 33), total energy, ΔEtotal (eq 32), and total entropy, TΔStotal (eq 35).
Thus, the relatively high difference, ΔEtotal = −7.2 kcal/mol is contributed mainly by water, ΔEwater = −5.4 kcal/mol (eq 31, and Tables 4 and 5). This energy difference for water is slightly counterbalanced by TΔSwater = −1.0 (Table 5) leading to ΔFwater = −4.4 kcal/mol. A similar effect is demonstrated (Table 5) for the total energy values (due to the small contributions of the loop discussed above), i.e., ΔEtotal = −7.2, and TΔStotal = −2.3 where ΔFtotal = −4.8 kcal/mol.
Our results also show that ΔEtotal = −7.2 correctly predicts the higher stability of the free microstate, and this value is not significantly different from ΔFtotal = −4.8 kcal/mol -the correct measure of stability due to a relatively small entropy effect, TΔStotal = −2.3 kcal/mol. Notice that the free microstate was found to be the more stable microstate also in implicit water (paper I); however, the free energy difference there is significantly larger than here, ΔFimplicit= −25.5 kcal/mol. This higher stability is expected because the bound loop structure was superimposed on the template of the free protein. However, one should bear in mind that this result is mainly due to water and it thus depends strongly on the model of water used, which is presently based on rshift=5 Å. Also, it is not clear how the number of water molecules and their density would affect the relative stability of the two microstates.
IV. Summary and conclusions
In paper I HSMD has been extended to a protein loop by treating the short loop (207–209) of pancreatic α-amylase modeled in vacuum and in the implicit solvent GB/SA. In the present paper we have made an important step further by extending HSMD to the same loop solvated by explicit water; treating the same loop in the free and bound microstates enables one to compare the effects of the different models. Computation of the entropy and free energy is divided into two stages, where the loop’s entropy is calculated first by reconstructing its structures in the presence of moving waters; this is followed by the calculation of the free energy of the surrounding water in the presence of a fixed loop structure. As in previous studies, we have found that already small reconstruction samples of 500 structures lead to the correct entropy difference, TΔSloop. Furthermore, the same difference was obtained from a partial sample of 200 configurations (rather than 600), which decreases computer time by a factor of 3, where other means to improve efficiency (discussed in the Summary of paper I but were not applied here) are expected to decrease computer time considerably further. The fast convergence of the results for TΔSloop supports (like previous calculations) theoretical arguments discussed in paper I that relatively large systematic errors in are cancelled to a large extent in differences, (eq 24). The relatively small statistical errors stem from the small system (loop and water) moved by MD. Notice that the calculations of the transition probabilities of different steps are completely independent and they are also independent of the integration of water. Therefore, the reconstruction steps and the TI of water can be fully parallelized.
Calculation of the free energy of water (second stage) was carried out successfully (and with relatively small error bars) by TI rather than HSMD, where again the difference in free energy ΔFwater obtained from a partial sample of 100 configurations is equal within the statistical error to that obtained from the entire sample Thus, the application of our entire methodology to a loop capped with water has been successful. However, the performance of the water model used with respect to other models has not been investigated; in particular, the effect of the number of waters capped, their volume, density, and the size of the shifting parameter on ΔFtotal and other thermodynamic parameters should be studied. Such a study is being carried out now with respect to the 4-residue mobile loop, 287–290 of the protein acetylcholinesterase (AChE) from Torpedo californica. Treating this loop has the advantage that ΔFtotal has been estimated from experimental data and was calculated by several techniques.67
In accordance with paper I, the quasi-harmonic approximation and the local states method overestimate the entropy significantly, which might reflect strong long-range correlations and an-harmonic effects within the loop due to the loop-template, loop-loop and loop-water interactions.
Acknowledgments
This work was supported by NIH grant 2-R01 GM066090-4 A2.
References
- 1.Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. J Chem Phys. 1953;21:1087. [Google Scholar]
- 2.Alder BJ, Wainwright TE. J Chem Phys. 1959;31:459. [Google Scholar]
- 3.McCammon JA, Gelin BR, Karplus M. Nature. 1977;267:585. doi: 10.1038/267585a0. [DOI] [PubMed] [Google Scholar]
- 4.Meirovitch H. Chem Phys Lett. 1977;45:389. [Google Scholar]
- 5.Meirovitch H, Vásquez M, Scheraga HA. Biopolymers. 1987;26:651. doi: 10.1002/bip.360260508. [DOI] [PubMed] [Google Scholar]
- 6.Meirovitch H, Koerber SC, Rivier J, Hagler AT. Biopolymers. 1994;34:815. doi: 10.1002/bip.360340703. [DOI] [PubMed] [Google Scholar]
- 7.Meirovitch H. Phys Rev A. 1985;32:3709. doi: 10.1103/physreva.32.3709. [DOI] [PubMed] [Google Scholar]
- 8.Meirovitch H, Scheraga HA. J Chem Phys. 1986;84:6369. [Google Scholar]
- 9.Meirovitch H. J Chem Phys. 2001;114:3859. [Google Scholar]
- 10.White RP, Meirovitch H. J Chem Phys. 2004;121:10889. doi: 10.1063/1.1814355. [DOI] [PubMed] [Google Scholar]
- 11.White RP, Meirovitch H. J Chem Phys. 2006;124:204108. doi: 10.1063/1.2199529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.White RP, Meirovitch H. J Chem Phys. 2005;123:214908. doi: 10.1063/1.2132285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cheluvaraja S, Meirovitch H. J Chem Phys. 2005;122:054903. doi: 10.1063/1.1835911. [DOI] [PubMed] [Google Scholar]
- 14.Cheluvaraja S, Meirovitch H. J Phys Chem B. 2005;109:21963. doi: 10.1021/jp052969l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cheluvaraja S, Meirovitch H. J Chem Phys. 2006;125:024905. doi: 10.1063/1.2208608. [DOI] [PubMed] [Google Scholar]
- 16.Cheluvaraja S, Meirovitch H. J Chem Theory Comput. 2008;4:192. doi: 10.1021/ct700116n. [DOI] [PubMed] [Google Scholar]
- 17.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Jr, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J Am Chem Soc. 1995;117:5179. [Google Scholar]
- 18.Qiu D, Shenkin PS, Hollinger FP, Still WC. J Phys Chem. 1997;101:3005. [Google Scholar]
- 19.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J Chem Phys. 1983;79:926. [Google Scholar]
- 20.Elber R, Karplus M. Science. 1987;235:318. doi: 10.1126/science.3798113. [DOI] [PubMed] [Google Scholar]
- 21.Stillinger FH, Weber TA. Science. 1984;225:983. doi: 10.1126/science.225.4666.983. [DOI] [PubMed] [Google Scholar]
- 22.Getzoff ED, Geysen HM, Rodda SJ, Alexander H, Tainer JA, Lerner RA. Science. 1987;235:1191. doi: 10.1126/science.3823879. [DOI] [PubMed] [Google Scholar]
- 23.Rini JM, Schulze-Gahmen U, Wilson IA. Science. 1992;255:959. doi: 10.1126/science.1546293. [DOI] [PubMed] [Google Scholar]
- 24.Constantine KL, Friedrichs MS, Wittekind M, Jamil H, Chu CH, Parker RA, Goldfarb V, Mueller L, Farmer BT. Biochemistry. 1998;37:7965. doi: 10.1021/bi980203o. [DOI] [PubMed] [Google Scholar]
- 25.Kessler H, Matter H, Gemmecker G, Kottenhahn M, Bates JW. J Am Chem Soc. 1992;114:4805. [Google Scholar]
- 26.Baysal C, Meirovitch H. Biopolymers. 1999;50:329. doi: 10.1002/(SICI)1097-0282(199909)50:3<329::AID-BIP8>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- 27.Korzhnev DM, Salvatella X, Vendruscolo M, Di Nardo AA, Davidson AR, Dobson CM, Kay LE. Nature. 2004;430:586. [Google Scholar]
- 28.Eisenmesser EZ, Millet O, Labeikovski W, Korzhnev DM, Wolf-Watz M, Bosco DA, Skalicky JJ, Kay LE, Kern D. Nature. 2005;438:117. doi: 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- 29.Beveridge DL, DiCapua FM. Annu Rev Biophys Biophys Chem. 1989;18:431. doi: 10.1146/annurev.bb.18.060189.002243. [DOI] [PubMed] [Google Scholar]
- 30.Kollman PA. Chem Rev. 1993;93:2395. [Google Scholar]
- 31.Jorgensen WL. Acc Chem Res. 1989;22:184. [Google Scholar]
- 32.Meirovitch H. In: Reviews in Computational Chemistry. Lipkowitz KB, Boyd DB, editors. Wiley-VCH; New York: 1998. p. 12.p. 1. [Google Scholar]
- 33.Gilson MK, Given JA, Bush BL, McCammon JA. Biophys J. 1997;72:1047. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Boresch S, Tettinger F, Leitgeb M, Karplus M. J Phys Chem B. 2003;107:9535. [Google Scholar]
- 35.Meirovitch H. Curr Opin Struct Biol. 2007;17:181. doi: 10.1016/j.sbi.2007.03.016. [DOI] [PubMed] [Google Scholar]
- 36.Gô N, Scheraga HA. J Chem Phys. 1969;51:4751. [Google Scholar]
- 37.Gô N, Scheraga HA. Macromolecules. 1976;9:535. [Google Scholar]
- 38.Hagler AT, Stern PS, Sharon R, Becker JM, Naider F. J Am Chem Soc. 1979;101:6842. [Google Scholar]
- 39.Karplus M, Kushick JN. Macromolecules. 1981;14:325. [Google Scholar]
- 40.White RP, Meirovitch H. J Chem Phys. 2003;119:12096. [Google Scholar]
- 41.Meirovitch H, Meirovitch E. J Phys Chem. 1996;100:5123. [Google Scholar]
- 42.Meirovitch H, Hendrickson TF. Proteins. 1997;29:127. [PubMed] [Google Scholar]
- 43.Baysal C, Meirovitch H. Biopolymers. 2000;53:423. doi: 10.1002/(SICI)1097-0282(20000415)53:5<423::AID-BIP6>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- 44.Qian M, Haser R, Payan F. J Mol Biol. 1993;231:785. doi: 10.1006/jmbi.1993.1326. [DOI] [PubMed] [Google Scholar]
- 45.Qian M, Haser R, Buisson G, Duee E, Payan F. Biochemistry. 1994;33:6284. doi: 10.1021/bi00186a031. [DOI] [PubMed] [Google Scholar]
- 46.Qian M, Haser R, Payan F. Protein Sci. 1995;4:747. doi: 10.1002/pro.5560040414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Machius M, Vertesy L, Huber R, Wiegand G. J Mol Biol. 1996;260:409. doi: 10.1006/jmbi.1996.0410. [DOI] [PubMed] [Google Scholar]
- 48.Brayer GD, Sidhu G, Maurus R, Rydberg EH, Braun C, Wang Y, et al. Biochemistry. 2000;39:4778. doi: 10.1021/bi9921182. [DOI] [PubMed] [Google Scholar]
- 49.Rydberg EH, Li C, Maurus R, Overall CM, Brayer GD, Withers SG. Biochemistry. 2002;41:4492. doi: 10.1021/bi011821z. [DOI] [PubMed] [Google Scholar]
- 50.Numao S, Maurus R, Sidhu G, Wang Y, Overall CM, Brayer GD, Withers SG. Biochemistry. 2002;41:215. doi: 10.1021/bi0115636. [DOI] [PubMed] [Google Scholar]
- 51.Steer ML, Levitzki A. FEBS Letters. 1973;31:89. doi: 10.1016/0014-5793(73)80079-1. [DOI] [PubMed] [Google Scholar]
- 52.Levitzki A, Steer ML. Eur J Biochem. 1974;41:171. doi: 10.1111/j.1432-1033.1974.tb03257.x. [DOI] [PubMed] [Google Scholar]
- 53.Aghajari N, Feller G, Gerday C, Haser R. Protein Sci. 2002;11:1435. doi: 10.1110/ps.0202602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Brayer GD, Luo Y, Withers SG. Protein Sci. 1995;4:1730. doi: 10.1002/pro.5560040908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ramasubbu N, Paloth V, Luo Y, Brayer GD, Levine MJ. Acta Crystallog sect D. 1996;52:435. doi: 10.1107/S0907444995014119. [DOI] [PubMed] [Google Scholar]
- 56.White RP, Meirovitch H. J Chem Theory Comput. 2006;2:1135. doi: 10.1021/ct600317d. [DOI] [PubMed] [Google Scholar]
- 57.Steinbach PJ, Brooks BR. Proc Natl Acad Sci USA. 1993;90:9135. doi: 10.1073/pnas.90.19.9135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Ponder JW. TINKER - software tools for molecular design, version 3.9. Department of Biochemistry and Molecular Biophysics, Washington University School of Medicine; St. Louis, Mo: 2001. [Google Scholar]
- 59.Meirovitch H, Alexandrowicz Z. J Stat Phys. 1976;15:123. [Google Scholar]
- 60.Meirovitch H. J Chem Phys. 1999;111:7215. [Google Scholar]
- 61.Szarecka A, White RP, Meirovitch H. J Chem Phys. 2003;119:12084. [Google Scholar]
- 62.Meirovitch H, Vásquez M, Scheraga HA. Biopolymers. 1988;27:1189. doi: 10.1002/bip.360270802. [DOI] [PubMed] [Google Scholar]
- 63.Brady J, Karplus M. J Am Chem Soc. 1985;107:6103. [Google Scholar]
- 64.Chang CE, Chen W, Gilson MK. J Chem Theory Comput. 2005;1:1017. doi: 10.1021/ct0500904. [DOI] [PubMed] [Google Scholar]
- 65.Allen MP, Tildesley DJ. Computer Simulation of Liquids. Clarenden Press; Oxford: 1987. [Google Scholar]
- 66.Zacharias M, Straatsma TP, McCammon JA. J Chem Phys. 1994;100:9025. [Google Scholar]
- 67.Olson MA. Proteins. 2004;57:645. doi: 10.1002/prot.20294. [DOI] [PubMed] [Google Scholar]